Как найти радиус вписанной в треугольник abc окружности: формула, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение радиуса вписанной в треугольник окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.
- Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Примеры задач
Формулы вычисления радиуса вписанной окружности
Произвольный треугольник
Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.
где a и b – катеты, c – гипотенуза треугольника.
Равнобедренный треугольник
Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:
где a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:
где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Радиус вписанной окружности в равносторонний треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в равносторонний треугольник окружности.
Содержание
- Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
- Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
- Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
Пусть известна сторона a равностороннего треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
Радиус вписанной в равнобедренный треугольник окружности через основание a и боковую сторону b вычисляется из следующей формулы:
Учитывая, что у равностороннего треугольника все стороны равны (\( \small a=b \)), имеем:
| \( \small r=\frac{\large a}{\large 2} \cdot \sqrt{\frac{\large 2a-a}{\large 2a+a}} \) \( \small =\frac{\large a}{\large 2} \cdot \sqrt{\frac{\large a}{\large 3a}} \) \( \small =\frac{\large a}{\large 2 \cdot \sqrt{3}} \) |
То есть
| \( \small r=\frac{\large a}{\large 2 \cdot \sqrt{3}} \) | (2) |
или, умножив числитель и знаменатель на \( \small \sqrt{3} \):
| \( \small r=\frac{\large \sqrt{3}}{\large 6 } \cdot a \) | (3) |
Пример 1. 2}{ 6h}\small =\large \frac{1}{3} \small \cdot h \)
2}{ 6h}\small =\large \frac{1}{3} \small \cdot h \)
То есть, радиус вписанной в равносторонний треугольник окружности по высоте вычисляется из формулы:
| \( \small r = \large \frac{1}{3} \small \cdot h \) | (6) |
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значение \( \small h=39 \) в (6):
Ответ:
3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
Пусть известна площадь S равностороннего треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется из следующей формулы:
\( \small S= 3\cdot \sqrt{3}r^2. 2= \large \frac{S}{3 \cdot \sqrt{3}} \) \( \small = \large \frac{\sqrt{3} \ \cdot \ S }{9} \) 2= \large \frac{S}{3 \cdot \sqrt{3}} \) \( \small = \large \frac{\sqrt{3} \ \cdot \ S }{9} \) |
Тогда:
| \( \small r= \large \frac{\sqrt[4]{3} }{3} \small \cdot \sqrt{S} \) | (7) |
Пример 3. Известна площадь равностороннего треугольника: \( \small S=42 . \) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (7). Подставим значение \( \small S=42 \) в (7):
Ответ:
Смотрите также:
- Окружность, описанная около треугольника
- Радиус описанной окружности около треугольника онлайн
- Радиус описанной окружности около равнобедренного треугольника онлайн
- Радиус описанной окружности около равностороннего треугольника онлайн
- Радиус описанной окружности около прямоугольного треугольника онлайн
- Радиус вписанной в треугольник окружности онлайн
геометрия — Нахождение радиуса окружности внутри треугольника
спросил
Изменено 4 месяца назад
Просмотрено 100 тысяч раз
$\begingroup$
Чему равен радиус окружности, вписанной в треугольник, стороны которого измеряются в $8$, $15$ и $17$ единицах?
Я легко могу понять, что это прямоугольный треугольник, по заданным сторонам.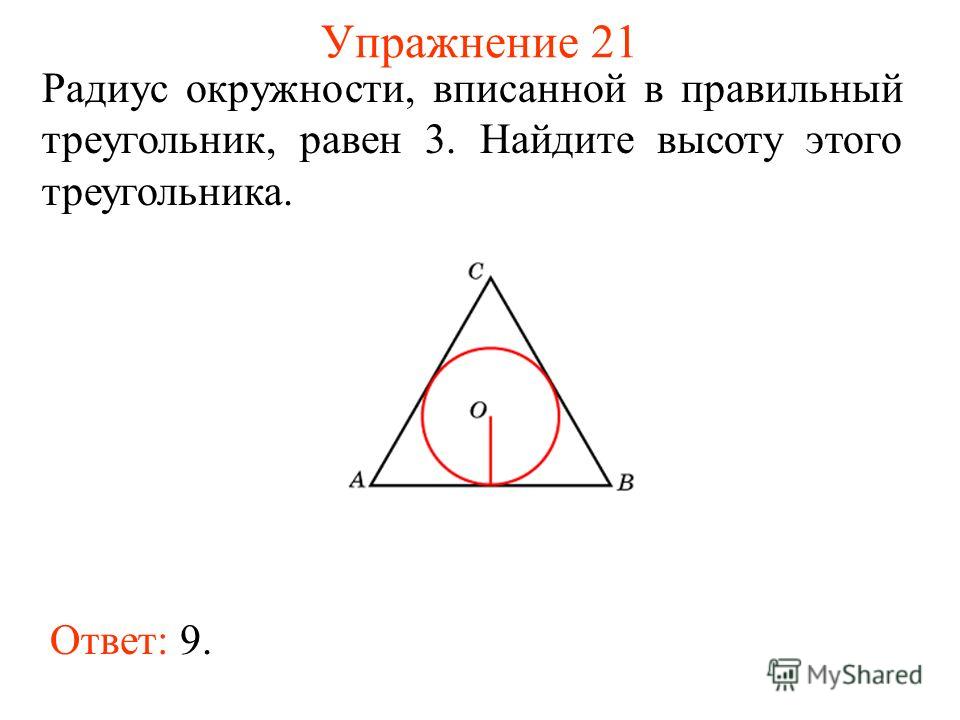 но я не нахожу простой формулы для нахождения радиуса круга.
но я не нахожу простой формулы для нахождения радиуса круга.
- геометрия
$\endgroup$
4
$\begingroup$
Подсказка:
используйте тот факт, что площадь $A$ (треугольника) определяется как: $A=\frac{pr}{2}$, где $p$ – периметр, а $r$ – радиус вписанной окружности. . Эта формула легко доказывается (разбить треугольник на три треугольника с общей вершиной в точке $O$) и верна для выпуклого многоугольника..
$\endgroup$
0
$\begingroup$
Вы можете легко вычислить площадь треугольника.
Затем разделите треугольник на три меньших: $AOB, BOC, COA$. Обратите внимание, что их площади соответственно равны $AB\cdot r/2, BC\cdot r/2, CA\cdot r/2$. Сложите их и сравните с площадью $ABC$, рассчитанной ранее.
Сложите их и сравните с площадью $ABC$, рассчитанной ранее.
$\endgroup$
$\begingroup$
Обнаружение того, что треугольник прямоугольный, очень помогает, но проблему можно решить и без нее.
Пусть стороны треугольника равны $a,b,c$, и определим полупериметр $s=\frac {a+b+c}2$, искомый радиус внутренней стороны как $r$ и площадь треугольника. треугольник как $A$.
Тогда у нас есть и $A=rs$, и формула Герона для площади треугольника при данных сторонах $A=\sqrt {s(s-a)(s-b)(s-c)}$, из которых мы получаем $$r=\ sqrt {\ frac {(sa) (sb) (sc)} {s}} = s \ sqrt {\ left (1- \ frac as \ right) \ left (1- \ frac bs \ right) \ left (1 -\frac cs\right)}$$ 92$, следовательно, треугольник прямоугольный.
площадь прямоугольного треугольника $$\Delta=\frac{1}{2}\times 8\times 15=60$$
полупериметр прямоугольного треугольника $$s=\frac{8+15+17} {2}=20$$
Радиус вписанной окружности определяется как $$r=\frac{\Delta}{s}=\frac{60}{20}=3$$
$\endgroup$
0
$\begingroup$
На самом деле, как только вы заметили, что это прямоугольный треугольник, существует простая формула для диаметра вписанной окружности. 92 = (a+b+c)(a+b-c)$
92 = (a+b+c)(a+b-c)$
С другой стороны
$2A = радиус * периметр = r (a+b+c)$
Объединив два, вы получите
$4A = 2r(a +b+c) = (a+b+c)(a+b-c)$
$\Rightarrow 2r = (a+b-c)$
$\endgroup$
1
$\begingroup$
Ответ равен $3$, потому что одна формула для внутреннего радиуса дается следующим образом:
$$\frac{\text{площадь треугольника}}{\text{полупериметр треугольника}}$$
$\endgroup$
2
геометрия — более простой способ определения радиуса окружности, вписанной в разносторонний треугольник, по двум сторонам и углу между ними
Задавать вопрос
спросил
Изменено 5 лет, 11 месяцев назад 92-2*119*202*cos(43)}}=35,5$
Есть ли более простой способ сделать это?
- геометрия
- круги
- треугольники
$\endgroup$
3
$\begingroup$
, используя правило косинуса, поскольку вы утверждаете, что третья сторона равна 140,73 $.
тогда, поскольку стороны касаются вписанной окружности, мы можем написать: $$ 119 = х + у \\ 202 = х+г \\ 140,73 = у + г $$ эти уравнения дают $x=9{\ круг} \\ & = 35,5 \end{выравнивание} $$ (извините, если мои расчеты ошибочны, но я думаю, что предложенный метод будет работать)
$\endgroup$
$\begingroup$
Поскольку центр вписанной окружности лежит на биссектрисе углов, вы можете разложить треугольник на три пары прямоугольных треугольников, проведя эти биссектрисы и каждый радиус к точкам касания $3$.
Каждый из этих маленьких треугольников имеет высоту радиуса вписанной окружности и общее основание (по всем шести маленьким треугольникам), равное периметру, что дает формулу для радиуса вписанной окружности: $$r_{\маленький I} = \frac{A_T}{s} $$ где $A_T$ — площадь треугольника, а $s$ — полупериметр (половина периметра).
Таким образом, вам все еще нужна третья сторона, как вы вычислили, чтобы получить (полу)периметр, а затем вы можете получить площадь по формуле Герона, $$A_T = \sqrt{s(s-a)(s-b)(s-c)}$$
или, объединяя эти два,
$$r_{\small I} = \sqrt{\frac{(sa)(s-b )(s-c)}{s}}$$
В вашем случае $s = (119+202+140,73)/2 = 230,87$, поэтому $r_{\small I} = \sqrt{\frac{(111,87)( 28,87)(90,14)}{230,87}} = \sqrt{1261} = 35,51$ .

Leave A Comment