СУНЦ УрФУ
Расписание
Электронный журнал
Поступающим
Олимпиады, турниры, конкурсы
Планы работы
Подготовительные курсы
Новости:
27.05.2023
Астрономы СУНЦ наблюдают
Демонстрационные наблюдения являются важной частью учебной программы по астрономии.
25.05.2023
Прозвенел последний звонок!
В СУНЦ УрФУ 23 мая для 237 выпускников прозвенел последний звонок.
21.05.2023
Два диплома на театральном фестивале
Литературный театр СУНЦ с успехом принял участие в региональном фестивале-конкурсе школьных театров «СоБытие».
15.05.2023
Проект из «магии и кирпичей»
Литературный театр СУНЦ показал спектакль «История одного рассказчика».
15.05.2023
«Милосердие сильнее мести»
Состоялась премьера спектакля литературного театра СУНЦ.
12.05.2023
И снова май, цветы, салют и слёзы
В преддверии Дня Победы в СУНЦ состоялся концерт, подготовленный учащимися и педагогами.
Больше новостей
Видеогалерея:
Дом в котором (Литературный театр СУНЦ УрФУ, май 2023)
День Победы (04.05.2023)
Игра в Шекспира (Литературный театр СУНЦ УрФУ, апрель 2023)
Больше видео
О нас:
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).
В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.
Иногородние обучающиеся проживают в уютном общежитии.
Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.
Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону
Как нас найти:
Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝
Проезд:
- автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
- автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
- троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
- троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.
Страница не найдена — ГБПОУ «КРЫМСКОЕ СРЕДНЕЕ ПРОФЕССИОНАЛЬНОЕ УЧИЛИЩЕ (ТЕХНИКУМ) ОЛИМПИЙСКОГО РЕЗЕРВА»
Чемпионат и Первенства России по горному бегу вверх-вниз.
 Республика Марий Эл. Куяр. 20.05.2023
Республика Марий Эл. Куяр. 20.05.2023Чемпионат и Первенства России по горному бегу вверх-вниз. Республика Марий Эл. Куяр. 20.05.2023 Девушки до 18 лет. Дистанция 2км. 6 место АЛИНА САКИР.
Читать далее
22 мая в УОР прозвенел Последний звонок для выпускников 9-х классов!
На торжественной линейке посвящённой празднику «Последний звонок» присутствовали гости: Министр спорта Республики Крым — Торубарова Ольга Александровна и Депутат Государственного совета Республики Крым, президент Региональной общественной организации соде .
Читать далее
ТРЕНЕРСКО-ПРЕПОДАВАТЕЛЬСКИЙ СОСТАВ УЧИЛИЩА
/*! elementor — v3.13.1 — 09-05-2023 */ .elementor-widget-image{text-align:center}.elementor-widget-image a{display:inline-block}.elementor-widget-image a img{width:48px}.elementor-widget-image img{vertical-align:middle;display:inline-block} …
Читать далее
«Крымский подснежник» 2023 г.
14 мая 2023 года перед матчем 6-го тура Чемпионата Республики Крым по футболу среди мужских любительских команд сезона 2023, между командами «УОР» — ФК «НовАвтоТранс», состоялась церемония награждения серебряных призёров Республиканского турнира по футбол .
Читать далее
Поздравляем студента 3 курса Серобян Геворга с серебряной медалью на V Боливарианских играх
Читать далее
Финал межрегионального творческого конкурса «Мы — наследники Победы!»
5 мая 2023 года состоялся Финал межрегионального творческого конкурса «Мы — наследники Победы!», который 9-й раз проводится Межрегиональной общественной организацией «РУССКОЕ ЕДИНСТВО» под патронатом Главы Республики Крым Сергея Аксёнова. В этом году …
В этом году …
Читать далее
Абитуриенту
Читать далее
Обучающемуся
Читать далее
Безопасность
Читать далее
Сведения об ОО
Читать далее
Математическая задача: Четырехугольники 7224 — Практическая математическая задача, Математическая олимпиада
В ABCDEFGHIJKL две смежные стороны перпендикулярны друг другу, и все стороны, кроме сторон AL и GF, идентичны.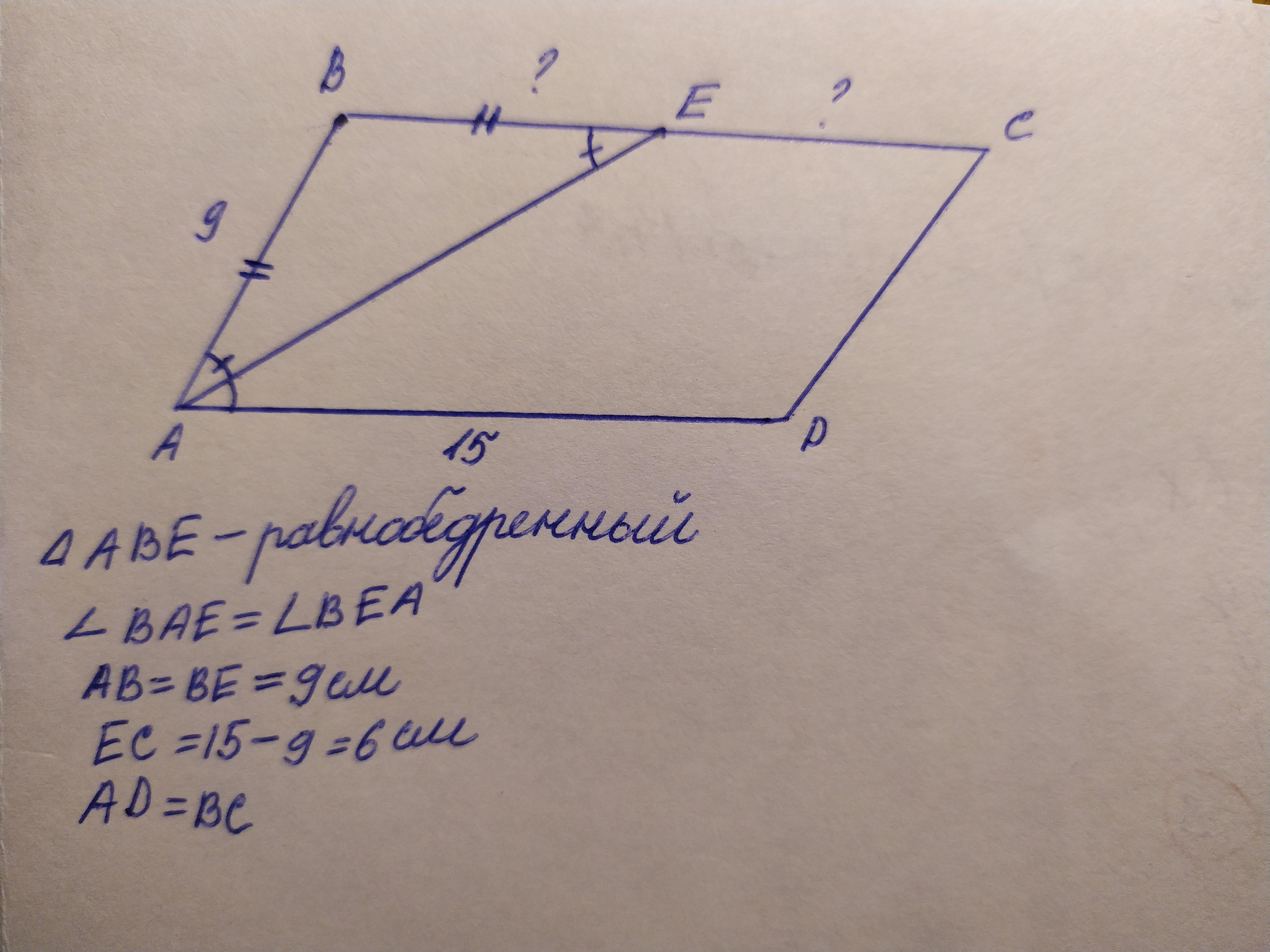 Стороны AL и GF в два раза длиннее остальных сторон. Прямые BG и EL пересекаются в точке M и делят двенадцатиугольник на шесть фигур (три треугольника, два четырехугольника и один пятиугольник). Квадрат EFGM имеет площадь 7 см 2 .
Стороны AL и GF в два раза длиннее остальных сторон. Прямые BG и EL пересекаются в точке M и делят двенадцатиугольник на шесть фигур (три треугольника, два четырехугольника и один пятиугольник). Квадрат EFGM имеет площадь 7 см 2 .Определите площадь остальных пяти отделов.
Правильный ответ:
S 1 = 7 см 2S 2 = 5 см 2 900 16 S 3 = 2 см 2
S 4 = 2 см 2
S 5 = 1 см 2
Пошаговое объяснение:
( 1/2 + 1/4 + 1) S0 S0=S6/(1+21+41)=7/(1+21+41)=4 см2 S0= a⋅ a a=S0 =4 = 2 см S1= S(ABML) S1=S6=7=7 см2S2 = S(CDEMB) S2=(1+1/4)⋅ S0=(1+1/4)⋅ 4=5 см2
S3 = S(JKL) S3=1/2 ⋅ S0=1/2⋅ 4=2 см2
S3= S(GIH) S4=S3=2=2 см2
S5 = S(MIJ) S5=41⋅ S0=41 ⋅ 4=41⋅ 4=44=1 см2
Нашли ошибку или неточность? Не стесняйтесь пишите нам .
 Спасибо!
Спасибо!Советы по использованию связанных онлайн-калькуляторов
Нужна помощь в вычислении суммы, упрощении или умножении дробей? Попробуйте наш калькулятор дробей.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой математической задачи вам необходимо знать следующие знания:
- планиметрия
- многоугольник
- площадь фигуры
- треугольник
- квадрат
- четырехугольник
- основные функции
- причина
- числа
- дроби
Единицы физических величин:
- площадь
- угол
Темы, темы:
- Математическая олимпиада
Класс задачи:
- Практика для 11-летних
Рекомендуем посмотреть обучающее видео по этой математической задаче : видео1
- Перпендикуляр 7223
В ABCDEFGHIJKL , две смежные стороны перпендикулярны друг другу, и все стороны, кроме сторон AL и GF, идентичны. Стороны AL и GF в два раза длиннее остальных сторон. Прямые BG и EL пересекаются в точке M. Четырехугольник
Стороны AL и GF в два раза длиннее остальных сторон. Прямые BG и EL пересекаются в точке M. Четырехугольник - Построение ромба
Постройте ромб ABCD, если его диагональ AC=9 см, а сторона AB = 6 см. Впишите в него окружность, касаясь всех сторон. - Треугольник ABC
В треугольнике ABC длина стороны BC 2 см. Точка К является средней точкой АВ. Точки L и M делят сторону АС на три равные линии. KLM равнобедренный треугольник с прямым углом в точке K. Определить длины сторон AB, AC треугольника A - Диагонали 3580
Длина ребра куба 5см. Нарисуйте разные диагонали. - Добавление фигур
Пять треугольников + 1 квадрат = сколько всего сторон? - Пятиугольник
Вывеска имеет форму пятиугольника ABCDE, в котором линия BC перпендикулярна линии AB, а EA перпендикулярна линии AB. Точка P является пяткой вертикали, начинающейся из точки D на линии AB. | АП | = | ПБ |, | Британская Колумбия | = | ЕА | = 6дм, | ПД | = 8,4 дм - Изготовлено 67424
Имеется шесть линий длиной 3 см, 4 см, 5 см, 7 см, 8 см и 9 см, по две каждой длины. Сколько равнобедренных треугольников можно составить из них? Перечислите все варианты.
Сколько равнобедренных треугольников можно составить из них? Перечислите все варианты. - Перпендикуляр 73574
Две линии треугольника перпендикулярны друг другу и равны 27 см и 36 см. Вычислите длину сторон треугольника и длину третьей линии. - Ящики для отправки по почте
У Лии есть шесть ящиков, которые она хочет отправить по почте. Пять одинаковых коробок весят по 3 и 7/8 фунта каждая. Последняя коробка весит в два раза больше, чем одна из других упаковок. Сколько фунтов весят все шесть ящиков? - Пересечение диагонали
Равнобедренная трапеция ABCD с длинными основаниями | АБ | = 6 см, CD | = 4 см делится на четыре треугольника диагоналями, пересекающимися в точке S. Какую часть площади трапеции составляют треугольники ABS и CDS? - Коэффициент подобия
В треугольнике ТМА длины сторон равны t = 5 см, m = 3,5 см и a = 6,2 см. Другой подобный треугольник имеет длины сторон 6,65 см, 11,78 см и 9,5 см. Определить коэффициент подобия этих треугольников и приписать друг другу подобные стороны.
- Диагональ прямоугольника
В прямоугольнике ABCD находится центр BC, точка E, а точка F — центр CD. Докажите, что прямые AE и AF делят диагональ BD на три равные части. - Диагонали 2
Диагонали AC и BD прямоугольника ABCD пересекаются в точке O. Если OA=4 см, найдите AC и BD. - Пересечение) 1566
В скольких точках пересекаются девять прямых на плоскости, из которых четыре параллельны, а из пяти других нет двух параллельных (и если предположить, что через каждое пересечение проходят только две прямые)? - Шестиугольник
Разделите правильный шестиугольник линиями на девять совершенно одинаковых частей; ни один из них не должен быть в зеркальном отображении (можно только произвольно вращать отдельные части). - Две двумерные фигуры
Определите, какие фигуры имеют большую площадь: (а) квадрат со стороной 8 см; или (б) два прямоугольника со сторонами 5 см и 15 см? Запишите результат в виде 1 или 2 (прямоугольники) - Докажите 2
Докажите, что минимальное количество прямых одиночных разрезов/штрихов, необходимых для разделения данного прямоугольного треугольника или тупоугольного треугольника на совокупность всех остроугольных треугольников семь (7).
- все задачи по математике17272
- алгебра 4981
- арифметика 3610
- основные функции 5336
- комбинаторика 910
- геометрия 2819
- гониометрия и тригонометрия 512
- числа 5451
- физическая величина 5649
- планиметрика 3122
- объемная геометрия 2124
- статистика 678
- темы, темы 2627
-
- Новые математические задачи
- Популярные математические задачи
- Более сложные математические задачи
- Самые простые задачи
В четырехугольнике ABCD с диагональю BD угол A=93, угол ADB=43, угол C=3x+5, угол BDC=x+19 и…
Выберите область веб-сайта для поискаMathAllУчебные пособияПомощь в выполнении домашних заданийПланы уроков
Искать на этом сайте
Цитата страницы Начать эссе значок-вопрос Задайте вопрос Начать бесплатную пробную версию Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяУкажите эту страницу следующим образом:
«В четырехугольнике ABCD с диагональю BD мера угла A=93, мера угла ADB=43, мера угла C=3x+5, мера угла BDC=x+19 и мера угла DBC=2x+6.
Ответы экспертов
Диагональ BD делит четырехугольник на треугольники: `Дельта` ABD и `Дельта` BCD. Сумма углов треугольника равна 180 градусам.
Два угла дельты ABD составляют 93 градуса и 43 градуса. Вычтите из 180 градусов, чтобы найти меру третьего угла: 180 — 93 — 43 = 44. Мера `/_` ABD = 44 градуса.
Углы дельты BCD равны (x + 19), (2x + 6) и (3x + 5). Их сумма составляет 180 градусов. Запишите это в виде уравнения и решите относительно х.
(x + 19) + (2x + 6) + (3x + 5) = 180
6x + 30 = 180
6x = 150
x = 25
Подставьте 25 вместо x, чтобы найти меры углов ` Дельта` BCD.
`/_` BDC = x + 19 = 25 + 19 = 44 градуса
`/_` DBC = 2x + 6 = 2 * 25 + 6 = 56 градусов + 5 = 80 градусов
Диагональ BD действует как поперечная, в результате чего `/_` ABD и « BDC являются чередующимися внутренними углами.
`/_` ABD = 44 градуса
`/_` BDC = 44 градуса
Следовательно, `/_` ABD = `/_` BDC.
Когда альтернативные внутренние углы конгруэнтны, противоположные стороны параллельны. Следовательно, сторона AB параллельна стороне CD.
Однако фигура не является параллелограммом, потому что в параллелограмме противоположные углы равны.
`/_` A = 93 градуса и `/_` C = 80 градусов. `/_` A `!=` `/_` C
« B = 100 градусов и `/_` D = 87 градусов. `/_` B « « D
Четырехугольник ABCD не является параллелограммом (2 пары параллельных сторон). Это трапеция (1 пара параллельных сторон).
Ответ: AB параллельна DC.
См. eNotes без рекламы
Запустите 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.
Получите 48 часов бесплатного доступа Уже зарегистрированы? Войдите здесь.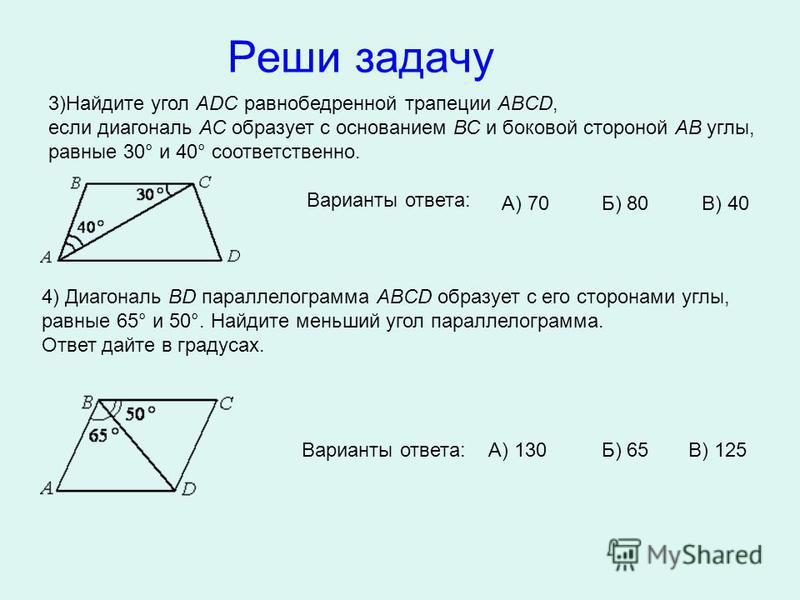

 Стороны AL и GF в два раза длиннее остальных сторон. Прямые BG и EL пересекаются в точке M. Четырехугольник
Стороны AL и GF в два раза длиннее остальных сторон. Прямые BG и EL пересекаются в точке M. Четырехугольник Сколько равнобедренных треугольников можно составить из них? Перечислите все варианты.
Сколько равнобедренных треугольников можно составить из них? Перечислите все варианты.

Leave A Comment