Раскрытие логарифмических уравнений
На предыдущем уроке из курса ВНО подготовки Вы познакомились с формулой раскрытия логарифмов
logaf(x)=c⇔f(x)=ac.
{x>0, x≠1, f(x)>0}
и ее частичными случаями:
логарифм основания равен единице
c=1⇔logaa=1⇔f(x)=a.
логарифм единицы равен нулю
c=1⇔loga1=0⇔f(x)=1.
Мы настолько часто пользуемся этими свойствами логарифмов, что после прочтения всех примеров Вы точно будете знать, где и для чего нужны эти формулы.
Примеры раскрытия логарифмических уравнений
Курс подготовки ВНО состоит из 40 примеров от простых до сложных, так что по номеру примера Вы можете следить, какой класс задач решается. По мере углубления Вы будете знакомиться с новыми формулами и свойствами логарифмов, без которых уравнение невозможно решить.
Пример 16.7 Решить уравнение log2(x+1)-log2(x-1)=1 и указать промежуток, которому принадлежит его корень.
Решение: Выписываем ОДЗ:
По правилу, разницу логарифмов выражений заменяем логарифмом частки + логарифм основания равен единице, в результате опускаем логарифмы и приравниваем выражения:
x=3 – корень заданного уравнения, принадлежащий промежутку (2,9;3,1). 2 в результате логарифмирования обеих его частей.
2 в результате логарифмирования обеих его частей.
Решение: ОДЗ: {x>0, x≠1}.
Прологарифмируем обе части уравнения по основанию 10.
При этом помните, что десятичный логарифм 10 равен 1
таким образом нашли уравнение, которое равносильно начальному.
(x1=1000 или x2=0,1).
Ответ: lg2(x)-2•lg(x)-3=0 – Д.
Пример 16.13 Указать уравнение, равносильное уравнению 2lgx2-lg2(-x)=4.
Решение: ОДЗ: -x>0, x<0.
Вынесем из под логарифма степень =2 и перегруппируем слагаемые
Это и есть все манипуляции, чтобы найти уравнение, которое равносильно заданному
2lgx2-lg2(-x)=4.
С помощью других преобразований Вы бы его не получили.
(x=-100).
Ответ: lg2(-x)-4•lg(-x)+4=0 – Г.
Пример 16.14 Решить уравнения
logalogblogcx=0.
Решение: ОДЗ: x>0.
Имеем три вложенные логарифмы, поэтому по свойствам добиваемся равных основ логарифмов справа и слева от знака равенства, и раскрываем уравнение за схемой
Такого плана задания в свое время были популярны на олимпиадах.
Ответ: cb – А.
Пример 16.15 Указать количество корней уравнения
А | Б | В | Г | Д |
Четыре | три | два | один | ни одного |
Решение: ОДЗ: x≠0.
Путем введения замены переменных уравнение сводим к квадратному, после вычисления которого решаем 2 простых логарифмических уравнения.
Подробные объяснения хода преобразований приведены в таблице
Все найденные значения (-8; -4; 4; 8) принадлежат ОДЗ, уравнение имеет четыре решения.
Ответ: Четыре – А.
Пример 16.24 Установить соответствие между уравнениями (1-4) и произведениями их корней (А–Д).
Решение: Все 4 варианта логарифмических уравнений сводим путем замены переменных к квадратным, после нахождения корней последних возвращаемся к замене и вычисляем простые уравнения с логарифмами. Так как в ответе нужно найти произведение корней, то условие ОДЗ допускает все значения.
Решение уравнений с логарифмами невозможно без знания их свойств. Обращайте внимание на подчеркивания в формулах, они даются не просто так, эти две формулы к концу занятий Вы должны выучить на память и поверьте, что у Вас это получится.
А сейчас переходите к новым готовым ответам с ВНО подготовки на логарифмические уравнения.
11.4.7. Логарифм произведения.
Логарифм произведения.
loga(x∙y)=logax+logay
Логарифм произведения равен сумме логарифмов сомножителей.
Под знаком логарифма могут быть только положительные числа, причем, основание логарифма не равно единице.
Используя формулу логарифма произведения, найти:
1) log36, если log32=a.
log36=log3(2∙3)=log32+log33=log32+1=a+1.
2) log2515, если log53=c. Ответ записать в виде многочлена.
log2515=(log5(3∙5))2=(log53+log55)
3) log210-log315, если log25=p, log35=k.
log210-log315=log2(2∙5) -log3(3∙5)=log22+log25- (log33+log35)=1+log25-1-log35=p-k.
Вычислить:
1) 10lg3+lg2+lg4=10lg (3∙2∙4)=10lg24=24.
2) 7lg2+lg5=7lg (2∙5)=7lg10=71=7.
3) 3log210+log23,2=3log2(10∙3,2)

Решить уравнение:
1) lgx+lg (x-1)=lg2.
lg (x∙(x-1))=lg2 – преобразовали сумму логарифмов в логарифм произведения. Потенцируем и получаем равенство:
x (x-1)=2;
x2-x-2=0. Дискриминант D=b2-4ac=12-4∙1∙(-2)=1+8=9=32. Дискриминант является полным квадратом.
По теореме Виета корни приведенного квадратного уравнения x2-x-2=0 найдем из условий: x1+x2=1; x1∙x2=-2. Подбором находим x
Значение х1=-1 не удовлетворяет условию существования логарифма. Сделаем проверку для х2=2.
lg2+lg (2-1)=lg2;
lg2+lg1=lg2;
lg2=lg2.
Ответ: 2.
2) ln (x-1)+ln (x+1)=ln8.
ln ((x-1)(x+1))=ln8;
(x-1)(x+1)=8;
x2-1=8;
x2=9;
x=±3.
Значение х=-3 не является корнем уравнения, так как не удовлетворяет условию существования логарифма ln (x-1) и ln (x+1). 50 и использовать двоичный поиск, чтобы найти p. это заняло бы около log (50) операций, но кажется немного чрезмерным и уродливым?
50 и использовать двоичный поиск, чтобы найти p. это заняло бы около log (50) операций, но кажется немного чрезмерным и уродливым?
Я нашел этот поток для решения C: вычислительные быстро логарифма по основанию 2 потолок
Однако это кажется немного уродливым, и я не был точно уверен, как преобразовать его в python.
python math logging binaryПоделиться Источник robert king 28 октября 2012 в 02:24
6 ответов
- Быстро вычислить логарифм с основанием 2 потолок
Как быстро вычислить (long int) ceiling(log_2(i)) , где вход и выход-целые числа 64-bit? Допустимы решения для целых чисел со знаком или без знака. Я подозреваю, что лучшим способом будет немного вертлявый метод , подобный тем, что можно найти здесь , но вместо того, чтобы пытаться использовать…
- Узнайте, сколько двоичных цифр имеет конкретное целое число
Возможный Дубликат : Быстро вычислить логарифм с основанием 2 потолок Каков самый быстрый способ узнать, сколько двоичных цифр имеет конкретное целое число, когда оно преобразуется из десятичного в двоичное в C/C++? Пример 47 (10) = 101111 (2 ) Таким образом, 47 имеет 6 цифр, представленных в.
 p <= x
p = 0
while 2**p <= x:
p += 1
return p-1 def easy(x):
return x.bit_length() — 1
p <= x
p = 0
while 2**p <= x:
p += 1
return p-1 def easy(x):
return x.bit_length() — 1 что дает
>>> brute(0), brute(2**3-1), brute(2**3) (-1, 2, 3) >>> easy(0), easy(2**3-1), easy(2**3) (-1, 2, 3) >>> brute(2**50-1), brute(2**50), brute(2**50+1) (49, 50, 50) >>> easy(2**50-1), easy(2**50), easy(2**50+1) (49, 50, 50) >>> >>> all(brute(n) == easy(n) for n in range(10**6)) True >>> nums = (max(2**x+d, 0) for x in range(200) for d in range(-50, 50)) >>> all(brute(n) == easy(n) for n in nums) TrueПоделиться DSM 28 октября 2012 в 02:54
4Вы указываете в комментариях, что ваш x является целым числом, но для тех, кто приходит сюда, где их x уже является плавающей точкой, то math.frexp() будет довольно быстро извлекать базу журнала 2:
log2_slow = int(floor(log(x, 2))) log2_fast = frexp(x)[1]-1Функция C, которую вызывает frexp(), просто захватывает и настраивает показатель степени.
 62:
62:>>> 2**np.log2(2**50) == 2**50 True >>> 2**np.log2(2**62) == 2**62 TrueВыше этого (по крайней мере для меня) он терпит неудачу из-за ограничений внутренних типов чисел numpy, но это будет обрабатывать данные в диапазоне, с которым вы говорите, что имеете дело.
Поделиться BrenBarn 28 октября 2012 в 02:35
- Как вычислить логарифм в Java ME?
Как я могу вычислить логарифм в Java ME? В классе Java ME Math для него нет никакого метода, но он доступен в классе Java SE Math .
- NumPy: логарифм с основанием n
Из документации numpy по логарифмам я нашел функции, которые принимают логарифм с основанием e , 2 и 10 : import numpy as np np.log(np.e**3) #3.0 np.log2(2**3) #3.0 np.log10(10**3) #3.0 Однако как мне взять логарифм с основанием n (например, 42) в numpy?
2Работает на меня, Python 2.
 6.5 (CPython) на OSX 10.7:
6.5 (CPython) на OSX 10.7:>>> x = 2**50 >>> x 1125899906842624L >>> p = int(log(x,2)) >>> p 50 >>> 2**p == x TrueОн продолжает работать, по крайней мере, для показателей до 1e9, и к этому времени математика начинает занимать довольно много времени. Что вы на самом деле получаете за
pв своем тесте? На какой версии Python, на какой OS вы работаете?Поделиться Russell Borogove 28 октября 2012 в 02:35
2Что касается «not accurate for large numbers», то ваша проблема здесь заключается в том, что представление с плавающей запятой действительно не так точно, как вам нужно (
49.999999999993 != 50.0). отличная ссылка-это » то, что каждый компьютерный ученый должен знать об арифметике с плавающей запятой .»Хорошая новость заключается в том, что трансформация процедуры C очень проста:
def getpos(value): if (value == 0): return -1 pos = 0 if (value & (value - 1)): pos = 1 if (value & 0xFFFFFFFF00000000): pos += 32 value = value >> 32 if (value & 0x00000000FFFF0000): pos += 16 value = value >> 16 if (value & 0x000000000000FF00): pos += 8 value = value >> 8 if (value & 0x00000000000000F0): pos += 4 value = value >> 4 if (value & 0x000000000000000C): pos += 2 value = value >> 2 if (value & 0x0000000000000002): pos += 1 value = value >> 1 return posДругой альтернативой является то, что вы можете округлить до ближайшего целого числа, а не усекать:
log(x,2) => 49. p
p
Это, вероятно, так же быстро, как вы можете получить, и использует исключительно побитовую целочисленную арифметику.
def log2_approx(val): from math import floor val = floor(val) approx = 0 while val != 0: val &= ~ (1<<approx) approx += 1 return approxВаше немного другое значение будет вычислено для данного n по формуле
log2_approx(n) - 1..- может быть. Но в любом случае побитовая арифметика может дать вам ключ к тому, как сделать это быстро.
Поделиться cefn 31 октября 2016 в 23:42
Похожие вопросы:
Как вычислить логарифм в iOS?Я хочу вычислить логарифм в iOS. Может ли Objective-C сделать это?
Неперианский логарифм на ActionScript 2?Как вычислить неперианский логарифм на AS2 ???
Матричный логарифм по основанию 2Logm() принимает логарифм матрицы, а log2() принимает логарифм основания 2 каждого элемента матрицы.
 Я пытаюсь вычислить энтропию фон Неймана, которая включает в себя логарифм матрицы базы 2. Как...
Я пытаюсь вычислить энтропию фон Неймана, которая включает в себя логарифм матрицы базы 2. Как...
Быстро вычислить логарифм с основанием 2 потолокКак быстро вычислить (long int) ceiling(log_2(i)) , где вход и выход-целые числа 64-bit? Допустимы решения для целых чисел со знаком или без знака. Я подозреваю, что лучшим способом будет немного...
Узнайте, сколько двоичных цифр имеет конкретное целое числоВозможный Дубликат : Быстро вычислить логарифм с основанием 2 потолок Каков самый быстрый способ узнать, сколько двоичных цифр имеет конкретное целое число, когда оно преобразуется из десятичного в...
Как вычислить логарифм в Java ME?Как я могу вычислить логарифм в Java ME? В классе Java ME Math для него нет никакого метода, но он доступен в классе Java SE Math .
NumPy: логарифм с основанием nИз документации numpy по логарифмам я нашел функции, которые принимают логарифм с основанием e , 2 и 10 : import numpy as np np.
 log(np.e**3) #3.0 np.log2(2**3) #3.0 np.log10(10**3) #3.0 Однако как...
log(np.e**3) #3.0 np.log2(2**3) #3.0 np.log10(10**3) #3.0 Однако как...
Логарифм с основанием 2 в Java в парном разрядеЯ пытаюсь вычислить энтропию английского языка, используя следующую функцию Java public static void calculateEntropy() { for(int i = 0; i < letterFrequencies[i]; i++) { entropy +=...
Основание 2 матричный логарифм в MATLABЯ знаю , что существует MATLAB функция для log и log2 , а для матричного логарифма существует logm . Но мне было интересно, как вычислить матричный логарифм для базы 2?
Как вы можете быстро вычислить целочисленный логарифм для любой базы?Как я могу быстро вычислить целочисленный логарифм для любой базы, а не только для базы 10? Этот вопрос имеет действительно эффективное решение для базы 10, но я хотел бы понять, как я могу обобщить...
логарифмы ЕГЭ | Профиль-математика
Решите неравенство lg4(x2 – 26)4 – 4lg2(x2 – 26)2 ≤ 240.

Применим формулу для логарифма степени и запишем
lg(x2 – 26)4 как 2lg(x2 – 26)2. А почему не как 4lg(x2 – 26)? Потому что в этом случае число под знаком логарифма должно быть положительным, а не просто не равным нулю, как мы записали в ОДЗ. Это значит, что преобразованное далее неравенство не будет равносильно данному. Итак:
lg4(x2 – 26)4 = (lg(x2 – 26)4 )4 = (2lg(x2 – 26)2 )4 = 24 · (lg(x2 – 26)2 )4 = 16lg4(x2 – 26)2.
Тогда данное неравенство примет вид:
16lg4(x2 – 26)2 – 4lg2(x2 – 26)2 ≤ 240. Делим обе части на 4.
4lg4(x2 – 26)2 – lg2(x2 – 26)2 – 60 ≤ 0.
Сделаем замену.
 Пусть lg2(x2 – 26)2 = t.
Пусть lg2(x2 – 26)2 = t.Решим неравенство. 4t2 – t – 60 ≤ 0.
Находим корни квадратного трёхчлена.
4t2 – t – 60 = 0. D = b2 – 4ac = 1 + 960 = 961 = 312.
0 ≤ lg2(x2 – 26)2 ≤ 4.
lg2(x2 – 26)2 ≤ 4. Извлекаем из обеих частей квадратные корни.
| lg(x2 – 26)2| ≤ 2.
-2 ≤ lg(x2 – 26)2 ≤ 2. (см. рис. 2)
Запишем числа -2 и 2 в виде десятичного логарифма.
lg0,01 ≤ lg(x2 – 26)2 ≤ lg100. Логарифмическая функция с основанием 10 является возрастающей, поэтому последнее неравенство равносильно неравенству
0,01 ≤ (x2 – 26)2 ≤ 100. А это неравенство равносильно системе неравенств
Решаем каждое неравенство системы по отдельности, а затем находим их общее решение. Оно и будет служить решением данного неравенства.

I. (x2 – 26)2 ≥ 0,01; (см. рис.3)
| x2 – 26| ≥ 0,1;
1) x2 – 26 ≤ -0,1
x2 ≤ 25,9.
2) x2 – 26 ≥ 0,1
x2 ≥ 26,1.
Решаем второе неравенство системы ( * )
II. (x2 – 26)2 ≤ 100;
| x2 – 26| ≤ 10;
-10 ≤ x2 – 26 ≤ 10
16 ≤ x2 ≤ 36;
Полученные решения неравенств I и II покажем синим и зелёным цветом на координатной прямой. Пересечение этих промежутков и будет решением нашего неравенства.
Как решить логарифмическое неравенство
Логарифмическое неравенство может встретиться вам в 13 задании ЕГЭ по математике.
 При решении логарифмического неравенства важно правильно определить область допустимых значений (ОДЗ). Как же решить логарифмическое неравенство? Давайте разберем основные правила.
При решении логарифмического неравенства важно правильно определить область допустимых значений (ОДЗ). Как же решить логарифмическое неравенство? Давайте разберем основные правила.- Как найти ОДЗ (область допустимых значений) логарифмического неравенства
- Решение логарифмического неравенства с основанием больше 1
- Решение логарифмического неравенства с основанием от 0 до 1
- Решение логарифмического неравенства с переменным основанием: классический подход и метод рационализации
Простейшее логарифмическое неравенство можно записать в виде:знак можно заменить на <, ≤ или ≥.
В логарифмическом неравенстве вначале решения нам важно определить область допустимых значений (ОДЗ).Далее мы смотрим на основание логарифма – a. Напомним, что основание логарифма должно быть положительным, и не должно равняться единице.
Если у логарифма в неравенстве а > 1, то знак неравенства не меняется.

Если у логарифма в неравенстве 0 < а < 1, то знак неравенства меняется на противоположный.
Рассмотрим, как это работает на практике.
Решение логарифмического неравенства с основанием больше 1Вначале определяем ОДЗ: 2х + 4 > 0
Решаем это простейшее неравенство и получаем х > -2.
Таким образом область допустимых значений данного неравенства х > -2.
Далее решаем непосредственно логарифмическое неравенство. Так как основание логарифмов (основание = 2) в неравенстве больше единицы, знак неравенства сохраняется:Так как логарифмы в неравенстве имеют одинаковое основание, то мы их можем просто отбросить и решить неравенство вида
Теперь вспоминаем про нашу ОДЗ и определяем окончательный ответ.Отметим полученные значения на числовой оси:
Решение логарифмического неравенства с основанием от 0 до 1Теперь разберем то же самое неравенство, только основание логарифма будет равно ½.
 Таким образом, получим:
Таким образом, получим:Определяем ОДЗ, как и в прошлом примере, х > -2.
Далее смотрим на основание логарифма. В данном случае основание равно ½, т.е. находится в области от 0 < а < 1. В этом случае знак исходного неравенства меняется на противоположный. Получим:
Решаем полученное неравенство. Так как основания у логарифмов в обеих частях равны, то их можно отбросить, в результате чего получим:Вспоминаем про ОДЗ и определяем окончательный ответ.Отметим полученные точки на числовой оси:Таким образом, решением нашего неравенства является:
Такие неравенства являются простыми, так как основания логарифмов, которые присутствовали в наших неравенствах, были четко определены.
Решение логарифмического неравенства с переменным основаниемА что делать, если основание логарифма, который присутствует в неравенстве, содержит Х? То есть нельзя четко сказать а > 1 или 0 < а < 1. Такое логарифмическое неравенство называется логарифмическим неравенством с переменным основанием.
 Решить его можно двумя способами – с помощью определения логарифма с переменным основанием и методом рационализации.
Решить его можно двумя способами – с помощью определения логарифма с переменным основанием и методом рационализации.Давайте рассмотрим оба способа. И для наглядности решим одно логарифмическое неравенство двумя этими способами.
Итак, мы имеем неравенство
Решение логарифмического неравенства с переменным основанием: классический подходКак правило, в школе учат решать логарифмические неравенства с переменным основанием только с помощью определения логарифма, поэтому-то его и назвали классическим подходом.
Выше мы говорили о том, что при решении неравенств, содержащих логарифмы, необходимо обращать внимание на основание логарифма, которое может быть либо больше единицы, либо меньше единицы, но при этом больше ноля. И в зависимости от этого определяем знак неравенства.
С помощью такого подхода можно решить и логарифмическое неравенство с переменным основанием, то есть с основанием, которое содержит Х, и о котором невозможно сказать больше оно единицы или меньше.
 В этом случае нам просто нужно рассмотреть два случая: когда исходное неравенство больше единицы, и когда исходное неравенство меньше единицы, но больше ноля.
В этом случае нам просто нужно рассмотреть два случая: когда исходное неравенство больше единицы, и когда исходное неравенство меньше единицы, но больше ноля.Вернемся к нашему примеру.Для начала нам нужно преобразовать данное неравенство в такой вид, где слева и справа будут логарифмы с одинаковым основанием. Для этого вспомним такое свойство логарифмов, как логарифмическая единица:То есть в нашем примере правую часть можно преобразовать следующим образом:Таким образом наше неравенство примет вид:
Теперь нам нужно рассмотреть два случая, когда основание логарифма больше единицы и, когда основание логарифма меньше единицы, но больше нуля. При этом не забываем про область допустимых значений.
Решение логарифмического неравенства с переменным основанием: метод рационализации
Отметим полученные точки на числовой оси:Таким образом, решением исходного неравенства является (-2/3;6) .Метод рационализации заключается в том, что исходное неравенство видаВместо V может стоять знак: >, <, ≤ или ≥.

Далее неравенство можно переписать в виде:
В этом случае необходимо поставить тот же знак, что и в изначальном неравенстве.
Далее нам необходимо учесть область допустимых значений:
Применим метод рационализации для решения нашего неравенства:Первое, что нам нужно сделать, это привести его к виду
Для этого снова воспользуемся свойством логарифмов – логарифмическая единица:Теперь перепишем неравенство, используя метод рационализации:
Нам необходимо учесть ОДЗ, тогда получим следующую систему:Первое неравенство системы решим методом интервалов:Таким образом, решение первого неравенства -2 < х < 6
Решение второго неравенства: х > -4½
Решение третьего неравенства: х < 7
Решение четвертого неравенства: х ≠ 6
Совместим решения всех неравенств на числовой оси:
На приведенном примере мы разобрали, как решить логарифмическое неравенство двумя способами. Часто решение методом рационализации бывает более коротким, соответственно, на него вы потратите гораздо меньше драгоценного времени, отведенного на ЕГЭ.
 5}{5}....$
5}{5}....$Когда упрощаются коэффициенты путем деления на множители факториала, они являются своего рода гармоническим рядом, который не сходится очень быстро. Числители - это последовательные степени х, а знаменатели простые числа, не факториалы.
Вы захотите логарифмы чисел больших, чем 2. Здесь скорость сходимости показана в нахождении логарифма 2 этим методом. На сходимость влияет: единственный уменьшающийся фактор гармонического ряда интегральных обратных чисел. Он колеблется между наивысшим значением, а значит, должен сходиться гораздо дальше, чтобы достичь своего наивысшего значения.
Логарифмические ряды: изменение
Вот трюк, для чего введены логарифмы. Если вы изменяете переменную снова, используя (1 + x)/(1 - x), по принципу логарифмов, логарифм этой переменной будет логарифмом (1 + x) минус логарифм (1 - x).
Во-первых, ряд логарифмов (l - x) был последовательностью степеней x разделенных на гармоническую последовательность интегральных чисел, меняющих свой знак.
 Ряды для log(l - x) используют те же численные члены, но все их знаки - отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными.
Ряды для log(l - x) используют те же численные члены, но все их знаки - отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными.Этот метод делает две вещи: удаляет четные степени x и и объединяет их. Эти ряды заключены в большие скобки, умноженные на 2.
Чтобы показать, насколько быстрее эти ряды сходятся, используйте это для вычисления log 2, что при применении первого метода заняло бы вечность. Решите (x + 1)/(x - 1) = 2. Здесь еще одна переменная изменится. Решая этого уравнения, переменная в ряде не 1, а 1/3. Так как каждый другой член выпал, последовательные члены уменьшаются на х (или 1/9). Это соотношение приводит к гораздо быстрому схождению. Он сходится так быстро, что только 4 члена необходимы для получения log2 c четырьмя цифрами после запятой.
Расчет логарифмов
Здесь вы рассчитываете два логарифма, чтобы найти сравнения в скорости сходимости. Для расчета log1,1 сделайте х = 1 / 21.
 Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой.
Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой.Как вы уже видели, для вычисления log2, х = 1/3, где сходимость около одной десятой за каждый дополнительный член. Для точности до шести цифр, требуется семь членов.
Теперь попробуйте найти значение log 3; x = 1/2. Этот ряд сходится более медленно, но попробуйте по-другому. Вы уже посчитали log 2. Log 3 = log 2 + log 1.5, потому что 3 = 2.1,5. Поэтому, найдите log1.5 и сложите его значение с log2. Log 1.5 использует x = 1/5 и его ряд сходится быстрее чем в случае с log 2. Теперь у вас есть значение с 6-ю цифрами для log 3.В примере выше вы пробовали найти значение логарифмов до 10. Обратите внимание, что есть способы для упрощения вычислений. Log 4 есть удвоенный log 2. Вы можете получить его либо из 4 = 2.2 или из 4 = 22. Log 5 есть log 4 + log 1.25. Log 6 есть log 2 + log 3. Log 7 есть log 4 + log 1.75. Log 8 есть log 2 взятый 3 раза, потому что 8 есть 23.
 Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5.
Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5. Общие логарифмы
Хотя все алгоритмы должны быть вычислены в их основной форме с основанием e, иногда называемыми гиперболическими или логарифмами Непера (от имени изобретателя логарифмов). Но более распространенное названия натуральные логарифмы или логарифмы с основанием e.
Log10x = y x = 10y Logε10 = t εt = 10
So x = (εt)y = εty Logεx = tyЕсли у логарифма основание 10, тогда логарифм 10 по основанию 10 равен 1. Вы можете изменить основание, разделив натуральный логарифм на логарифм 10.
Использование логарифмов: умножение и деление
Конечно, нахождение логарифмов с помощью карманных калькуляторов намного проще, чем использование таблиц. Калькулятор вычисляет логарифмы обоих видов, натуральные и общие.
 Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln.
Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln.Примеры, которые мы здесь приводим, взяты из таблиц с логарифмами с четырьмя цифрами. Ваш калькулятор, возможно, показывает больше цифр, чем таблица. На своем калькуляторе я ввел логарифм 32 и получил 1.505149978; значение логарифма 256 равно 2.408239965. Суммируя их, получим 3.9133889944. Используя сдвиг, ответ равен точно 8192!
Последний пример показывает еще одну разницу с таблицами. Таблица дала только мантиссу - дробную часть. Вам необходимо вставить характеристику - целое число слева от запятой. 0.0969 есть мантиссой (в четырехзначных таблицах) для чисел 125. Риска над 1 указывает, что характеристика отрицательная. Поэтому, log есть -1 + 0.0969. Мой калькулятор пишет -0.903089987. Однако, если я ввожу 1.25 вместо 0.125, калькулятор пишет 0.096910013. Если число больше 1, мантисса не меняется, только характеристика изменяется и смещается десятичная точка.
Использование логарифмов: индексы
Здесь снова примеры, которые были приготовлены с помощью четырехзначных логарифмических таблиц.
 Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора.
Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора.Логарифм 12 считается калькулятором как 1.079181246. Умножая на 3, получаем 3.23764 3738. Используя смещение и логарифм дает точно 1728. Вводим 12 снова. Нажимаем xy, затем 3, и =. Калькулятор снова высвечивает 1728.
В следующем примере log 2 равен 0.301029995, правильный ответ снова. Однако, если ввести log 1024, высвечивается предыдущее значение 3.010299957 с одной дополнительной цифрой.
Выше использованы логарифмы или xy клавиши, где индексы были очевидны. Иногда ответ не такой простой. Возьмем следующее: 354/5. С использованием калькулятора: Log 35 = 1.544068044. Используя клавиши xy, получаем тот же ответ.
Кроме того, можно вычислить это значение используя биномиальное разложение, если калькулятор оснащен достаточной памятью.
 Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.
Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро. Биноминальным разложением
Биноминальным разложением
В этот раз, 4-х значные логарифмы довольно ограниченны. Используя тот же калькулятор с клавишами логарифмов или с xy, результат равен 353.5533906. Биноминальное разложение дает тот же результат за исключением последних двух цифр.
Конечно, ваш калькулятор не сделает биномиальный ряд для вас. Для того-то и упражнения, чтобы показать, что биномиальный ряд работает. Как калькулятор это делает? Он имеет встроенные программы, которые вычисляют логарифмические ряды очень быстро - за доли секунды. Помните, что калькулятор работает в двоичной системе, даже если он высвечивает десятичные цифры.
Использование логарифмов с формулами
Формула здесь связывает давление и объем в физическом расширение и сжатии газа.
 Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4.
Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4.В таблице приведены значения v от 10 до 30 (предполагается, что этот диапазон охватывает необходимые значения в нашей конкретной задаче) и используются логарифмы для расчета соответствующего значения р (в последнем столбце). В 3-й колонке приведены значения 0,4logv в качестве помощи нахождения log1,4v. Табулирование с помощью этого метода облегчало процесс до появления калькуляторов.
Четвертая колонка есть вычитание из 3, что есть log1000. Чтобы сделать это на калькуляторе, у вас есть выбор: использовать клавишу logs или xy. В любом случае, вы должны вставить k в это. Если k было другим, чем степень 10, это немного усложнит вычисление. Метод: использовать клавишу 1/x (обратное значение) а потом умножить на 1000 (или на соответсвующее значение к).
Поиск закона логарифмов
Вы знаете, что v и p относится друг к другу по закону типа: pvn = k.
 Это показывает, как это делались вычисления с помощью логарифмов до появления калькуляторов. Вы можете использовать ваш калькулятор, но использование клавиши xy является не таким легким; использование клавиши log есть более легким.
Это показывает, как это делались вычисления с помощью логарифмов до появления калькуляторов. Вы можете использовать ваш калькулятор, но использование клавиши xy является не таким легким; использование клавиши log есть более легким.Возьмем логарифмы значения p: 1.361727836 и 1.176091259. После вычитания получим 0.185636579. Возьмем логарифмы значения v: 1.176091259 и 1.301029996. После вычитания получим: 0.124938736. Разделим первое значение на второе: 0.185636579/0.124938736= 1.485820827 - значение n. Такое вычисление требовало использование ячейки памяти вашего калькулятора. И все эти цифры после запятой точные, но необязательные. Числа, с которыми вам необходимо работать, скорее всего, имеют две значащие цифры.
Вопросы и задачи
1. Рассмотрим следующий рисунок. Эти функции нарисованы на логарифмической шкале. Перерисуйте приближения этих функций в полулогарифмическом масштабе (ось х - линейные, ось у - логарифмическая). Выберите масштаб, который является обоснованными для угла значения в каждом конкретном случае.

2. Нарисуйте приблизительные значения функции в прямоугольных координатах поверх приведенного графика. Выберите масштаб, который является наиболее подходящим для диапазона значений в каждом случае. Масштабы могут быть неодинаковыми на каждой оси, но обе оси должны быть линейными.
3. Рассмотрите следующий рисунок. Эти функции нарисованы в прямоугольных координатах. Нарисуйте приблизительные значения функции в полулогарифмическом масштабе (ось х - линейная и ось у - логарифмическая). Выберите подходящий масштаб для диапазона значений в каждом случае.
4. Нарисуйте приблизительные значения функции в логарифмическом масштабе . Выберите подходящий масштаб для диапазона значений в каждом случае. Масштабы могут быть неодинаковыми на каждой оси, но обе оси должны быть линейными.
5. Используя формулу log10xy = log10x + log10y, найдите значения следующих множителей путем сложений чисел. Вы можете использовать калькулятор. Запишите ответы с тремя цифрами после запятой.

(a) 5.44 • 3.67 (b) 10.5 • 0.567
(c) 36.7 • 2.56 (d) 0.987 • 0.8226. Используя формулу log10xy = ylog10x, найдите значения (стремя цифрами после запятой). Вы можете использовать калькулятор.
(a) 5.443,67 (b) 10.53,67
(c) 36.72,56 (d) 0.9870,8227. Если бы в решении задачи №6 натуральные логарифмы (с основанием e) были бы использованы вместо логарифмов с основанием 10 был бы результат верным?
8. Если бы в решении задачи №6 логарифмы по основанию 7 были бы использованы вместо десятичных логарифмов, был бы результат верным?
Модуль math | Python 3 для начинающих и чайников
Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для работы с числами.
math.ceil(X) – округление до ближайшего большего числа.
math.copysign(X, Y) - возвращает число, имеющее модуль такой же, как и у числа X, а знак - как у числа Y.

math.fabs(X) - модуль X.
math.factorial(X) - факториал числа X.
math.floor(X) - округление вниз.
math.fmod(X, Y) - остаток от деления X на Y.
math.frexp(X) - возвращает мантиссу и экспоненту числа.
math.ldexp(X, I) - X * 2i. Функция, обратная функции math.frexp().
math.fsum(последовательность) - сумма всех членов последовательности. Эквивалент встроенной функции sum(), но math.fsum() более точна для чисел с плавающей точкой.
math.isfinite(X) - является ли X числом.
math.isinf(X) - является ли X бесконечностью.
math.isnan(X) - является ли X NaN (Not a Number - не число).
math.modf(X) - возвращает дробную и целую часть числа X. Оба числа имеют тот же знак, что и X.
math.trunc(X) - усекает значение X до целого.
math.exp(X) - eX.
math.expm1(X) - eX - 1. При X → 0 точнее, чем math.
 exp(X)-1.
exp(X)-1.math.log(X, [base]) - логарифм X по основанию base. Если base не указан, вычисляется натуральный логарифм.
math.log1p(X) - натуральный логарифм (1 + X). При X → 0 точнее, чем math.log(1+X).
math.log10(X) - логарифм X по основанию 10.
math.log2(X) - логарифм X по основанию 2. Новое в Python 3.3.
math.pow(X, Y) - XY.
math.sqrt(X) - квадратный корень из X.
math.acos(X) - арккосинус X. В радианах.
math.asin(X) - арксинус X. В радианах.
math.atan(X) - арктангенс X. В радианах.
math.atan2(Y, X) - арктангенс Y/X. В радианах. С учетом четверти, в которой находится точка (X, Y).
math.cos(X) - косинус X (X указывается в радианах).
math.sin(X) - синус X (X указывается в радианах).
math.tan(X) - тангенс X (X указывается в радианах).
math.hypot(X, Y) - вычисляет гипотенузу треугольника с катетами X и Y (math.
 sqrt(x * x + y * y)).
sqrt(x * x + y * y)).math.degrees(X) - конвертирует радианы в градусы.
math.radians(X) - конвертирует градусы в радианы.
math.cosh(X) - вычисляет гиперболический косинус.
math.sinh(X) - вычисляет гиперболический синус.
math.tanh(X) - вычисляет гиперболический тангенс.
math.acosh(X) - вычисляет обратный гиперболический косинус.
math.asinh(X) - вычисляет обратный гиперболический синус.
math.atanh(X) - вычисляет обратный гиперболический тангенс.
math.erf(X) - функция ошибок.
math.erfc(X) - дополнительная функция ошибок (1 - math.erf(X)).
math.gamma(X) - гамма-функция X.
math.lgamma(X) - натуральный логарифм гамма-функции X.
math.pi - pi = 3,1415926...
math.e - e = 2,718281...
логарифмов
логарифмовЛогарифм - показатель степени. Логарифм - это показатель степени, который указывает, в какой степени база должна быть увеличена, чтобы получить заданное число.

г = b x экспоненциальная форма
х = log b y логарифмический форма
x - логарифм y по основанию b
log b y - степень, в которую мы должны возвести b, чтобы получить y
Мы выражаем x через y
Примеры
x = журнал b y
x = журнал 2 8 Это означает логарифм 8 с основанием 2.Это экспонента, до которой нужно возвести 2, чтобы получить 8. Мы знаем, что 2 (2) (2) = 8. Следовательно, x = 3. x = бревно 6 36 Это означает логарифм 36 по основанию 6.  Это
показатель степени, до которого нужно возвести 6, чтобы получить 36. Мы знаем, что 6 (6)
= 36. Следовательно, x = 2.
Это
показатель степени, до которого нужно возвести 6, чтобы получить 36. Мы знаем, что 6 (6)
= 36. Следовательно, x = 2.x = журнал 10 10,000 Это означает логарифм 10000 с основанием 10.Это - показатель степени, до которого нужно поднять 10, чтобы получить 10 000. Мы знаем что 10 (10) (10) (10) = 10,000. Следовательно, x = 4. журнал b b = 1 Логарифм любого числа по тому же основанию равен 1. x = журнал 11 11 Это означает логарифм 11 по основанию 11. Это показатель степени. на которое нужно поднять 11, чтобы получить 11.Мы знаем, что 1 (1) = 11. Следовательно, x = 1. журнал b 1 = 0 Логарифм 1 всегда равен 0.

Любое число может служить базой b.
Общий (Бриггсиан) логарифмы Основание 10.Логарифмы к базе 10 широко используются. Таким образом, обычно опускают нижний индекс.Если база не указана, подразумевается, что она равна 10.
журнал 10 y = журнал y
Натуральный (Наперианские) логарифмы Основание - e.
Помните e - иррациональное число, где e = 2,71828 ... Символ "ln" относится к натуральным логарифмам.журнал e x = ln x ln x - показатель степени, до которого необходимо возвести e, чтобы получить x.
Почему мы хотим использовать логарифмы? Для упрощения расчетов во многих случаях.
Правила логарифмовПравило продукта Правило частного Правило силы Это правило полезно, потому что оно позволяет нам решать уравнения где переменная - показатель степени. 
Экспоненциальные и логарифмические функции являются обратными функциямиРассмотрим следующие таблицы и связанные с ними графики:
x
f (x) = e x
х
f (x) = ln x
0
1
1
0
1
2.7
2,7
1
2
7,39
7,39
2
3
20
20
3
[индекс]
Работа с показателями и логарифмами
Что такое экспонента?
Показатель степени показывает , сколько раз
до использовать число в умножении.
В этом примере: 2 3 = 2 × 2 × 2 = 8
(2 используется 3 раза при умножении, чтобы получить 8)
Что такое логарифм?
Логарифм идет другим путем.
Возникает вопрос «какой показатель произвел это?»:
И отвечает так:
В этом примере:
- Экспонента принимает 2 и 3 и дает 8 (2, использованные 3 раза в умножении, дает 8)
- Логарифм берет 2 и 8 и дает 3 (2 дает 8 при 3-кратном умножении)
Логарифм показывает , сколько одного числа нужно умножить, чтобы получить другое число
Таким образом, логарифм фактически дает вам показатель степени в качестве ответа :
(Также посмотрите, как связаны экспоненты, корни и логарифмы.)Работаем вместе
Показатели и логарифмы хорошо работают вместе, потому что они «отменяют» друг друга (при условии, что основание «а» одинаково):
Это «обратные функции»
Выполнение одного, затем другого вернет вас к тому, с чего вы начали:
Выполнение a x , затем log a вернет вам снова x : Выполнение log a , затем a x вернет вам снова x :Жаль, что они написаны так иначе .
 .. это заставляет вещи выглядеть странно. Так что может помочь думать о x как о «верхнем» и логарифмически a (x) как о «нижнем»:
.. это заставляет вещи выглядеть странно. Так что может помочь думать о x как о «верхнем» и логарифмически a (x) как о «нижнем»:вверх, затем вниз, снова возвращает вас обратно: вниз (вверх (x)) = x
вниз, затем вверх, снова возвращает вас обратно: вверх (вниз (x)) = x
Во всяком случае, важно то, что:
Логарифмическая функция "отменяется" экспоненциальной функцией.
(и наоборот)
Как в этом примере:
Пример, что такое
x в журнале 3 (x) = 5Начать с: log 3 (x) = 5
Мы хотим «отменить» журнал 3 , чтобы получить «x =»
Используйте экспоненциальную функцию (с обеих сторон): И мы это знаем, так что: x = 3 5Ответ: x = 243
А также:
Пример: вычислить y в
y = log 4 (1/4)Начать с: y = log 4 (1/4)
Используйте экспоненциальную функцию с обеих сторон:Упростить: 4 y = 1/4
Теперь простой трюк: 1/4 = 4 −1
Итак: 4 y = 4 −1
Итак: y = −1
Свойства логарифмов
Одна из сильных сторон логарифмов заключается в том, что они могут превратить умножение в сложение .

log a (m × n) = log a m + log a n
«логарифм умножения - это сумма журналов»
Почему это правда? См. Сноску.
Используя это свойство и законы экспонент, мы получаем следующие полезные свойства:
лог a (м × n) = лог a м + лог a n логарифм умножения - сумма логов бревно a (м / п) = бревно a м - бревно a n бревно деления разность бревен журнал a (1 / n) = −log a n это просто следует из предыдущего правила «деления», потому что log a (1) = 0 бревно a (м r ) = r (лог a м) логарифм m с показателем r равен r, умноженному на логарифм m Помните: основание «а» всегда одинаково!
История: Логарифмы были очень полезны до изобретения калькуляторов.
 .. например, вместо умножения двух больших чисел, используя логарифмы, вы можете превратить его в сложение (намного проще!)
.. например, вместо умножения двух больших чисел, используя логарифмы, вы можете превратить его в сложение (намного проще!)В помощь были книги, полные таблиц логарифмов.
Давайте повеселимся, используя свойства:
Пример: Упростить
журнал a ((x 2 +1) 4 √x)Начать с: log a ((x 2 +1) 4 √x)
Используйте log a (mn) = log a m + log a n : log a ((x 2 +1) 4 ) + log a (√x)
Используйте log a (m r ) = r (log a m) : 4 log a (x 2 +1) + log a (√x)
Также √x = x ½ : 4 log a (x 2 +1) + log a (x ½ )
Используйте log a (m r ) = r (log a m) снова : 4 log a (x 2 +1) + ½ log a (x)
Это насколько мы можем упростить.
 .. мы ничего не можем сделать с логом a (x 2 +1).
.. мы ничего не можем сделать с логом a (x 2 +1).Ответ: 4 журнала a (x 2 +1) + ½ журнала a (x)
Примечание: нет правила для обработки журнала a (m + n) или журнала a (m − n)
Мы также можем применить правила логарифмирования «назад», чтобы объединить логарифмы:
Пример: превратите это в один логарифм:
log a (5) + log a (x) - log a (2)Начинается с: log a (5) + log a (x) - log a (2)
Используйте log a (mn) = log a m + log a n : log a (5x) - log a (2)
Используйте бревно a (м / п) = бревно a м - бревно a n : бревно a (5x / 2)
Ответ: журнал a (5x / 2)
Натуральный логарифм и натуральные экспоненциальные функции
Когда основание равно e («Число Эйлера» = 2.
 718281828459 ...) получаем:
718281828459 ...) получаем:- Натуральный логарифм log e (x) , который чаще записывается ln (x)
- Естественная экспоненциальная функция e x
И та же идея, что одно может "отменить" другое, все еще верна:
ln (e x ) = x
e (ln x) = x
А вот их графики:
Натуральный логарифм
Естественная экспоненциальная функция
График f (x) = ln (x) График f (x) = e x
Проходит через (1,0) и (e, 1)
Проходит через (0,1) и (1, e)
Это такая же кривая с перевернутыми осями x и y .

Это еще одна вещь, чтобы показать вам, что они являются обратными функциями.
На калькуляторе натуральный логарифм - это кнопка «ln».
Всегда старайтесь использовать натуральные логарифмы и натуральную экспоненциальную функцию, когда это возможно.
Десятичный логарифм
Если база равна 10 , вы получите:
- Общий логарифм log 10 (x) , который иногда записывается как log (x)
Инженеры любят его использовать, но в математике он мало используется.
На калькуляторе десятичный логарифм - это кнопка "журнал".
Это удобно, потому что показывает, насколько «большое» число в десятичной системе (сколько раз вам нужно использовать 10 при умножении).
Пример: расчет журнала
10 100Ну, 10 × 10 = 100, поэтому, когда 10 используется 2 раз при умножении, вы получаете 100:
журнал 10 100 = 2
Аналогично log 10 1000 = 3, log 10 10 000 = 4 и т.
 Д.
Д.Пример: расчет журнала
10 369Хорошо, лучше всего использовать кнопку "журнал" моего калькулятора:
журнал 10 369 = 2,567 ...
Замена основания
Что, если мы хотим изменить основание логарифма?
Легко! Просто используйте эту формулу:
"x поднимается, a понижается"
Или другой способ думать об этом: log b a - это как «коэффициент преобразования» (та же формула, что и выше):
Итак, теперь мы можем преобразовать любую базу в любую другую.
Еще одно полезное свойство:
Видите, как меняются местами «x» и «a»?
Пример: вычислить 1 / лог
8 21 / лог 8 2 = лог 2 8
И 2 × 2 × 2 = 8, поэтому, когда 2 используется 3 раз при умножении, вы получаете 8:
1 / лог 8 2 = лог 2 8 = 3
Но мы чаще используем натуральный логарифм, поэтому стоит запомнить:
Пример: расчет журнала
4 22В моем калькуляторе нет кнопки « log 4 ».
 ..
..... но у него есть кнопка " ln ", поэтому мы можем использовать это:
журнал 4 22 = ln 22 / ln 4
= 3,09 ... / 1,39 ...
= 2,23 (до 2 знаков после запятой)
Что означает этот ответ? Это означает, что 4 с показателем 2,23 равняется 22. Итак, мы можем проверить этот ответ:
Чек: 4 2,23 = 22,01 (достаточно близко!)
Вот еще один пример:
Пример: расчет журнала
5 125журнал 5 125 = ln 125 / ln 5
= 4.83 ... / 1,61 ...
= 3 (точно)
Я знаю, что 5 × 5 × 5 = 125, (5 используется 3 раз, чтобы получить 125), поэтому я ожидал ответа 3 , и это сработало!
Использование в реальном мире
Вот несколько примеров использования логарифмов в реальном мире:
Землетрясения
Магнитуда землетрясения в логарифмической шкале.

В знаменитой «шкале Рихтера» используется эта формула:
M = журнал 10 A + B
Где A - амплитуда (в мм), измеренная сейсмографом
и B - поправочный коэффициент расстоянияВ настоящее время есть более сложные формулы, но они все еще используют логарифмическую шкалу.
Звук
Громкость измеряется в децибелах (сокращенно дБ):
Громкость в дБ = 10 log 10 (p × 10 12 )
, где p - звуковое давление.
Кислый или щелочной
Кислотность (или щелочность) измеряется в pH:
pH = −log 10 [H + ]
, где H + - молярная концентрация растворенных ионов водорода.
Примечание: в химии [] означает молярную концентрацию (моль на литр).Другие примеры
Пример: решить 2 журнала
8 x = журнал 8 16Начать с: 2 журнала 8 x = журнал 8 16
Введите "2" в журнал: журнал 8 x 2 = журнал 8 16
Убрать бревна (они же основа): 2 = 16
Решите: x = −4 или +4
Но .
 .. но ... но ... у вас не может быть журнала с отрицательным числом!
.. но ... но ... у вас не может быть журнала с отрицательным числом!Таким образом, случай −4 не определен.
Ответ: 4
Проверка: воспользуйтесь калькулятором, чтобы убедиться, что это правильный ответ ... также попробуйте случай «−4».
Пример: Решите e
−w = e 2w + 6Начнем с: e −w = e 2w + 6
Применить ln с обеих сторон: ln (e −w ) = ln (e 2w + 6 )
И ln (e w ) = w : −w = 2w + 6
Упростить: −3w = 6
Решить: w = 6 / −3 = −2
Ответ: w = −2
Чек: e - (- 2) = e 2 и e 2 (−2) +6 = e 2
Сноска: Почему
log (m × n) = log (m) + log (n) ?Чтобы увидеть , почему , мы будем использовать и:
Сначала превратите m и n в «показатели логарифмов»: Затем используйте один из законов экспонент
Наконец отмените экспоненты.

Это одна из тех умных вещей, которые мы делаем в математике, которую можно описать как «мы не можем сделать это здесь, поэтому давайте пройдемся по там , затем сделаем это, затем вернемся»
РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ1. Чтобы решить логарифмическое уравнение, перепишите уравнение в экспоненциальной форме и решите относительно переменной.
Пример 1: Решите относительно x в уравнении Ln ( x ) = 8.
Решение:
- Шаг 1: Пусть обе стороны будут степенями основания e. Уравнение Ln ( x ) = 8 можно переписать.
- Шаг 2: К настоящему моменту вы должны знать, что когда основание экспоненты и основание логарифма одинаковы, в левой части можно записать x. Теперь уравнение можно записать
.

- Шаг 3: Точный ответ:
и приблизительный ответ
Чек: Вы можете проверить свой ответ двумя способами.Вы можете построить график функции Ln ( x ) -8 и посмотреть, где она пересекает ось x. Если вы правы, график должен пересекать ось x в ответе, который вы получили алгебраически.
Вы также можете проверить свой ответ, подставив значение x в начальное уравнение и определите, равна ли левая часть правой. За Например, если Ln (2,980.95798704) = 8, вы правы. Это так, и вы правы.Пример 2: Решите относительно x в уравнении 7 Log (3 x ) = 15.
Решение:
- Шаг 1: Выделите логарифмический член перед преобразованием логарифмического уравнения в экспоненциальное уравнение. Разделите обе части исходного уравнения на 7:
- Шаг 2: Преобразуйте логарифмическое уравнение в экспоненциальное уравнение: если основание не указано, это означает, что основание логарифма равно 10.
 Напомним также, что логарифмы являются показателями степени, поэтому показатель степени равен
.Уравнение
Напомним также, что логарифмы являются показателями степени, поэтому показатель степени равен
.Уравнениетеперь можно написать
- Шаг 3: Разделите обе части приведенного выше уравнения на 3:
это точный и приблизительный ответ.
Чек: Вы можете проверить свой ответ двумя способами: построив график функции
или подставив значение x в исходное уравнение. Если вы выберете построение графика, точка пересечения по оси X должна быть такой же, как и ответ, который вы полученный ( ).
Если вы выберете замену, значение левой части оригинала уравнение должно равняться значению правой части уравнения после того, как вы вычислили значение каждой стороны на основе вашего ответа для x.Пример 3: Решите относительно x в уравнении
Решение:
- Шаг 1: Обратите внимание, что первый член Ln ( x -3) действителен только тогда, когда x > 3; термин Ln ( x -2) действителен только тогда, когда x > 2; и термин Ln (2 x +24) действителен только тогда, когда x > -12.
 Если мы потребуем, чтобы x был любым действительным числом больше 3, все три члена будут действительными. Если все три члена верны, то уравнение действительно.
Если мы потребуем, чтобы x был любым действительным числом больше 3, все три члена будут действительными. Если все три члена верны, то уравнение действительно. - Шаг 2: Упростите левую часть приведенного выше уравнения: по свойствам логарифмов мы знаем, что
- Шаг 3: Теперь уравнение можно записать
- Шаг 4: Пусть каждая сторона приведенного выше уравнения будет показателем степени основания e:
- Шаг 5: Упростите приведенное выше уравнение:
Другой способ взглянуть на уравнение на шаге 3 - понять, что если Ln ( a ) = Ln ( b ), тогда a должно быть равно b.В случае этой проблемы, тогда
- Шаг 6: Упростите левую часть приведенного выше уравнения:
- Шаг 7: Вычтем 2x + 24 с каждой стороны:
- Шаг 8: Разложите на множители левую часть приведенного выше уравнения:
- Шаг 9: Если произведение двух множителей равно нулю, по крайней мере один из множителей должен быть равен нулю.
 Если . Если
. x = 9 - наше единственное решение. Почему 9 - единственное решение? Мы определили наш домен как все действительные числа больше 3.
Если . Если
. x = 9 - наше единственное решение. Почему 9 - единственное решение? Мы определили наш домен как все действительные числа больше 3.
Чек: Вы можете проверить свой ответ, построив график функции
и определение того, равен ли отрезок оси x также 9. Если это так, вы правильно сработали проблему.
Вы также можете проверить свой ответ, заменив 9 слева x и правые части исходного уравнения. Если после подстановки левый сторона уравнения имеет то же значение, что и правая часть уравнения, вы правильно решили проблему.Если вы хотите просмотреть другой пример, нажмите «Пример».
Решите следующие задачи. Если вы хотите просмотреть ответ и решение, нажмите "Ответить".
Задача 1: Решите относительно x в уравнении
Ответ
Задача 2: Решите относительно x в уравнении
Ответ
Задача 3: Решите относительно x в уравнении
Ответ
Задача 4: Решите относительно x в уравнении
Ответ
Задача 5: Решите относительно x в уравнении
Ответ
Задача 6: Решите относительно x в уравнении
Ответ
[Назад к правилам логарифмов] [Назад к экспоненциальным функциям] [Алгебра] [Тригонометрия] [Сложный Переменные] S. Домашняя страница O.S MATHematics
Домашняя страница O.S MATHematicsВам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор: Нэнси Маркус
Copyright 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. - П.О. Box 12395 - El Paso TX 79913 - США
пользователей онлайн за последний часЛогарифмы - Темы в предварительном исчислении
20
Определение
Десятичный логарифм
Натуральные логарифмы
Три закона логарифмов
Доказательство законов логарифмов
Изменение базы
КОГДА МЫ ДАЕМ, например, основание 2 и показатель степени 3, тогда мы можем вычислить 2 3 .
2 3 = 8.
И наоборот, если даны основание 2 и его степень 8 -
2 ? = 8
- тогда какой показатель даст 8?
Этот показатель называется логарифмом.
 Мы называем показатель степени 3 логарифмом 8 с основанием 2. Запишем
Мы называем показатель степени 3 логарифмом 8 с основанием 2. Запишем3 = журнал 2 8.
Мы пишем основание 2 как нижний индекс.
3 - это показатель степени , до которого нужно поднять 2, чтобы получить 8.
Логарифм - это показатель степени.
С
10 4 = 10 000
, затем
журнал 10 10,000 = 4.
"Логарифм 10 000 по основанию 10 равен 4."
4 - это показатель степени , до которого необходимо поднять 10, чтобы получить 10 000.
«10 4 = 10 000» называется экспоненциальной формой.
"log 10 10,000 = 4" называется логарифмической формой.
Вот определение:
журнал b x = n означает b n = x .
Основание с этой экспонентой дает x .
Пример 1. Запишите в экспоненциальной форме: log 2 32 = 5.

Ответ . 2 5 = 32,
Пример 2.Запишите в логарифмической форме: 4 −2 = .1
16. Ответ. журнал 4 1
16= -2. Задача 1. Какие числа имеют отрицательный логарифм?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!Правильные дроби.
Урок 20 арифметики
Пример 3. Анализ журнала 8 1.
Ответ . 8 до какой степени дает 1? 8 0 = 1.
журнал 8 1 = 0.
Мы можем заметить, что по любому основанию логарифм 1 равен 0.
Пример 4.Анализировать журнал 5 5.
Ответ .
 5 с каким показателем даст 5? 5 1 = 5. Следовательно,
5 с каким показателем даст 5? 5 1 = 5. Следовательно,журнал 5 5 = 1.
В любом основании логарифм самого основания равен 1.
Пример 5. журнал 2 2 м =?
Ответ . 2 поднятый на какой показатель даст 2 м ? м , очевидно.
бревно 2 2 м = м .
Следующее важное формальное правило, действительное для любой базы b :
Это правило воплощает сам смысл логарифма. x - справа - это показатель степени , до которого необходимо поднять основание b , чтобы получить b x .
Правило также показывает, что экспоненциальная функция b x является обратной функцией log b x .Мы увидим это в следующей теме.
Пример 6.  Анализировать журнал 3
Анализировать журнал 3 1
9. Ответ. 1
9равно 3 с какой степенью? 1
9= 3 −2 журнал 3 1
9= журнал 3 3 −2 = −2. Сравните предыдущее правило.
Пример 7. log 2 . 25 =?
Ответ . . 25 = ¼ = 2 2 . Следовательно,
журнал 2 . 25 = лог 2 2 −2 = −2.
Пример 8. журнал 3 =?
Ответ. = 3 1/5 .(Определение рациональной экспоненты.) Следовательно,
журнал 3 = журнал 3 3 1/5 = 1/5.

Задача 2. Запишите каждое из следующих утверждений в логарифмической форме.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).a) b n = x журнал b x = n б) 2 3 = 8 журнал 2 8 = 3 c) 10 2 = 100 журнал 10 100 = 2 г) 5 −2 = 1/25. лог 5 1/25 = −2. Задача 3. Запишите каждое из следующих утверждений в экспоненциальной форме.
a) бревно b x = n b n = x б) журнал 2 32 = 5 2 5 = 32 c) 2 = лог 8 64 8 2 = 64 г) лог 6 1/36 = −2 6 −2 = 1/36 Проблема 4.
 Оцените следующее.
Оцените следующее.а) журнал 2 16 = 4 б) журнал 4 16 = 2 в) бревно 5 125 = 3 г) бревно 8 1 = 0 e) журнал 8 8 = 1 е) журнал 10 1 = 0 Проблема 5.Какой номер n ?
a) журнал 10 n = 3 1000 б) 5 = журнал 2 n 32 c) журнал 2 n = 0 1 d) 1 = журнал 10 n 10 e) журнал n 1
16= −2 4 f) журнал n 1
5= -1 5 г) бревно 2 1
32= n −5 ч) журнал 2 1
2= n -1 Проблема 6.
 журнал b b x = х
журнал b b x = х Проблема 7. Оцените следующее.
а) журнал 9 1
9= лог 9 9 -1 = -1 б) журнал 9 1
81= −2 в) журнал 2 1
4= −2 г) бревно 2 1
8= −3 д) журнал 2 1
16= -4 е) журнал 10 .01 = −2 г) бревно 10 .  001
001= −3 h) бревно 6 = 1/3 i) журнал b = 3/4 Десятичный логарифм
Система десятичного логарифма имеет основу 10.Когда база не указана,
журнал 100 = 2
, то подразумевается система десятичных логарифмов - основание 10.
Вот степени десяти и их логарифмы:
Полномочия 10: 1
10001
1001
101 10 100 1000 10 000 Логарифмы: −3 −2 -1 0 1 2 3 4 Логарифмы заменяют геометрический ряд арифметическим.

Проблема 8. Журнал 10 n =? № . База 10.
Задача 9. log 58 = 1,7634. Следовательно, 10 1.7634 =?
58. 1,7634 - десятичный логарифм 58. Когда 10 возводится в этот показатель, получается 58.
Задача 10. Журнал (журнал x ) = 1. Какое число x ?
log a = 1, подразумевает a = 10, что является основанием.
Пример 4.
Следовательно, log (log x ) = 1 означает log x = 10. Поскольку 10 является основанием,
x = 10 10 = 10 000 000 000
Натуральные логарифмы
В системе натуральных логарифмов в основе лежит число e . ( e назван в честь швейцарского математика 18 века Леонарда Эйлера.) e - база, используемая в исчислении.Его называют «натуральной» базой из-за определенных технических соображений.
e x имеет простейшую производную.
 Урок 14 из Подход к исчислению .)
Урок 14 из Подход к исчислению .)e можно вычислить из следующих рядов, выраженных факториалами:
и = 1 + 1
1!+ 1
2!+ 1
3!+ 1
4!+.. . e - иррациональное число; его десятичное значение примерно
2 . 71828182845904.
Чтобы указать натуральный логарифм числа, мы пишем «ln».
ln x означает журнал e x .
Проблема 11. Какой номер ln e ?
ln e = 1.Логарифм самого основания всегда равен 1. e - основание.
Пример 4.
Задача 12. Запишите в экспоненциальной форме (Пример 1): y = ln x .
e y = x .

е - база.
Три закона логарифмов
1 . log b xy = log b x + log b y
" Логарифм произведения равен сумме
логарифмов каждого множителя. "2 . журнал b = бревно b x - лог b y " Логарифм частного равен логарифму числителя
минус логарифм знаменателя. "3 . журнал b x n = n журнал b x
" Логарифм x с рациональной степенью равен
степени, умноженной на логарифм."Мы докажем эти законы ниже.
Пример 9. Применить законы логарифмов к логарифму .
abc 2
d 3. Ответ. Согласно первым двум законам,
журнал abc 2
d 3= журнал ( abc 2 ) - журнал d 3 = журнал a + журнал b + журнал c 2 - журнал d 3 = журнал a + журнал b + 2 журнал c -3 журнала d , по третьему закону.
Ответ выше показывает полные теоретические шаги. На практике, однако, писать строку
необязательно.журнал abc 2
d 3= журнал ( abc 2 ) - журнал d 3 . 
Студент должен иметь возможность сразу перейти к следующей строке -
журнал abc 2
d 3= журнал a + журнал b + журнал c 2 - журнал d 3 - если не до самой последней строки
log abc 2
d 3= журнал a + журнал b + 2 журнал c - 3 журнала d . Пример 10. Применить законы логарифмов к логарифму
z 5. Ответ. журнал
z 5= журнал x + журнал - журнал z 5 Сейчас, = y ½ .
 (Урок алгебры 29.) Следовательно, согласно третьему закону:
(Урок алгебры 29.) Следовательно, согласно третьему закону:журнал
z 5= журнал x + ½ журнала y - 5 журнал z . Пример 11. Используйте законы логарифмов, чтобы переписать ln.
Решение .
пер. = ln (sin x ln x ) ½ = ½ ln (sin x ln x ), 3-й закон = ½ (ln sin x + ln ln x ), 1-й закон. Обратите внимание, что множители sin x ln x являются аргументами функции логарифма.
Пример 12. Решите это уравнение для x :
журнал 3 2 x + 5 = 1 Решение .  Согласно 3-му Закону мы можем написать
Согласно 3-му Закону мы можем написать(2 x + 5) журнал 3 = 1. Теперь лог 3 - это просто число. Следовательно, при раздаче лога 3, 2 x · журнал 3 + 5 журнал 3 = 1 2 x · журнал 3 = 1-5 журнал 3 x = 1-5 журнала 3
2 журнала 3С помощью этой техники мы можем решить уравнения, в которых неизвестное появляется в экспоненте.
Задача 13. Используйте законы логарифмов, чтобы переписать следующее.
а) журнал ab
c= журнал a + журнал b - журнал c б) бревно ab 2
c 4= журнал a + 2 журнал b - 4 журнала c в) бревно
z= 1/3 журнала x + 1/2 журнала y - журнал z d) ln (sin 2 x ln x ) = ln sin 2 x + ln ln x = 2 ln sin x + ln ln x
д) пер. 
= ½ ln (cos x · x 1/3 ln x ) = ½ (ln cos x + 1/3 ln x + ln ln x ) f) ln ( a 2 x - 1 b 5 x + 1 ) = ln a 2 x - 1 + ln b 5 x + 1 = (2 x - 1) ln a + (5 x + 1) ln b Проблема 14.Решите относительно x .
пер 2 3 x + 1 = 5. (3 x + 1) пер 2 = 5 3 x пер 2 + пер 2 = 5 3 x ln 2 = 5 - пер 2 x = 5 - пер 2
3 пер 2Проблема 15.  Докажите: −ln x
Докажите: −ln x = ln 1
x. −ln x = (−1) ln x = пер. х -1 , Третий закон = пер. 1
xДоказательство законов логарифмов
Законы логарифмов будут действительны для любого основания.Мы докажем их для основания e, то есть для y = ln x .
1 . ln ab = ln a + ln b .
Функция y = ln x определена для всех положительных действительных чисел x . Следовательно, существуют действительные числа p и q , такие что
p = ln a и q = ln b .

Это означает
a = e p и b = e q .
Следовательно, по правилам экспонент
ab = e p · e q = e p + q .
И, следовательно,
ln ab = ln e p + q = p + q = ln a + ln b .
Это то, что мы хотели доказать.
Аналогичным образом доказывается второй закон. Вот 3-й:
3 . ln a n = n ln a .
Существует действительное число p такое, что
p = ln a ;
то есть
a = e p .
И правила экспонент действительны для всех рациональных чисел n (Урок 29 алгебры; иррациональное число - это предел последовательности рациональных чисел).
 Следовательно,
Следовательно,a n = e pn .
Это означает
ln a n = ln e pn = pn = np = n ln a .
Это то, что мы хотели доказать.
Изменение базы
Скажем, мы знаем значения логарифмов по основанию 10, но не, например, по основанию 2. Затем мы можем преобразовать логарифм с основанием 10 в единицу с основанием 2 - или с любым другим основанием - понимая, что значения будет пропорциональным.
Каждое значение в базе 2 будет отличаться от значения в базе 10 той же константой k .
Теперь, чтобы найти эту константу, мы знаем, что
Следовательно, положив сверху x = 2:
Это означает
Следовательно,
То есть
Зная значения логарифмов по основанию 10, мы можем таким образом вычислить их значения по основанию 2.

В общем, тогда, если мы знаем значения в базе a , то константа пропорциональности при переходе к основанию b - это , обратная его логарифму в базе a .
Задача 16. Напишите правило перехода к основанию 8 от основания e .
Следующая тема: Логарифмические и экспоненциальные функции
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Экспоненциальные и логарифмические уравнения
Экспоненциальные и логарифмические уравненияСодержание: Эта страница соответствует § 4.4 (с. 348) текста.
Предлагаемые задачи из текста:
с.
 355 # 13,17,21,25,27,29,31,51,53,57,59,81,89
355 # 13,17,21,25,27,29,31,51,53,57,59,81,89Экспоненциальные уравнения
Логарифмические уравнения
Экспоненциальные уравнения
Некоторые экспоненциальные уравнения можно решить, используя тот факт, что экспоненциальные функции взаимно однозначны. В другом словами, экспоненциальная функция не принимает два разных значения к одному и тому же числу.
Пример 1.
3 x = 9
3 x = 3 2
Функция f (x) = 3 x является взаимно однозначной, поэтому она не принимает два разных значения до 9, поэтому x должен быть равен 2.
х = 2
Уравнение в примере 1 было легко решить, потому что мы могли выразить 9 как степень 3. Однако часто это необходимо использовать логарифм при решении экспоненциального уравнения.
Пример 2.
e x = 20
Мы собираемся использовать тот факт, что натуральный логарифм является обратной экспоненциальной функцией, поэтому ln e x = x по логарифмическому тождеству 1.Мы должны взять натуральный логарифм от обеих сторон уравнения.
ln e x = ln 20
Теперь левая часть упрощается до x, а правая часть представляет собой число. Это примерно 2,9957.
х = 2,9957
Упражнение 1 :
Воспользуйтесь калькулятором, чтобы проверить найденный ответ на уравнение в примере 2.
Пример 3.
5 x = 16 Мы решим это уравнение двумя разными способами.
Первый подход: мы используем тот факт, что log 5 5 x = x (логарифмический тождество 1 снова).
5 x = 16
журнал 5 5 x = журнал 5 16
x = журнал 5 16
x = ln 16 / ln 5, по формуле замены базы.

x = 1,7227 (приблизительно)
Второй подход: мы будем использовать натуральный логарифм и свойство 3.
5 x = 16 Возьмите натуральный логарифм обеих частей.
ln 5 x = ln 16
x ln 5 = ln 16
х = пер 16 / пер 5
x = 1,7227 (приблизительно)
При втором подходе мы могли использовать любой логарифм.Второй подход - тот, который вы видите больше всего довольно часто.
Упражнение 2 :
Воспользуйтесь калькулятором, чтобы проверить найденный ответ на уравнение в примере 3.
Уравнения, подобные приведенному в следующем примере, часто встречаются в приложениях.
Пример 4.
200 е 0,07 т = 500
Сначала мы выделяем экспоненциальную часть, разделив обе части уравнения на 200.
e 0,07 т = 2,5
Теперь возьмем натуральный логарифм обеих частей.

ln e 0,07 t = ln 2,5
Левая часть упрощается до 0,07t по логарифмическому тождеству 1.
0,07t = ln 2,5
t = ln (2,5) / 0,07
t = 13,1 (приблизительно)
Упражнение 3 :
Решите следующие уравнения и проверьте ответы.
(а) 3 x = 10
(б) 150 д 0,05 т = 350
Ответ
Вернуться к содержанию
Логарифмические уравнения
При решении экспоненциальных уравнений мы часто использовали логарифмическое тождество 1, потому что оно включает в себя применение логарифмическая функция для «отмены» эффекта экспоненциальной функции. При работе с логарифмическими уравнениями мы будем использовать логарифмическую идентичность 2, где экспоненциальная функция применяется для «отмены» эффекта логарифмическая функция.

Пример 5.
2 журнала x = 12
Мы хотим изолировать бревно x, поэтому мы делим обе стороны на 2.
журнал x = 6
Поскольку log - это логарифм с основанием 10, мы применяем экспоненциальную функцию с основанием 10 к обеим сторонам уравнения.
10 журнал x = 10 6
По логарифмическому тождеству 2 левая часть упрощается до x.
х = 10 6 = 1000000
Пример 6.
7 + 3 ln x = 15 Сначала выделить ln x.
3 дюйма x = 8
дюйм x = 8/3
Теперь примените экспоненциальную функцию к обеим сторонам.
e ln x = e 8/3
x = e 8/3
Это точный ответ .Если вы используете калькулятор для вычисления этого выражения, у вас будет приближение к ответу.

x примерно равно 14,39.
Упражнение 4 :
Проверьте ответы в примерах 5 и 6.
Пример 7.
ln (x + 4) + ln (x - 2) = ln 7
Сначала мы используем свойство 1 логарифмов, чтобы объединить члены слева.
ln (x + 4) (x - 2) = ln 7
Теперь примените экспоненциальную функцию к обеим сторонам.
e ln (x + 4) (x - 2) = e ln 7
Логарифмическое тождество 2 позволяет упростить обе стороны.
(х + 4) (х - 2) = 7
x 2 + 2x - 8 = 7
x 2 + 2x - 15 = 0
(х - 3) (х + 5) = 0
x = 3 или x = -5
x = 3 проверки, для ln 7 + ln 1 = ln 7.
x = -5 не проверяет , поскольку, когда мы пытаемся заменить -5 на x в исходном уравнении, мы берем натуральный логарифм отрицательных чисел, который не определен.

Итак, x = 3 - единственное решение.
Вернуться к содержанию
Решение логарифмических уравнений - подробные решения
Решите логарифмические уравнения, включая некоторые сложные вопросы.Представлены подробные решения. Логарифмические уравнения в примерах 4, 5, 6 и 7 включают логарифмы с разными основаниями и поэтому являются сложными.
- Как вычислить логарифм в Java ME?

 p <= x
p = 0
while 2**p <= x:
p += 1
return p-1 def easy(x):
return x.bit_length() — 1
p <= x
p = 0
while 2**p <= x:
p += 1
return p-1 def easy(x):
return x.bit_length() — 1  62:
62: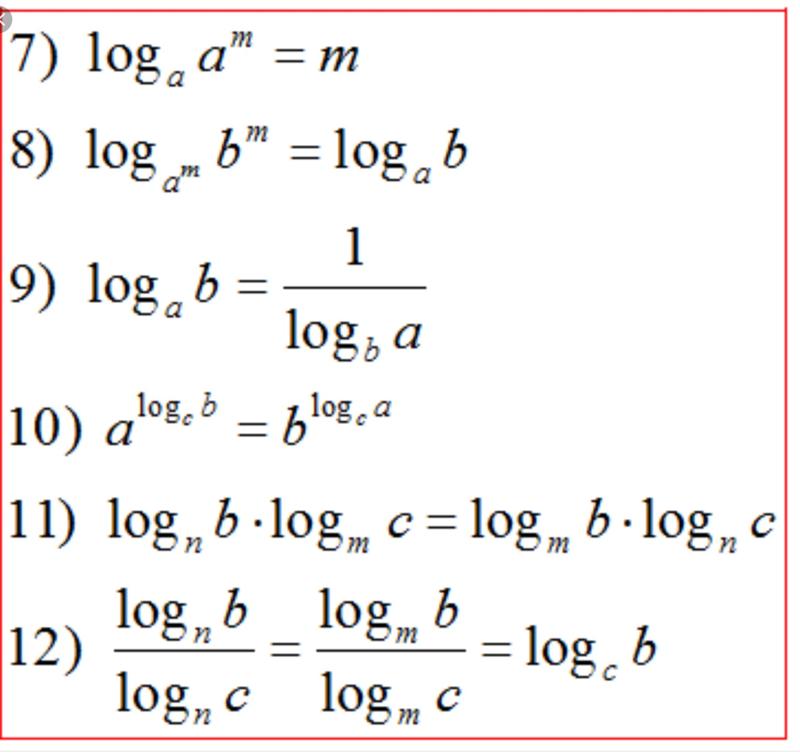 6.5 (CPython) на OSX 10.7:
6.5 (CPython) на OSX 10.7: p
p
 Я пытаюсь вычислить энтропию фон Неймана, которая включает в себя логарифм матрицы базы 2. Как...
Я пытаюсь вычислить энтропию фон Неймана, которая включает в себя логарифм матрицы базы 2. Как... log(np.e**3) #3.0 np.log2(2**3) #3.0 np.log10(10**3) #3.0 Однако как...
log(np.e**3) #3.0 np.log2(2**3) #3.0 np.log10(10**3) #3.0 Однако как...
 Пусть lg2(x2 – 26)2 = t.
Пусть lg2(x2 – 26)2 = t.
 При решении логарифмического неравенства важно правильно определить область допустимых значений (ОДЗ). Как же решить логарифмическое неравенство? Давайте разберем основные правила.
При решении логарифмического неравенства важно правильно определить область допустимых значений (ОДЗ). Как же решить логарифмическое неравенство? Давайте разберем основные правила.
 Таким образом, получим:
Таким образом, получим: Решить его можно двумя способами – с помощью определения логарифма с переменным основанием и методом рационализации.
Решить его можно двумя способами – с помощью определения логарифма с переменным основанием и методом рационализации. В этом случае нам просто нужно рассмотреть два случая: когда исходное неравенство больше единицы, и когда исходное неравенство меньше единицы, но больше ноля.
В этом случае нам просто нужно рассмотреть два случая: когда исходное неравенство больше единицы, и когда исходное неравенство меньше единицы, но больше ноля.
 5}{5}....$
5}{5}....$ Ряды для log(l - x) используют те же численные члены, но все их знаки - отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными.
Ряды для log(l - x) используют те же численные члены, но все их знаки - отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными. Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой.
Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой.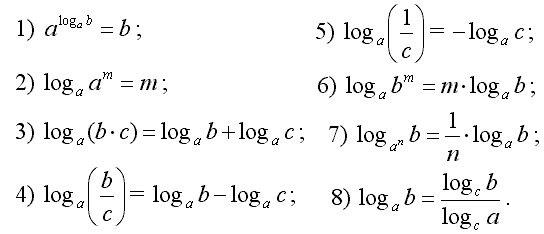 Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5.
Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5.  Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln.
Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln. Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора.
Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора. Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.
Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.  Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4.
Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4. Это показывает, как это делались вычисления с помощью логарифмов до появления калькуляторов. Вы можете использовать ваш калькулятор, но использование клавиши xy является не таким легким; использование клавиши log есть более легким.
Это показывает, как это делались вычисления с помощью логарифмов до появления калькуляторов. Вы можете использовать ваш калькулятор, но использование клавиши xy является не таким легким; использование клавиши log есть более легким.


 exp(X)-1.
exp(X)-1. sqrt(x * x + y * y)).
sqrt(x * x + y * y)).
 Это
показатель степени, до которого нужно возвести 6, чтобы получить 36. Мы знаем, что 6 (6)
= 36. Следовательно, x = 2.
Это
показатель степени, до которого нужно возвести 6, чтобы получить 36. Мы знаем, что 6 (6)
= 36. Следовательно, x = 2.


 .. это заставляет вещи выглядеть странно. Так что может помочь думать о x как о «верхнем» и логарифмически a (x) как о «нижнем»:
.. это заставляет вещи выглядеть странно. Так что может помочь думать о x как о «верхнем» и логарифмически a (x) как о «нижнем»:
 .. например, вместо умножения двух больших чисел, используя логарифмы, вы можете превратить его в сложение (намного проще!)
.. например, вместо умножения двух больших чисел, используя логарифмы, вы можете превратить его в сложение (намного проще!) .. мы ничего не можем сделать с логом a (x 2 +1).
.. мы ничего не можем сделать с логом a (x 2 +1). 718281828459 ...) получаем:
718281828459 ...) получаем:
 Д.
Д. ..
..
 .. но ... но ... у вас не может быть журнала с отрицательным числом!
.. но ... но ... у вас не может быть журнала с отрицательным числом!

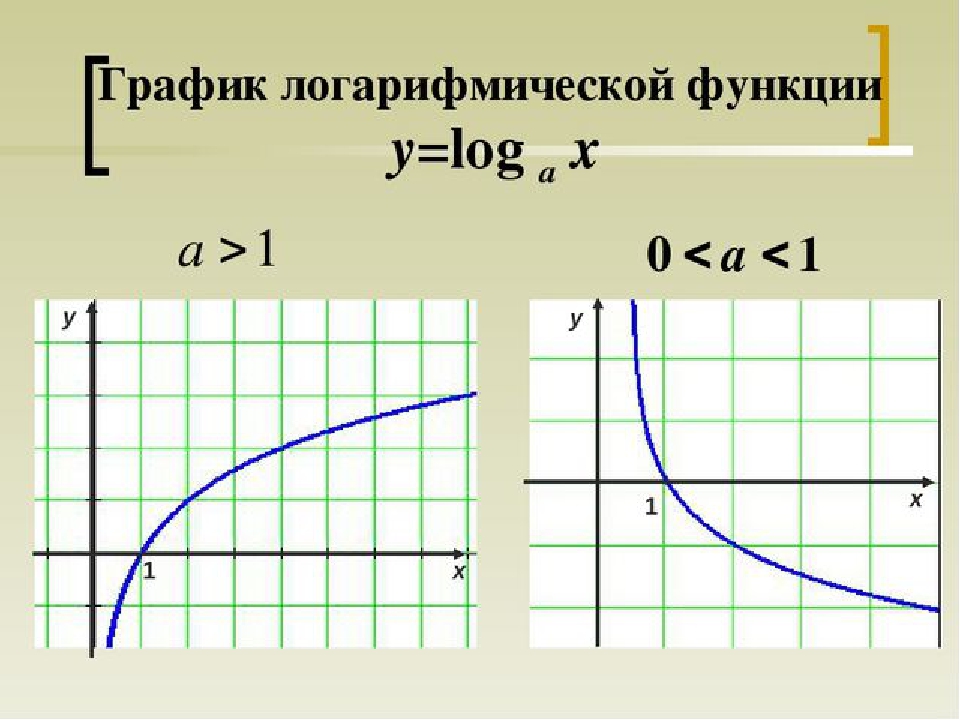 Напомним также, что логарифмы являются показателями степени, поэтому показатель степени равен
.Уравнение
Напомним также, что логарифмы являются показателями степени, поэтому показатель степени равен
.Уравнение Если мы потребуем, чтобы x был любым действительным числом больше 3, все три члена будут действительными. Если все три члена верны, то уравнение действительно.
Если мы потребуем, чтобы x был любым действительным числом больше 3, все три члена будут действительными. Если все три члена верны, то уравнение действительно. Если . Если
. x = 9 - наше единственное решение. Почему 9 - единственное решение? Мы определили наш домен как все действительные числа больше 3.
Если . Если
. x = 9 - наше единственное решение. Почему 9 - единственное решение? Мы определили наш домен как все действительные числа больше 3. Домашняя страница O.S MATHematics
Домашняя страница O.S MATHematics Мы называем показатель степени 3 логарифмом 8 с основанием 2. Запишем
Мы называем показатель степени 3 логарифмом 8 с основанием 2. Запишем
 5 с каким показателем даст 5? 5 1 = 5. Следовательно,
5 с каким показателем даст 5? 5 1 = 5. Следовательно, Анализировать журнал 3
Анализировать журнал 3 
 Оцените следующее.
Оцените следующее. журнал b b x = х
журнал b b x = х  001
001
 Урок 14 из Подход к исчислению .)
Урок 14 из Подход к исчислению .)


 (Урок алгебры 29.) Следовательно, согласно третьему закону:
(Урок алгебры 29.) Следовательно, согласно третьему закону: Согласно 3-му Закону мы можем написать
Согласно 3-му Закону мы можем написать
 Докажите: −ln x
Докажите: −ln x 
 Следовательно,
Следовательно,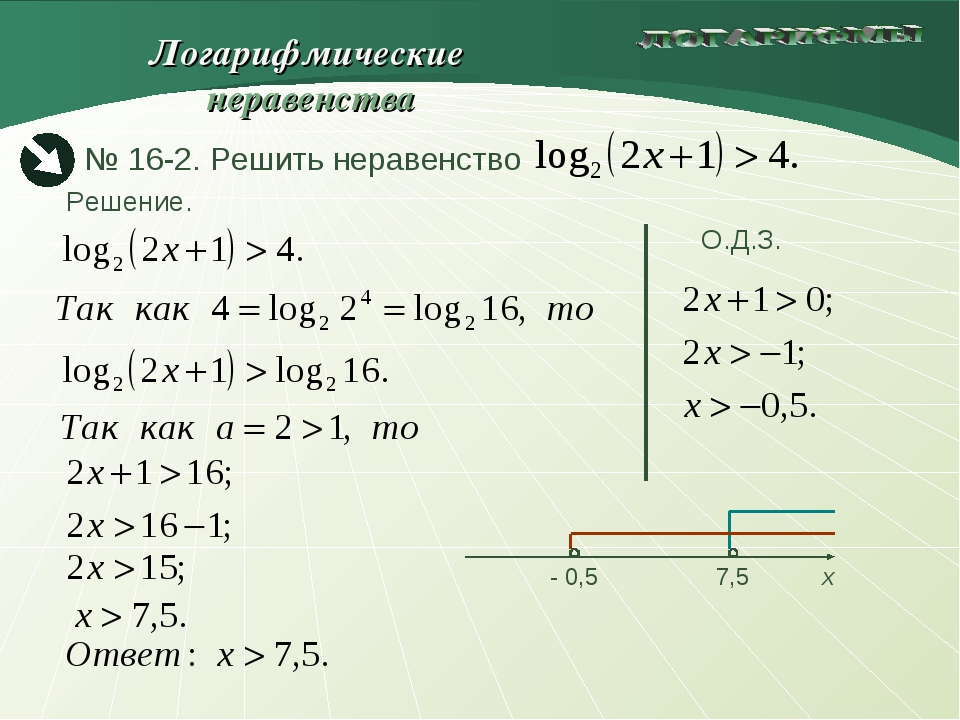
 355 # 13,17,21,25,27,29,31,51,53,57,59,81,89
355 # 13,17,21,25,27,29,31,51,53,57,59,81,89





 Решение примера 1
Решение примера 1 
 2 + 139)
2 + 139) Решение примера 4
Решение примера 4 

 5 (х - 4) = 20. Решение примера 5
5 (х - 4) = 20. Решение примера 5  Решение для примера 7
Решение для примера 7 
 Логарифмы
в основном другой способ написания
экспоненты и логарифмические функции являются обратными экспоненциальным функциям.
Логарифмы
в основном другой способ написания
экспоненты и логарифмические функции являются обратными экспоненциальным функциям. лин (х) .Натуральный логарифм имеет основание и , которое, как мы обнаружили, представляет собой уникальную экспоненту.
функция. Многие проблемы будут связаны с и , и нам придется использовать естественный
log ln , чтобы оценить и построить график функции.
лин (х) .Натуральный логарифм имеет основание и , которое, как мы обнаружили, представляет собой уникальную экспоненту.
функция. Многие проблемы будут связаны с и , и нам придется использовать естественный
log ln , чтобы оценить и построить график функции. Хотя мы обычно подключаем
в значениях x, чтобы найти наши значения y, в этой форме гораздо проще подключать различные
значения для y.
Хотя мы обычно подключаем
в значениях x, чтобы найти наши значения y, в этой форме гораздо проще подключать различные
значения для y. Если наш ввод больше 5, наш вывод
не будет определяться. Перехват по оси x задается как
Если наш ввод больше 5, наш вывод
не будет определяться. Перехват по оси x задается как Это подтверждает, что журналы - это еще один способ записи
экспоненты, как и вычитание, - это еще один способ написания сложения и деления
это еще один способ записи умножения. Опять же, это свойство работает, только если
база b такая же, как база b бревна.
Это подтверждает, что журналы - это еще один способ записи
экспоненты, как и вычитание, - это еще один способ написания сложения и деления
это еще один способ записи умножения. Опять же, это свойство работает, только если
база b такая же, как база b бревна.
Leave A Comment