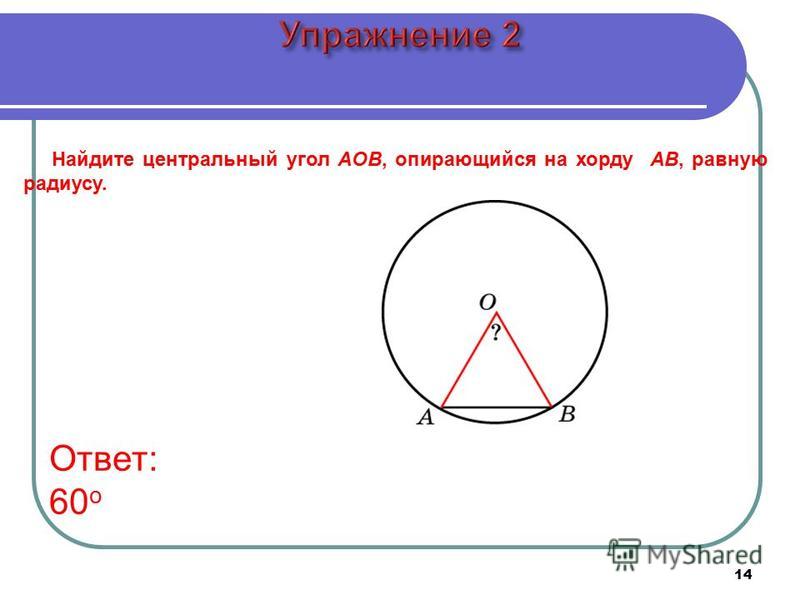
1. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах
1.
Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
2.
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
3.
Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
4.
Дуга окружности AC, не содержащая точки B, составляет 200°. А дуга окружности BC, не содержащая точки A, составляет 80°. Найдите вписанный угол ACB. Ответ дайте в градусах.
5.
Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно и Ответ дайте в градусах.
6.
Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек
Градусная величина дуги AB окружности, не содержащей точек
7.
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 61°, угол CAD равен 37° Найдите угол ABC. Ответ дайте в градусах.
8.
В треугольнике ABC сторона AB равна угол С равен 135°. Найдите радиус описанной около этого треугольника окружности.
9. Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
10. Хорда AB стягивает дугу окружности в 92°. Найдите угол
11.
Через концы А и В дуги окружности с центром О проведены касательные АС и ВС.
 Угол СAB равен 32°. Найдите угол AОB. Ответ дайте в градусах.
Угол СAB равен 32°. Найдите угол AОB. Ответ дайте в градусах.
12.
Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
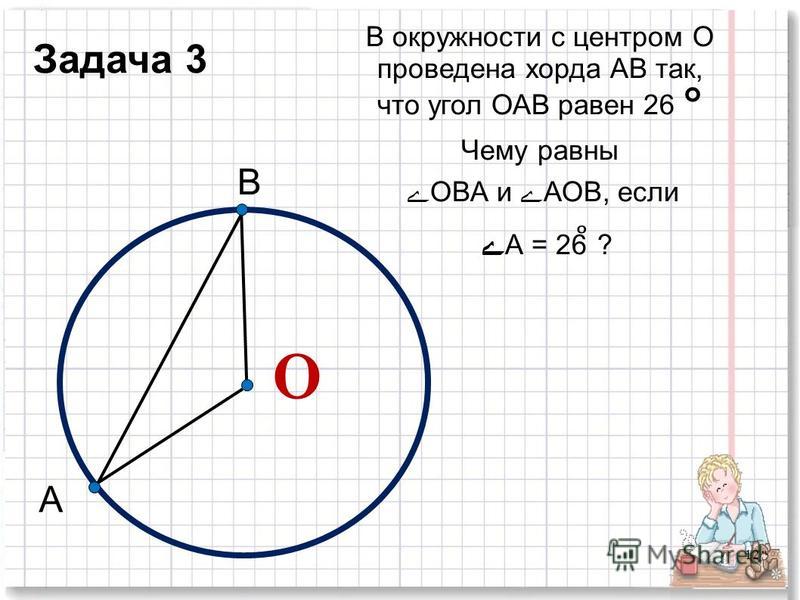
13. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона
14.
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона CO пересекает окружность в точках B и D, а дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.
Ключ
|
№ п/п |
№ задания |
Ответ |
|
|
27857 |
30 |
|
2 |
27859 |
150 |
|
3 |
27864 |
36 |
|
4 |
27866 |
40 |
|
5 |
27885 |
40 |
|
6 |
27886 |
20 |
|
7 |
525110 |
98 |
|
8 |
541371 |
3 |
|
9 |
27867 |
105 |
|
10 |
27877 |
46 |
|
11 |
27878 |
64 |
|
12 |
27879 |
118 |
|
13 |
27881 |
26 |
|
14 |
27883 |
26 |
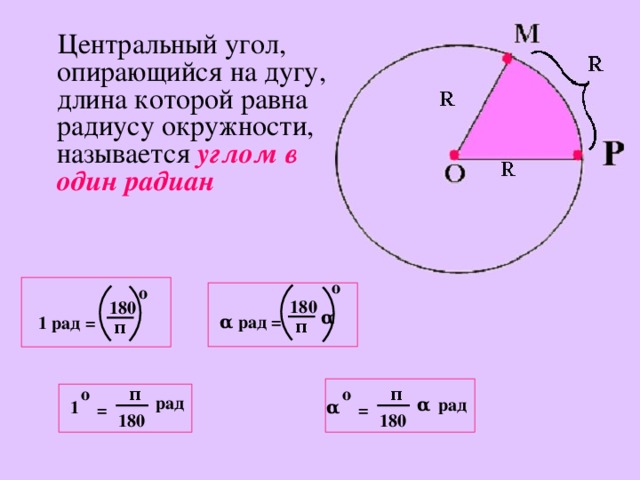
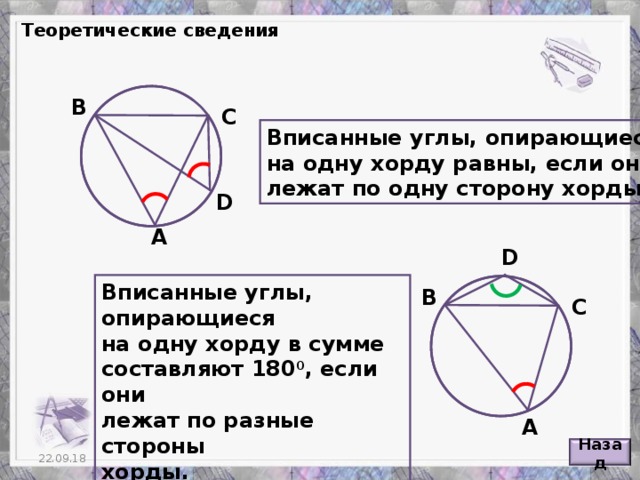
Чему равен вписанный и центральный угол.
 Угол
УголПрерывание беременности
Угол ABC — вписанный угол. Он опирается на дугу АС, заключённую между его сторонами (рис. 330).
Теорема . Вписанный угол измеряется половиной дуги, на которую он опирается.
Это надо понимать так: вписанный угол содержит столько угловых градусов, минут и секунд, сколько дуговых градусов, минут и секунд содержится в половине дуги, на которую он опирается.
При доказательстве этой теоремы надо рассмотреть три случая.
Первый случай. Центр круга лежит на стороне вписанного угла (рис. 331).
Пусть ∠ABC — вписанный угол и центр круга О лежит на стороне BC. Требуется доказать, что он измеряется половиной дуги AC.
Соединим точку A с центром круга. Получим равнобедренный \(\Delta\)AOB, в котором АО = OB, как радиусы одного и того же круга. Следовательно, ∠A = ∠B.
∠AOC является внешним по отношению к треугольнику AOB, поэтому ∠AOC = ∠А + ∠В, а так как углы А и В равны, то ∠В составляет 1 / 2 ∠AOC.
Но ∠AOC измеряется дугой АС, следовательно, ∠В измеряется половиной дуги АС.
Например, если \(\breve{AC}\) содержит 60°18’, то ∠В содержит 30°9’.
Второй случай.
Пусть ∠ABD — вписанный угол. Центр круга О лежит между его сторонами. Требуется доказать, что ∠ABD измеряется половиной дуги АD.
Для доказательства проведём диаметр BC. Угол ABD разбился на два угла: ∠1 и ∠2.
∠1 измеряется половиной дуги АС, а ∠2 измеряется половиной дуги СD, следовательно, весь ∠АВD измеряется 1 / 2 \(\breve{AC}\) + 1 / 2 \(\breve{CD}\), т. е. половиной дуги АD.
Например, если \(\breve{AD}\) содержит 124°, то ∠В содержит 62°.
Третий случай. Центр круга лежит вне вписанного угла (рис. 333).
Пусть ∠MAD — вписанный угол. Центр круга О находится вне угла. Требуется доказать, что ∠MAD измеряется половиной дуги MD.
Для доказательства проведём диаметр AB. ∠MAD = ∠MAB — ∠DAB.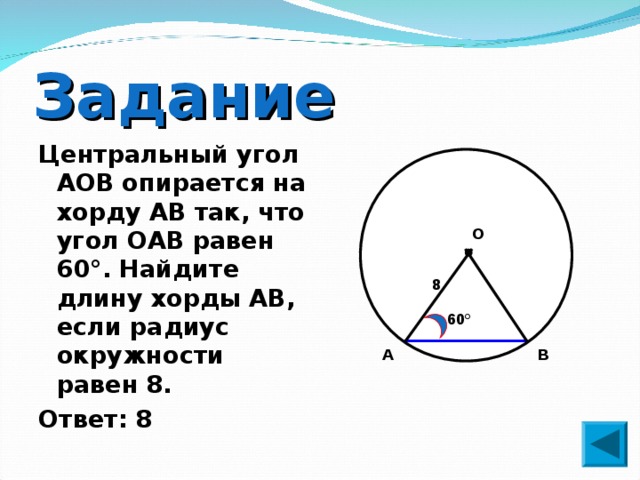 Но ∠MAB измеряется 1 / 2 \(\breve{MB}\), а ∠DAB измеряется 1 / 2 \(\breve{DB}\).
Но ∠MAB измеряется 1 / 2 \(\breve{MB}\), а ∠DAB измеряется 1 / 2 \(\breve{DB}\).
Следовательно, ∠MAD измеряется 1 / 2 (\(\breve{MB} — \breve{DB})\), т. е. 1 / 2 \(\breve{MD}\).
Например, если \(\breve{MD}\) содержит 48° 38″, то ∠MAD содержит 24° 19’ 8″.
Следствия
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги (рис. 334, а).
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности. Половина окружности содержит 180 дуговых градусов, значит, угол, опирающийся на диаметр, содержит 90 угловых градусов (рис. 334, б).
Сегодня мы рассмотрим очередной тип задач 6 — на этот раз с окружностью. Многие ученики не любят их и считают сложными. И совершенно напрасно, поскольку такие задачи решаются элементарно , если знать некоторые теоремы. Или не решаются вообще, если их не знать.
Прежде чем говорить об основных свойствах, позвольте напомнить определение:
Вписанный угол — тот, у которого вершина лежит на самой окружности, а стороны высекают на этой окружности хорду.
Центральный угол — это любой угол с вершиной в центре окружности. Его стороны тоже пересекают эту окружность и высекают на ней хорду.
Итак, понятия вписанного и центрального угла неразрывно связаны с окружностью и хордами внутри нее. А теперь — основное утверждение:
Теорема. Центральный угол всегда в два раза больше вписанного, опирающегося на ту же самую дугу.
Несмотря на простоту утверждения, существует целый класс задач 6, которые решаются с помощью него — и никак иначе.
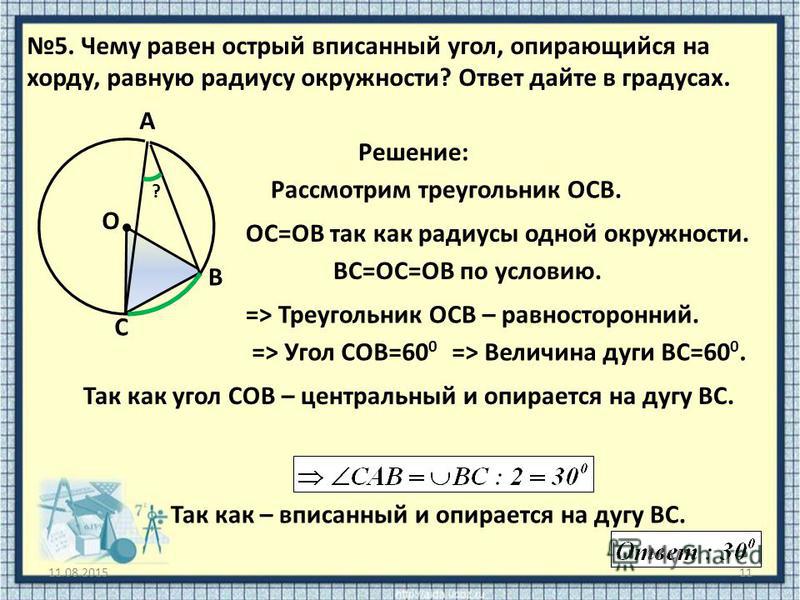
Задача. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.
Пусть AB — рассматриваемая хорда, O — центр окружности. Дополнительное построение: OA и OB — радиусы окружности. Получим:
Рассмотрим треугольник ABO . В нем AB = OA = OB — все стороны равны радиусу окружности. Поэтому треугольник ABO — равносторонний, и все углы в нем по 60°.
Пусть M
— вершина вписанного угла.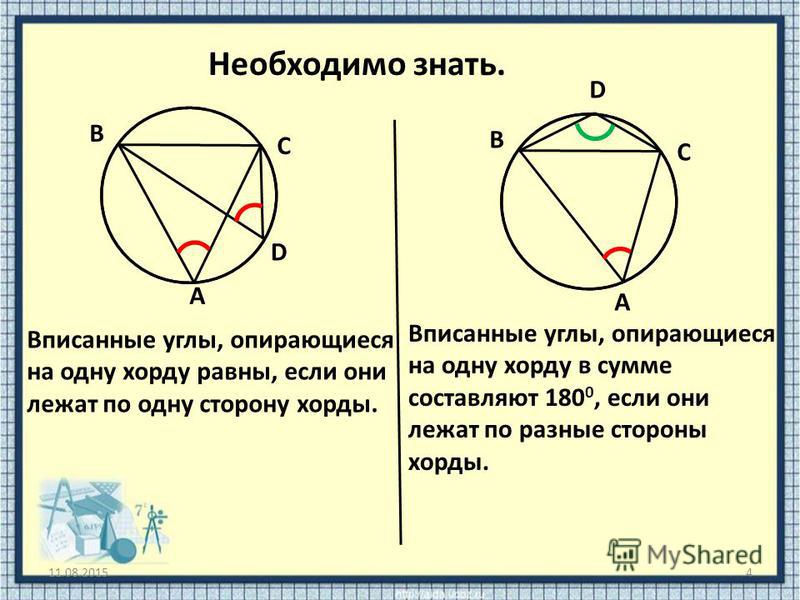 Поскольку углы O
и M
опираются на одну и ту же дугу AB
, вписанный угол M
в 2 раза меньше центрального угла O
. Имеем:
Поскольку углы O
и M
опираются на одну и ту же дугу AB
, вписанный угол M
в 2 раза меньше центрального угла O
. Имеем:
M = O : 2 = 60: 2 = 30
Задача. Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.
Введем обозначения:
- AB — хорда окружности;
- Точка O — центр окружности, поэтому угол AOB — центральный;
- Точка C — вершина вписанного угла ACB .
Поскольку мы ищем вписанный угол ACB , обозначим его ACB = x . Тогда центральный угол AOB равен x + 36. С другой стороны, центральный угол в 2 раза больше вписанного. Имеем:
AOB
= 2 · ACB
;
x
+ 36 = 2 · x
;
x
= 36.
Вот мы и нашли вписанный угол AOB — он равен 36°.
Окружность — это угол в 360°
Прочитав подзаголовок, знающие читатели, наверное, сейчас скажут: «Фу!» И действительно, сравнивать окружность с углом не совсем корректно. Чтобы понять, о чем речь, взгляните на классическую тригонометрическую окружность:
К чему эта картинка? А к тому, что полный оборот — это угол в 360 градусов. И если разделить его, скажем, на 20 равных частей, то размер каждой из них будет 360: 20 = 18 градусов. Именно это и требуется для решения задачи B8.
И если разделить его, скажем, на 20 равных частей, то размер каждой из них будет 360: 20 = 18 градусов. Именно это и требуется для решения задачи B8.
Точки A , B и C лежат на окружности и делят ее на три дуги, градусные меры которых относятся как 1: 3: 5. Найдите больший угол треугольника ABC .
Для начала найдем градусную меру каждой дуги. Пусть меньшая из них равна x . На рисунке эта дуга обозначена AB . Тогда остальные дуги — BC и AC — можно выразить через AB : дуга BC = 3x ; AC = 5x . В сумме эти дуги дают 360 градусов:
AB
+ BC
+ AC
= 360;
x
+ 3x
+ 5x
= 360;
9x
= 360;
x
= 40.
Теперь рассмотрим большую дугу AC , которая не содержит точку B . Эта дуга, как и соответствующий центральный угол AOC , равна 5x = 5 · 40 = 200 градусов.
Угол ABC — самый большой из всех углов треугольника. Это вписанный угол, опирающийся на ту же дугу, что и центральный угол AOC . Значит, угол ABC в 2 раза меньше AOC . Имеем:
ABC = AOC : 2 = 200: 2 = 100
Это и будет градусная мера большего угла в треугольнике ABC
.
Окружность, описанная вокруг прямоугольного треугольника
Эту теорему многие забывают. А зря, ведь некоторые задачи B8 без нее вообще не решаются. Точнее, решаются, но с таким объемом вычислений, что вы скорее уснете, чем дойдете до ответа.
Теорема. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.
Что следует из этой теоремы?
- Середина гипотенузы равноудалена от всех вершин треугольника. Это прямое следствие теоремы;
- Медиана, проведенная к гипотенузе, делит исходный треугольник на два равнобедренных. Как раз это и требуется для решения задачи B8.
В треугольнике ABC провели медиану CD . Угол C равен 90°, а угол B — 60°. Найдите угол ACD .
Поскольку угол C равен 90°, треугольник ABC — прямоугольный. Получается, что CD — медиана, проведенная к гипотенузе. Значит, треугольники ADC и BDC — равнобедренные.
В частности, рассмотрим треугольник ADC
.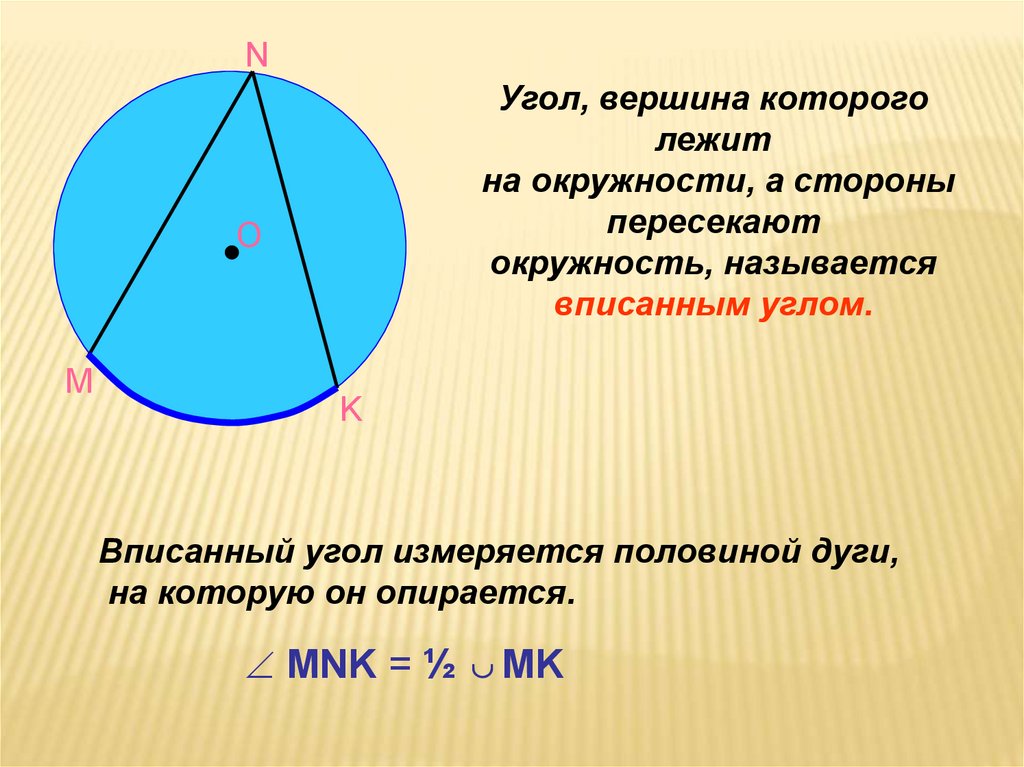 В нем AD
= CD
. Но в равнобедренном треугольнике углы при основании равны — см. «Задача B8: отрезки и углы в треугольниках ». Поэтому искомый угол ACD
= A
.
В нем AD
= CD
. Но в равнобедренном треугольнике углы при основании равны — см. «Задача B8: отрезки и углы в треугольниках ». Поэтому искомый угол ACD
= A
.
Итак, осталось выяснить, чему равен угол A . Для этого снова обратимся к исходному треугольнику ABC . Обозначим угол A = x . Поскольку сумма углов в любом треугольнике равна 180°, имеем:
A
+ B
+ BCA
= 180;
x
+ 60 + 90 = 180;
x
= 30.
Разумеется, последнюю задачу можно решить по-другому. Например, легко доказать, что треугольник BCD — не просто равнобедренный, а равносторонний. Значит, угол BCD равен 60 градусов. Отсюда угол ACD равен 90 − 60 = 30 градусов. Как видите, можно использовать разные равнобедренные треугольники, но ответ всегда будет один и тот же.
\[{\Large{\text{Центральные и вписанные углы}}}\]
Определения
Центральный угол – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности.
Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.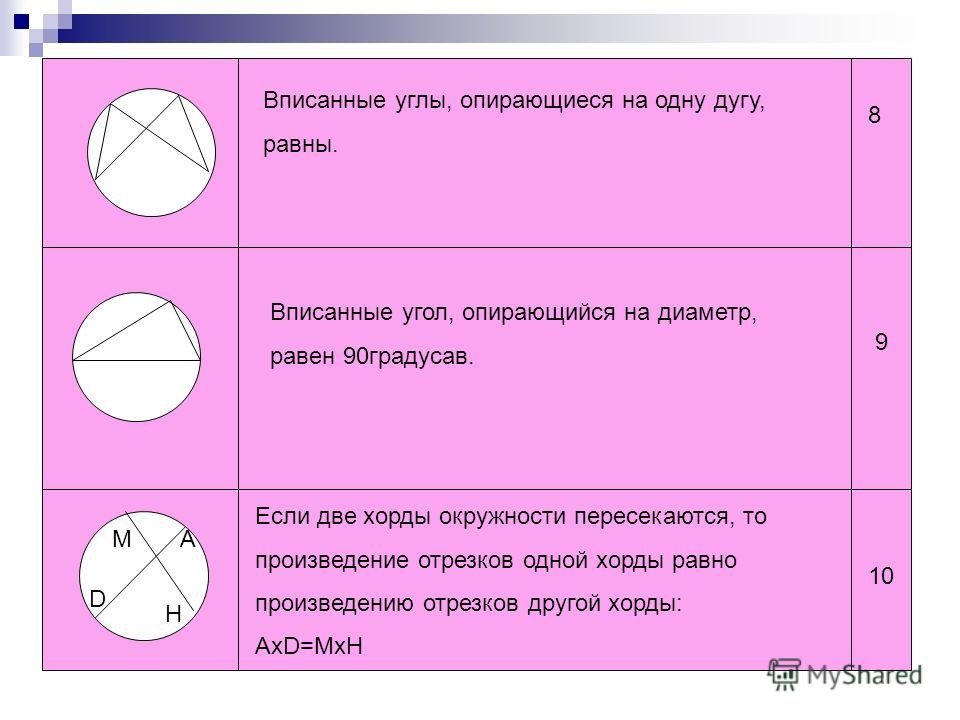
Теорема
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:
Треугольник \(AOB\) – равнобедренный, \(AO = OB\) , \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\) , откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over{AC}\) .
Теперь рассмотрим произвольный вписанный угол \(ABC\) . Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:
1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\)
(для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается).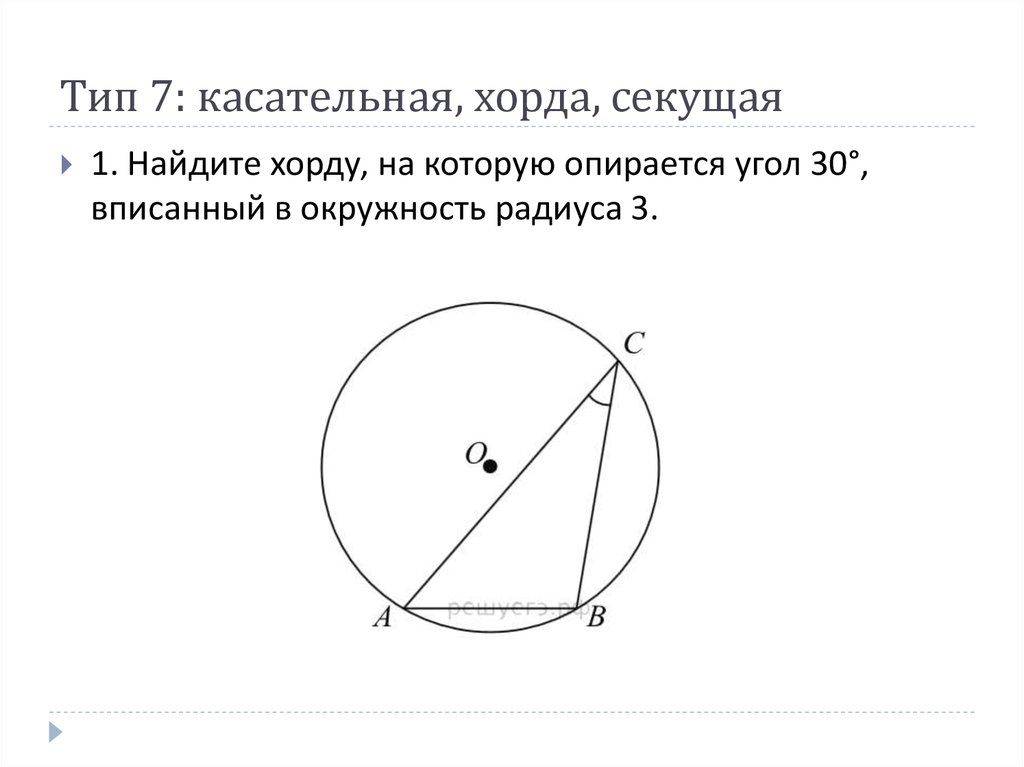 Рис. 1.
Рис. 1.
2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.
Следствия
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на полуокружность, прямой.
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
\[{\Large{\text{Касательная к окружности}}}\]
Определения
Существует три типа взаимного расположения прямой и окружности:
1) прямая \(a\)
пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\)
от центра окружности до прямой меньше радиуса \(R\)
окружности (рис.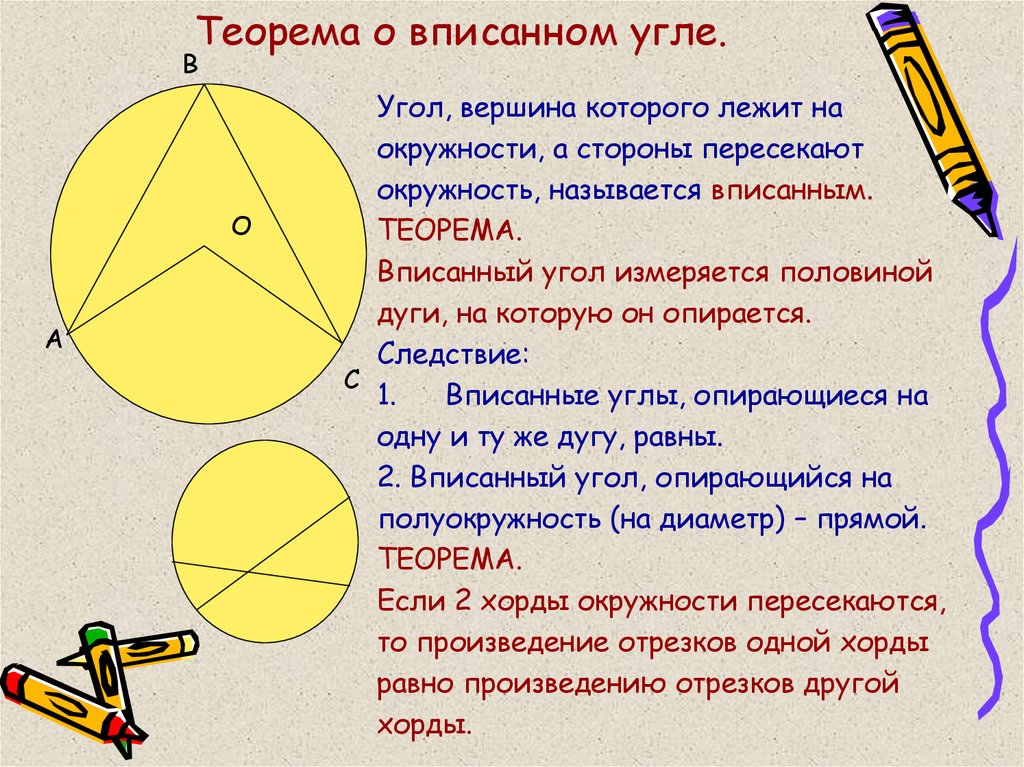 3).
3).
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).
Теорема
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.
Следствие
Отрезки касательных, проведенных из одной точки к окружности, равны.
Доказательство
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\) :
Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\) .
Следствие
Центр окружности \(O\) лежит на биссектрисе угла \(AKB\) , образованного двумя касательными, проведенными из одной точки \(K\) .
\[{\Large{\text{Теоремы, связанные с углами}}}\]
Теорема об угле между секущими
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.
Доказательство
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:
Покажем, что \(\angle DMB = \dfrac{1}{2}(\buildrel\smile\over{BD} — \buildrel\smile\over{CA})\) .
\(\angle DAB\) – внешний угол треугольника \(MAD\) , тогда \(\angle DAB = \angle DMB + \angle MDA\) , откуда \(\angle DMB = \angle DAB — \angle MDA\) , но углы \(\angle DAB\) и \(\angle MDA\) – вписанные, тогда \(\angle DMB = \angle DAB — \angle MDA = \frac{1}{2}\buildrel\smile\over{BD} — \frac{1}{2}\buildrel\smile\over{CA} = \frac{1}{2}(\buildrel\smile\over{BD} — \buildrel\smile\over{CA})\) , что и требовалось доказать.
Теорема об угле между пересекающимися хордами
Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over{AB}+\buildrel\smile\over{CD}\right)\]
Доказательство
\(\angle BMA = \angle CMD\) как вертикальные.
Из треугольника \(AMD\)
: \(\angle AMD = 180^\circ — \angle BDA — \angle
CAD = 180^\circ — \frac12\buildrel\smile\over{AB} — \frac12\buildrel\smile\over{CD}\)
. \circ — \alpha =
\frac12\cdot\buildrel\smile\over{AB}\)
.
\circ — \alpha =
\frac12\cdot\buildrel\smile\over{AB}\)
.
Теорема о дугах, стягиваемых равными хордами
Равные хорды стягивают равные дуги, меньшие полуокружности.
И наоборот: равные дуги стягиваются равными хордами.
Доказательство
1) Пусть \(AB=CD\) . Докажем, что меньшие полуокружности дуги .
По трем сторонам, следовательно, \(\angle AOB=\angle COD\) . Но т.к. \(\angle AOB, \angle COD\) — центральные углы, опирающиеся на дуги \(\buildrel\smile\over{AB}, \buildrel\smile\over{CD}\) соответственно, то \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\) .
2) Если \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\) , то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\) . Следовательно, и \(AB=CD\) .
Теорема
Если радиус делит хорду пополам, то он ей перпендикулярен.
Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.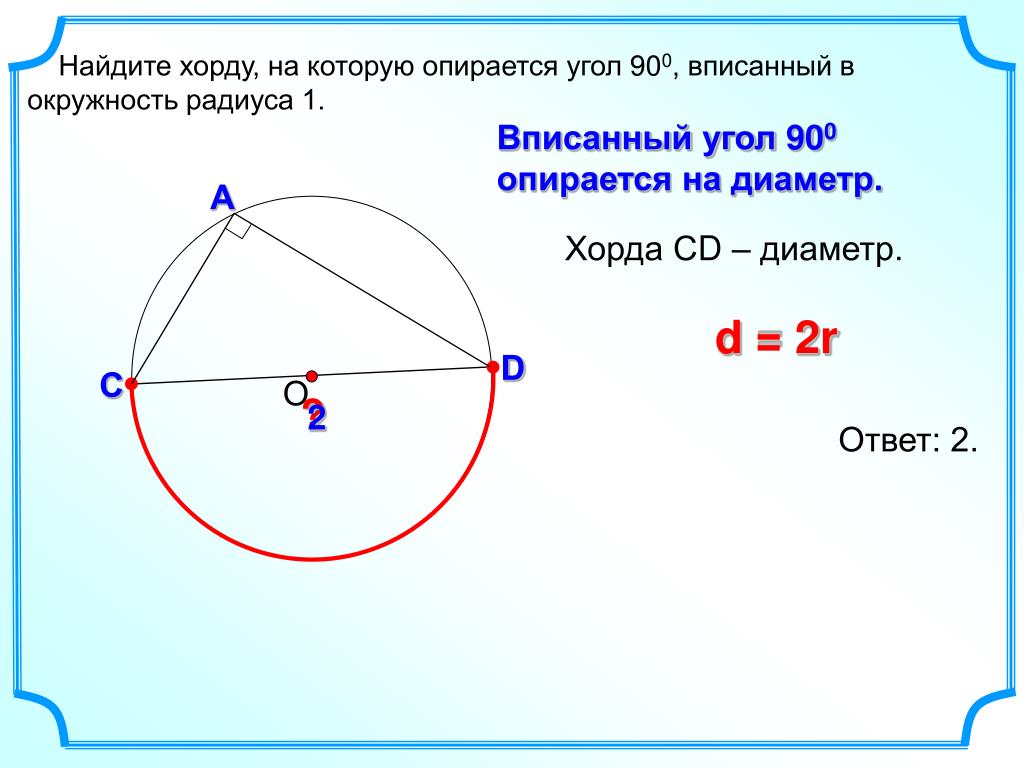
Доказательство
1) Пусть \(AN=NB\) . Докажем, что \(OQ\perp AB\) .
Рассмотрим \(\triangle AOB\) : он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\) .
2) Пусть \(OQ\perp AB\) . Докажем, что \(AN=NB\) .
Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\) .
\[{\Large{\text{Теоремы, связанные с длинами отрезков}}}\]
Теорема о произведении отрезков хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство
Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\) .
Рассмотрим треугольники \(ADE\)
и \(CBE\)
. В этих треугольниках углы \(1\)
и \(2\)
равны, так как они вписанные и опираются на одну и ту же дугу \(BD\)
, а углы \(3\)
и \(4\)
равны как вертикальные.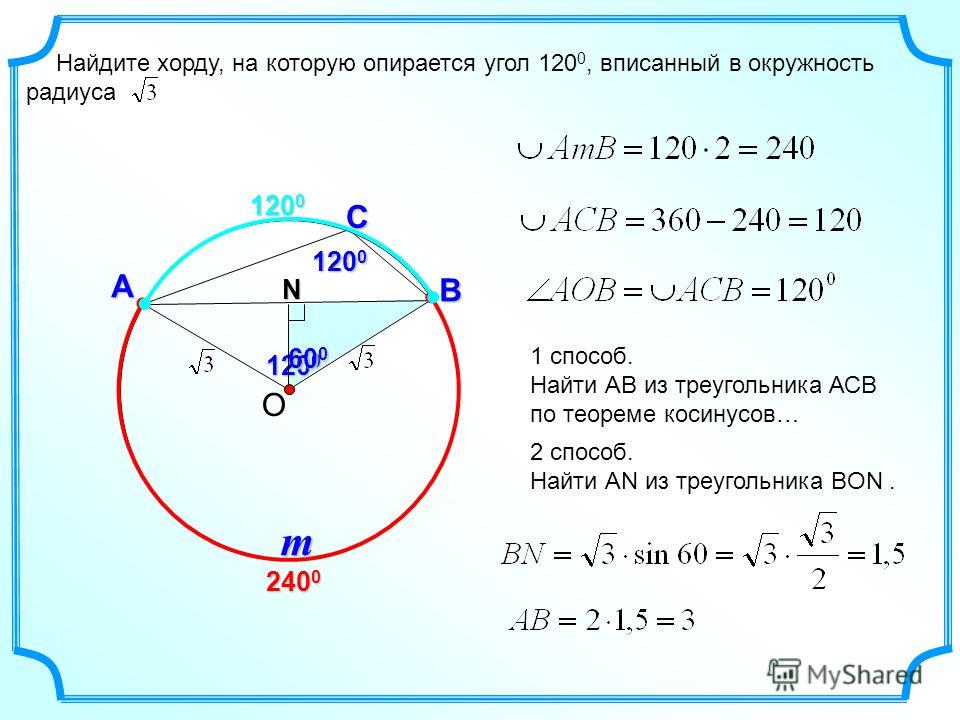 2\)
.
2\)
.
Следствие
Произведение секущей, проведённой из точки \(O\) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\) .
Понятие вписанного и центрально угла
Введем сначала понятие центрального угла.
Замечание 1
Отметим, что градусная мера центрального угла равна градусной мере дуги, на которую он опирается .
Введем теперь понятие вписанного угла.
Определение 2
Угол, вершина которого лежит на окружности и стороны которого пересекают эту же окружность, называется вписанным углом (рис. 2).
Рисунок 2. Вписанный угол
Теорема о вписанном угле
Теорема 1
Градусная мера вписанного угла равняется половине градусной меры дуги, на которую он опирается.
Доказательство.
Пусть нам дана окружность с центром в точке $O$. Обозначим вписанный угол $ACB$ (рис. 2). Возможны три следующих случая:
- Луч $CO$ совпадает с какой либо стороной угла. Пусть это будет сторона $CB$ (рис.
 \circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:
\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:- Луч $CO$ делит внутренний угол на два угла. Пусть он пересекает окружность в точке $D$ (рис. 4).
Рисунок 4.
Получаем
- Луч $CO$ не делит внутренний угол на два угла и не совпадает ни с одной его стороной (Рис. 5).
Рисунок 5.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
Теорема доказана.
Приведем следствия из данной теоремы.
Следствие 1: Вписанные углы, которые опираются на одну и туже дугу равны между собой.
Следствие 2: Вписанный угол, который опирается на диаметр — прямой.
Вписанный угол, теория задачи. Друзья! В этой статье речь пойдёт о заданиях, для решения которых необходимо знать свойства вписанного угла.
 Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.
Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.Есть задачи посложнее, но и они большой трудности для вас не представят, необходимо знать свойства вписанного угла. Постепенно мы разберём все прототипы задач, приглашаю вас на блог!
Теперь необходимая теория. Вспомним, что такое центральный и вписанный угол, хорда, дуга, на которые опираются эти углы:
Центральным углом в окружности называется плоский угол с вершиной в ее центре .
Часть окружности, расположенная внутри плоского угла, называется дугой окружности.
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность.
Отрезок соединяющий две точки окружности называется хордой . Самая большая хорда проходит через центр окружности и называется диаметр.

Для решения задач на вписанные в окружность углы, вам необходимо знать следующие свойства:
1. Вписанный угол равен половине центрального, опирающегося на ту же дугу.
2. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.
3. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.
4. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.
Следствие: противолежащие углы четырёхугольника вписанного в окружность в сумме составляют 180 градусов.
5. Все вписанные углы, опирающиеся на диаметр, прямые.
Вообще, это свойство является следствием из свойства (1), это его частный случай. Посмотрите – центральный угол равен 180 градусам (и этот развёрнутый угол есть не что иное, как диаметр), значит по первому свойству вписанный угол С равен его половине, то есть 90 градусам.

Знание данного свойства помогает в решении многих задач и часто позволяет избежать лишних расчётов. Хорошо усвоив его — вы более половины задач такого типа сможете решать устно. Два следствие, которые можно сделать:
Следствие 1: если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным (вершина прямого угла лежит на окружности).
Следствие 2: центр описанной около прямоугольного треугольника окружности совпадает с серединой его гипотенузы.
Многие прототипы стереометрических задач также решаются благодаря использованию этого свойства и данных следствий. Запомните сам факт: если диаметр окружности является стороной вписанного треугольника, то этот треугольник прямоугольный (угол лежащий против диаметра равен 90 градусов). Все остальные выводы и следствия вы сможете сделать сами, учить их не надо.
Как правило, половина задач на вписанный угол даётся с эскизом, но без обозначений.
 Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать.
Рассмотрим задачи:
Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать.
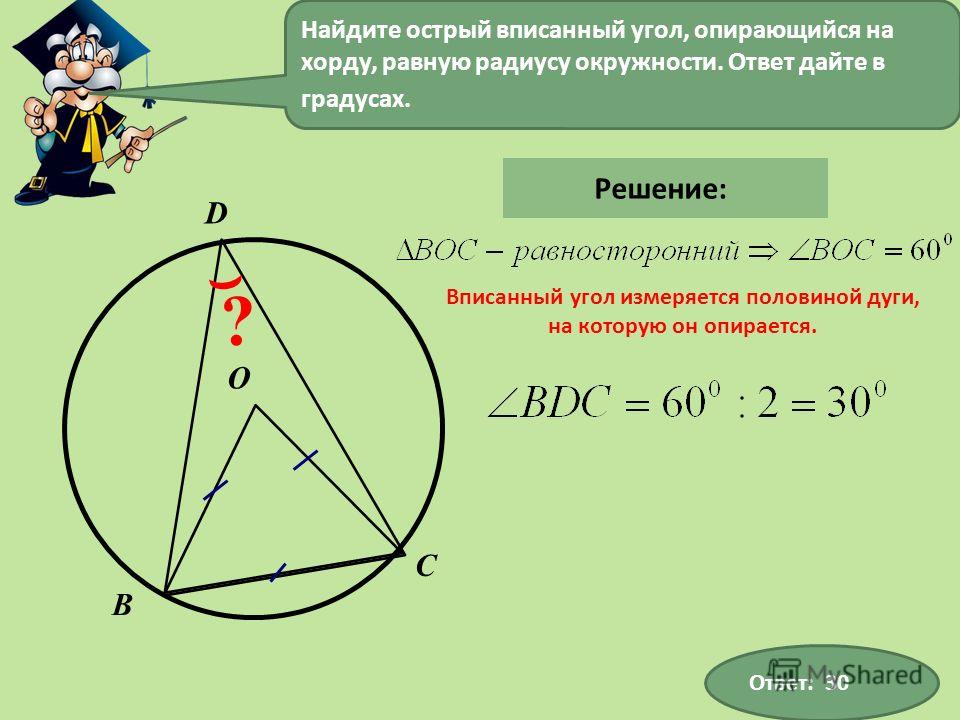
Рассмотрим задачи:Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Построим центральный угол для заданного вписанного угла, обозначим вершины:
По свойству вписанного в окружность угла:
Угол АОВ равен 60 0 , так как треугольник АОВ равносторонний, а в равностороннем треугольнике все углы равны по 60 0 . Стороны треугольника равны, так как в условии сказано, что хорда равна радиусу.
Таким образом, вписанный угол АСВ равен 30 0 .
Ответ: 30
Найдите хорду, на которую опирается угол 30 0 , вписанный в окружность радиуса 3.
Это по сути обратная задача (предыдущей). Построим центральный угол.
Он в два раза больше вписанного, то есть угол АОВ равен 60 0 . От сюда можно сделать вывод, что треугольник АОВ равносторонний.
 Таким образом, хорда равна радиусу, то есть трём.
Таким образом, хорда равна радиусу, то есть трём.Ответ: 3
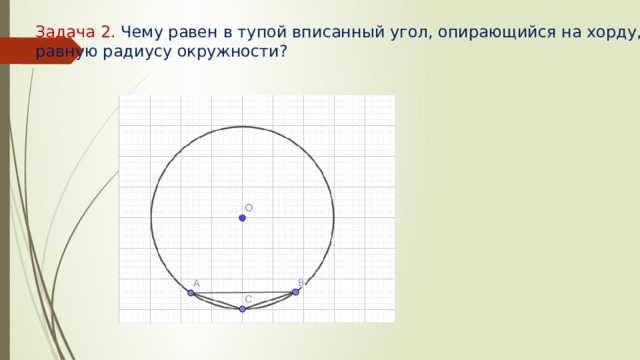
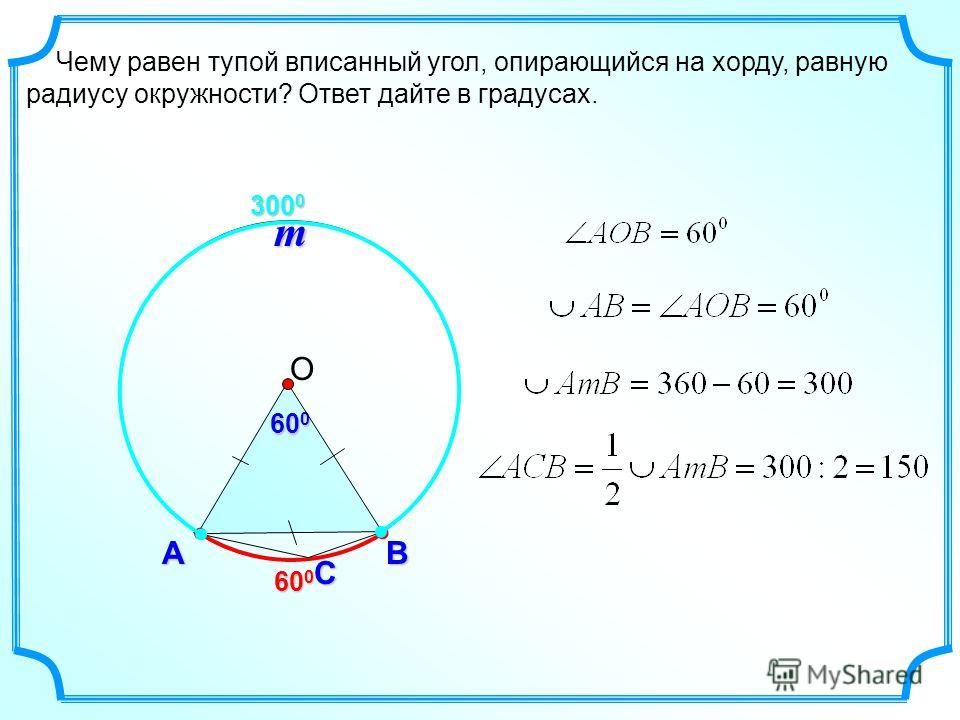
Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.
Построим центральный угол:
Зная радиус и хорду мы можем найти центральный угол АСВ. Это можно сделать по теореме косинусов. Зная центральный угол мы без труда найдём вписанный угол АСВ.
Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Следовательно, второй центральный угол равен 360 0 – 90 0 = 270 0 .
Угол АСВ по свойству вписанного угла равен его половине, то есть 135 градусам.
Ответ: 135
Найдите хорду, на которую опирается угол 120 градусов, вписанный в окружность радиуса корень из трёх.
Соединим точки А и В с центром окружности. Обозначим её как О:
Нам известен радиус и вписанный угол АСВ.
 Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.
Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.По свойству вписанного угла центральный угол АОВ (который больше 180 градусов) будет равен вдвое больше вписанного, то есть 240 градусам. Значит, угол АОВ в треугольнике АОВ равен 360 0 – 240 0 = 120 0 .
По теореме косинусов:
Ответ:3
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.
По свойству вписанного угла он вдвое меньше центрального угла, опирающегося на ту же дугу, в данном случае речь идёт о дуге АВ.
Сказано, дуга АВ составляет 20 процентов от окружности. Это означает, что центральный угол АОВ составляет так же 20 процентов от 360 0 . *Окружность это угол в 360 градусов. Значит,
Таким образом, вписанный угол АСВ равен 36 градусам.
Ответ: 36
Дуга окружности AC , не содержащая точки B , составляет 200 градусов.
 А дуга окружности BC, не содержащая точки A , составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.
А дуга окружности BC, не содержащая точки A , составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.Обозначим для наглядности дуги, угловые меры которых даны. Дуга соответствующая 200 градусам – синий цвет, дуга соответствующая 80 градусам – красный цвет, оставшаяся часть окружности – жёлтый цвет.
Таким образом, градусная мера дуги АВ (жёлтый цвет), а значит и центральный угол АОВ составляет: 360 0 – 200 0 – 80 0 = 80 0 .
Вписанный угол АСВ вдвое меньше центрального угла АОВ,то есть равен 40 градусам.
Ответ: 40
Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Теоремы о круге — Математика GCSE Revision
Теоремы
В этом разделе объясняется теорема о круге, включая касательные, сектора, углы и доказательства.
В приведенном ниже видео показаны правила, которые необходимо запомнить для работы с теоремами о кругах.

Равнобедренный треугольник
Два радиуса и хорда образуют равнобедренный треугольник.
Перпендикулярная хорда пополам
Перпендикуляр из центра окружности к хорде всегда делит хорду пополам (делит ее на две равные части). Углы, опирающиеся на одну дугу
Угол в полуокружности
Углы, образованные проведением линий от концов диаметра круга к его окружности, образуют прямой угол. Так c — прямой угол .
Доказательство
Мы можем разделить треугольник пополам, проведя линию из центра круга в точку на окружности, которой касается наш треугольник.
Мы знаем, что все линии, являющиеся радиусом окружности (зеленые линии), имеют одинаковую длину.
 Следовательно, каждый из двух треугольников равнобедренный и имеет пару равных углов.
Следовательно, каждый из двух треугольников равнобедренный и имеет пару равных углов.Но сумма всех этих углов должна составлять 180°, поскольку они являются углами исходного большого треугольника.
Следовательно, x + y + x + y = 180, другими словами, 2(x + y) = 180.
и, следовательно, x + y = 90. Но x + y — это величина угла, который мы хотели найти.Касательные
Касательная к окружности — это прямая, которая касается окружности только в одной точке (поэтому она не пересекает окружность, а только касается ее).
Касательная к окружности образует прямой угол с радиусом окружности в точке касания.
Кроме того, если на окружности проведены две касательные и они пересекаются, длины двух касательных (от точки, где они касаются окружности, до точки, где они пересекаются) будут одинаковыми.
Угол в центре
Угол, образованный в центре круга линиями, исходящими из двух точек на окружности, в два раза больше угла, образованного на окружности круга линиями, исходящими из той же точки.
 точки. то есть а = 2b .
точки. то есть а = 2b .Доказательство
Возможно, вам придется доказать этот факт:
OA = OX, так как оба они равны радиусу окружности. Таким образом, треугольник AOX равнобедренный, поэтому ∠OXA = a
Аналогично, ∠OXB = bПоскольку сумма углов треугольника равна 180, мы знаем, что ∠XOA = 180 — 2a
Аналогично, ∠BOX = 180 — 2b
Поскольку сумма углов вокруг точки равна 360, имеем, что ∠AOB = 360 — ∠XOA — ∠BOX
= 360 — (180 — 2a) — (180 — 2b)
= 2a + 2b = 2(a + b) = 2 ∠AXBТеорема об альтернативных сегментах
На этой диаграмме показана теорема об альтернативных сегментах . Короче говоря, красные углы равны друг другу, а зеленые углы равны друг другу.
Доказательство
Возможно, вам придется доказать теорему об альтернативном отрезке:
Мы используем факты о связанных углах
Касательная с радиусом окружности 90 , поэтому мы знаем, что ∠OAC + x = 90.

Угол в полуокружности равен 90, поэтому ∠BCA = 90.
Сумма углов треугольника равна 180, поэтому ∠BCA + ∠OAC + y = 180
Следовательно, 90 + ∠OAC + y = 180 и, следовательно, ∠OAC + y = 90
Но OAC + x = 90, поэтому ∠OAC + x = ∠OAC + y
Следовательно, x = yВписанные четырехугольники
четырехугольник, касающийся окружности окружности. Противоположные углы такого четырехугольника в сумме составляют 180 градусов.
Площадь сектора и длина дуги
Если радиус круга равен r,
Площадь сектора = πr 2 × A/360
Длина дуги = 2πr × A/360Другими словами, площадь сектора = площадь круга × A/360
длина дуги = длина окружности × A/360Для получения дополнительной информации в определениях окружностей нажмите здесь
Дуги и стягиваемые углы | Решенные примеры | Геометрия
В окружности есть различные углы, которые могут быть образованы при соединении концов дуг, и эти углы называются вытянутыми углами.
 Существуют разные категории углов, образованных этими дугами, например, углы в одном отрезке, углы в полуокружности, углы на окружности и т.д. Давайте узнаем об этом подробно в этом уроке.
Существуют разные категории углов, образованных этими дугами, например, углы в одном отрезке, углы в полуокружности, углы на окружности и т.д. Давайте узнаем об этом подробно в этом уроке.1. Как найти угол, образуемый дугой окружности? 2. Угол, опирающийся на дугу в центре 3. Углы на одном отрезке окружности равны Как найти угол, образуемый дугой окружности?
дуга окружности — это любая часть окружности. 9Угол 0004, опирающийся на дугу в любой точке, – это угол, образованный между двумя отрезками, соединяющими эту точку с конечными точками дуги. На следующем рисунке показанная дуга окружности образует угол α в точке окружности и угол β в центре O.
на окружность и угол, на который эта дуга опирается в центре окружности. Связь между ними проста и чрезвычайно важна.

Угол, опирающийся на дугу в центре
В центре круга, если есть два отрезка прямой, исходящие из конечных точек дуги пересечения окружности, этот угол называется углом, опирающимся на дугу в центре. Разберемся с теоремой и ее доказательством на ее основе.
Теорема:
Угол, образуемый дугой окружности в ее центре, в два раза больше угла, который она образует в любой точке окружности.
Доказательство этой теоремы довольно простое и использует теорему о внешнем угле – внешний угол треугольника равен сумме противоположных внутренних углов. Если два противоположных внутренних угла равны, то внешний угол будет вдвое больше любого из противолежащих внутренних углов.
Доказательство:
Рассмотрим следующий рисунок, на котором дуга (или сегмент) AB стягивает ∠AOB в центре O и ∠ACB в точке C на окружности.
Нам нужно доказать, что ∠AOB = 2 × ∠ACB. Проведите линию через О и С и дайте ей снова пересечь окружность в точке D, как показано на рисунке.

Имеются два треугольника, образованные ΔOAC и ΔOBC. Итак, делаем следующие наблюдения.
1. В ΔOAC ∠OAC = ∠OCA, поскольку OA = OC
2. В ΔOBC ∠OBC = ∠OCB, поскольку OB = OC.
Отсюда, используя теорему о внешнем угле, получаем :
∠AOD+ ∠DOB= 2× (∠ACO+ ∠OCB)
⇒ ∠AOB= 2× ∠ACB
Это завершает доказательство теоремы. Вы можете поэкспериментировать с симуляцией ниже, чтобы понять взаимосвязь между углами, стягиваемыми дугой в центре и в точке на окружности.
Что, если дуга AB такова, что образует рефлекторный угол в центре? Что ж, наше доказательство не меняется, как показано на следующем рисунке.
Теперь вы можете применить те же шаги, что и раньше, и получить тот же результат: ∠AOB= 2× ∠ACB. Другая конфигурация была бы, когда O не лежит в пределах ∠ACB. Сохранится ли результат, как показано на следующем рисунке?
Да, будет. Снова соедините C с O и расширьте его до D по окружности круга.

Снова воспользуемся теоремой о внешнем угле и заметим, что эти углы не выделены на рисунке, но внимательно соблюдайте их. Вычтите уравнение (2) из (1)
∠BOD- ∠AOD= 2× (∠BCD- ∠ACD)
⇒ ∠AOB= 2× ∠ACB
Эта теорема приводит к интересному следствию, которое обсуждается далее.
Следствие:
Угол в полуокружности прямой. Рассмотрим рисунок ниже, где AB — диаметр окружности. Нам нужно доказать, что ЧАКБ = 90 ∘
Доказательство:
Поскольку ♂AOB = 180 º , ладк = 1/2 × nTAOB = 90 º
Это и LEADEM. следующий результат.
Углы на одном отрезке окружности равны
В круге есть два сегмента — большие сегменты и второстепенные сегменты. Углы, образованные концами хорды как на большом, так и на малом отрезках, всегда равны. Давайте разберемся в этой теореме и ее доказательстве в деталях.
Теорема:
Углы на одном отрезке окружности равны.
 Другими словами, дуга окружности образует равные углы в любом месте окружности. Рассмотрим следующий рисунок, на котором показана дуга AB, образующая углы ACB и ADB в двух произвольных точках C и D на окружности. О — центр круга.
Другими словами, дуга окружности образует равные углы в любом месте окружности. Рассмотрим следующий рисунок, на котором показана дуга AB, образующая углы ACB и ADB в двух произвольных точках C и D на окружности. О — центр круга.Нам нужно доказать, что ∠ACB= ∠ADB.
Доказательство:
Используя нашу предыдущую теорему, мы имеем, что ) и (2), получаем ∠ACB= ∠ADB.
Важные примечания:
- Конгруэнтные дуги окружности образуют равные углы в центре.
- Угол, образуемый дугой в центре, в два раза больше угла, образуемого дугой в любой точке оставшейся части окружности.
- Углы одного сегмента окружности равны.
- Угол в полуокружности является прямым углом.
Аналитический центр:
- Если углы, образуемые хордами окружности в центре, равны, равны ли хорды?
- Хорды конгруэнтных окружностей образуют равные углы в своих центрах.
 Аккорды равны?
Аккорды равны?
Часто задаваемые вопросы по дугам и вытянутым углам
Что означает слово Subtended?
В геометрии стягиваемый означает продолжение под. Стягивающий угол образуется при пересечении более чем одной линии или лучей, соединяющих конечные точки линии или дуги.
Что такое вытянутый центральный угол?
Вытянутый центральный угол — это угол, образованный в центре окружности, а катеты угла — это радиусы окружности, пересекающие окружность в двух разных точках.
Как найти угол, образуемый дугой в центре?
Чтобы найти значение угла, образуемого дугой в центре, мы должны умножить угол, образованный через те же концы дуги на окружности, на два. Например, если угол, образуемый в любой точке окружности, равен 60 º , это означает, что угол, образуемый той же дугой в центре, равен 120 º .
Что такое центральный угол окружности?
Центральный угол окружности — это угол, вершина которого совпадает с центром окружности.


 \circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:
\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем: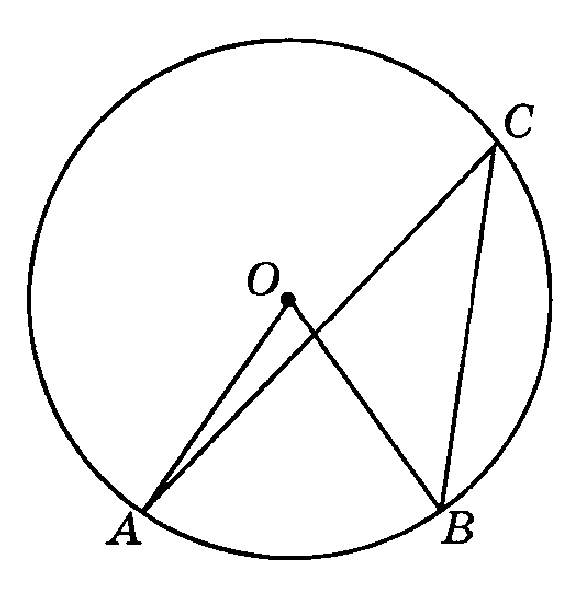 Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.
Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.

 Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать.
Рассмотрим задачи:
Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать.
Рассмотрим задачи: Таким образом, хорда равна радиусу, то есть трём.
Таким образом, хорда равна радиусу, то есть трём. Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.
Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ. А дуга окружности BC, не содержащая точки A , составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.
А дуга окружности BC, не содержащая точки A , составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.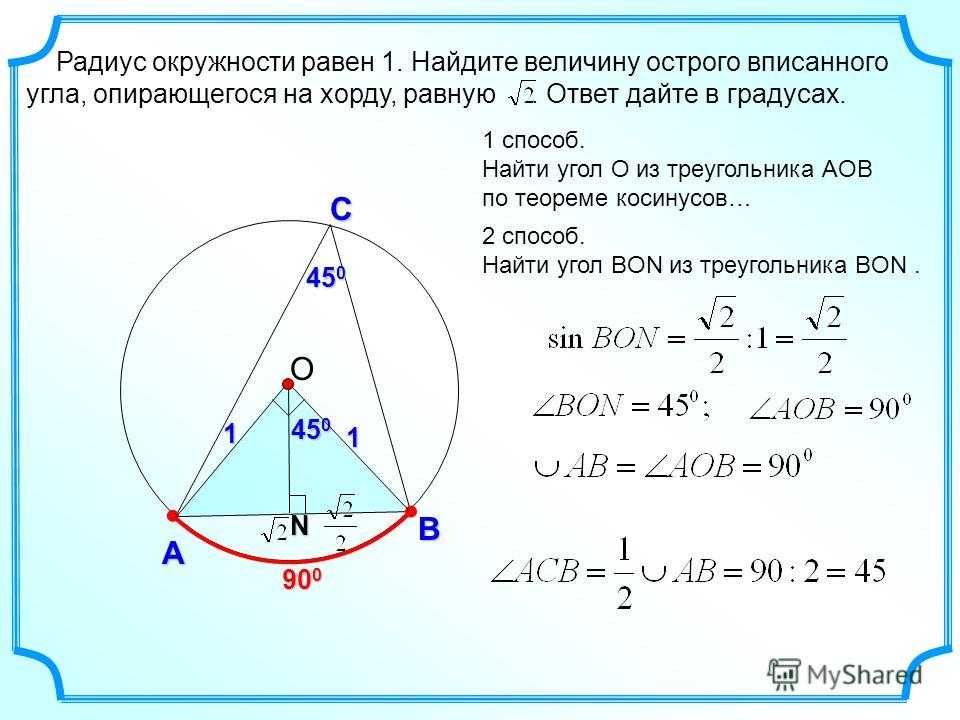
 Следовательно, каждый из двух треугольников равнобедренный и имеет пару равных углов.
Следовательно, каждый из двух треугольников равнобедренный и имеет пару равных углов.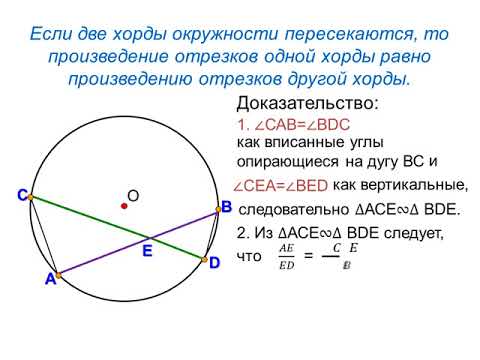 точки. то есть а = 2b .
точки. то есть а = 2b .
 Существуют разные категории углов, образованных этими дугами, например, углы в одном отрезке, углы в полуокружности, углы на окружности и т.д. Давайте узнаем об этом подробно в этом уроке.
Существуют разные категории углов, образованных этими дугами, например, углы в одном отрезке, углы в полуокружности, углы на окружности и т.д. Давайте узнаем об этом подробно в этом уроке.

 Другими словами, дуга окружности образует равные углы в любом месте окружности. Рассмотрим следующий рисунок, на котором показана дуга AB, образующая углы ACB и ADB в двух произвольных точках C и D на окружности. О — центр круга.
Другими словами, дуга окружности образует равные углы в любом месте окружности. Рассмотрим следующий рисунок, на котором показана дуга AB, образующая углы ACB и ADB в двух произвольных точках C и D на окружности. О — центр круга.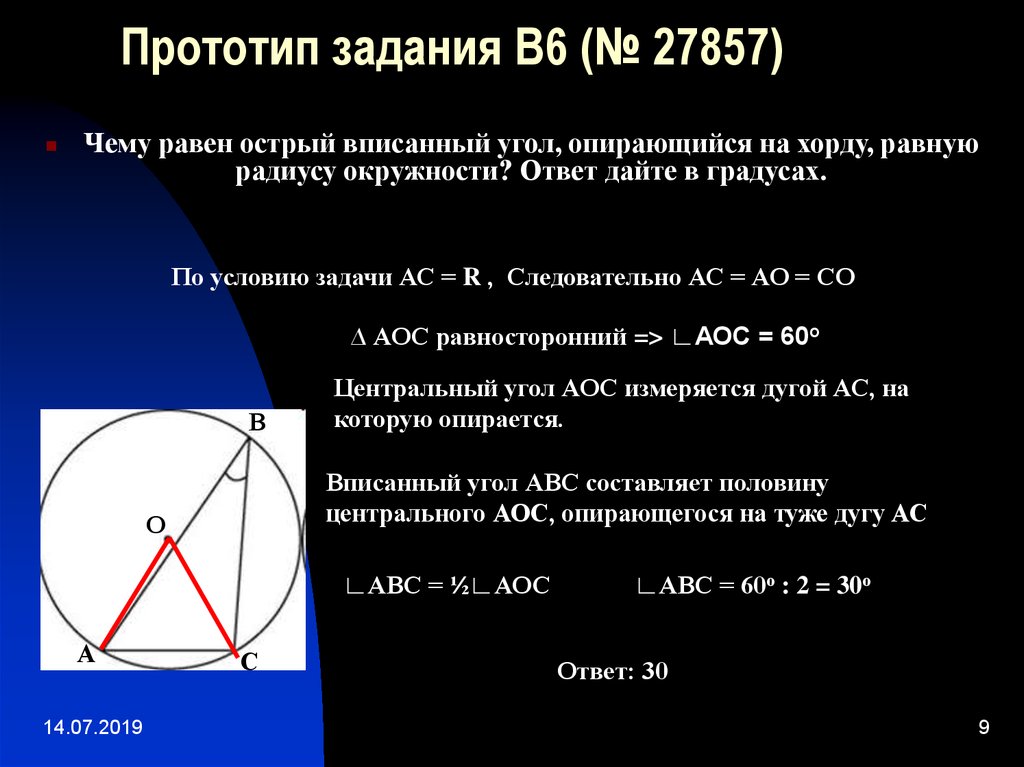 Аккорды равны?
Аккорды равны?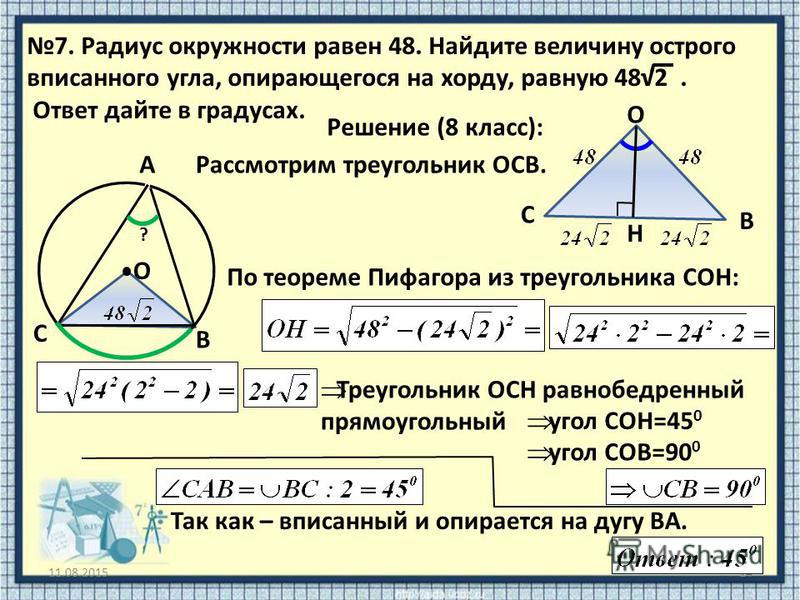
Leave A Comment