Вариант 20. Часть 1. Задание 5. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите указать номера – Рамблер/класс
Вариант 20. Часть 1. Задание 5. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите указать номера – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
На рисунках изображены графики функций вида у = aх
Установите соответствие между графиками функций и знаками коэффициентов а и с.
1) а>0, с<0 2) а<0, с>0 3) а>0, с>0
В таблице под каждой буквой укажите соответствующий номер.
ответы
Ответ:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Олимпиады
Экзамены
Оценки
3 класс
похожие вопросы 5
Решите уравнение 5х2+ 20х = 0.
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
ГДЗМатематикаОГЭ9 классЯщенко И.В.
Вариант 13.
Часть 1. Задание 12. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Найдите расстояние от точки до середины отрезка
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: А, В и С. Найдите расстояние от точки А до середины отрезка ВС.
(Подробнее…)
ГДЗМатематикаОГЭ9 классЯщенко И.В.
ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№33. Зад.№14.Под руководством Ященко. Помогите поставить в соответствие.
Здравствуйте! На рисунке изображён график функции у =f(х). Точки a, b, с, d и е задают на оси х четыре интервала. Помогите пользуясь (Подробнее…)
ГДЗЭкзаменыМатематикаЯщенко И.В.
2. В чем заключается принцип Ферма? Громов, Шаронова 11 класс Физика. Вопросы к параграфу 1
2. В чем заключается принцип Ферма?
ГДЗФизикаГромов С.В.11 класс
ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№34. Зад.№13.Под руководством Ященко.
Здравствуйте! В сосуде, имеющем форму конуса, уровеньжидкости достигает 1/3 высоты. Объём сосударавен 270 мл. Чему равен объём (Подробнее…)
ГДЗЭкзаменыМатематикаЯщенко И.В.
Вероятность выпадения кубика. Игра в кости Вероятность IV
Цели урока:
Учащиеся должны знать:
- определение вероятности случайного события;
- уметь решать задачи на нахождение вероятности случайного события;
- уметь применять теоретические знания на практике.
Цели урока:
Образовательная: создать условия для овладения учащимися системой знаний, умений и навыков с понятиями о вероятности события.
Образовательная: формировать у учащихся научное мировоззрение
Развивающая: развивать у учащихся познавательный интерес, творческие способности, волю, память, речь, внимание, воображение, восприятие.
Методы организации учебно-познавательной деятельности:
- наглядная,
- практичный,
- по умственной деятельности: индуктивная,
- на усвоение материала: частично ознакомительный, репродуктивный,
- по степени самостоятельности: самостоятельная работа,
- стимулирующие: награды,
- видов контроля: проверка самостоятельно решаемых задач.
План урока
- Устные упражнения
- Изучение нового материала
- Решение задач.
- Самостоятельная работа.
- Подведение итогов урока.
- Комментирование домашнего задания.
Оборудование: мультимедийный проектор (презентация), карточки (самостоятельная работа)
Во время занятий
I. Организационный момент.
Организация занятий на протяжении всего урока, готовность учащихся к уроку, порядок и дисциплина.
Постановка целей обучения учащимся, как на весь урок, так и на отдельные его этапы.
Определить значимость изучаемого материала, как в данной теме, так и во всем курсе.
II. Повторение
1. Что такое вероятность?
Вероятность – возможность осуществления, осуществимость чего-либо.
2. Какое определение дал основоположник современной теории вероятностей А.Н. Колмогоров?
Математическая вероятность — числовая характеристика степени возможности наступления определенного события в определенных определенных условиях, которое может повторяться неограниченное число раз.
3. Какое классическое определение вероятности дают авторы школьных учебников?
Вероятность P(A) события А в испытании с равновозможными элементарными исходами есть отношение числа исходов m, благоприятных для события А, к числу n всех исходов испытания.
Вывод: в математике вероятность измеряется числом.
Сегодня мы продолжим рассмотрение математической модели «Игральная кость».
Предметом исследования в теории вероятностей являются события, возникающие при определенных условиях, которые могут воспроизводиться неограниченное количество раз. Каждая реализация этих условий называется тестом.
Тест — бросание игральных костей.
Событие — падение шестерки или выпадает из четного числа точек.
Каждая грань с одинаковой вероятностью выпадет при нескольких бросках костей (кубик правильный).
III. Вербальное решение проблемы.
1. Игральная кость (кубик) бросается один раз.
Какова вероятность того, что выпадет 4 очка?
Раствор. Случайный эксперимент — бросание игральной кости. Событие — число на выпавшем лице. Всего шесть лиц. Перечислим все события: 1, 2, 3, 4, 5, 6. Итак, NS = 6. Событие А = (выпало 4 очка) одно событие благоприятствует: 4. Следовательно, T = 1. События равновозможны, так как предполагается, что кость честная. Следовательно, Р(А) = т/н
2. Кости (кубики) подбрасываются один раз. Какова вероятность того, что будет набрано не более 4 очков?
NS = 6. Событие А = (выпало не более 4 баллов) предпочтение отдается 4 событиям: 1, 2, 3, 4. Следовательно, T = 4. Следовательно, P(A) = t/n = 4/6 = 0,67.
3. Кости (кубики) подбрасываются один раз. Какова вероятность того, что выпадет менее 4 очков?
Раствор. Случайный эксперимент — бросание игральной кости. Событие — число на выпавшем лице. Означает NS = 6. Событие A = (выпало менее 4 баллов) благоприятствует 3 событиям: 1, 2, 3.
Следовательно,
4. Кости (кубики) подбрасываются один раз. Какова вероятность нечетного количества очков?
Решение. Случайный эксперимент — бросание игральной кости. Событие — число на выпавшем лице. Означает NS = 6. Событие A = (выпало нечетное количество очков) благоприятствует 3 событиям: 1,3,5. Вот почему Т = 3. Р(А) = т/н = 3/6 = 0,5.
IV. Изучение нового
Сегодня мы рассмотрим задачи, когда в случайном эксперименте используются две игральные кости или производится два-три броска.
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Округлите ответ до сотых 9.0079 .
Раствор. Конечным результатом этого опыта является упорядоченная пара чисел. Первое число выпадет на первом кубике, второе — на втором. Многие результаты удобно представить в виде таблицы.
Строки соответствуют количеству очков на первом кубике, столбцы — на втором кубике. Всего элементарных событий NS = 36.
| 1 | 2 | 3 | 5 | 6 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Запишем в каждую ячейку сумму выпавших очков и закрасим ячейки, где сумма равна 6.
Таких ячеек 5. Это означает, что событию A = (сумма выпавших очков равна 6) благоприятствуют 5 исходов. Отсюда Т = 5. Следовательно, Р(А) = 5/36 = 0,14.
2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме будет 3 очка. Округлите результат до сотых .
NS = 36.
Событие A = (сумма 3) 2 исхода в пользу. Отсюда T = 2.
Следовательно, P(A) = 2/36 = 0,06.
3. В случайном эксперименте бросают две игральные кости. Найти вероятность того, что сумма будет больше 10 очков. Округлите результат до сотых .
Раствор. Конечным результатом этого опыта является упорядоченная пара чисел. Всего событий NS = 36.
Событие A = (всего более 10 очков) благоприятствуют 3 исходам.
Отсюда T
4. Люба дважды бросает кости. Всего она набрала 9 баллов. Найти вероятность того, что в одном из бросков будет 5 очков .
Решение Результатом этого эксперимента является упорядоченная пара чисел.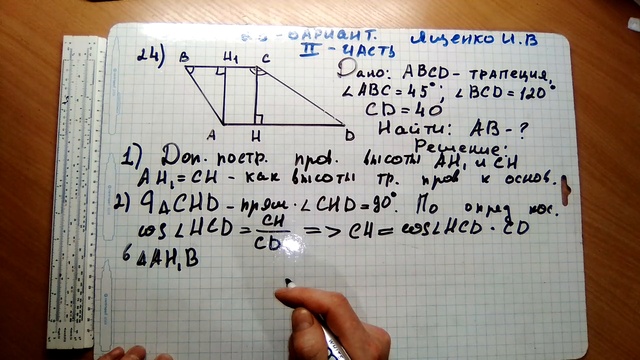
Первый номер выпадет при первом броске, второй — при втором. Многие результаты удобно представить в виде таблицы.
Строки соответствуют результату первого броска, столбцы — результату второго броска.
Всего событий, для которых сумма очков равна 9, будет NS = 4. Событие A = (при одном из бросков выпало 5 очков) благоприятствует 2 исходам. Отсюда T = 2.
Следовательно, P(A) = 2/4 = 0,5.
5. Света дважды бросает кости. Всего она набрала 6 баллов. Найти вероятность того, что один из бросков принесет 1 очко.
Первый бросок | Второе литье | Всего баллов | ||
Равновозможных исходов — 5.
Вероятность события p = 2/5 = 0,4.
6. Оля дважды бросает кубик. Всего она набрала 5 баллов. Найти вероятность того, что при первом броске выпало 3 очка.
Первый бросок | Второе литье | Всего баллов | ||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = |
Равновозможных исходов — 4.
Благоприятных исходов — 1.
Вероятность события R = 1/4 = 0,25.
7. Наташа и Витя играют в кости. Они бросают кубик один раз.
Победитель тот, кто накинул больше всего очков. Если очки делятся поровну, то происходит ничья. Всего было сброшено 8 очков. Найдите вероятность того, что Наташа выиграла.
Всего баллов | ||||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = |
Равновозможные исходы — 5.
Благоприятные исходы — 2.
Вероятность события Р = 2/5 = 0,4.
8. Таня и Наташа играют в кости. Они бросают кубик один раз. Победителем становится тот, кто накинул больше всех очков. Если очки делятся поровну, то происходит ничья. Всего выпало 6 очков. Найдите вероятность того, что Таня проиграла.
| Таня | Наташа | Всего очков | ||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = | |||
| + | = |
Равновозможные исходы — 5.
Благоприятные исходы — 2.
Вероятность события Р = 2/5 = 0,4.
9. Коля и Лена играют в кости. Они бросают кубик один раз. Выигрывает тот, кто накинул больше всех очков. Если очки делятся поровну, то происходит ничья. Коля бросил первым, набрав 3 очка. Найдите вероятность того, что Лена не выиграет.
Коля получил 3 очка.
Лена имеет 6 равновозможных исходов.
Исходы, благоприятные для проигрыша — 3 (при 1 и при 2 и при 3).
Вероятность события R = 3/6 = 0,5.
10. Маша бросает кости три раза. Какова вероятность того, что все три раза четные числа.
Маша имеет равновозможные исходы — 6 6 6 = 216.
Исходы, благоприятные для проигрыша — 3 · 3 · 3 = 27.
Вероятность события R = 27/216 = 1/8 = 0,125.
11. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме будет 16 очков. Округлите результат до сотых.
Решение.
| Второй | Третий | Всего очков | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = | ||||
| + | + | = |
Равновозможные исходы — 6 6 6 = 216.
Благоприятные исходы — 6.
Вероятность события R = 6/216 = 1/36 = 0,277 … = 0,28. Отсюда Т = 3. Следовательно, Р(А) = 3/36 = 0,08.
В. Самостоятельная работа.
Вариант 1.
- Кубик бросается один раз. Какова вероятность того, что будет набрано не менее 4 очков? (ответ: 0,5)
- В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме будет 5 очков. Округлите результат до сотых. (ответ: 0,11)
- Аня дважды бросает кости. Всего она получила 3 балла. Найти вероятность того, что при первом броске будет набрано 1 очко. (ответ: 0,5)
- Катя и Ира играют в кости. Они бросают кубик один раз. Победителем становится тот, кто накинул больше всех очков. Если очки делятся поровну, то происходит ничья. Всего выпало 9 очков. Найдите вероятность того, что Ира проиграл. (ответ: 0,5)
- В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме будет 15 очков. Округлите результат до сотых. (ответ: 0,05)
Найдите вероятность того, что в сумме будет 15 очков. Округлите результат до сотых. (ответ: 0,05)Вариант 2.
- Кубик бросается один раз. Какова вероятность того, что будет набрано не более 3 очков? (ответ: 0,5)
- В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что всего будет разыграно 10 очков. Округлите результат до сотых. (ответ: 0,08)
- Женя дважды бросает кости. Всего она набрала 5 баллов. Найти вероятность того, что при первом броске выпало 2 очка. (ответ: 0,25)
- Маша и Даша играют в кости. Они бросают кубик один раз. Победителем становится тот, кто накинул больше всех очков. Если очки делятся поровну, то происходит ничья. Всего было сброшено 11 очков. Найдите вероятность того, что Маша выиграла. (ответ: 0,5)
- В случайном эксперименте бросают три игральные кости. Найти вероятность того, что в сумме будет 17 очков. Округлить результат
Ви.
Домашнее задание
- В случайном эксперименте бросают три игральные кости. Всего было снято 12 очков. Найти вероятность того, что при первом броске выпало 5 очков. Округлите результат до сотых.
- Катя бросает кости три раза. Какова вероятность того, что все три раза будет одно и то же число?
VII. Итог урока
Что нужно знать, чтобы найти вероятность случайного события?
Для расчета классической вероятности необходимо знать все возможные исходы события и благоприятные исходы.
Классическое определение вероятности применимо только к событиям с равновероятными исходами, что ограничивает его область применения.
Зачем мы изучаем теорию вероятностей в школе?
Многие явления окружающего нас мира поддаются описанию только с помощью теории вероятностей.
Литература
- Алгебра и начало математического анализа. 10-11 классы: учеб. для общеобразовательных учреждений: базовый уровень / [Ш.А.Алимов, Ю.М.Колягин, М.В. Ткачева и др.]. — 16-е изд., испр. — М.: Просвещение, 2010. — 464 с.
- Семенов А.Л. ЕГЭ: 3000 задач с ответами по математике. Все задачи группы Б/ — 3-е изд., испр. и доп. – М.: Издательство «Экзамен», 2012. – 543с.
- Высоцкий И.Р., Ященко И.В. ЕГЭ 2012. Математика. Задача Б10. Теория вероятности. Рабочая тетрадь / Под ред. А.Л. Семенова и И.В. Ященко. – М.: МЦШМО, 2012. – 48 с.
10-11 классы: учеб. для общеобразовательных учреждений: базовый уровень / [Ш.А.Алимов, Ю.М.Колягин, М.В. Ткачева и др.]. — 16-е изд., испр. — М.: Просвещение, 2010. — 464 с.Задачи на вероятность выпадения не менее популярны, чем задачи на подбрасывание монеты. Условие такой задачи обычно звучит так: при бросании одного или нескольких кубиков (2 или 3) какова вероятность того, что сумма очков будет равна 10, или количество очков равно 4, или произведение числа очков или кратное 2 произведение количества очков и так далее.
Использование классической формулы вероятности является основным методом решения задач такого типа.
Один кубик, вероятность.
С одним кубиком все просто. определяется по формуле: P = m/n, где m — число исходов, благоприятных для события, а n — число всех элементарных равновозможных исходов опыта с подбрасыванием игральной кости или игральной кости.
Задача 1. Кубик бросают один раз. Какова вероятность получить четное количество очков?
Так как игральная кость является кубом (или ее еще называют правильной игральной костью, кубик выпадет на все грани с одинаковой вероятностью, так как он сбалансирован), у куба 6 граней (количество очков от 1 до 6 , которые обычно обозначаются точками), это означает, что задача имеет общее число исходов: n = 6. Событию благоприятствуют только исходы, в которых выпадает грань с четными точками 2,4 и 6, куб имеет таких граней: m = 3. Теперь мы можем определить искомую вероятность выпадения кости: P = 3/6 = 1/2 = 0,5.
Задача 2. Игральная кость подбрасывается один раз. Какова вероятность того, что выпадет не менее 5 очков?
Эта задача решается по аналогии с примером, указанным выше.
При бросании игральной кости общее количество равновозможных исходов равно: n = 6, а условие задачи (выпало не менее 5 очков, то есть выпало 5 или 6 очков) всего 2 исхода, значит, m = 2. Далее находим искомую вероятность: P = 2/6 = 1/3 = 0,333.
Две кости, вероятность.
При решении задач с броском 2 игральных костей очень удобно пользоваться специальной таблицей выпадения очков. На нем по горизонтали откладывается количество очков, выпавших на первом кубике, а по вертикали — количество очков, выпавших на втором кубике. Заготовка выглядит так:
Но возникает вопрос, что будет в пустых ячейках таблицы? Это зависит от проблемы, которую необходимо решить. Если задача о сумме баллов, то там пишется сумма, а если о разнице, то пишется разница и так далее.
Задача 3. Одновременно бросают две игральные кости. Какова вероятность получить менее 5 баллов?
Во-первых, вам нужно выяснить, каково будет общее количество результатов эксперимента. Все было очевидно при бросании одной кости 6 граней куба — 6 исходов эксперимента.
Но когда игральных костей уже две, то возможные исходы можно представить в виде упорядоченных пар чисел вида (х, у), где х показывает, сколько очков выпало на первой кости (от 1 до 6), а у — сколько очков выпало на втором кубике (от 1 до 6). Всего таких числовых пар будет: n = 6 * 6 = 36 (им соответствует 36 ячеек в таблице исходов).
Теперь можно заполнить таблицу, для этого в каждую ячейку вносится число суммы очков, выпавших на первом и втором кубике. Заполненная таблица выглядит так:
Благодаря таблице определим количество исходов в пользу события «всего будет меньше 5 очков». Подсчитаем количество ячеек, значение суммы в которых будет меньше числа 5 (это 2, 3 и 4). Для удобства закрасьте такие клетки, они будут m=6:
Учитывая данные таблицы, вероятность умереть равна: P = 6/36 = 1/6.
Задача 4. Бросили две игральные кости. Определить вероятность того, что произведение количества очков будет делиться на 3.
Для решения задачи составим таблицу произведений очков, выпавших на первом и втором кубике.
В ней сразу выбираем числа, кратные 3:
Записываем общее количество исходов эксперимента n = 36 (рассуждение такое же, как и в предыдущей задаче) и количество благоприятных исходов ( количество ячеек, которые заполнены в таблице) m = 20. Вероятность события: P = 20/36 = 5/9.
Задача 5. Игральная кость подбрасывается дважды. Какова вероятность того, что разница в количестве очков будет от 2 до 5 на первом и втором кубике?
Для определения вероятности выпадения Запишем таблицу различий очков и выделим в ней те ячейки, значение разницы в которых будет между 2 и 5:
Количество благоприятных исходов (количество ячейки, заполненные в таблице) равно m = 10, общее количество равновозможных элементарных исходов будет n = 36. Определяет вероятность события: P = 10/36 = 5/18.
В случае простого события и при броске 2 игральных костей нужно построить таблицу, затем выделить в ней нужные ячейки и разделить их количество на 36, это будет считаться вероятностью.
Объясните принцип решения задачи. Кости бросали один раз. Какова вероятность того, что выпадет менее 4 очков? и получил лучший ответ
Ответ от Дивергента [гуру]
50 процентов
Принцип предельно прост. Всего исходов 6: 1,2,3,4,5,6
Три из них удовлетворяют условию: 1,2,3, а три не удовлетворяют: 4,5,6. Следовательно, вероятность 3/6 = 1/2 = 0,5 = 50%
Ответ от Я супермен [гуру]
Всего может быть шесть вариантов (1,2,3,4,5,6 )
А из этих вариантов 1, 2 и 3 меньше четырех
Значит 3 ответа из 6
Для расчета вероятности делим благоприятный расклад на все, т.е. 3 на 6 = 0,5 или 50%
Ответ от Юрий Довбыш [active]
50%
разделить 100% на количество чисел на кубике,
и потом полученный процент умножить на сумму которую нужно узнать, то есть на 3)
Ответ от Иван Панин [гуру]
Точно не знаю, готовлюсь к ГИА, но мне сегодня препод что-то говорил, только про вероятность машин, как я понял, отношение показано в виде дроби, от сверху номер благоприятный, а снизу, на мой взгляд, вообще общий, ну у нас так было по машинам: Таксомоторная компания на данный момент свободна 3 черных, 3 желтых и 14 зеленых машин.
Одна из машин подъехала к заказчику. Найти вероятность того, что к нему подъедет желтое такси. Итак, желтых такси 3 и из общего количества машин 3, получается, что сверху дроби пишем 3, так как это выгодное количество машин, а снизу пишем 20, так как есть 20 машин в таксопарке, значит получаем вероятность 3 к 20 или дробь 3/20, ну я так понял… точно не знаю как с костями, но может с чем помогло..
Ответ от 3 ответа [гуру]
Привет! Вот подборка тем с ответами на ваш вопрос: Объясните принцип решения задачи. Кости бросали один раз. Какова вероятность того, что выпадет менее 4 очков?
Задача 19 ( ОГЭ — 2015, Ященко И.В.)
Оля, Денис, Витя, Артур и Рита кинули жребий — кто должен начать игру. Найдите вероятность того, что Рите придется начать игру.
Решение
Всего игру могут начать 5 человек.
Ответ: 0,2.
Задача 19 ( ОГЭ — 2015, Ященко И.В.)
В кармане у Миши было четыре конфеты — «Грильяж», «Маска», «Белочка» и «Красная шапочка», а также ключи от квартира.
Вынимая ключи, Миша случайно уронил одну конфету. Найдите вероятность того, что конфета-маска будет потеряна.
Решение
Всего 4 варианта.
Вероятность того, что Миша уронил конфету «Маска», равна
Ответ: 0,25.
Задача 19 ( ОГЭ — 2015, Ященко И.В.)
Игральная кость (игральная кость) подбрасывается один раз. Какова вероятность того, что количество выпавших очков будет не менее 3?
Решение
Всего существует 6 различных вариантов выпадения очков на кубике.
Количество точек, не менее 3, может быть: 3,4,5,6 — то есть 4 варианта.
Значит, вероятность P = 4/6 = 2/3.
Ответ: 2/3.
Задача 19 ( ОГЭ — 2015, И. В. Ященко)
Бабушка решила подарить внуку Илье наугад выбранные фрукты в дорогу. У нее было 3 зеленых яблока, 3 зеленых груши и 2 желтых банана. Найдите вероятность того, что Илья получит от бабушки зеленый фрукт.
Раствор
3 + 3 + 2 = 8 — всего фруктов.
Leave A Comment