Задание №13 ОГЭ по математике
неравенства и системы неравенств
Первичный бал: 1 Сложность (от 1 до 3): 3 Среднее время выполнения: 5 мин.
В задании №13 проверяется умение решать уравнения, неравенства и их системы. Конечно, под такие слова подходит огромный спектр заданий. Уточнение, пожалуй, одно. Надо применять графическое представление решения и показа результатов этого решения. В демонстрационном варианте ОГЭ предложена система двух линейных неравенств и графические представления вариантов ответов. Полезно понимать, что главным здесь является решение конкретных неравенств и понимание геометрического смысла полученного решения.
Теория к заданию №13
Определение:
Неравенством называется выражение вида: a < b (a ≤ b), a > b (a ≥ b)
Полезным для нас окажется метод интервалов:
Задание 13OM21R Укажите решение неравенства 8х – х- [0; +∞)
- [8; +∞)
- [0; 8]
- (-∞;0]∪[8;+∞)
8х – х2≥0
Вынесем -х за скобки: -х(-8 + х) ≥0
Теперь разделим на -1, не забывая изменить знак неравенства на противоположный: х(х – 8) ≤0
Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8.
Итак, имеем нули функции 0 и 8.
Теперь расставляем их на числовом луче и решаем неравенство методом интервалов.
Теперь находим промежуток чисел, соответствующий неравенству х(х – 8) ≤0, т.е. промежуток отрицательных или равных нулю чисел. Это будет промежуток [0; 8]
В соответствии с его номером, это будет ответ под №3.
Ответ: 3pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1506oУкажите неравенство, решение которого изображено на рисунке.
Тут нужно сразу отметить два важных момента.
- Графическим решением неравенств из вариантов ответа является парабола, которая пересекает координатную ось в точках, соответствующих корням неравенств.
- Так как все неравенства, представленные в вариантах ответов, имеют нестрогий знак, то точки пересечения корней неравенства с координатной осью будут закрашенными, т.е. входящими в искомые промежутки (решения).

Анализируем неравенства.
1) х2–36≤0 х2≤36Корни этого неравенства равны ±6. Поскольку знак неравенства «меньше», то для ответа следует взять ту часть параболы, которая располагается ниже коорд.оси. Получаем:
Полученный промежуток-решение не соответствует заданному в качестве ответа в условии. 2) х2+36≥0 х2≥–36 Это неравенство не имеет решений, поскольку для получения решения здесь требуется извлечь корень из отрицательные числа (из –36), а это невозможно.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1505oУкажите решение неравенства:
Выполняем тождественные преобразования неравенства и приводим его к простейшему виду. Для этого сначала группируем слагаемые, перенося те, что с «х», в левую сторону, а свободные члены в правую:
4х–6х≥–2–5
Приводим подобные:–2х≥–7
Находим х. Знак неравенства при этом поменяется на противоположный, поскольку делить будем на –2, т.е. на отрицательное число:х≤3,5
Далее на коорд.прямой теперь нужно отложить точку со значением 3,5, причем точка будет закрашенная, т.к. знак неравенства нестрогий: Т.к. знак полученного неравенства «≤», то выделить следует часть прямой слева от точки 3,5: Это графическое решение соответствует ответу под №2.Ответ:pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1504o Решите систему неравенств: На каком рисунке изображено множество её решений?Итак, решим систему неравенств – оставим х в левой части, а остальное перенесём в правую, получим:
х ≤ 0 -2,6
х ≥ 1 – 5
Вычислив, получаем ответ:
х ≤ -2,6
х ≥ -4
Найдем его на координатной прямой – это №2.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1503oУкажите множество системы неравенств:
⌈ x — 4 ≥ 0
⌊ x — 0,3 ≥ 1
Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:
⌈ x ≥ 4
⌊ x ≥ 1,3
В отличие от первого примера, решение более простое, но в данном случае нужно сравнить промежутки и выбрать общий. Первое неравенство требует, чтобы x был больше 4, а второе – более 1,3, на координатной прямой это будет выглядеть следующим образом:
Промежутки перекрывают друг друга начина с 4, значит ответ выглядит следующим образом (не забываем, что неравенство нестрогое):
[ 4 ; + ∞ ) или
Ответ: [4 ;+∞ )pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1502oУкажите множество решений неравенства: 7 x — x2 < 0
Существуют несколько способов решения квадратных неравенств, но я приведу самый простой и надежный.
x ( 7 – x ) < 0
Затем находим ноли функции x ( 7 – x ) = 0, приравнивая каждый множитель к нолю:
x = 0
7 – x = 0
Получаем:
x = 0
x = 7
Таким образом, мы получили три интервала:
( -∞ ; 0 )
( 0 ; 7 )
( 7 ; +∞)
Подставим любое значение x из первого интервала и посмотрим на получившийся ответ.
Подставим -1:
x ( 7 – x ) = – 1 ( 7 – (-1) ) = -8
Значение отрицательно, значит в интервале ( -∞ ; 0 ) функция отрицательна, что нам и подходит для ответа, так как в условии:
x ( 7 – x ) < 0
Подставим 1:
x ( 7 – x ) = 1 ( 7 – 1 ) = 6
Значение положительно, и промежуток ( 0 ; 7 ) нам не подходит.
Подставим 8:
x ( 7 – x ) = 8 ( 7 – 8 ) = – 8
Значение отрицательно, и это подходит под условия, следовательно ответ:
( -∞ ; 0 ) и ( 7 ; +∞)
или графически:
Ответ: (-∞;0) и (7;+∞)pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1501o Укажите решение неравенства: 2 x — 3 ( x — 7) ≤ 3Для решения линейного неравенства достаточно выполнить действия, аналогичные действию решений линейных уравнений.
Для решения этого примера вначале раскроем скобки, не забывая, что -3 умножается на -7 и дает + 21:
2 x – 3 x + 21 ≤ 3
Затем приводим подобные, перенося числа в правую сторону:
2 x – 3 x ≤ 3 – 21
– x ≤ -18
Нам необходимо умножить неравенство на -1, чтобы получить диапазон x, не забывая, что при этом меняется знак неравенства:
x ≥ 18
Таким образом, мы получаем, что x должен быть больше либо равен 18.
Ответ:pазбирался: Даниил Романович | обсудить разбор | оценить
👀 24.9k |
Страница не найдена (ошибка 404)
- Родителям и ученикам
- Полезная информация
- Правила посещения школы
- Права и обязанности учащихся
- Школьная форма
- Информационная безопасность
- Доступная среда
- Вакантные места для приема (перевода) обучающихся
- Помощь в трудной ситуации
- Будущим первоклассникам
- Правила приема, перевода, отчисления
- Детям с ограниченными возможностями здоровья
- Безопасность учащихся
- Отдых и оздоровление учащихся
- Условия питания учащихся
- Правила дорожной безопасности
- Платные образовательные услуги
- Новости
- Каникулы
- Государственная итоговая аттестация (ОГЭ, ЕГЭ, ГВЭ)
- Всероссийские олимпиады школьников
- Стипендии и меры поддержки обучающихся
- Всероссийские проверочные работы
- Секции и кружки
- Школьный спортивный клуб
- Профориентационная работа
- Российское движение школьников (РДШ)
- Военно-исторический музей
- Школьный театр
- Полезная информация
- Наша школа
- О школе
- Администрация
- Педагогический состав
- Профильные направления
- Естественнонаучный профиль
- Технологический профиль
- Социально-гуманитарный профиль
- Наши классы
- Достижения и победы
- Доска почета
- Педагогам и сотрудникам
- Объявления для учителей
- Электронный журнал
- Образовательные ресурсы
- Аттестация педагогических работников
- Повышение квалификации
- Профсоюзная организация
- Вакансии
- Инновационная деятельность
- Наставничество
- Сведения об образовательной организации
- Организация питания в образовательной организации
- Отзывы о качестве питания
- Руководство.
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав - Структура и органы управления образовательной организацией
- Методический совет
- Педагогический совет
- Родительский совет
- Ученический совет
- Общее собрание работников
- Материально-техническое обеспечение и оснащенность образовательного процесса
- Основные сведения
- Документы
- Образование
- Образовательные стандарты и требования
- Стипендии и меры поддержки обучающихся
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приема (перевода) обучающихся
- Доступная среда
- Международное сотрудничество
- Организация питания в образовательной организации
- Независимая оценка качества образования
- Независимая оценка качества условий образовательной деятельности
- Независимая оценка качества подготовки обучающихся
- Отзывы о качестве питания
- Расписание
- Политика в отношении обработки персональных данных
- Сведения об образовательной организации
- Вопросы и ответы
- Контакты
Алгебра — линейные неравенства
Онлайн-заметки Пола
Главная
/
Алгебра
/
Решение уравнений и неравенств
/ Линейные неравенства
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.11: Линейные неравенства
До сих пор в этой главе мы сосредоточились на решении уравнений. Настало время немного переключиться и начать думать о решении неравенства. Прежде чем мы приступим к решению неравенств, мы должны сначала пройтись по паре основ.
На данном этапе вашей математической карьеры предполагается, что вы знаете, что
\[а <б\]
означает, что \(a\) — это некоторое число, которое строго меньше, чем \(b\). Также предполагается, что вы знаете, что
\[а \ge б\]
означает, что \(a\) — это некоторое число, которое либо строго больше, чем \(b\), либо точно равно \(b\). Точно так же предполагается, что вы знаете, как поступить с оставшимися двумя неравенствами. > (больше) и \( \le \) (меньше или равно).
Точно так же предполагается, что вы знаете, как поступить с оставшимися двумя неравенствами. > (больше) и \( \le \) (меньше или равно).
Мы хотим обсудить некоторые проблемы с обозначениями и некоторые тонкости, которые иногда достаются студентам, когда они действительно начинают работать с неравенствами.
Во-первых, помните, что когда мы говорим, что \(a\) меньше, чем \(b\), мы имеем в виду, что \(a\) находится слева от \(b\) на числовой прямой. Итак,
\[- 1000 < 0\]
— истинное неравенство.
Далее не забудьте правильно интерпретировать \( \le \) и \( \ge \). Оба следующих неравенства являются истинными.
\[4 \le 4\hspace{0,25 дюйма}\hspace{0,25 дюйма}\hspace{0,25 дюйма} — 6 \le 4\]
В первом случае 4 равно 4 и, следовательно, «меньше или равно» 4. Во втором случае -6 строго меньше 4 и, следовательно, «меньше или равно» 4. Наиболее распространенная ошибка состоит в том, чтобы решить, что первое неравенство не является истинным неравенством. Также будьте осторожны, чтобы не использовать эту интерпретацию и не переводить ее в < и/или >. Например,
Также будьте осторожны, чтобы не использовать эту интерпретацию и не переводить ее в < и/или >. Например,
\[4 < 4\]
не является истинным неравенством, поскольку 4 равно 4 и строго не меньше 4.
Наконец, в этом и последующих разделах мы будем встречать много двойных неравенств , так что мы не можем забыть о них. Далее следует двойное неравенство.
\[ — 9 < 5 \le 6\]
В двойном неравенстве мы говорим, что оба неравенства должны быть верны одновременно. В этом случае 5 определенно больше, чем -9и в то же время меньше или равно 6. Следовательно, это двойное неравенство является истинным неравенством.
С другой стороны,
\[10 \le 5 < 20\]
не является истинным неравенством. Хотя верно, что 5 меньше 20 (поэтому верно второе неравенство), неверно, что 5 больше или равно 10 (поэтому первое неравенство неверно). Если хотя бы одно из неравенств двойного неравенства неверно, то неверно и все неравенство. Этот момент важнее, чем вы можете себе представить на данный момент. В следующем разделе мы столкнемся с ситуациями, когда многие студенты пытаются объединить два неравенства в двойное неравенство, которое просто невозможно объединить, поэтому будьте осторожны.
Если хотя бы одно из неравенств двойного неравенства неверно, то неверно и все неравенство. Этот момент важнее, чем вы можете себе представить на данный момент. В следующем разделе мы столкнемся с ситуациями, когда многие студенты пытаются объединить два неравенства в двойное неравенство, которое просто невозможно объединить, поэтому будьте осторожны.
Следующей темой, которую нам нужно обсудить, является идея записи интервалов . Интервальное обозначение — очень удобное сокращение для неравенств, и оно будет широко использоваться в следующих нескольких разделах этой главы.
Лучший способ определить обозначение интервала — это следующая таблица. В таблице три столбца. Каждая строка содержит неравенство, график, представляющий неравенство, и, наконец, обозначение интервала для данного неравенства.
Помните, что квадратная скобка «[» или «]» означает, что мы включаем конечную точку, а скобка «(» или «)» означает, что мы не включаем конечную точку.
Теперь, с первыми четырьмя неравенствами в таблице, обозначение интервала на самом деле не что иное, как график без числовой линии на нем. С последними четырьмя неравенствами обозначение интервала является почти графом, за исключением того, что нам нужно добавить соответствующую бесконечность, чтобы убедиться, что мы получили правильную часть числовой прямой. Также обратите внимание, что бесконечность НИКОГДА не ставится в скобки. Они получают только скобки.
Прежде чем перейти к решению неравенств, необходимо сделать одно последнее замечание по поводу записи интервалов. Всегда помните, что когда мы пишем интервальную нотацию для неравенства, число слева должно быть меньшим из двух.
Пришло время подумать о решении линейных неравенств. При решении неравенств мы будем использовать следующий набор фактов. Обратите внимание, что факты приведены для <. Однако мы можем записать эквивалентный набор фактов для оставшихся трех неравенств.
- Если \(a < b\), то \(a + c < b + c\) и \(a - c < b - c\) для любого числа \(c\).
 Другими словами, мы можем прибавить или вычесть число к обеим частям неравенства, но само неравенство не изменится.
Другими словами, мы можем прибавить или вычесть число к обеим частям неравенства, но само неравенство не изменится. - Если \(a < b\) и \(c > 0\), то \(ac < bc\) и \(\frac{a}{c} < \frac{b}{c}\). Таким образом, при условии, что \(c\) является положительным числом, мы можем умножить или разделить обе части неравенства на число без изменения неравенства.
- Если \(a < b\) и \(c < 0\), то \(ac > bc\) и \(\frac{a}{c} > \frac{b}{c}\). В этом случае, в отличие от предыдущего факта, если \(c\) отрицательно, нам нужно изменить направление неравенства, когда мы умножаем или делим обе части неравенства на \(c\).
Это почти те же факты, которые мы использовали для решения линейных уравнений. Единственным реальным исключением является третий факт. Это важный факт, так как его чаще всего неправильно используют и/или забывают при решении неравенств.
Если вы не уверены, что считаете, что знак \(c\) имеет значение для второго и третьего фактов, рассмотрите следующий пример числа.
\[ — 3 < 5\]
Надеюсь, мы все согласимся, что это истинное неравенство. Теперь умножьте обе части на 2 и на -2.
\[\begin{align*}- 3 & < 5\hspace{0.5in} & - 3 & < 5\\ - 3\left( 2 \right) & < 5\left( 2 \right)\hspace{0.5 in} & - 3\left( { - 2} \right) & > 5\left( { — 2} \right)\\ — 6 & < 10 \hspace{0.5in} & 6 & > — 10\end{ выровнять*}\]
Действительно, при умножении на положительное число направление неравенства остается прежним, однако при умножении на отрицательное число направление неравенства меняется.
Хорошо, давайте решим некоторые неравенства. Мы начнем с неравенств, которые содержат только одно неравенство. Другими словами, мы отложим решение двойных неравенств до следующего набора примеров.
Здесь нужно помнить, что мы просим определить все значения переменной, которые мы можем подставить в неравенство и получить истинное неравенство. Это означает, что наши решения в большинстве случаев будут сами неравенствами.
Это означает, что наши решения в большинстве случаев будут сами неравенствами.
Пример 1 Решение следующих неравенств. Приведите решение в форме неравенства и интервальной записи.
- \( — 2\влево( {m — 3} \вправо) < 5\влево( {m + 1} \вправо) - 12\)
- \(2\влево( {1 — x} \вправо) + 5 \le 3\влево( {2x — 1} \вправо)\)
Показать все решения Скрыть все решения
Показать обсуждение
Решение одиночных линейных неравенств происходит почти так же, как и решение линейных уравнений. Мы упростим обе стороны, получим все члены с переменной с одной стороны и числами с другой, а затем умножим/разделим обе части на коэффициент переменной, чтобы получить решение. Единственное, что вы должны помнить, это то, что если вы умножаете/делите на отрицательное число, вы меняете направление неравенства.
a \( — 2\влево( {m — 3} \вправо) < 5\влево( {m + 1} \вправо) - 12\) Показать решение
Здесь действительно нечего делать, кроме как следовать описанному выше процессу.
\[\begin{align*} — 2\left( {m — 3} \right) & < 5\left( {m + 1} \right) - 12\\ - 2m + 6 & < 5m + 5 - 12 \\ - 7 м & < - 13\\ м & > \frac{{13}}{7}\end{align*}\]
Вы уловили тот факт, что здесь изменилось направление неравенства, не так ли? Мы разделили на «-7», поэтому нам пришлось изменить направление. Форма неравенства решения: \(m > \frac{{13}}{7}\). Обозначение интервала для этого решения: \(\left({\frac{{13}}{7},\infty} \right)\).
b \(2\left( {1 — x} \right) + 5 \le 3\left( {2x — 1} \right)\) Показать решение
Опять же, здесь особо нечего делать.
\[\begin{align*}2\left( {1 — x} \right) + 5 & \le 3\left( {2x — 1} \right)\\ 2 — 2x + 5 & \le 6x — 3 \\ 10 & \le 8x\\ \frac{{10}}{8} & \le x\\ \frac{5}{4} & \le x\end{align*}\]
Теперь, с этим неравенством, мы получили переменную с правой стороны, хотя более традиционно с левой стороны. Итак, давайте поменяем местами, чтобы переменная оказалась слева. Обратите внимание, однако, что нам нужно будет также изменить направление неравенства, чтобы убедиться, что мы не изменим ответ. Итак, вот запись неравенства для неравенства.
Итак, давайте поменяем местами, чтобы переменная оказалась слева. Обратите внимание, однако, что нам нужно будет также изменить направление неравенства, чтобы убедиться, что мы не изменим ответ. Итак, вот запись неравенства для неравенства.
\[x \ge \frac{5}{4}\]
Обозначение интервала для решения: \(\left[ {\frac{5}{4},\infty} \right)\).
Теперь решим двойные неравенства. Этот процесс в чем-то похож на решение одиночных неравенств, но в чем-то он сильно отличается. Поскольку есть два неравенства, нет никакого способа получить переменные «с одной стороны» неравенства, а числа — с другой. Легче увидеть, как они работают, если мы сделаем пример или два, поэтому давайте сделаем это.
Пример 2. Решите каждое из следующих неравенств. Приведите решения в форме неравенства и интервала.
- \( — 6 \le 2\влево( {x — 5} \вправо) < 7\)
- \( — 3 < \frac{3}{2}\left( {2 - x} \right) \le 5\)
- \( — 14 < - 7\влево( {3x + 2} \вправо) < 1\)
Показать все решения Скрыть все решения
a \( — 6 \le 2\left( {x — 5} \right) < 7\) Показать решение
Этот процесс очень похож на процесс для одиночных неравенств, но сначала нам нужно быть осторожным в нескольких местах. Нашим первым шагом в этом случае будет удаление скобок в среднем термине.
Нашим первым шагом в этом случае будет удаление скобок в среднем термине.
\[ — 6 \le 2x — 10 < 7\]
Теперь нам нужен \(x\) сам по себе в среднем члене и только числа в двух внешних терминах. Для этого мы будем складывать/вычитать/умножать/разделять по мере необходимости. Единственное, что нам нужно помнить, это то, что если мы делаем что-то со средним термином, нам нужно сделать то же самое с ОБОИМИ терминами. Одна из наиболее распространенных ошибок на этом этапе — добавить что-то, например, в середину и добавить это только к одной из двух сторон.
Хорошо, мы добавим 10 ко всем трем частям, а затем разделим все три части на два.
\[\begin{array}{c} 4 \le 2x < 17\\ 2 \le x < \displaystyle \frac{{17}}{2}\end{array}\]
Это ответ в форме неравенства. Интервальная форма записи ответа: \(\left[ {2,\frac{{17}}{2}} \right)\).
b \( — 3 < \frac{3}{2}\left( {2 - x} \right) \le 5\) Показать решение
В этом случае первое, что нам нужно сделать, это очистить дроби, умножив все три части на 2. Затем мы действуем так же, как и в первой части.
\[\begin{array}{c} — 6 < 3\left( {2 - x} \right) \le 10\\ - 6 < 6 - 3x \le 10\\ - 12 < - 3x \le 4\ конец {массив}\]
Здесь мы еще не совсем закончили, но нам нужно быть очень осторожными со следующим шагом. На этом шаге нам нужно разделить все три части на -3. Однако помните, что всякий раз, когда мы делим обе части неравенства на отрицательное число, нам нужно изменить направление неравенства. Для нас это означает, что оба неравенства должны изменить направление здесь.
\[4 > х \ge — \frac{4}{3}\]
Итак, решение имеет форму неравенства. Нам нужно быть осторожными с обозначением интервала для решения. Во-первых, запись интервала НЕ \(\left( {4, — \frac{4}{3}} \right]\). Помните, что в записи интервала меньшее число всегда должно идти слева! Следовательно, правильное обозначение интервала для решения: \(\left[ { — \frac{4}{3},4} \right)\).
Нам нужно быть осторожными с обозначением интервала для решения. Во-первых, запись интервала НЕ \(\left( {4, — \frac{4}{3}} \right]\). Помните, что в записи интервала меньшее число всегда должно идти слева! Следовательно, правильное обозначение интервала для решения: \(\left[ { — \frac{4}{3},4} \right)\).
Обратите внимание, что это также совпадает с формой решения в виде неравенства. Неравенство говорит нам, что \(x\) — это любое число между 4 и \( — \frac{4}{3}\) или, возможно, \( — \frac{4}{3}\) само по себе, и это точно о чем говорит нам интервальное обозначение.
Кроме того, неравенство можно перевернуть, чтобы получить меньшее число слева, если мы захотим. Вот эта форма,
\[ — \frac{4}{3} \le x < 4\]
При этом также убедитесь, что правильно обработаны неравенства.
c \( — 14 < - 7\left( {3x + 2} \right) < 1\) Показать решение
Не так уж и много. Мы поступим так же, как и с предыдущими двумя.
Мы поступим так же, как и с предыдущими двумя.
\[\begin{array}{c} — 14 < - 21x - 14 < 1\\ 0 < - 21x < 15\end{массив}\]
Не радуйтесь тому, что одна из сторон теперь равна нулю. Это не проблема. Опять же, как и в предыдущей части, мы будем делить на отрицательное число, поэтому не забудьте поменять направление неравенств.
\[\begin{array}{c} \displaystyle 0 > x > — \frac{{15}}{{21}}\\ \displaystyle 0 > x > — \frac{5}{7}\hspace{0,25 in}{\mbox{OR}}\hspace{0,25in} — \frac{5}{7} < x < 0\end{массив}\]
Для решения подойдет любое из неравенств во второй строке. Интервальное обозначение решения: \(\left( { — \frac{5}{7},0} \right)\).
При решении двойных неравенств обязательно обращайте внимание на неравенства, которые есть в исходной задаче. Одна из наиболее распространенных ошибок здесь состоит в том, чтобы начать с задачи, в которой одно из неравенств равно < или >, а другое — \( \le \) или \( \ge \), как мы делали это в первых двух частях книги. предыдущий пример, а затем по окончательному ответу они оба < или > или они оба \( \le \) или \( \ge \). Другими словами, легко внезапно сделать оба неравенства одинаковыми. Будьте осторожны с этим.
предыдущий пример, а затем по окончательному ответу они оба < или > или они оба \( \le \) или \( \ge \). Другими словами, легко внезапно сделать оба неравенства одинаковыми. Будьте осторожны с этим.
Последний пример, который мы хотим здесь обработать.
Пример 3. Если \( — 1 < x < 4\), то определить \(a\) и \(b\) в \(a < 2x + 3 < b\).
Показать решение
Это проще, чем может показаться на первый взгляд. Все, что мы действительно собираемся сделать, это начать с заданного неравенства, а затем манипулировать средним членом, чтобы он выглядел как второе неравенство. Опять же, нам нужно помнить, что все, что мы делаем со средним термином, нам также нужно делать с двумя внешними терминами.
Итак, сначала умножим все на 2.
\[- 2 < 2x < 8\]
Теперь прибавьте ко всему 3.
\[1 < 2x + 3 < 11\]
Теперь у нас есть средний член, идентичный второму неравенству в условии задачи, поэтому все, что нам нужно сделать, это выбрать \(a\) и \(b\). Из этого неравенства видно, что \(a = 1\) и \(b = 11\).
Из этого неравенства видно, что \(a = 1\) и \(b = 11\).
Решение линейных неравенств (Алгебра 1, Линейные неравенства) – Mathplanet
График линейного неравенства с одной переменной представляет собой числовую прямую. Используйте открытый кружок для < и > и закрытый кружок для ≤ и ≥.
График для x > -3
График для x ≥ 2
Неравенства, имеющие одно и то же решение, называются эквивалентными. Есть свойства неравенства, а есть свойства равенства. Все приведенные ниже свойства верны и для неравенств с участием ≥ и ≤.
Свойство сложения неравенства гласит, что добавление одного и того же числа к каждой части неравенства дает эквивалентное неравенство
$$If \: x>y,\: then\: x+z>y+z$$
$$If\: x Свойство вычитания неравенства говорит нам, что вычитание одного и того же числа из обеих частей неравенства дает эквивалентное неравенство. $$If \: x>y,\: then\: x-z>y-z$$ $$If\: x Свойство умножения неравенства говорит нам, что умножение обеих частей неравенства с положительным числом дает эквивалентное неравенство. $$Если \: x>y \: и\: z>0,\: то\: xz>yz$$ $$If\: x Умножение в каждой части неравенства с отрицательным числом, с другой стороны, не дает эквивалентного неравенства, если мы также не поменяем направление символа неравенства $$Если \: x>y \: и\: z<0,\: то\: xz $$Если\: x То же самое относится и к свойству деления неравенства. Деление обеих частей неравенства на положительное число дает эквивалентное неравенство. $$If \: x>y \: and\: z>0,\: then\: \frac{x}{z}>\frac{y}{z}$$ $$If\: x И деление в обе стороны неравенства с отрицательным числом дает эквивалентное неравенство, если символ неравенства перевернуть. $$If \: x>y \: and\: z<0,\: then\: \frac{x}{z}<\frac{y}{z}$$ $$If\: x при решении многошаговых уравнений. Возьмите одну вещь за раз, желательно, начиная с изоляции переменной от констант.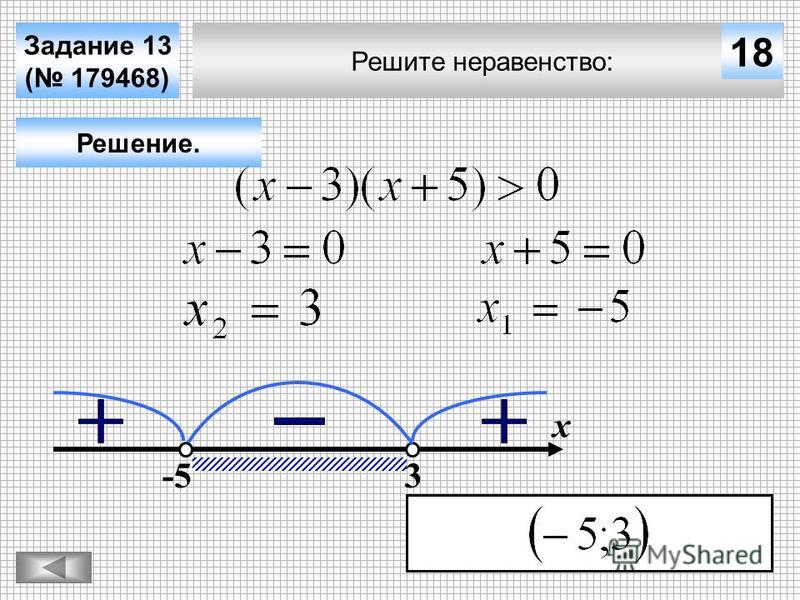


 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав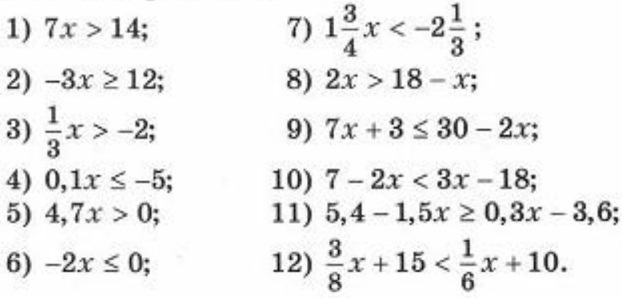 Другими словами, мы можем прибавить или вычесть число к обеим частям неравенства, но само неравенство не изменится.
Другими словами, мы можем прибавить или вычесть число к обеим частям неравенства, но само неравенство не изменится.
Leave A Comment