Задания типа С5 — презентация онлайн
1. Задания типа С5
8. Найти все значения а, при каждом из которыхуравнение 1=|x – 3| — |2x + a| имеет единственное
решение.
у
Решение:
Перепишем
уравнение:
|2x + a| = |x – 3| — 1.
Построим графики
функций:
у = |x – 3| — 1 и
у = |2x + a|.
0
2
4
х
Очевидно, что данное уравнение будет иметь
единственное решение, если вершина движущегося
«уголка» попадет в точку с координатами (2; 0) или
(4; 0). Следовательно, координаты этих точек
удовлетворяют уравнению у = |2x + a|. Значит,
0 = |4 + a|
а=-4
или
0 = |8 + a|
а = — 8.
Ответ: — 8 или – 4.
2
ПАМЯТКА
x, если х ≥ 0
Пользоваться определением модуля |x| = – x, если х ˂ 0
А так же |x|< а → -а < x < а |x|> а → x < -а и х > а
Знать и строить: уравнение, линию, алгоритм построения:
надо иметь, хотя бы, 2 точки
y = kx + b – линейная, прямая
*направление ветвей
y = аx² + bх + с – квадратная, парабола
*пересечение с ОХ
*х₀ = -b/2a – абсцисса вершины – ось симметрии
*выделять полный квадрат
x² + y² = R² – окружность,
Центр (0;0), R — радиус
(x-а)² + (y-b)² = R² – окружность, Центр (a; b), R — радиус
k>0
y = — гипербола
y = f(x)
график
y = |f(x)|
график
линии выше ОХ
оставляем
точки оси ОХ
линии ниже ОХ симметрично
в верхнюю полуплоскость
Преобразования графика
3
y = Ikf(mx + c) + bI
y = Ikf(m (x + a)) + bI
1.
 y
y= f(х)
Как построить график …
исходная
по точкам
m = ¹∕₃
2. y
= f(mх)
растянуть в 3 раза
вдоль оси ОХ
a = -2
сдвинуть на 2 вправо
3. y
= f(m(х + a)
4. y
= kf(m(х + a))
5. y
= kf(m(х + a)) + b
6. y
а, если
а, если
— —
k=2
растянуть в 2 раза
вдоль оси ОY
b = -2
сдвинуть на 2
вниз
= kf(m( IхI + a)) + b
a=2?
—
m = -2 ?
❹
❸
❷
—❺— — — а, если k = -¹∕₂ ?
сжать и (-)
влево
сжать и (-) а, если
? вверх
b = ¹∕₂ ?
Линия при Х ≥ 0 и
симметричная ей
при Х ≤ 0
относительно оси ОУ
9 Найдите все значения параметра а, при
которых уравнение 2 х а х 3 1имеет
единственное решение.
у
4
А
В
2
-4
-2
0
х
РЕШЕНИЕ.
Правая часть этого уравнения задает неподвижный
«уголок», левая – «уголок», вершина которого
двигается по оси абсцисс.
Очевидно, что данное уравнение будет иметь
единственное решение, если вершина движущегося
«уголка» попадет в точку А, или точку В.
 Имеем,
Имеем,х 3 1 0 х 4, х 2,
тогда А(-4; 0), В(-2; 0) и координаты этих точек
удовлетворяют уравнению у 2х а .
у
8 а 0
а 8
.
а 4
4 а 0
Ответ:
а 8, а 4
А
-4
В 2
-2
0
х
8. Задача 2. Найдите все значения a, при каждом из которых функция имеет более двух точек экстремума.
Задача 2. Найдите все значения a, при каждом из которых функцияимеет более двух точек
f x x 2 2 x a 2 8x
экстремума.
Решение.
1. Функция f имеет вид:
а) при
, поэтому ее график есть часть параболы
с ветвями, направленными вверх, и осью симметрии x=5;
б) при
, поэтому ее график есть часть параболы с
ветвями, направленными вверх, и осью симметрии x=3.
Все возможные виды графика функции f(x) показаны на рисунках:
9. Задача 2. Найдите все значения a, при каждом из которых функция
f ( x) x 2 2 x a 2 8 xимеет более двух точек экстремума.
5
2) График обеих квадратичных функций проходят через точку (a2;f(a2)) .

3) Функция y=f(x)имеет более двух точек экстремума, а именно – три, в
единственном случае (рис. 1):
2
3 a 5 3 a 5.
5 a 3;
Ответ:
3 a 5.
10. С5.Найдите все положительные значения a, при каждом из которых система уравнений имеет единственное решение.
7С5.Найдите все положительные значения a,
при каждом из которых система уравнений
2
2
х 9 у 5 9,
2
2
2
х 3 у а
имеет единственное решение.
По определению модуля:
Заметим:
x – 9, если х ≥ 0 ,
|x| – 9 = – x – 9, если х ˂ 0 ,
х² = ( – х)² = ( –1∙ х)² = ( –1)² ∙ х² = х²
(– x – 9)²= (-(х+9))² =( –1)² ∙(х+9)² = (х+9)²
х ≥0
(х – 9)² + (у – 5)² = 9
центры
(-(хх+–9)²
9)²++(у(у––5)²
5)²==99
График уравнения — совокупность
(9; 5) двух окружностей. R = 3
х<0
(-9; 5)
х 9 у 5
Первые
Второе
уравнения
График
1-гоуравнение
уравнения
системы:
у
(х + 9)² + (у – 5)² = 9
Центр (-9; 5)
первый
ответ:
2
R 61 3
окружность Центр (-3;0)
Радиус
МЕНЯЕТСЯ
5
3
8
9
(х – 9)² + (у – 5)² = 9
Центр (9; 5)
АС = 13
R 13 3 16
BC² = 61
ВB R=3
2
R=3 А
3
13
-9-9
-6
С
-3
О 1
Ответ :
61 3; 16.

99
6
12
12
Второй случай
R=а2
х 3 у а
2
2
х
10
Найти значения а, при которых уравнение
2
имеет более двух корней.
х+1 = a|x-5| на [0; + ∞)
Корни
— абсциссы точек
пересечения
f(x)=
2
х+1
гипербола 5
на [0; + ∞]
f(x) g(x)
g(x) =a|x-5|
y = x-5
y = |x-5|
a(5-x)
a(x-5)
величина «УГОЛКА» модуля
зависит от а
при х = 0 → а = ²⁄5 3 корня
2 ●❶
0,5
2 корня левый луч «УГОЛКА»
● ●❷
касается гиперболы
❸
●
1 корень точку
2 корня
Определим
касания
2
g(x)
f(x)
=
Должны выполняться условия:
х+1 = a(5-x) – левый
луч
f ′(x) =g ′(x) -2 = — a
3
5
(х+1)²
-5
2 = 2(5-x) х+1
5-x х = 2 в точке касания
|∙
1=
а = ²⁄9 (2 корня)
х+1 (х+1)²
х+1
2
Ответ: лучи «УГОЛКА»
а Є (²⁄5; ²⁄9]
ЕГЭ. 07.06.12.
ЗАДАЧИ ИЗ КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ И
ДЕМОНСТРАЦИОННЫХ МАТЕРИАЛОВ ЕГЭ ПО МАТЕМАТИКЕ
Пример 1.
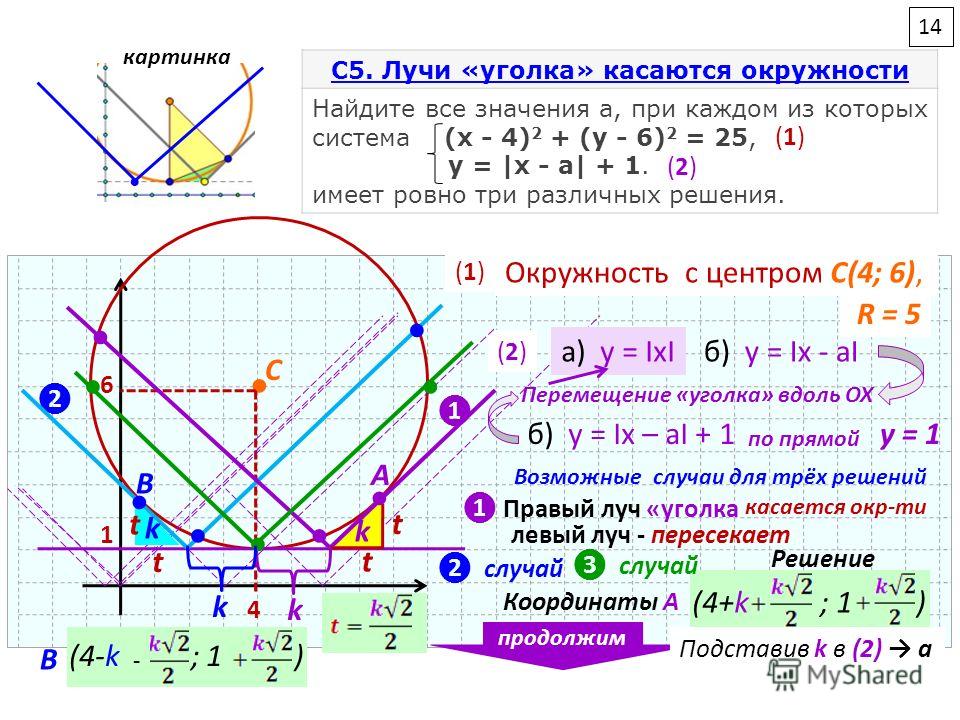 Найдите сумму целых значений параметра а , при которых
Найдите сумму целых значений параметра а , при которыхуравнение a 2 x x 2 19 a 3 x 4 0 имеет три корня.
Решение.
a x 2 2 x 19
Исходное уравнение равносильно совокупности уравнений:
a x 4 3 ,
График этой совокупности — объединение
«уголка» и параболы.
Подвижная прямая а=а0 пересекает график
совокупности в трёх точках, если а=а1,
а=а2, а=а3.
1) а=а1 а = 3.
2) При х >4 x2 2x 19 x 4 3,
х2-3х-18=0, х1=-3, х2=6. Число -3
не удовлетворяет условию х >4.
а(6) = 6-4+3 = 5 а2= 5.
2
3) При x < 4 x 2 x 19 ( х 4) 3 ,
x2 x 26 0, x1,2 Z а3 .
а
.
а33 = ?
а2=
=5?
а1= 3
3
0 1
4
-20
Ответ: 8.
х
ЗАДАЧИ ИЗ КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ И
ДЕМОНСТРАЦИОННЫХ МАТЕРИАЛОВ ЕГЭ ПО МАТЕМАТИКЕ
Пример 1. Найдите сумму целых значений параметра а , при которых
уравнение a 2 x x 2 19 a 3 x 4 0 имеет три корня.
Решение.
a x 2 2 x 19
Исходное уравнение равносильно совокупности уравнений:
a x 4 3 ,
График этой совокупности — объединение
«уголка» и параболы.

Подвижная прямая а=а0 пересекает график
совокупности в трёх точках, если а=а1,
а=а2, а=а3.
1) а=а1 а = 3.
2) При х >4 x2 2x 19 x 4 3,
х2-3х-18=0, х1=-3, х2=6. Число -3
не удовлетворяет условию х >4.
а(6) = 6-4+3 = 5 а2= 5.
2
3) При x < 4 x 2 x 19 ( х 4) 3 ,
x2 x 26 0, x1,2 Z а3 .
а
.
а33 =
?Z
а2=
=5?
а1= 3
3
0 1
4
-20
Ответ: 8.
х
10. Найдите все значения р, при каждом из которых
найдётся q такое, что система имеет единственное
решение:
2
2
x y 1,
y q | x | p
Решение:
у
Графиком функции х2 + у2 = 0
является окружность с
центром (0; 0) и R = 1.
1) q = 0, у = р; р = 1 или р = -1.
2) q > 0, y = q | x | + p; p = 1.
3) q < 0, y = q | x | + p; p = -1.
Ответ: р = 1 или р = -1.
1
х
-1
0
-1
1
С5. Найдите все значения параметра а, при каждом из
которых система уравнений 4 у 3 12 3 х ,
2
y a 2 3 2у 3 х 2 .

имеет ровно 4 решения.
Решение. Преобразуем данную систему:
3 х 4 у 3 12,
3 х 4 у 3 12,
2
2
2
2
2
2
y
6
у
9
х
a
;
y
3
х
a
.
Пусть t = y – 3, тогда система примет вид:
3 х 4 t 12,
2
t х 2 a 2 .
1
2
Заметим, что количество решений полученной системы
совпадает с количеством решений исходной системы.
Построим графики уравнений (1) и (2) в системе координат Oxt.
С5.
t
График первого уравнения – ромб,
диагонали которого, равные 8 и 6,
лежат на осях Ох и Оt, а графиком
3
второго уравнения является
окружность с центром в начале
координат и радиусом r = a .
Графики уравнений системы имеют -4
ровно четыре общих точки, и,
следовательно, система имеет ровно
-3
4 решения, тогда и только тогда,
когда окружность либо вписана в ромб,
либо ее радиус удовлетворяет условию
3 < r < 4.
В первом случае радиус окружности является высотой
прямоугольного треугольника с катетами 3 и 4, откуда
3 4
r a
2,4;
5
х
4
a 2,4.
 {3}+a) — 2log_{3} \sqrt{x+1} = log_{3}x\) имеет хотя бы один действительный корень.
{3}+a) — 2log_{3} \sqrt{x+1} = log_{3}x\) имеет хотя бы один действительный корень.ПодробнееУзнать ответКомментировать
Вопрос B18 #2890 Математика (профиль)
Найдите все значения параметра \(а\), при каждом из которых уравнение
имеет ровно три различных действительных корня.
ПодробнееУзнать ответКомментировать
Вопрос B18 #2907 Математика (профиль)
Найдите все значения \(a\), при каждом из которых система уравнений
имеет хотя бы одно решение.
ПодробнееУзнать ответКомментировать
Вопрос B18 #2928 Математика (профиль)
При каких значениях параметра \(a\) система
\(\displaystyle \begin{cases}|x+a|+|y-a|+|a+1+x|+|a+1-y|=2 \\ y=2|x-4|-5 \end{cases}\)
имеет единственное решение?
ПодробнееУзнать ответКомментировать
Вопрос B18 #2947 Математика (профиль)
Найдите все значения \(a\) , при которых система
\(\begin{cases}|x^{2} -x -6|=(y-1)^{2}+x-7\\3y=2x-a\end{cases}\)
имеет ровно один или два корня. {x}-1}=2a+2\) имеет ровно один корень.
{x}-1}=2a+2\) имеет ровно один корень.
ПодробнееУзнать ответКомментировать
Вопрос B18 #3262 Математика (профиль)
Для каждого допустимого значения а решите неравенство
ПодробнееУзнать ответКомментировать
Вопрос B18 #3323 Математика (профиль)
Определите, при каких значениях параметра \(a\) пересечение множеств
представляет собой круг.
ПодробнееУзнать ответКомментировать
Вопрос B18 #3405 Математика (профиль)
При каждом значении параметра «a» решить неравенство
ПодробнееУзнать ответКомментировать
Вопрос B18 #3424 Математика (профиль)
Определите, при каких значениях параметра а, неравенство
\( \left | \left( \frac{5}{8} \right )^{x} — a \right | имеет ровно 2 целочисленных решения.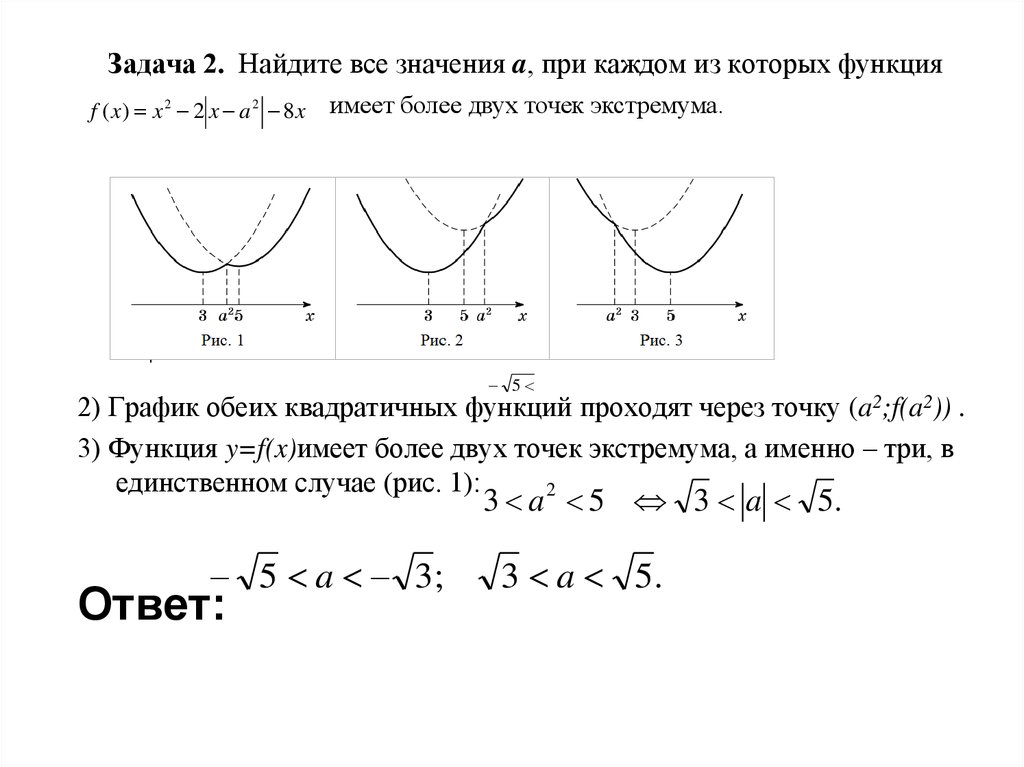
ПодробнееУзнать ответКомментировать
Вопрос B18 #3653 Математика (профиль)
При каких значениях параметра \(a\), уравнение \(g(sin x)=a\)
имеет хотя бы одно решение на отрезке \( \left [ 0; \frac{5 \pi }{6} \right ]\).
ПодробнееУзнать ответКомментировать
Вопрос B18 #3672 Математика (профиль)
Задана функция
При каких действительных значениях параметра \(a\) уравнение \({f}'(x)=0\) имеет на отрезке \(\left [ \frac{73}{12} \pi ; \frac{155}{24} \pi \right ]\) ровно два корня?
ПодробнееУзнать ответКомментировать
Вопрос B18 #3796 Математика (профиль)
При каких значениях a уравнение
имеет ровно 4 решения?
ПодробнееУзнать ответКомментировать
Вопрос B18 #3815 Математика (профиль)
При каких значениях параметра \(a\) область значений функции
\(y=ax^{2}+(2-3a)x+ \frac{9}{4}a\)
содержит отрезок \([1;4]\)
ПодробнееУзнать ответКомментировать
Вопрос B18 #3834 Математика (профиль)
Найдите все значения параметра а, при каждом из которых уравнение имеет ровно два различных действительных корня.
ПодробнееУзнать ответКомментировать
python — Найдите все положительные решения для набора линейных уравнений, используя sympy
Я не уверен, что понимаю ваш вопрос, но…
Вы можете решить первые 3 уравнения для 3 неизвестных и исключить их из 4-го уравнение вида
В [60]: s = решить([eq1, eq2, eq3], [b, g, t])
В [61]: с
Out[61]: {b: иди + sa + 11, g: -2⋅go - 2⋅sa + 48, t: -2⋅f - go + 95}
В [62]: eq4_subs = eq4.subs(s)
В [63]: eq4_subs
Out[63]: -2⋅f + go⋅(f + go) - go + sa + 95 = результат
Таким образом, b, g и t всегда являются целыми числами, если таковыми являются другие переменные.
В идеале вы могли бы решить это с помощью диофантина кроме:
В [64]: диофантина (eq4_subs) -------------------------------------------------- ------------------------- ... NotImplementedError: Решатель для inhomogeneous_general_quadratic не написан.
Похоже, что решатель для этого случая не реализован в sympy. Это частные случаи, но общий случай — нет, поэтому давайте попробуем частные случаи…
Это частные случаи, но общий случай — нет, поэтому давайте попробуем частные случаи…
Только разница результат - sa имеет значение, поэтому мы установим sa на ноль и попробуем значения для результата:
В [65 ]: для r в диапазоне (200):
...: print('result =', r, 'go, f =', diophantine(eq4_subs.subs(sa, 0).subs(result, r), syms=(go, f)))
...:
результат = 0 перейти, f = {(1, 95)}
результат = 1 иди, f = {(1, 94)}
результат = 2 иди, f = {(1, 93)}
результат = 3 иди, f = {(1, 92)}
результат = 4 иди, f = {(1, 91)}
...
результат = 94 иди, f = {(1, 1)}
результат = 95 иди, f = {(0, 0)}
результат = 96 иди, f = set()
результат = 97 иди, f = {(-t_0 - 1, t_0), (2, n1)}
результат = 98 иди, f = set()
результат = 99 иди, f = set()
результат = 100 иди, f = set()
результат = 101 иди, f = set()
результат = 102 иди, f = {(3, 1)}
результат = 103 иди, f = {(3, 2)}
...
результат = 121 иди, f = {(3, 20), (4, 7), (5, 2)}
результат = 122 иди, f = {(3, 21)}
результат = 123 иди, f = {(4, 8), (3, 22)}
результат = 124 иди, f = {(3, 23), (5, 3)}
результат = 125 иди, f = {(4, 9), (3, 24)}
.
..
результат = 193 go, f = {(8, 7), (10, 1), (6, 17), (5, 26), (4, 43), (3, 92)}
результат = 194 иди, f = {(3, 93)}
результат = 195 иди, f = {(4, 44), (3, 94), (9, 4)}
результат = 196 иди, f = {(5, 27), (3, 95)}
результат = 197 иди, f = {(6, 18), (4, 45), (7, 12), (3, 96)}
результат = 198 иди, f = {(3, 97)}
результат = 199, f = {(4, 46), (8, 8), (3, 98), (5, 28)}
Я не уверен, как это выразить в общем, но это говорит о том, что существует:
- уникальное решение для других параметров, если
результат <= 95. - конечное число решений для любого результата
>= 102. - бесконечных решений для
результатов = 97. - Никакие решения для
Преобразование отрицательного числа в положительное в Excel [Удалить отрицательный знак]
Смотреть видео – Преобразование отрицательного числа в положительное в Excel
youtube.com/embed/qDM6gbGjUkE?feature=oembed" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen="">Большинство людей, работающих с электронными таблицами Excel, имеют дело с числами в больших/малых наборах данных.
И когда вы работаете с числами, у вас будут все их типы (положительные, отрицательные, десятичные, дата/время).
Одной из распространенных задач, которую часто приходится выполнять многим из нас, является преобразование этих чисел из одного формата в другой.
И, наверное, самый распространенный из них, когда вам нужно заменить отрицательные числа на положительные числа ( удалить знак минус ) для некоторых вычислений.
И опять же, есть несколько способов сделать это в Excel.
В этом уроке я покажу вам несколько простых способов изменить отрицательные числа на положительные в Excel (используя формулы, метод копирования-вставки и другие замечательные методы).
Если вам интересно, продолжайте читать!
В этом учебном пособии рассматриваются:
Умножение на минус 1 для преобразования отрицательного числа в положительное
Если у вас есть столбец, полный чисел, и вы хотите быстро получить числа, в которых отрицательные числа были преобразованы в положительные, вы можете легко сделать это с помощью умножив эти отрицательные значения на -1.
Но вы также должны убедиться, что вы умножаете только отрицательные числа, а не положительные.
Предположим, у вас есть набор данных, как показано ниже:
Ниже приведена формула, которая преобразует отрицательные числа в положительные и оставляет остальные без изменений: В приведенной выше формуле используется функция ЕСЛИ, чтобы сначала проверить, является ли число положительным или нет. Если он положительный, знак не меняется, а если отрицательный, к ссылке добавляется отрицательный знак, что в итоге дает нам только положительное число.
Если у вас также есть текстовые значения в наборе данных, эта функция будет игнорировать это (и будут изменены только отрицательные значения)
Теперь, когда у вас есть требуемый результат, вы можете преобразовать эти формулы в значения (и скопировать
Используйте функцию ABS для замены всех отрицательных чисел на положительные
В Excel есть специальная функция, которая убирает отрицательный знак и дает вам абсолютное значение.
.. Функция ABS
Предположим, у вас есть набор данных, как показано ниже, и вы хотите изменить отрицательные значения на положительные значения.
Ниже приведена формула, которая это сделает:
=ABS(A2)
Приведенная выше функция ABS не влияет на положительные числа, но преобразует отрицательные числа в положительные значения.
Теперь, когда у вас есть требуемый результат, вы можете преобразовать эти формулы в значения (и скопировать их поверх исходных данных, если они вам не нужны)
Один небольшой недостаток функции ABS заключается в том, что она может работать только с числами. Если у вас есть текстовые данные в некоторых ячейках и вы используете функцию ABS, она даст вам #ЗНАЧ! ошибка.
Умножение с использованием специальной вставки для изменения знака
Если вы хотите изменить знак числа на противоположный (т. е. изменить отрицательное число на положительное, а положительное на отрицательное), вы также можете использовать эту специальную технику умножения вставки.
Предположим, у вас есть набор данных, как показано ниже, и вы хотите изменить знак:
Ниже приведены шаги для изменения знака с помощью специальной вставки:
- В любой пустой ячейке на листе введите -1
- Скопируйте эту ячейку (со значением -1)
- Выберите диапазон, в котором вы хотите изменить знак.
- Щелкните правой кнопкой мыши любую из выделенных ячеек
- Щелкните "Специальная вставка". Откроется диалоговое окно «Специальная вставка» .
- В опции «Вставить» выберите «Значения».
- В параметрах операции выберите «Умножение»
- Нажмите "ОК"
- Удалить -1 из ячейки
Вы заметите, что приведенные выше шаги мгновенно изменяют знак числа (т. е. положительные числа становятся отрицательными, а отрицательные числа становятся положительными).
Но что, если вы хотите преобразовать только отрицательные числа в положительные числа, а не наоборот?
В этом случае вам каким-то образом сначала нужно выбрать все отрицательные числа, а затем выполнить описанные выше действия.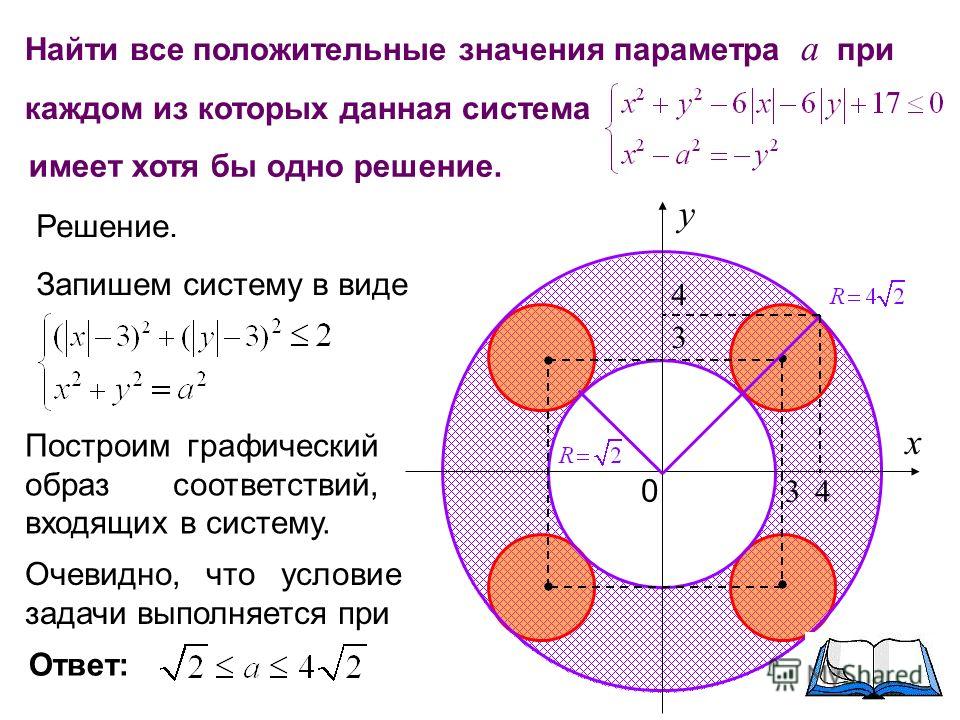
Вот как выбрать только отрицательные числа в Excel:
- Выбрать весь набор данных
- Удерживая клавишу Control, нажмите клавишу F. Это откроет диалоговое окно «Найти и заменить».
- В поле Найти введите - (знак минус)
- Нажмите «Найти все»
- Удерживая клавишу Control, нажмите клавишу A.
Вышеуказанные шаги будут выбирать только те ячейки, которые имеют отрицательный знак. Теперь, когда вы выбрали эти ячейки, вы можете использовать технику «Специальная вставка», чтобы изменить знак только отрицательных чисел.
Этот метод имеет два преимущества по сравнению с методом формул (два метода, рассмотренные ранее):
- Вам не нужно добавлять дополнительный столбец, а затем использовать формулу для получения результата в этом столбце. Вы можете использовать это в своем существующем наборе данных.
- Вам не нужно преобразовывать формулы в значения (поскольку результат, который вы получите, уже является значением, а не формулой)
Быстрое заполнение для удаления знака минуса
Быстрое заполнение — это новая функция, представленная в Excel 2013.
Позволяет быстро идентифицировать шаблоны, а затем выдает результат, в котором шаблон был применен ко всему набору данных.
Это можно использовать, когда у вас есть имена, и вы хотите разделить имя и фамилию. Как только вы пару раз наберете имя в соседней ячейке, Flash Fill определит шаблон и выдаст вам все имена.
Точно так же можно использовать для быстрого удаления отрицательного знака из числа, в то время как положительные значения остаются неизменными.
Ниже приведен набор данных, в котором у меня есть отрицательные числа, и я хочу изменить их на положительные значения.
Ниже приведены шаги по изменению отрицательных чисел на положительные с помощью Flash Fill:
- В соседнем с данными введите ожидаемый результат вручную. В этом примере я вручную введу 874
- В ячейку ниже введите ожидаемый результат (в данном примере 162)
- Выберите обе ячейки
- Поместите курсор в правую нижнюю часть выделения.
 Он изменится на значок плюса
Он изменится на значок плюса - Щелкните и перетащите, чтобы заполнить столбец (или дважды щелкните)
- Щелкните значок «Параметры автозаполнения».
- Нажмите на мгновенное заполнение
Вышеуказанные шаги дадут вам ожидаемый результат, где отрицательный знак был удален.
При использовании этого метода необходимо помнить, что Excel полагается на угадывание шаблона. Так что вам нужно будет хотя бы показать Excel, что вы конвертируете отрицательное число в положительное.
Это означает, что вам придется вручную вводить ожидаемый результат, пока вы не закроете хотя бы одно отрицательное число.
Преобразование отрицательных чисел в положительные одним щелчком мыши (VBA)
И, наконец, вы также можете использовать VBA для преобразования отрицательных значений в положительные значения.
Я бы рекомендовал использовать этот метод, если вам приходится делать это часто. Может быть, вы регулярно получаете набор данных из базы данных или от коллеги, и вам приходится делать это каждый раз.
В таком случае вы можете создать и сохранить код макроса VBA в личной книге макросов и поместить VBA на панель быстрого доступа. Таким образом, в следующий раз, когда вы получите набор данных, где вы должны сделать это, вы просто выбираете данные и щелкаете значок в QAT…
… и готово!
Не волнуйтесь, я покажу вам точные шаги, чтобы настроить и запустить это приложение.
Ниже приведен код VBA, который преобразует отрицательные значения в положительные значения в выбранном диапазоне:
Sub ChangeNegativetoPOsitive()
Для каждой выбранной ячейки
Если Ячейка.Значение < 0 Тогда
Ячейка.Значение = -Ячейка.Значение
Конец, если
Следующая ячейка
End Sub Приведенный выше код использует цикл For Next для прохождения каждой ячейки в выделенном фрагменте. Он использует оператор IF, чтобы проверить, является ли значение ячейки отрицательным или нет. Если значение отрицательное, знак меняется на противоположный, а если нет, то игнорируется.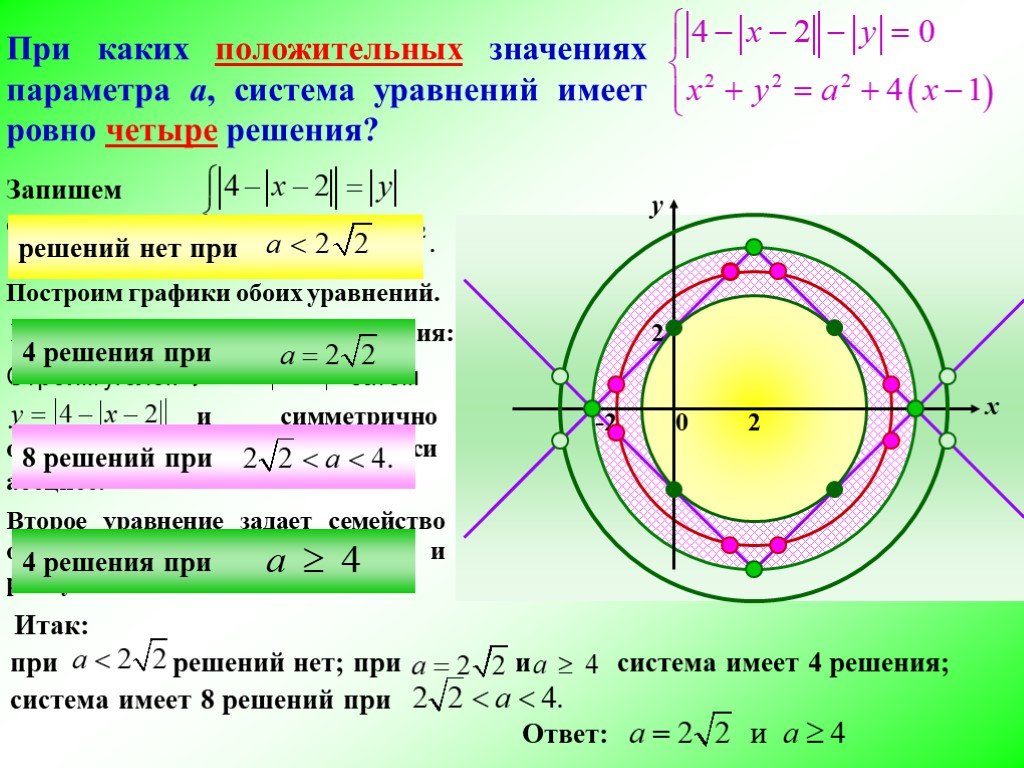
Вы можете добавить этот код в обычный модуль в рабочей книге (если вы хотите использовать его только в этой рабочей книге). И если вы хотите использовать этот код макроса в любой книге вашей системы, вы можете сохранить его в личной книге макросов.
Вот шаги для получения личной книги макросов (PMW).
Вот шаги для сохранения этого кода в PMW.
Теперь позвольте мне показать вам, как добавить этот код на панель быстрого доступа (шаги одинаковы, независимо от того, сохраняете ли вы этот код в отдельной книге или в PMW)
- Откройте книгу, в которой у вас есть данные
- Добавьте код VBA в рабочую книгу (или в PMW)
- Щелкните параметр «Настроить панель быстрого доступа» в QAT .
- Нажмите «Дополнительные команды»
- В диалоговом окне «Параметры Excel» щелкните раскрывающийся список «Выбрать команды из».
- Щелкните Макросы. Это покажет вам все макросы в книге (или личной книге макросов)
- Нажмите кнопку «Добавить»
- Нажмите OK
Теперь у вас будет значок макроса в QAT.

 Он изменится на значок плюса
Он изменится на значок плюса
Leave A Comment