Как решать задание 13 ЕГЭ по математике базового уровня – разбор заданий

Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 13 проверяются навыки решения задач по стереометрии. Школьник должен знать основные формулы по стереометрии и уметь применять их на практике. Здесь вы можете узнать, как решать задание 13 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.

ЕГЭ база все задания (263) ЕГЭ база задание 1 (5) ЕГЭ база задание 2 (6) ЕГЭ база задание 3 (45) ЕГЭ база задание 4 (33) ЕГЭ база задание 5 (2) ЕГЭ база задание 6 (44) ЕГЭ база задание 7 (1) ЕГЭ база задание 8 (12) ЕГЭ база задание 10 (22) ЕГЭ база задание 12 (5) ЕГЭ база задание 13 (20) ЕГЭ база задание 15 (13) ЕГЭ база задание 19 (23) ЕГЭ база задание 20 (32)

Все заданияЕГЭ база все задания (263)ЕГЭ база задание 1 (5)ЕГЭ база задание 2 (6)ЕГЭ база задание 3 (45)ЕГЭ база задание 4 (33)ЕГЭ база задание 5 (2)ЕГЭ база задание 6 (44)ЕГЭ база задание 7 (1)ЕГЭ база задание 8 (12)ЕГЭ база задание 10 (22)ЕГЭ база задание 12 (5)ЕГЭ база задание 13 (20)ЕГЭ база задание 15 (13)ЕГЭ база задание 19 (23)ЕГЭ база задание 20 (32)

Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна K, а боковое ребро равно N.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами K и M. Площадь ее поверхности равна S. Найдите высоту призмы.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами K и M, высота призмы равна H. Найдите площадь ее поверхности.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной K см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на N см. Ответ дайте в кубических сантиметрах.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Объем одного куба в K раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Если каждое ребро куба увеличить на K, то его объем увеличится на N. Найдите ребро куба.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Если каждое ребро куба увеличить на K, то его площадь поверхности увеличится на N. Найдите ребро куба.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Во сколько раз увеличится объем куба, если его ребра увеличить в K раз?

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в K раз?

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Диагональ куба равна d. Найдите площадь его поверхности.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.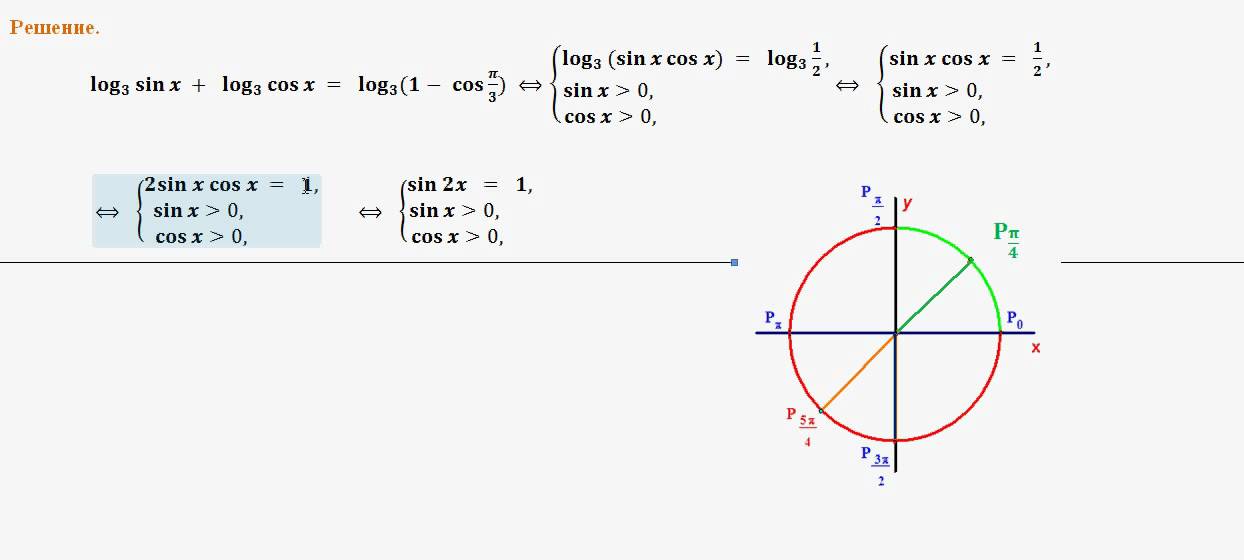

Объем куба равен V. Найдите его диагональ.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Площадь поверхности куба равна S. Найдите его диагональ.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Объем куба равен V. Найдите площадь его поверхности.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Площадь поверхности куба равна S. Найдите его объем.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Радиус основания цилиндра равен M, а его образующая равна N. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное K. Найдите площадь этого сечения.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Два ребра прямоугольного параллелепипеда равны A и B, а объём параллелепипеда равен D. Найдите площадь поверхности этого параллелепипеда.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Вода в сосуде цилиндрической формы находится на уровне h = N см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в K раз больше/меньше, чем у первого? Ответ дайте в сантиметрах.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

Объём конуса равен N. Через точку, делящую высоту конуса в отношении A:B, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

В сосуде, имеющем форму конуса, уровень жидкости достигает K/L высоты. Объём сосуда N мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

В бак, имеющий форму прямой призмы, налито N л воды. После полного погружения в воду детали уровень воды в баке поднялся в K раз. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13.

ЕГЭ. Задание 13. Тригонометрические (и не только) уравнения

Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.

Полезные материалы

Подборки видео и онлайн-курсы

  • Все ролики с заданием 13 
  • Все ролики про тригонометрию
  • Мини-курс «Как решать задачи по тригонометрии»
  • Мини-курс «Логарифм и экспонента»

Тригонометрические формулы

Геометрическая иллюстрация тригонометрических формул

 

а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} — \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.

 

а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.

Подборка заданий прошлых лет

  1. а) Решите уравнение $\dfrac{\sin x}{\sin^2\dfrac{x}{2}} = 4\cos^2\dfrac{x}{2}$. 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
    б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
  2. а) Решите уравнение $2 \sin\left( 2x + \dfrac{\pi}{3} \right) — \sqrt{3} \sin x = \sin 2x + \sqrt3$.
    б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
  3. а) Решите уравнение $2\sqrt3 \sin\left( x + \dfrac{\pi}{3} \right) — \cos 2x = 3\cos x — 1$.
    б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
  4. а) Решите уравнение $2\sin\left( 2x + \dfrac{\pi}{6} \right) — \cos x = \sqrt3\sin 2x — 1$.
    б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; 4\pi \right]$. (ЕГЭ-2018. Основная волна)
  5. а) Решите уравнение $\sqrt2\sin\left( \dfrac{\pi}{4} + x \right) + \cos 2x = \sin x — 1$. 2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ — \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)

Подготовка к тестам (для подростков)

Вы только что узнали, что в пятницу у вас будет контрольная по математике — в тот же день, что и ваш большой контрольный по истории и еженедельная викторина по испанским глаголам. Они сумасшедшие? Как вы будете делать все свое обучение?

Не паникуйте. Есть несколько секретов хорошей учебы. Эти 5 советов по обучению помогут вам уверенно сдавать тесты.

1. Начните учиться в школе

Подготовка к тестам и викторинам фактически начинается задолго до того, как вы даже узнаете, что вам предстоит сдавать тест. Хорошие методы обучения начинаются в классе, когда вы делаете записи. Ведение заметок — это способ вспомнить, чему вас учили или о чем вы читали.

Одним из способов ведения заметок является запись фактов, которые учитель упоминает или пишет на доске во время урока. Если вы что-то упустили, попросите учителя обсудить с вами факты после урока.

Организуйте свои заметки по темам и убедитесь, что их легко читать и просматривать. Это может означать, что вам нужно переписать некоторые заметки дома или в свободное время, пока урок еще свеж в вашей памяти.

К сожалению, в большинстве школ нет классов, на которых учат делать заметки. Когда дело доходит до хороших заметок, может потребоваться некоторое время, чтобы понять, что работает, поэтому не сдавайтесь.

2. Планируйте свое учебное время

Когда вы садитесь за учебу, подумайте, сколько времени вы хотите посвятить каждой теме. Это поможет вам не переутомляться.

Если сегодня понедельник, а в пятницу у вас три контрольных, подсчитайте, сколько времени вам нужно на учебу в этот период. Затем подсчитайте, сколько времени займет изучение каждого предмета. Например, еженедельный тест по испанским глаголам, вероятно, не будет таким интенсивным, как большой тест по истории. Таким образом, вам не нужно будет выделять столько времени на изучение испанского языка, а если вы будете разбивать его на небольшое количество каждый вечер, это даже лучше.

Еще один метод обучения называется «разбиение на части» — разбиение больших тем на части. Допустим, у вас есть тест по истории Второй мировой войны. Вместо того, чтобы думать об изучении всей Второй мировой войны (что может ошеломить даже эксперта), попробуйте разбить свои учебные сессии на двухгодичные периоды или изучить материал по конкретным сражениям.

Большинство людей могут хорошо концентрироваться в течение примерно 45 минут. После этого вы, вероятно, захотите сделать небольшой перерыв. Если вы обнаружите, что отвлекаетесь и думаете о других вещах во время учебы, верните свое внимание назад. Напомните себе, что когда ваши 45 минут учебы истекут, вы можете сделать 15-минутный перерыв.

стр. 2

3. Обучение в зависимости от типа экзамена, который вы сдаете

Многие учителя заранее сообщают учащимся формат экзамена. Это может помочь вам адаптировать то, как вы учитесь. Например, если вы знаете, что у вас будут вопросы с несколькими вариантами ответов о Второй мировой войне, вы будете знать, что нужно сосредоточиться на изучении фактов и деталей. Но если экзамен будет содержать вопросы для эссе, вам следует подумать о том, какие темы, скорее всего, будут затронуты. Затем придумайте несколько возможных тем для эссе и используйте свои заметки, книги и другие справочные источники, чтобы выяснить, как вы могли бы ответить на вопросы по этим темам.

Во время учебы просматривайте свои заметки и любую специальную информацию из учебника. Если нужно, прочитайте несколько раз и запишите любые фразы или мысли, которые помогут вам запомнить основные идеи или концепции.

Пытаясь запомнить даты, имена или другую фактическую информацию, имейте в виду, что обычно требуется несколько попыток, чтобы что-то вспомнить правильно. Это одна из причин, по которой стоит начать заниматься задолго до экзамена. Используйте специальные триггеры памяти, которые мог предложить учитель или которые вы придумываете сами.

В случае задач или уравнений по математике или естествознанию, сделайте несколько практических задач. Обращайте особое внимание на все, на что учитель делал акцент в классе. (Вот тут-то и пригодится хорошее ведение записей!)

Некоторым людям помогает преподавание того, что они изучают, вслух воображаемому ученику. Или работайте с партнером по учебе и по очереди учите вслух. Другой метод обучения – это создание карточек, в которых кратко изложены некоторые важные факты или концепции. Затем вы можете использовать их для просмотра теста.

стр. 3

4. Не поддавайтесь желанию откладывать

Заманчиво откладывать учебу до последней минуты (также известное как прокрастинация). К сожалению, к тому времени, когда учащиеся переходят в старшие классы, происходит так много всего, что обычно нет места для прокрастинации.

Если вы прокрастинатор (а кто иногда не прокрастинирует?), один из лучших способов преодолеть это — оставаться организованным. После того, как вы записали даты тестов и сроков выполнения проекта в календаре, их трудно игнорировать. А когда вы садитесь за организацию и планирование своей работы, вы действительно показываете, сколько времени это занимает. Организация усложняет прокрастинацию.

Иногда люди откладывают учебу, потому что чувствуют себя подавленными из-за того, что отстают, или просто чувствуют себя неорганизованными. Не позволяйте этому случиться с вами. Держите свои заметки в порядке, следите за необходимым чтением и следуйте другим советам по обучению, упомянутым ранее, чтобы оставаться сосредоточенным и контролировать ситуацию. Ваши учителя предупредят вас о важных тестах, чтобы у вас было достаточно времени для подготовки к тому типу экзамена, который вы будете сдавать.

Но что, если вы чувствуете себя перегруженным всеми делами, которые вам нужно сделать? Ограничивают ли занятия или внеклассные мероприятия ваше время для надлежащей учебы? Попросите учителей помочь расставить приоритеты. Возможно, вам придется привлечь людей, ответственных за вашу деятельность, например вашего тренера, учителя музыки или драмы, к выработке решения.

Не ждите до последней минуты, чтобы поговорить со своими учителями, иначе вы просто будете выглядеть как прокрастинатор! И не бойтесь просить о помощи. Учителя уважают студентов, которые вдумчивы и заинтересованы в учебе и успеваемости.

5. Начать учебную группу

Иногда может быть полезно обсудить вещи с людьми, которые готовятся к тому же тесту: Вы можете убедиться, что ваши записи верны и что вы понимаете предмет. Учебные группы также полезны, потому что вы можете работать вместе, чтобы придумать способы запомнить концепции, а затем проверить друг друга.

Тем не менее, для некоторых людей, которые легко отвлекаются, учебные группы означают катастрофу, потому что они отвлекаются от темы. Когда вы в компании друзей или одноклассников, вы можете проводить больше времени за общением, чем за учебой. Один из способов обеспечить тишину и концентрацию при занятиях в группе — это заниматься в библиотеке. Вам придется вести себя более сдержанно, чем если бы вы сидели за чьим-то кухонным столом.

В конце концов, все сводится к тому, что лучше всего подходит именно вам. Если вам нравится учиться в одиночестве и вы чувствуете себя наиболее уверенно, делая это таким образом, это здорово. Если вы думаете, что хотели бы работать в группе, попробуйте — просто помните о недостатках.

Расплата

Когда вы закончите изучение, вы должны чувствовать, что можете с уверенностью подойти к тесту или викторине — не обязательно, что вы получите 100% правильных ответов, но что вы хорошо понимаете информацию .

Прежде всего, не паникуйте, если вы не можете вспомнить некоторые факты в ночь перед тестом. Даже если вы потратили весь вечер на изучение, мозгу нужно время, чтобы переварить всю эту информацию. Вы будете удивлены тем, что вернется к вам после сна.

Проверил: D’Arcy Lyness, PhD

Дата проверки: сентябрь 2016 г.

12 математических приемов, которые помогут решать задачи без калькулятора | by Andrew Jamieson

Разработайте это в уме

Photo by Crissy Jarvis на Unsplash

1.

Дополнение

Первый трюк состоит в том, чтобы упростить задачу, разбив ее на более мелкие части. Например, мы можем переписать

 567 + 432 
 = 567 + (400 + 30 + 2) 
 = 967 + 30 + 2 
 = 997 + 2 
 =  999

Переключить

Часто проще работать с добавлением меньшего числа, поэтому вместо 131 + 858 поменяйте местами числа

 858 + 131 
 = 858 + 100 
 =  989

2. Вычитание

Использование дополнения числа может облегчить вычитание. Дополнение — это разница между исходным числом и круглым числом, скажем, 100, 1000.

Вот несколько примеров с числом и его дополнением по сравнению со 100:

 67:33, 45:55, 89:11, 3:97

Обратите внимание, что вторые цифры в сумме составляют 10, а первая цифра в сумме составляет 9.

Вот как это может быть полезно

 721– 387 
 # дополнение 87 равно 13, поэтому мы можем поменять местами 387 с 400 – 13 
 -> 721 – (400 – 13) 
 = 321 – -13 
 = 321 + 13 
 =  334

Другой метод: чтобы записать большее число, чтобы оно заканчивалось на 99. Тот же пример:

 721 -> (699 + 22) 
 = 699 – 387 + 22 
 = 312 + 22 
 =  334
Photo by Chris Liverani on Unsplash

умножение:

 35 x 11 
 -> 3  _  5 
 -> 3+5 = 8 
 -> 3  8  5

Если сумма больше 10, добавьте разряд десятков в следующий столбец влево и впишите в ответ цифру единиц. Например, 4+8 = 12, запишите 2 и перенесите 1 в следующий столбец.

 48 x 11 
 -> 4_8 
 -> 4+8 = 12 
 -> 4,12,8 
 ->  528

Процесс немного сложнее для трехзначных и более чисел, но он работает аналогичным образом. На этот раз сохраните первую и последнюю цифру и суммируйте цифры попарно

 725 X 11 
 -> 7__5 
 -> 7_,(7+2=9), (2+5=7), _5 
 ->  7975  51973 x 11 
 -> 5__3 
 -> 5_,(5+1=6),(1+9=10), (9+7=16), (7+3=10), _3 
 # где сумма больше десяти, мы перемещаем цифру десятков в следующий столбец 
 -> 5,(6+1),(0+1),(6+1),(0),3 
 ->  571703

4.

Девятки

Умножение на девятки можно упростить, умножив на 10 и вычитание исходного числа

 799 x 9 
 = 799 x (10 -1) 
 = 7990 – 799 
 =  7191

. (90–1)
= (70 х 90) + (2 х 90) — 72
= 6300 + 180–72
= 6408

5. Как решать квадраты 92


= 4200 + 25
= 4225

6. Метод сближения

Аналогичный метод работает для умножения близких друг к другу чисел. Формула работает для всех чисел, но она не упрощается, если числа не похожи.

Вот формула. n — «базовое» число

 (n+a)(n+b) = n(n + a + b) + ab

Пример:

 47 x 43 
 = (40 + 7)(40 + 3) 
 = 40 х (40 + 3 + 7) + (7 х 3) 
 = (40 х 50) + (7 х 3) 
 = 2000 + 21 
 =  2021

В этом примере сумма единиц составляет десять, поэтому наше «базовое» число и множитель — круглые числа (40 и 50).

Вот еще один пример. Уменьшите меньшее число, чтобы получить ближайшее круглое число — наше базовое число, в данном случае 40. Добавьте разницу к большему числу. Умножьте основание и большее число. Наконец, добавьте произведение разницы между исходными числами и базовым числом.

 47 х 42 
 = (40 + 7) х (40 + 2) 
 = (40 + 7 + 2) х 40 + (7 х 2) 
 = (49 х 40) + (7 х 2) 
 = (40 х 40) + (40 х 9) + (7 х 2) 
 = 1600 + 360 + 14 
 =  1974

Можно также округлить до основания. Поскольку исходные числа меньше основания, мы добавляем произведение двух отрицательных чисел.

 47 х 42 
 = (50 х 39) + (-3 х -8) 
 = (50 х 30) + (50 х 9) + (-3 х -8) 
 = 1500 + 450 + 24 
 =  1974

Это работает и для трехзначных чисел. В этом случае основное число находится между нашими числами, поэтому произведение является отрицательным числом.

 497 х 504 
 = (500 – 3) х (500 + 4) 
 = (500) х (500 + 4 – 3) + (-3 х 4) 
 = 500 х 501 – 12 
 = 250 000 + 500 – 12 
 =  250 488
Photo by Sandro Schuh на Unsplash

7.

Упрощение вычислений

Вы можете упростить некоторые уравнения еще до того, как начнете. Например, разделить и делитель, и делимое на два.

 898 / 4 
 = 449 / 2 
 = 224 и ½

Обратите внимание, что при использовании этого метода остаток нужно записать в виде дроби:

 898/4 имеет остаток 2 — делится на 4 
 449/2 имеет остаток 1 — делится на 2

Дробь та же, но абсолютное число другое.

При делении на 5 измените уравнение, умножив на 2. Гораздо проще делить на 10. Например:

 1753/5 
 = 3506 / 10 
 =  350,6

8. Признак делимости 900

Есть много способов быстро определить, является ли число фактором.

2 : Число четное.

 Пример: 28790 четно, поэтому делится на 2.

3 : Сумма цифр делится на 3.

 Пример: 1281 -> 1+2+8+1 = 12 
 -> 12 кратно 3, поэтому 1281 делится на 3

4 : Последние две цифры делятся на 4. Почему это работает? 100 кратно 4, поэтому нам нужно проверить только две последние цифры.

 Пример: 1472, 72 делится на 4, поэтому 1472 делится на 4.

5 : Число оканчивается на 5 или 0.

 Пример: 575 оканчивается на 5, поэтому оно делится на ноль

6 : Число четное, сумма цифр делится на 3 6 — это 3 x 2, поэтому применяются правила 2 и 3.

 Пример: 774 четно и 7+7+4 = 18 
 -> 18 делится на 3, поэтому 774 делится на 6. заканчивается нулем. Отбросьте последнюю цифру с нулем и повторите процесс. Продолжайте, пока не сможете определить, делится ли результат на 7. 
 
 Пример: 2702 добавить 98 (7 x 14) -> 2800, отбросить нули 
 -> 28 кратно 7, поэтому 2702 делится на 7. 
  8  : Последние три цифры делятся на 8
 Пример: 79256, 256 делится на 8, поэтому 79256 делится на 8. (Альтернативное правило: если цифра сотен  четная  , последние  2  цифр делятся на 8, если цифра сотен  нечетная  , последние  2  цифр  + 4  делится на 8) 
  9  : То же правило, что и для 3, но с 9. Если сумма цифр делится на 9, то число делится на 9.
 Пример: 13671 -> 1+3+6+7+1 = 18 
 -> 18 делится на 9, поэтому 13671 делится на 9 
  10  : Число оканчивается на 0.
 Пример: 280 оканчивается на 0, 280 делится на 10 
 10:0909 Аналогичное правило до 3 и 9, начните с правой цифры и попеременно вычитайте и добавляйте оставшиеся цифры. Если ответ равен нулю или кратен 11, то число делится на 11.
 Пример: 12727 -> 1 - 2 + 7 - 2 + 7 = 11, поэтому 12727 делится на 11. 
 Вы можете ознакомиться с некоторыми дополнительными методами здесь.
 9. Деление больших чисел на 9
 Пример: 
 -> 10520/9 
 Напишите первую цифру над уравнением и напишите «R» (для остатка) над последней цифрой. Добавьте число, которое вы только что написали, и число по диагонали ниже и справа от него. Запишите это новое число во втором месте. Добавьте это число к числу по диагонали ниже и справа. Продолжайте этот процесс, пока не дойдете до R.
 Суммируйте числа одного цвета, чтобы получить следующую цифру.
 Наконец, добавьте последнюю цифру к числу под буквой R, чтобы получить остаток.
 10520/9 
 =  1168 R8  
 или 1168,889 
 Вот еще пример:
 -> 57423/9 
 внизу и справа больше десяти (5+7=12). Ставим единицу над первой цифрой и вычитаем девять  от него. (Мы делим по основанию девять, поэтому мы вычитаем девять, а не десять). Поместите полученное число на вторую позицию (12–9 = 3). Продолжайте тот же процесс.
 В этом примере остаток больше 9 (9+3 = 12). Снова переносим единицу выше предыдущей цифры и вычитаем девять из остатка, оставляя три. Теперь добавьте результат и цифры переноса.
 57423 / 9 
 =  6380 R3 
  или 6380,333 
Фото Элисон Панг на Unsplash
 10. Переверните вопрос
 Проценты являются ассоциативными, поэтому иногда обратный порядок вопросов облегчает вычисления.
 Пример: 
 Что составляет 36% от 25 
 -> равно 25% от 36 
 -> 25% равно ¼ 
 -> 36/4 = 9 
 36% от 25 равно  9  
 11.
 Дроби
 Как вы видите, использование ¼ в последнем примере помогает узнать дроби и то, как они связаны с процентами.
 1/2 = 50 %1/3 = 33,33 %, 2/3 = 66,67 %, 1/4 = 25 %, 3/4 = 75 %1/5 = 20 %, 2/5 = 40 % …1 /6 = 16,67%, 5/6 = 83,33% (2/6 = 1/3, 3/6 = 1/2, 4/6 = 2/3) 1/7 = 14,2857%, 2/7 = 28,5714% , 3/7 = 42,8571 %, 4/7 = 57,1428 % (обратите внимание на повторяющийся шаблон 0,142857) 1/8 = 12,5 %, 3/8 = 37,5 %, 5/8 = 62,5 %, 7/8 = 87,5 %1 /9= 11,11 %, 2/9 = 22,22 %, 3/9 = 33,33 % … 1/10 = 10 %, 2/10 = 20 % … 1/11 = 9,09 %, 2/11 = 18,18 %, 3/11 = 27,27% …1/12 = 8,33%, 5/12 = 41,67%, 7/12 = 58,33%, 11/12 = 91,67% 
 12. Правило 72
 Правило 72 позволяет оценить, сколько лет потребуются инвестиции, чтобы удвоить стоимость при заданном процентном доходе. Он работает путем деления 72 на процент, а ответом является количество лет, которое потребуется, чтобы удвоиться.
 2% -> 72/2 = 36, примерно 36 лет, чтобы удвоить 
 8% -> 72/8 = 9, примерно 9 лет, чтобы удвоить 
 Обратите внимание, что правило 72 является ориентиром, основанным на натуральном логарифме 2, что дает 0,693.