Результаты ЕГЭ по математике: ряд наблюдений
Единый государственный экзамен по математике в нашей стране обязан сдавать каждый школьник, оканчивающий курс средней школы. Не будем вдаваться в подробности возможных изменений формы экзамена и тех исключительных случаев, когда выпускник, являясь победителем, например, Всероссийской олимпиады, автоматически получает за ЕГЭ 100 баллов.
Рассмотрим результаты Единого государственного экзамена по математике в предыдущие годы, когда он содержал одновременно и совсем простые задачи, и усложненные, но решаемые выпускниками обычных школ, и очень сложные, требующие специальной подготовки. Если опираться на статистику, опубликованную на Официальном информационном портале Единого государственного экзамена ( http://ege.edu.ru/ru/main/satistics-ege/ ), картина получается следующая:
Результаты недавнего ЕГЭ по математике
Фактически весь 11-й класс (а иногда – и дольше) готовятся школьники к выпускному экзамену, который для некоторых из них является и вступительным.
Интересно сравнить результаты ЕГЭ по математике с результатами ЕГЭ по русскому языку.
Результаты ЕГЭ по математике и по русскому языку
Мы видим, что успешно сдать русский язык было несравненно легче. Перелом в баллах происходит в районе 60-ти. Это показывает и средний балл: по русскому языку – 63,4, по математике – 48,7.
При этом на 100 баллов работу написали: по русскому языку – 2559 человек, а по математике – 538 (т.е. почти в пять раз меньше), что менее 0,07% от всех результатов.
Именно по математике – самый низкий процент максимальных результатов среди всех предметов, сдаваемых в форме ЕГЭ! И это еще «оптимистичная» статистика! Не так давно, после серии скандалов вокруг ЕГЭ, высокие результаты тщательно перепроверили, и в итоге по математике максимальный балл получили только 64 человека – в 8,4 раза меньше, чем за год до этого! Уменьшилась в результате проверок и доля выпускников, сдавших более, чем на 80 баллов.
Теперь рассмотрим результаты выпускников того же года, прошедших обучение в «Математушке». Более 70-ти баллов здесь набрали 32 человека, из них: 71-80 – 19 человек, 81-90 – 9 человек, 91-100 – 4 человека.
Сейчас – это студенты Московского государственного университета им. М.В. Ломоносова, Национального исследовательского института «Высшая школа экономики», Российского экономического университета им. Г.В. Плеханова, Московского государственного института международных отношений (МГИМО), Московского государственного технического университета им. Н.Э. Баумана, Федерального университета при правительстве Российской Федерации и других престижных вузов нашей столицы.
Есть среди выпускников «Математушки» и 100-балльный результат за ЕГЭ. Его получил Иван Павлов в год, когда на максимальный балл экзамен сдали всего 157 человек из 43 регионов России. Логично, что среди всех факультетов Иван выбрал мехмат МГУ. Очень близок к этому результату был Константин Славнов, поступивший на факультет ВМиК МГУ.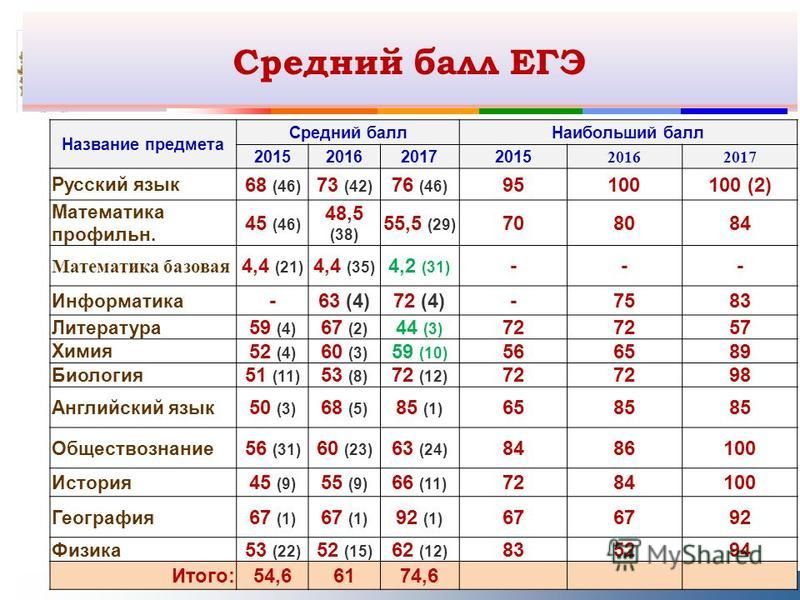 Он сдал ЕГЭ на 98% (тогда на 100 баллов ЕГЭ по математике сдали 214 человек, что составило 0,03% от всех выпускников).
Он сдал ЕГЭ на 98% (тогда на 100 баллов ЕГЭ по математике сдали 214 человек, что составило 0,03% от всех выпускников).
Таким образом, «Математушка» тщательно готовит своих выпускников, и они успешно сдают Единый государственный экзамен не только на высокие, но даже на максимальные баллы! Что, как можно было видеть по статистике ЕГЭ, является весьма и весьма редким результатом.
Автор статьи: Елена Чач
Павлов Иван
Победитель олимпиады в МГТУ им. Баумана (диплом 1-й степени), Московской математической олимпиады (диплом 3-й степени), олимпиады «Покори Воробьёвы горы» (диплом 2-й степени), Межвузовской олимпиады (диплом 1-й степени), межпрофильной олимпиады НИУ-ВШЭ (профиль «прикладная математика») (диплом 1-й степени), олимпиады «Ломоносов-2010» (диплом 2-й степени).
Результат ЕГЭ 100
Поступил на механико-математический ф-т МГУ.
Литвинова Анна
Победительница олимпиады «Физтех» по математике (диплом 3-й степени), межрегиональной олимпиады школьников по математике САММАТ (диплом 3-й степени)
Результат ЕГЭ 99
Поступила в МГУ им.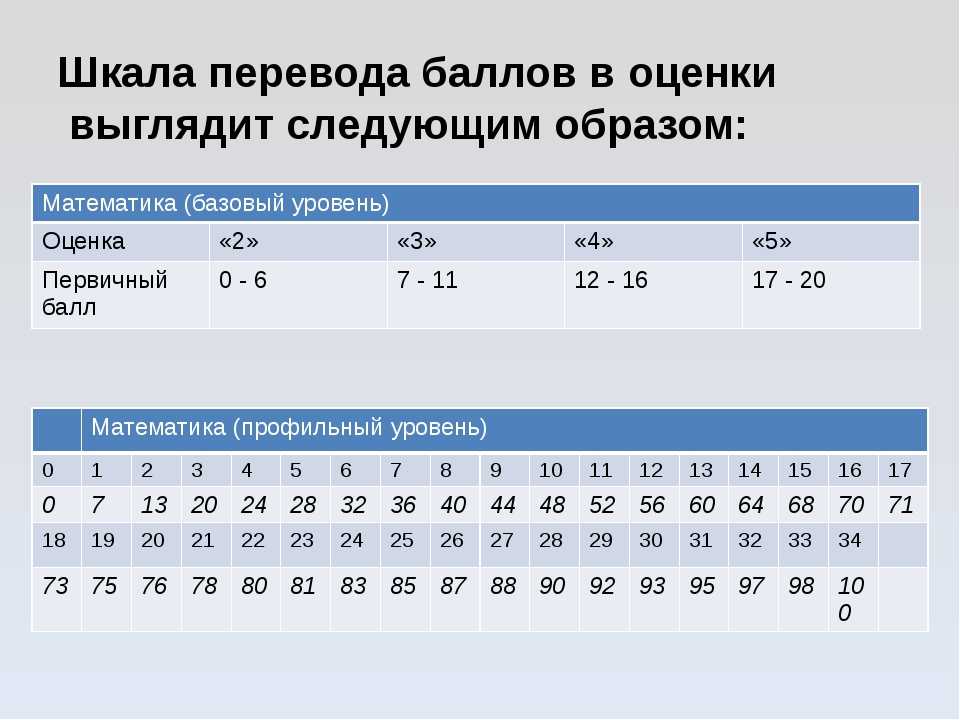 Ломоносова, экономический ф-т.
Ломоносова, экономический ф-т.
Горовцов Пётр
Победитель отраслевой физико-математической олимпиады школьников «Росатом» по математике (диплом 2-й степени), объединённой межвузовской математической олимпиады (диплом 3-й степени)
Результат ЕГЭ 100
Поступил в МФТИ, ф-т физической и квантовой электроники.
Макаров Станислав
Победитель объединённой межвузовской математической олимпиады (диплом 3-й степени), олимпиады МФТИ (диплом 3-й степени)
Результат ЕГЭ 98
Поступил в НИУ ВШЭ, ф-т международный институт экономики и финансов.
Самойлова Ульяна
Победительница объединённой межвузовской математической олимпиады (диплом 3-й степени), СПбГУ (диплом 2 — й степени), олимпиады МФТИ (диплом 3 — й степени)
Результат ЕГЭ 100 (победительница олимпиады)
Поступила в МГУ, экономический ф-т
Колчин Дмитрий
Победитель олимпиады школьников «Ломоносов» по математике (диплом 3-й степени), объединённой межвузовской математической олимпиады (диплом 1-й степени)
Результат ЕГЭ 92
Поступил в ИТМО, ф-т информационных технологий и программирования.
Купцова Анастасия
Победительница олимпиады МГУ «Ломоносов» (диплом 2-й степени), олимпиады МФТИ (диплом 2-й степени), объединённой межвузовской математической олимпиады (диплом 3-й степени)
Результат ЕГЭ 95
Поступила в НИУ ВШЭ, ф-т экономики
Смотреть ещё…
Шкала перевода баллов ЕГЭ 2023
Школьный портал → Перевод баллов ЕГЭ в 2023 году
Как переводить первичные баллы в тестовые по результатам ЕГЭ 2023 года.
Первичный балл — сумма баллов за правильно выполненные задания экзамена. Вторичный (тестовый) балл учитывается при поступлении в вуз.
Внимание: данные регулярно актуализируются по мере поступления официальной информации.
Содержание:
- Оценки по математике (база)
- Баллы по математике (профиль)
- Баллы по русскому языку
- Баллы по литературе
- Баллы по биологии
- Баллы по истории
- Баллы по информатике и ИКТ
- Баллы по обществознанию
- Баллы по химии
- Баллы по физике
- Баллы по географии
- Баллы по иностранным языкам
- Количество баллов за каждое задание
- Минимальные баллы для вуза и аттестата
Шкала перевода баллов ЕГЭ в 100-балльную систему
Математика (база)
| Балл | Оценка |
| 0-6 | 2 |
| 7-11 | 3 |
| 12-16 | 4 |
| 17-20 | 5 |
Баллы по математике (база) не учитываются при поступлении в ВУЗ!
Математика (профиль)
| Первичный балл | Тестовый балл |
| 1 | 5 |
| 2 | 9 |
| 3 | 14 |
| 4 | 18 |
| 5 | 23 |
| 6 | 27 |
| 7 | 33 |
| 8 | 39 |
| 9 | 45 |
| 10 | 50 |
| 11 | 56 |
| 12 | 62 |
| 13 | 68 |
| 14 | 70 |
| 15 | 72 |
| 16 | 74 |
| 17 | 76 |
| 18 | 78 |
| 19 | 80 |
| 20 | 82 |
| 21 | 84 |
| 22 | 86 |
| 23 | 88 |
| 24 | 90 |
| 25 | 92 |
| 26 | 94 |
| 27 | 96 |
| 28 | 98 |
| 29 | 99 |
| 30 | 100 |
| 31 | 100 |
| 32 | 100 |
Русский язык
| Первичный балл | Тестовый балл |
| 1 | 3 |
| 2 | 5 |
| 3 | 8 |
| 4 | 10 |
| 5 | 12 |
| 6 | 15 |
| 7 | 17 |
| 8 | 20 |
| 9 | 22 |
| 10 | 24 |
| 11 | 26 |
| 12 | 28 |
| 13 | 30 |
| 14 | 32 |
| 15 | 34 |
| 16 | 36 |
| 17 | 38 |
| 18 | 39 |
| 19 | 40 |
| 20 | 41 |
| 21 | 43 |
| 22 | 44 |
| 23 | 45 |
| 24 | 46 |
| 25 | 48 |
| 26 | 49 |
| 27 | 50 |
| 28 | 51 |
| 29 | 53 |
| 30 | 54 |
| 31 | 55 |
| 32 | 56 |
| 33 | 57 |
| 34 | 59 |
| 35 | 60 |
| 36 | 61 |
| 37 | 62 |
| 38 | 64 |
| 39 | 65 |
| 40 | 66 |
| 41 | 67 |
| 42 | 69 |
| 43 | 70 |
| 44 | 71 |
| 45 | 72 |
| 46 | 73 |
| 47 | 76 |
| 48 | 78 |
| 49 | 80 |
| 50 | 82 |
| 51 | 85 |
| 52 | 87 |
| 53 | 89 |
| 54 | 91 |
| 55 | 94 |
| 56 | 96 |
| 57 | 98 |
| 58 | 100 |
Литература
| Первичный балл | Тестовый балл |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| 7 | 15 |
| 8 | 18 |
| 9 | 20 |
| 10 | 22 |
| 11 | 24 |
| 12 | 26 |
| 13 | 28 |
| 14 | 30 |
| 15 | 32 |
| 16 | 34 |
| 17 | 35 |
| 18 | 36 |
| 19 | 37 |
| 20 | 38 |
| 21 | 40 |
| 22 | 41 |
| 23 | 42 |
| 24 | 43 |
| 25 | 44 |
| 26 | 45 |
| 27 | 47 |
| 28 | 48 |
| 29 | 49 |
| 30 | 50 |
| 31 | 51 |
| 32 | 52 |
| 33 | 54 |
| 34 | 55 |
| 35 | 56 |
| 36 | 57 |
| 37 | 58 |
| 38 | 59 |
| 39 | 61 |
| 40 | 62 |
| 41 | 63 |
| 42 | 64 |
| 43 | 65 |
| 44 | 66 |
| 45 | 68 |
| 46 | 69 |
| 47 | 70 |
| 48 | 71 |
| 49 | 72 |
| 50 | 73 |
| 51 | 77 |
| 52 | 80 |
| 53 | 84 |
| 54 | 87 |
| 55 | 90 |
| 56 | 94 |
| 57 | 97 |
| 58 | 100 |
Биология
| Первичный балл | Тестовый балл |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 12 |
| 6 | 14 |
| 7 | 16 |
| 8 | 18 |
| 9 | 21 |
| 10 | 23 |
| 11 | 25 |
| 12 | 27 |
| 13 | 30 |
| 14 | 32 |
| 15 | 34 |
| 16 | 36 |
| 17 | 38 |
| 18 | 39 |
| 19 | 40 |
| 20 | 42 |
| 21 | 43 |
| 22 | 44 |
| 23 | 46 |
| 24 | 47 |
| 25 | 48 |
| 26 | 50 |
| 27 | 51 |
| 28 | 52 |
| 29 | 53 |
| 30 | 55 |
| 31 | 56 |
| 32 | 57 |
| 33 | 59 |
| 34 | 60 |
| 35 | 61 |
| 36 | 63 |
| 37 | 64 |
| 38 | 65 |
| 39 | 66 |
| 40 | 68 |
| 41 | 69 |
| 42 | 70 |
| 43 | 72 |
| 44 | 73 |
| 45 | 74 |
| 46 | 76 |
| 47 | 77 |
| 48 | 78 |
| 49 | 79 |
| 50 | 82 |
| 51 | 84 |
| 52 | 86 |
| 53 | 89 |
| 54 | 91 |
| 55 | 93 |
| 56 | 96 |
| 57 | 98 |
| 58 | 100 |
История
| Первичный балл | Тестовый балл |
| 1 | 4 |
| 2 | 8 |
| 3 | 11 |
| 4 | 15 |
| 5 | 18 |
| 6 | 22 |
| 7 | 25 |
| 8 | 29 |
| 9 | 32 |
| 10 | 34 |
| 11 | 35 |
| 12 | 36 |
| 13 | 37 |
| 14 | 38 |
| 15 | 40 |
| 16 | 41 |
| 17 | 42 |
| 18 | 43 |
| 19 | 44 |
| 20 | 45 |
| 21 | 47 |
| 22 | 48 |
| 23 | 49 |
| 24 | 50 |
| 25 | 51 |
| 26 | 52 |
| 27 | 54 |
| 28 | 55 |
| 29 | 56 |
| 30 | 57 |
| 31 | 58 |
| 32 | 60 |
| 33 | 61 |
| 34 | 62 |
| 35 | 63 |
| 36 | 64 |
| 37 | 65 |
| 38 | 67 |
| 39 | 68 |
| 40 | 69 |
| 41 | 70 |
| 42 | 71 |
| 43 | 72 |
| 44 | 75 |
| 45 | 77 |
| 46 | 79 |
| 47 | 81 |
| 48 | 83 |
| 49 | 85 |
| 50 | 88 |
| 51 | 90 |
| 52 | 92 |
| 53 | 94 |
| 54 | 96 |
| 55 | 98 |
| 56 | 100 |
Информатика
| Первичный балл | Тестовый балл |
| 1 | 7 |
| 2 | 14 |
| 3 | 20 |
| 4 | 27 |
| 5 | 34 |
| 6 | 40 |
| 7 | 42 |
| 8 | 44 |
| 9 | 46 |
| 10 | 48 |
| 11 | 50 |
| 12 | 51 |
| 13 | 53 |
| 14 | 55 |
| 15 | 57 |
| 16 | 59 |
| 17 | 61 |
| 18 | 62 |
| 19 | 64 |
| 20 | 66 |
| 21 | 68 |
| 22 | 70 |
| 23 | 72 |
| 24 | 73 |
| 25 | 75 |
| 26 | 77 |
| 27 | 79 |
| 28 | 81 |
| 29 | 83 |
| 30 | 84 |
| 31 | 88 |
| 32 | 92 |
| 33 | 96 |
| 34 | 100 |
| 35 | 100 |
Обществознание
| Первичный балл | Тестовый балл |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
| 6 | 12 |
| 7 | 14 |
| 8 | 16 |
| 9 | 18 |
| 10 | 20 |
| 11 | 21 |
| 12 | 23 |
| 13 | 25 |
| 14 | 27 |
| 15 | 29 |
| 16 | 31 |
| 17 | 33 |
| 18 | 35 |
| 19 | 37 |
| 20 | 39 |
| 21 | 41 |
| 22 | 42 |
| 23 | 44 |
| 24 | 45 |
| 25 | 46 |
| 26 | 47 |
| 27 | 48 |
| 28 | 49 |
| 29 | 51 |
| 30 | 52 |
| 31 | 53 |
| 32 | 54 |
| 33 | 55 |
| 34 | 56 |
| 35 | 57 |
| 36 | 59 |
| 37 | 60 |
| 38 | 61 |
| 39 | 62 |
| 40 | 63 |
| 41 | 64 |
| 42 | 66 |
| 43 | 67 |
| 44 | 68 |
| 45 | 69 |
| 46 | 70 |
| 47 | 71 |
| 48 | 72 |
| 49 | 74 |
| 50 | 76 |
| 51 | 77 |
| 52 | 79 |
| 53 | 81 |
| 54 | 83 |
| 55 | 85 |
| 56 | 86 |
| 57 | 88 |
| 58 | 90 |
| 59 | 92 |
| 60 | 93 |
| 61 | 95 |
| 62 | 97 |
| 63 | 99 |
| 64 | 100 |
Химия
| Первичный балл | Тестовый балл |
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| 5 | 15 |
| 6 | 18 |
| 7 | 21 |
| 8 | 24 |
| 9 | 27 |
| 10 | 30 |
| 11 | 33 |
| 12 | 36 |
| 13 | 39 |
| 14 | 41 |
| 15 | 42 |
| 16 | 43 |
| 17 | 44 |
| 18 | 46 |
| 19 | 47 |
| 20 | 48 |
| 21 | 49 |
| 22 | 50 |
| 23 | 52 |
| 24 | 53 |
| 25 | 54 |
| 26 | 55 |
| 27 | 56 |
| 28 | 58 |
| 29 | 59 |
| 30 | 60 |
| 31 | 61 |
| 32 | 62 |
| 33 | 64 |
| 34 | 65 |
| 35 | 66 |
| 36 | 67 |
| 37 | 68 |
| 38 | 70 |
| 39 | 71 |
| 40 | 72 |
| 41 | 73 |
| 42 | 74 |
| 43 | 76 |
| 44 | 77 |
| 45 | 78 |
| 46 | 79 |
| 47 | 80 |
| 48 | 82 |
| 49 | 84 |
| 50 | 85 |
| 51 | 87 |
| 52 | 89 |
| 53 | 90 |
| 54 | 92 |
| 55 | 94 |
| 56 | 95 |
| 57 | 97 |
| 58 | 99 |
| 59 | 100 |
| 60 | 100 |
Физика
| Первичный балл | Тестовый балл |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
| 4 | 14 |
| 5 | 17 |
| 6 | 20 |
| 7 | 23 |
| 8 | 27 |
| 9 | 30 |
| 10 | 33 |
| 11 | 36 |
| 12 | 38 |
| 13 | 39 |
| 14 | 40 |
| 15 | 41 |
| 16 | 42 |
| 17 | 44 |
| 18 | 45 |
| 19 | 46 |
| 20 | 47 |
| 21 | 48 |
| 22 | 49 |
| 23 | 51 |
| 24 | 52 |
| 25 | 53 |
| 26 | 54 |
| 27 | 55 |
| 28 | 57 |
| 29 | 58 |
| 30 | 59 |
| 31 | 60 |
| 32 | 61 |
| 33 | 62 |
| 34 | 64 |
| 35 | 66 |
| 36 | 68 |
| 37 | 70 |
| 38 | 72 |
| 39 | 74 |
| 40 | 76 |
| 41 | 78 |
| 42 | 80 |
| 43 | 81 |
| 44 | 83 |
| 45 | 85 |
| 46 | 87 |
| 47 | 89 |
| 48 | 91 |
| 49 | 93 |
| 50 | 95 |
| 53 | 100 |
География
| Первичный балл | Тестовый балл |
| 1 | 4 |
| 2 | 7 |
| 3 | 11 |
| 4 | 14 |
| 5 | 17 |
| 6 | 21 |
| 7 | 24 |
| 8 | 27 |
| 9 | 31 |
| 10 | 34 |
| 11 | 37 |
| 12 | 39 |
| 13 | 40 |
| 14 | 41 |
| 15 | 42 |
| 16 | 43 |
| 17 | 44 |
| 18 | 45 |
| 19 | 46 |
| 20 | 47 |
| 21 | 49 |
| 22 | 50 |
| 23 | 51 |
| 24 | 52 |
| 25 | 53 |
| 26 | 54 |
| 27 | 55 |
| 28 | 56 |
| 29 | 57 |
| 30 | 58 |
| 31 | 60 |
| 32 | 61 |
| 33 | 62 |
| 34 | 63 |
| 35 | 64 |
| 36 | 65 |
| 37 | 66 |
| 38 | 67 |
| 39 | 68 |
| 40 | 69 |
| 41 | 74 |
| 42 | 78 |
| 43 | 83 |
| 44 | 87 |
| 45 | 92 |
| 46 | 96 |
| 47 | 100 |
Иностранные языки: английский, немецкий, французский, испанский
1 первичный балл = 1 тестовому.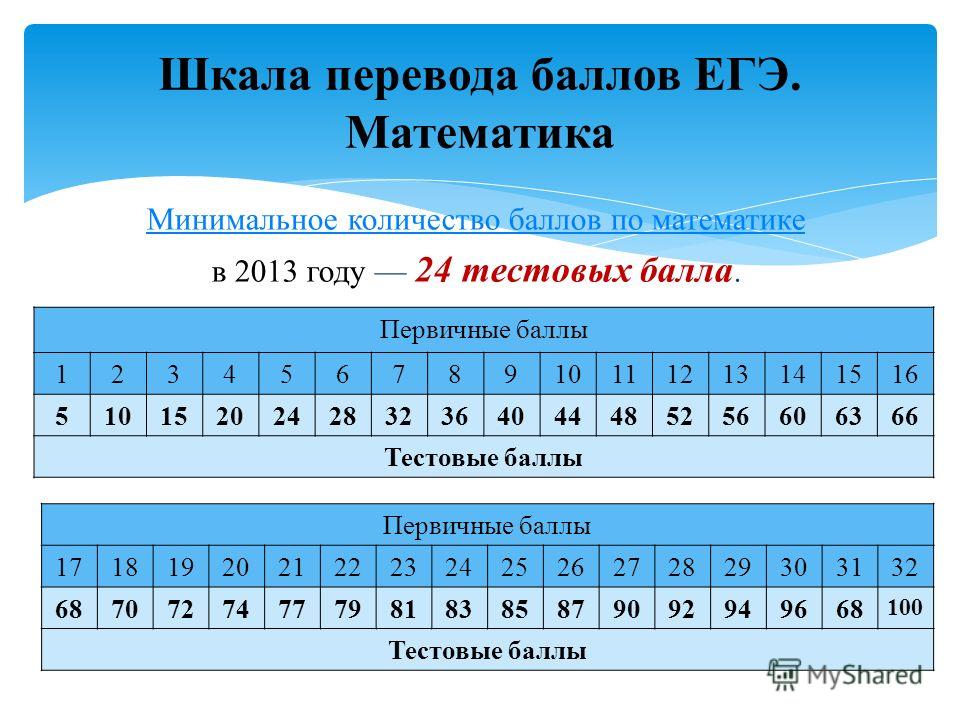 Всего 100 первичных.
Всего 100 первичных.
Порог — 22 балла. Порог в вузы Минобрнауки — 30 баллов.
Китайский язык
| Первичный балл | Тестовый балл |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 7 |
| 6 | 8 |
| 7 | 9 |
| 8 | 10 |
| 9 | 12 |
| 10 | 13 |
| 11 | 14 |
| 12 | 15 |
| 13 | 17 |
| 14 | 18 |
| 15 | 19 |
| 16 | 20 |
| 17 | 22 |
| 18 | 23 |
| 19 | 24 |
| 20 | 25 |
| 21 | 27 |
| 22 | 28 |
| 23 | 29 |
| 24 | 30 |
| 25 | 32 |
| 26 | 33 |
| 27 | 34 |
| 28 | 35 |
| 29 | 37 |
| 30 | 38 |
| 31 | 39 |
| 32 | 40 |
| 33 | 42 |
| 34 | 43 |
| 35 | 44 |
| 36 | 45 |
| 37 | 47 |
| 38 | 48 |
| 39 | 49 |
| 40 | 50 |
| 41 | 52 |
| 42 | 53 |
| 43 | 54 |
| 44 | 55 |
| 45 | 57 |
| 46 | 58 |
| 47 | 59 |
| 48 | 60 |
| 49 | 62 |
| 50 | 63 |
| 51 | 64 |
| 52 | 65 |
| 53 | 67 |
| 54 | 68 |
| 55 | 69 |
| 56 | 70 |
| 57 | 72 |
| 58 | 73 |
| 59 | 74 |
| 60 | 75 |
| 61 | 77 |
| 62 | 78 |
| 63 | 79 |
| 64 | 80 |
| 65 | 82 |
| 66 | 83 |
| 67 | 84 |
| 68 | 85 |
| 69 | 87 |
| 70 | 88 |
| 71 | 89 |
| 72 | 90 |
| 73 | 92 |
| 74 | 93 |
| 75 | 94 |
| 76 | 95 |
| 77 | 97 |
| 78 | 98 |
| 79 | 99 |
| 80 | 100 |
Количество баллов за каждое задание
В этом разделе представлено распределение баллов за задания единого государственного экзамена по каждому предмету — сколько первичных баллов дается за каждое задание (в соответствии со спецификацией ФИПИ).
Математика (база)
1 балл — 1-20 задания
Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа, или конечной десятичной дроби, или последовательности цифр.
Математика (профиль)
1 балл — 1-12 задания
2 балла — 13-15 задания
3 балла — 16-17 задания
4 балла — 18-19 задания
Максимальный первичный балл за всю работу — 32.
Русский язык
1 балл — 1-7, 9-15, 17-25 задания
2 балла — 16 задание
4 балла — 26 задание
5 баллов — 8 задание
25 баллов — 27 задание
Максимальный первичный балл за всю работу — 59.
Литература
1 балл — 1-7, 10-14 задания
6 баллов — 8 и 15 задания
10 баллов — 9 и 16 задания
14 баллов — 17 задание
Максимальный первичный балл за всю работу — 58.
Биология
1 балл — 1-3, 6 задания
2 балла — 4-5, 7-22 задания
3 балла — 23-28 задания
Максимальный первичный балл за всю работу — 58.
История
1 балл — 1, 4, 10, 13-15, 18-19 задания
2 балла — 2-3, 5-9, 12, 16-17, 20-22 задания
3 балла — 11 и 23 задания
4 балла — 24 задание
12 баллов — 25 задание
Максимальный первичный балл за всю работу — 56.
Информатика
1 балл — 1-24 задания
2 балла — 25-27 задание
Максимальный первичный балл за всю работу — 30.
Обществознание
1 балл — 1-3, 10, 12, 16 задания
2 балла — 4-9, 11, 13-15, 17-22 задания
3 балла — 23-24, 26-27 задания
4 балла — 25 и 28 задания
6 баллов — 29 задание
Максимальный первичный балл за всю работу — 64.
Химия
1 балл — 1-6, 11-15, 19-21, 26-29 задания
2 балла — 7-10, 16-18, 22-25, 30-31 задания
3 балла — 35 задание
4 балла — 32 и 34 задания
5 баллов — 33 задание
Максимальный первичный балл за всю работу — 60.
Физика
1 балл — 1-4, 8-10, 13-15, 19-20, 22-23, 25-26 задания
2 балла — 5-7, 11-12, 16-18, 21, 24, 28 задания
3 балла — 27, 29-32 задания
Максимальный первичный балл за всю работу — 53.
География
1 балл — 1-2, 5-10, 12-13, 16-17, 19-27 задания
2 балла — 3-4, 11, 14-15, 18, 28-34 задания
Максимальный первичный балл за всю работу — 47.
Иностранные языки (кроме китайского)
1 балл — 3-9, 12-38, 41 задания
5 баллов — 42 задание
6 баллов — 1, 11, 39 задания
7 баллов — 2, 10, 43-44 задания
14 баллов — 40 задание
Максимальный первичный балл за всю работу — 100.
Китайский язык
1 балл — 15-27 задания
3 балла — 12-14 задания
4 балла — 2-9, 11 задания
5 баллов — 30 задание
6 баллов — 1 и 10 задания
7 баллов — 31 задание
8 баллов — 28 и 32 задания
12 баллов — 29 задание
Максимальный первичный балл за всю работу — 80.
Эта же информация в сводной таблице доступна на этой странице.
Проходные баллы ЕГЭ
Сколько баллов нужно набрать на экзаменах для получения школьного аттестата и поступления в вуз (включая образовательные учреждения Минобрнауки).
Минимальные баллы ЕГЭ на 2023 год
Для поступления в вузы:
- Русский язык — 36
- Литература — 32
- Математика — 27
- Информатика — 40
- Биология — 36
- История — 32
- Химия — 36
- Физика — 36
- Обществознание — 42
- География — 37
- Иностранные языки — 22
- Китайский язык — 17
Для получения аттестата:
- Русский язык — 24
- Математика — 27
- Математика (база) — оценка 3
Для поступления в подведомственные образовательные учреждения Минобрнауки:
- Русский язык — 40
- Литература — 40
- Математика — 39
- Информатика — 44
- Биология — 39
- История — 35
- Химия — 39
- Физика — 39
- Обществознание — 45
- География — 40
- Иностранные языки — 30
Неофициальный перевод баллов ЕГЭ в оценки смотрите на этой странице.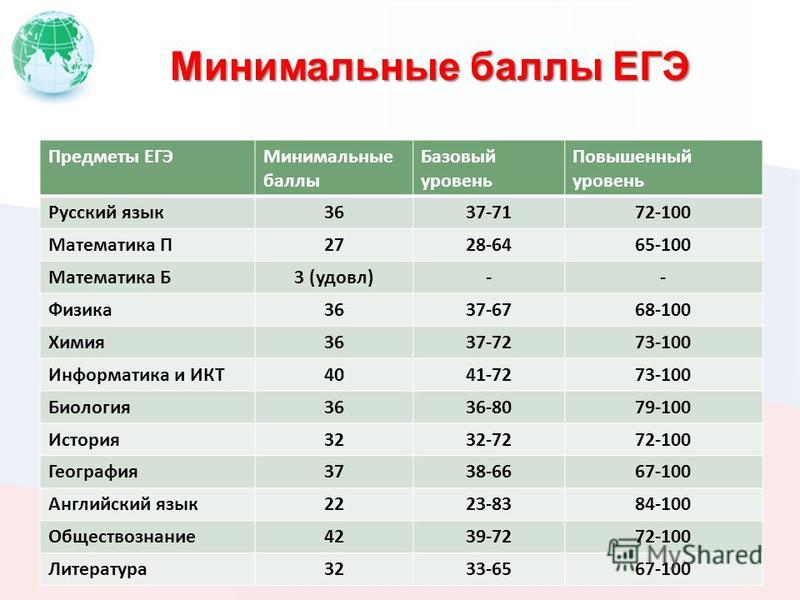
алгебраическая геометрия. Примеры базовых точек линейных систем
Задавать вопрос
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 2к раз
$\begingroup$
Я читаю книгу Фултона об алгебраических кривых, и у нас есть следующие определения:
- Делитель $D=n_1P_1+\ldots,n_kP_k$ ($n_i$ — целые числа, а $P_i$ — точки) над изгиб.
- Линейная система как множество дивизоров $\{(f)+D\mid f\in L(D)\}$
- Базовая точка линейной системы — это точка, которая содержится в каждом делителе линейной системы.
Я действительно новичок в этом вопросе, который мне кажется очень сложным. Я ищу простые примеры базовых точек линейной системы. Это было бы отличной мотивацией для меня, чтобы изучить эти концепции и определения.
Я ищу простые примеры базовых точек линейной системы. Это было бы отличной мотивацией для меня, чтобы изучить эти концепции и определения.
Любая помощь приветствуется!
Спасибо
- алгебраическая геометрия
- алгебраические кривые
$\endgroup$
3
$\begingroup$
Пусть $C$ — гладкая проективная кривая рода $g$ над алгебраически замкнутым полем.
Пусть $p_1,\cdots, p_n$ — $n$ точек на $C$.
Тогда, если рассмотреть дивизор $D=p_1+\cdots+ p_n$, то линейная система $\mathcal E\subset |D|$, состоящая из дивизоров $E\in |D|$ с $p_1$ в их носителе, будет тавтологически (неполная) линейная система, имеющая $p_1$ в качестве базовой точки.
Если $n\geq 2g$, то линейная система $\mathcal E$ является гиперплоскостью в проективном пространстве $|D|$ размерности $n-g$ и, следовательно, имеет размерность $n-g-1$ . 1)$ — линейно эквивалентные делители в $X$.
1)$ — линейно эквивалентные делители в $X$.
$\endgroup$
База номеров | Brilliant Math & Science Wiki
Гаутам Шарма, Нихил Амминабхави, Алоизиус Нг, и
способствовал
Содержимое
- Целочисленные базы чисел
- Числовая база — преобразование в другие базы
- Преобразование в десятичную систему
- От десятичной системы к другим основаниям
- От одной базы к другой
- Числовая база — решение проблем
Поскольку наиболее часто используемой системой счисления является десятичная, мы разделим преобразования на три части:
- от любого основания до десятичной системы счисления
- от десятичной до любой системы счисления
- с любой базы на любую другую базу.

Сейчас мы изучим преобразование целых чисел и преобразование десятичных чисел с плавающей запятой.
Предположим, у нас есть натуральное число \(\overline{c_nc_{n-1}\cdots c_3c_2c_1c_0.c_{-1}c_{-2}\cdots c_{-m}}\) по основанию \(b\) и мы хотим преобразовать его в базу 10 с \(n\) цифрами до десятичной точки и \(m\) цифрами после десятичной точки. 9{-1})=1,5. \ _\квадрат\]
Для целых чисел:
Для перевода из десятичной системы в другую выполните следующие действия:
- Разделите десятичное число, которое необходимо преобразовать, на новую систему счисления и запишите остаток.
- Разделите частное, полученное при предыдущем делении, на новое основание и запишите остаток.
- Повторяйте шаг 2, пока частное не станет равным 0.
- Теперь, когда частное станет равным 0, запишите полученные остатки справа налево в том порядке, в котором они были получены; если вы получили 1 в качестве остатка от первого деления, 3 от второго деления и 6 от третьего деления, то запишите это как 631.

Преобразовать \(27_{10}\) в основание 8.
Используя описанные выше шаги, мы имеем следующее:
- делим 27 на 8, получаем остаток 3 и частное 3,
- деля 3 на 8, получаем остаток 3 и частное 0.
Следовательно, его эквивалентное восьмеричное представление равно \(33_8\). \(_\квадрат\)
Для десятичных чисел с плавающей запятой:
Предположим, что у нас есть натуральное число \(\overline{c_nc_{n-1}\cdots c_3c_2c_1c_0.c_{-1}c_{-2}\cdots c_{-m} }\) в десятичной системе счисления с \(n\) цифрами до десятичной точки и \(m\) цифрами после. Затем целая часть и дробная часть могут быть преобразованы отдельно, а затем добавлены.
Целую часть можно преобразовать, как в приведенном выше примере, поэтому теперь нам нужно преобразовать дробную часть. То есть \(0.c_{-1}c_{-2}\cdots c_{-m}\) в десятичной системе счисления нужно преобразовать в базу \(b\). Это можно сделать, выполнив следующие действия:
- Умножьте десятичную дробную часть на \(b\).

- Обратите внимание на целую часть полученного числа.
- Теперь снова возьмите дробную часть предыдущего результирующего числа в качестве новой дробной части. Если он равен нулю, то мы закончили. Если нет, то повторим вышеописанные шаги.
- Все отмеченные целые части записываются слева направо в том порядке, в котором они были получены, с предшествующей десятичной точкой.
Наглядно понятно на примере:
Преобразование \(987.11111111111\ldots\) в восьмеричную систему счисления.
Во-первых, целая часть \(987\) будет равна \(1733\) в восьмеричной системе счисления по вышеуказанной теории.
Теперь возьмем дробную часть \(0,111111111111\ldots\).
- Умножая на 8, получаем \(0,8888888888888888888\ldots\).
- Теперь целая часть равна нулю, а новая дробная часть равна \(0,888888888888\ldots\).
- Снова умножив эту новую дробную часть на 8, мы получим \(7,1111111111111\ldots\).
- Теперь целая часть равна 7, а новая дробная часть равна \(0,111111111\ldots\).
- Здесь мы видим, что у нас снова \(0,111111111\ldots\), поэтому цифры будут повторяться.
Следовательно, восьмеричное представление \(0,11111111111\ldots\) равно \(0,070707070707\ldots\).
Таким образом, новый номер будет \(1733.07070707\ldots\) в восьмеричной системе счисления. \(_\квадрат\)
Это можно легко сделать, сначала преобразовав исходное число в десятичную систему счисления, а затем в требуемую базу.
Преобразовать \(10_2\) в основание 8.
Мы можем легко преобразовать его в десятичное число, то есть 2.
Затем мы можем преобразовать его в восьмеричное число, которое также равно 2.
Следовательно, \(10_2=2_8\). \(_\квадрат\)Примечание. Этот пример дает нам еще одну идею: если начальное значение меньше основания, в которое его нужно преобразовать, то число остается прежним. Например, \(7_8=7_{10}=7_{16}=7_{100} \) и т. д. 92, \ldots\), где каждую степень числа 5 можно использовать не более трех раз?
Пусть \(f\) — многочлен с целыми неотрицательными коэффициентами.
Если \(f(1)=7\) и \(f(7)=7597\), то что такое \(f(10)?\)
Да №
\[\large (11221133112211)_{12}\]
Делится ли указанное выше число на \((143)_{10}?\) (Калькуляторы не нужны!)
\(\)
Уточнение: Нижний индекс 12 означает, что мы работаем с основанием 12.Попробуйте больше вопросов по базам.
0 1 2 3 4 5 6 7
\[\large (102030405060504030201)_7\]
Какое целое число \(0 \leq n \leq 7\) нужно вычесть из приведенного выше числа, чтобы оно делилось на \((8)_{ 10}\)?
\(\)
Уточнение:
- Пожалуйста, без калькуляторов!
- Нижний индекс 7 указывает на то, что мы работаем в базе 7.




 Если \(f(1)=7\) и \(f(7)=7597\), то что такое \(f(10)?\)
Если \(f(1)=7\) и \(f(7)=7597\), то что такое \(f(10)?\)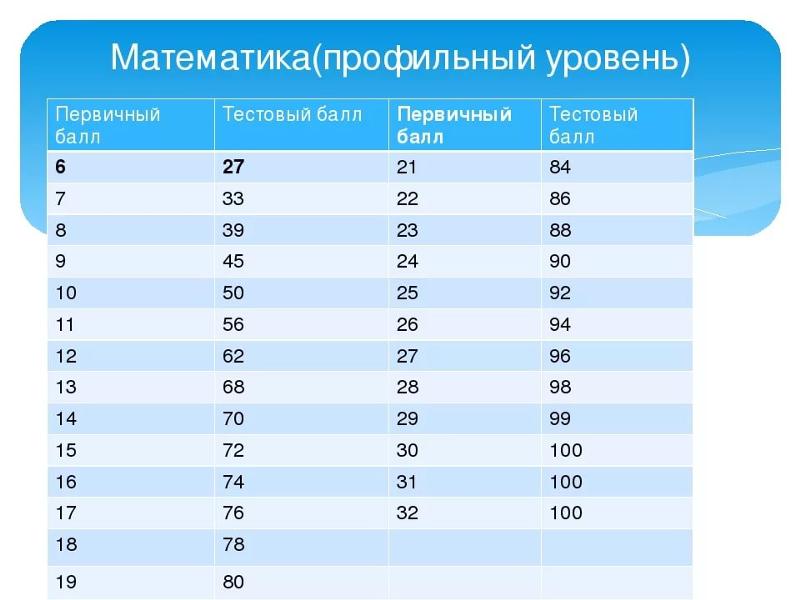
Leave A Comment