Задание 14 Профильного ЕГЭ по математике. Стереометрия. Задача 1

Высота правильной треугольной пирамиды равна 4, а угол между боковой гранью и плоскостью основания равен 60 градусов. Найдите расстояние от вершины основания до плоскости противолежащей ей боковой грани.

Обратите внимание на эту задачу. Она содержит базовые схемы для решения очень многих задач по стереометрии.

Прежде всего, определим, где на нашем чертеже угол между плоскостью основания и боковой гранью SBC. Пусть точка М — середина ВС.

Проведем AМ — медиана и высота правильного треугольника АВС, значит,

Проведем SМ — медиана и высота равнобедренного треугольника SВС, значит,

Отсюда следует, что , а угол АМS — угол между боковой гранью и плоскостью основания, равный (по определению угла между плоскостями).

Будем искать расстояние от точки А до плоскости (SBC).

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.

Нам надо построить прямую, проходящую через точку А перпендикулярно плоскости SBC. Вот еще одно определение.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим этой плоскости.

Значит, надо построить отрезок с одним из концов в точке А, перпендикулярный двум пересекающимся прямым в плоскости (SBC).

Проведем в плоскости (ASM).

Заметим, что нужно обязательно указывать, в какой плоскости идет построение. Мы не можем провести линию просто в воздухе. Необходима плоскость, в которой лежит эта линия.

Кроме того, так как

Получается, что отрезок АН перпендикулярен двум пересекающимся прямым в плоскости SBC, поэтому Значит, — расстояние от А до плоскости SBC.

Чтобы найти это расстояние, сделаем плоский чертеж сечения пирамиды плоскостью АSM.

Пусть точка О — проекция точки S на плоскость основания пирамиды. По условию, как высота пирамиды.

Из треугольника SOM, где угол М равен , а угол О — прямой, найдем ОМ:

Катет, лежащий напротив угла OSM, равного , равен половине гипотенузы, поэтому

У правильной пирамиды вершина S проецируется в центр основания — точку О, которая является центром вписанной и описанной окружностей треугольника АВС. Также для правильного треугольника АВС точка О — точка пересечения его высот, медиан и биссектрис. Значит, по свойству медиан точка О лежит на АМ и делит АМ в отношении 2:1, считая от вершины А.

Следовательно,

Воспользуемся методом площадей, записав площадь треугольника АВС двумя способами.

Ответ: 6.

Второй способ решения этой задачи:

Покажем, как решить данную задачу методом объемов. Суть метода — в том, чтобы разными способами записать объем нашей пирамиды, а затем найти неизвестное расстояние от вершины до противоположной грани, которое является высотой пирамиды. Ведь в качестве основания пирамиды мы можем выбрать любую ее грань.

Из прямоугольного треугольника SOM найдем Тогда и , так как (по свойству правильного треугольника). Отсюда

Мы нашли площадь основания пирамиды.

Объем пирамиды

С другой стороны, объем пирамиды , где АН — неизвестное нам расстояние от вершины А до плоскости SBC, которое мы и хотим найти.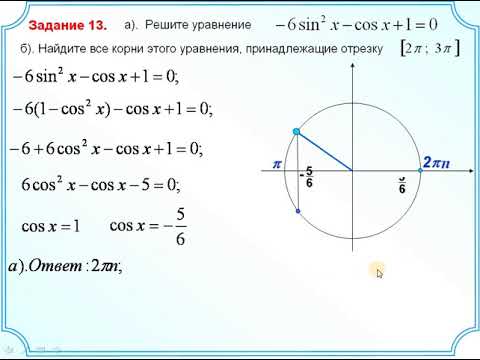

Отсюда

Задание 14 Профильного ЕГЭ по математике. Стереометрия

Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Задание 14 Профильного ЕГЭ по математике. Стереометрия. Задача 1» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена: 09.03.2023

Профильный ЕГЭ по математике. Задание №2. Стереометрия

Задание 2 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.

Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.

Как решать задания по стереометрии из первой части Профильного ЕГЭ?

Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)

Проверим себя – умеем ли мы рисовать чертежи?

Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.

Запоминаем один из главных лайфхаков решения задач по стереометрии:

Отношение объемов подобных тел  равно кубу коэффициента подобия.

Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в  раз, а объем в  раз.

 

И решаем задачи. У нас все получится!

1. Во сколько раз увеличится площадь поверхности и объем куба, если его ребро увеличить в два раза?

Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.

2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

 

 

Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого.

Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.

3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.

 

 

Меньшая пирамида подобна большой, коэффициент подобия Отношение объемов  подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен 

4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.

 

Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен

5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна   Найти объем пирамиды SABCD .

 

 

Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника  SAE получаем, что Соответственно, сторона основания пирамиды равна Если обозначить центр основания за H, то высоту пирамиды  найдем по теореме Пифагора, для треугольника SHE – она равна 2.

Применяя формулу для объема пирамиды , получаем ответ: 16.

Многие задания №2 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.

Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.

6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.

Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу).

Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.

Радиус описанной окружности найдем по формуле

Площадь найдем по формуле Герона:

, где   – полупериметр.

Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.

7. В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми и  . Ответ дайте в градусах.

Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку  и  параллельны, найдем угол между  и . Он равен 45 градусов, так как грань   –  квадрат.

Ответ: 45.

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Профильный ЕГЭ по математике. Задание №2. Стереометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена: 09.03.2023

Математика — Школа Святого Павла

Факультет математики школы Святого Павла имеет международную репутацию. Мы не учим к экзамену, мы учим математике – и успех на экзамене является следствием.

Наши ученики не только обладают высокими навыками, но и проявляют энтузиазм и настоящее понимание, а в школе существует живая математическая культура. В любой день вы услышите, как ученики всех возрастов со знанием дела и интересом обсуждают математику, и сотрудники математики одинаково находят время каждый день подбрасывать математические идеи. В коридорах математического факультета есть доски, на которых отображаются вопросы, и вы увидите, как ученики обсуждают проблемы и предлагают решения. Мощная интеллектуальная любознательность, характерная для школы Святого Павла, подтверждается страстью к математике, проявляемой как сотрудниками, так и учениками.

Центральная часть образовательного кредо школы заключается в том, что мы не ускоряем наших учеников, зачисляя их раньше времени на государственные экзамены. Вместо этого мы расширяем их, добавляя дополнительную глубину и, в частности, используя широкий спектр более сложных вопросов и задач. Мы неизменно добиваемся выдающихся успехов на национальных соревнованиях, таких как Британская математическая олимпиада.

Математика является основным предметом GCSE. На уровне A он очень популярен: обычно более 85% учеников изучают математику уровня A и около 40% изучают высшую математику. В 2022/23 учебном году 182 ученика 13-х классов изучают математику уровня A, а 83 ученика изучают дополнительную математику.

GCSE

В четвертом, пятом и шестом классах (9–11 классы) все мальчики проходят курс, ведущий к экзамену EdExcel International GCSE. Программа обучения включает в себя инновационную программу повышения квалификации, основанную на навыках решения задач, необходимых для соревнований по математике и олимпиад.

Уровень A

На уровне A мы следуем спецификации OCR A Linear как для отдельной математики, так и для дополнительной математики. Все экзамены сдаются в конце двухгодичного курса. Одиночная математика A Level состоит из трех, двухчасовых работ, которые включают чистую математику, механику и статистику. Все наши дальнейшие математики сдают варианты статистики и механики, а наши наиболее способные ученики сдают дополнительный вариант чистой математики. Те дополнительные математики, которые изучают информатику уровня A, также могут дополнительно выбрать вариант дискретной математики.

Подготовка предлагается как для тех, кто хочет изучать математику в лучших университетах, так и для тех, для кого математика является важным элементом их предполагаемого курса обучения, например, физики, естественных наук или инженерии. Неудивительно, что у нас в Оксбридже высокий уровень успеха.

Совместная учебная программа

Центральное место в математическом профиле школы занимают различные национальные соревнования по математике, проводимые UK Mathematics Trust (UKMT) – соревнования по математике среднего и старшего уровней, олимпиада среднего уровня (Кейли, Гамильтон и Маклорен) и Британский математический конкурс. Олимпиады 1 и 2 туры. Математический факультет также предлагает широкий спектр внеклассных математических кружков. Дополнительную информацию можно найти здесь.

Сводка результатов экзамена по математике 2022

Поздравляем всех учеников, добившихся отличных результатов на экзаменах по математике IGCSE и A Level
летом 2022 года. Сводная статистика:

Математика IGCSE

99% 8/9 класс

100% 7/8/9 класс

Уровень A Математика

84% Класс A*

97% Класс A*/A 9% A*/A

3

3 9 /Б

Ясно, что ученики ценят выдающееся обучение, которое они все получают. Для получения дополнительной информации о результатах и ​​сравнениях с последним набором результатов за 2019 год см. документ ниже:

Новости математики

Математические олимпиады 2021-22

В конкурсе Intermediate Mathematical Challenge принимают участие более 200 000 учеников из
стран. 600 лучших учеников 9-го, 10-го и 11-го классов получают право на участие в следующем раунде олимпиады
. учащиеся 9-х классов Адавья, Ананго и Аман; Ученики 10 класса Самир
и Александр; и ученики 11-х классов Эгэ, Нил и Хаолинь, все они вошли в число 100 лучших
в стране и были награждены медалями. Адавья, Нил и Хаолинь вошли в число
лучших 20 лучших в стране и были награждены золотой медалью.

Hans Woyda 2021-22

Математическое соревнование Hans Woyda проводится каждый год между 64 школами Лондона и организовано в 16 лиг по 4 команды. Каждая команда состоит из одного ученика 9-го класса, одного 11-го класса, одного 12-го класса и одного ученика 13-го класса от каждой школы. Задача состоит в том, чтобы решить сложные математические задачи в условиях времени. Сент-Пол стал совместным победителем в сезоне 2020-21. В том году финала не было из-за карантина. В сезоне 2021-22 «Сент-Пол» снова очень успешно вышел в финал, что оказалось захватывающим событием. Нажмите здесь, чтобы ознакомиться с результатами каждого раунда и отчетом о финале.

Математический кружок

Математический факультет активно участвует в школьной информационно-просветительской программе. Одним из основных событий года является двухдневная программа математических презентаций и секционных мероприятий. Мы принимаем учеников 10-х классов из школ Лондона (включая школу епископа Чаллонера, школу для мальчиков Фулхэма, больницу Грей Коут, академию Хаммерсмит и бесплатную школу Западного Лондона). Для краткого описания презентаций, пожалуйста, нажмите здесь.

Приглашения на летнюю школу UKMT для Хаолиня и Нила

Хаолинь Чжао и Нил Прабху были приглашены в Национальную летнюю школу по математике после их отличного выступления в промежуточном математическом конкурсе этого года. Подробнее здесь.

Опыт работы в области управления инвестициями

В 2021/22 году учащиеся младших восьмых классов Чарльз, Алексей, Арджун и Шашват работали над финансовым проектом
с ведущими аналитиками компании по управлению инвестициями Cheyne Capital. Нажмите здесь, чтобы прочитать об их опыте.

Премия Толлера по математике

В течение двух недель после летних экзаменов младших классов восьмой школы все последующие математики проводят небольшой исследовательский проект, кульминацией которого является
презентация их работы. Лучшие четыре презентации проходят в финал, который проходит в
Colet Hall. Четыре финалиста в 2022 году:
Джаш Джавери:
Эйлер, Базельская проблема и бесконечная серия
Арджун Раджкумар:
Математика покера
Аксель Ла Пира:
Математическая логика
Элиягу Глушов-Коппель:
Математическое моделирование инфекционных заболеваний

Ряд презентаций Toller Prize прошлых лет можно посмотреть ниже.

13 шагов к хорошей оценке

Тело

Математика как спорт. Этому можно научиться только через активное участие.
Вот несколько мыслей об изучении математики и достижении успеха, или0030 классные заметки и подробно прочитать учебный план . Учебный план содержит значительный объем информации для вас.

  • Понимание математики — это тяжелая работа, и процесс приобретения знаний требует согласованных усилий со стороны учащегося. Планируйте потратить около двух часов на каждое задание . Иногда вам может понадобиться потратить больше. Обязательно делайте больше, чем просто назначенные задачи.
  • Как можно скорее после занятий изучите свои конспекты занятий и примеры. Возможно, вы даже захотите переписать свои заметки для большей ясности. (Этот процесс перезаписи служит для того, чтобы вы начали думать об идеях, что является первым шагом в обучении.)
  • Затем внимательно прочитайте раздел(ы) учебника , относящийся к материалу, уделяя особое внимание словарному запасу, основным понятиям. и проблемные примеры. Вы можете связать это чтение с вашими заметками в классе, выделив концепции, которые обсуждались.
  • Теперь приступайте к заданию . Делать это раньше — безрассудно, так как задание предназначено для практики и применения идей и концепций, которые вам действительно необходимо усвоить и понять, прежде чем выполнять задание; следовательно, предварительное изучение идей необходимо!
  • Проверяйте свои ответы в конце учебника по ходу чтения. Если у вас возникли трудности, вернитесь и повторите изучение, просматривая примеры, сделанные в классе и в учебнике, на предмет сходства с вашей проблемой; затем повторите попытку.
  • Если на этом этапе возникают трудности, и вы не можете решить их самостоятельно или друг с другом (рекомендуется групповое обучение — мы можем учиться на проблемах и анализах друг друга), то пришло время  обратиться за помощью . Обратитесь за помощью непосредственно к лектору и/или Т. А. в рабочее время или пойти в комнату репетитора по математике. Не ждите следующего занятия, чтобы задать вопрос; может не хватить времени, или преподаватель не сможет разобраться с вашей проблемой.
  • Когда вы успешно выполните задание, вернитесь назад и еще раз перечитайте текстовые разделы и примечания  к классу, чтобы подчеркнуть и повторить концепции. Это не займет много времени, и это принесет большие дивиденды, закрепив концепции, процессы и терминологию в вашем «банке памяти».
  • Успешные учащиеся обнаруживают, что следующим шагом в выполнении задания является заглядывание вперед на то, что будет в следующем классе; вы можете легко увидеть, какой раздел будет обсуждаться, взглянув на ваш учебный план. Быстро прочитайте соответствующие разделы текста не для усвоения, а для общего обзора. Ознакомьтесь с новыми терминами и основными понятиями, чтобы они не казались вам такими «чужими», когда они будут представлены в классе.
  • Наконец, успешные учащиеся также обнаружили, что незадолго до следующего занятия (возможно, за пятнадцать минут до начала занятия или даже по дороге на занятие) быстрое перечитывание «старых» заметок , а также « новый» текстовый раздел дает им преимущество, особенно если есть викторина (объявленная или необъявленная).