Графики движения: равномерное, равноускоренное движения. Тест
Всего вопросов: 8
Вопрос 1. Движение двух тел заданы уравнениями: и (м). Какой из нижеприведенных рисунков соответствует данным уравнениям в начальный момент времени?
| A. | D |
| B. | C |
| C. | A |
| D. | B |
Вопрос 2. На рисунке изображены графики зависимости скорости движения четырех тел от времени. Какое из тел прошло наибольший путь за первые 3с движения?
| A. | 1 |
| B. | 3 |
| C. | 2 |
D. | 4 |
Вопрос 3. На рисунке изображен график зависимости проекции скорости некоторого тела от времени. Путь и перемещение этого тела вдоль оси х за 10 с равны:
| A. | 21 м, 15 м |
| B. | 15 м, 15 м |
| C. | 21 м, 21 м |
| D. | 0 м, 15 м |
| E. | 15 м, 21 м |
Вопрос 4. На рисунке представлена зависимость проекции скорости от времени. Какой из нижеприведенных графиков отражает зависимость проекции ускорения от времени?
| A. | D |
| B. | C |
C. |
E |
| D. | B |
| E. | A |
Вопрос 5. На рисунке представлен график зависимости проекции ускорения тела от времени. Какой из нижеприведенных графиков наиболее точно соответствует зависимости проекции скорости от времени? (Начальная скорость равна нулю)
| A. | A |
| B. | C |
| C. | D |
| D. | E |
| E. | B |
Вопрос 6. Тело, имеющее начальную скорость 10 м/с, в течение первых 5 секунд двигается равноускоренно с ускорением 2 м/с2, следующие две секунды оно двигается равномерно в течение следующих трех секунд — равнозамедленно с ускорением 3 м/с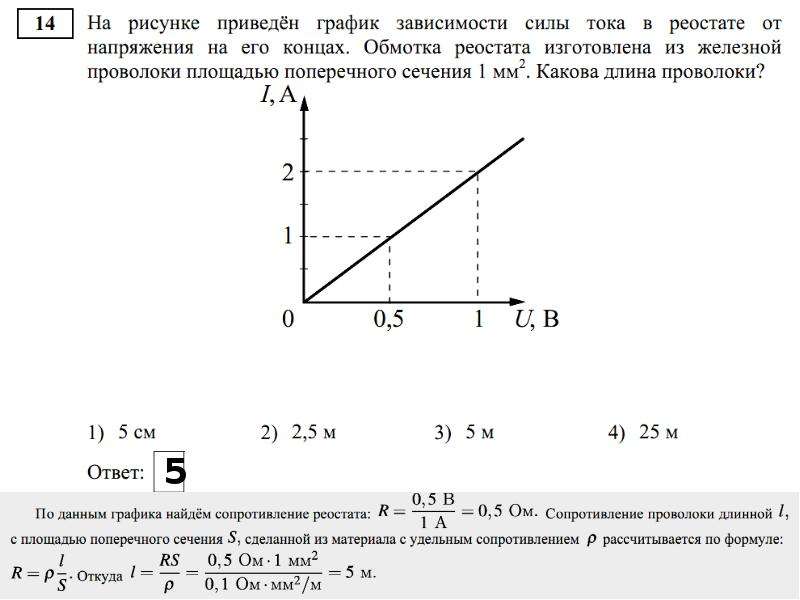 Какой из нижеприведенных графиков соответствует данному движению?
Какой из нижеприведенных графиков соответствует данному движению?
| A. | A |
| B. | D |
| C. | B |
| D. | C |
| E. | E |
Вопрос 7. Шарику, находящемуся на некотором расстоянии от наклонной плоскости, сообщили небольшую скорость. Какой из нижеприведенных графиков отражает зависимость проекции скорости этого шарика от времени. (Трением пренебречь).
| A. | C |
| B. | D |
| C. | E |
| D. | A |
E. |
B |
Вопрос 8. На рисунке приведена зависимость проекции скорости от времени. Какой из нижеприведенных графиков наиболее точно отражает зависимость проекции перемещения от времени?
| A. | E |
| B. | B |
| C. | A |
| D. | C |
| E. | D |
10класс. Равномерное движение. Относительность движения(профиль)
10 кл. Профиль.Равномерное движение, относительность движения
1. Задание 1 № 133
На рисунке представлен график зависимости пути S велосипедиста от времени t.
Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью
1) от 50 с до 70 с
2) от 30 с до 50 с
3) от 10 с до 30 с
4) от 0 до 10 с
Решение.
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась
На других интервалах скорость была иная.
Правильный ответ указан под номером 4.
2. Задание 1 № 134
На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
Пункт A находится в точке а пункт Б — в точке Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Решение.
Для того чтобы по графику зависимости координаты от времени найти
скорость движения тела в некоторый момент, необходимо вычислить тангенс угла
наклона графика в соответствующей точке. Максимальной скорости соответствует
максимальный угол наклона.
Ответ: 60.
Ответ: 60
3. Задание 1 № 138
На рисунке приведен график зависимости проекции скорости тела от времени.
Чему равно ускорение тела в интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)
Решение.
Из графика видно, что в интервале времени от 30 до 40 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Ответ: 0.
Ответ: 0
4. Задание 1 № 317
Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки: Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение:
Ответ: 0,7.
Ответ: 0,7
5. Задание 1 № 3540
Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Решение.
Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: То есть, буквально, надо весь пройденный телом путь разделить на всё время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
Разберёмся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
Вычислим теперь среднюю путевую скорость. Обозначим расстояние
между двумя пунктами через тогда
весь путь, пройденный велосипедистом, равен На
первую половину пути велосипедист затратил время На
обратную дорогу — время Всё
время пути составило Окончательно,
находим, что средняя путевая скорость велосипедиста равна
Обозначим расстояние
между двумя пунктами через тогда
весь путь, пройденный велосипедистом, равен На
первую половину пути велосипедист затратил время На
обратную дорогу — время Всё
время пути составило Окончательно,
находим, что средняя путевая скорость велосипедиста равна
Ответ: 10.
Ответ: 10
6. Задание 1 № 3541
Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
Решение.
Из графика видно, что начальная координата тела равна Модуль перемещения тела относительно исходной точки в любой момент определяется выражением: Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при и равен 20 м.
Ответ: 6.
Ответ: 6
7. Задание 1 № 3544
Движение двух велосипедистов задано уравнениями и Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
Решение.
Встреча двух велосипедистов означает, что у них в некоторый момент времени совпадут координаты. Определим, когда именно произойдет встреча, для этого решим уравнение Теперь не составляет труда определить координату места встречи:
Ответ: 20.
Ответ: 20
8. Задание 1 № 3545
На рисунке приведен график движения x(t) электрокара. Определите по этому графику путь, проделанный электрокаром за интервал времени от t1 = 1 c до t2 = 4 c. (Ответ дайте в метрах.)
Решение.
Путь — это физическая величина, показывающая пройденное телом
расстояние. Иначе говоря, это длина пройденного участка траектории. Из графика
видно, что в интервале времени от 1 до 3 с электрокар двигался в положительном
направлении оси При
этом его координата изменилась на Последнюю,
четвертую, секунду электрокар двигался в обратном направлении, изменение его
координаты на этом участке равно Таким
образом, путь, пройденный машинкой за интервал времени от 1 до 4 с равен
Из графика
видно, что в интервале времени от 1 до 3 с электрокар двигался в положительном
направлении оси При
этом его координата изменилась на Последнюю,
четвертую, секунду электрокар двигался в обратном направлении, изменение его
координаты на этом участке равно Таким
образом, путь, пройденный машинкой за интервал времени от 1 до 4 с равен
Ответ: 3.
Ответ: 3
9. Задание 1 № 3548
Пешеход идет по прямолинейному участку дороги со скоростью 4 км/ч. Навстречу ему движется автобус со скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
Решение.
Обозначим искомую скорость велосипедиста через Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью а к автобусу — со скоростью
Приравняв эти две скорости, находим требуемую скорость велосипедиста:
Ответ: 18.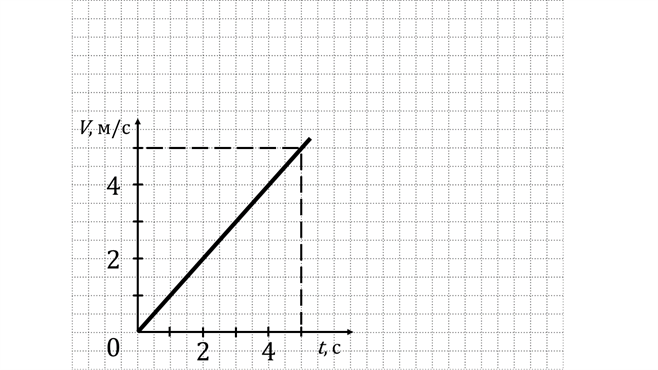
Ответ: 18
10. Задание 1 № 3549
Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Обозначим искомую скорость течения реки через а скорость парохода в стоячей воде — через Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна Скорость парохода вверх по течению: Решая систему из двух этих уравнений, для скорости течения воды имеем
Ответ: 1,5.
Ответ: 1,5
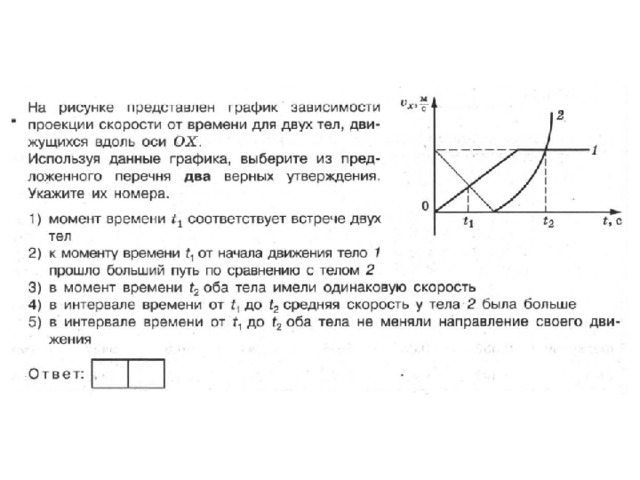
11. Задание 1 № 3783
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v2 больше скорости первого тела v1? (Ответ дайте в метрах в секунду.)
Решение.
Из графика видно, что для обоих тел пройденный путь линейно
зависит от времени, а значит, оба тела двигались с постоянными по величине
скоростями. Модуль скорости первого тела равен Скорость
же второго тела: Следовательно,
скорость второго тела больше скорости первого тела на величину
Модуль скорости первого тела равен Скорость
же второго тела: Следовательно,
скорость второго тела больше скорости первого тела на величину
Ответ: 10.
Ответ: 10
12. Задание 1 № 3867
Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
Решение.
Используя график, определим проекции скоростей обоих тел. Для тела 1 имеем
Для тела 2:
Таким образом модуль скорости одного тела относительно другого равен
Ответ: 18.
Ответ: 18
13. Задание 1 № 4077
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с.
Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса,
двигаясь от задней двери к кабине водителя.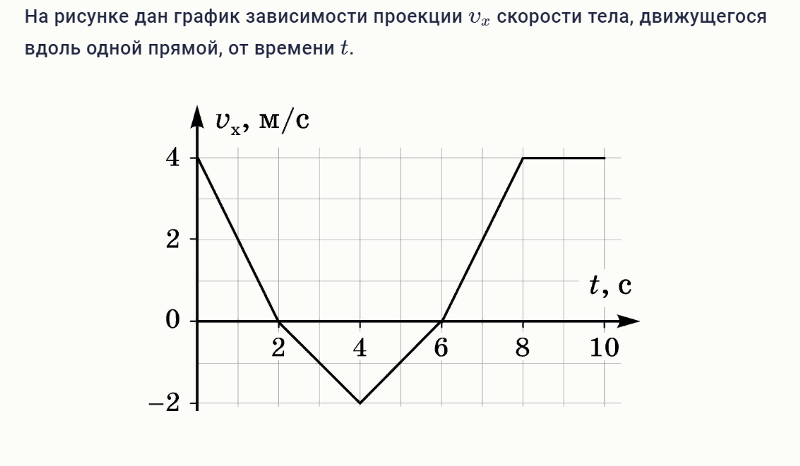 Чему равен модуль скорости
пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Чему равен модуль скорости
пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Решение.
Согласно закону сложения скоростей, скорость тела относительно «неподвижной системы отсчёта» связана со скоростью этого тела относительно «подвижной системы отсчёта» и скоростью движения «подвижной с. о.» относительно «неподвижной» при помощи следующего соотношения: В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем:
Ответ: 11.
Ответ: 11
14. Задание 1 № 6038
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Решение.
Перейдём в систему отсчёта, связанную с автомобилем. Модуль
скорости движения мотоцикла в данной системе отсчёта будет равен
50 + 70 = 120 км/ч.
Ответ: 120.
Ответ: 120
15. Задание 1 № 6073
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Решение.
Перейдём в систему отсчёта, связанную с автомобилем. Модуль скорости движения мотоцикла в данной системе отсчёта будет равна |50 − 70| = 20 км/ч.
Ответ: 20.
Ответ: 20
16. Задание 1 № 7995
На рисунке представлен график зависимости пути S велосипедиста от времени t. Найдите скорость велосипедиста в интервале времени от 50 до 70 с.
Решение.
За время от 50 до 70 с велосипедист проехал 250 − 100 = 150 м, значит, его скорость равна 150 м : 20 с = 7,5 м/с.
Ответ: 7,5.
Ответ: 7,5
17. Задание 1 № 8341
На рисунке
представлен график зависимости координаты х велосипедиста от
времени t. Чему равен наибольший модуль проекции скорости
велосипедиста на ось Оx? Ответ выразите в м/с.
Чему равен наибольший модуль проекции скорости
велосипедиста на ось Оx? Ответ выразите в м/с.
Решение.
Из графика видно, что координата на каждом отдельном интервале времени изменяется линейно, следовательно, движение на каждом участке происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на каждом интервале времени можно определить разделив разность координат в начале и в конце интервала на длительность интервала времени.
Интервал от 0 до 10 с:
Интервал от 10 до 30 с:
Интервал от 30 до 50 с:
Интервал от 50 до 70 с:
Наибольший модуль скорости составляет 10 м/с.
Ответ: 10.
Ответ: 10
18. Задание 1 № 8342
На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наименьший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.
Решение.
Из графика видно, что координата на каждом отдельном интервале
времени изменяется линейно, следовательно, движение на каждом участке
происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на
каждом интервале времени можно определить разделив разность координат в начале
и в конце интервала на длительность интервала времени.
Проекцию скорости велосипедиста на ось x на
каждом интервале времени можно определить разделив разность координат в начале
и в конце интервала на длительность интервала времени.
Интервал от 0 до 10 с:
Интервал от 10 до 30 с:
Интервал от 30 до 50 с:
Интервал от 50 до 70 с:
Наименьший модуль скорости составляет 2,5 м/с.
Ответ: 2,5.
Ответ: 2,5
19. Задание 1 № 8343
На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наибольший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.
Решение.
Из графика видно, что координата на каждом отдельном интервале
времени изменяется линейно, следовательно, движение на каждом участке
происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на
каждом интервале времени можно определить разделив разность координат в начале
и в конце интервала на длительность интервала времени.
Интервал от 0 до 10 с:
Интервал от 10 до 30 с:
Интервал от 30 до 50 с:
Интервал от 50 до 70 с:
Наибольший модуль скорости составляет 10 м/с.
Ответ: 10.
Ответ: 10
20. Задание 1 № 8344
На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наименьший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.
Решение.
Из графика видно, что координата на каждом отдельном интервале времени изменяется линейно, следовательно, движение на каждом участке происходит с постоянной скоростью. Проекцию скорости велосипедиста на ось x на каждом интервале времени можно определить разделив разность координат в начале и в конце интервала на длительность интервала времени.
Интервал от 0 до 10 с:
Интервал от 10 до 30 с:
Интервал от 30 до 50 с:
Интервал от 50 до 70 с:
Наименьший модуль скорости составляет 2,5 м/с.
Ответ: 2,5.
Ответ: 2,5
21. Задание 1 № 9493
Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.
Решение.
Вектор скорости катера относительно воды разложим на две компоненты: где вектор направлен параллельно берегу, а вектор — перпендикулярно берегу. Для того чтобы катер в системе отсчёта, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонента скорости катера относительно воды вдоль реки в точности компенсировала скорость течения Тогда модуль скорости катера относительно воды будет равен (по теореме Пифагора)
Ответ: 7,5 км/ч.
Ответ: 7,5
22. Задание 1 № 9525
Катер плывёт по прямой реке, двигаясь относительно берега
перпендикулярно береговой линии.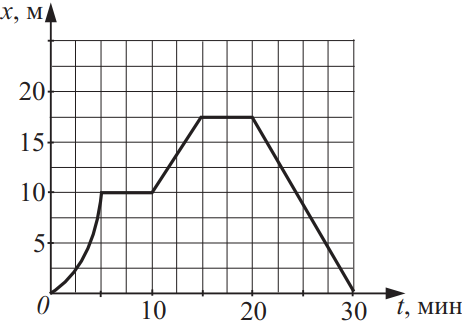 Модуль скорости катера относительно берега
равен 4,8 км/ч. Река течёт со скоростью 3,6 км/ч. Чему равен модуль скорости
катера относительно воды? Ответ выразите в км/ч.
Модуль скорости катера относительно берега
равен 4,8 км/ч. Река течёт со скоростью 3,6 км/ч. Чему равен модуль скорости
катера относительно воды? Ответ выразите в км/ч.
Решение.
Вектор скорости катера относительно воды разложим на две компоненты: где вектор направлен параллельно берегу, а вектор — перпендикулярно берегу. Для того, чтобы катер в системе отсчета, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонента скорости катера относительно воды вдоль реки в точности компенсировала скорость течения u. Тогда модуль скорости катера относительно воды будет равен (по теореме Пифагора)
Ответ: 6 км/ч.
Ответ: 6
2.3 Графики зависимости положения от времени — Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Объяснять значение наклона на графиках зависимости положения от времени
- Решение задач с использованием графиков положения и времени
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции.
 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:- (A) создание и интерпретация графиков и диаграмм, описывающих различные типы движения, включая использование технологий реального времени, таких как детекторы движения или фотодатчики.
Основные термины раздела
| зависимая переменная | независимая переменная | тангенс |
Поддержка учителей
Поддержка учителей
[BL][OL] Опишите сценарий, например, в котором вы запускаете в воздух водяную ракету. Он поднимается на 150 футов, останавливается и снова падает на землю. Предложите учащимся оценить ситуацию. Куда бы они поставили свой ноль? Что такое положительное направление, и что такое отрицательное направление? Попросите одного из учащихся нарисовать сценарий на доске. Затем нарисуйте график зависимости положения от времени, описывающий движение. Попросите учащихся помочь вам заполнить график. Линия прямая? Он изогнут? Он меняет направление? Что они могут сказать, глядя на график?
Затем нарисуйте график зависимости положения от времени, описывающий движение. Попросите учащихся помочь вам заполнить график. Линия прямая? Он изогнут? Он меняет направление? Что они могут сказать, глядя на график?
[AL] После того, как учащиеся просмотрели и проанализировали график, проверьте, могут ли они описать различные сценарии, в которых линии были бы прямыми, а не изогнутыми? Где линии будут прерывистыми?
График позиции как функции времени
График, как и картинка, стоит тысячи слов. Графики не только содержат числовую информацию, они также показывают отношения между физическими величинами. В этом разделе мы исследуем кинематику, анализируя графики положения во времени.
Графики в этом тексте имеют перпендикулярные оси, одна горизонтальная, а другая вертикальная. Когда две физические величины нанесены друг против друга, горизонтальная ось обычно считается независимой переменной, а вертикальная ось — зависимой переменной. В алгебре вы бы назвали горизонтальную ось осью x , а вертикальную ось осью y . Как и на рис. 2.10, линейный график имеет общий вид y=mx+by=mx+b.
Как и на рис. 2.10, линейный график имеет общий вид y=mx+by=mx+b.
Здесь м — уклон, определяемый как подъем, деленный на длину (как видно на рисунке) прямой. Буква b представляет собой точку пересечения y , которая является точкой, в которой линия пересекает вертикальную ось y . С точки зрения физической ситуации в реальном мире эти величины приобретут особое значение, как мы увидим ниже. (Рисунок 2.10.)
Рисунок 2.10 На схеме изображен линейный график. Уравнение прямой линии y равно m x + b .
В физике время обычно является независимой переменной. Говорят, что другие величины, такие как смещение, зависят от него. Таким образом, график зависимости положения от времени будет иметь положение на вертикальной оси (зависимая переменная) и время на горизонтальной оси (независимая переменная). К чему в этом случае относятся наклон и y -intercept? Давайте вернемся к нашему исходному примеру при изучении расстояния и смещения.
К чему в этом случае относятся наклон и y -intercept? Давайте вернемся к нашему исходному примеру при изучении расстояния и смещения.
Дорога в школу находилась в 5 км от дома. Предположим, что поездка заняла 10 минут, и ваш родитель все это время ехал с постоянной скоростью. График зависимости положения от времени для этого участка пути будет выглядеть так, как показано на рисунке 2.11.
Рисунок 2.11 Показан график зависимости положения от времени по дороге в школу. Как бы выглядел график, если бы мы добавили обратный путь?
Как мы уже говорили, d 0 = 0, потому что мы называем домом 9.0055 O и начните расчет оттуда. На рис. 2.11 линия также начинается с d = 0. Это b в нашем уравнении для прямой линии. Нашей начальной позицией на графике зависимости положения от времени всегда является место, где график пересекает ось x в точке t = 0. Каков наклон? подъем — это изменение положения (т. е. смещение), а прогон — это изменение во времени. Это отношение также можно записать
Каков наклон? подъем — это изменение положения (т. е. смещение), а прогон — это изменение во времени. Это отношение также можно записать
ΔdΔt.ΔdΔt.
2,4
Это соотношение было тем, как мы определили среднюю скорость. Следовательно, наклон графика d по сравнению с t представляет собой среднюю скорость.
Советы для успеха
Иногда, как в случае, когда мы наносим на график и поездку в школу, и обратную дорогу, поведение графика выглядит по-разному в разные промежутки времени. Если график выглядит как серия прямых линий, то вы можете рассчитать среднюю скорость для каждого временного интервала, глядя на наклон. Если затем вы хотите рассчитать среднюю скорость за всю поездку, вы можете сделать средневзвешенное значение.
Давайте посмотрим на другой пример. На рис. 2.12 показан график зависимости положения автомобиля с реактивным двигателем от времени на очень плоском высохшем дне озера в Неваде.
Рисунок 2.12 На диаграмме показан график зависимости положения автомобиля с реактивным двигателем от времени на соляных равнинах Бонневилля.
Используя взаимосвязь между зависимыми и независимыми переменными, мы видим, что наклон на графике на рис. 2.12 представляет собой среднюю скорость, v avg , а точка пересечения представляет собой перемещение в нулевое время, то есть д 0 . Подстановка этих символов в y = m x + b дает
d=vt+d0d=vt+d0
2,5
или
d=d0+vt.d=d0+vt.
2.6
Таким образом, график зависимости положения от времени дает общее соотношение между перемещением, скоростью и временем, а также дает подробную числовую информацию о конкретной ситуации. Из рисунка видно, что машина имеет позицию 400 м при т = 0 с, 650 м при t = 1,0 с и т.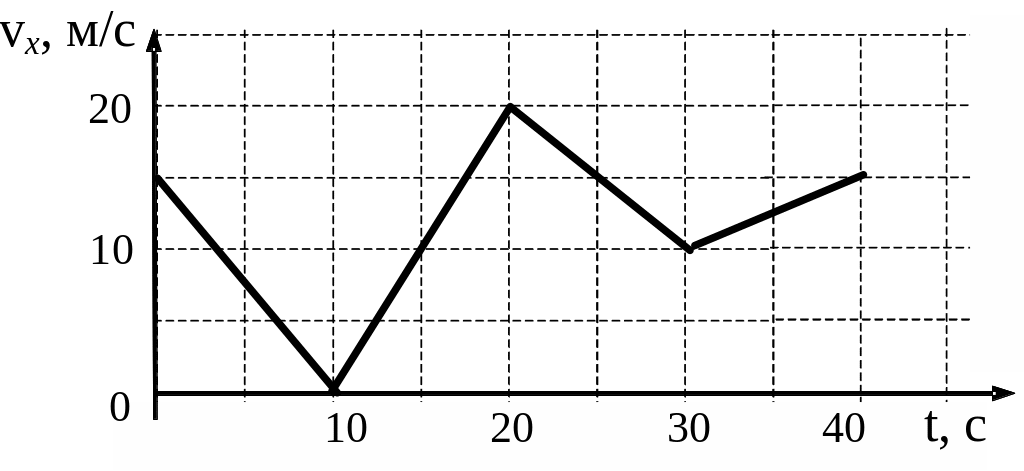 д. И мы также можем узнать о скорости объекта.
д. И мы также можем узнать о скорости объекта.
Поддержка учителей
Поддержка учителей
Демонстрация учителя
Помогите учащимся узнать, как выглядят различные графики зависимости перемещения от времени.
[Визуально] Установите метр.
- Если вы можете найти машину с дистанционным управлением, попросите одного из учащихся записать время, когда вы отправляете машину вперед вдоль палки, затем назад, а затем снова вперед с постоянной скоростью.
- Возьмите записанное время и изменение положения и соедините их.
- Попросите учеников научить вас рисовать график зависимости позиции от времени.
Каждый этап пути должен представлять собой прямую линию с различным уклоном. Участки, где машина ехала вперед, должны иметь положительный уклон. Часть, где он движется назад, будет иметь отрицательный наклон.
[ПР] Спросите, влияет ли место, которое они занимают как ноль , на график.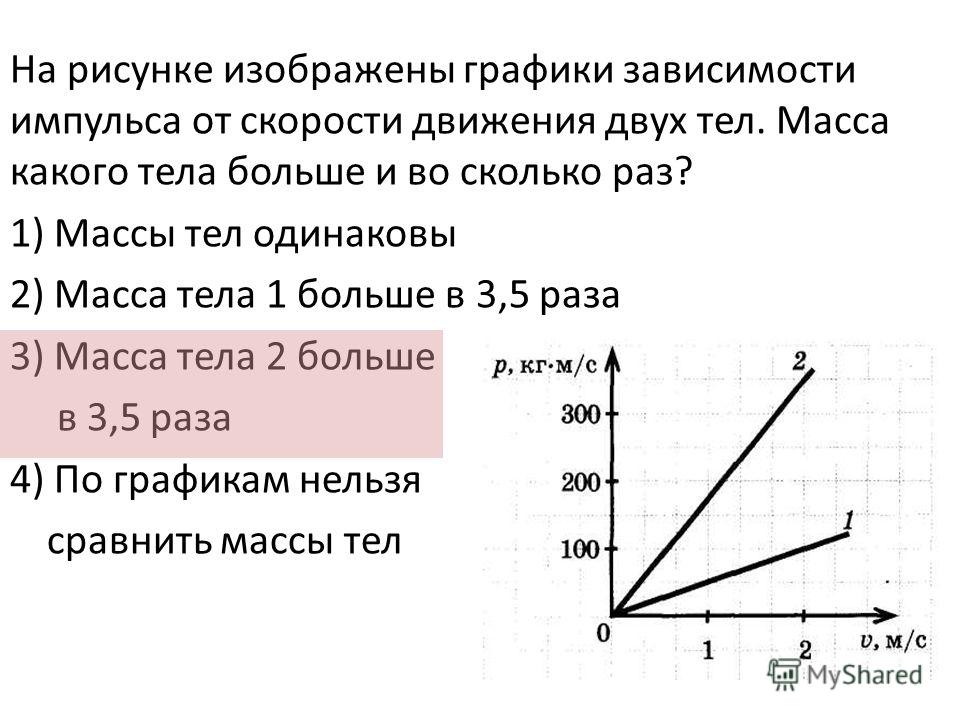
[AL] Реально ли нарисовать любой график положения, который начинается в состоянии покоя без какой-либо кривой? Почему мы можем пренебречь кривой в некоторых сценариях?
[Все] Обсудите, что можно узнать из этого графика. Учащиеся должны уметь читать чистое перемещение, но они также могут использовать график для определения общего пройденного расстояния. Затем спросите, как скорость или скорость отражены на этом графике. Укажите учащимся, что крутизна линии (наклона) является мерой скорости, а направление уклона является направлением движения.
[AL] Некоторые учащиеся могут понять, что кривая на линии представляет собой своего рода наклон склона, предварительный просмотр ускорения, о котором они узнают в следующей главе.
Снап Лаборатория
График движения
В этом упражнении вы запустите мяч вниз по пандусу и нарисуете график смещения мяча в зависимости от времени.
- Выберите открытое место с большим пространством для расстановки, чтобы было меньше шансов споткнуться или упасть из-за катящихся шаров.

- 1 шарик
- 1 плата
- 2 или 3 книги
- 1 секундомер
- 1 рулетка
- 6 шт. малярной ленты
- 1 лист миллиметровой бумаги
- 1 карандаш
Процедура
- Постройте пандус, поместив один конец доски поверх стопки книг. При необходимости отрегулируйте местоположение до тех пор, пока на пути прямой линии от нижней части пандуса до следующих 3 м не будет препятствий.
- Отметьте расстояния 0,5 м, 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части пандуса. Запишите расстояния на ленте.
- Пусть один человек возьмет на себя роль экспериментатора. Этот человек выпустит мяч с вершины рампы. Если мяч не достигает отметки 3,0 м, увеличьте наклон пандуса, добавив еще одну книгу. Повторяйте этот шаг по мере необходимости.
- Попросите экспериментатора отпустить мяч. Попросите второго человека, таймера, начать отсчет времени, как только мяч достигнет нижней части пандуса, и остановить отсчет времени, когда мяч достигнет 0,5 м.
 Попросите третьего человека, регистратора, записать время в таблицу данных.
Попросите третьего человека, регистратора, записать время в таблицу данных. - Повторите шаг 4, остановив время на расстоянии 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части рампы.
- Используйте свои измерения времени и смещения, чтобы построить график зависимости положения от времени движения мяча.
- Повторите шаги с 4 по 6, при этом разные люди берут на себя роли экспериментатора, таймера и записывающего устройства. Получаете ли вы одинаковые значения измерений независимо от того, кто выпускает мяч, измеряет время или записывает результат? Обсудите возможные причины расхождений, если таковые имеются.
Верно или неверно: средняя скорость мяча будет меньше средней скорости мяча.
Правда
Ложь
Поддержка учителей
Поддержка учителей
[BL][OL] Подчеркните, что движение в этой лабораторной работе — это движение мяча, когда он катится по полу. Спросите учащихся, где должен быть ноль.
Спросите учащихся, где должен быть ноль.
[AL] Спросите учащихся, как бы выглядел график, если бы они начали отсчет времени сверху, а не снизу рампы. Почему график будет выглядеть иначе? Что может объяснить разницу?
[BL][OL] Предложите учащимся сравнить графики, построенные для разных людей, играющих разные роли. Попросите их определить и сравнить средние скорости для каждого интервала. Каковы были абсолютные различия в скоростях и каковы процентные различия? Являются ли различия случайными или существуют систематические различия? Почему могут быть систематические различия между двумя наборами измерений с разными людьми в каждой роли?
[BL][OL] Предложите учащимся сравнить графики, построенные для разных людей, играющих разные роли. Попросите их определить и сравнить средние скорости для каждого интервала. Каковы были абсолютные различия в скоростях и каковы процентные различия? Являются ли различия случайными или существуют систематические различия? Почему могут быть систематические различия между двумя наборами измерений с разными людьми в каждой роли?
Решение проблем с использованием графиков зависимости положения от времени
Итак, как мы можем использовать графики для решения вещей, которые мы хотим знать, таких как скорость?
Рабочий пример
Использование графика положение-время для расчета средней скорости: реактивный автомобиль
Найдите среднюю скорость автомобиля, положение которого показано на рис.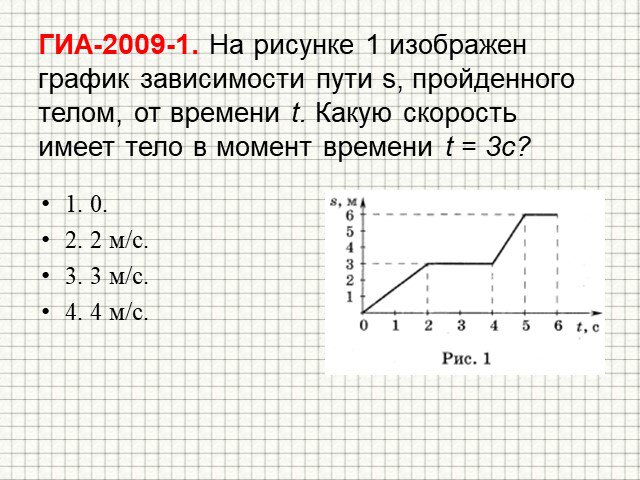 1.13.
1.13.
Стратегия
Наклон графика d по сравнению с t представляет собой среднюю скорость, поскольку наклон равен превышению над пробегом.
наклон =ΔdΔt=vslope =ΔdΔt=v
2,7
Поскольку здесь наклон постоянный, для определения наклона можно использовать любые две точки на графике.
Решение
- Выберите две точки на линии. В этом случае выбираем точки, отмеченные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Обратите внимание, однако, что вы можете выбрать любые две точки.)
- Подставьте значения d и t выбранных точек в уравнение. Помните, что при расчете изменения (Δ) мы всегда используем конечное значение минус начальное значение.
v=ΔdΔt=2000 м-525 м6,4 с-0,50 с=250 м/с, v=ΔdΔt=2000 м-525 м6,4 с-0,50 с=250 м/с,
2,8
Обсуждение
Это впечатляюще высокая скорость на суше (900 км/ч, или около 560 миль/ч): намного больше, чем типичный предел скорости на шоссе в 27 м/с или 96 км/ч, но значительно меньше рекорд 343 м/с или 1234 км/ч, установленный в 1997 году.
Поддержка учителей
Поддержка учителей
Если график положения представляет собой прямую линию, то единственное, что нужно знать учащимся для расчета средней скорости, — это наклон линии, подъем/бег. Они могут использовать любые точки на линии, которые наиболее удобны.
А что, если график позиции сложнее прямой линии? Что, если объект ускорится или развернется и пойдет назад? Можем ли мы узнать что-нибудь о его скорости из графика такого движения? Давайте еще раз посмотрим на автомобиль с реактивным двигателем. График на рис. 2.13 показывает его движение по мере того, как он набирает скорость после старта из состояния покоя. Время для этого движения начинается с нуля (как если бы его измеряли секундомером), а перемещение и скорость изначально равны 200 м и 15 м/с соответственно.
Рисунок
2.13
На диаграмме показан график положения автомобиля с реактивным двигателем в течение промежутка времени, когда он разгоняется.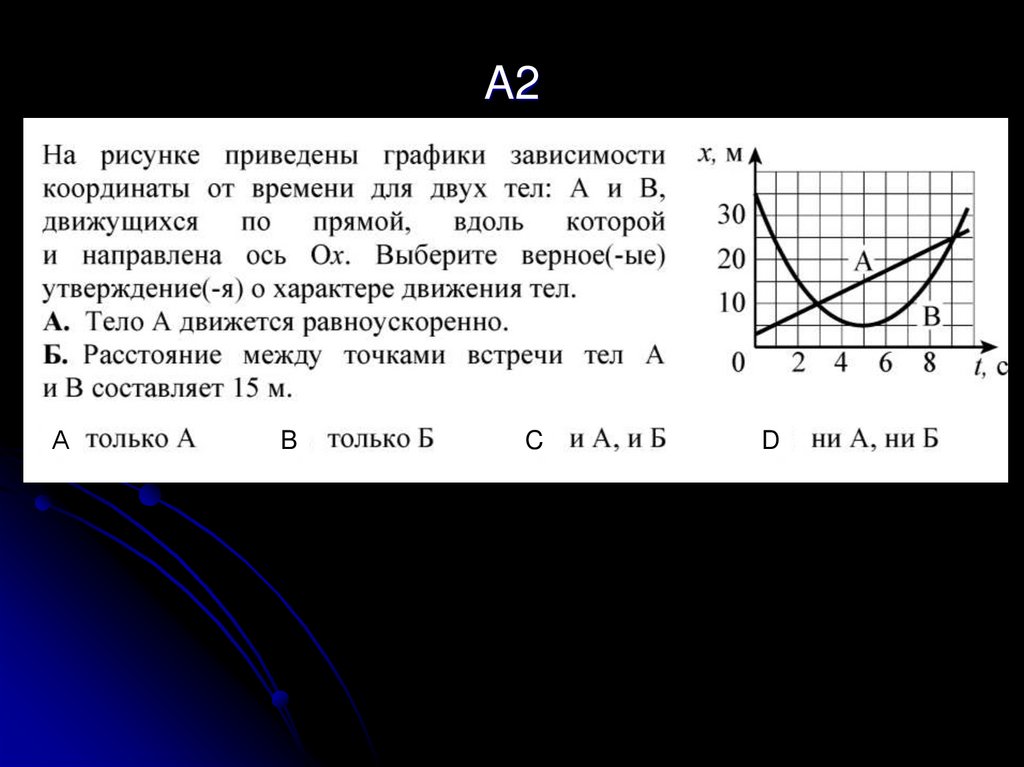 Наклон графика зависимости расстояния от времени — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке равна наклону касательной в этой точке.
Наклон графика зависимости расстояния от времени — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке равна наклону касательной в этой точке.
Рисунок 2.14 Реактивный автомобиль ВВС США мчится по трассе. (Мэтт Тростл, Flickr)
График зависимости положения от времени на рис. 2.13 представляет собой кривую, а не прямую линию. Наклон кривой становится круче с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости положения от времени представляет собой мгновенную скорость в этой точке. Его находят, проводя прямую линию, касающуюся кривой в интересующей точке, и измеряя наклон этой прямой. Касательные линии показаны для двух точек на рисунке 2.13. Средняя скорость равна чистому перемещению, деленному на пройденное время.
Рабочий пример
Использование графика положение-время для расчета средней скорости: реактивный автомобиль, дубль два
Рассчитайте мгновенную скорость реактивного автомобиля через 25 с, найдя наклон касательной в точке Q на рис.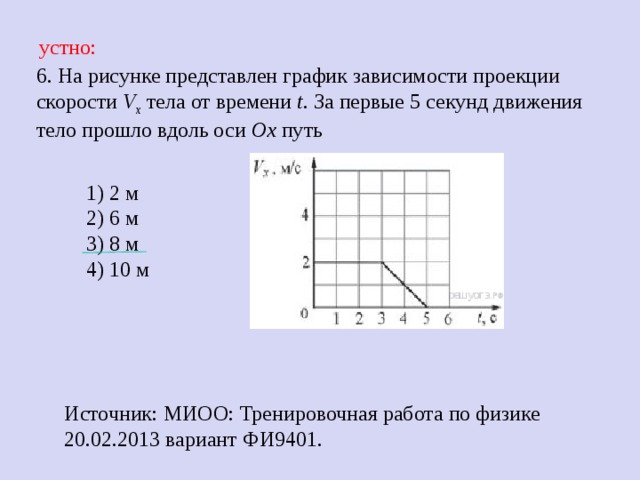 2.13.
2.13.
Стратегия
Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке.
Решение
- Найдите касательную к кривой в момент времени t=25 st=25 с .
- Определить конечные точки касательной. Они соответствуют положению на 1300 м в момент времени 19 с и положению на 3120 м в момент времени 32 с.
- Подставьте эти конечные точки в уравнение для определения наклона v .
уклон=vQ=ΔdQΔtQ=(3120−1300) м(32−19) с=1820 м13 с=140 м/с уклон=vQ=ΔdQΔtQ=(3120−1300) м(32−19) с=1820 м13 с= 140 м/с
2,9
Обсуждение
Полный график v против t может быть получен таким образом.
Поддержка учителей
Поддержка учителей
Кривая линия — более сложный пример. Определить касательную как линию, которая касается кривой только в одной точке. Покажите, что когда прямая линия меняет свой угол рядом с кривой, она на самом деле несколько раз пересекается с кривой в основании, но только одна линия никогда не касается ее вообще. Эта линия образует прямой угол с радиусом кривизны, но на этом уровне они могут просто увидеть ее на глаз. Наклон этой линии дает мгновенную скорость. Наиболее полезная часть этой линии заключается в том, что учащиеся могут сказать, когда скорость увеличивается, уменьшается, положительна, отрицательна и равна нулю.
Покажите, что когда прямая линия меняет свой угол рядом с кривой, она на самом деле несколько раз пересекается с кривой в основании, но только одна линия никогда не касается ее вообще. Эта линия образует прямой угол с радиусом кривизны, но на этом уровне они могут просто увидеть ее на глаз. Наклон этой линии дает мгновенную скорость. Наиболее полезная часть этой линии заключается в том, что учащиеся могут сказать, когда скорость увеличивается, уменьшается, положительна, отрицательна и равна нулю.
[AL] Вы можете найти мгновенную скорость в каждой точке на графике, и если вы начертите график каждой из этих точек, у вас будет график скорости.
Практические задачи
16.
Рассчитайте среднюю скорость объекта, показанного на графике ниже, за весь интервал времени.
- 0,25 м/с
- 0,31 м/с
- 3,2 м/с
- 4,00 м/с
17.
Верно или неверно: Взяв наклон кривой на графике, вы можете убедиться, что скорость реактивного автомобиля равна 125\,\text{м/с} при t = 20\,\text{с}.
Правда
Ложь
Проверьте свое понимание
18.
Какую из следующих сведений о движении можно определить, глядя на график зависимости положения от времени, который представляет собой прямую линию?
- система отсчета
- среднее ускорение
- скорость
- направление приложенной силы
19.
Верно или неверно: график зависимости положения от времени ускоряющегося объекта представляет собой прямую линию.
Правда
Ложь
Поддержка учителей
Поддержка учителей
Используйте Проверьте свое понимание вопросов для оценки достижения учащимися целей обучения раздела. Если учащиеся испытывают затруднения при выполнении определенной задачи, тест Check Your Understanding поможет определить, как направить учащихся к соответствующему содержанию.
На рисункепоказан график зависимости скорости от tie для частицы, движущейся вдоль оси X. Найди. ускорение, б. Расстояние, пройденное за время от 0 до 10 с и c. смещение от 0 до 10 с.

HC VERMA-ОТДЫХ И ДВИЖЕНИЕ: КИНЕМАТИКА-Упражнения
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Обновлено: 27-06-2022
Текст Решение
Ответ
Правильный ответ: A::B::C
Решение
a. Начальная скорость u=2мс
FiNAlvelocity
v=8мс
Время=10сек
Ae≤ration=v−ut,=8−210=610=0,6ms2,b.v2−u2=2aS< br>→Расстояние
S=v2−u22a
=82−222×0,6=50м
c. Перемещение равно пройденному расстоянию. Водоизмещение = 50 м
Ответить
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Похожие видео
На рисунке показан график зависимости x-координаты частицы, движущейся вдоль оси X, от времени. Найдите a. te средняя скорость от 0 до 10 с, b. мгновенная скорость на 2,5,8 и 12с.
9515254
На рис.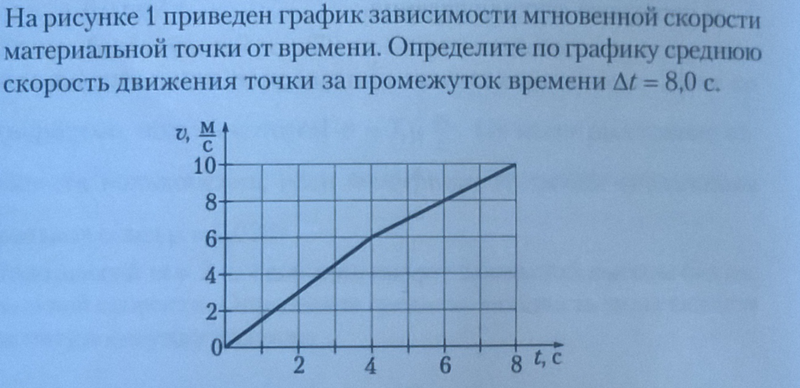 показан график зависимости скорости от времени для тела, движущегося вдоль оси x. Найти: а) ускорение, б) расстояние, пройденное за время от 0 до 10 с, в) перемещение за время от 0 до 10 с.
показан график зависимости скорости от времени для тела, движущегося вдоль оси x. Найти: а) ускорение, б) расстояние, пройденное за время от 0 до 10 с, в) перемещение за время от 0 до 10 с.
10955425
На рис. показан график зависимости координаты х частицы, идущей по оси абсцисс, от времени. Найдите: а) среднюю скорость в период от 0 до 10 с, б) мгновенную скорость через 2, 5, 8 и 12 с.
10955426
Частица движется вдоль оси x. Считайте, что это t-график. Если начальная скорость равна 10 м/с, начертите график v-t и рассчитайте перемещение в интервале времени от t=0 до 12 с.
13396064
График зависимости скорости (v) от смещения (s) частицы, движущейся по прямой линии, показан на рисунке. Соответствующий график зависимости ускорения (a) от скорости (v) будет равен
14527193
Частица движется вдоль положительного направления x и испытывает постоянное ускорение 4 м/с2 в отрицательном направлении x. В момент времени t=3 секунды было замечено, что его скорость составляет 10 м/с в положительном направлении x.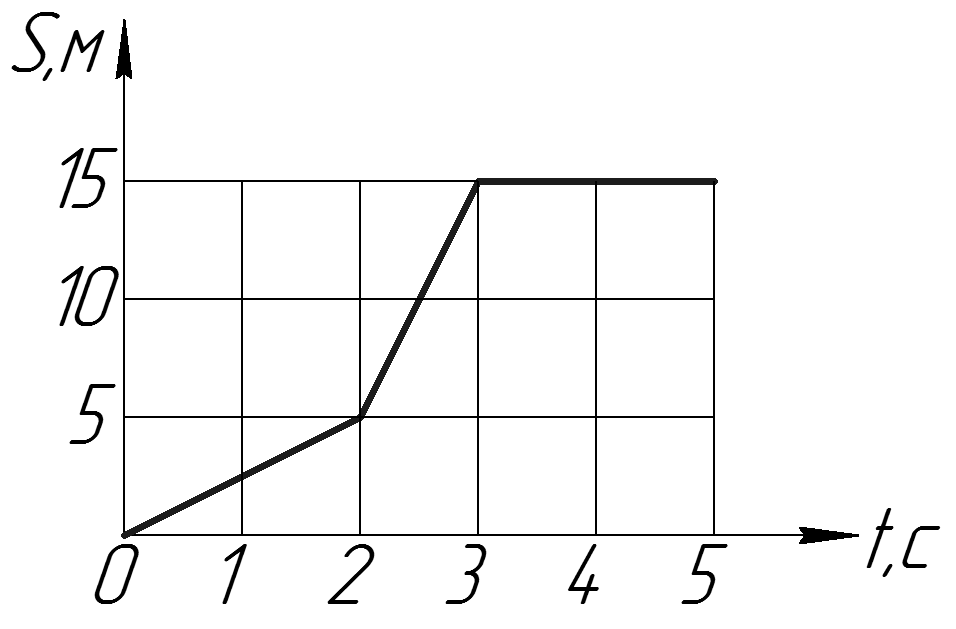
(а) Найдите расстояние, пройденное частицей в интервале от t=0 до t=3с. Также найдите расстояние, пройденное в интервале от t = 0 до t = 7,5 с..
(b) Постройте график зависимости смещения от времени для интервала от t = 0 до 7,5 с.
15084789
Текст Решение
График v-t для частицы, движущейся вдоль оси абсцисс, показан на рисунке, найти
(а) Средняя скорость в интервале от 0 до 8 с.
(б) Средняя скорость в интервале от 0 до 8 с.
(c) Среднее ускорение в интервале от 0 до 4 с.
(г) Мгновенное ускорение при t = 2,5 с.
69127328
График ускорения частицы, движущейся вдоль оси x, показан на рисунке. Если частица стартовала со скоростью 3 м/с в момент t = 0, найти скорость частицы в момент t = 4 с.
69127329
x -अक्ष के गतिशील कण का समय- ज्ञात कीजिए : (i) त्वरण 0, (ii) 0 से 4 सेकण्ड तक चली गयी दी|री
109999876
चित्र में x — अक्ष प000 (а) कण का त्वरण निकले | (b) t = 0 से t = 10 s के बीच चली गई दुरी तथा (c) t = 0 से t = 10 S के अंत अंत अंत में विस्थापन निकले |
110486291
На рисунке показан график зависимости скорости от времени для частицы, движущейся вдоль оси x.

 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
 Попросите третьего человека, регистратора, записать время в таблицу данных.
Попросите третьего человека, регистратора, записать время в таблицу данных.
Leave A Comment