Решаем ЕГЭ 2020 Ященко Математика профильный Вариант 7

содержание видео

Рейтинг: 4.0; Голоса: 1

Решаем ЕГЭ 2020 Ященко Математика профильный Вариант 7 Sr. : Здравствуйте. Я похоже что-то не понимаю, но в 19. Б. нужно было сравнить с средней ценой книг Без бирки выгодно До выставки (по условию их цена должна быть >=100, а вы взяли 90, т. е. эта книга была с биркой, что противоречит условию в пункте Б. по сравнению со средней ценой КНИГ БЕЗ бирки выгодно ДО открытия. я подозреваю, что ошибка где-то у меня, но. где?
Дата: 2021-09-22

← Математик решает ЕГЭ по русскому языку 2020 Цыбулько вариант 1. Новогодний выпуск

Решаем ОГЭ 2020 Ященко 7 вариант →

Похожие видео

Факты и мифы про холестерин

• Доктор Комаровский

Зачем ВАТИКАН выставляет МУМИИ людей в своих ХРАМАХ?

• Альтернативная история

От каких мужчин женщины бегут без оглядки? Горькая Правда! Девушка сказала Я тебя не люблю! Причины

• Дмитрий Петров

Девушка общается с бывшим? Дружит и переписывается с бывшим? Что делать? Женщина общается с бывшим.

• Максим Вердикт

Вот как ПОДМЕНИЛИ веру РУСИ! О чем молчат старые ЦЕРКВИ?

• Альтернативная история

Тайны острова Уруп Русское географическое общество

• Русское географическое общество

Комментарии и отзывы: 8

Григорий
В восьмой задаче лучше и понятнее обьяснить через подобные треугольники и отношение площадей как отношение квадратов соответствуюших сторон. А через 4 одинаковых треугольника ничего не понятно, в пособиях такого свойства нету и по рисунку эти треугольники ни разу не одинаковые.

Agent
Ребят, представьте, что вы в 10 классе, математику знаете не плохо, 70+ уже, а другие предметы, которые сдаешь, в душе не чаеш, что делать, начинать готовиться, или пытаться делать какие-то проекты по зароботку (требуют все свободное время, вложится в учебу, или в заработок?

Persivan
19в) выгодных: 15 по 80 и 1 по 96, средняя цена до подорожания 81, а после стало 15 по 90 со средней ценой 90. Тут правильно НО
Не выгодных: 4 по 226, средняя цена до подорожания 226, а после стало 4 по 226 и 1 по 106 СРЕДНЯЯ ЦЕНА СТАЛА 202.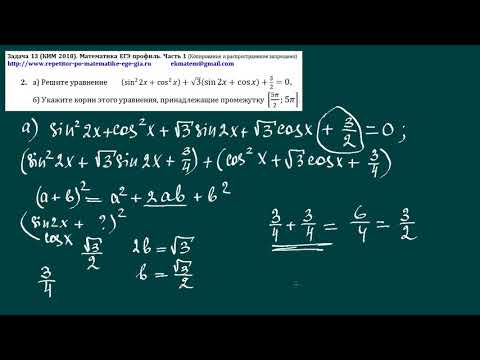 А по условия должна стать 210.
Где я ошибся?

anoter
Добрый вечер, учусь в 11 классе, уже долго смотрю ваши видео и не всегда понятно каким правилом руководствуетесь, в решениях некоторых задач, конкретно не скажу, но хотелось бы, чтобы в следующем видео вы ссылались на ту, или иную формулу, спасибо за внимание

Onlylafro
Капец, хорошо что я после девятого ушел, а то бы у меня мозг взорвался на математике. У меня ад флешбеки были где я сижу на математике и ничего не понимаю и тупо срисовываю у своего френдана задачи, словно иероглифы.

neMagomedov
Здравствуйте, я посмотрел ваш курс, там написано, что с 1 до 12 задания идёт обучение, а в отзывах вас благодарят за то, что вы научили делать из 17, 19 и др задания
Не могли бы вы объяснить мне поподробнее

ПЕРВЫЙ
сдавал егэ в 2008 году, дело было так я почти не ходил в школу 2 года, побухивал, покуривал, гулял с телками а потом просто пришел на егэ и сдал на 4 и 3. далее попал на бесплатное в технарь изи бля

edinson
Привет всем, удачи и здоровья вам и вашим родителям. Всем денег и благо! Что бы всё хорошо было в жизни у вас! Всего хорошего)Еще раз всего хорошего)

Официальный информационный портал Государственной итоговой аттестации выпускников Камчатского края

Новости и обновления на сайте

  • новость за

    28.04.2023, категория: Новости ГИА-9

    Опубликованы результаты ОГЭ по дисциплине «Математика» за 21.04.2023 и «Русский язык» за 24.04.2023. С результатами можно ознакомиться в разделе «ГИА-9(ОГЭ, ГВЭ-9) — Посмотреть результаты ОГЭ, ГВЭ-9».

    ВНИМАНИЕ!

    С 2023 года бланки ОГЭ, ГВЭ-9 можно посмотреть на сайте sdr.ixora.ru

    Пожалуйста используйте указанный сервис для просмотра бланков своих работ!

    Также результаты размещены в сетевых папках ГИС «Сетевой город» органов местного самоуправления, осуществляющих управление в сфере образования.

    Официальный день объявления результатов — 02.05.2023.

    Прием апелляций осуществляется – 03.05.2023 и 04.05.2023.

  • новость за

    27.04.2023, категория: Новости ГИА-9

    Ключ для КИМ по КОГЭ 27.04.2023 ссылка

  • новость за

    26.04.2023, категория: Новости ГИА-9

    Форма ППЭ-10 (Отчет члена(ов) ГЭК о проведении ГИА в ППЭ)

  • новость за

    25. 04.2023, категория: Новости ГИА-9

    Пароль к экзаменационным материалам тренировочного тестирования по математике на 25.04.2023 @/:ZeZ?3

  • новость за

    24.04.2023, категория: Новости ГИА-11

    Опубликованы результаты ЕГЭ, ГВЭ-11 по дисциплинам «Химия», «История» за 10.04.2023. С результатами можно ознакомиться в разделе «ГИА-11(ЕГЭ, ГВЭ-11) — Посмотреть результаты ЕГЭ, ГВЭ-11».

    Также результаты размещены в сетевых папках ГИС «Сетевой город» органов местного самоуправления, осуществляющих управление в сфере образования.

    Официальный день объявления результатов — 25. 04.2023.

    Прием апелляций осуществляется – 26.04.2023 и 27.04.2023.

  • новость за

    24.04.2023, категория: Новости ГИА-9

    Пароль к экзаменационным материалам по русскому языку на 24.04.2023 Fx2YWD7#

  • новость за

    21.04.2023, категория: Новости ГИА-9

    Пароль к экзаменационным материалам по математике на 21.04.2023 5shkV%2s

  • новость за

    18. 04.2023, категория: Новости ГИА-11

    Опубликованы результаты ЕГЭ, ГВЭ-11 по дисциплинам «Обществознание» за 06.04.2023, «Английский язык» за 30.03.2023, 03.04.2023. С результатами можно ознакомиться в разделе «ГИА-11(ЕГЭ, ГВЭ-11) — Посмотреть результаты ЕГЭ, ГВЭ-11».

    Также результаты размещены в сетевых папках ГИС «Сетевой город» органов местного самоуправления, осуществляющих управление в сфере образования.

    Официальный день объявления результатов — 18.04.2023.

    Прием апелляций осуществляется – 19.04.2023 и 20.04.2023.

  • новость за

    14.04.2023, категория: Новости ГИА-9

    В разделе Документы опубликованы приказы Министерства образования Камчатского края, утверждающие минимальные баллы для прохождения государственной итоговой аттестации по программам основного общего образования (ГИА-9).

  • новость за

    12.04.2023, категория: Новости ГИА-11

    Опубликованы результаты ЕГЭ, ГВЭ-11 по дисциплинам «Биология», «Физика» за 30.03.2023. С результатами можно ознакомиться в разделе «ГИА-11(ЕГЭ, ГВЭ-11) — Посмотреть результаты ЕГЭ, ГВЭ-11».

    Также результаты размещены в сетевых папках ГИС «Сетевой город» органов местного самоуправления, осуществляющих управление в сфере образования.

    Официальный день объявления результатов — 13.04.2023.

    Прием апелляций осуществляется – 14.04.2023 и 17.04.2023.

  • новость за

    10. 04.2023, категория: Новости ГИА-11

    Опубликованы результаты ЕГЭ, ГВЭ-11 по дисциплине «Математика» за 27.03.2023. С результатами можно ознакомиться в разделе «ГИА-11(ЕГЭ, ГВЭ-11) — Посмотреть результаты ЕГЭ, ГВЭ-11».

    Также результаты размещены в сетевых папках ГИС «Сетевой город» органов местного самоуправления, осуществляющих управление в сфере образования.

    Официальный день объявления результатов — 11.04.2023.

    Прием апелляций осуществляется – 12.04.2023 и 13.04.2023.

  • новость за

    05.04.2023, категория: Новости ГИА-11

    Опубликованы результаты ЕГЭ, ГВЭ-11 по дисциплине «Русский язык» за 23. 03.2023. С результатами можно ознакомиться в разделе «ГИА-11(ЕГЭ, ГВЭ-11) — Посмотреть результаты ЕГЭ, ГВЭ-11».

    Также результаты размещены в сетевых папках ГИС «Сетевой город» органов местного самоуправления, осуществляющих управление в сфере образования.

    Официальный день объявления результатов — 05.04.2023.

    Прием апелляций осуществляется – 06.04.2023 и 07.04.2023.

  • новость за

    04.04.2023, категория: Обновления

    На технологической странице сайта gia41.ru размещены материалы для проведения апробации КОГЭ 05.04 и 06.04

  • новость за

    30. 03.2023, категория: Обновления

    В разделе Методические материалы — Презентации, Методические материалы — Видеоматериалы опубликованы презентации и записи вебинаров, которые проходили с 21.03.2023 по 29.03.2023 для работников ППЭ на ГИА-11 и ГИА-9

  • новость за

    15.03.2023, категория: Новости ГИА-9

    На технологической странице в разделе «Программное обеспечение для проведения ГИА-9 (ОГЭ)» размещены варианты КИМ для проведения итогового собеседования выпускников 9 классов по русскому языку 15.03.2023

  • новость за

    14. 03.2023, категория: Новости ГИА-9

    На технологической странице сайта размещен «Школьный модуль» версии 13.0.0.1 для ввода результатов собеседования 15.03.2023.

  • новость за

    17.02.2023, категория: Обновления

    Напоминаем о размещённых на сайте баннерах на разделы «ГИА» и «Навигатор ГИА» официального сайта Рособрнадзора, телефонов «горячей линии» Рособрнадзора по вопросам ЕГЭ и телефона доверия ЕГЭ.

    Также размещены баннеры на официальные сайты ФГБНУ «ФИПИ» и ФГБУ «ФЦТ».

    Вышеназванные ресурсы содержат в том числе методические рекомендации для выпускников по самостоятельной подготовке к экзаменам, видеоконсультации разработчиков КИМ ЕГЭ 2023 года, а также полезную информацию для учителей школ.

  • новость за

    16.02.2023, категория: Новости ГИА-11

    На технологической странице размещены два дистрибутива: «Дистрибутив Планирование ГИА (ЕГЭ) 2023» и «Дистрибутив для проведения АПРОБАЦИИ Планирование ГИА (ЕГЭ) 2023» в разделе «Программное обеспечение для проведения ГИА-11 (ЕГЭ)» — «Программное обеспечение АИС»

  • новость за

    08.02.2023, категория: Новости ГИА-9

    На технологической странице в разделе «Программное обеспечение для проведения ГИА-9 (ОГЭ)» размещены варианты для проведения итогового собеседования выпускников 9 классов по русскому языку.

  • новость за

    27.01.2023, категория: Новости ГИА-11

    Пароль к архиву с материалами итогового изложения на 1.02.2023: 3e14k

Смотреть архив

Памятка участникам . Графические материалы

Полезные ссылки

  • НАВИГАТОР ГИА

    Федеральная служба по надзору в сфере образования и науки

  • ГИА

    Федеральная служба по надзору в сфере образования и науки

  • фипи

    Федеральный институт педагогических измерений

  • ФЦТ

    Федеральный центр тестирования

  • Российское образование

    Федеральный портал Рособрнадзора

  • Минпросвещения России

    Министерство просвещения Российской Федерации

Assessment, Research & Program Evaluation / Honor Math 7

Этот экзамен предназначен для учащихся, которые с отличием завершили 6-й класс по математике и хотят перейти на курс с отличием по алгебре I в следующем учебном году. Это ускорит учащихся, прошедших курс математики 7 с отличием. В Plano ISD курс Honors Math 7 охватывает примерно половину государственных стандартов по математике для 7-го класса, а также все государственные стандарты для 8-го класса. Ниже приведены результаты обучения по этим государственным стандартам, которые учащиеся должны продемонстрировать на этом CBE.

Кредит по экзамену:     1.0 —  *Оценка не рассчитывается в среднем балле (GPA)

Полученный курс PISD:  Почетная математика 7

9000 2 Экзамен: Район создан

Экзамен Ограничение по времени:  4 часа

Формат экзамена:  

  • 96 вопросов с несколькими вариантами ответов

Дополнительные материалы к экзамену:

  • Справочная таблица Math 7 STAAR (предоставляется в онлайн-тесте)
  • Справочная таблица Math 8 STAAR (предоставляется в онлайн-тесте)
  • Научный калькулятор (предоставляется в онлайн-тестировании)

Информация о содержании экзамена — Государственные стандарты (TEKS) по математике с отличием 7:

  • Учащиеся могут подготовиться, изучив любые ресурсы, соответствующие этим TEKS по математике для 7 и 8 классов, перечисленным ниже.

Числа и операции

(7.2) Количество и операции. Учащийся применяет стандарты математических процессов для представления и использования рациональных чисел в различных формах. Ожидается, что учащийся расширит предыдущие знания о множествах и подмножествах, используя визуальное представление для описания отношений между наборами рациональных чисел.

(8.2)  Количество и операции. Учащийся применяет стандарты математических процессов для представления и использования действительных чисел в различных формах. Ожидается, что учащийся:
(A) расширить предыдущие знания о наборах и подмножествах, используя визуальное представление для описания отношений между наборами действительных чисел;
(B) приблизить значение иррационального числа, включая π и квадратные корни из чисел меньше 225, и найти это приближение рационального числа на числовой прямой;
(D) заказать набор действительных чисел, возникающих из математических и реальных контекстов.

(8.6)  Выражения, уравнения и отношения. Учащийся применяет стандарты математических процессов для разработки математических отношений и установления связей с геометрическими формулами. Студент должен:
(C) использовать модели и диаграммы для объяснения теоремы Пифагора.

(8.7)  Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для решения задач. Ожидается, что учащийся:
(C) будет использовать теорему Пифагора и ее обращение для решения задач; и
(D) определяют расстояние между двумя точками на координатной плоскости, используя теорему Пифагора.


Геометрия

(7.5) Пропорциональность. Учащиеся применяют стандарты математических процессов, чтобы использовать геометрию для описания или решения проблем, связанных с пропорциональными отношениями. Ожидается, что учащийся:
(A) обобщать критические признаки подобия, включая отношения внутри и между подобными формами;
(B) описывают π как отношение длины окружности к ее диаметру; и
(C) решают математические и практические задачи, связанные с похожими формами и чертежами в масштабе.

(8.10) Двумерные формы. Студент применяет стандарты математического процесса для разработки концепций трансформационной геометрии. Ожидается, что учащийся:
(A) обобщит свойства ориентации и конгруэнтности вращений, отражений, перемещений и расширений двумерных фигур на координатной плоскости;
(B) провести различие между преобразованиями, сохраняющими конгруэнтность, и теми, которые ее не сохраняют;
(C) объясняют эффект перемещений, отражений по оси x или y и поворотов, ограниченных 90°, 180°, 270° и 360°, применительно к двумерным формам на координатной плоскости, используя алгебраический представление;
(D) смоделируйте влияние расширенных двумерных форм на линейные и площадные измерения.

(8.3)  Пропорциональность. Учащийся применяет стандарты математического процесса, чтобы использовать пропорциональные отношения для описания расширений. Студент должен:
(A) обобщить, что отношение соответствующих сторон подобных форм пропорционально, включая форму и ее расширение;
(B) сравнить и сопоставить атрибуты формы и ее расширения на координатной плоскости; и
(C) используют алгебраическое представление для объяснения эффекта данного положительного рационального коэффициента масштабирования, применяемого к двумерным фигурам на координатной плоскости с началом координат в качестве центра расширения.

(8.8)  Выражения, уравнения и отношения. Учащийся применяет стандарты математического процесса, чтобы использовать уравнения или неравенства с одной переменной в проблемных ситуациях. Ожидается, что учащийся:
(D) используют неформальные аргументы для установления фактов о сумме углов и внешнем угле треугольников, углах, образующихся при пересечении параллельных прямых секущей, и критерии угол-угол для подобия треугольников.


Пропорциональность и линейные зависимости

(7.4)  Пропорциональность. Учащийся применяет стандарты математических процессов для представления и решения задач, связанных с пропорциональными отношениями. Ожидается, что учащийся:
(C) определит константу пропорциональности (k = y/x) в математических и реальных задачах;

(7.7) Выражения, уравнения и отношения. Учащийся применяет стандарты математического процесса для представления линейных отношений с использованием нескольких представлений. Ожидается, что учащийся представит линейные отношения, используя словесные описания, таблицы и уравнения, которые упрощаются до формы y=mx+b.

(8.5)  Пропорциональность. Учащийся применяет стандарты математических процессов, чтобы использовать пропорциональные и непропорциональные отношения для разработки основных концепций функций. Студент должен:
(A) представляют линейно-пропорциональные ситуации с помощью таблиц, графиков и уравнений в виде y = kx;
(B) представляют линейные непропорциональные ситуации с помощью таблиц, графиков и уравнений в виде y = mx + b, где b ≠ 0;
(E) решать задачи, связанные с прямой вариацией;
(F) различать пропорциональные и непропорциональные ситуации, используя таблицы, графики и уравнения в форме y = kx или y = mx + b, где b ≠ 0;
(G) идентифицировать функции, используя наборы упорядоченных пар, таблиц, отображений и графиков;
(H) определить примеры пропорциональных и непропорциональных функций, которые возникают из математических и реальных задач; и 
(I) написать уравнение в форме y = mx + b для моделирования линейной зависимости между двумя величинами с использованием вербального, числового, табличного и графического представления.

(8.8)  Выражения, уравнения и отношения. Учащийся применяет стандарты математического процесса, чтобы использовать уравнения или неравенства с одной переменной в проблемных ситуациях. Ожидается, что учащийся:
(A) написать уравнения с одной переменной или неравенства с переменными с обеих сторон, которые представляют задачи с использованием коэффициентов и констант рациональных чисел;
(B) написать соответствующую задачу из реальной жизни, когда дано уравнение с одной переменной или неравенство с переменными по обе стороны от знака равенства с использованием коэффициентов и констант рациональных чисел;
(C) моделировать и решать уравнения с одной переменной с переменными по обе стороны от знака равенства, которые представляют математические и реальные задачи с использованием коэффициентов и констант рациональных чисел;


Вероятность

(7.6)  Пропорциональность. Учащийся применяет стандарты математических процессов, чтобы использовать вероятность и статистику для описания или решения проблем, связанных с пропорциональными отношениями. Ожидается, что учащийся:
(A) представит примеры пространств для простых и составных событий, используя списки и древовидные диаграммы;
(B) выбирать и использовать различные симуляции для представления простых и сложных событий с использованием технологий и без них;
(C) делать прогнозы и находить решения, используя экспериментальные данные для простых и сложных событий;
(D) делать прогнозы и находить решения, используя теоретическую вероятность для простых и сложных событий;
(E) найти вероятности простого события и его дополнения и описать отношения между ними;
(H) решать проблемы, используя качественные и количественные прогнозы и сравнения из простых экспериментов; и
(I) определяют экспериментальные и теоретические вероятности, связанные с простыми и составными событиями, используя данные и выборочные пространства.


Выражения, уравнения и отношения

(8.4)  Пропорциональность. Учащийся применяет стандарты математического процесса для объяснения пропорциональных и непропорциональных отношений, связанных с уклоном. Ожидается, что учащийся:
(A) использует подобные прямоугольные треугольники, чтобы развить понимание того, что наклон m, заданный как скорость сравнения изменения значений y с изменением значений x, (y2 — y1)/(x2 ‐ x1), одинаково для любых двух точек (x1, y1) и (x2, y2) на одной прямой;
(B) нарисуйте пропорциональные отношения, интерпретируя удельную ставку как наклон линии, которая моделирует отношения; и
(C) использовать данные из таблицы или графика для определения скорости изменения или наклона и точки пересечения с координатой Y в математических и реальных задачах.

(8.9)  Выражения, уравнения и отношения. Учащийся применяет стандарты математического процесса, чтобы использовать несколько представлений для разработки основных концепций одновременных линейных уравнений. Ожидается, что учащийся
(A) определит и проверит значения x и y, которые одновременно удовлетворяют двум линейным уравнениям в форме y = mx + b, из пересечений графических уравнений.


Трехмерное измерение

(7. 8)  Выражения, уравнения и отношения. Учащийся применяет стандарты математического процесса для разработки геометрических соотношений с объемом. Ожидается, что учащийся:
(A) смоделирует отношение между объемом прямоугольной призмы и прямоугольной пирамиды, имеющих конгруэнтные основания и высоты, и свяжет это отношение с формулами;
(B) объясните словесно и символически отношение между объемом треугольной призмы и треугольной пирамиды, имеющих конгруэнтные основания и высоты, и свяжите это отношение с формулами; и

(7.9)  Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для решения геометрических задач. Ожидается, что учащийся:
(A) решит задачи на объем прямоугольных призм, треугольных призм, прямоугольных и треугольных пирамид;
(B) определить длину окружности и площадь кругов;
(C) определить площадь составных фигур, содержащих комбинации прямоугольников, квадратов, параллелограммов, трапеций, треугольников, полуокружностей и четвертей окружности
(D) решить задачи, связанные с боковой и общей площадью поверхности прямоугольной призмы, прямоугольной пирамиды, треугольной призмы и треугольной пирамиды, путем определения площади сетки формы.

(8.7)  Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для решения задач. Ожидается, что учащийся:
(A) решит задачи на объем цилиндров, конусов и сфер;
(B) использовать предыдущие знания о площади поверхности, чтобы установить связи с формулами для поперечной и общей площади поверхности и найти решения для задач, связанных с прямоугольными призмами,
треугольные призмы и цилиндры;

(8.6)  Выражения, уравнения и отношения. Учащийся применяет стандарты математических процессов для разработки математических отношений и установления связей с геометрическими формулами. Ожидается, что учащийся:
(A) опишет формулу объема V = Bh цилиндра через его площадь основания и высоту;
(B) смоделируйте взаимосвязь между объемом цилиндра и конуса, имеющих конгруэнтные основания и высоты, и свяжите эту взаимосвязь с формулами ;


Анализ данных

(7.6)  Пропорциональность. Учащийся применяет стандарты математических процессов, чтобы использовать вероятность и статистику для описания или решения проблем, связанных с пропорциональными отношениями. Ожидается, что учащийся:
(F) будет использовать данные из случайной выборки, чтобы делать выводы о населении;
(G) решать задачи, используя данные, представленные в виде гистограмм, точечных и круговых диаграмм, включая сравнения частей с целыми и частями и эквиваленты;
(H) решать проблемы, используя качественные и количественные прогнозы и сравнения из простых экспериментов; и

(7.12) Измерения и данные. Учащийся применяет стандарты математических процессов, чтобы использовать статистические представления для анализа данных. Ожидается, что учащийся:
(B) будет использовать данные из случайной выборки, чтобы делать выводы о населении; и
(C) сравнивают две популяции на основе данных случайных выборок из этих популяций, включая неформальные сравнительные выводы о различиях между двумя популяциями.

(8.5)  Пропорциональность. Учащийся применяет стандарты математического процесса, чтобы использовать пропорциональные и непропорциональные отношения для разработки основных концепций функций. Ожидается, что учащийся:
(C) сопоставит двумерные наборы данных, которые предполагают линейную связь, с двумерными наборами данных, которые не предполагают линейной зависимости от графического представления;
(D) использовать линию тренда, которая аппроксимирует линейную зависимость между двумерными наборами данных, чтобы делать прогнозы;

(8.11)  Измерения и данные. Студент применяет стандарты математических процессов, чтобы использовать статистические процедуры для описания данных. Ожидается, что учащийся:
(A) построит диаграмму рассеяния и опишет наблюдаемые данные, чтобы ответить на такие вопросы, как связь, например, линейная, нелинейная и отсутствие связи между двумерными данными;
(B) определить среднее абсолютное отклонение и использовать эту величину в качестве меры среднего расстояния данных от среднего, используя набор данных не более  10 точек данных; и
(C) имитируют создание случайных выборок одинакового размера из совокупности с известными характеристиками, чтобы разработать понятие случайной выборки, репрезентативной для совокупности, из которой она была отобрана.

(8.2)  Количество и операции. Учащийся применяет стандарты математических процессов для представления и использования действительных чисел в различных формах. Ожидается, что учащийся:
(C) преобразует стандартную десятичную систему счисления в экспоненциальную систему счисления;


Личная финансовая грамотность

(7.13) Личная финансовая грамотность. Учащийся применяет стандарты математического процесса, чтобы развить экономическое мышление и решение проблем, полезных в жизни знающего потребителя и инвестора. Ожидается, что учащийся:
(B) определит компоненты личного бюджета, включая доход, запланированные сбережения на колледж, пенсию и чрезвычайные ситуации, налоги, а также постоянные и переменные расходы, а также подсчитает, какой процент составляет каждая категория от общего бюджета. ;
(C) создать и организовать учет финансовых активов и обязательств и составить отчет о чистой стоимости;
(D) использовать оценщик семейного бюджета, чтобы определить минимальный семейный бюджет и среднюю почасовую заработную плату, необходимые семье для удовлетворения своих основных потребностей в городе студента или другом крупном городе поблизости;
(E) рассчитать и сравнить доходы по простым и сложным процентам; и

(8. 12) Личная финансовая грамотность. Учащийся применяет стандарты математического процесса для развития экономического образа мышления и решения проблем, полезных как для знающего потребителя, так и для инвестора. Ожидается, что учащийся:
(A) решить реальные проблемы, сравнивая, как процентная ставка и срок кредита влияют на стоимость кредита;
(B) рассчитать общую стоимость погашения кредита, включая кредитные карты и кредиты с легким доступом, под различные процентные ставки и за разные периоды с помощью онлайн-калькулятора;
(C) объясните, как небольшие суммы денег, регулярно инвестируемые, включая деньги, отложенные на обучение в колледже и выход на пенсию, со временем растут;
(D) рассчитать и сравнить простые проценты и доходы по сложным процентам;

Экзаменационные кредиты средней школы | Кафедра математики Калифорнийского университета в Беркли


КАФЕДРА МАТЕМАТИИ
Калифорнийский университет в Беркли

Предметный балл по математике ~ Часто задаваемые вопросы

См. ниже наши правила в отношении расширенного размещения,
Международный бакалавриат и экзамены A-Level

 

ЭКЗАМЕНЫ ДЛЯ ПРОДВИНУТОГО РАЗМЕЩЕНИЯ (AP)

 

Математический факультет принимает: 
AP Исчисление AB с оценкой 3, 4 или 5 по математике 1A.
AP Исчисление BC с оценкой 3 или 4 по математике 1A.
AP Исчисление BC с оценкой 5 по математике 1A и математике 1B.

Обратите внимание: другие факультеты и колледжи могут использовать свои собственные шкалы для определения предмета AP по математике. Пожалуйста, свяжитесь с ними напрямую и планируйте соответственно.

В:      Итак, если я получил 3 или 4 балла по математике AB, я могу сразу записаться на курс математики 1B?
A:      Да (за исключениями, указанными выше).

Хотя Департамент математики установил, что 3 или 4 балла показывают, что учащийся готов сдавать математические расчеты в колледже, это не является точным показателем того, как учащийся будет успевать по курсу математики в колледже. Исчисление в средней школе не обязательно совпадает с исчислением в колледже. Ожидания профессора относительно того, что ученики должны знать и усвоить (а не просто запомнить), могут сильно отличаться от того, что могут ожидать старшеклассники.

Различные факторы, такие как сильные математические способности учащегося, расписание на первый семестр, работа, поездки на работу и любые другие временные обязательства, играют решающую роль в определении того, как учащийся справится со своим первым математическим курсом в школе. Кал. Если вы чувствуете, что ваши знания математики не так сильны, как вам хотелось бы, вы можете выбрать математику 1А, даже если ваш балл AP может не соответствовать требованиям. Единицы будут учитываться как часть ваших минимальных единиц, необходимых для семестра, но вы не будете получать единицы ни за баллы AP, ни за класс к выпуску.

В:      Если я получил 5 баллов по математике в Британской Колумбии, могу ли я зарегистрироваться непосредственно на курс математики 53, , исчисление многих переменных или математику 54, , линейная алгебра и дифференциальные уравнения, ?
A:      Да. Единственным предварительным условием для Math 53 и Math 54 является Math 1B. Math 53 и Math 54 не зависят друг от друга.

Обратите внимание:  Математика 1B охватывает больше материала по дифференциальным уравнениям, чем курсы математического анализа для первого года обучения в большинстве учебных заведений (он охватывает ОДУ первого порядка, динамику населения, ОДУ второго порядка, колебание и демпфирование, а также ряд решений ОДУ). . Если вы зарегистрируетесь на Math 54, вам нужно будет самостоятельно изучить вышеупомянутые темы.

 

ЭКЗАМЕНЫ НА МЕЖДУНАРОДНЫЙ БАКАЛАВР

Экзамены IB по математике до 2021 года:

IB Math (стандартный уровень) SL:  Никакой балл не засчитывается

IB Math (Higher Level) HL, без возможности исчисления: Оценка 5, 6 или 7 может быть использована для выполнения математики 1A. Никаких исключений для математики 1B.

IB Math (Higher Level) HL с опцией исчисления: балл 5, 6 или 7 может быть использован для соответствия математике 1A. Оценка 7 может быть использована для выполнения заданий по математике 1A и 1B.

IB Math (дальнейший уровень) FL: 7 баллов можно использовать для выполнения заданий по математике 1A и 1B. Оценка 6 может быть использована только для выполнения математики 1A.

 

Экзамены IB по математике с 2021 г. и последующие:

 

Математика, анализ и подходы IB (стандартный уровень):   Ни один балл не засчитывается.

IB Математика, анализ и подходы (высший уровень): 5, 6 или 7 баллов могут быть использованы для выполнения заданий по математике 1A или 16A. Оценка 7 может быть использована для выполнения математики 1A и математики 1B.

IB Math, Applications and Interpretations (стандартный уровень): не засчитывается ни один балл.

IB Math, Applications and Interpretations (Высший уровень): 5, 6 или 7 баллов можно использовать для выполнения задания по математике 16A. Оценка 6 или 7 может быть использована для выполнения Математики 10A.