С помощью масштаба определите расстояние до каждого из объектов: Страница 6

Страница 6 — 7. План местности

Опубликовано 26.07.201916.05.2021 автором mmetalnik

Все рабочие тетради (главная страница сайта)
ГДЗ к контурным картам по географии. 6 класс «Дрофа»

Комментарий: Перед выполнением работы, обязательно изучите Правила оформления контурных карт. В них вы найдёте информацию о том, как должны быть сделаны надписи к различным географическим объектам. Например, что все водные объекты подписываются синим цветом, а остальные — чёрным.

При этом, если вы внимательно рассмотрите наши ГДЗ, то увидите, что на наших картах объекты подписаны самыми разными цветами.

Это сделано специально, ведь наша главная цель — помочь вам сориентироваться в огромном количестве информации, которой насыщена любая карта. Разноцветные надписи помогут вам быстро найти нужное: города и реки, моря и равнины. Вы сможете быстро увидеть что добавилось на карте в результате выполнения следующего задания и лучше понять что и где находится.

Так что пользуйтесь нашими картами «с умом», чтобы ваши оценки не были снижены из-за тонкостей оформления. Работу лучше выполнять по шагам, последовательно выполняя задания к контурным картам. Для того, чтобы увеличить карту, просто нажмите на неё. Также можно увеличивать и уменьшать размер страницы при помощи одновременного клавиш Ctrl и «+» или Ctrl и «-«.

ЗАДАНИЯ

Для выполнения заданий будем рассматривать атлас на странице 9.

1. Группа туристов находится на местности, обозначенной на плане точкой А.

а) Выберите по четыре объекта, расположенные к северу и югу от места нахождения туристов. Обведите их синим карандашом, а расположенные к югу — красным.

Объекты, расположенные к северу от точки А (обведены синей окружностью):

отдельно стоящее дерево;
посёлок Харино;
мельница;
дом лесника.

Объекты, расположенные к югу от точки А (обведены красной окружностью):

школа;
мост;
пристань;
песчаный карьер.

б) По каким азимутам должны следовать туристы, чтобы дойти до этих объектов?

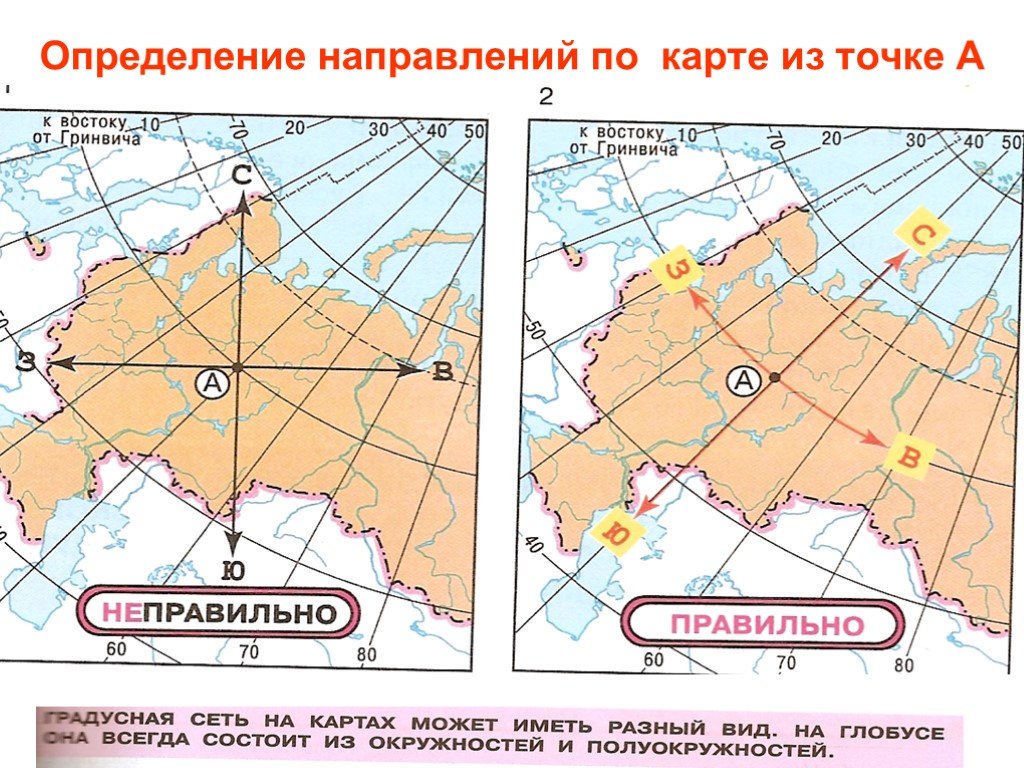
Комментарий: Азимут маршрута — это угол между направлением движения по маршруту и северным направлением. Азимут маршрута измеряется в градусах и всегда только по часовой стрелке.

Для вычисления азимутов проведём вспомогательную линию — стрелку, указывающую строго на север (обозначена синим ветом и буквой С).

Теперь при помощи транспортира измерим азимуты маршрута к объектам (углы между направлениями к объектам и стрелкой на север):

отдельно стоящее дерево — 308°;
посёлок Харино — 324°;
мельница — 3°;
дом лесника — 40°;
школа — 160°;
мост — 195°;
пристань — 232°;
песчаный карьер — 213°.

в) С помощью масштаба определите расстояние до каждого из объектов.

При помощи линейки измерим расстояние от точки А до объектов, а потом определим реальное расстояние между объектами (масштаб карты 1 : 10 000 или 1 см = 100 метрам):

до отдельно стоящего дерева — 4 см, то есть 400 метров;
до посёлка Харино — 4 см, то есть 400 метров;
до мельницы — 5,8 см, то есть 580 метров;
до дома лесника — 3,1 см, то есть 310 метров;
до школы- 4,7 см, то есть 470 метров;
до моста — 2,3 см, то есть 230 метров;
до пристани- 4,2 см, то есть 420 метров;
до песчаного карьера — 12 см, то есть 1200 метров.

Результаты занесите в таблицу.

Объект	Азимут относительно точки А	Расстояние на местности от точки А
отдельно стоящее дерево	308°	400 метров
посёлок Харино	324°	400 метров
мельница	3°	580 метров
дом лесника	40°	310 метров
школа	160°	470 метров
мост	195°	230 метров
пристань	232°	420 метров
песчаный карьер	213°	1200 метров

2. Внимательно рассмотрите план местности на с. 6. Где бы вы разместили футбольное поле? Почему вы выбрали именно это место? Свой ответ аргументируйте.

Я бы разместил поле уго-восточнее населенного пункта Арсентьево (место отмечено зелёным прямоугольником). Это место выбрал по следующим причинам:

Это достаточно ровная поверхность без большого уклона. Определить ровность земной поверхности можно по карте — в этом месте расстояние между ближайшими горизонталями на карте 3 см или 300 метров на реальной местности (показано на карте фиолетово вспомогательной линией). Согласно легенде, горизонтали на данной карте проведены через 2,5 метра изменения уровня земной поверхности. То есть на протяжении 300 метров уклон составляет не более 2,5 метров. Так как длина стандартного футбольного поля примерно равна 100 метрам, то такой уклон не помешает сооружению этого спортивного объекта.
Арсентьево — довольно крупный населённый пункт. В нем проживает 3 200 человек (цифры под названием населённого пункта обозначают количество жителей в тысячах человек). Кроме того, это место находится на пересечении дорог, ведущих из соседних населённых пунктов. То есть жителям окрестных деревень и поселков будет легко добраться до нового футбольного поля.

3. Напишите рассказ о своём пути в школу, заменив как можно больше слов условными знаками.

Все рабочие тетради (главная страница сайта)
ГДЗ к контурным картам по географии. 6 класс «Дрофа»

Ответы

2019, 6 класс, ГДЗ, география, готовые домашние задания, Дрофа, Касимов, контурки, контурные карты, Курбский, решения

ГДЗ Рабочая тетрадь по географии 5 класс Николина.

17. Практическая работа Номер •

Учебники
5 класс
География 👍
Николина
№•

авторы: Николина.

издательство: «Экзамен»

Раздел:

Предыдущее
Следующее

Практическая работа. Работаем с картой.
Девизом при выполнении заданий будут слова известного географа, океа нолога, картографа Ю. М. Шокальского: «Карта есть удивительное орудие изучения земного шара, которое одно только и сможет дать человеку дар провидения».
В рабочей тетради выполните задания § 17 в учебнике (стр. 58−59). Определите, можете ли вы пользоваться планом и картой. Для этого поставьте знак «+», если можете, или знак «−», если затрудняетесь.
_ Определять направление на плане и карте.
_ Определять расстояние на плане и карте с помощью масштаба.
_ Определять взаиморасположение объектов на плане и карте.
_ Определять географические координаты точки на карте.
_ Находить точку на карте по её географическим координатам.
_ Определять абсолютные высоты и глубины на плане и карте.
_ Составлять описания местности по топографическим картам.
Выставите себе отметку _ и выполняйте задания далее.
1) Выполните задание I. Для этого выделите признаки для сравнения.

Признаки для сравнения	План	Карта

Вывод_
2) По рисунку 24 (стр.38 учебника) опишите маршрут по топографической карте. Для этого ответьте на вопросы задания II.
3) Выполните задание III в учебнике.
Изучите топографическую карту на рисунке 37 (стр. 59 учебника). С помощью масштаба определите расстояние по прямой:
а) от точки B до точки A _
б) от точки B до точки C _
Абсолютная высота точки B _ .
Выявите, какой из этапов эстафеты вам кажется самым простым: _
Самым сложным _ . Почему? _
4) Выполните проектное задание и запишите:
Наилучший вариант освоения земельного участка _ потому что _ .
При ответе опирайтесь на вопросы, поставленные в тексте учебника. Выполняя этот проект, представьте себя предпринимателем, который приобрёл участок земли за свои деньги, осваивает его с целью производить продукты для общества, получать прибыль для себя, культивировать окружающую местность. Как вы думаете, у вас получилось?
5) Оцените изученный материал. Как вы считаете, вы освоили тему «План и карта»? Вам понравилось выполнять задания? Какие оказались сложными? Какие − интересными?

reshalka.com

Решение

Практическая работа. Работаем с картой.
+ Определять направление на плане и карте.
+ Определять расстояние на плане и карте с помощью масштаба.
+ Определять взаиморасположение объектов на плане и карте.
+ Определять географические координаты точки на карте.
+ Находить точку на карте по её географическим координатам.
+ Определять абсолютные высоты и глубины на плане и карте.
+ Составлять описания местности по топографическим картам.
Отметка «5»
Сравнение плана и карты.

Признаки для сравнения	План	Карта
Форма изображения земной поверхности	Плоская	Плоская
Учет кривизны земной поверхности	Не учитывается	Картографическая проекция
Охват территории	Небольшие, выбранные участки земной поверхности	Вся Земля, материки, страны, океаны и т.д.
Масштаб	Крупный 1:5000 и более	Мелкий 1:10 000 и меньше
Расположение сторон горизонта	На планах стрелкой обозначают направление на север. Остальные направления определяются исходя из северного направления: противоположное ему − южное, слева − западное, справа − восточное.	Направление с севера на юг определяют меридианы, с запада на восток − параллели.
Содержание	Наносятся все объекты и детали определённой местности в заданом масштабе.	Отбираются только сущственные объекты и свойства.
Условные знаки	Условные обозначения похожи на реальные объекты. Так, деревья изображают зеленым цветом, горы − коричневым, воду − голубым.	Условные знаки разнообразны, зависят от выбранной темы, лишь на физической карте, приближены к реальной действительности (горы − коричневым, воду − голубым).
Градусная сетка	Не всегда; если участок изображаемой местности небольшой , то элементов градусной сетки не наносят.	Указывают все элементы градусной сетки.

Вывод: Географические план и карта представляют собой изображения участков земной поверхности с помощью условных обозначений и в определенном масштабе. План используется для отображения небольших участков земной поверхности, а карта позволяет отбразить очень большие участки земной поверхности (хоть и в сильно уменьшенном масштабе).
2) Описание маршрута.
Мы отправляемся в поход. Утром собираемся у церки в селе Барсуки, затем спускаемся к реке Зайке отправляемся на лодке вниз по ее течению в северо−восточном, затем в юго−восточном направлении до деревянного моста. При движении по реке на правом берегу мы увидим полевые дороги, двухпутные железные дороги и насыпи. На левом берегу располагается крупное село Красное. Далее пойдем пешком до села Клёново. Пешком нам предстоит пройти 1500 м в северном направлении. При движении к селу Клёново нам предстоит подниматься вверх. У железнодорожной насыпи сделаем остановку. К северо−западу от железнодорожной насыпи расположен очень большой овраг. Нас могут подстерегать различные опасности болота, ямы и овраги, пересечение железнодорожного полотна. Перед путешествием мы изучили правила безопасности на воде, открытой местности, подготовили необходимый инвентарь, аптечку. В рюкзаке у каждого должен быть компас, карта местности (маршрута), индивидуальные средсва оказания доврачебной медицинской помощи, желательно средства связи.
3) Расстояния.
а) от точки B до точки A − 440 м.
б) от точки B до точки C − 410 м.
Абсолютная высота точки B − 140 м.
Самым простым этапом эстафеты стало описание маршрута по топографическому плану. Сложным выбор маршрута.
4) Наилучший вариант освоения земельного участка: развитие сельского хозяйства (животноводство и растениеводство), потому что есть все необходимые условия для строительства фермы, выпаса животных, есть луговая растительность, можно использовать под сенокос, наличие воды (река и озеро).
Какие участки подходят: а) для распашки под поля; б) под сенокосы; в) для
строительства домов; г) для лыжной трассы; д) для других объектов (предложите)?

Описание териториии.
На представленном участке нет объектов, построенных человеком. В центральной части протекает река с севера на юг. С запада и востока впадают притоки. На северо−западе березовый лес, в центре которого имеется холм высотой 133 м, на северо−востоке − холм с высотой 128 м, в центральной части кленового леса. На юго−западе кленовый лес, на юго−востоке участок кустарниковой растительности. Кутизна склонов одинаковая, выровненные участки в центральной части местности. Дорогу нужно проложить с севера на юг, построить небольшой мост через приток реки. Для лучшего использования местности, нужно строить мост (переправу через русло главной реки).

Участки, подходящие для:
а) для распашки под поля;
б) под сенокосы;
в) для строительства домов;
г) для лыжной трассы.
5) Изучение темы «План и карта» было сложным, но интересным. Для выполнения заданий необходимо было изучить легенду карты и плана, понимать расположение обектов по сторонам света, расположение холмов и других обьектов.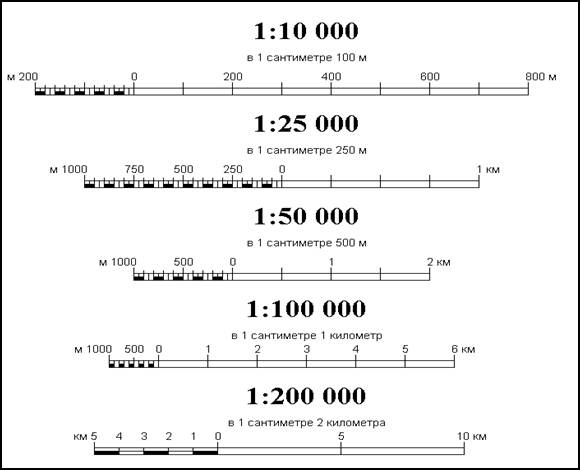 Творческие задания выполять оказалось непросто, так как помимо желания расположить те или иные обьекты, нужно было оценить реальные условия для местности.

Предыдущее
Следующее

Задумывались ли вы когда-нибудь о размерах планет в Солнечной системе или о расстояниях между ними? В этом проекте вы создадите собственную масштабную модель Солнечной системы, научившись вычислять масштабные расстояния, относительные размеры планет или и то, и другое. Затем используйте бусины и веревку, мел для тротуара или материалы, которые вы сами творчески подберете, чтобы построить модель, которую вы сможете исследовать или, возможно, даже носить!

Расстояния в Солнечной системе могут быть огромными! Расстояние от Солнца до Нептуна составляет почти три миллиарда миль (четыре миллиарда километров). Поскольку расстояния между планетами очень велики, астрономы иногда описывают расстояния в астрономических единицах (а.е.). Одна а.е. равна среднему расстоянию между Солнцем и Землей, примерно 93 миллиона миль (150 миллионов километров). Это позволяет ученым более эффективно описывать и рассчитывать расстояния. Например, вместо того, чтобы сказать: «Марс находится в 130 миллионах миль от Солнца», ученые могут сказать: «Марс находится в 1,5 а.е. от Солнца».

Велико не только расстояние между планетами. Существуют также огромные различия в размерах каждой планеты. Из-за этого может быть сложно или даже невозможно точно отобразить размер планеты и расстояние, особенно в моделях меньшего масштаба, таких как изображение.

Watch en Español: Seleccione subtítulos en Español bajo el ícono de configuración. | Смотрите на YouTube
Дополнительные ресурсы о размерах и масштабах Солнечной системы:
Справочное руководство по размерам и расстояниям Солнечной системы – скачать PDF
Коллекционные карточки Солнечной системы
2. Решите, какую модель вы хотите построить.
Решите, хотите ли вы, чтобы ваша модель отображала размеры планет в масштабе или расстояния между планетами в масштабе.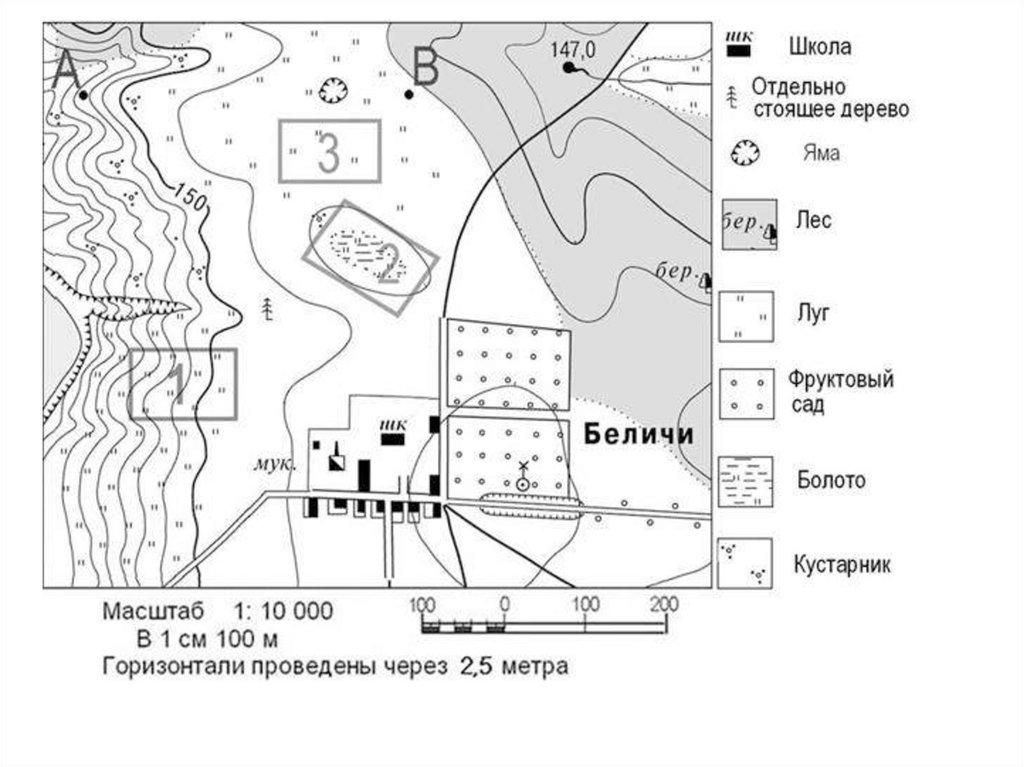 Вы можете комбинировать модель размером с планету одного масштаба с дистанционной моделью другого масштаба. Но если вы хотите, чтобы размер и расстояние были в одном масштабе, вам нужно растянуть модель как минимум на полмили! См. Шаг 6 для получения инструкций по построению комбинированной модели размера и расстояния.
+ Развернуть изображение
3. Выберите, куда будет установлена ваша модель солнечной системы.
Выберите место для установки вашей модели солнечной системы. Это может быть через стену спальни, вдоль пола в коридоре или большой комнате, снаружи во дворе или на тротуаре.
Помните о своем выборе при расчете размеров планет и расстояний между ними на следующих шагах. Вам понадобится достаточно материалов, и ваша модель должна поместиться в том месте, которое вы выберете.
Инструкции по сборке модели из бисера и ниток, тротуарного мела или дворовых маркеров приведены ниже, но вы можете использовать любые материалы и любое пространство, которое вам нравится!
+ Развернуть изображение
4.
Расчет масштабных расстояний
Если вы создаете масштабную модель, продолжайте читать, чтобы узнать о двух разных методах расчета масштабных расстояний. Для масштабной модели перейдите к шагу 5.
Рассчитать вручную:
Загрузите таблицу расчета расстояния (DOCX).
Умножьте масштабный коэффициент на диаграмме на расстояние до каждой планеты в астрономических единицах (а.е.). Примечание. При использовании предлагаемых 10 сантиметров на 1 а.е. вам потребуется около 10 футов между Солнцем и Нептуном. Если вы хотите, чтобы ваша модель охватывала большее или меньшее расстояние, вы можете соответствующим образом изменить значение масштаба.

Расчет с использованием электронной таблицы:
Загрузите таблицу «Масштабное расстояние» (XLSX или CSV).
Создайте в электронной таблице формулу, которая будет вычислять расстояние от Солнца до каждой планеты (в сантиметрах) в вашей модели. Формула должна умножать значение AU на количество сантиметров, которое вы хотите, чтобы каждая AU представляла, значение вашей шкалы.
Формула умножения в электронной таблице имеет следующий формат: =B3*10, где B3 — ячейка с расстоянием до планеты в астрономических единицах, а 10 — значение масштаба. B относится к столбцу ячейки, а 3 относится к строке ячейки.
Попробуйте разные значения масштаба, чтобы масштабная модель охватывала меньшее или большее расстояние, в зависимости от того, где вы хотите ее разместить.
Выполнив расчеты, перейдите к шагам 8-10, чтобы получить несколько различных идей по созданию и отображению вашей модели. Вы также можете придумать свой собственный творческий дисплей, используя выбранные вами материалы.
+ Развернуть изображение
5. Расчет размеров планет в масштабе
Если вы создаете модель в масштабе, продолжайте читать, чтобы узнать о двух различных методах расчета размеров планет в масштабе. Для модели масштаба-расстояния см. шаг 4 выше.
Рассчитать вручную:
Скачать таблицу расчета размера (DOCX).
Выберите размер (диаметр) Земли в вашей модели (например, 1 см).
Для каждой планеты умножьте размер, выбранный вами для Земли, на значение множителя, указанное в таблице. Множитель — это размер планеты по сравнению с Землей. Это даст вам масштабный размер каждой планеты.

Расчет с использованием электронной таблицы:
Загрузите электронную таблицу калькулятора масштаба (XLSX или CSV).
Выберите размер (диаметр) Земли в вашей модели (например, 10 см).
Создайте в электронной таблице формулу, которая будет вычислять диаметр (расстояние) каждой планеты в сантиметрах. Формула должна умножать размер, который вы выбрали для Земли, на значение множителя для каждой планеты. Множитель — это размер планеты по сравнению с Землей.
Формула умножения в электронной таблице имеет следующий формат: =B3*10, где B3 — это ячейка с множителем планеты (ее размер по сравнению с Землей), а 10 — размер, который вы выбрали для Земли. B относится к столбцу ячейки, а 3 относится к строке ячейки.
Попробуйте разные значения для Земли, чтобы сделать масштабные планеты больше или меньше, в зависимости от доступных материалов для представления размера каждой планеты.
Выполнив расчеты, перейдите к шагу 9, чтобы узнать, как сделать модель тротуара в масштабе мела. Вы также можете придумать свой собственный творческий дисплей, используя выбранные вами материалы.
Об изображении: Рендеринг этого художника (доступен в виде загружаемого плаката) показывает планеты нашей Солнечной системы, выстроенные в линию, как если бы они проходили транзитом через Солнце. Хотя в действительности такой вид был бы невозможен, рисунок предназначен для отображения точного масштаба планет относительно друг друга и Солнца. › Полное изображение и подпись
6. Вычислить комбинированное масштабное расстояние и размер планеты
Если вы заинтересованы в более точном представлении Солнечной системы и имеете много пространства (не менее полумили!) для работы, попробуйте создать модель Солнечная система, отображающая расстояние и размер планеты в одном масштабе. В противном случае пропустите этот шаг.
Шаги:
Загрузите таблицу размеров и расстояний в масштабе (XLSX или CSV) или справочное руководство по размерам и расстояниям Солнечной системы, если рассчитываете вручную.
Определите диаметр Земли в масштабной модели. Имейте в виду, что размер Земли в 1 см означает, что масштабное расстояние от Солнца до Нептуна составляет около двух миль. Подумайте о том, чтобы сделать вашу масштабную Землю всего в несколько миллиметров в поперечнике. Чтобы рассчитать масштаб Солнечной системы, вам нужно будет работать с пропорциями и отношениями, как показано в этом уравнении.
Диаметр шкалы / Расстояние шкалы = Фактический диаметр / Фактическое расстояние | + Развернуть изображение
Используя фактический диаметр и расстояние до планеты, а также масштабный диаметр Земли, вы можете изменить уравнение, чтобы найти неизвестные размеры и расстояния. Для начала используйте масштабный диаметр, который вы выбрали для Земли, и измените уравнение, как показано ниже, чтобы найти неизвестное масштабное расстояние от Земли до Солнца. Вы можете рассчитать это вручную или создать функцию электронной таблицы, которая вычисляет это значение.
Диаметр шкалы (фактическое расстояние) / фактический диаметр = расстояние шкалы | + Expand image
В этом примере функция электронной таблицы делит произведение диаметра Земли в масштабе (B5) и фактического расстояния от Солнца (E5) на фактический диаметр Земли (D5), используя =(B5*E5)/D5, чтобы найти шкала расстояния от Земли до Солнца. | + Развернуть изображение
Чтобы рассчитать масштабный диаметр других планет, вам нужно переставить пропорциональные отношения и написать уравнения, аналогичные тому, что вы делали в предыдущем шаге, используя масштабный диаметр Земли в своем уравнении. Изменив приведенное ниже уравнение, вы можете рассчитать вручную или создать формулу в электронной таблице, чтобы найти как диаметр шкалы, так и расстояние шкалы для остальных планет. Примечание. Если вы измените масштабный диаметр Земли в электронной таблице, это заставит функции пересчитать значения масштаба и для других планет.
Масштаб диаметра планеты / Масштаб диаметра Земли = Фактический диаметр планеты / Фактический диаметр Земли | + Увеличить изображение
В этом примере произведение масштабного диаметра Земли (B5) и фактического диаметра Марса (D6) делится на фактический диаметр Земли (D5) с использованием =(B5*D6)/D5, чтобы найдите масштабный диаметр Марса. | + Развернуть изображение
Затем, используя шкалу диаметра Земли и коэффициенты пропорциональности, найдите шкалу расстояний до других планет, перестроив приведенное ниже уравнение.
Масштаб расстояния до планеты / Масштаб диаметра Земли = Фактическое расстояние до планеты / Фактический диаметр Земли | + Развернуть изображение
В этом примере функция электронной таблицы вычисляет произведение масштабного диаметра Земли (B5) и фактического расстояния до Марса (E6), деленное на фактический диаметр Земли (D5), используя =(B5*E6) /Д5. | + Развернуть изображение
Повторите предыдущие шаги для остальных планет.
С помощью линейки, циркуля, веревки, транспортира или другого инструмента начертите круги соответствующих размеров для каждой планеты. Вы можете раскрасить круги, чтобы они напоминали внешний вид планет.
Используя программное обеспечение для онлайн-картографирования, такое как карты Google или Bing, щелкните правой кнопкой мыши место, представляющее Солнце (например, ваш дом), и выберите «Измерить расстояние», чтобы определить, где должны быть планеты на шкале. В зависимости от рассчитанного размера масштабной модели вы можете проверить у соседей и друзей, могут ли они разместить более отдаленные планеты в вашей масштабной модели.
+ Развернуть изображение
7. Создайте и отобразите свою модель
Теперь пришло время создать свою модель! Есть много способов создать и отобразить масштабную солнечную систему. Рассчитав свои измерения, выберите один из вариантов ниже или придумайте свой собственный.
8.
Соберите Солнечную систему на нитке (масштабная модель расстояния)
Привяжите цветные бусины к нитке, чтобы сделать масштабную модель расстояний между планетами в Солнечной системе. Вы можете носить свою модель или даже повесить ее на стену.
Материалы:
Веревка (достаточная, чтобы натянуть расстояние до Нептуна, плюс дополнительные 30 см)
Бусины, шайбы или другие предметы для обозначения расстояния до каждой планеты на нитке
Расчетные расстояния из шага 4

Шаги:
Отмерьте и отрежьте кусок веревки примерно на 30 см длиннее, чем рассчитанное вами расстояние от Солнца до Нептуна.
Привяжите бусину, изображающую Солнце, к одному концу нити двойным узлом. Если у вас нет бусинок, вы можете привязать к нитке металлические шайбы, прикрепить вырезки планет или коллекционные карточки или просто использовать ленту, чтобы отметить положение Солнца.
Используя рассчитанные вами расстояния (в сантиметрах), измерьте расстояние от Солнца по нитке до каждой планеты и привяжите цветную бусину двойным узлом. Если можете, выбирайте бусины цветов планет и Солнца.
После того, как вы каким-то образом прикрепите все свои бусины или обозначите свои планеты на нитке, выпрямите нить, чтобы увидеть свою Солнечную систему в масштабе!
+ Развернуть изображение
9. Солнечная система на тротуаре (масштабная модель расстояний и/или размеров)
С помощью мела сделайте масштабную модель расстояний между планетами и/или размеров планет в Солнечной системе. Пригласите свою семью и друзей на прогулку по вашей масштабной модели.
Материалы:
Тротуарный мел
Расчетные расстояния из шага 4 или расстояния и размеры из шага 6

Ступени:
С помощью тротуарного мела нарисуйте солнце на земле.
Измерьте рассчитанное вами расстояние до каждой планеты и нарисуйте их в масштабе их расстояний.
Если вы рассчитали размеры планет по сравнению друг с другом, измерьте эти размеры, когда вы их рисуете, давая вашим планетам правильный диаметр.
Вы можете нарисовать свои планеты вдоль одной прямой линии от Солнца, но если у вас достаточно места, подумайте о том, чтобы нарисовать их на правильном расстоянии в разных точках на орбите вокруг Солнца.
+ Развернуть изображение
10. Солнечная система во дворе (модель в масштабе)
Используйте маркеры расстояния, такие как конусы или палочки от эскимо, во дворе или на открытой площадке, чтобы создать масштабную модель расстояний между планетами в солнечной системе.
Материалы:
Палочки от эскимо, конусы или другие предметы для обозначения расстояний
Расчетные расстояния из шага 4

Ступени:
Используйте маркеры расстояний, такие как конусы, наземные колья или палочки от эскимо, чтобы отметить расположение планет на рассчитанных вами расстояниях.
Прикрепите рисунки или вырезы планет к их маркерам.
+ Развернуть изображение
ЗемляЮпитерМарсМеркурийНептунСатурнсолнечная системав масштабемасштабные моделимасштабная модель солнечной системымодельразмеррасстояниемоделированиеэлектронные таблицыСолнцеУранВенера
Материалы
1. Узнайте о размерах и расстояниях в нашей Солнечной системе
2. Решите, какую модель вы хотите построить
2 00 4.03 9003 900 900 Рассчитать расстояния по шкале
5. Рассчитать размеры планеты по шкале
6. Рассчитать комбинированное расстояние по шкале и размер планеты
7. Создайте и отобразите свою модель
8. Создайте Солнечную систему на струне (масштабная модель расстояния)
9. Солнечная система на тротуаре (масштабная модель расстояния и/или размера)
10. Солнечная система в Двор (масштабная дистанционка)
Нахождение масштаба космоса – наука в школе
Автор(ы): Маркус Пёссель
Как астрономы измеряют расстояния до звезд? Использование цифровой камеры для записи смещения параллакса является точным и аутентичным методом, который можно использовать в классе.
Астрономы — удаленные наблюдатели, находящиеся на большом расстоянии от изучаемых ими объектов. Знание расстояния до небесных объектов имеет решающее значение: оно обеспечивает ключевой фактор в различении очень яркого, далекого объекта от объекта, который намного ближе, но по своей сути менее яркий, и, таким образом, в определении того, что это за объект. Даже отдельные звезды и целые галактики могут выглядеть одинаково — до тех пор, пока мы не узнаем, что одна из них находится в миллиард раз дальше другой и, следовательно, в действительности в триллионы раз ярче.
Важнейшим астрономическим методом определения расстояний от Земли до звезд является параллакс – видимое смещение положения наблюдаемого объекта при изменении положения наблюдателя. Мы замечаем эффект параллакса, когда смотрим в окно поезда: близлежащие объекты кажутся движущимися мимо гораздо быстрее, чем удаленные. Используя этот эффект, мы можем определить расстояние до объекта, измеряя видимое изменение его положения при изменении нашего положения как наблюдателей.
Проблема, конечно, в точности. Как сделать измерения расстояний на основе параллакса максимально точными? В этой второй статье об измерении расстояний с помощью параллакса мы используем аутентичный метод, очень похожий на тот, который используют астрономы, который был адаптирован для использования в классе (о предыдущей статье см. Pössel, 2017). Вместо того, чтобы использовать устройства для измерения угла (как в предыдущей статье, основанные на измерениях теодолита) для определения расстояния до «звезды», здесь мы делаем фотографии с разных точек и используем их для получения измерений, необходимых для расчета нашей звезды. расстояние.

Когда мы смотрим на ночное небо, яркие звезды вдали выглядят похожими на более тусклые, расположенные ближе звезды. Измерения параллакса позволяют нам различать их.
Изображение предоставлено ESO / B Tafreshi

Вариант этого фотографического метода, описанный далее в этой статье, еще более достоверен и точен, хотя и немного сложнее. Он включает в себя использование фиксированной точки отсчета за пределами классной комнаты — так же, как астрономы используют очень удаленные фоновые объекты (например, активные галактики, называемые квазарами) в качестве фиксированных точек отсчета при измерении звездного параллакса, вместо того, чтобы полагаться на свои телескопы, направленные в одном и том же направлении для каждого наблюдения.
Для этих занятий вам понадобится цифровая камера, установленная (по возможности) на оптической скамье (см. рис. 1). Мероприятия могут выполняться группами учащихся. Выделите около 30 минут на настройку и проведение измерений и еще 30 минут на анализ и расчеты.
Материалы
Цифровой фотоаппарат с объективом с известным фокусным расстоянием (не менее 50 мм)
Оптическая скамья (или аналогичная установка для перемещения камеры вбок и измерения сдвига, например, плоская столешница и длинная линейка)
Модель-звезда (небольшой шар диаметром не более 1 см или светодиод, закрепленный на палочке)
Объект известной длины с четкой маркировкой (например, измерительная линейка) в качестве калибровочного объекта
Рулетка
Программа обработки изображений, напр. Адоб Фотошоп, GIMP
Процедура
Установите камеру на оптическую скамью так, чтобы можно было сместить камеру вбок на известное расстояние. Камера должна быть направлена под прямым углом к длине скамьи (рис. 1). Если у вас нет оптической скамьи, прикрепите длинную линейку к поверхности стола, чтобы вы могли перемещать камеру вдоль линейки и измерять расстояние сдвига.

Рис. 1. Камера, установленная на оптической скамье для легкого бокового смещения
Изображение предоставлено HdA / M Pössel

Установите модель звезды так, чтобы она находилась на уровне глаз камеры и в нескольких метрах от скамьи для камеры.

Сдвиньте камеру к одному концу скамейки, убедившись, что через камеру видна звезда. Сфотографируйте звезду с этого места.

Затем переместите камеру вдоль оптической скамьи так, чтобы звезда все еще была видна через объектив. Запишите пройденное расстояние, а затем сделайте еще один снимок с этого места.

Верните камеру в центральное положение. Теперь поместите калибровочный объект (например, измерительную линейку) под прямым углом к направлению взгляда камеры и сделайте его снимок. Это изображение будет использоваться для калибровки ваших измерений.

С помощью рулетки найдите и запишите расстояние от камеры до метра.
Расчет расстояния до звезды
Экспериментальная ситуация показана на рис. 2. Здесь b представляет собой расстояние смещения вдоль базовой линии камеры (оптическая скамья или стол) между первой и второй позициями (A и B), а C — положение звезды модели, а d — это расстояние от базовой линии камеры до звезды — то есть расстояние, которое мы пытаемся рассчитать.
Шаги для расчета расстояния d приведены ниже.
Если провести линию, параллельную базовой линии и находящуюся на том же расстоянии d, что и звезда, линия обзора камеры из положения А пересечет новую линию в точке ОА, а из точки В — в точке ОВ. Углы между лучами зрения камеры и направлением на звезду в положениях камеры А и В равны α и ß соответственно.
Рисунок 2: Модель звезды в позиции C, сфотографированная с двух разных положений камеры, A и B, разделенных сдвигом расстояния b
Изображение предоставлено HdA / M Pössel
В отличие от теодолитов, камеры не позволяют измерять углы напрямую. Таким образом, нам необходимо связать расположение изображений звезды на экране детектора изображения камеры с углом световых лучей от звезды, когда камера находится в разных положениях.

Для этого нам нужно представить ситуацию в несколько упрощенном и выдуманном виде. Во-первых, мы относимся к объективу камеры как к пинхолу — как показано на рисунке 3, где P — это положение объектива. Таким образом, луч света от звезды проходит по прямой линии через объектив камеры и попадает на фотодетектор на экране изображения на расстоянии f (фокусное расстояние объектива) позади передней части камеры.
Рисунок 3: Упрощенная модель установки параллакса
Изображение предоставлено HdA / M Pössel
Начиная с рисунка 2, мы затем думаем о ситуации с точки зрения камеры, когда она перемещается из точки А в точку В, как если бы мы были наблюдателем, постоянно сидящим на камере. Мы можем добиться этого, фактически сдвинув положение положения камеры A (и линии AC) вправо на расстояние b , на которое была перемещена камера, так что теперь положения двух камер совпадут. Точка обзора камеры показана на рисунке 3. Видимое местоположение звезды будет в точке C 9.0385 A , когда камера находится в первой позиции (A), а ее изображение будет расположено в точке D _A на экране детектора. Точно так же, после перемещения камеры в точку B, видимое местоположение звезды будет в точке C _B, а ее изображение — в точке D _B. (Здесь отрезок линии OQ представляет собой расстояние между плоскостью изображения камеры и параллельной плоскостью, содержащей звезду.) Длина C _B C _A равна расстоянию b на рис. 2, а углы a и ß остаются прежними.

Глядя на геометрию, мы видим несколько похожих треугольников. Использование этих треугольников дает формулу, связывающую расстояние d с другими известными длинами b и f , что позволяет вычислить его значение. Как вывести эту формулу, вы можете узнать в разделе дополнительных материалов ^w1. Формула:
Где:
d = расстояние до звезды
L = фактическая длина калибровочного объекта
b = фактическое расстояние, на которое была перемещена камера (которое соответствует расстоянию от C _A до C _B )
d _L = фактическое расстояние калибровочного объекта от базовой линии камеры (по линии OQ)
p = расстояние как количество пикселей между изображениями звезд (по D _A и D _B )
p _L = длина как количество пикселей изображения калибровочного объекта

Чтобы использовать эту формулу, вам сначала нужно использовать программу обработки изображений, чтобы найти p , количество пикселей (по горизонтальной оси), которые разделяют положения изображения звезды между двумя фотографиями, когда вы просматриваете их на экране. Вы также можете использовать программу, чтобы найти p _L , длину калибровочного объекта как количество пикселей на экране.
Когда вы определили значение для d , вы успешно использовали измерение параллакса для определения расстояния до звезды.
Теперь используйте рулетку, чтобы найти расстояние d напрямую и сравните это со значением, рассчитанным на основе измерения параллакса. Насколько точным было вычисленное измерение?
Вы можете повторить это действие со «звездой», расположенной на разных расстояниях, чтобы выяснить, меняется ли точность измерения параллакса с расстоянием (см. ниже раздел «Какую точность мы можем ожидать?»).
Параллаксная фотография с контрольной точкой
Для еще большего астрономического реализма мы можем адаптировать метод параллаксной фотографии для использования контрольного объекта за пределами класса, который должен быть значительно дальше, чем «звезда». С помощью этой процедуры вместо того, чтобы полагаться на камеру, направленную в том же направлении после перемещения из точки А в точку В, мы выбираем удаленный эталонный объект, видимый на каждом из двух изображений. Затем мы измеряем расстояние в пикселях изображения звезды от эталонного объекта на каждом изображении. Этот альтернативный подход, который мы здесь описываем, должен давать более точные результаты.
Процедура
Для эталонного объекта найдите небольшую деталь самого удаленного объекта, видимого на обоих изображениях — он должен быть намного дальше, чем модельная звезда. В нашем случае в качестве маркера мы выбрали опорный объект на одном из куполов обсерватории Института астрономии им. Макса Планка, который находился примерно в 80 м от нашей камеры.

Проведите вертикальную линию через эталонный объект на каждом изображении. Это опорная линия. Теперь мы можем использовать опорную линию, чтобы найти сдвиг пикселей между двумя изображениями, как показано на рисунке 4.9.0070 Рис. 4. Два примера изображений активности камеры, показывающих сдвиг пикселей по горизонтали p. На изображениях эталонный объект (элемент купола на заднем плане) лежит на красной базовой линии.
Изображение предоставлено HdA / M Pössel
Чтобы вычислить p , расстояние на экране в пикселях, сначала нужно найти горизонтальное расстояние модели звезды в пикселях от опорной линии на обоих изображениях по отдельности. Затем просто добавьте эти (исправленные) значения горизонтальных пикселей друг к другу, чтобы найти стр . Например, -24 пикселя соответствует 24 пикселям слева от контрольной метки, а +36 пикселям — 36 пикселям вправо, что дает расстояние p в 60 пикселей.

Начиная с этого момента расчеты такие же, как и в предыдущем методе (см. выше раздел «Расчет звездного расстояния»).
На какую точность можно рассчитывать?
Итак, насколько точны результаты, полученные с помощью этого усовершенствованного метода? Наши данные показывают, что они могут быть удивительно точными (по сравнению с прямыми измерениями расстояний), как показано на рисунке 5. Наибольшая относительная ошибка составляет всего 3,2%.
Рис. 5: Вверху: расстояния до модели звезды, измеренные методом параллакса, в зависимости от расстояний, полученных с помощью рулетки
Внизу: относительные погрешности расстояний, измеренных с использованием метода фотографии параллакса опорной точки, по сравнению с расстояниями, полученными с помощью рулетки
Изображение предоставлено HdA / M Pössel

Обратите внимание, что на больших расстояниях наблюдается увеличение как относительной ошибки, так и фактической ошибки. Это связано с изменением геометрии: расстояние до звезды модели становится больше по сравнению с расстоянием до эталонного объекта, поэтому ошибка, вносимая параллаксом эталонного объекта, становится все больше.
При простом методе измерения угла, описанном в предыдущей статье (Pössel, 2017), точность измерения расстояния была значительно ниже – обычно в пределах примерно 10%, как показано на рис. 6. Таким образом, метод, описанный в текущей статье, обеспечивает значительное улучшение точности по сравнению с предыдущим методом, где основными источниками ошибок являются угловые измерения.
Рис. 6: Вверху: параллаксные расстояния, измеренные с помощью теодолитов, в зависимости от расстояний, измеряемых рулеткой. (Для идеальной точности все точки данных должны лежать на пунктирной линии.)
Внизу: относительные погрешности расстояний, измеренных с помощью теодолитов, по сравнению с рулеткой. Наука в школе 39 : 40-44.
Веб-ссылки
w1 – Алгебраический вывод формулы для расчета расстояния до звезды с использованием подобных треугольников можно скачать в разделе дополнительных материалов.
Ресурсы
Для получения информации о том, как выполнять реальные астрономические измерения параллакса с помощью небольших инструментов, см.:
Cenadelli D et al. (2016) Геометрия может привести вас на Луну. Наука в школе 35 : 41-46.
Cenadelli D et al. (2009) Международная кампания параллакса для измерения расстояния до Луны и Марса. Европейский журнал физики 30 : 35-46. дои: 10.1088/0143-0807/30/1/004
Хиршфельд А.В. (2013) Параллакс: Гонка за измерением космоса . Минеола, Нью-Йорк, США: Dover Publications. ISBN: 9780486490939
Вариации этих опытов уже давно используются на лабораторных курсах астрономии. Например:
Де Йонг М.Л. (1972) Упражнение на звездный параллакс для вводного курса астрономии. Американский журнал физики 40(5) : 762-763. дои: 10.1119/1.1986635
Дойчман WA (1977) Параллакс без боли. American Journal of Physics 45(5) : 490. doi: 10.1119/1.11009
Автор(ы)
Маркус Пёссель является управляющим научным сотрудником Haus der Astronomie (центр астрономического образования и информационно-пропагандистской деятельности) и старшим научным сотрудником Института астрономии Макса Планка в Гейдельберге, Германия.

Обзор
В этой статье описывается инновационный способ определения расстояний до небесных тел методом параллакса.