Элементарные функции и их графики

Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».

И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.

Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.

Существует всего пять типов элементарных функций:

1. Степенные
К этому типу относятся линейные, квадратичные, кубические, , , . Все они содержат выражения вида xα.

2. Показательные
Это функции вида y = ax.

3. Логарифмические
y = logax.

4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.

5. Обратные тригонометрические
Содержат arcsinx, arccosx, arctgx, arcctgx.

Элементарными они называются, потому что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x2 · ex — произведение квадратичной и показательной функций; y = sin(ax) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.

Графики и свойства основных элементарных функций следует знать наизусть.

Степенные функции

1. Линейная функция y = x
2. Квадратичная парабола y = x2
3. Функция y = xn,
n — натуральное, n > 1
n — чётное
n = 2, 4, 6,…
n — нечётное
n = 3, 5, 7,…
4.Гипербола
5.
6.

 

Показательная функция y = ax

a > 1
0 < a < 1

 

Логарифмическая функция y = logax

a > 1
0 < a < 1

 

Тригонометрические функции

1.
2.
3.
4.

 

Обратные тригонометрические функции

1.
2.
3.
4.

 

Выше приведены основные, «базовые» графики. А как будут выглядеть, например, графики функций y = sin(2x) или y = 4x2 + 5? Об этом — статья «Преобразования графиков функций».

Обратите внимание: уравнения, которые вы решаете, обычно относятся к одному из этих пяти типов. Для каждого типа — свои способы решения. Это и понятно: они основаны на тех или иных свойствах функций.

Почему в уравнении 3x = 35 мы можем «отбросить» основания и записать, что x = 5? Да потому что показательная функция y = 3x возрастает и каждое значение принимает только один раз.

Почему уравнение имеет бесконечно много решений, которые записываются в виде серии: , где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.

Зная графики элементарных функций, вы уже не запутаетесь с ОДЗ уравнений и неравенств. Вы сможете решать сложные задачи графически — а это часто во много раз легче и быстрее, чем аналитически.

Есть еще и такие уравнения, где слева и справа стоят функции разных типов. Для их решения есть графический способ, а также специальные приемы, о которых рассказывается в статье «Метод оценки».

Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Элементарные функции и их графики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 09.03.2023

Принципы решения задачи 9 ЕГЭ по математике 2022

В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы.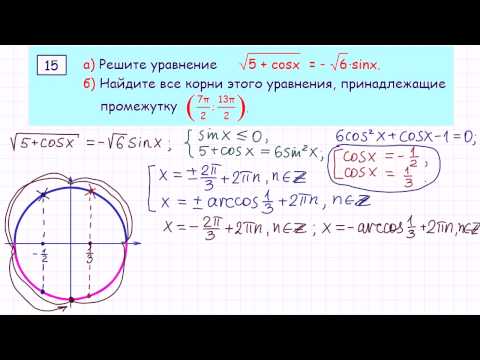 Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике. 

9 задание по математике профильного уровня 2022 получится решить четырьмя методами. 

Первый вариант

Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом: 

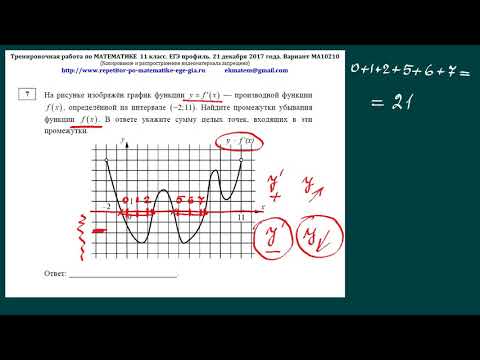
Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки: 

Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты: 

16a — 4b + c = -3

Аналогичным образом записываем выражение, используя две остальные точки: 

9a — 3b + c = -2

4a — 2b + c = 1

Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем: 

b = 8;

c = 13. 

Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы: 

f(x) = x2 + 8x + 13

f(-12) = 144 — 96 + 13 = 61

Второй вариант

Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы: 

Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x2, сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x0 = -b / 2a. По рисунку видно: x0 = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще. 

Третий вариант

9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример: 

y = x2

Сдвиг влево записывается: 

y = (x + 4)2

Сдвиг вниз: 

y = (x + 4)2 — 3

Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61. 

Четвертый вариант

Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат: 

Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!

В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum. 

Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации! 

Изучение задач обучения при использовании математического мышления учащихся

  • Баруди, А.Дж., Цибульскис, М., Лай, М. и Ли, X.: 2004, «Комментарии к использованию траекторий обучения в разработке учебных программ и исследованиях» ‘, Математическое мышление и обучение 6 (2), 227–260.

    Артикул Google Scholar

  • Борко, Х., Мэйфилд, В., Марион, С. , Флексер, Р. и Камбо, К.: 1997, «Учителя», развивающие идеи и методы оценки успеваемости по математике: успехи, камни преткновения и последствия для повышения квалификации»,

    Преподавание и педагогическое образование 13, 259–278.

    Артикул Google Scholar

  • Карпентер, Т.П., Феннема, Э. и Франке, М.Л.: 1996, «Когнитивное обучение: база знаний для реформирования начального обучения математике», Elementary School Journal 97(1), 3–20.

    Артикул Google Scholar

  • Конфри Дж. и Смит Э.: 1994, «Экспоненциальные функции, скорость изменения и мультипликативная единица», Образовательные исследования по математике 26 (2–3), 135–164.

    Артикул Google Scholar

  • Конфри, Дж. и Смит, Э.: 1995, «Расщепление, ковариация и их роль в развитии экспоненциальных функций», Journal for Research in Mathematics Education 26(1), 66–86.

    Артикул Google Scholar

  • Креспо, С.: 2000, «Видеть больше, чем правильные и неправильные ответы: будущие учителя интерпретируют математические работы учащихся», Journal of Mathematics Teacher Education 3, 155–181.

    Артикул Google Scholar

  • Дэвис, Б.: 1996, « Преподавание математики: на пути к надежной альтернативе », Гарленд, Нью-Йорк.

  • Дэвис, Б.: 1997, «Прислушиваться к различиям: развивающаяся концепция преподавания математики», Журнал исследований в области математического образования 28 (3), 355–376.

    Артикул Google Scholar

  • Дэвис, Б. и Симмт, Э.: 2003, «Понимание систем обучения: математическое образование и наука о сложности», Journal for Research in Mathematics Education 34(2), 137–167.

    Артикул Google Scholar

  • Дорр, Х.

    М. и Леш, Р.А.: 2003, «Перспектива моделирования развития учителей», в Р.А. Леш и Х.М. Дорр (ред.), За пределами конструктивизма: модели и перспективы моделирования решения математических задач, преподавания и обучения , Lawrence Erlbaum Associates, Mahwah, NJ, стр. 125–139.

    Google Scholar

  • Доерр, Х.М.: 1998, «Студент думает о моделях роста и упадка», в книге А. Оливье и К. Ньюстеда (ред.), Труды 22-й конференции Международной группы психологии математического образования. , Том. 2, Стелленбосский университет, Стелленбос, Южная Африка, стр. 256–263.

    Google Scholar

  • Doerr, H.M.: 2000, «Как найти закономерность в этих случайных данных?» Сходимость мультипликативных и вероятностных рассуждений»,

    Journal of Mathematical Behavior 18(4), 431–454.

    Артикул Google Scholar

  • Дубинский, Э. и Харел, Г. (ред.): 1992, Понятие функции: аспекты эпистемологии и педагогики , Математическая ассоциация Америки, Вашингтон, округ Колумбия.

    Google Scholar

  • Инглиш, Л. и Леш, Р.А.: 2003, «Конечные задачи», в Р. Леш и Х.М. Дорр (ред.), За пределами конструктивизма: модели и перспективы моделирования решения математических задач, обучения and Teaching

    , Lawrence Erlbaum Associates, Mahwah, NJ, стр. 297–316.

    Google Scholar

  • Эвен, Р.: 1993, «Предметные знания и знание педагогического содержания: будущие учителя средней школы и концепция функции», Журнал исследований в области математического образования 24 (2), 94–116.

    Артикул Google Scholar

  • Эвен, Р. и Тирош, Д.: 1995, «Предметные знания и знания о студентах как источники презентации преподавателем предмета», Образовательные исследования по математике 29(1), 1–20.

    Артикул Google Scholar

  • Эвен, Р. и Уоллах, Т.: 2003, «О наблюдении за учениками и оценке учащихся», в Л. Брэгг, К. Кэмпбелл, Г. Герберт и Дж. Моусли (ред.), Исследования в области математического образования. : Инновации, создание сетей, возможности: материалы 26-й ежегодной конференции Исследовательской группы по математическому образованию Австралии, , Vol. 1, Университет Дикина, Мельбурн, Австралия, стр. 316–323.

    Google Scholar

  • Фелтович П.Дж., Спиро Р.Дж. и Коулсон, Р.Л.: 1997, «Проблемы экспертной гибкости в контекстах, характеризующихся сложностью и изменением», в П.Дж. Фелтович, К.М. Форд и Р. Р. Хоффман (редакторы), Опыт в контексте: человек и машина , AAAI / MIT Press, Кембридж, Массачусетс, стр. 125–146.

    Google Scholar

  • Феннема Э. и Карпентер Т.П.: 1996, «Продольное исследование обучения использованию детского мышления в обучении математике», Journal for Research in Mathematics Education 27(4), 403–434.

    Артикул Google Scholar

  • Франке, М.Л., Карпентер, Т., Феннема, Э., Анселл, Э. и Беренд, Дж.: 1998, «Понимание самоподдерживающихся, генеративных изменений учителей в контексте профессионального развития», Преподавание и педагогическое образование 14, 67–80.

    Артикул Google Scholar

  • Хайд, М.К., Блюм, Г.В., Збиек, Р.М. и Эдвардс, Б.С.: 1999, «Факторы, влияющие на учителей, которые учатся проводить интервью, чтобы понять математические представления учащихся», Educational Studies in Mathematics 37, 223–249.

    Артикул Google Scholar

  • Хеннингсен, М. и Штейн, М.К.: 1997, «Математические задачи и познание учащихся: факторы в классе, которые поддерживают и препятствуют математическому мышлению и рассуждениям высокого уровня», Журнал исследований в области математического образования 28 (5), 524–549.

    Артикул Google Scholar

  • Якобсен, К. и Лерер, Р.: 2000, «Присвоение учителями и изучение геометрии учениками посредством проектирования», Journal for Research in Mathematics Education 31(1), 71–88.

    Артикул Google Scholar

  • Ламперт, М.: 2001, Проблемы обучения и проблемы обучения , Издательство Йельского университета, Нью-Хейвен, Коннектикут.

    Google Scholar

  • Лав, Дж. и Венгер, Э.: 1991, Обучение на месте: законное периферийное участие , издательство Кембриджского университета, Кембридж, Англия.

    Google Scholar

  • Лейнхардт, Г.: 1990, «Получение ремесленных знаний в обучении», Исследователь в области образования 19(2), 18–25.

    Артикул Google Scholar

  • Лейнхардт Г. , Заславский О. и Штейн М.К.: 1990, «Функции, графики и графики: задачи, обучение и преподавание», Review of Educational Research 50(1), 1–64.

    Артикул Google Scholar

  • Леш, Р.А., Крамер, К., Дорр, Х.М., Пост, Т. и Завоевски, Дж.С.: 2003, «Последовательности разработки моделей», в Р.А. Леш и Х.М. Дорр (ред.), За пределами конструктивизма: модели и перспективы моделирования решения математических задач, преподавания и обучения, Lawrence Erlbaum Associates, Mahwah, NJ, стр. 35–58.

    Google Scholar

  • Леш, Р., Гувер, М. и Келли, А.: 1992, «Справедливость, технологии и развитие учителей», в И. Виршуп и Р. Стрейт (ред.), Развитие школьного математического образования Вокруг света , Vol. 3, Национальный совет учителей математики, Рестон, Вирджиния, стр. 104–129..

    Google Scholar

  • Леш Р. А. и Келли, А.Э.: 1999, «Многоуровневые обучающие эксперименты», в книге А.Э. Келли и Р.А. Леш (ред.), Справочник по дизайну исследований в области математики и естественнонаучного образования , Lawrence Erlbaum Associates Mahwah, NJ, стр. 197–230.

    Google Scholar

  • Национальный совет учителей математики 2000, Принципы и стандарты школьной математики , Национальный совет учителей математики, Рестон, Вирджиния.

  • Ромберг Т., Феннема Э. и Карпентер Т. (ред.): 1993, Интеграция исследований по графическому представлению функций , Lawrence Erlbaum Associates, Hillsdale, NJ.

    Google Scholar

  • Шифтер, Д.: 1998, «Изучение математики для преподавания: от учительского семинара до классной комнаты», Journal of Mathematics Teacher Education 1(1), 55–87.

    Артикул Google Scholar

  • Шифтер Д. и Фоснот К.Т.: ​​1993, Реконструкция математического образования: истории учителей, преодолевающих трудности реформы , Teachers College Press, Нью-Йорк.

    Google Scholar

  • Сфард, А.: 1991, «О двойственной природе математических понятий: размышления о процессах и объектах как о разных сторонах одной медали», Образовательные исследования по математике 22, 1–36.

    Артикул Google Scholar

  • Саймон, Массачусетс: 1995, «Реконструкция математической педагогики с конструктивистской точки зрения», Journal for Research in Mathematics Education 26(2), 114–145.

    Артикул Google Scholar

  • Саймон, М.А. и Шифтер, Д.: 1991, «На пути к конструктивистской перспективе: интервенционное исследование развития учителей математики», Образовательные исследования по математике 22, 309–331.

    Артикул Google Scholar

  • Саймон, М.А. и Цур, Р.: 2004, «Объяснение роли математических задач в концептуальном обучении: разработка гипотетической траектории обучения», Математическое мышление и обучение 6 (2), 91–104.

    Артикул Google Scholar

  • Штейн, М.К., Гровер, Б.В. и Хеннингсен, М.: 1996, «Развитие способностей учащихся к математическому мышлению и рассуждениям: анализ математических задач, используемых в классах реформ», American Education Research Journal 33, 455–488.

    Артикул Google Scholar

  • Штраус, А. и Корбин, Дж.: 1998, Основы качественного исследования: методы и процедуры разработки обоснованной теории , 2-е изд., Sage Publications, Thousand Oaks, CA.

    Google Scholar

  • Тирош, Д.: 2000, «Повышение знаний будущих учителей о детских представлениях: случай деления дробей», Журнал исследований в области математического образования 31 (1), 5–25.

    Артикул Google Scholar

  • Цур, Р.: 1999, «Комплексное исследование построения детьми неправильных дробей и роли учителя в продвижении этого обучения», Journal for Research in Mathematics Education 30(4), 390–416.

    Артикул Google Scholar

  • Вакц, Н.Н. и Брайт, Г.В.: 1999, «Изменение убеждений учителей начальной школы и использование в обучении детского математического мышления», Journal for Research in Mathematics Education 30(1), 89–110.

    Артикул Google Scholar

  • Виннер, С. и Дрейфус, Т.: 1989, «Образы и определения понятия функции», Журнал исследований в области математического образования 20 (4), 356–366.

    Артикул Google Scholar

Ссылки на скачивание

Задания для итогового оценивания

Наши итоговые задачи делятся на три класса — Новичок , Ученик и Эксперт . Это не показатель сложности содержания, а указывает, в какой степени они требуют от учащихся автономного применения своих математических знаний: Задания для новичков явно проверяют определенные элементы знаний о содержании, Задания для экспертов гораздо менее структурированы и требуют навыков стратегического решения проблем в дополнение к знанию содержания. Для правильной оценки Математические практики.

Каждое задание включает критерий оценки, набор предварительно оцененных образцов работ учащихся и такой же набор работ без оценок. Практика подсчета очков для этого типа задач может быть эффективной деятельностью по профессиональному развитию.

Также доступен набор тестовых форм с использованием этих стилей задач.

Выбор задач

Существует несколько способов навигации:

  1. Используйте меню слева для просмотра по оценкам и темам или для поиска по ключевой фразе.
  2. Перейдите на вкладку «Стандарты», чтобы найти задачи, связанные с определенным стандартом контента или практикой.