Разбор задания для подготовки к ЕГЭ по математике: базовый уровень
Базовая математика — обязательный предмет ЕГЭ, который ежегодно сдают все российские школьники. Для того, чтобы получить школьный аттестат, вполне достаточно минимального балла по базовой математике, а вот для поступления в вуз может потребоваться экзамен по профильной математике. Минимальный балл, который необходимо набрать для получения аттестата — 23. Чтобы поступить в вуз, понадобится не менее 27 баллов. Рассмотрим демовариант ЕГЭ по математике 2019 и разберем некоторые из этих заданий.
Задание №1
Это задание основано на проверке простейших математических навыков: сложение, вычитание, деление, умножение, а также действия десятичными дробями и перевод одних единиц измерения в другие.
Пример задачи
В 23.50 минут по московскому времени из Санкт-Петербурга в Москву выехал поезд. В Москву он приехал на следующие сутки в 7 часов 50 минут. Необходимо вычислить, какое количество времени поезд был в пути.
Решение
Зная о том, что в сутках всего 24 часа, и их начало приходится на 00:00, а конец — на 24 часа, вычисляем: в первые сутки поезд находился в пути десять минут, во вторые — 7 часов и 50 минут.
7 ч. 50 мин. + 0 ч. 10 мин. = 7 ч. 60 мин. или 8 часов
Задание №2
Задание проверяет, насколько хорошо выпускники умеют интерпретировать различные таблицы, графики и диаграммы, а также совершать с их помощью простейшие вычисления. Как правило, речь идет об анализе графика функции и поиске наибольших и наименьших значений.
Пример задачи
В задаче представлен график, отображающий среднюю температуру Сочи за каждый месяц 1920 года. Необходимо определить, сколько месяцев в году температура была выше 18 градусов Цельсия.
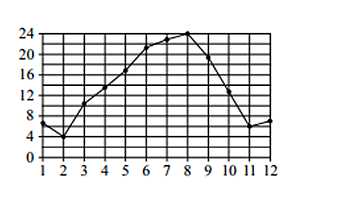
Решение
Для того, чтобы найти правильное решение, необходимо провести горизонтальную линию от точки с цифрой 18 (указана температура в градусах Цельсия). Таким образом станет очевидно, что такая температура держалась 4 месяца подряд: в июне, июле, августе и сентябре.
Задание №3
Школьники должны продемонстрировать знание основ планиметрии, а именно: уметь вычислять площадь фигур, рассчитывать градусные меры углов, диаметры и находить другие значения. Например, найти площадь треугольника, начерченного на бумаге с размером клеток 1х1. В этом задании важно продемонстрировать знание формул и умение пользоваться различными способами решения задачи.
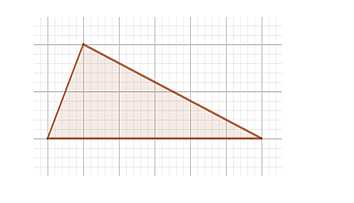
Задание №4
Задача из курса “Теория вероятностей и статистика”. Выпускникам предлагается высчитать вероятность того или иного события, произошедшего в повседневной ситуации.
Пример задачи
Ученикам предложено выучить 25 билетов по биологии. Лишь два из них содержат вопрос о грибах. Каждому школьнику предстоит ответить лишь на один билет. Вычислите вероятность того, что вопрос о грибах будет содержаться именно в этом билете.
Решение
Вероятность события можно рассчитать по формуле Р(А) = m/n, где m — количество благоприятных исходов, а n — общее их количество. 25 билетов означают 25 исходов, 2 из которых — благоприятные. Значит, вероятность равна 2/25, то есть 0,08.
Задача №5
Здесь проверяется умение решать уравнения, находить неизвестные, извлекать корни и т. д.
Пример задачи
Найти корень уравнения 3x-5 = 81
Решение
3х-5 = 34
х-5 = 4
х = 9
Задание №6
Здесь необходимо продемонстрировать умение моделировать различные ситуации при помощи геометрических понятий. Важно знание теорем, умение определять длину, градус угла и другие величины.
Пример задачи
Треугольник с углами А, B и С вписан в окружность с центром О. Угол BAC — 32 градуса. необходимо найти угол BOC.
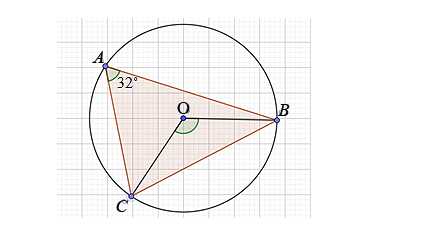
Решение
COB — центральный угол, равный дуге CB
САВ — вписанный угол, равный ½ дуги СВ
Значит, САВ = ½ СОВ. Так как ½ угла СОВ равна 32 градусам, то угол СОВ равен 64о
Ответ: 64о
Задача №7
Выпускник должен продемонстрировать знание понятия “функция” и умение выполнять с ним различные действия: руководствуясь графиком, описывать свойства и поведение функции; находить наибольшие и наименьшие значения; самостоятельно строить графики.
Пример задачи
На графике дифференцируемой функции y = f(x) на оси абсцисс отмечены девять точек. Необходимо найти все точки, в которых производная функции f(х) отрицательна.
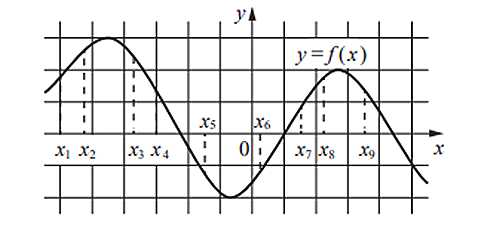
Решение
Необходимо проследить, в каких местах графика убывает функция: именно там ее производная будет отрицательна. Всего на этом графике 4 таких точки.
Задача №8
Задачи на знание основ стереометрии, простейших геометрических понятий и умение использовать при решении стереометрических задач планиметрические методы.
Пример задачи
В условии даны два цилиндрических сосуда. Уровень жидкости в первом достигает 16 сантиметров. Всю жидкость перелили во второй сосуд, диаметр которого дважды превышает диаметр основания первого. Необходимо определить уровень жидкости во втором сосуде.
Решение
Для вычисления объема цилиндра следует воспользоваться этой формулой: V = πR2H, где R — это радиус цилиндра, а Н — его высота. Так как уровень жидкости поднимается до 16 см, значит, высота также равна 16.
V = πR2H = πR216
Зная о том, что диаметр второго сосуда в два раза больше первого, мы можем сделать вывод, что радиус второго сосуда в два раза больше первого (2R). Вычисляем объем жидкости во втором сосуде: V = π(2R)2h или V = 4R2h
При переливании жидкости из одного сосуда в другой ее объем не изменился.
πR216 = π4R2h
4h = 16
Задача №9
В этом разборе задания очень важно уметь выполнять простейшие вычисления и преобразования, поэтому знание формул просто необходимо.
Пример задачи
Необходимо найти sin2α, если учесть, что cosα = 6, а π
Решение
sin2α = 2sinα х cosα
(sinα)2 + (cosα)2 = 1
(sinα)2 + (0,6)2 = 1
(sinα)2 = 1 — 0,36
(sinα)2 = ±0,8
sinα = –0,8
sin2α = 2 х (–0,8) х (0,6)
sin2α = –0,96
Задача №10
Здесь выпускники демонстрируют умение решать прикладные задачи социально-экономической и физической направленности. Необходимо знать и уметь пользоваться формулами, быть точным в расчетах и внимательным при записи ответа.
Пример задачи
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий̆ первым, окажется из России.
Решение
Вероятность определяется, как количество положительных вариантов к количеству всех вариантов. Например, у вас есть 10 монеток и только 2 из них — десятирублёвые, то если вы возьмёте одну монетку, вероятность того, что она будет десятирублёвой, составит
В нашей задаче 35 спортсменов, из которых 7 — из России.
Значит, вероятность того, что первый спортсмен будет из России, составляет:
Ответ: 0.2.
Задача №11
Текстовые задачи с чуть более сложными условиями нужны для того, чтобы экзаменуемый продемонстрировал не только свои знания, но также аналитические способности и умение мыслить логически.
Пример задачи
На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.
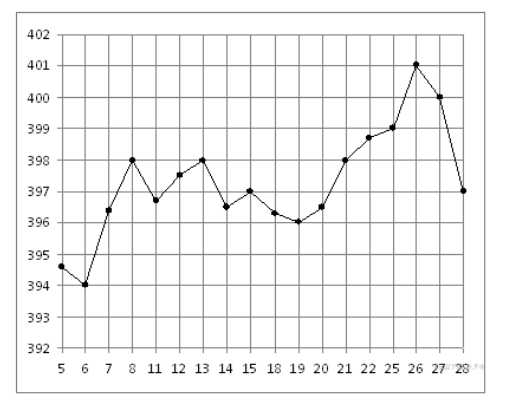
Решение
Из графика видно, что наименьшей цена была 6 марта.
Ответ: 6.
Задача №12
12 задача из демоверсии ЕГЭ по математике базового уровня посвящена теме “экстремум”. Здесь необходимо найти производную функции и ее критические точки.
Пример задачи
Турист подбирает себе экскурсионную программу. Сведения о некоторых музеях и парках, подготовленные туристическим бюро, представлены в таблице.
Пользуясь таблицей, подберите экскурсионную программу так, чтобы турист посетил не ме-нее трёх достопримечательностей за один день.
В ответе для подобранной программы укажите номера экскурсий без пробелов, запятых и других дополнительных символов.
Решение
У туриста всего 10 часов. Если он выберет шестую экскурсию, то на третью экскурсию времени уже не хватит, а вот если выберет пятую, то вполне успевает и на первую. Та-ким образом, 5 и 1.
При выборе четвертой успевает только на вторую. Таким образом, 4 и 2. При выборе третьей посмотреть три достопримечательности никак не успеет.
Ответ: 1 и 5 или 2 и 4.
Задача №13
Задания из этого раздела демо-варианта ЕГЭ проверяют знание стереометрии. Необходимо знать формулы нахождения площадей разных фигур: прямоугольного параллелепипеда, призмы, пирамиды, куба, цилиндра и т. д.
Пример задачи
В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 4. Найдите длину отрезка OS.
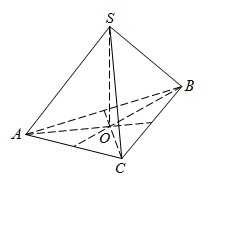
Решение
Отрезок OS высотой треугольной пирамиды SABC, ее объем выражается формулой
Значит,
Ответ: 6.
Задача №14
Для решения этого задания стоит повторить свойства функций. Необходимо знать, что такое область определения и область значений, экстремальные значения, убывание и возрастание.
Пример задачи
На диаграмме показано количество запросов со словом СНЕГ, сделанных на поисковом сайте Yandex.ru во все месяцы с марта 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество запросов за данный месяц.
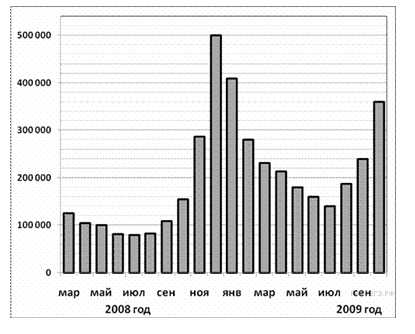
Пользуясь диаграммой, установите связь между промежутками времени и характером изме-нения количества запросов.
ПРОМЕЖУТКИ ВРЕМЕНИ | ХАРАКТЕР ИЗМЕНЕНИЯ КОЛИЧЕСТВА ЗАПРОСОВ |
А) Весна 2008 года | 1) Количество запросов резко снижалось |
Б) Лето 2008 года | 2) Количество запросов заметно увеличивалось |
В) Осень 2008 года | 3) Количество запросов практически не менялось |
Г) Зима 2008-2009 года | 4) Количество запросов плавно снижалось |
Решение
Весной 2008 года количество запросов падало примерно со 120 000 до 100 000.
Летом 2008 года количество запросов изменялось примерно с 82 000 до 80 000.
Осенью 2008 года количество запросов возрастало примерно со 115 000 до 283 000.
Зимой 2008 года количество запросов падало с 500 000 до 280 000.
Таким образом, получаем следующее: A — 4, Б — 3, В — 2, Г — 1.
Ответ: 4321.
Задача №15
Еще одна задача по планиметрии, для решения которой необходимо повторить формулы нахождения площади фигур на плоскости. и основные теоремы.
Пример задачи
В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, AD=8. Найдите синус угла B.
Решение
Ответ: 0,5.
Задача №16
Задача на знание стереометрии. Для ее решения необходимо разбираться в типах пространственных фигур, знать их элементы, а также основные формулы: объем, площадь поверхности и т. д.
Пример задачи
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение
Площадь основания конуса равна Sосн = πr2, а площадь боковой поверхности Sбок = πrl. Из условия имеем:
Значит, в прямоугольном треугольнике, образованном высотой, образующей и ра-диусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Значит, угол между образующей конуса и плоскостью осно-вания равен 60°.
Задача №17
Решение простейших неравенств. В этом задании необходимо составить математическую модель и прописать, что является здесь переменной x, p и переменной z. Даже если само уравнение решить не получится, за правильно составленную задачу вы сможете получить один балл.
Пример задачи
На координатной прямой отмечены точки A, B, C, и D.
Число m равно log54.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответ-ствие между указанными точками и числами.
ТОЧКИ ЧИСЛА
А) A
Б) B
В) C
Г) D
В таблице под каждой буквой укажите соответствующий номер.
Решение
Ответ: 2431.
Задача №18
Выпускникам предлагается решить задачу с параметром, в которой необходимо будет проявить аналитические способности и владение логикой.
Пример задачи
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение
Согласно условию, если кошка идёт по забору, то Шарик лает. Рассмотрим предложенные утверждения:
- Если Шарик не лает, значит, по забору идёт кошка — неверно, так как, если кошка идёт, то Шарик обязательно лает.
- Если Шарик молчит, значит, кошка по забору не идёт — верно, так как, если молчит — значит, никакая кошка не идет.
- Если по забору идёт чёрная кошка, Шарик не лает — неверно, так как, если любая кошка идет по забору — Шарик лает.
- Если по забору пойдет белая кошка, Шарик будет лаять — верно, согласно условию.
Задача №19
Чтобы решить задание под номером 19 по математике базового уровня, необходимо владеть следующими понятиями: числа и их свойства, числовые последовательности и прогрессии, признаки делимости чисел. В самом задании выпускникам для разбора будет предложена задача.
Пример задачи
Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что его квадрат делится на 16.
Решение
Разложим число 25 на слагаемые: 25 = 9 + 9 + 7 = 9 + 8 + 8.
Квадрат числа делится на 16, значит, само число делится на 4. Это значит, что оно заканчивается на чётную цифру. То есть первый набор отпадает, так как в нём нет четных чисел. Из второго мы можем составить числа 988 и 898. Первое число походит по условия задачи.
Ответ: 988.
Задача №20
Одно из самых интересных заданий заставляет задействовать не только логику, но и смекалку: правильный ответ необходимо найти при помощи рассуждений и внимательного отношения к каждой детали.
Пример задачи
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение
Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14 + 4 + 6 = 24 линии, следовательно, кусков будет 25.
Ответ: 25.
Таким образом видим, что разбор заданий для подготовки к ЕГЭ не представляет особых трудностей: при желании к экзамену можно как следует подготовиться и сдать его на максимально высокие баллы.
Читать похожие статьи
ruseducenter.ru
Задание №13 ЕГЭ по математике базовый уровень
Наглядная стереометрия
В 13 задании ЕГЭ базового уровня мы будем иметь дело с задачами по стереометрии, но не абстрактными, а наглядными примерами. Это могут быть задачи на уровень жидкости в сосудах, которую я разобрал ниже, или же задачи на модификации фигуры — например, у которой отрезали вершины. Нужно быть готовым к решению простых задач по стереометрии — они обычно сводятся сразу к задачам на плоскости, необходимо только правильно посмотреть на чертеж.
Разбор типовых вариантов заданий №13 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
Алгоритм выполнения:
- Записать формулу объема цилиндра.
- Подставить значения для цилиндра с жидкостью в первом и во втором случае.
- Объем жидкости не изменялся, следовательно, можно приравнять объемы.
- Полученное уравнение решить относительно второй высоты h2.
- Подставить данные и вычислить искомую величину.
Решение:
Запишем формулу объема цилиндра.
Если вы забыли формулу объема цилиндра, то напомню, как ее можно легко вывести. Объем простых фигур, таких как куб и цилиндр, можно вычислить умножив площадь основания на высоту. Площадь основания в случае с цилиндром равна площади окружности, которую, вы, наверняка помните: π • r2.
Следовательно, объем цилиндра равен π • r2 • h
Подставим значения для цилиндра с жидкостью в первом и во втором случае.
V1 = π r12 h1
V2 = π r22 h2
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
Левые части равны, значит можно приравнять и правые.
π r12 h1 = π r22 h2
Полученное уравнение решим относительно второй высоты h2.
h2 – неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
h2 =( π r12 h1)/ π r22
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 .
Подставим r2 = 4 r1 в выражение для h1.
Получим: h2 =( π r12 h1)/ π (4 r1) 2
Полученную дробь сократим на π, получим h2 =( r12 h1)/ 16 r12
Полученную дробь сократим на r1, получим h2 = h1/ 16.
Подставим известные данные: h2 = 80/ 16 = 5 см.
Ответ: 5.
Второй вариант задания
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй),
b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2) = 4,5/9 = ½.
Объем первой коробочки в 2 раза меньше объема второй.
Ответ: 2.
Третий вариант задания
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 1,5 c2 (первая коробка в полтора раза выше второй), b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 1,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2) = 1,5/9 = 15/(10 · 9) = 3/(2 · 9) = 1/ (2 · 3) = 1/6.
Объем первой коробочки в 6 раза меньше объема второй.
Ответ: 6.
Вариант тринадцатого задания 2017
От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?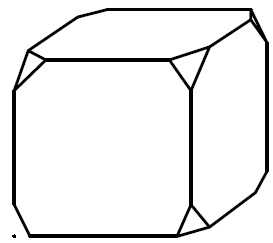
Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
Вариант тринадцатого задания 2019 года(1)
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
Алгоритм выполнения
- Записываем ф-лу для вычисления объема цилиндра.
- Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
- Формируем формулы для объема 1-го и 2-го цилиндров.
- Вычисляем отношение объемов.
Решение:
Объем цилиндра равен: V=πR2H. Обозначим радиус основания 1-го цилиндра через R1, а его высоту – через Н1. Соответственно, радиус основания 2-го цилиндра обозначим через R2, а высоту – через Н2.
Отсюда получим: V1=πR12H1, V2=πR22H2.
Запишем искомое отношение объемов:
.
Подставляем в полученное отношение числовые данные:
.
Вывод: объем 2-го цилиндра больше объема 1-го в 6 раз.
Вариант тринадцатого задания 2019 года(2)
В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
Алгоритм выполнения
- Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V1 и V2.
- Фиксируем значение для V1. Выражаем V2 через V1. Находим значение V2.
- Переводим результат, полученный в литрах, в куб.см.
Решение:
Объем бака до погружения V1=5 (л). Т.к. после погружения детали объем стал равным V2. Согласно условию, увеличение составило 1,4 раза, поэтому V2=1,4V1.
Отсюда получаем: V2=1,4·5=7 (л).
Т.о., разница объемов, которая и составляет объем детали, равна:
V2–V1=7–5=2 (л).
2 л=2·1000=2000 (куб.см).
Вариант тринадцатого задания 2019 года(3)
Вода в сосуде цилиндрической формы находится на уровне h=80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.
Алгоритм выполнения
- Записываем ф-лу для расчета объема цилиндра.
- На основании этой формулы записываем 2 уравнения – для вычисления объема воды в 1-м и 2-м сосудах. Для этого используем в формуле соответствующие индексы 1 и 2.
- Поскольку воду просто переливают их одного сосуда в другой, то ее объем не изменяется. Поэтому приравниваем полученные уравнения. Из полученного единственного уравнения находим уровень воды во 2-м сосуде, выраженный высотой h2.
Решение:
Объем цилиндра равен: V=Sоснh=πR2h.
Объем воды в 1-м сосуде: V1=πR12h1.
Объем во 2-м сосуде: V2=πR22h2.
Приравниваем V1 и V2: πR12h1=πR22h2.
Сокращаем на π, выражаем h2:
.
По условию R2=2R1. Отсюда:
.
Вариант тринадцатого задания 2019 года(4)
От деревянной правильной треугольной призмы отпилили все ее вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые ребра на рисунке не изображены)?
Алгоритм выполнения
- Определяем количество вершин у треугольной призмы.
- Анализируем изменения, которые произойдут при отпиливании всех вершин. Подсчитываем кол-во вершин у нового многогранника.
Решение:
Вершины призмы формируют вершины оснований (верхнего и нижнего). Поскольку основаниями прав.треугольной призмы являются прав.треугольники, то вершин у такой призмы 3·2=6 штук.
Спилив вершины призмы, получим вместо них небольшие (по сравнению с размерами самой призмы) треугольники. Это отображено и на рисунке. Т.е. вместо каждой вершины образуется 3 новых. Следовательно, их кол-во станет равным: 6·3=18.
Вариант тринадцатого задания 2019 года(5)
Даны две коробки, имеющие форму правильной четырехугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза ниже второй, а вторая второе уже первой. Во сколько раз объем первой коробки больше объема второй?
Алгоритм выполнения
- Вводим обозначения для линейных параметров коробок и их объемов.
- Определяем зависимость линейных параметров согласно условию.
- Записываем формулу для вычисления объема призмы.
- Адаптируем эту формулу для объемов коробок.
- Находим отношение объемов.
Решение:
Т.к. форма коробок – правильная призма, то в их основании лежат квадраты. Поэтому можем обозначить длину и ширину каждой коробки одинаково. Пусть для первой коробки это а1, а для второй а2. Высоты коробок обозначим соответственно h1 и h2. Объемы – V1 и V2.
Согласно условию, h2=4,5h1, а1=3а2.
Объем призмы равен: V=Sоснh. Т.к. в основании коробок лежит квадрат, то Sосн=а2. Отсюда: V=a2h.
Для 1-й коробки имеем: V1=a12h1. Для 2-й коробки: V2=a22h2.
Тогда получаем отношение:
Вариант тринадцатого задания 2019 года(6)
В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
Алгоритм выполнения
- Доказываем, что данные в условии конусы подобны.
- Определяем коэффициент подобия.
- Используя свойство для объемов подобных тел, находим объем жидкости.
Решение:
Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.
По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.
Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V1, малого – V2. Получим:
.
Поскольку по условию V1=1600 мл, то V2=1600/8=200 мл.
Вариант тринадцатого задания 2019 года(7)
Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?
Алгоритм выполнения
- Записываем формулу для вычисления объема шара.
- Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
- Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.
Решение:
Объем шара вычисляется по ф-ле: .
Отсюда объем 1-го (большего) шара равен , 2-го (меньшего) шара – .
Составим отношение объемов:
.
Подставляем в полученную формулу числовые данные из условия:
.
Вывод: объем большего шара в 64 раза больше.
Вариант тринадцатого задания 2019 года(8)
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Алгоритм выполнения
- Записываем формулу для определения площади бок.поверхности цилиндра.
- Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
- Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.
Решение:
Площадь бок.поверхности цилиндра вычисляется так: S=2πRH.
Для 1-го цилиндра имеем: S1=2πR1H1. Для 2-го цилиндра: S2=2πR2H2.
Составим отношение этих площадей:
.
Найдем числовое значение полученного отношения:
.
Вывод: площадь бок.поверхности 1-го цилиндра больше в 12 раз.
Вариант тринадцатого задания 2019 года(9)
Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
Алгоритм выполнения
- Записываем формулу для определения массы большего шаров через плотность и объем.
- Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).
- Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
- Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.
Решение:
Масса большего (1-го) шара равна: m1=ρV1. Объем этого шара составляет V1=(4/3)πR13. Отсюда получаем: m1=(4/3)πρR13. Из этого уравнения выразим плотность: .
Масса меньшего (2-го) шара равна: m2=ρV2. Объем шара: V2=(4/3)πR23. В ур-ние для m2 подставим выражения для ρ и V2. Получаем:
.
Вычисляем m2:
.
Вариант тринадцатого задания 2019 года(10)
В бак, имеющий форму правильной четырехугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объем детали сложной формы, ее полностью погружают в эту жидкость. Найдите объем детали, если после ее погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Алгоритм выполнения
- Определяем часть призмы, соответствующую объему погруженной детали.
- Вычисляем объем детали на основании ф-лы для определения объема прямой призмы с квадратом в основании.
Решение:
Погруженная в жидкость деталь занимает объем, соответствующий столбу жидкости, высота которого равна 10 см, т.е. разнице, возникшей между начальной высотой жидкости и конечной (после погружения). Это означает, что деталь имеет объем, равный части жидкости, занимающей объем 40х40х10 (см).
Найдем этот объем:
V=40·40·10=16000 (см3).
spadilo.ru
разбор с решением и теория – Российский учебник
Демонстрационная версия ЕГЭ (базовый уровень) – 2019 год
Задание 20
В обменном пункте можно совершить одну из двух операций:
- За 2 золотых монеты получить 3 серебряных и одну медную
- За 5 серебряных монет получить 3 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
Т.к. у Николая нет золотых монет, значит он может начинать со второй операции, пусть таких операций он совершил b,
Тогда количество первых операций будет a.
Составим уравнение для золотых монет:
2a = 3b
a = 1,5b
Общее количество операций: a + b = 50
1,5b + b = 50
2,5b = 50
b = 20
Первая операция была проделана: a = 20 · 1,5 = 30 раз
Получено: 3 · 30 = 90 серебряных монет
Вторая операция проделана 20 раз (b = 20)
Получено: 5 · 20 = 100 серебряных монет
Количество серебряных монет у Николая уменьшилось на 10 монет:
100 – 90 = 10 монет.
Ответ: 10
Или
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трех из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвертого прямоугольника.
Решение:
Выразим периметры прямоугольников:
2 · (a + b) = 24
2 · (a + c) = 28
2 · (d + c) = 16
2 · (d + b) = ?
d + b = 8 – 2
d + b = 6
2 · (d + b) = 2 · 6 = 12
Ответ: 12.
#ADVERTISING_INSERT#
rosuchebnik.ru
Задание №1 ЕГЭ по математике базовый уровень
Элементарные математические вычисления
В задании №1 ЕГЭ по математике базового уровня необходимо провести элементарные вычисления — сложение, вычитание, деление и умножение дробей. Более того, данное задание аналогично первому заданию ОГЭ по математике, поэтому теория для успешного выполнения одинакова. Поэтому мы перейдем непосредственно к разбору типовых вариантов.
Разбор типовых вариантов заданий №1 ЕГЭ по математике базового уровня
Первый вариант задания
Найдите значение выражения:Алгоритм решения:
- Определить порядок действий.
- Выполнить действия в скобках.
- Преобразовать смешанное число в неправильную дробь.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Произвести действия в числителе.
- Знаменатель оставить наименьший общий.
- Умножить числитель получившейся дроби на 9.
- Полученный результат сократить и преобразовать в десятичную дробь.
Решение в общем виде:
Пояснения к решению:
Первым всегда выполняется действие в скобках, в данном случае вычитание.
Преобразуем смешанное число
в неправильную дробь. Для этого умножим целую часть на знаменатель, и прибавим числитель
3 • 15 + 1 = 46
Запишем результат в числитель, знаменатель оставим без изменения.
Действие в скобках примет вид:
Ищем наименьший общий знаменатель для дробей 4/9 и 46/15. 15 не делится на 9, удвоим наибольший знаменатель. 30 не делится на 9. утроим наибольший знаменатель, 45 делится на 9. Следовательно, 45 делится одновременно и на 15, и на 9. То есть 45 – наименьший общий знаменатель дробей 4/9 и 46/15.
Приводим дроби к общему знаменателю – 45. Для этого по основному свойству дроби необходимо и числитель и знаменатель дроби умножить на одно и то же число, чтобы дробь не изменилась. Это число называется дополнительным множителем. Дополнительный множитель к первой дроби — 5 (9*5=45). Чтобы получить в знаменателе первой дроби 45 необходимо умножить на 5 и числитель и знаменатель.
Вторую дробь умножим на 3 (15 • 3=45)
Действие в скобках после преобразования будет выглядеть так:
Произведем вычитание дробей с одинаковыми знаменателями. Для этого в числителе запишем вычитание числителей, а знаменатель оставим без изменений.
Выполним действие за скобками, в данном случае умножение на целое число. Для этого умножим числитель дроби на 9, а знаменатель оставим без изменений. Числитель и знаменатель полученной дроби сократим на 9, то есть разделим и числитель и знаменатель дроби на 9. По основному свойству дроби дробь не изменится.
Минус в числителе выносится за дробную черту.
Полученную дробь преобразуем в десятичную, поделив в столбик.
Не забудьте о знаке «минус» в ответе.
Ответ: 23,6
Второй вариант задания
Найдите значение выражения:Алгоритм решения:
- Определить порядок действий.
- Выполнить действие в скобках.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Выполнить вычитание числителей, знаменатель оставить без изменений.
- Выполнить деление. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае вычитание.
Для того чтобы выполнить вычитание дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 4, и на 9. 9 на 4 не делится. Удвоим больший знаменатель: 18 не делится на 4. Утроим больший знаменатель: 27 не делится на 4. Увеличим больший знаменатель в 4 раза: 36 делится и на 9, и на 4 одновременно. Следовательно, 36 – наименьший общий знаменатель для дробей 1/4 и 2/9.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 1/4 и 2/9. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 1/4 нужно умножить на 9(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36. Дробь 2/9 нужно умножить на 4 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36.
В результате получим:
Действие в скобках примет вид:
Выполним вычитание дробей с одинаковыми знаменателями. Для этого вычтем из числителя первой дроби числитель второй, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель и знаменатель) полученную дробь на 12.
Ответ: 21
Третий вариант задания
Найти значение выражения:Алгоритм решения:
- Определить порядок действий.
- Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
- Перевести смешанное число в неправильную дробь.
- Привести полученные дроби к наименьшему общему знаменателю.
- Выполните сложение дробей с одинаковыми знаменателями. Для этого сложить числители, результат записать в числитель, знаменатель оставить без изменений.
- Выполнить деление.
- Перевести смешанное число в неправильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
- Числитель первой дроби умножить на знаменатель второй – записать в числитель. Знаменатель первой дроби умножить на числитель второй результат записать в знаменатель.
- Сократить получившуюся дробь.
- Привести результат к десятичному виду.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
Нужно сложить смешанное число и правильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним. Переведем смешанное число в неправильную дробь:
Действие в скобках примет вид:
Для того, чтобы выполнить сложение дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 5, и на 7. 7 на 5 не делится. Удвоим больший знаменатель: 14 не делится на 5. Утроим больший знаменатель: 21 не делится на 5. Увеличим больший знаменатель в 4 раза: 28 не делится 5. Увеличим больший знаменатель в 5 раз: 35 делится одновременно и на 5, и на 7. Следовательно, 35 – наименьший общий знаменатель для дробей 9/5 и 3/7.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 9/5 и 3/7. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 9/5 нужно умножить на 7(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35. Дробь 3/7 нужно умножить на 5 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35.
В результате получим:
Действие в скобках примет вид:
Выполним сложение дробей с одинаковыми знаменателями. Для этого сложим числители, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Переведем смешанное число в неправильную дробь, для этого целую часть нужно умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
Выполнить деление дробей. Числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель, и знаменатель на одно и то же число) полученную дробь на 39.
Переведем полученную дробь в десятинную.
Ответ: 8,75
Вариант первого задания 2017 года (1)
Найдите значение выражения:(6,7 − 3,2) ⋅ 2,4
В данном случае первым действием мы выполняем вычитание в скобках, а затем производим умножение:
6,7 − 3,2 = 3,5
3,5⋅ 2,4 = 8,4
Отдельно остановлюсь на последнем действии. Его можно вычислить умножением в столбик, либо посчитать устно, воспользовавшись следующими логическими операциями:
2,4 ⋅ 3 + 2,4 ⋅ 0,5 = 2 ⋅ 3 + 0,4 ⋅ 3 + 2,4/2 = 6 + 1,2 +1,2 = 8,4
Ответ: 8,4
Вариант первого задания 2017 года (2)
Найдите значение выражения:В данном случае необходимо выполнить сложение обыкновенных дробей. Общий знаменатель для дробей в скобках — 15 (если вы забыли как определять общий знаменатель, смотрите здесь). Первую дробь домножаем на 5, вторую на 3. Получаем:
(5 + 3)/15
После сложения:
8/15
Теперь выполняем умножение:
8•6/15 = 48/15
В таком варианте дробь в ответ записать мы не можем, выделяем сначала целую часть, это 3 (45/15=3), в остатке получим:
3/15
После сокращения на 3:
1/5
и перевода в десятичный вид:
1/5 = 20/100 = 2/10 = 0,2
Не забываем про целую часть и получаем ответ:
3,2
Ответ: 3,2
Вариант первого задания 2019 года (1)
Найдите значение выражения:- Если представить черту дроби в виде знака деления, то получим выражение: (2,7+5,8):6,8. Отсюда получаем приоритет действий: 1) сложение в скобках; 2) деление. Поэтому сначала выполняем действие в числителе.
- Избавляемся от десят. запятых в числителе и знаменателе. Для этого применяем основное свойство дроби и умножаем числитель и знаменатель на 10.
- Делим 85 на 68 в столбик.
Решение

Ответ: 1,25
Вариант первого задания 2019 года (2)
- Учитываем приоритетность операций. Здесь 1-м действием выполняется умножение, а затем вычитание.
- При умножении числа записываем друг под другом, выровняв их по последней цифре. В результирующем числе отделяем столько знаков после запятой, сколько имеется суммарно в обоих множителях. В данном случае нужно отделить 2 знака.
- При выполнении вычитания в столбик числа располагают так, чтобы десят.запятые располагались на друг под другом.
Решение
Ответ: 26,7
Вариант первого задания 2019 года (3)
- Умножаем 1/5 на 5,5. При этом 5,5 переходит в числитель дроби.
- Выполняем сокращение полученной дроби на 5. Получаем десят.дробь
- Находим конечную разность.
Решение
Ответ:0,1
Вариант первого задания 2019 года (4)
- Находим разность в скобках. Для этого находим НОК (25, 38) и приводим дроби к общему знаменателю.
- Делим результат в скобках на дробь 6/19. Для этого переходим к умножению дробей, перевернув 9/16 и получив 16/9. Далее сокращаем множители в числителе и знаменателе и находим результирующую дробь.
- Полученную дробь записываем в десят.виде.
Решение
spadilo.ru
Задание №10 ЕГЭ по математике базовый уровень
Вероятность и статистика
В задании №10 ЕГЭ по математике базового уровня нам предстоит решить задачу по теории вероятности. Задачи довольно простые и адаптированы под реальные жизненные ситуации, что делает их решение интересным для школьников. Разберем с Вами несколько подробных примеров.
Разбор типовых вариантов задания №10 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что первым будет россиянин) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 7, так как россиян 7 и каждый из них имеет равные шансы выступать первым.
Всего общее число вариантов 35, так как спортсменов всего 35 и каждый из них может выступать первым.
Подставим значения и вычислим вероятность.
7/35 = 1/5 = 0,2
Ответ: 0,2.
Второй вариант задания
Олег, Петя, Миша и Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет не Миша.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что игру должен будет начинать не Миша) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 3, так как «не Миш» трое и каждый из них имеет равные шансы начинать игру.
Всего общее число вариантов 4, так как мальчиков всего 4 и каждый из них может начинать игру.
Подставим значения и вычислим вероятность.
3/4 = 0,75
Вариант решения в общем виде:
При бросании жребия начинает игру один из 4 мальчиков. Вероятность этого события составляет P = 1/4 (для любого мальчика, в том числе и для Миши). Тогда обратная вероятность того, что Миша не будет начинать игру, равна:
Ответ: 0,75.
Третий вариант задания
Вася, Петя, Олег, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Вася или Петя.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что игру должен будет начинать Вася или Петя) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 2, так как Вася и Петя – это два мальчика, каждый из них имеет равные шансы начинать игру.
Всего общее число вариантов 4, так как мальчиков всего 5 и каждый из них может начинать игру.
Подставим значения и вычислим вероятность.
2/5 = 0,4
Решение в общем виде:
Всего при бросании жребия может быть n = 5 исходов (для 5 человек). Обозначим через событие А – жребий выпал Васе или Пете. Число благоприятных исходов для события A равно m = 2. Следовательно, искомая вероятность, равна:
Ответ: 0,4.
Четвертый вариант задания
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,1. Найдите вероятность того, что в течение года обе лампы перегорят.
Алгоритм выполнения:
- Определить вероятность каждого события в отдельности.
- Перемножить вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Решение:
Определим вероятность каждого события в отдельности.
Вероятность того, что перегорит первая лампа по условию 0,1. Вероятность того, что перегорит вторая лампа по условию 0,1.
Перемножим вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Ответ: 0,01.
Пятый вариант задания
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,15. Найдите вероятность того, что в течение года обе лампы перегорят.
Алгоритм выполнения:
- Определить вероятность каждого события в отдельности.
- Перемножить вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Решение:
Определим вероятность каждого события в отдельности.
Вероятность того, что перегорит первая лампа по условию 0,15. Вероятность того, что перегорит вторая лампа по условию 0,15.
Перемножим вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Ответ: 0,0225.
Вариант десятого задания 2017
Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной?
Данная задача даже проще, чем предыдущая. В начале, нам необходимо найти количество исправных лампочек:
100 — 3 = 97
После этого находим вероятность, она равна отношению количества исправных лампочек к общему количеству:
97 / 100 = 0,97
Ответ: 0,97
Вариант десятого задания 2019 года(1)
На семинар приехали 6 ученых из Норвегии, 5 из России и 9 из Испании. Каждый ученый подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Алгоритм выполнения
- Поскольку событие, описанное в условии, является независимым, то вероятность того, что ученый из России выступит именно 8-м, такая же, как и вероятность выступления под любых другим номером. Поэтому для решения можем применить формулу-определение для вероятности P=Nб/N, где Nб – кол-во благоприятствующих данному событию исходов, N – общее кол-во исходов.
- Подсчитываем общее кол-во исходов. Оно равно сумме всех докладов.
- Определяем кол-во благоприятствующих исходов как число докладов от российских ученых.
- Подставляем полученные данные в формулу, вычисляем вероятность.
Решение:
P=Nб/N
N=6+5+9=20
Nб=5
P=5/20=0,25
Вариант десятого задания 2019 года(2)
В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 4 раза больше, чаем пакетиков с зеленым. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зеленым чаем.
Алгоритм выполнения
- Обозначаем через х кол-во пакетиков с зеленым чаем. Выражаем затем через х кол-во пакетиков с черным чаем.
- Записываем ф-лу для нахождения вероятности, имея в виду, что число благоприятствующих исходов равно кол-ву пакетиков зеленого чая, а общее число исходов – общему кол-ву пакетиков.
- Вычисляем вероятность.
Решение:
Пусть х – кол-во пакетиков зеленого чая. Тогда кол-во пакетиков черного составляет 4х.
Вероятность P=Nб/N. Здесь Nб=х, поскольку вероятность определяется именно для пакетиков с зеленым чаем. N=х+4х=5х.
Получаем: P=х/(5х)=1/5=0,2.
Вариант десятого задания 2019года(3)
В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекает. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Алгоритм выполнения
- Из 1400 вычитаем 14. Получаем кол-во исправных насосов.
- По ф-ле P=Nб/N (где Nб – кол-во исправных насосов, N – общее кол-во насосов) находим искомую вероятность.
Решение:
1400 – 14 = 1386 (шт.) – исправных насосов поступило в продажу.
1386 / 1400 = 0,99 – вероятность того, что случайно подобранный насос исправен (не подтекает).
Вариант десятого задания 2019 года(4)
В кармане у Дани было пять конфет – «Ласточка», «Взлетная», «Василек», «Грильяж» и «Гусиные лапки», а также ключи от квартиры. Вынимая ключи, Даня случайно выронил из кармана одну конфету. Найдите вероятность того, что упала конфета «Взлетная».
Алгоритм выполнения
- Определяем общее кол-во конфет. Фиксируем, что упала единственная конфета.
- Применяя ф-лу для вероятности P=Nб/N, находим искомую вероятность.
Решение:
В кармане у Дани находится 6 предметов – 5 конфет и ключи. Ключи для расчета не учитываем, поскольку их извлечение из кармана не является случайным событием. Тогда общее кол-во случайных событий N=5. Кол-во благоприятных исходов для этих событий в данном случае равно 1, т.к. падает 1 конфета. Отсюда Nб=1.
Вероятность находим по ф-ле P=Nб/N. Подставляем числовые данные, получаем: P=1/5=0,2.
Вариант десятого задания 2019 года(5)
На борту самолета 26 мест рядом с запасными выходами и 10 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Д. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Д. достанется удобное место, если всего в самолете 300 мест.
Алгоритм выполнения
- Суммируем 26 и 10, чтобы найти общее кол-во удобных для пассажира Д. мест.
- Используя ф-лу P=Nб/N, где Nб – кол-во удобных мест, N – общее кол-во мест, находим искомую вероятность.
Решение:
26 + 10 = 36 – кол-во мест, которые удобны для пассажира Д
Р = 36 / 300 = 0,1233 – вероятность того, что при случайном выборе пассажиру достанется удобное место
Вариант десятого задания 2019 года(6)
Вероятность того, что новая шариковая ручка пишет плохо или вовсе не пишет, равна 0,21. Покупатель не глядя берет одну шариковую ручку из коробки. Найдите вероятность того, что эта ручка пишет хорошо.
Алгоритм выполнения
- Анализируем ситуацию, описанную в условии. Определяем, что существует только 2 варианта возможных событий.
- Находим искомую вероятность как разность единицы и вероятности того, что ручка пишет плохо.
Решение:
Вариантов событий в данном случае имеется два – ручка пишет хорошо или она пишет плохо. При этом ручка в любом случае будет из коробки взята, т.е. событие состоится. Это означает, что его вероятность равна 1.
Поскольку вероятность того, что ручка пишет плохо, составляет 0,21, то вероятность того, ручка будет писать хорошо, равна:
1 – 0,21 = 0,79.
Вариант десятого задания 2019 года(7)
На олимпиаде по русскому языку участников рассаживают по трем аудиториям. В первых двух по 130 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Алгоритм выполнения
- Умножаем 130 на 2, получаем кол-во участников в первых двух аудиториях.
- Из 400 вычитаем полученное произведение. Узнаем, сколько участников находилось в запасной аудитории.
- Делим полученную разность на 400. Находим искомую вероятность.
Решение:
130 · 2 = 260 – участников писали олимпиаду в первых 2-х аудиториях.
400 – 260 = 140 – участников находилось в запасной аудитории.
Вероятность P = Nб / N. Здесь Nб = 140, N = 400.
Получаем: Р = 140 / 400 = 0,35.
Вариант десятого задания 2019 года(8)
В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдет в магазин?
Алгоритм выполнения
- Записываем ф-лу P=Nб/N, где Nб – кол-во благоприятных исходов для ситуации, N – общее кол-во исходов.
- Благоприятным исходом в данном случае является попадание туриста Д. в группу из 2 человек, которым нужно идти в магазин. Т.е. Nб=2.
- Общее кол-во исходов – число туристов, составляющих полную группу.
- Подставляем определенные числовые величины в ф-лу, находим искомую вероятность.
Решение:
Вероятность равна: P = Nб / N.
Nб = 2, т.к. по условию для похода в магазин требуется 2 человека.
N = 8, т.к. всего в группе 8 туристов.
Р = 2 / 8 = 0,25.
Вариант десятого задания 2019 года(9)
На тарелке лежат одинаковые на вид пирожки: 1 с мясом, 12 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что этот пирожок окажется с капустой.
Алгоритм выполнения
- Для вычисления вероятности используем ф-лу P=Nб/N, где Nб – кол-во благоприятных исходов ситуации, N – общее кол-во исходов.
- Определяем кол-во благоприятных исходов. Здесь таковым является кол-во пирожков с капустой.
- Находим общее кол-во исходов. Это – кол-во всех (любых) пирожков.
- Подставляем числовые данные в формулы, определяем требуемую вероятность.
Решение:
Искомую вероятность найдем по ф-ле P=Nб/N.
В данном случае Nб = 12, поскольку именно столько на тарелке пирожков с капустой.
Общее число исходов N = 1 + 12 + 3 = 16 (пирожков).
Р = 12 / 16 = 0,75.
Вариант десятого задания 2019 года(10)
Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 14 выступлений, остальные распределены поровну между оставшимися днями.
Алгоритм выполнения
- Из 50 вычитаем 14. Получаем кол-во незапланированных выступлений, которые приходятся на 2–5-й дни.
- Полученную разность делим на 4, т.е. на кол-во дней, в течение которых будет заслушано выступление российского исполнителя. Получим кол-во выступлений, которые приходятся на каждый из этих дней.
- По ф-ле P=Nб/N (где Nб – кол-во выступлений в каждый из дней, кроме первого; N – общее кол-во выступлений в эти дни) находим искомую вероятность.
Решение:
50 – 14 = 36 – кол-во незапланированных выступлений, в числе которых как раз и предполагается выступление россиянина.
5 – 1 = 4 – кол-во дней, в течение которых распределены поровну 36 выступлений.
36 : 4 = 9 – кол-во выступлений, приходящихся на каждый день, начиная со 2-го.
Поскольку выступление в 3-й день, равно как и в любой другой, начиная со 2-го, является независимым и равновероятным событием, то вероятность его положит.исхода можно определить по ф-ле P=Nб/N. Здесь Nб = 9, N = 36. Тогда: Р = 9 / 36 = 0,25.
spadilo.ru
разбор с решением и теория – Российский учебник
Демонстрационная версия ЕГЭ (базовый уровень) – 2019 год
Задание 5
Найдите cosα, если sinα = 0,8 и 90° < α < 180°
Решение:
(sinα)2 + (cosα)2 = 1
(cosα)2 = 1 – (sinα)2
(cosα)2 = 1 – (0,8)2
(cosα)2 = 1 – 0,64
(cosα)2 = 0,36
cosα = ±0,6
т.к. 90° < α < 180°, значит угол принадлежит 2 четверти и cosα < 0,
cosα = –0,6
Ответ: cosα = –0,6
Или
Найдите значение выражения
Решение:
Применим формулу разности квадратов (a – b)(a + b) = a2 – b2
Ответ: 51
Или
Найдите значение выражения
Решение:
Используем свойство:
am+n = am · an
Используем свойство:
Ответ: 30
#ADVERTISING_INSERT#
rosuchebnik.ru
Задание №15 ЕГЭ по математике базового уровня
Планиметрия
В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.
Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.
Алгоритм выполнения:
- Вспомнить определение косинуса угла.
- Записать выражение для нахождения косинуса угла.
- Выразить неизвестную величину.
- Вычислить.
Решение:
Вспомним определение косинуса угла.
Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.
Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.
Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.
Прилежащий к углу А катет – АН.
Получим cos A = АН/АС.
Выразим неизвестную величину.
АН = АС · cos A
Вычислим.
АН = АС · cos A = 4 · 0,8 = 3,2
Ответ: 3,2.
Второй вариант задания
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.
Алгоритм выполнения:
- Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
- Вычислить градусную меру угла, на который опирается дуга.
- Вычислить вписанный угол.
Решение:
Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.
Вычислим градусную меру угла, на который опирается дуга.
Весь круг составляет 360°, а 5/18 от его длины это
Вычислим вписанный угол.
Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
100°:2 = 50°.
Ответ: 50.
Третий вариант задания
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.
Алгоритм выполнения:
- Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
- Вычислить градусную меру угла, на который опирается дуга.
- Вычислить вписанный угол.
Решение:
Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.
Вычислим градусную меру угла, на который опирается дуга.
Весь круг составляет 360°, а 11/36 от его длины это
Вычислим вписанный угол.
Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
110°:2 = 55°.
Ответ: 55.
Вариант пятнадцатого задания 2019 года(1)
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.
Алгоритм выполнения
- Определяем вид треугольника.
- Доказываем, что медиана ВМ является и высотой.
- Из прямоугольного треугольника АМВ по т.Пифагора находим медиану ВМ.
Решение:
Если АВ=ВС, то ∆АВС – равнобедренный.
В равнобедр.треугольнике медиана, опущенная на основание, является еще и высотой. Тогда угол АМВ=900, и ∆АМВ – прямоугольный с катетами АМ и ВМ и гипотенузой АВ.
По т.Пифагора АМ2+ВМ2=АВ2. Отсюда: .
Т.к. АМ медиана, то
AM=АС:2=24:2=12.
Тогда:
.
Вариант пятнадцатого задания 2019 года(2)
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.
Алгоритм выполнения
- Находим ЕС.
- Определяем значение СD.
- Из прямоугольного треугольника АСD по т.Пифагора находим ЕD.
Решение:
Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.
Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.
ЕС=ВС–ВЕ=17–12=5.
Рассмотрим ∆ЕСD. Т.к. АВСD прямоугольник, то угол С=900, и ∆ЕСD прямоугольный.
Тогда по т.Пифагора ЕD2=ЕC2+СD2. Получаем:
.
Вариант пятнадцатого задания 2019 года(3)
В треугольнике АВС угол С равен 900, АВ=25, АС=24. Найдите cos B.
Алгоритм выполнения
- По т.Пифагора находим величину катета ВС.
- По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.
Решение:
Из прямоугольного ∆АВС по т.Пифагора имеем: АВ2=АС2+ВС2.
Отсюда: .
.
Вариант пятнадцатого задания 2019 года(4)
В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.
Алгоритм выполнения
- Из вершины В проводим высоту BD к основанию ∆АВС. Получаем прямоугольного ∆ADB.
- Из ∆ADB находим катет ВD, используя sin A.
- Находим АD из ∆ADB по т.Пифагора. Далее определяем АС как 2AD.
- Находим площадь ∆АВС по формуле S=ah/2.
Решение
В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.
Из ∆ADB по т.Пифагора имеем: AB2=AD2+BD2 →
Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.
Площадь ∆АВС равна: .
Вариант пятнадцатого задания 2019 года(5)
В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.
Алгоритм выполнения
- Доказываем, что ∆АВМ прямоугольный.
- Из ∆АВМ, используя формулу-определение для тангенса, находим АМ.
- Из ∆АВМ по т.Пифагора находим АВ.
Решение:
Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.
Из ∆АВМ имеем:
.
Из ∆АВМ по т.Пифагора АВ2=АМ2+ВМ2 →
Вариант пятнадцатого задания 2019 года(6)
В треугольнике АВС угол В равен 1200. Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.
Алгоритм выполнения
- Определяем величину угла АВМ.
- Доказываем, что ∆АМВ прямоугольный.
- Находим АВ, используя формулу-определение для косинуса.
Решение:
По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет
1200:2=600.
Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.
В прямоугольного ∆АМВ: .
Отсюда:
.
Вариант пятнадцатого задания 2019 года(7)
В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.
Алгоритм выполнения
- Доказываем, что ∆АКВ прямоугольный.
- Из ∆АКВ по т.Пифагора находим АК.
- Находим АС как 2АК.
- Находим МN как среднюю линию.
Решение:
Т.к. ∆АВС равнобедренный, то медиана ВК, опущенная на основание АС, является и высотой. Поэтому угол АКВ равен 900, и ∆АКВ прямоугольный.
Из прямоугольного ∆АКВ по т.Пифагора АВ2=АК2+ВК2.
Отсюда:
.
Поскольку ВК медиана, то АС=2АК=2·24=48.
Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).
Значит, MN=AC:2=48:2=24.
Вариант пятнадцатого задания 2019 года(8)
В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.
Алгоритм выполнения
- Находим длину отрезков АМ и МС как половину от АС.
- Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС.
- Находим АН как сумму АМ и МН.
Решение:
Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.
По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.
АН=АМ+МН=28+14=42.
Вариант пятнадцатого задания 2019 года(9)
Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.
Алгоритм выполнения
- Находим величину 2-го (неизвестного) катета по т.Пифагора.
- Определяем площадь треугольника как полупроизведение катетов.
Решение:
Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.
По т.Пифагора a2+b2=c2. Отсюда:
.
Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.
Вариант пятнадцатого задания 2019 года(10)
В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.
Алгоритм выполнения
- Используя формулу для площади треугольника S=ah/2 и зная величину а (по условию – основание АС), найдем высоту ∆АВС. Отображаем высоту на рисунке, обозначив ее пересечение с основанием буквой К.
- Доказываем, что высота ВК является и его медианой. Отсюда находим АК.
- Из ∆АКВ по т.Пифагора находим АВ.
Решение:
Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.
Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.
Из прямоугольного ∆АКВ по т.Пифагора АВ2=АК2+ВК2. Получаем:
.
spadilo.ru

Leave A Comment