Двоичный калькулятор
+−×÷
Количество знаков после запятой в ответе
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100
Что такое двоичная система счисления
Двоичная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в двоичной системе счисления используется две цифры 0 и 1. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 10012 или 10001012.
Как складывать, вычитать, делить и умножать числа в двоичной системе счисления
Для того чтобы выполнить математическую операцию с двоичными числами необходимо:
- Перевести эти числа в десятичную систему счисления.

- Выполнить математическую операцию (сложение, вычитание, умножение, деление) с десятичными числами.
- Перевести полученный результат в двоичную систему счисления.
Приведем пример на сложение, допустим необходимо сложить два числа 110 и 101.
Первым делом переведем эти числа в десятичную систему счисления:
Переведем число 1102 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе с права налево, начиная с нуля
| Позиция в числе | 2 | 1 | 0 |
| Число | 1 | 1 | 0 |
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число 110
1102 = 1 ⋅ 22 + 1 ⋅ 21 + 0 ⋅ 20 = 610
Переведем число 1012 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе с права налево, начиная с нуля
| Позиция в числе | 2 | 1 | 0 |
| Число | 1 | 0 | 1 |
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число 1012 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
1012 = 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 510
Теперь сложим получившиеся десятичные числа 610 + 510 = 1110 и переведем ответ в двоичную систему счисления
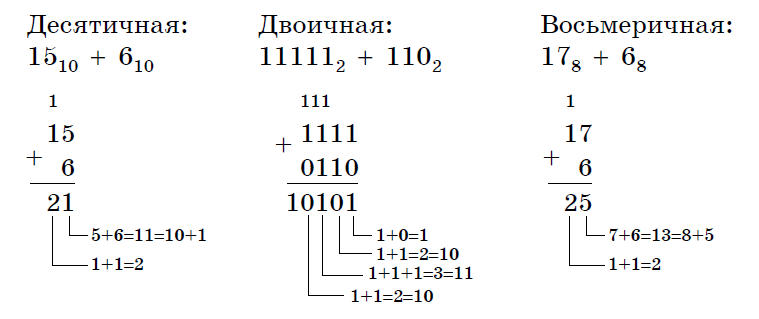 В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.| 11 | : | 2 | = | 5 | остаток: 1 |
| 5 | : | 2 | = | 2 | остаток: 1 |
| 2 | : | 2 | = | 1 | остаток: 0 |
| 1 | : | 2 | = | 0 | остаток: 1 |
1110 = 10112
110 + 101 = 10112
Вычитание двоичных чисел выполняется аналогичным образом, если бы нам было необходимо из числа 110 вычесть число 101, то также как в примере на сложения необходимо перевести эти числа в десятичную систему счисления, получим 1102 = 610 и 1012 = 510. Затем произведем вычитание 610 – 510 = 110. И далее переведем число 1 в двоичную систему счисления
Переведем число 110 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю.
| 1 | : | 2 | = | 0 | остаток: 1 |
110 – 101 = 1
Умножение и деление также, как и сложение и вычитание требует сначала перевести числа из двоичной системы счисления в десятичную, а затем выполнить математические вычисления с последующим переводом результата в двоичное число.
Приведем пример, возьмём два двоичных числа 110 и 101 из предыдущего примера, (так будет удобнее, так как мы уже перевели их в десятичную систему счисления) и выполним умножение данных чисел.
Итак 1102 = 610 и 1012 = 510, тогда 610 × 510 = 3010. И далее переведем число 3010 в двоичную систему счисления
Переведем число 3010 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.
| 30 | : | 2 | = | 15 | остаток: 0 |
| 15 | : | 2 | = | 7 | остаток: 1 |
| 7 | : | 2 | = | 3 | остаток: 1 |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
110 × 101 = 111102
И в завершении, чтобы научиться делить двоичные числа разделим 110 на 101.
1102 = 610 и 1012 = 510, тогда 610 : 510 = 1.210.
Переведем число 1.210 в двоичную систему счисления:
Переведем целую часть 1 числа 1.210 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.
| 1 | : | 2 | = | 0 | остаток: 1 |
110 = 12
Переведем дробную часть 0.2 числа 1.210 в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
0.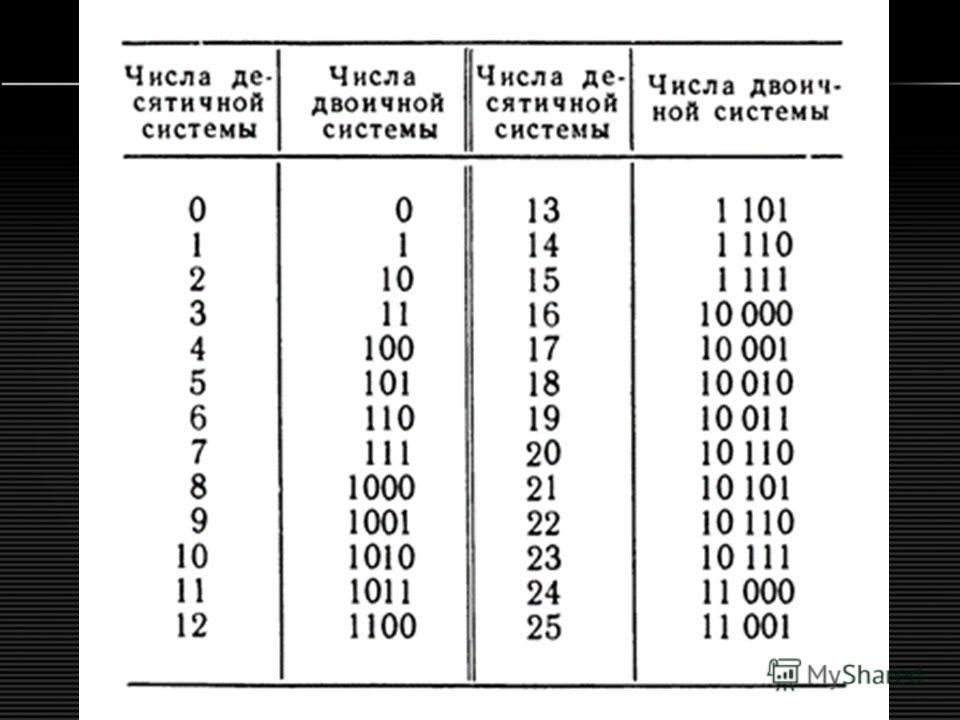 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
0.210 = 0.001100112
1.210 = 1.001100112
Нужно сразу оговориться, что, умножая дробную часть на 2 мы все равно не получим ноль, так как десятичная дробь 1.2 в двоичной системе бесконечная. Поэтому, для примера оставим 8 знаков после запятой. Получим 110 : 101 = 1.00110011.2
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.
Двоичная система счисления | Презентация к уроку:
Слайд 1
Двоичная система счисления Система счисления. Часть2
Слайд 2
Историческая справка 1703г. – великий немецкий математик Лейбниц ввел в математику двоичную систему счисления. 1936-1938гг. – американский инженер и математик Клод Шеннон предложил использовать двоичную систему счисления для конструирования электрических схем. В двоичной системе счисления для записи чисел используются всего две цифры: 0 и 1, q = 2 .
– великий немецкий математик Лейбниц ввел в математику двоичную систему счисления. 1936-1938гг. – американский инженер и математик Клод Шеннон предложил использовать двоичную систему счисления для конструирования электрических схем. В двоичной системе счисления для записи чисел используются всего две цифры: 0 и 1, q = 2 .
Слайд 3
Перевод чисел из двоичной системы счисления в десятичную ( N 2 N 10 ) ( через развернутую форму записи числа ) Пример: 1011,01 2 =1*2 3 +0*2 2 +1*2 1 +1*2 0 +0*2 -1 +1*2 -2 =8+2+1+ ¼ =11 ¼ . Таблица степеней числа 2 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7 2 8 2 9 2 10 ___________________________________________________________________________________________________________________ 2 4 8 16 32 64 128 256 512 1024 Задание 8: переведите в десятичную систему счисления 10110,011 2 110101,1 2 10101,101 2
Слайд 4
Перевод целых чисел из десятичной системы счисления в двоичную ( N 10 N 2 ) Способ – деление на основание системы счисления 22 10 =10110 2 Задание 9: переведите десятичные числа 27; 35; 54; 66 в двоичную систему счисления
Слайд 5
Арифметические операции с двоичными числами. Рассмотрим правила выполнения арифметических операций над одноразрядными числами. Представим их в виде таблиц. Правило сложения Правило вычитания Правило умножения 0+0=0 0-0=0 0*0=0 0+1=1 1-0=1 0*1=0 1+0=1 1-1=0 1*0=0 1+1=10 0-1=-1 1*1=1 1+1+1=11
Рассмотрим правила выполнения арифметических операций над одноразрядными числами. Представим их в виде таблиц. Правило сложения Правило вычитания Правило умножения 0+0=0 0-0=0 0*0=0 0+1=1 1-0=1 0*1=0 1+0=1 1-1=0 1*0=0 1+1=10 0-1=-1 1*1=1 1+1+1=11
Слайд 6
Арифметические операции с двоичными числами. Примеры. 1. 1010+10101=11111 1010 10101 11111 2. 10101-1010=1011 10101 1010 1011 3. 10111*11=1000101 10111 11 10111 10111 1000101
Слайд 7
Упражнения Произведите сложение двоичных чисел: 111+101; 11011+1110 Выполните вычитание двоичных чисел: 111-101; 11011-01110 Умножьте двоичные числа: 111*101; 11011*1110
Слайд 8
Перевод десятичных дробей в двоичную систему счисления ( N 10 N 2 ) (умножением на 2) Пример: 0,5625 10 = N 2 = 0,1001 2 0, 5625 2 1 1250 2 0 2500 2 0 5000 2 1 0000 Задание 10: переведите десятичные дроби в двоичную систему счисления с точностью до 6 знаков после запятой: 0,7 10 0,4622 10 0,5198 10 0,5803 10
Слайд 9
Перевод смешанных чисел из десятичной системы счисления в двоичную Алгоритм перевода: 1) перевести целую часть; 2) перевести дробную часть; 3) сложить полученные результаты. Пример : перевести 17,25 10 в двоичную систему счисления. Решение: 17 10 = 10001 2 0,25 10 = 0,01 2 17,25 10 = 10001,01 2 Задание 11: переведите в двоичную систему счисления числа: 40,5 10 31,75 10 124,25 10
Пример : перевести 17,25 10 в двоичную систему счисления. Решение: 17 10 = 10001 2 0,25 10 = 0,01 2 17,25 10 = 10001,01 2 Задание 11: переведите в двоичную систему счисления числа: 40,5 10 31,75 10 124,25 10
Слайд 10
Упражнения: Переведите в двоичную запись десятичные числа: 17; 48; 193; 513 используя правило деления на 2. 2. Переведите в десятичную запись двоичные числа: 1001; 10111; 1011000; 10111011
Слайд 11
Основной недостаток двоичной системы – ее громоздкость. Более компактной является восьмеричная система счисления с основанием 8. В ней используется восемь символов 0,1,2,3,4,5,6,7, заимствованных из десятичной. Для представления двоичных чисел восьмеричными цифрами разряды двоичного числа объединяют в группы по три (триады), начиная с младшего разряда, а дробную часть, со старшего и каждую триаду преобразуют в восьмеричный эквивалент: 11111101 2 = 011 111 101 =375 =3*8 2 +7*8 1 +5*8 0 =253 Восьмеричная и шестнадцатиричная система счисления.
Слайд 12
Если для образования триад не хватает разрядов, то добавляют незначащие нули. Еще более компактную форму записи двоичных чисел дает шестнадцатиричная система счисления, в которой используется 16 символов: 0,1,2,3,4,5,6,7,8,9,А,В,С, D ,Е, F . Десять символов заимствованы из десятичной системы, а в качестве недостающих использованы буквы латинского алфавита: А-10, В-11, С-12, D -13, Е-14, F -15. Процедура преобразования двоичного числа в шестнадцатиричное довольно проста. Двоичное число разбивается на четверки (тетрады),начиная с младшего разряда, а дробная часть со старшего и каждая тетрада заменяется шестнадцатиничным символом: 10101011111101 =0010 1010 1111 1101 =2А FD 1111000101111011 2 = Восьмеричная и шестнадцатиричная система счисления.
Еще более компактную форму записи двоичных чисел дает шестнадцатиричная система счисления, в которой используется 16 символов: 0,1,2,3,4,5,6,7,8,9,А,В,С, D ,Е, F . Десять символов заимствованы из десятичной системы, а в качестве недостающих использованы буквы латинского алфавита: А-10, В-11, С-12, D -13, Е-14, F -15. Процедура преобразования двоичного числа в шестнадцатиричное довольно проста. Двоичное число разбивается на четверки (тетрады),начиная с младшего разряда, а дробная часть со старшего и каждая тетрада заменяется шестнадцатиничным символом: 10101011111101 =0010 1010 1111 1101 =2А FD 1111000101111011 2 = Восьмеричная и шестнадцатиричная система счисления.
Слайд 13
Таблица двоичных кодов десятичных и шестнадцатеричных 1 2 3 4 5 6 7 8 9 A B C D E F 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
Слайд 14
1111000101111011 2 = F17B 16 Ответ
Слайд 15
1. выполните сложение и проведите проверку 11010101 2 +1110 2 2. выполните вычитание и результат переведите в десятичную СС: 110101110 2 -10111111 2 3. выполните умножение и результат переведите в десятичную СС: 111100 2 *100100 2 4. переведите из 10-ой СС в 2-ичную, 8 –ричную,16- ричную СС числа: 126, 533 5. запишите в развернутом виде (по формуле) числа: 657; 15А12 Самостоятельная работа
выполните умножение и результат переведите в десятичную СС: 111100 2 *100100 2 4. переведите из 10-ой СС в 2-ичную, 8 –ричную,16- ричную СС числа: 126, 533 5. запишите в развернутом виде (по формуле) числа: 657; 15А12 Самостоятельная работа
Калькулятор двоичных сложений
Автор Rita Rain
Отзыв от Dominik Czernia, PhD и Steven Wooding
Последнее обновление: 12 февраля 2023 г.
Содержание:- Что такое двоичная система?
- Как пользоваться калькулятором двоичного сложения?
- Каковы правила двоичного сложения?
- Двоичная сумма: сложение двоичных чисел
- Часто задаваемые вопросы
Этот калькулятор двоичного сложения суммирует числа, представленные нулями и единицами (вы можете сгенерировать их с помощью двоичного преобразователя).
Прочтите этот текст, чтобы узнать больше о языке компьютеров и о том, как складывать двоичные числа без двоичного математического калькулятора. Как только вы освоите сложение двоичных чисел, вы можете научиться вычитать их с помощью нашего калькулятора двоичного вычитания.
Как только вы освоите сложение двоичных чисел, вы можете научиться вычитать их с помощью нашего калькулятора двоичного вычитания.
🔎 Помимо суммирования, вы можете вычитать, умножать и делить эти типы чисел с помощью нашего двоичного калькулятора.
Что такое двоичная система?
Чтобы понять двоичную систему, давайте сначала посмотрим на более привычную десятичную систему .
В десятичной системе мы используем десять цифр (0-9) и, в зависимости от их положения, умножаем их на соответствующие степени десяти. Например, разложим число 1934 :
1934 = 1000 + 900 + 30 + 4
1934 = 1×1000 + 9×100 + 3×10 + 4×1
1934 = 1×10³ + 9×10² + 3×10¹ + 4×10⁰
Если бы мы составили формулу для 4-значного числа, она могла бы выглядеть так:
Символ «a» здесь представляет цифру от 0 до 9.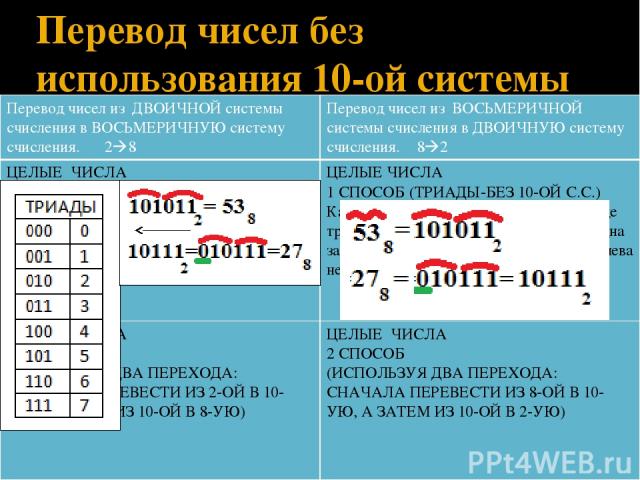 Индекс рядом с «a» обозначает место цифры (мы счет от 0, справа налево).
Индекс рядом с «a» обозначает место цифры (мы счет от 0, справа налево).
Теперь, , двоичная система работает аналогично, но мы используем только две цифры и умножаем их на степени двойки. Таким образом, формула будет следующей:
а₃а₂а₁а₀ = а₃ × 2³ + а₂ × 2² + а₁ × 2¹ + а₀ × 2⁰
В этой системе мы умножаем две цифры (0 и 1) на 2 в степени, соответствующей на свое место в номере.
Например, мы запишем «9» как «1001», потому что:
1001 = 1 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰ = 8 + 0 + 0 + 1 = 9
Аналогично:
«2» в двоичном формате равно «10», потому что 1 × 2¹ + 0 × 2⁰ = 2
«3» в двоичном формате равно «11», потому что 1 × 2¹ + 1 × 2⁰ = 2 + 1 = 3
«4» в двоичном формате равно «100», потому что 1 × 2² + 0 × 2¹ + 0 × 2⁰ = 4
Как пользоваться калькулятором двоичного сложения?
Чтобы двоичный математический калькулятор выполнял сложение двоичных чисел, выполните следующие действия:
Введите первое число в первое поле калькулятора двоичного сложения.
 Помните, что для используйте только нули и единицы . Вам не нужно вводить ведущие нули, например, для «00001111» вы можете ввести просто «1111».
Помните, что для используйте только нули и единицы . Вам не нужно вводить ведущие нули, например, для «00001111» вы можете ввести просто «1111».Введите второе двоичное число во второй строке.
Калькулятор двоичного сложения отобразит результат в третьем поле .
В расширенном режиме
Каковы правила двоичного сложения?
Существует четыре основных правила двоичного сложения:
-
0 + 0 = 0 -
0 + 1 = 1 -
1 + 0 = 1 -
1 + 1 = 10(запишите «0» в столбце и перенесите 1 на следующий бит)
Приведенные выше уравнения работают так же, как и в десятичной системе, только здесь вам нужно перевести 1, когда сумма превышает 1 (в десятичной системе мы делаем это, когда она превышает 9).
Двоичная сумма: Сложение двоичных чисел
Как складывать двоичные числа? Вы всегда можете преобразовать двоичные числа в десятичные, сложить их, как обычно, и восстановить результат в двоичной форме.
Другой способ состоит в том, чтобы использовать приведенные выше правила двоичного сложения и выполнить длинное сложение . Давайте посмотрим на эту двоичную сумму:
перенос: 1 1 ___________ 1001 + 1101 ___________ =10110\text{carry:} \ \ \ \ 1\ \ \ \ 1 \\\ \_\_\_\_\_\_\_\_\_\_\_ \\\ \\\\\\\\\\\\\1001\\\ \\\\\\\+\\\1101\\\ \_\_\_\_\_\_\_\_\_\_\_ \\\ \ \ \ \ \ \ \ = 10110carry: 1 1 ___________ 1001 + 1101 ___________ =10110
🔎 Наш калькулятор длинных сложений может помочь понять описанную выше операцию.
В первом столбце справа 1 + 1 дает нам 2, поэтому нам нужно перенести 1 во второй столбец (1, помещенный во второй столбец, равен двум, потому что 1 × 2¹ = 2) и записать 0 в первый столбец. Во втором столбце
Во втором столбце 0 + 0 = 0 , поэтому мы просто записываем 1, которую перенесли. В третьем столбце справа 0 + 1 = 1 . В четвертом столбце у нас есть 1 + 1 , так что снова пишем 0 и переносим 1. Так как добавить больше нечего, пишем «1» в начале результата (слева).
Приложения двоичного сложения присутствуют во многих методах исправления и обнаружения ошибок, таких как бит четности и расстояние Хэмминга!
Часто задаваемые вопросы
Что такое двоичное сложение?
Двоичное сложение — это операция суммирования чисел в двоичной форме . Он работает как «обычное» (десятичное) сложение, но в числе могут быть только нули и единицы в качестве цифр, поэтому, если сумма превышает 1, вы должны перенести 1 в следующий бит. Например, 101 + 101 = 1010 .
Как решить двоичное сложение?
Чтобы решить двоичное сложение, выполните длинное сложение — расположите числа вертикально и добавьте цифры в столбцы, идущие справа налево.

Если сумма в столбце равна 2, перенести 1 в следующий столбец (слева). Если сумма равна 1 или 0, запишите ее и перейдите к следующему столбцу.
Продолжайте таким образом, пока не просуммируете все столбцы (включая переносимые числа).
Как обнаружить переполнение при двоичном сложении?
Проверить, имеет ли смысл сумма двоичных чисел. Если сумма двух отрицательных чисел положительна или сумма двух положительных чисел равна , что-то не так. Эта ошибка означает, что сумма переполняла — то есть двоичное представление результата не помещалось в выделенное количество бит.
Рита Рейн
Посмотреть 11 похожих бинарных калькуляторов 1️0️
Двоичное делениеДвоичная дробьДвоичное умножение… Еще 8
Калькулятор двоичного вычитания
Создано Wojciech Sas, PhD 0003 Содержание:
- Вычитание двоичного числа
- Методы вычитания двоичных чисел
- Как пользоваться калькулятором двоичного вычитания?
- Как мы представляем знак в двоичных числах?
- Часто задаваемые вопросы
Этот калькулятор двоичного вычитания поможет вам понять, как вычитать двоичные числа. Здесь вы можете найти описания двух основных методов, которые имеют дело с вычитанием двоичных чисел, а именно Метод заимствования и Метод дополнения . В конце также есть короткое примечание о различных представлениях двоичных чисел со знаком и без знака.
Здесь вы можете найти описания двух основных методов, которые имеют дело с вычитанием двоичных чисел, а именно Метод заимствования и Метод дополнения . В конце также есть короткое примечание о различных представлениях двоичных чисел со знаком и без знака.
Если вам нужно сложить числа, давайте попробуем наш калькулятор двоичного сложения.
Вычитание двоичных чисел
Вычитание двоичных чисел практически такое же, как и для десятичной, шестнадцатеричной или любой другой системы счисления.
Для пояснения: двоичные числа — это значения, содержащие только два типа цифр, 0 или 1. Каждая цифра относится к последовательным степеням 2 и к тому, следует ли умножать ее на 0 или 1. Например, 13 в десятичной записи эквивалентно 1101 в двоичной записи, потому что 13 = 8 + 4 + 1 или 13 = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ в экспоненциальном представлении. Используйте двоичный преобразователь всякий раз, когда вам нужно переключиться между десятичной и двоичной записью.
Используйте двоичный преобразователь всякий раз, когда вам нужно переключиться между десятичной и двоичной записью.
Итак, как вычитать двоичные числа, например, 1101 — 110 ? Мы всегда можем преобразовать эти значения в десятичные числа, классически вычесть их, а затем снова преобразовать в двоичную форму:
1101₂ — 110₂ = 13₁₀ — 6₁₀ = 7₁₀ = 111₂
Здесь 900 23 ₂ обозначает двоичное число, и ₁₀ — десятичное число. Пока количество цифр относительно невелико, мы можем сделать это вручную. Для длинных чисел это становится довольно сложно. А что, если мы хотим вычесть большее число из меньшего ? Вот где калькулятор двоичного вычитания пригодится! Давайте перейдем к следующему разделу, чтобы узнать о различных методах решения этих проблем.
Методы вычитания двоичных чисел
В этой части мы опишем два метода вычитания двоичных чисел, Метод заимствования и метод дополнения . Есть еще несколько приемов, но эти два являются наиболее распространенными и помогают лучше понять проблему.
Есть еще несколько приемов, но эти два являются наиболее распространенными и помогают лучше понять проблему.
Метод заимствования — все, что вам нужно сделать, это выровнять числа, как при обычном десятичном вычитании. Процедура почти такая же! Единственная разница в том, что вы оперируете только двумя цифрами, а не десятью. Вам нужно вычитать цифры в том же столбце, соблюдая следующие правила:
-
1 - 0 = 1; -
1 - 1 = 0; -
0 - 0 = 0; и -
0 - 1 = 1, что на самом деле происходит от10 - 1 = 1, поскольку вы заимствуете1из ближайшей цифры слева, и после всего этого1, которое вы заимствовали, становится 9012 3 0 .
-
Метод дополнения – процесс состоит из нескольких шагов:
- Выровняйте числа как обычно;
- Заполните второе число ведущими
нулямитак, чтобы оба значения имели одинаковое количество цифр; - Заменить второе число его дополнением до двух ;
- Сложите эти два двоичных числа;
- Удалить из результата
1, так как будет на одну цифру больше, чем нужно; и - Вот оно! Оставшаяся часть – конечный результат.

Если вы хотите увидеть пошаговое решение вашей проблемы с помощью метода дополнения, выберите «Да» внизу нашего калькулятора двоичного вычитания. Для более подробного объяснения также проверьте наш калькулятор дополнения до двух.
Кстати, знаете ли вы, что концепция двоичного вычитания довольно распространена в некоторых частях набора инструментов для разработчиков? Например, команда chmod является одной из них.
Как использовать калькулятор двоичного вычитания?
Давайте посмотрим, как вычесть два двоичных числа, например, 110 0101 — 1000 1100 . Это довольно сложно, потому что второе число имеет больше цифр, чем первое, поэтому мы собираемся вычесть большее число из меньшего .
Есть умный способ обойти эту задачу. Мы можем использовать тождество a — b = -(b — a) , поэтому мы собираемся изменить порядок вычитания и добавить знак минус в конце . Другими словами, мы оцениваем абсолютное значение и в конце концов присваиваем ему знак минус. Воспользуемся методом дополнения:
Воспользуемся методом дополнения:
В обратном порядке получаем 1000 1100 — 110 0101 .
Заполните второе значение одним ведущим нулем, 1000 1100 — 0110 0101 .
Найдите дополнение второго числа – поменяйте местами цифры ( 0→1, 1→0 ) и добавьте 1, 0110 0101 → 1001 1011 .
Сложите первое число и дополнение ко второму вместе, 1000 1100 + 1001 1011 = 1 0010 0111 .
Удалить ведущие 1 и все соседние 0 , 1 0010 0111 → 10 0111 .
Не забудьте добавить знак минус, чтобы результат стал -10 0111 .
Окончательный результат вычитания этих двоичных чисел: 110 0101 — 1000 1100 = -10 0111 .
Мы также можем преобразовать значения в десятичные числа, чтобы подтвердить вычисления: 110 0101₂ — 1000 1100₂ = 101₁₀ — 140₁₀ = -39₁₀ = -10 0111₂ .
 Замечательный!
Замечательный!
Прежде чем производить какие-либо вычисления, мы должны принять во внимание одну важную вещь — представление чисел в двоичном коде , особенно знак . Мы объясним это в следующем разделе.
Существует как минимум три метода:
Используйте знак минус (
-) как мы обычно делаем с десятичными числами. В 8-битном коде5в двоичном виде равно 9.0123 0000 0101 , а-5это-0000 0101.Используйте первую цифру в качестве знака, обычно 0 для положительного числа и 1 для отрицательного . Теперь
-5становится1000 0101.Представьте отрицательное число как дополнение к положительному , поэтому
-5теперь равно1111 1011. Первая цифра по-прежнему указывает на знак числа.
Наш калькулятор двоичного вычитания использует знак минус , т.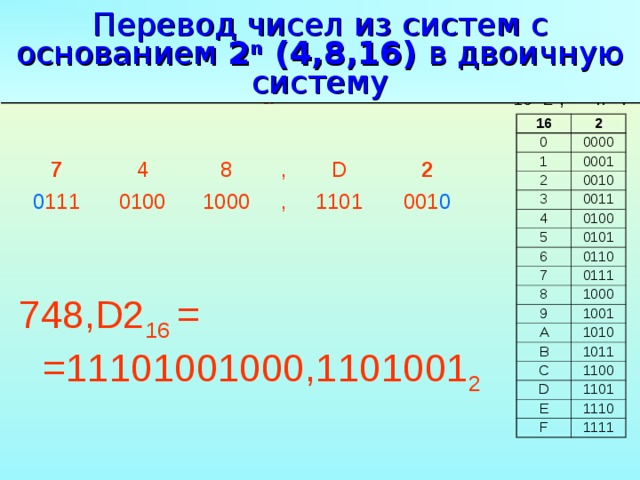 е. 1-й метод. Всякий раз, когда вы копируете значение в наш инструмент, убедитесь, что вы вводите число, используя соответствующее представление, например, если оно имеет первую цифру, представляющую знак, замените
е. 1-й метод. Всякий раз, когда вы копируете значение в наш инструмент, убедитесь, что вы вводите число, используя соответствующее представление, например, если оно имеет первую цифру, представляющую знак, замените 1 на - или оставьте 0 как есть.
Часто задаваемые вопросы
Как вычитать двоичные числа?
Существует как минимум три метода вычитания двоичных чисел:
- Метод заимствования — выровняйте числа и вычтите путем заимствования, как всегда, помня, что
0 - 1разрешается в1. - Метод дополнения — идея состоит в том, чтобы заменить вычитаемое число его дополнением и добавить два числа. Не забудьте опустить начальный
1из результата! - Метод преобразования — преобразуйте двоичные числа в десятичные числа , вычтите, а затем преобразуйте их обратно в двоичные.
 Эффективен для небольших количеств.
Эффективен для небольших количеств.
Как найти дополнение двоичного числа?
Чтобы определить дополнение двоичного числа в 8-битной системе, выполните следующие действия:
- Убедитесь, что ваш двоичный код содержит 8 цифр . Если их меньше, добавьте несколько ведущих нулей.
- Замените каждую цифру на напротив :
0→1и1→0. - Увеличить число на
1. Вот и все!
Каков результат двоичного вычитания 101 — 11?
101 - 11 = 10 . Действительно, используя метод заимствования, мы видим, что последняя цифра результата должна быть 1 - 1 = 0 . Затем для выполнения 0 - 1 нам нужно одолжить 1 : 0 - 1 = 10 - 1 = 1 . И все: так как мы заимствовали, цифр не осталось. Следовательно, результат равен 10 .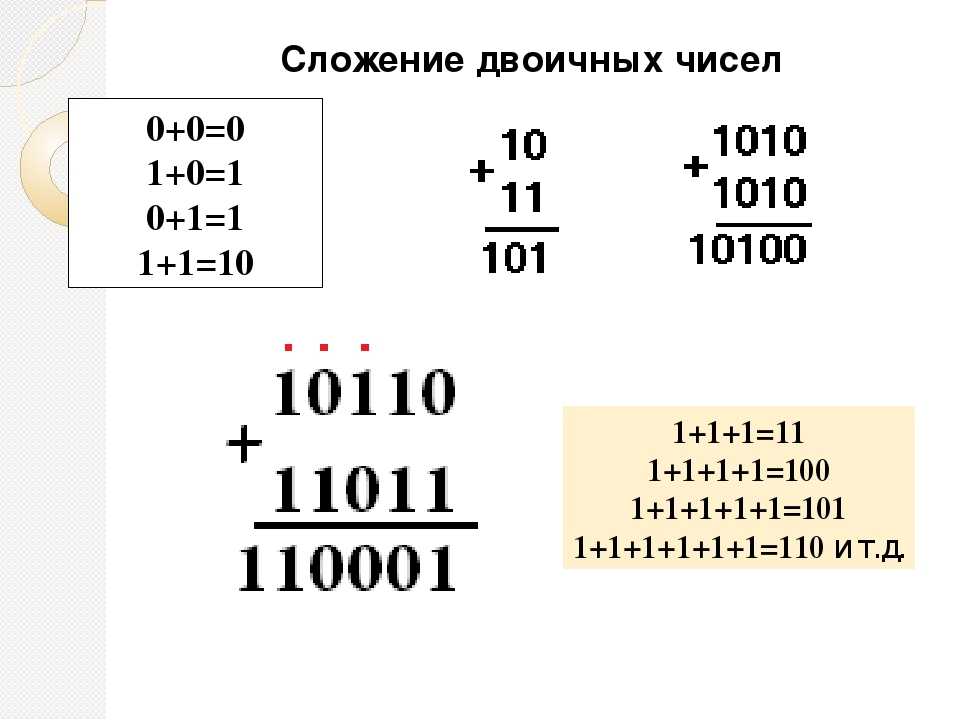


 Помните, что для используйте только нули и единицы . Вам не нужно вводить ведущие нули, например, для «00001111» вы можете ввести просто «1111».
Помните, что для используйте только нули и единицы . Вам не нужно вводить ведущие нули, например, для «00001111» вы можете ввести просто «1111».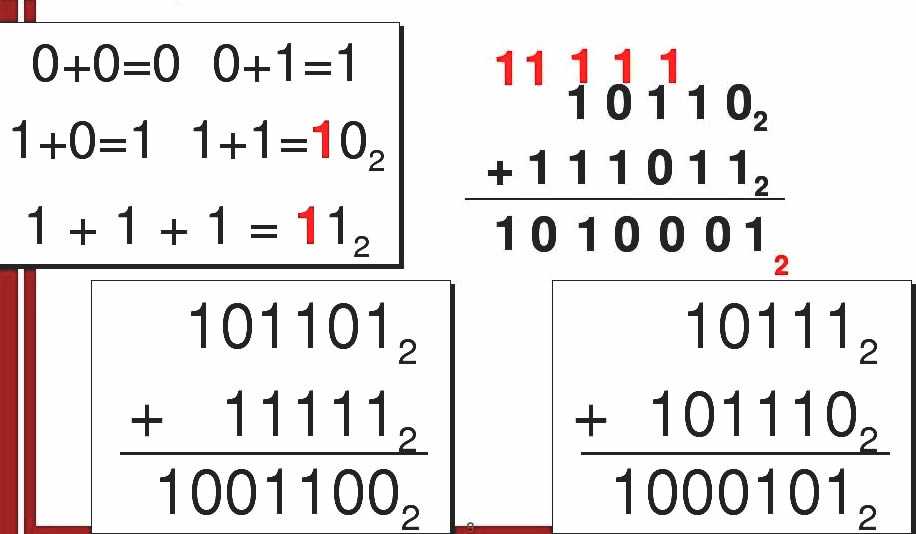

 Замечательный!
Замечательный!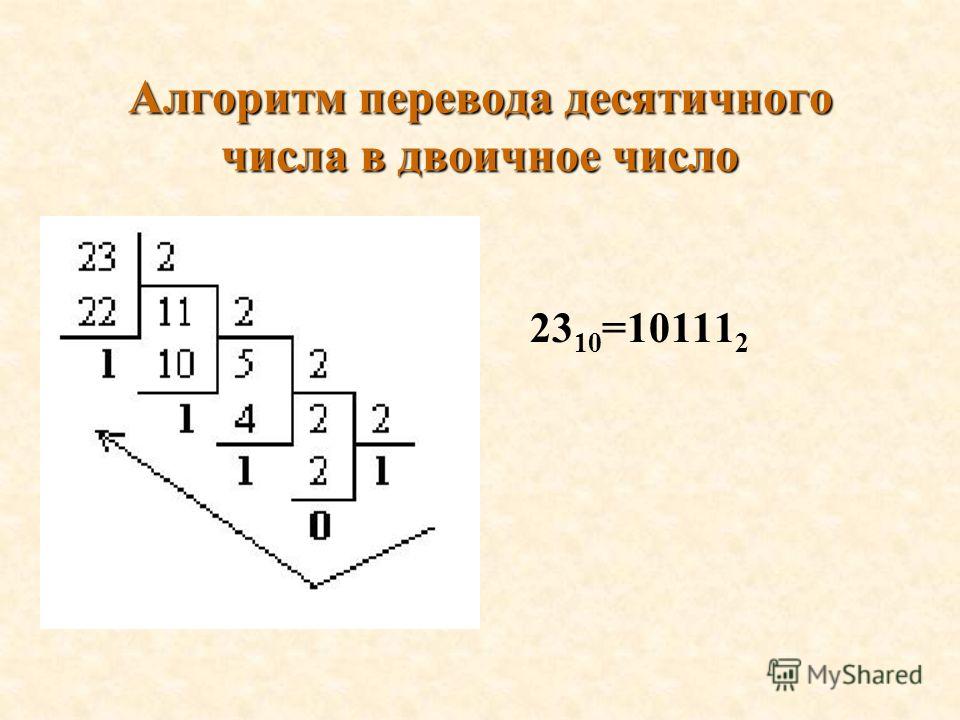 Эффективен для небольших количеств.
Эффективен для небольших количеств.
Leave A Comment