05028 — Тренировочный вариант ОГЭ (ГИА) № 144 по математике от Ларина 2017 года
Ответы
Ответы к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Решения
Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 683 | 110 | Загрузок |
|---|---|---|---|
| Добавил | Yagubova | 13.05.2017 | Дата |
| День | Суббота | 21:51 | Время |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: Александр Александрович Ларин
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Оценивание
| № задания | 1-20 | 21-26 | Всего |
|---|---|---|---|
| Баллы | 1 | 2 | 32 |
Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Всего в работе 26 заданий. Модуль «Алгебра» содержит 11 заданий: в части 1 — восемь заданий; в части 2 — три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания. Модуль «Реальная математика» содержит семь заданий: все задания этого модуля — в части 1.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 2, 3, 8, 14 записываются в виде одной цифры, которая соответствует номеру правильного ответа. Эту цифру запишите в поле ответа в тексте работы.
Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите её в десятичную. В случае записи неверного ответа на задания части 1 зачеркните его и запишите рядом новый.
При выполнении работы Вы можете воспользоваться справочными материалами.
Баллы, полученные за верно выполненные задания, суммируются. Для успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов, из них не менее 3 баллов в модуле «Алгебра», не менее 2 баллов в модуле «Геометрия» и не менее 2 баллов в модуле «Реальная математика». За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания оцениваются в 2 балла.
Файлы критерий доступны
для бесплатного скачивания
только зарегистрированным
пользователям проекта!
Справочные материалы
Загрузка формул…
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Решения ОГЭ (ГИА) alexlarin.net | ЕГЭ решебник
Здесь представлены решения тренировочных вариантов ОГЭ (ГИА) по математике с сайта alexlarin.net, публикуемые еженедельно каждую среду.
Решение задач тренировочного варианта 202
вариант от 26 декабря 2018 г.
Решение задач тренировочного варианта 200
вариант от 12 декабря 2018 г.
Решение задач тренировочного варианта 199
вариант от 05 декабря 2018 г.
Решение задач тренировочного варианта 198
вариант от 28 октября 2018 г.
Решение задач тренировочного варианта 193
вариант от 24 октября 2018 г.
Решение задач тренировочного варианта 191
вариант от 11 октября 2018 г.
Решение задач тренировочного варианта 189
вариант от 26 сентября 2018 г.
Решение задач тренировочного варианта 188
вариант от 19 сентября 2018 г.
Решение задач тренировочного варианта 187
вариант от 12 сентября 2018 г.
Решение задач тренировочного варианта 184
вариант от 16 мая 2018 г.
Решение задач тренировочного варианта 183
вариант от 09 мая 2018 г.
Решение задач тренировочного варианта 182
вариант от 02 мая 2018 г.
Решение задач тренировочного варианта 181
вариант от 25 апреля 2018 г.
Решение задач тренировочного варианта 180
вариант от 18 апреля 2018 г.
Решение задач тренировочного варианта 179
вариант от 11 апреля 2018 г.
Решение задач тренировочного варианта 178
вариант от 04 апреля 2018 г.
Решение задач тренировочного варианта 177
вариант от 28 марта 2018 г.
Решение задач тренировочного варианта 176
вариант от 21 марта 2018 г.
Решение задач тренировочного варианта 175
вариант от 14 марта 2018 г.
Решение задач тренировочного варианта 173
вариант от 28 февраля 2018 г.
Решение задач тренировочного варианта 172
вариант от 21 февраля 2018 г.
Решение задач тренировочного варианта 171
вариант от 14 февраля 2018 г.
Решение задач тренировочного варианта 170
вариант от 07 февраля 2018 г.
Решение задач тренировочного варианта 169
Решение задач тренировочного варианта 168
вариант от 24 января 2018 г.
Решение задач тренировочного варианта 167
вариант от 17 января 2018 г.
Решение задач тренировочного варианта 166
вариант от 10 января 2018 г.
Решение задач тренировочного варианта 165
вариант от 03 января 2018 г.
Решение задач тренировочного варианта 164
вариант от 27 декабря 2017 г.
Решение задач тренировочного варианта 163
вариант от 20 декабря 2017 г.
Решение задач тренировочного варианта 162
вариант от 13 декабря 2017 г.
Решение задач тренировочного варианта 161
вариант от 06 декабря 2017 г.
Решение задач тренировочного варианта 160
вариант от 29 ноября 2017 г.
Решение задач тренировочного варианта 159
вариант от 22 ноября 2017 г.
Решение задач тренировочного варианта 158
вариант от 15 ноября 2017 г.
Решение задач тренировочного варианта 157
вариант от 08 ноября 2017 г.
Решение задач тренировочного варианта 156
вариант от 01 ноября 2017 г.
Решение задач тренировочного варианта 155
вариант от 25 октября 2017 г.
Решение задач тренировочного варианта 154
вариант от 18 октября 2017 г.
Решение задач тренировочного варианта 153
вариант от 11 октября 2017 г.
Решение задач тренировочного варианта 152
вариант от 04 октября 2017 г.
Решение задач тренировочного варианта 151
вариант от 27 сентября 2017 г.
Решение задач тренировочного варианта 150
вариант от 20 сентября 2017 г.
Решение задач тренировочного варианта 149
вариант от 13 сентября 2017 г.
Решение задач тренировочного варианта 148
вариант от 06 сентября 2017 г.
Решение задач тренировочного варианта 145
вариант от 17 мая 2017 г.
Решение задач тренировочного варианта 144
вариант от 10 мая 2017 г.
Решение задач тренировочного варианта 143
вариант от 03 мая 2017 г.
Решение задач тренировочного варианта 142
вариант от 19 апреля 2017 г.
Решение задач тренировочного варианта 141
вариант от 19 апреля 2017 г.
Решение задач тренировочного варианта 140
вариант от 12 апреля 2017 г.
Решение задач тренировочного варианта 139
вариант от 05 апреля 2017 г.
Решение задач тренировочного варианта 138
вариант от 29 марта 2017 г.
Решение задач тренировочного варианта 137
вариант от 22 марта 2017 г.
Решение задач тренировочного варианта 136
вариант от 15 марта 2017 г.
Решение задач тренировочного варианта 135
вариант от 08 марта 2017 г.
Решение задач тренировочного варианта 134
вариант от 01 марта 2017 г.
Решение задач тренировочного варианта 133
вариант от 22 февраля 2017 г.
Решение задач тренировочного варианта 132
вариант от 15 февраля 2017 г.
Решение задач тренировочного варианта 131
вариант от 08 февраля 2017 г.
Решение задач тренировочного варианта 130
вариант от 01 февраля 2017 г.
Решение задач тренировочного варианта 129
вариант от 25 января 2017 г.
Решение задач тренировочного варианта 128
вариант от 18 января 2017 г.
Решение задач тренировочного варианта 127
вариант от 11 января 2017 г.
Решение задач тренировочного варианта 126
вариант от 04 января 2017 г.
Решение задач тренировочного варианта 125
вариант от 28 декабря 2016 г.
Решение задач тренировочного варианта 124
вариант от 21 декабря 2016 г.
Решение задач тренировочного варианта 123
вариант от 14 декабря 2016 г.
Решение задач тренировочного варианта 122
вариант от 07 декабря 2016 г.
Решение задач тренировочного варианта 121
вариант от 30 ноября 2016 г.
Решение задач тренировочного варианта 120
вариант от 23 ноября 2016 г.
Решение задач тренировочного варианта 119
вариант от 16 ноября 2016 г.
Решение задач тренировочного варианта 118
вариант от 09 ноября 2016 г.
Решение задач тренировочного варианта 117
вариант от 02 ноября 2016 г.
Решение задач тренировочного варианта 116
вариант от 26 октября 2016 г.
Решение задач тренировочного варианта 115
вариант от 19 октября 2016 г.
Решение задач тренировочного варианта 114
вариант от 12 октября 2016 г.
Решение задач тренировочного варианта 113
вариант от 05 октября 2016 г.
Решение задач тренировочного варианта 112
вариант от 28 сентября 2016 г.
Решение задач тренировочного варианта 111
вариант от 21 сентября 2016 г.
Решение задач тренировочного варианта 110
вариант от 14 сентября 2016 г.
Решение задач тренировочного варианта 109
вариант от 07 сентября 2016 г.
ege4.me
ОГЭ математика 2019. Разбор варианта Алекса Ларина № 197.
В треугольнике КЕМ длина стороны КЕ равна 27, длина биссектрисы КВ равна 24, а длина отрезка МВ равна 8. Найдите периметр треугольника КМВ.
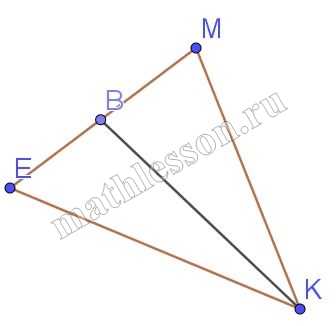
1) Пусть KE=a=27; KM=b; EB=x; BM=y=8; KB=m=24; $$\angle EKB=\angle BKM=\alpha$$
2) По свойству биссектрисы: $$\frac{x}{y}=\frac{a}{b}(1)$$
3) Рассмотрим теорему косинусов для $$\Delta EBK$$ и $$\Delta BMK$$:
$$\left\{\begin{matrix}y^{2}=m^{2}+b^{2}-2mb \cos \alpha\\x^{2}=m^{2}+a^{2}-2ma \cos \alpha\end{matrix}\right.$$
Умножим первое и второе уравнения на a и b соответственно и вычтем из первого второе :
$$\left\{\begin{matrix}y^{2}a =m^{2}a+b^{2}a-2mab \cos \alpha\\x^{2}b=m^{2}b+a^{2}b-2mab \cos \alpha\end{matrix}\right.$$
Получим: $$y^{2}a-x^{2}b=m^{2}a+b^{2}a-m^{2}b-a^{2}b$$
Рассмотрим левую часть равенства: $$y^{2}a-x^{2}b=xy(\frac{ya}{x}-\frac{xb}{y})$$ .С учетом , что $$\frac{x}{y}=\frac{a}{b}$$, получим : $$xy(\frac{b}{a}*a-\frac{a}{b}*b)=xy(b-a).$$
Рассмотрим правую часть равенства: $$m^{2}a+b^{2}a-m^{2}b-a^{2}b=m^{2}(a-b)-ba(a-b)$$. Получим : $$xy(b-a)=m^{2}(a-b)-ba(a-b)$$.
Т.к. $$a\neq b$$ (иначе получим равнобедренный), то поделим $$a-b$$: $$-xy=m^{2}-ba\Rightarrow m^{2}=ab-xy(2)$$ — вообще, это формула длины биссектриссы через две стороны и отрезки третьей, но в учебниках за 7-9 класс ее не встречал, потому необходимо ее выводить.
4) Итого имеем систему: $$\left\{\begin{matrix}\frac{x}{y}=\frac{a}{b}\\m^{2}=ab-xy\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{x}{8}=\frac{27}{b}\\24^{2}=27b-8x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{216}{b}\\576=27b-\frac{8*216}{b}\end{matrix}\right.$$
$$576b=27b^{2}-1728\Leftrightarrow$$ $$27b^{2}-576b-1728=0|:9\Leftrightarrow$$ $$3b^{2}-64b-192=0$$
$$D=4096+2304=6400$$
$$b_{1}=\frac{64+80}{6}=\frac{144}{6}=24$$
$$b_{2}=\frac{64-80}{6}<0$$
5) $$P_{BMK}=m+y+b=24+8+24=56$$
mathlesson.ru

Leave A Comment