22. Движение заряженных частиц в постоянном магнитном поле.
1. Рассмотрим движение заряженных частиц в однородном магнитном поле. Считаем, что на частицы не действуют никакие электрические поля, сила Лоренца имеет только магнитную составляющую: .
Если частица влетает в однородное магнитное поле так, что ее скорость направлена вдоль линии магнитной индукции (угол между v и В равен 0 или ), то . Частица будет продолжать двигаться в магнитном поле равномерно и прямолинейно.
Если же угол , т.е. частица влетает в магнитное поле в направлении, перпендикулярном линиям магнитной индукции, то на нее действует сила Лоренца , модуль которой: .
Под
действием этой силы траектория частицы
искривляется – частица равномерно
движется в однородном поле по дуге
окружности, плоскость которой
перпендикулярна линиям индукции. Радиус
окружности легко найти из условия, что
сила Лоренца играет роль центростремительной
силы, сообщающей частице нормальное
ускорение.
, , где m – масса частицы, — ее удельный заряд. Если скорость частицы v<<c, то радиус окружности зависит от v линейно: .
2. Направления силы Лоренца и вызываемого ею отклонения заряженной частицы в магнитном поле зависят не только от направления скорости v частицы, но и от знака ее заряда q. Если частица движется в плоскости чертежа слева направо, а магнитное поле направлено из-за чертежа перпендикулярно ее плоскости, то положительно заряженная частица отклоняется вниз, а отрицательно заряженная – вверх. Т.о., по характеру отклонения частицы в поле можно сразу же судить о знаке заряда частицы. Этим широко пользуются в экспериментах с элементарными частицами.
Частица движется по окружности радиуса r равномерно. Поэтому период обращения частицы: . , где W – полная энергия частицы. Для частицы, движущейся с нерелятивистской скоростью (v<<c), период обращения не зависит от скорости: .
3.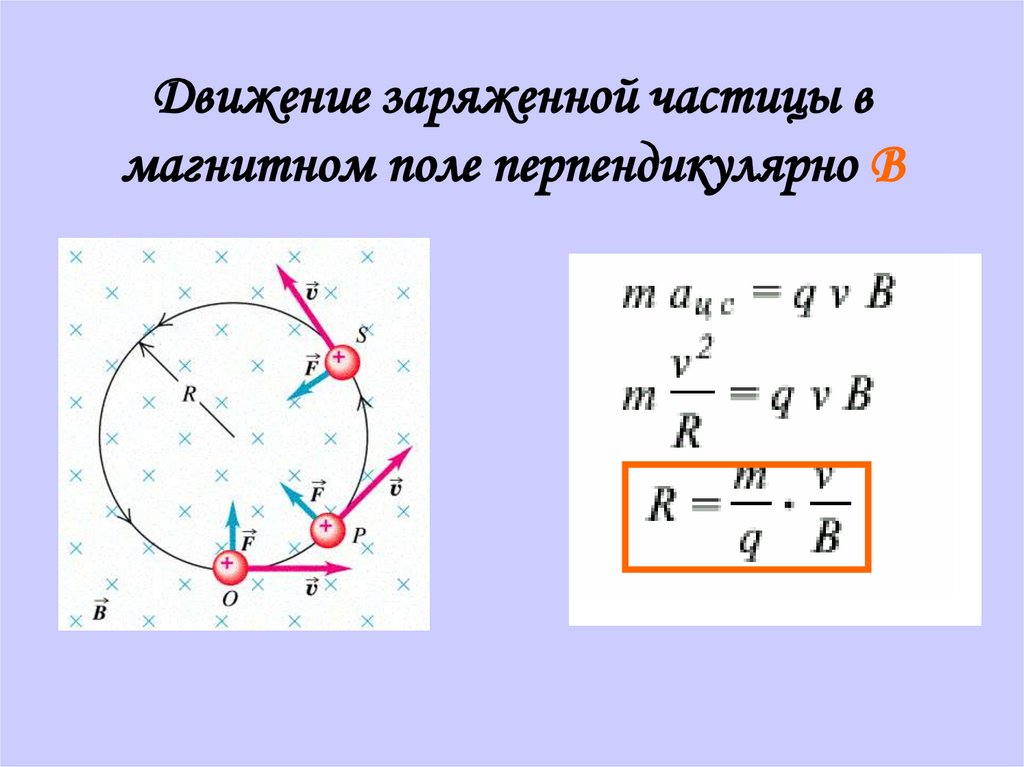 Рассмотрим общий случай движения
заряженной частицы в однородном магнитном
поле, когда ее скорость v
направлена под произвольным острым
углом
к вектору магнитной индукции поля.
Разложим вектор v
на две составляющие: параллельную
вектору В и перпендикулярную ему:
Рассмотрим общий случай движения
заряженной частицы в однородном магнитном
поле, когда ее скорость v
направлена под произвольным острым
углом
к вектору магнитной индукции поля.
Разложим вектор v
на две составляющие: параллельную
вектору В и перпендикулярную ему:
Скорость в магнитном поле не изменяется. Частица одновременно участвует в двух движениях: она равномерно вращается со скоростью по окружности радиуса: и движется поступательно с постоянной скоростью в направлении, перпендикулярном плоскости вращения. Поэтому траектория заряженной частицы представляет собой винтовую линию, ось которой совпадает с линией индукции магнитного поля. Расстояние между соседними витками равно h= Т.
.
4.
Если заряженная частица движется в неоднородном поле, индукция которого возрастает в
направлении движения частицы, то по
мере перемещения частицы значения r
и h
уменьшаются. Следовательно, частица
движется по скручивающейся спирали,
которая навивается на линию магнитной
индукции поля.
Курс общей физики, Т.2
Курс общей физики, Т.2
ОглавлениеПРЕДИСЛОВИЕМЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ § 1. Электрический заряд § 2. Закон Кулона § 3. Системы единиц § 4. Рационализованная запись формул § 5. Электрическое поле. Напряженность поля § 6. Потенциал § 7. Энергия взаимодействия системы зарядов § 8. Связь между напряженностью электрического поля и потенциалом § 9. Диполь § 10. Поле системы зарядов на больших расстояниях § 11. Описание свойств векторных полей Дивергенция. Циркуляция. Теорема Стокса. § 12. Циркуляция и ротор электростатического поля § 13. Теорема Гаусса § 14. Вычисление полей с помощью теоремы Гаусса Поле двух разноименно заряженных плоскостей. Поле объемно-заряженного шара. ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ § 15. Полярные и неполярные молекулы § 16. Поляризация диэлектриков § 17.  Поле внутри диэлектрика Поле внутри диэлектрика§ 18. Объемные и поверхностные связанные заряды § 19. Вектор электрического смешения § 20. Примеры на вычисление поля в диэлектриках § 21. Условия на границе двух диэлектриков § 22. Силы, действующие на заряд в диэлектрике § 23. Сегнетоэлектрики ГЛАВА III. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 24. Равновесие зарядов на проводнике § 25. Проводник во внешнем электрическом поле § 27. Конденсаторы ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ § 28. Энергия заряженного проводника § 29. Энергия заряженного конденсатора § 30. Энергия электрического поля ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 31. Электрический ток § 32. Уравнение непрерывности § 33. Электродвижущая сила § 34. Закон Ома. Сопротивление проводников § 35. Закон Ома для неоднородного участка цепи § 36. Разветвленные цепи. Правила Кирхгофа § 37. Мощность тока § 38. Закон Джоуля — Ленца ГЛАВА VI. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ § 39.  § 40. Магнитное поле § 41. Поле движущегося заряда § 42. Закон Био — Савара § 43. Сила Лоренца § 44. Закон Ампера § 45. Магнитное взаимодействие как релятивистский эффект § 46. Контур с током в магнитном поле § 47. Магнитное поле контура с током § 48. Работа, совершаемая при перемещении тока в магнитном § 49. Дивергенция и ротор магнитного поля § 50. Поле соленоида и тороида ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ § 51. Намагничение магнетика § 52. Напряженность магнитного поля § 53. Вычисление поля в магнетиках § 54. Условия на границе двух магнетиков § 56. Магнитомеханические явления § 57. Диамагнетизм § 58. Парамагнетизм § 59. Ферромагнетизм ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 60. Явление электромагнитной индукции § 61. Электродвижущая сила индукции § 62. Методы измерения магнитной индукции § 63. Токи Фуко § 64. Явление самоиндукции § 65.  Ток при замыкании и размыкании цепи Ток при замыкании и размыкании цепи§ 66. Взаимная индукция § 67. Энергия магнитного поля § 68. Работа перемагничивания ферромагнетика ГЛАВА IX. УРАВНЕНИЯ МАКСВЕЛЛА § 69. Вихревое электрическое поле § 70. Ток смещения § 71. Уравнения Максвелла ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями § 74. Определение заряда и массы электрона § 75. Определение удельного заряда ионов. Масс-спектрографы § 76. Ускорители заряженных частиц ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ § 77. Природа носителей тока в металлах § 78. Элементарная классическая теория металлов § 79. Эффект Холла ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ § 80. Несамостоятельная и самостоятельная проводимость § 81. Несамостоятельный газовый разряд § 82. Ионизационные камеры и счетчики § 83.  § 84. Газоразрядная плазма § 85. Тлеющий разряд § 86. Дуговой разряд § 87. Искровой и коронный разряды ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ § 88. Квазистационарные токи § 89. Свободные колебания в контуре без активного сопротивления § 90. Свободные затухающие колебания § 91. Вынужденные электрические колебания § 92. Переменный ток ЧАСТЬ 2. ВОЛНЫ § 93. Распространение волн в упругой среде § 94. Уравнения плоской и сферической волн § 95. Уравнение плоской волны, распространяющейся в произвольном направлении § 97. Скорость упругих волн в твердой среде § 98. Энергия упругой волны § 99. Стоячие волны § 100. Колебания струны § 101. Звук § 102. Скорость звука в газах § 103. Эффект Доплера для звуковых волн ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 104. Волновое уравнение для электромагнитного поля § 105.  Плоская электромагнитная волна Плоская электромагнитная волна§ 106. Экспериментальное исследование электромагнитных волн § 107. Энергия электромагнитных волн § 108. Импульс электромагнитного поля § 109. Излучение диполя ЧАСТЬ 3. ОПТИКА § 110. Световая волна § 111. Представление гармонических функций с помощью экспонент § 112. Отражение и преломление плоской волны на границе двух диэлектриков § 113. Световой поток § 114. Фотометрические величины и единицы § 115. Геометрическая оптика § 116. Центрированная оптическая система § 117. Тонкая линза § 118. Принцип Гюйгенса ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА § 119. Интерференция световых волн § 120. Когерентность § 121. Способы наблюдения интерференции света § 122. Интерференция света при отражении от тонких пластинок § 123. Интерферометр Майкельсона § 124. Многолучевая интерференция ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА § 126. Принцип Гюйгенса—Френеля § 127. Зоны Френеля § 128. Дифракция Френеля от простейших преград § 129.  Дифракция Фраунгофера от щели Дифракция Фраунгофера от щели§ 130. Дифракционная решетка § 131. Дифракция рентгеновских лучей § 132. Разрешающая сила объектива § 133. Голография ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА § 134. Естественный и поляризованный свет § 135. Поляризация при отражении и преломлении § 136. Поляризация при двойном лучепреломлении § 137. Интерференция поляризованных лучей § 138. Прохождение плоскополяризованного света через кристаллическую пластинку § 139. Кристаллическая пластинка между двумя поляризаторами § 140. Искусственное двойное лучепреломление § 141. Вращение плоскости поляризации ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ § 142. Дисперсия света § 143. Групповая скорость § 144. Элементарная теория дисперсии § 145. Поглощение света § 146. Рассеяние света § 147. Эффект Вавилова — Черенкова ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД § 148. Скорость света § 149. Опыт Физо § 150. Опыт Майкельсона § 151.  Эффект Доплера Эффект ДоплераПРИЛОЖЕНИЯ I. Единицы электрических и магнитных величин в СИ и в гауссовой системе Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе Приложение III. Векторный потенциал |
8.3 Движение заряженной частицы в магнитном поле. Введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Объяснить, как заряженная частица во внешнем магнитном поле совершает круговое движение
- Объясните, как определить радиус кругового движения заряженной частицы в магнитном поле
Заряженная частица испытывает силу при движении через магнитное поле. Что произойдет, если это поле будет однородным по движению заряженной частицы? По какому пути движется частица? В этом разделе мы обсудим круговое движение заряженной частицы, а также другие движения, возникающие в результате попадания заряженной частицы в магнитное поле.
Простейший случай имеет место, когда заряженная частица движется перпендикулярно однородному -полю (рис. 8.3.1). Если поле находится в вакууме, магнитное поле является доминирующим фактором, определяющим движение. Поскольку магнитная сила перпендикулярна направлению движения, заряженная частица движется по криволинейному пути в магнитном поле. Частица продолжает следовать по этому изогнутому пути, пока не образует полный круг. Другой способ взглянуть на это состоит в том, что магнитная сила всегда перпендикулярна скорости, так что она не действует на заряженную частицу. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость.
(рис. 8.3.1)
Рисунок 8.3.1 Отрицательно заряженная частица движется в плоскости бумаги в области, где магнитное поле перпендикулярно бумаге (обозначается маленькой буквой s — как хвостики стрелок). Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. В результате получается равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.)
В результате получается равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна по направлению предсказанию правила правой руки.)В этой ситуации магнитная сила дополняет центростремительную силу. Учитывая, что скорость перпендикулярна магнитному полю, величина магнитной силы уменьшается до . Поскольку магнитная сила обеспечивает центростремительную силу, мы имеем
(8.3.1)
Решение для выходов
(8.3.2)
Здесь — радиус кривизны пути заряженной частицы с массой и зарядом, движущейся со скоростью, перпендикулярной магнитному полю напряженностью . Время прохождения заряженной частицей круговой траектории определяется как период, равный пройденному расстоянию (окружности), деленному на скорость. На основании этого и 8.3.1 мы можем получить период движения как
(8.3.3)
Если скорость не перпендикулярна магнитному полю, то мы можем сравнивать каждую составляющую скорости отдельно с магнитным полем. Составляющая скорости, перпендикулярная магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
Составляющая скорости, перпендикулярная магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
(8.3.4)
, где это угол между и . Составляющая, параллельная магнитному полю, создает постоянное движение в том же направлении, что и магнитное поле, также показанное в 8.3.4. Параллельное движение определяет шаг спирали, то есть расстояние между соседними витками. Это расстояние равно параллельной составляющей скорости, умноженной на период:
(8.3.5)
В результате получается спиральное движение , как показано на следующем рисунке.
(рис. 8.3.2)
Рисунок 8.3.2 Заряженная частица, движущаяся со скоростью, отличной от направления магнитного поля. Составляющая скорости, перпендикулярная магнитному полю, создает круговое движение, тогда как составляющая скорости, параллельная полю, перемещает частицу по прямой линии. Шаг — это горизонтальное расстояние между двумя последовательными кругами.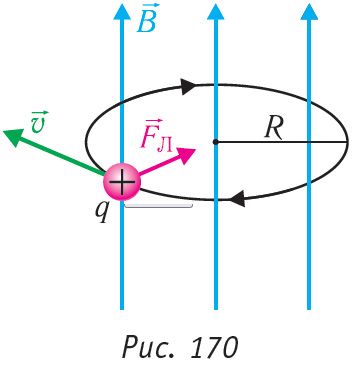 Результирующее движение является спиральным.
Результирующее движение является спиральным.Когда заряженная частица движется по винтовой траектории, она может попасть в область, где магнитное поле не является однородным. В частности, предположим, что частица перемещается из области сильного магнитного поля в область более слабого поля, а затем обратно в область более сильного поля. Частица может отразиться назад, прежде чем попасть в область более сильного магнитного поля. Это похоже на волну на струне, идущую от очень легкой тонкой струны к твердой стене и отражающуюся назад. Если отражение происходит с обоих концов, частица попадает в так называемую магнитную бутылку.
Частицы, захваченные магнитными полями, обнаружены в радиационных поясах Ван Аллена вокруг Земли, которые являются частью магнитного поля Земли. Эти пояса были обнаружены Джеймсом Ван Алленом при попытке измерить поток космических лучей на Земле (высокоэнергетические частицы, поступающие из-за пределов Солнечной системы), чтобы увидеть, похож ли он на поток, измеренный на Земле. Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в открытом космосе. Северное сияние , как и знаменитое северное сияние (Северное сияние) в Северном полушарии (рис. 8.3.3), представляет собой прекрасное проявление света, испускаемого при рекомбинации ионов с электронами, попадающими в атмосферу по спирали вдоль силовых линий магнитного поля. (Ионы в основном представляют собой атомы кислорода и азота, которые первоначально ионизируются в результате столкновений с энергичными частицами в атмосфере Земли.) Полярные сияния также наблюдались на других планетах, таких как Юпитер и Сатурн.
Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в открытом космосе. Северное сияние , как и знаменитое северное сияние (Северное сияние) в Северном полушарии (рис. 8.3.3), представляет собой прекрасное проявление света, испускаемого при рекомбинации ионов с электронами, попадающими в атмосферу по спирали вдоль силовых линий магнитного поля. (Ионы в основном представляют собой атомы кислорода и азота, которые первоначально ионизируются в результате столкновений с энергичными частицами в атмосфере Земли.) Полярные сияния также наблюдались на других планетах, таких как Юпитер и Сатурн.
(рис. 8.3.3)
Рисунок 8.3.3 (a) Радиационные пояса Ван Аллена вокруг Земли улавливают ионы, образующиеся при попадании космических лучей в атмосферу Земли. (b) Великолепное зрелище северного сияния, или северного сияния, сияет в северном небе над Медвежьим озером возле базы ВВС Эйлсон, Аляска. Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота. (кредит b: модификация работы старшего летчика ВВС США Джошуа Странга)
Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота. (кредит b: модификация работы старшего летчика ВВС США Джошуа Странга)ПРИМЕР 8.3.1
Дефлектор луча
Исследовательская группа изучает короткоживущие радиоактивные изотопы. Им нужно разработать способ транспортировки альфа-частиц (ядер гелия) из места их образования в место, где они столкнутся с другим материалом, чтобы сформировать изотоп. Пучок альфа-частиц преломляется через градусную область с однородным магнитным полем (рис. 8.3.4). а) В каком направлении должно быть приложено магнитное поле? б) Сколько времени требуется альфа-частицам, чтобы пересечь область однородного магнитного поля?
(рис. 8.3.4)
Рисунок 8.3.4 Вид сверху на установку дефлектора луча.Стратегия
а. Направление магнитного поля показывает RHR-1. Ваши пальцы указывают в направлении , а большой палец должен указывать в направлении силы, влево. Следовательно, поскольку альфа-частицы заряжены положительно, магнитное поле должно быть направлено вниз.
Следовательно, поскольку альфа-частицы заряжены положительно, магнитное поле должно быть направлено вниз.
б. Период обращения альфа-частицы по окружности равен
.(8.3.6)
Поскольку частица проходит только четверть круга, мы можем вычислить время, необходимое для прохождения этого пути, умноженное на период.
Решение
а. Давайте начнем с фокусировки на альфа-частице, входящей в поле в нижней части изображения. Во-первых, наведите большой палец вверх на страницу. Чтобы ваша ладонь открылась влево, куда указывает центростремительная сила (и, следовательно, магнитная сила), ваши пальцы должны изменить ориентацию, пока они не укажут на страницу. Это направление приложенного магнитного поля.
б. Период обращения заряженной частицы по окружности рассчитывается по заданным в задаче массе, заряду и магнитному полю. Получается
Однако для данной задачи альфа-частица проходит четверть круга, поэтому время, которое потребуется, будет равно
Значение
Этого времени может быть достаточно, чтобы добраться до материала, который мы хотим бомбардировать, в зависимости от того, насколько короткоживущий радиоактивный изотоп продолжает испускать альфа-частицы. Если бы мы могли увеличить магнитное поле, приложенное к области, это сократило бы время еще больше. Путь, который должны пройти частицы, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
Если бы мы могли увеличить магнитное поле, приложенное к области, это сократило бы время еще больше. Путь, который должны пройти частицы, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 8.2
Однородное магнитное поле магнитудой направлено горизонтально с запада на восток. а) Какова магнитная сила, действующая на протон в тот момент, когда он движется вертикально вниз в поле со скоростью ? (б) Сравните эту силу с весом протона.
ПРИМЕР 8.3.2
Винтовое движение в магнитном поле
Протон входит в однородное магнитное поле со скоростью . Под каким углом должно быть магнитное поле от скорости, чтобы шаг результирующего винтового движения был равен радиусу спирали?
Стратегия
Шаг движения относится к параллельной скорости, умноженной на период кругового движения, тогда как радиус относится к перпендикулярной составляющей скорости.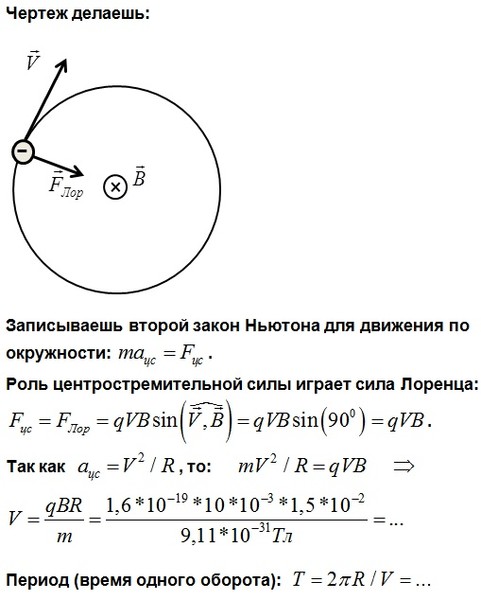 Установив радиус и шаг равными друг другу, найдите угол между магнитным полем и скоростью или .
Установив радиус и шаг равными друг другу, найдите угол между магнитным полем и скоростью или .
Решение
Шаг определяется уравнением 8.3.5, период определяется уравнением 8.3.3, а радиус кругового движения определяется уравнением 8.3.2. Обратите внимание, что скорость в уравнении радиуса связана только с перпендикулярной скоростью, при которой происходит круговое движение. Поэтому подставим синусоидальную составляющую общей скорости в уравнение радиуса, чтобы приравнять шаг и радиус:
Значение
Если бы этот угол был , возникла бы только параллельная скорость, и спираль не образовалась бы, потому что не было бы кругового движения в перпендикулярной плоскости. Если бы этот угол был , произошло бы только круговое движение и не было бы движения окружностей, перпендикулярных движению. Именно это создает спиральное движение.
Цитаты Кандела
Содержимое по лицензии CC, конкретное указание авторства
- Загрузите бесплатно по адресу http://cnx.
 org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Движение заряженной частицы в магнитном поле
Это уже известно о взаимодействии электрического и магнитного полей, а также о движении заряженных частиц в присутствии как электрического, так и магнитного полей. Мы также вывели зависимость силы, действующей на заряженную частицу, которая определяется соотношением сила Лоренца в данном случае. Мы также узнали о магнитной силе, действующей на проводящий стержень с током, когда он подвергается воздействию магнитного поля.
Что же происходит, когда заряженная частица движется в присутствии магнитного поля? Как определить траекторию такой частицы? Об этом будет подробно рассказано в этой статье.
Когда на частицу действует сила, считается, что она производит работу, если составляющая силы направлена в направлении движения частицы. Магнитная сила действует перпендикулярно движению частицы в обсуждаемой ситуации, когда заряженная частица, несущая заряд q, движется в однородном магнитном поле величиной B. В этом случае мы утверждаем, что магнитная сила не совершает работы над частицей и, следовательно, нельзя увидеть никакого изменения скорости частицы. Когда скорость частицы v перпендикулярна направлению магнитного поля, мы можем написать
Магнитная сила действует перпендикулярно движению частицы в обсуждаемой ситуации, когда заряженная частица, несущая заряд q, движется в однородном магнитном поле величиной B. В этом случае мы утверждаем, что магнитная сила не совершает работы над частицей и, следовательно, нельзя увидеть никакого изменения скорости частицы. Когда скорость частицы v перпендикулярна направлению магнитного поля, мы можем написать
F = q (v × B)
В этом случае магнитная сила направлена к центру кругового движения объекта и действует как центростремительная сила. В результате, если v и B перпендикулярны, частица описывает окружность. В других ситуациях, если компонента скорости существует в направлении магнитного поля B, ее величина остается постоянной во время движения, поскольку на нее не влияет магнитное поле. Кроме того, как упоминалось ранее, движение, вызванное перпендикулярной составляющей скорости, носит круговой характер.
Круговое движение заряженной частицы в магнитном поле
Когда заряженная частица движется через магнитное поле, на нее действует сила. Что произойдет, если это поле будет однородным поперек движения заряженной частицы? По какому пути пойдет частица? В этом разделе мы рассмотрим круговое движение заряженной частицы, а также другие движения, возникающие, когда заряженная частица входит в магнитное поле.
Что произойдет, если это поле будет однородным поперек движения заряженной частицы? По какому пути пойдет частица? В этом разделе мы рассмотрим круговое движение заряженной частицы, а также другие движения, возникающие, когда заряженная частица входит в магнитное поле.
Простейший случай, когда заряженная частица движется перпендикулярно однородной, как показано на рисунке ниже. Если поле находится в вакууме, магнитное поле является решающим фактором движения. Заряженная частица в магнитном поле движется по криволинейному маршруту, потому что магнитная сила перпендикулярна направлению движения.
В области, где магнитное поле перпендикулярно бумаге, отрицательно заряженная частица движется в плоскости бумаги.
По этой кривой траектории следует частица, пока не образует полный круг. Другой способ думать об этом состоит в том, что магнитная сила всегда перпендикулярна скорости, поэтому она не действует на заряженную частицу. В результате кинетическая энергия и скорость частицы остаются постоянными. Скорость не меняется, а вот направление.
Скорость не меняется, а вот направление.
Винтовое движение
Когда вектор скорости не перпендикулярен вектору магнитного поля, возникает винтовое движение.
Движение, возникающее, когда одна составляющая скорости постоянна по амплитуде и направлению (т. е. прямолинейное движение), а другая составляющая постоянна по скорости, но равномерно меняет направление (т. движение . Это результат сочетания прямолинейного и кругового движения.
Когда заряженная частица движется перпендикулярно однородному B-полю, как показано на рис. , возникает простейшая ситуация. (Если это происходит в вакууме, магнитное поле является наиболее важным элементом, влияющим на движение.) Магнитная сила (сила Лоренца) обеспечивает в этом случае центростремительную силу, так как
Fc = mv 2 / r
Поскольку, здесь sin θ = 1
Тогда магнитная сила:
F = qvB
Теперь, если магнитная сила Лоренца обеспечивает центростремительную силу, следовательно, эти силы должны быть равны:
qvB = mv 2 / r
Решите приведенное выше выражение для r как скорость v, перпендикулярная магнитному полю напряженностью B, обозначается r, также известным как гирорадиус или циклотронный радиус.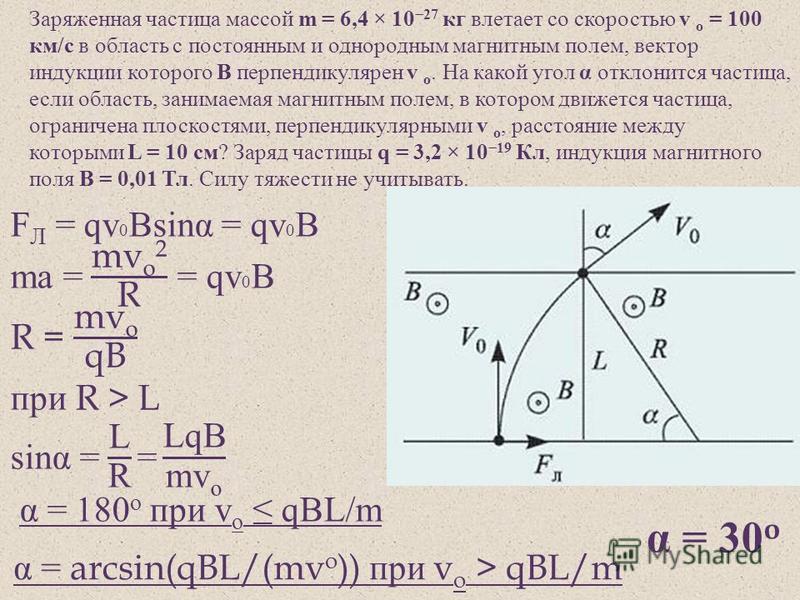 Другими словами, это радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.
Другими словами, это радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.
Если скорость не перпендикулярна магнитному полю, то v — перпендикулярная составляющая скорости. Поскольку магнитная сила равна 0 для движения, параллельного полю, составляющая скорости, параллельная полю, не изменяется. В следующем разделе, посвященном спиральному движению, мы рассмотрим последствия этой ситуации.
A Циклотронный резонанс возникает, когда частица совершает круговое движение под действием однородного магнитного поля. Это слово происходит от названия циклического ускорителя частиц, известного как циклотрон, который был продемонстрирован в. для v, приведенного выше, и подставив в частоту обращения такую, что
f = v / 2πr
or
f = qB / 2πm
Hence, The cyclotron frequency is easily expressed in radians per second as:
ω = qB / m
Magnetic MirrorРасположение магнитного поля, при котором напряженность поля изменяется вдоль силовой линии.
Зеркальный эффект заставляет заряженные частицы отскакивать от области сильного поля, такое явление называется Магнитным зеркалом .
Магнитное зеркало и спиральное движение
Если v обозначает частоту вращения частицы. Следовательно, промежуток времени для одного оборота может быть выражен следующим образом:
Время для одного оборота, T = 2π / ω = 1 / v
Шаг частицы — это расстояние, которое она проходит вдоль направления магнитного поля. поле за один оборот. тогда:
Шаг, p = v || T = 2πm v || / qB
, где v || — скорость, параллельная магнитному полю.
Примеры задач
Задача 1: Опишите, как будет двигаться заряженная частица в циклотроне, если частота радиочастотного поля (r f ) удвоится.
Решение:
Требование резонанса нарушается, и период времени радиочастотного (РЧ) поля уменьшается вдвое, когда частота радиочастотного (r f ) поля удваивается.
В результате радиочастота завершает цикл за время, необходимое частице для совершения половины оборота внутри буквы D.
Задача 2: Какая частица из протонов, нейтронов и электронов может иметь самую низкую частоту вращения при движении с той же скоростью, нормальной к магнитному полю?
Решение:
Когда заряженная частица с массой m и зарядом q попадает в магнитное поле B, она начинает вращаться с частотой,
f = Бк / 2πm
В результате высокое отношение q/m указывает на более высокую частоту, а электрон имеет самое высокое отношение q/m из трех из-за его малой массы. 9Частота электрона 0017 будет самой высокой.
Задача 3. Когда протон движется в однородном магнитном поле, его скорость изменяется, а кинетическая энергия остается неизменной. Почему?
Решение:
Магнитная сила будет перпендикулярна направлению движения протона.
Мы знаем, что когда сила, действующая перпендикулярно направлению движущегося заряда, совершаемая работа равна нулю. Это указывает на то, что кинетическая энергия остается постоянной. Сила может изменить направление (скорость) протона, но не его скорость (величину). В результате импульс и скорость меняются.
Задача 4. Может ли магнитное поле ускорить заряженную частицу? Можно ли увеличить его скорость?
Решение:
Магнитное поле ускоряет заряженную частицу, изменяя направление ее скорости. Скорость заряженной частицы не зависит от магнитного поля. Магнитное поле не влияет на скорость, так как оно действует перпендикулярно движению. В результате сила не может совершить работу над частицей. В результате кинетическая энергия частицы не может быть изменена. Поэтому он не может регулировать скорость.
Задача 5. Что такое сила Лоренца? Объяснять.
Решение:
Сила Лоренца, сила, действующая на заряженную частицу q, движущуюся со скоростью v через электрическое и магнитное поля E и B.
Сила Лоренца (названа в честь голландского ученого Хендрика А. Лоренца) полная электромагнитная сила F, действующая на заряженную частицу, и определяется выражением
F = qE + qv × B
Электрическое поле дает первый член. Магнитная сила, которая имеет направление, перпендикулярное как скорости, так и магнитному полю, является вторым членом. Магнитная сила пропорциональна q, а также размеру векторного векторного произведения v × B. Величина силы равна qvB sin с точки зрения угла между v и B.
Скорость заряженной частицы в однородном магнитном поле является интригующим следствием силы Лоренца. Если v перпендикулярна B (т. е. между v и B угол 90°), частица будет следовать по круговой траектории с радиусом r = mv/qB. Орбита частицы будет представлять собой спираль с осью, параллельной силовым линиям, если угол меньше 90°.
Если ϕ равно 0, на частицу не будет действовать магнитная сила, и она будет продолжать двигаться вдоль силовых линий без отклонения. Ускорители частиц, использующие заряженные частицы, такие как циклотроны, используют тот факт, что частицы движутся по круговой орбите, когда v и B находятся под прямым углом.


 org/contents/
org/contents/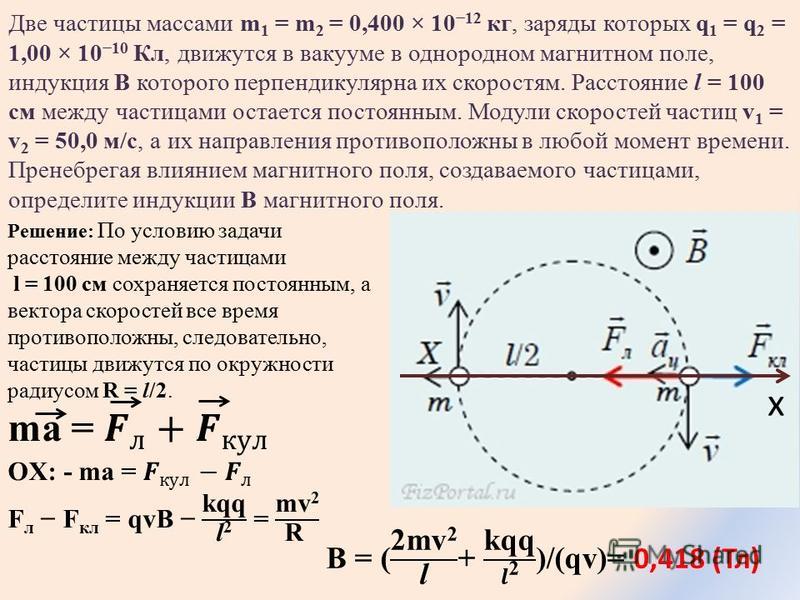 Зеркальный эффект заставляет заряженные частицы отскакивать от области сильного поля, такое явление называется Магнитным зеркалом .
Зеркальный эффект заставляет заряженные частицы отскакивать от области сильного поля, такое явление называется Магнитным зеркалом . В результате радиочастота завершает цикл за время, необходимое частице для совершения половины оборота внутри буквы D.
В результате радиочастота завершает цикл за время, необходимое частице для совершения половины оборота внутри буквы D. Мы знаем, что когда сила, действующая перпендикулярно направлению движущегося заряда, совершаемая работа равна нулю. Это указывает на то, что кинетическая энергия остается постоянной. Сила может изменить направление (скорость) протона, но не его скорость (величину). В результате импульс и скорость меняются.
Мы знаем, что когда сила, действующая перпендикулярно направлению движущегося заряда, совершаемая работа равна нулю. Это указывает на то, что кинетическая энергия остается постоянной. Сила может изменить направление (скорость) протона, но не его скорость (величину). В результате импульс и скорость меняются. Сила Лоренца (названа в честь голландского ученого Хендрика А. Лоренца) полная электромагнитная сила F, действующая на заряженную частицу, и определяется выражением
Сила Лоренца (названа в честь голландского ученого Хендрика А. Лоренца) полная электромагнитная сила F, действующая на заряженную частицу, и определяется выражением
Leave A Comment