Задачи на силу Лоренца с решением

Решение задач – обязательная практика в жизни всех студентов-технарей. В сегодняшней статье разберемся, как решать задачи на силу Лоренца. 

Если вам скучно читать про решение задач, переходите в наш телеграм-канал. Там найдется интересная информация и новости для всех специальностей. А еще, у нас есть второй канал, где мы рассказываем об акциях нашего сервиса и дарим приятные скидки. Проверьте — и не упустите выгоду!

Задачи по теме «сила Лоренца»

Даже если вы не новичок, прежде чем решать задачи, прочтите общую памятку и на всякий случай держите под рукой полезные формулы. 

Задача на силу Лоренца №1

Условие 

Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона.

Решение

Скорость электрона можно найти из формулы кинетической энергии:

Eк=m·v22v=2Eкm

Сила Лоренца является центростремительной силой, значит, по второму закону Ньютона, можно записать:

Магнитная индукция равна напряженности, умноженной на магнитную постоянную.  Подставив ранее найденное выражение для скорости в формулу для радиуса и силы Лоренца, запишем:

R=m2Eктqμ0H=2Eктqμ0HFл=q2Eктμ0H​

Теперь осталось только подставить значения и вычислить:

v=2·4,8·10-169,1·10-31=3,25·107 мсFл=4·3,14·10-7·465·1,6·10-19·3,25·107=3·10-15НR=2·4,8·10-16·9,1·10-314·3,14·10-7·465·1,6·10-19=0,32 м

Ответ: v=3,25·107 мс; Fл=3·10-15Н; R=0,32 м.

Задача на силу Лоренца №2

Условие

Альфа-частица влетает в магнитное поле с индукцией 1 Тл перпендинулярно силовым линиям. Найти момент импульса частицы относительно центра окружности, по которой она будет двигаться.

Решение

Когда частица влетает в поле перпендикулярно силовым линиям, на нее начинает действовать сила Лоренца, которая выполняет роль центростремительной силы. Радиус окружности, по которой будет двигаться частица:

R=mvQBm=6,65·10-27 кг — масса альфа частицыQ=2e=3,2·10-19Кл — заряд альфа частицы

Момент импульса частицы относительно центра окружности найдем по формуле:

L=mvR=m2v2QB=6,65·10-272·0,35·10723,2·10-19·1=5,42·10-21кг·м2с

Ответ: 5,42·10-21 кг·м2с.

Задача на силу Лоренца №3

Условие

В однородном магнитном поле с индукцией  В = 0,5 Тл вращается с частотой n = 10 с-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определите разность потенциалов U на концах стержня.

Решение

Рассмотрим физическую суть процессов, проходящих в стержне. Когда стержень движется в магнитном поле, в нем возникает ЭДС индукции, которая обусловлена действием силы Лоренца на заряды стержня.

Под действием этой силы в стержне происходит разделение зарядов: свободные электроны перемещаются вверх и между концами стержня возникает разность потенциалов.

Заряды на концах стержня создают поле E, препятствующее дальнейшему разделению зарядов. В какой-то момент сила Лоренца уравновесится с силой возникающего поля:

Fл=e·ЕЕ=Fле=evBe=vB

Скорость нижнего конца стержня, а значит, и скорость электронов в нем, можно найти, зная частоту вращения и длину стержня:

v=2π·n·l

C учетом этого, перепишется выражения для напряженности электрического поля:

 Е=2πnlB

Индуцируемая разность потенциалов, по определению, равна:

U=Е·lU=2πnl2B=2·3,14·10-1·0,22·0,5=1,3В

Ответ: 1,3 В.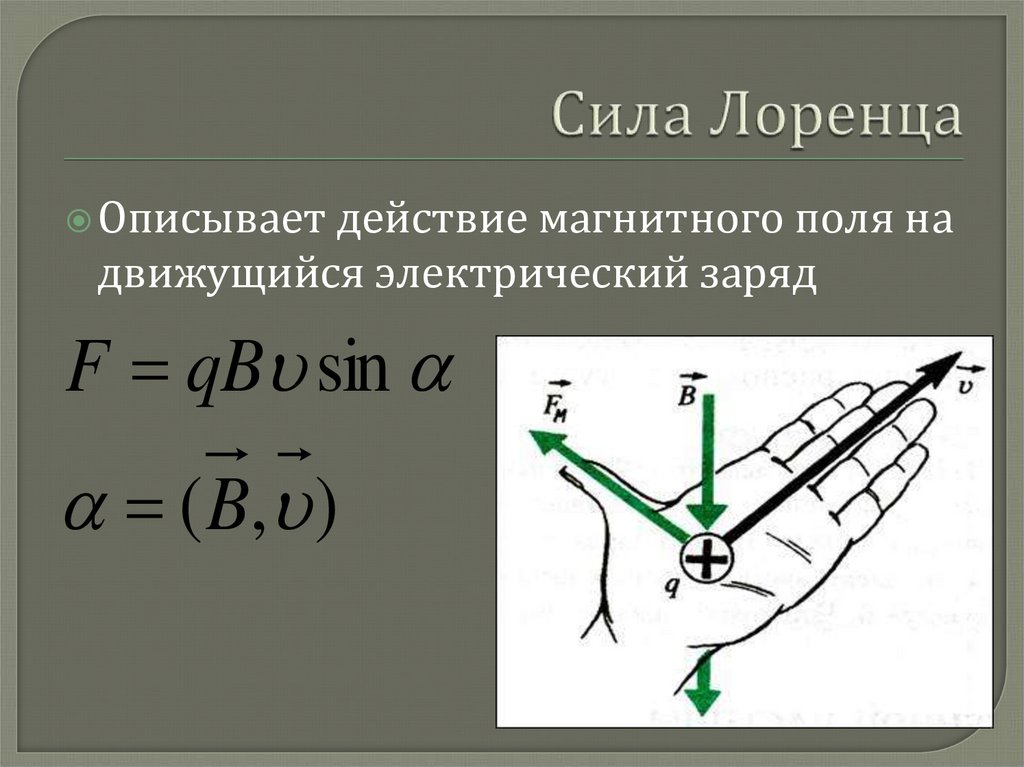

Задача на силу Лоренца №4

Условие

Какая сила действует на заряд 0,005 Кл, движущийся в магнитном поле с индукцие 0,5 Тл со скоростью 150 м/с под углом 45 градусов к вектору магнитной индукции?

Решение

Это простейшая задача на определение силы Лоренца. Вспомним формулу и запишем, что на заряд действует сила Лоренца, равная:

F=q·v·B·sinα

Подставим значения и вычислим:

F=0,005·150·0,5·22=0,26 Н

Ответ: 0,26 Н.

Задача на силу Лоренца №5

Условие

На тело с зарядом 0,8 мКл, движущееся в магнитном поле, со стороны поля действует сила, равная 32Н. Какова скорость тела, если вектор магнитного поля перпендикулярен ей?

Решение

Это классическая задача на применение формулы силы Лоренца. Так как векторы скорости и магнитной индукции перпендикулярны, можно записать:

F=qvBsinα=qvBv=FqB=320,8·10-3·2=20·103 мс

Ответ: 20000 м/с.

Проходите магнитостатику? Вам также может быть интересно:

  1. Задачи на закон Био-Савара-Лапласа.
  2. Задачи на теорему о циркуляции магнитного поля.

Вопросы на тему «Сила Лоренца»

Вопрос 1. Что такое сила Лоренца?

Ответ. Сила Лоренца — это сила, с которой магнитное поле действует на заряженную частицу, движущуюся в нем.

Сила Лоренца действует только на движущиеся заряды.

Вопрос 2. Как определить направление силы Лоренца?

Ответ. Направление силы Лоренца определяется по правилу левой руки:

Если левую руку расположить так, чтобы составляющая вектора В, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движении положительного заряда (= против движения отрицательного заряда), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.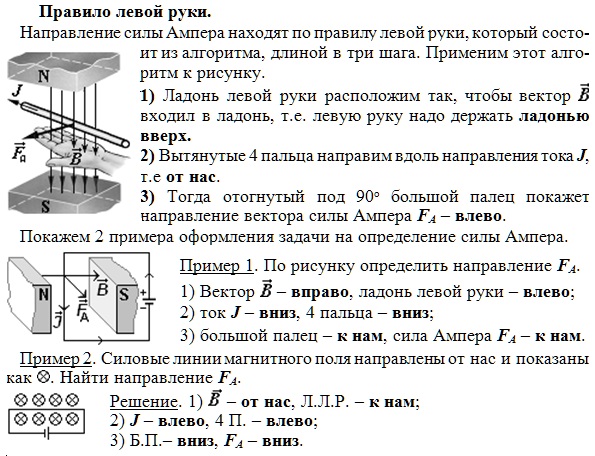

Вопрос 3. Зависит ли сила Лоренца от знака заряда?

Ответ. Да, зависит. Для противоположных зарядов сила Лоренца будет направлена в противоположные стороны.

Вопрос 4. Совершает ли сила Лоренца работу?

Ответ. Нет. Сила Лоренца не совершает работу, т.к., являясь перпендикулярной вектору скорости частицей, может изменить лишь направление скорости, но не ее значение. Работа силы Лоренца всегда равна нулю!

Вопрос 5. По какой траектории движется частица, попадающая в магнитное поле, перпендикулярное вектору скорости?

Ответ. Частица, влетающая в магнитное поле перпендикулярно линиям магнитной индукции, будет двигаться в этом поле по окружности определенного радиуса под действием силы Лоренца.

Нужна помощь в решении задач и других заданий по учебе? Профессиональный сервис для студентов посодействует, обращайтесь в любое время!

Сила Ампера.

Сила Лоренца. Примеры решения задач по физике. 10-11 класс
Подробности
Обновлено 03.07.2018 18:36
Просмотров: 2488

Задачи по физике — это просто!

Вспомним формулы, которые :

Не забываем, что решать задачи надо всегда в системе СИ!


А теперь к задачам!

Элементарные задачи из курса школьной физики

Задача 1

Определить силу, с которой однородное магнитное поле действует на проводник длиной 20 см, если сила тока в нем 300 мА, расположенный под углом 45o к вектору магнитной индукции. Магнитная индукция составляет 0,5 Тл.

Задача 2

Проводник с током 5 А находится в магнитном поле с индукцией 10 Тл.
Определить длину проводника, если магнитное поле действует на него с силой 20 Н и перпендикулярно проводнику.



Задача 3

Определить силу тока в проводнике длиной 20 см, расположенному перпендикулярно силовым линиям магнитного поля с индукцией 0,06 Тл, если на него со стороны  магнитного поля действует сила 0,48 Н.

Задача 4

Проводник длиной 20 см с силой тока 50 А находится в однородном магнитном поле с индукцией 40 мТл.
Какую работу совершит источник тока, если проводник переместится на 10 см перпендикулярно вектору магнитной индукции (вектор магнитной индукции перпендикулярен направлению тока в проводнике).

Задача 5

Проводник длиной 0,15 м перпендикулярен вектору магнитной индукции однородного магнитного поля, модуль которого В=0,4 Тл. Сила тока в проводнике  8 А. 

Найдите работу, которая  была совершена при перемещении проводника на 0,025 метра по направлению действия силы Ампера.

Задача 6

Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.

Задача 7

Какова скорость заряженного тела, перемещающегося в магнитном поле с индукцией 2 Тл, если на него со стороны магнитного поля действует сила 32 Н.

Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.

Задача 8

Определить центростремительную силу, действующую на протон в однородном магнитном поле с индукцией 0,01 Тл (вектор магнитной индукции перпендикулярен вектору скорости), если радиус окружности, по которой он движется, равен 5 см.

Задача 9

С каким ускорением движется электрон в однородном магнитном поле (вектор магнитной индукции перпендикулярен вектору скорости) с индукцией 0,05 Тл, если сила Лоренца, действующая на него, равна 5×10-13 Н.

(Так как сила Лоренца является одновременно и центростремительной силой, и электрон движется по окружности, в задаче требуется рассчитать центростремительное ускорение, которое приобретает электрон в результате действия центростремительной силы.)


Следующая страница « Магнитный поток. Магнитная индукция 9-11 класс»

Назад в раздел «Решение типовых задач по физике»

Сила Лоренца: решенные примеры задач

Физика: Магнетизм и магнитные эффекты электрического тока: сила Лоренца: решены примеры задач с ответами, решением и объяснением

1.

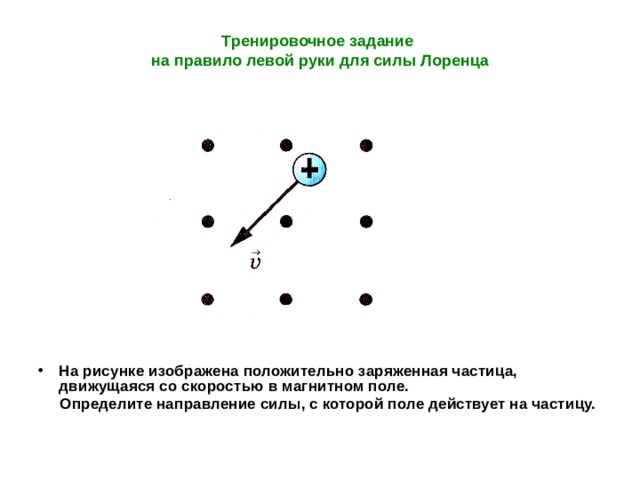Сила, действующая на движущийся заряд в магнитном поле:  Решенные примеры задач

ПРИМЕР 3.20

Частица с зарядом q движется с положительной скоростью вдоль оси y магнитного поля. Вычислите силу Лоренца, действующую на частицу (а), когда магнитное поле направлено в положительном направлении по оси y (б), когда магнитное поле направлено в положительном направлении по оси z (в), когда магнитное поле находится в плоскости zy и составляет угол θ со скоростью частицы. Отметьте направление магнитной силы в каждом случае.

Решение

Скорость частицы

(a) Магнитное поле направлено в положительном направлении y, отсюда следует,


Из силы Лоренца,

Итак, при движении частицы никакая сила не действует на нее направление магнитного поля.

(b) Магнитное поле направлено в положительном направлении по оси z, что означает,


Из силы Лоренца,


Следовательно, величина силы Лоренца равна qvB, а направление направлено вдоль положительного направления x.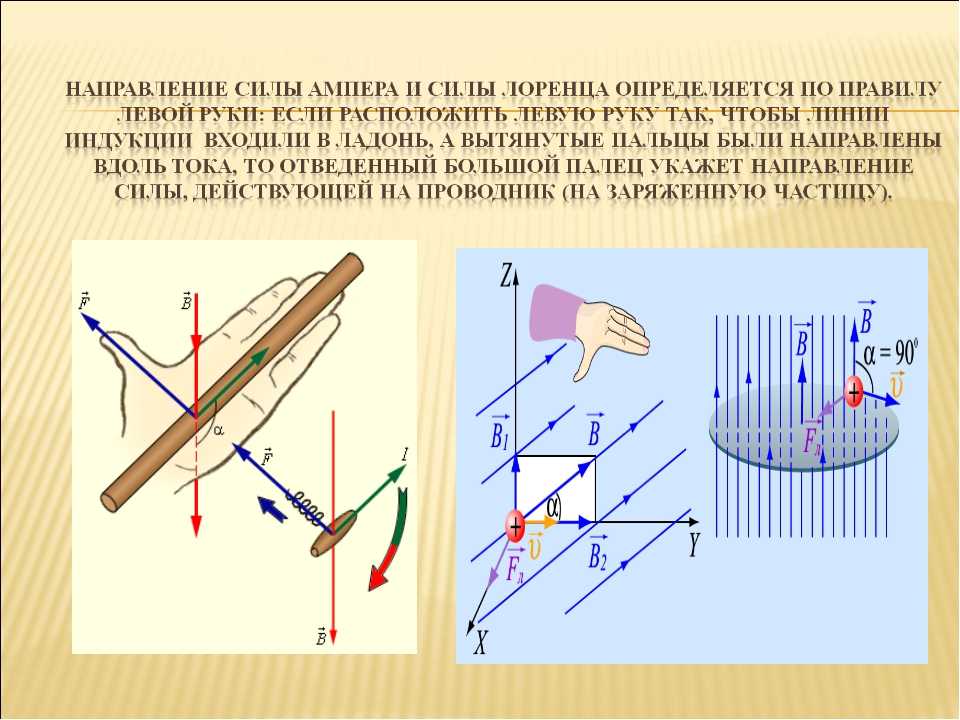

(c) Магнитное поле находится в Zy — плоскости и создает угол θ с скоростью частицы, которая подразумевает


от силы Лорента,


3,21

. Компьюция совершенная работа и мощность, переданная силой Лоренца частице с зарядом q, движущейся со скоростью  . Рассчитайте угол между силой Лоренца и скоростью заряженной частицы, а также интерпретируйте результат.

Решение

Для заряженной частицы, движущейся в магнитном поле,


Работа, совершаемая магнитным полем, равна


. Из теоремы о кинетической энергии работы (см. раздел 4-й главы XI стандарта, том I) Угол между силой Лоренца и скоростью заряженной частицы равен 90º. Таким образом, сила Лоренца изменяет направление скорости, но не величину скорости. Следовательно, сила Лоренца не совершает работы и не изменяет кинетическую энергию частицы.

2. Движение заряженной частицы в однородном магнитном поле:

Решенные примеры задач

ПРИМЕР 3.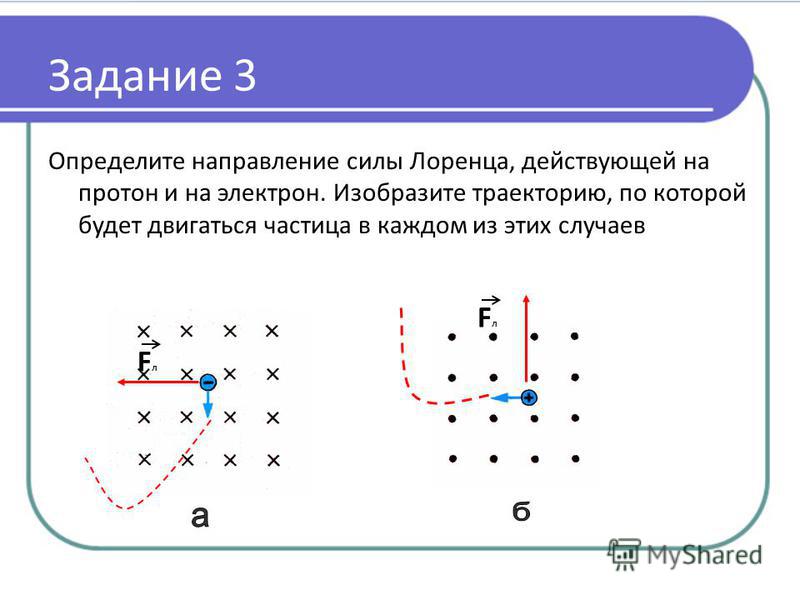 22

Электрон, движущийся перпендикулярно однородному магнитному полю 0,500 Тл, совершает круговое движение радиусом 2,80 мм. Какова скорость электрона?

Раствор

Заряд электрона q = -1,60 × 10-19 Кл

⟹ |q| = 1,60 × 10–19 Кл

Величина магнитного поля B = 0,500 Тл

Масса электрона, m = 9,11 × 10–31 кг

Радиус орбиты, r = 2,50 мм = 2,50 × 10–3 м

Скорость электрона, v = |q| rB/m


v = 2,195 × 108 м/с

 

В начальный момент времени t = 0 с протон имеет скорость. Найти

а) Каково ускорение протона в начальный момент времени?

(b) Является ли траектория круговой или спиральной?. Если спиральная, рассчитайте радиус винтовой траектории, а также рассчитайте шаг спирали (Примечание: шаг спирали — это расстояние, пройденное вдоль оси спирали за один оборот).

Решение


Шаг спирали — это расстояние, пройденное по оси x за время T, равное P = vx T

Но время,


Протон испытывает заметное ускорение в магнитном поле, поэтому шаг спирали почти в шесть раз больше радиуса спирали.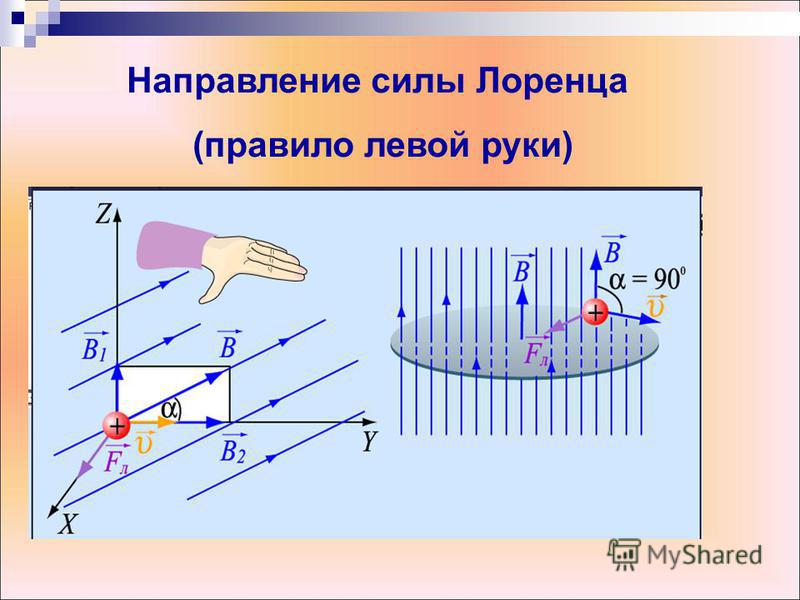 Пример 3.24 . Вычислите расстояние между двумя изотопами после того, как они закончат полукруг. Также вычислите время, затрачиваемое каждым изотопом на прохождение одного полукруга. (Дано: массы изотопов: m235 = 3,90 x 10-25 кг и m238 = 3,95 x 10-25 кг)


Раствор

Поскольку изотопы однократно ионизированы, они имеют одинаковый заряд, равный заряду электрона, q = — 1,6 × 10 -19 С. Масса урана 23592U и 23892U составляет 3,90 × 10–25 кг и 3,95 × 10–25 кг соответственно. Приложено магнитное поле, B = 0,500 Тл. Скорость электрона 1,00 × 105 м с-1, тогда

(а) радиус пути 23592U равен r235


Диаметр полукруга из-за до 23892U равно d238 = 2r238 = 98,8 см

Следовательно, расстояние между изотопами равно Δd = d238 − d235 = 1,2 см

(б) Время, затрачиваемое каждым изотопом на прохождение одного полукруга, равно

9 Обратите внимание, что даже несмотря на то, что разница между массами двух изотопов очень мала, такое расположение помогает нам преобразовать эту небольшую разницу в легко измеримое расстояние разделения. Это устройство известно как масс-спектрометр. Масс-спектрометр используется во многих областях науки, особенно в медицине, космонавтике, геологии и т. д. Например, в медицине анестезиологи используют его для измерения дыхательных газов, а биологи используют его для определения механизмов реакции при фотосинтезе.

3. Движение заряженной частицы в скрещенных электрическом и магнитном полях (селектор скорости):

Решенные примеры задач

ПРИМЕР 3.25

величина магнитного поля 0,83 Тл. Предположим, электрон ускоряется с потенциалом 200 В, будет ли он показывать нулевое отклонение?. Если нет, то при каком потенциале он покажет нулевое отклонение.

Решение:

Электрическое поле, E = 6,0 × 106 НКл-1, и магнитное поле, B = 0,83 Тл.

Затем


Когда электрон движется с этой скоростью, он демонстрирует нулевое отклонение. Поскольку ускоряющий потенциал равен 200 В, электрон приобретает кинетическую энергию благодаря этому ускоряющему потенциалу. Следовательно,


Поскольку масса электрона m = 9,1×10−31 кг и заряд электрона |q| = e = 1,6 × 10−19 Кл. Скорость за счет ускоряющего потенциала 200 В


Поскольку скорость v200 > v, электрон отклоняется в сторону направления силы Лоренца. Итак, чтобы иметь нулевое отклонение, потенциал, который мы должны предоставить, равен


V = 148 65 В

4. Циклотрон:

Решанные примеры задачи

Пример 3.26

Предположим, что циклотрон работает для аккуратных протонов с магнитным полем. Вычислите частоту, при которой электрическое поле между двумя Ди может быть изменено на противоположное.

Раствор

Магнитное поле B = 1 Тл

Масса протона, mp = 1,67 × 10–27 кг

Заряд протона, q = 1,60 × 10–19C


5. Сила, действующая на проводник с током, помещенный в магнитное поле:

Решенные примеры задач

ПРИМЕР 3.

27

Металлический стержень лежит горизонтально на поверхности а линейной плотностью 0,25 кг. гладкая наклонная плоскость, образующая с горизонтом угол 45º. Стержень не может соскальзывать вниз при пропускании через него тока, когда на него действует магнитное поле напряженностью 0,25 Тл в вертикальном направлении. Вычислите силу тока, протекающего по стержню, чтобы он оставался неподвижным.


Решение

Линейная плотность стержня, т. е. масса на единицу длины стержня, равна 0,25 кг м-1

⇒  м / l  0 = 0,25 кг м3–1. ток, протекающий по металлическому стержню. Направление электрического тока в бумагу. Направление магнитной силы IBl задается правилом левой руки Флеминга.


Для равновесия,

мг  sin 45º =  IBl  cos 45 º

⇒ I  = I/B m/l   g tan 45 º

⇒ I = 9,8 А

Итак, нам нужно обеспечить ток 9,8 А, чтобы металлический стержень оставался неподвижным.

Метки: Физика, 12-й курс Физика: Магнетизм и магнитные эффекты электрического тока

Учебный материал, Лекционные заметки, Задание, Справочник, Вики-описание, краткое описание

12-й курс Физика: Магнетизм и магнитные эффекты электрического тока: Сила Лоренца: Решенные примеры задач | Физика

Сила Лоренца – определение, формула, примеры

Когда заряды движутся под действием магнитного поля. Они испытывают на себе силы, которые заставляют их иногда менять свое направление, или если они не в состоянии это сделать. Силы этих отдельных зарядов становятся силой, действующей на проводник, несущий их. Применений этого конкретного явления в реальной жизни очень много. Все двигатели, которые используются во многих устройствах вокруг нас, работают по этому принципу. Чтобы понять и оценить работу этих устройств, необходимо понять эту концепцию. Рассмотрим это понятие подробнее.

Магнитное поле и сила Лоренца

Допустим, имеется точечный заряд «q», который движется со скоростью «v» и находится в точке «r» в момент времени «t» в присутствии обоих электрических полей E(r ) и магнитное поле B(r). Оба этих поля действуют на заряд под своим воздействием с некоторой силой. Сила заряда за счет их влияния впервые была указана Х. А. Лоренцем. Формула этой силы была выведена Лоренцем на основе тщательных экспериментов, проведенных Ампером и другими.

Сила, действующая на электрический заряд «q» за счет обоих этих полей, определяется формулой mag

Эта сила называется Сила Лоренца .

Глядя на формулу, известна связь между электрическим полем и силой, которую заряды испытывают под его воздействием. В случае силы, испытываемой под действием магнитного поля, делаются следующие наблюдения: 

  1. Зависит от q, v и B (заряд, скорость частицы и магнитное поле). В случае отрицательного заряда направление силы меняется на противоположное.
  2. Существует векторное произведение между скоростью и магнитным полем. Направление силы перпендикулярно обеим величинам. В этом случае скорость и магнитное поле становятся параллельными. Сила, действующая на заряд, становится равной нулю.
  3. Магнитная сила на любом заряде равна нулю, если он не движется, то есть |v| = 0,

На приведенном выше рисунке показано направление магнитной силы, действующей на частицу. Сила, действующая на положительно заряженную частицу со скоростью v и составляющую угол θ с направлением магнитного поля, определяется правилом правой руки.

На нем изображена движущаяся заряженная частица, которая отклоняется от своего пути из-за магнитного поля. Обратите внимание, что оба заряда отклоняются в разные стороны.

Примеры задач

Вопрос 1: Определите величину силы, возникающей при выдерживании единичного заряда под действием электрических полей силой 5 Н/Кл.

Ответ:

Для заряда определяется выражением

F = qE

⇒ F = (1)(5)

⇒ F = 5 Н/с.

Вопрос 2: Определите величину силы, действующей, когда заряд 5 Кл находится под действием электрических полей напряженностью 25 Н/Кл.

Ответ: 

Значение for для заряда определяется формулой: 

F = qE

⇒ F = (5)(25) 

⇒ F = 125 Н/с.

Вопрос 3: Определите величину силы, действующей, когда заряд 5 Кл движется со скоростью 10 м/с под действием электрического поля напряженностью 25 Н/Кл. Магнитное поле величиной 10 перпендикулярно направлению электрического поля и скорости. Найдите величину силы, действующей на заряд.

Ответ: 

Для заряда определяется выражением 90))

⇒ F = 125 + 5(250)

⇒ F = 125 + 1250

⇒ F = 1375 Н

со скоростью 10 м/с под действием электрических полей напряженностью 5 Н/Кл. Магнитное поле величиной 5 перпендикулярно направлению электрического поля и скорости. Найдите величину силы, действующей на заряд.

Ответ:

Для на заряде дается выражение (90))

⇒ F = 50 + 500 

⇒ F = 550 Н

Вопрос 4: Определите величину силы, действующей при движении заряда -2 Кл со скоростью 10 м/с под действием 5 Н/З электрические поля.