Формулы для базового егэ по математике: задания, ответы, решения. Обучающая система Дмитрия Гущина.

Год до ЕГЭ по математике: как подготовиться? / TeachMePlease

В 2018 году Единый государственный экзамен (ЕГЭ) по математике останется обязательным и будет разделён на два экзамена: базовый и профильный. Какой из них сдавать, на какие темы обратить внимание и как подготовиться к экзамену – ответы ищите в нашем материале.

Что выбрать: базовый экзамен или профильный

Результата базового экзамена хватит, чтобы получить аттестат и выпуститься из школы, с ним нельзя поступить на специальность, где в перечне экзаменов указана математика. Также оценку по базовому экзамену засчитывают в техникумах и колледжах. Базовый экзамен состоит из 20-ти простых заданий по алгебре, геометрии, началам математического анализа, теории вероятности и статистике, длится 3 часа. За каждый верный ответ даётся один балл. Экзамен оценивается по пятибалльной системе. В 2017 году экзамен считался пройденным, если ученик верно выполнил 7 заданий и более.

Профильный ЕГЭ проводится для выпускников, которые планируют поступить на специальности с математикой в списке вступительных экзаменов. Он состоит из двух частей: первая включает 8 базовых заданий с кратким ответом; вторая часть содержит задания повышенного уровня сложности: 4 задания с кратким ответом и 7 – с развёрнутым. Экзамен длится 3 часа 55 минут. Экзамен оценивается по стобалльной шкале, для поступления в высшее учебное заведение в 2017 году нужно было набрать минимум 27 баллов.

Выпускник имеет право сдавать оба экзамена: профильный и базовый. Если вы точно решили, что математика при поступлении в ВУЗ не нужна, выбирайте базовый экзамен. Математика значится среди вступительных предметов – идите только на профильный экзамен. Не уверены, понадобится ли математике при поступлении, сдавайте оба экзамена: базовый для аттестата, профильный для вуза.

Не стоит опрометчиво считать, что для всех гуманитарных специальностей не потребуется математика. При поступлении на направления «Фундаментальная и прикладная лингвистика», «Клиническая психология», «Психология служебной деятельности» в Московский государственный университет требуется сдать ЕГЭ по математике профильного уровня. Внимательно изучите требования к поступлению на специальности в каждом конкретном ВУЗе.

Чаще всего выпускники на ЕГЭ по математике невнимательно читают задания, ошибаются в расчётах и заданиях по геометрии

Как избежать ошибок

В методических рекомендациях 2017 года Федерального института педагогических измерений (ФИПИ) названы главные ошибки, которые совершают все выпускники на экзамене по математике: ученики невнимательно читают задания, ошибаются при счёте, неверно читают геометрические фигуры.

Не совершить глупые ошибки на экзамене по математике помогут следующие рекомендации:

Внимательно читайте задания. Прочтите вопрос несколько раз про себя, не пробегайте условие задачи глазами. Потраченная минута не отнимет большого количества времени на экзамене, зато предостережёт от обидной ошибки.
Не пренебрегайте геометрией. В базовом ЕГЭ 4 задачи по геометрии из 20-ти, в профильном 5 из 19-ти. Выпускники, сдающие базовый вариант, могут не налегать на задания по геометрии, два из них можно решить, используя базовые знания по геометрии за 7-9 классы: вычисление площадей треугольника и трапеции, длин отрезков, углов геометрических фигур. Тому, кто выбрал профильную математику, нужно обратить особое внимание на задания по стереометрии, выпускники 2017 года совершили в них до 57% ошибок.

Считайте и пересчитывайте. Сложные вычисления обязательно стоит выполнять на черновике. Записывайте все шаги в решении аккуратно и последовательно. В примерах не забывайте ставить скобки, это поможет не запутаться в порядке выполнения действий.
Внимание на тригонометрию. Выучите назубок формулы корней простейших тригонометрических уравнений, табличные значения тригонометрических функций – в заданиях на решение тригонометрических уравнений ошибаются 63,7% выпускников.

Методисты ФИПИ не рекомендуют ограничивать подготовку к ЕГЭ по математике вариантами прошлых лет. Ученик привыкает решать похожие задания по аналогии и может быть не готов к решению непривычной задачи на экзамене. Более успешный метод подготовки – решать большое количество задач по каждой теме от простой к сложной, изучать методы решения задач. Занятия по сборникам могут быть полезны, чтобы привыкнуть к формату проведения экзамена, записи ответов, научиться следить за временем.

Как подготовиться

Прорешать несколько открытых вариантов прошлых лет. Разбить задания на три типа: первый тип – задачи, которые решаются без проблем; второй тип – бывают случайные ошибки; третий тип – не знаешь, как решать такие задания.
Довести до совершенства решение заданий второго типа. Это база, знание которой поможет в решении более сложных заданий.
Не реже раза в неделю решать несколько заданий первого типа. Это поможет контролировать ситуацию.
Для изучения заданий третьего типа понадобится дополнительная помощь. Разобрать сложные задачи можно на подготовительных занятиях к ЕГЭ по математике или самостоятельно, поискав и проанализировав решения подобных задач в открытых источниках.

Получение аттестата и поступление на специальность с профильной математикой требуют разной подготовки. Гуманитариям достаточно повторить базовые математические формулы и понятия, научиться внимательно читать условия заданий, не ошибаться в вычислениях. Математикам придётся потратить больше сил на построение логических доказательств в заданиях по геометрии, решение задач по стереометрии, сосредоточиться на текстовых задачах. Также тому, кто выбрал профильный экзамен, придётся научиться организовывать порядок выполнения заданий, контролировать время их выполнения, перепроверять решения задач.

Подробнее о том, как подготовиться к профильному экзамену по математике, мы напишем в следующем материале. Следите за обновлениями в блоге.

Базовый экзамен по математике

В отличие от других ЕГЭ базовый экзамен по математике оценивают по пятибалльной шкале, а для того чтобы получить право на аттестат, выпускнику достаточно заслужить хотя бы тройку.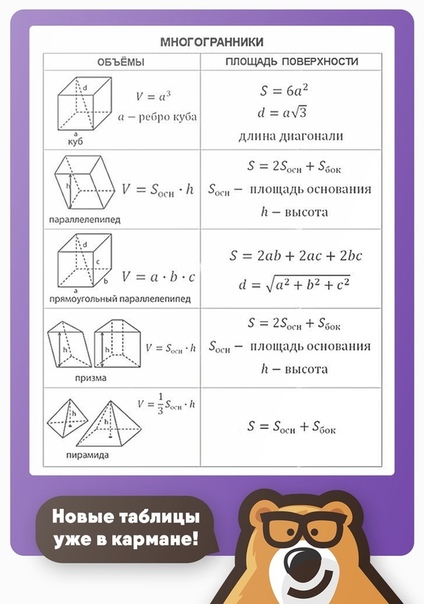

Всего в 2019 году ЕГЭ по математике базового уровня сдают более 300 000 одиннадцатиклассников. Это те ребята, которые выбрали для поступления вузы и направления подготовки, где не требуется математика. Кстати, профильный уровень экзамена выбрали более 400 000 человек.

Школьники должны будут написать контрольную работу, состоящую из 20 заданий, ровно за три часа.

На какие моменты требуется обратить особое внимание?

Самое главное: внимательно читайте текст задачи. Наиболее распространенная ошибка в течение уже нескольких лет – школьники решают не ту задачу, которая была предложена. Так происходит даже с несложными заданиями.

Второй момент, который надо иметь в виду, – это вычисления. Не стоит спешить и считать в уме, возьмите черновик и внимательно решайте примеры столбиком. Самое обидное, как отмечают эксперты ЕГЭ, когда выпускники, правильно решая сложную задачу, делают ошибки просто в вычислениях.

Большая часть ошибок старшеклассников на базовом экзамене по математике – это материал из учебников пятого-шестого класса. Поэтому ребятам совет: не забудьте повторить эту часть программы, даже если она кажется вам несложной.

По итогам ЕГЭ прошлых лет, многие школьники испытывают сложности, решая задания с элементами матанализа: менее 50 процентов ребят способны дать характеристику производной, опираясь на график ее функции (задание N 14).

В задании N 17 не могут решить логарифмические неравенства.

Трудности вызывает весь блок задач по геометрии (планиметрии и стереометрии, номера 8, 15, 13, 16).

Эксперты советуют выполнять задания блоками. Распределяя время, в первую очередь заниматься более легкими для вас заданиями, в которых вы уверены. И уже после них начинайте работать с трудными задачами.

Чтобы не допустить ошибок, полезно записывать свои рассуждения в черновике, проверять вычисления и только после этого, переписывать задачу в бланк.

Ознакомьтесь заранее со справочными материалами, размещенными на официальном сайте ФИПИ (Федеральный институт педагогических измерений). В частности в них содержатся формулы, необходимые для измерения объемов тел, площадей фигур и другие.

Все эти данные будут доступны и на базовом экзамене по математике, а вот на профильном ЕГЭ выпускники лишены такой возможности.

Likes(0)Dislikes(0)

ЕГЭ математика 2020: все, что нужно знать

Ежегодно все одиннадцатиклассники сдают Единый Государственный Экзамен по математике. Последние несколько лет его разделили на два уровня профильный и базовый.

ЕГЭ математика база 2020 предназначена для ребят, для которых математика не является обязательным при поступлении в высшее учебное заведение, например филологи, историки, журналисты, художники сдают именно базовую часть экзамена.

Если же школьник решил поступать на факультет, где математика профиль, то он ЕГЭ по математике 2020 профильный уровень.

Что такое базовый уровень ЕГЭ по математике

Базовый уровень нужен для тех ребят, которые дальше не будут продолжать обучения в заведениях высшего или среднего-профессионального образования, если оценка нужно только для аттестата, или же предмета нет среди тех, которые требуются в ВУЗе.

В него входит двадцать заданий разной степени сложности. Оцениваются они в баллах от 0 до 2, и для того, чтобы получить тройку, ученик должен справиться хотя бы с семью задачами.

ЕГЭ математика база 2020 включает в себя задачи с первого по девятый класс школьной программы. Первые шестнадцать заданий относительно простые. Оставшиеся три ближе к профильному уровню.

Профильный уровень ЕГЭ по математике

Для ребят, которым при поступлении требуется математика, нужно сдавать ЕГЭ по математике 2020 профильный уровень. Он состоит из девятнадцати заданий. Их можно разделить на две части. В первую входит восемь заданий, которые требуют краткий ответ. Они по уровню сложности похожи на задачи из базового уровня.

Остальные одиннадцать — задания повышенного уровня сложности. Хотя с 2015 года отметили часть C, задачи на логику никто не отменял. С девятого по двенадцатое задание нужно в ответе указать десятичную дробь или целое число. Остальные задания требуют от ученика развернутого ответа.

Для того, чтобы успешно сдать как профиль, так и базу, нужно усердно готовится. Решение простых задач доводить до автоматизма. Ребенок должен знать основные формулы и уметь быстро и правильно считать без калькулятора.

Первые простые задания проверяет компьютер. Поэтому очень важно научиться правильно заполнять бланки. Даже если ученик верно написал ответ, но компьютер его не распознал, балл не засчитывается.

Задания повышенной сложности ЕГЭ по математике 2020 профильный уровень проверяет комиссия. Здесь главное правильно построенное рассуждение. Ребенок должен уметь грамотно излагать свои мысли.

#Математика

Читайте нас первыми — добавьте сайт в любимые источники.

Добавить комментарий

{«commentics_url»:»\/\/express-novosti.ru\/comments\/»,»page_id»:722608,»enabled_country»:false,»enabled_state»:false,»state_id»:0,»enabled_upload»:false,»maximum_upload_amount»:3,»maximum_upload_size»:5,»maximum_upload_total»:5,»securimage»:true,»securimage_url»:»\/\/express-novosti.ru\/comments\/3rdparty\/securimage\/securimage_show.php?namespace=cmtx_722608″,»lang_error_file_num»:»\u041c\u0430\u043a\u0441\u0438\u043c\u0443\u043c %d \u0444\u0430\u0439\u043b\u043e\u0432 \u043c\u043e\u0436\u0435\u0442 \u0431\u044b\u0442\u044c \u0437\u0430\u0433\u0440\u0443\u0436\u0435\u043d\u043e.»,»lang_error_file_size»:»\u041f\u043e\u0436\u0430\u043b\u0443\u0439\u0441\u0442\u0430, \u0437\u0430\u0433\u0440\u0443\u0437\u0438\u0442\u0435 \u0444\u0430\u0439\u043b \u0440\u0430\u0437\u043c\u0435\u0440\u043e\u043c \u043d\u0435 \u0431\u043e\u043b\u0435\u0435 %d MB.»,»lang_error_file_total»:»\u041e\u0431\u0449\u0438\u0439 \u0440\u0430\u0437\u043c\u0435\u0440 \u0432\u0441\u0435\u0445 \u0444\u0430\u0439\u043b\u043e\u0432 \u0434\u043e\u043b\u0436\u0435\u043d \u0431\u044b\u0442\u044c \u043d\u0435 \u0431\u043e\u043b\u0435\u0435 %d MB. «,»lang_error_file_type»:»\u041c\u043e\u0436\u043d\u043e \u0437\u0430\u0433\u0440\u0443\u0436\u0430\u0442\u044c \u0442\u043e\u043b\u044c\u043a\u043e \u0438\u0437\u043e\u0431\u0440\u0430\u0436\u0435\u043d\u0438\u044f.»,»lang_text_loading»:»\u0417\u0430\u0433\u0440\u0443\u0437\u043a\u0430 ..»,»lang_placeholder_state»:»\u0420\u0435\u0433\u0438\u043e\u043d»,»lang_text_country_first»:»\u0421\u043d\u0430\u0447\u0430\u043b\u0430 \u0432\u044b\u0431\u0435\u0440\u0438\u0442\u0435 \u0441\u0442\u0440\u0430\u043d\u0443″,»lang_button_submit»:»\u0414\u043e\u0431\u0430\u0432\u0438\u0442\u044c»,»lang_button_preview»:»\u041f\u0440\u0435\u0434\u0432\u0430\u0440\u0438\u0442\u0435\u043b\u044c\u043d\u044b\u0439 \u043f\u0440\u043e\u0441\u043c\u043e\u0442\u0440″,»lang_button_remove»:»\u0423\u0434\u0430\u043b\u0438\u0442\u044c»,»lang_button_processing»:»\u041f\u043e\u0434\u043e\u0436\u0434\u0438\u0442\u0435…»}

{«commentics_url»:»\/\/express-novosti.ru\/comments\/»,»auto_detect»:false}

ЕГЭ по математике: материалы для подготовки

Алгебра
• Графики числовых функций
1-3. Преобразование графиков
4. Чтение графиков
• Неравенства (1)
1. Числовые неравенства и их свойства
2. Графическое решение неравенств
3. Двойное неравенство
4. Числовые промежутки
5. Линейные неравенства
6. Системы линейных неравенств
7. Квадратные неравенства
8. Дробно — рациональные неравенства
• Неравенства (2)
1. Метод интервалов
2. Показательные неравенства
3. Логарифмические неравенства
4. Тригонометрические неравенства
5. Графическое решение неравенств
6. Неравенства с двумя переменными
• Производные
1. Производные основных функций
2. Вычисление производной
3. Исследование функции с помощью производной
4. Касательная к графику функции
5. Наибольшее и наименьшее значения функций
6. График производной функции
7.

Вторая производная функции. Выпуклость функции, точки экстремумов и перегиба
• Решение уравнений (1)
1. Линейные уравнение с одной переменной
2-3. Системы уравнений с двумя переменными
4. Неполные квадратные уравнения
5. Квадратные уравнения
6. Теорема Виета
7. Дробные уравнения
8. Уравнения с двумя переменными и их графики
9. Графическое решение уравнений
10. Графическое решение систем линейных уравнений
11. Графическое решение систем НЕлинейных уравнений
12. Выражения. Тождества. Уравнения
• Решение уравнений (2)
1. Методы решения уравнений
2-3. Иррациональные уравнение
4. Показательные уравнения
5. Логарифмические уравнения
6. Тригонометрические уравнения
7-8. Решение тригонометрических уравнений
9. Графическое решение уравнений
• Тригонометрия и логарифмы
1-3. Формулы тригонометрии
4-6. Логарифм и его свойства
• Формулы и преобразование выражений
1-2. Формулы сокращенного умножения
3. Степени с натуральным и целым показателями
4. Степень с рациональным показателем
5. Квадратный корень и его свойства
6. Действия с квадратными корнями
7. Корни натуральной степени
8. Одночлены и многочлены
9. Действия с многочленами
10. Разложение многочлена на множители
• Функции (1)
1. Прямая пропорциональность
2. Обратная пропорциональность
3. Линейная функция
4. Функции y=x2 и y=x3
5. Функции с корнем
6-7. Квадратичная функция
8. Функции и их графики
• Функции (2)
1. Тригонометрическая окружность. Синус и косинус угла
2. Тригонометрическая окружность. Тангенс и котангенс угла
3. Тригонометрические функции — синус и косинус
4. Тригонометрические функции — тангенс и котангенс
5. Обратные тригонометрические функции — арксинус и арккосинус
6. Обратные тригонометрические функции — арктангенс и арккотангенс
7.

Степенная функция
8. Показательная функция
9. Логарифмическая функция
10. Графики функций
11. Взаимно-обратные функции
12. Свойства функций
13. Асимптоты графиков функций
• Числа, последовательности, проценты
1. Числовые множества
2. Числовые последовательности
3. Арифметическая прогрессия
4-5. Геометрическая прогрессия
6. Сложные проценты

Геометрия (планиметрия)

• Многоугольник
1. Свойства параллелограммов
2. Трапеция
3. Признаки параллелограмма и его видов
4. Свойства многоугольников
5. Теорема Фалеса
6. Правильные треугольник и четырехугольник
7. Правильные шестиугольник и восьмиугольник
8-9. Площадь многоугольника
• Окружность
1. Окружность. Хорды и касательные
2. Окружность, описанная около треугольника
3. Окружность, вписанная в треугольник
4. Центральные и вписанные углы
5. Свойства хорд и секущих
6. Вписанные и описанные четырехугольники
7. Длина окружности и площадь круга
• Треугольник
1. Виды треугольников. Равные треугольники
2. Признаки равенства треугольников
3. Основные линии в треугольнике
4. Равнобедренный треугольник
5. Отношения отрезков в треугольнике
6. Прямоугольный треугольник
7. Теорема Пифагора
8. Синус, косинус, тангенс прямоугольного треугольника
9. Подобие треугольников
10. Теорема косинусов
11. Теорема синусов
12-13. Площадь треугольника
• Углы
1. Измерение отрезков и углов
2. Смежные и вертикальные углы
3. Биссектриса угла. Перпендикулярные прямые
4. Признаки параллельности прямых
5. Свойства параллельных прямых
6. Сумма углов треугольника. Внешний угол

Геометрия (стереометрия)

• Вычисление расстояний и углов
1. Расстояние между двумя точками
2. Расстояние от точки до прямой
3. Расстояние от точки до плоскости
4.

Расстояние между скрещивающимися прямыми
5. Угол между скрещивающимися прямыми
6. Угол между прямой и плоскостью
7. Двугранные углы
8. Угол между двумя плоскостями
• Круглые тела
1. Цилиндр
2. Конус
3. Шар. Сфера
4-5. Комбинации шара и пирамиды
6. Комбинации конуса и пирамиды
7. Комбинации цилиндра и призмы
8. Комбинации шара и призмы
9. Площади поверхностей круглых тел (S)
10. Объёмы круглых тел и их частей (V)
• Многогранники
1. Призма
2. Параллелепипед
3. Пирамида
4. Виды пирамид
5. Правильная пирамида
6. Усеченная пирамида
7. Площади поверхностей и объемы

Курс подготовки к ЕГЭ по базовой (непрофильной) Математике

Скидка 20% до 15.02.2021 (цена с учетом скидки)

Курс подготовки к ЕГЭ по математике включает все теоретические знания и практические навыки, необходимые для успешного прохождения итоговой аттестации на базовом уровне. В течение 4,5 месяцев, обучающиеся, под руководством репетитора по математике, смогут обобщить и углубить свои знания по всем содержательным разделам.

Подготовка к ЕГЭ по математике (базовый уровень) актуальна для всех выпускников 11-х классов, желающих получить аттестат, но не планирующих поступать в вуз, или поступающих на направления подготовки, не требующих в качестве вступительного испытания экзамена по предмету «Математика».

Цель и структура курс

Цель – проработка с обучающимися заданий базового уровня с упором на применение полученных знаний на практике, на формирование логического мышления и умения работать с информацией (анализ данных графиков и таблиц, использование вероятностных и статистических моделей, умение исследовать простейшие геометрические конструкции).

Вариант экзаменационной работы представляет собой один блок, содержащий 20 заданий, предполагающих наличие краткого ответа. Задания имеют базовый уровень сложности. ЕГЭ математика (базовый) направлен на диагностику того, насколько полно выпускники освоили базовые умения и практические навыки, позволяющие применить математические знания в повседневных ситуациях.

Технология обучения

За основу наших занятий принята строго классическая модель организаций уроков: от классной работы к домашнему заданию. Онлайн-уроку в группе присущи все элементы обычного урока в школе:

объяснение учителем нового материала у доски (экран Zoom, Disсord, Scype) с использованием платформы mathematicos.com;
приглашение ученика к доске и парная работа с ним;
выполнение самостоятельной работы слушателями в своих тетрадях под руководством виртуального преподавателя на платформе mathematicos;
обсуждение в виртуальном классе тонкостей процесса решения примеров и упражнений.

При выполнении домашнего задания слушателей консультирует виртуальный онлайн преподаватель, который step – by – step оказывает индивидуальную помощь по исправлению допущенных ошибок и неверных математических действий.

Особенности нашей технологии

Благодаря применению инновационной технологии Mathematicos мы достигаем увеличения объема и интенсивности прохождения материала. В основе этой интерактивной технологии изучения математики – система искусственного интеллекта.

Рядом с учеником в режиме реального времени ежесекундно находится электронный тьютор. Встроенные подсказки и комментарии сопровождают этапы решения и выполняемые действия учеником. Виртуальный преподаватель готов предупредить возможные ошибки. Вместе с нашим онлайн-репетитором, у вас есть возможность в несколько раз повысить объем изученного материала в единицу времени!

«ПОДГОТОВКА К ЕГЭ. БАЗОВЫЙ УРОВЕНЬ.»

Открытый урок по геометрии в 11 кл..( слайд 1)

Данный урок является одним из уроков, отведенных в 11 классе на подготовку к ЕГЭ.

С темой «Площади» учащиеся начинают знакомиться в 8 классе при изучении свойств геометрических фигур на плоскости. В связи с введением новой версии ЕГЭ по математике, процент геометрического материала в заданиях увеличился и составляет 27% от всей работы профильного уровня и 20% базового уровня. Для решения этих задач необходимо твердое владение теоретическим материалом, а именно свойствами заданных плоских и пространственных фигур, применять эти свойства в ходе вычислений. Для успешного решения геометрических задач необходимо иметь прочные базовые знания, что поможет выделить ключевую идею задачи и наметить план ее решения. Решение геометрических задач требует также иметь необходимые умения логически мыслить, быть внимательным.

( слайд 2)

Тема: «Решение геометрических задач ЕГЭ на вычисление площадей плоских фигур на сетке и в координатной плоскости №8 базового уровня и №3 профильного уровня. ( слайд 2)

Триединая цель урока:

Образовательная:

систематизировать и обобщить знания учащихся по теме «Площади плоских фигур».

Развивающая:

способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения;
способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях.

Воспитательная:

содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.

Оборудование: компьютер, мультимедийный проектор, презентация, раздаточный материал : листы с заданиями, листы самооценки.

Методы: проблемно поисковый, личностно-ориентированное обучение, самостоятельная работа.

Тип урока: урок обобщения и систематизации знаний.

Задачи урока:

1.Повторить теоретический материал (формулы площадей плоских фигур).

2.Рассмотреть типы и виды задач на вычисление площадей плоских фигур на сетке и в координатной плоскости..

3.Совершенствовать умения применять различные способы решения задач данного вида.

4.Совершенствовать умение использовать образовательные ресурсы сети Internet.

План урока.

Организационный момент.

– Приветствие учащихся.
– Психологический настрой для вовлечения в работу по теме.
– Объяснение учащимся правил работы на уроке.
– Мотивация учебной деятельности через осознание учащимися значимости изучаемого материала.
– Сообщение темы, цели и задачи урока, этапов урока.

Актуализация знаний и систематизация теоретического материала.

Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).
На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.
Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.

Решение заданий.

Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно. Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике».

Создание проблемной ситуации.

Методы вычисления площадей плоских фигур. Исследование.
Рефлексия.
Итог урока.
Домашнее задание.

Организационный момент.

Здравствуйте, ребята, садитесь.

«Умение решать задачи — такое же практическое искусство, как умение плавать или бегать на лыжах.

Ему можно научиться только путём подражания или упражнения» (Джордж Пойа). (венгерский, швейцарский и американский математик 19-20вв.) . .( слайд 3)

Мы с вами закончили изучение школьного курса геометрии и теперь занимаемся вопросами повторения основных ее разделов и подготовкой к ЕГЭ.

Что помогает подготовке к ЕГЭ:

С психологической точки зрения. Неоднократная репетиция ситуации экзамена, формирование адекватной самооценки, позитивный настрой на экзамен.

С методической точки зрения. Тренинг по совершенствованию вычислительных навыков, организация зачетов, регулярное проведение уроков обобщения, проведение в течении года диагностических работ и репетиционных экзаменов, анализ результатов и работа по коррекции.

На предыдущих уроках мы решали задачи на нахождение площадей плоских фигур, и площадей поверхности геометрических тел.

Тема «Площади» является ключевой в курсе геометрии.

А что необходимо знать, чтобы решать хорошо задачи по этой теме?

Для решения этих задач необходимо твердое владение теоретическим материалом, а именно свойствами плоских и пространственных фигур, применять эти свойства в ходе вычислений, формулами.

Тема «Площади» имеет большое значение для успешной сдачи экзамена, но не только.

Скажите, а эта тема может найти свое применение в практической жизни человека?

Именно задачи по геометрии у большинства учащихся вызывают затруднения. Встретив геометрическую задачу в тексте, многие даже не прочитав ее, пропускают. А ведь эти задачи бывают проще, чем задачи из курса алгебры или математики. Их решение занимает гораздо меньше времени и не требуют громоздких вычислений.

Сегодня на занятии мы обобщим и систематизируем основные вопросы теории, необходимые для решения геометрических задач Единого государственного экзамена. Разберем решения основных типов задач по геометрии ЕГЭ.

В экзаменационную работу по математике базового уровня включено четыре задач из курса геометрии – это №№ 8,3,15 и 16. Мы сегодня рассмотрим методы решения задания №8.

Актуализация знаний и систематизация теоретического материала.

Чтобы решить задания 8 нужно хорошо знать площади плоских фигур.

Учитель: «А теперь давайте вспомним формулы площадей некоторых фигур.

Начнём с треугольника. Сейчас мы составим кластер.

У вас на столах находятся два листа формата А4. Один для самооценки второй для кластера . На листе для кластера делается надпись «Площади плоских фигур». Затем учащимся предлагается с лева записать виды плоских фигур и справа, их площади. На листе самоанализа также с лева название фигуры , а с права «+» если вы знаете формулу и «-» если не знаете.

Учащиеся в произвольной последовательности перечисляют формулы площадей треугольника, а учитель, открывает названные формулы.

(Слайды 4, 5)

Учитель: «Давайте вспомним ещё несколько формул, связанных с понятием «Площадь треугольника».

Учитель: Какие формулы площадей четырёхугольников вы знаете? Давайте вспомним формулы площади круга и сектора.

Учащиеся перечисляют формулы площадей параллелограмма, прямоугольника, ромба, квадрата, трапеции, а учитель, открывает названные формулы.( Слайды 6).

Решение заданий. Практическая работа.

Раздать модели геометрических фигур, площади которых , нужно найти.

Задание: Сделать необходимые измерения и найти площадь данной плоской фигуры.

Треугольник.
Трапеция.
Прямоугольник.

Внимание на доску.

Сложность задания зависит от того как расположена фигура по отношению к линии сетки. Существуют несколько способов решения таких задач.

Мы сейчас исследуем эти методы.

Методы вычисления площадей плоских фигур. Исследование.

Объект исследования: задачи на клетчатой бумаге

Предмет исследования: задач на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.

Методы исследования: сравнение, обобщение, аналогии, изучение литературы и Интернет-ресурсов, анализ информации.

Цель исследования:

выбрать главную, интересную, понятную информацию
Проанализировать и систематизировать полученную информацию
Найти различные методы и приёмы решения задач на клетчатой бумаге
проверить формулы вычисления площадей геометрических фигур с помощью формулы Пика.

1). Способ подсчета клеток. (слайд №7)

Задание для самостоятельного решения. (слайд №8).

2) Применение формул длы вычисления площадей известных фигур.

(Слайд №9 )

Задание для самостоятельного решения. (слайды № 10).

3) Метод разбиения на части. (слайд №11).

Задание для самостоятельного решения (слайд №12).

4). Метод достраивания до прямоугольника. (слайд №143.

Задание для самостоятельного решения (слайд №14).

5.Способ нахождение площади по координатам вершин.

А теперь посмотрите на следующие фигуры.

(слайд №15) и (слайд №16).

6.) Метод Пике. (слайд №17). . (слайд №18).

Эксперимент.

Найти площадь фигуры на ксетке (слайд №219).

Методом достроения до прямоугольника.
Методом Пике.

Рефлексия.

Ребята мы рассмотрели с вами несколько методов нахождения площади плоских фигур. Перечислите их.

– Что дает нам прием «Кластер»?
– Имеет ли практическое значение данная тема?
– Понравился ли вам урок?

Домашнее задание. Задания из банка открытых заданий ЕГЭ распечатанные с сайта «Решу ЕГЭ»

Итог урока.

Сегодня на уроке мы с вами обобщили тему «Площади» и систематизировали основные формулы с помощью приема «Кластер», увидели практическое применение данной темы для решения задач, применили знания при решении задач ЕГЭ.
Работа по закреплению данной темы будет продолжаться, так как в нашем кластере остались не заполненные места и вопросы.

Лист самооценки уч. 11 кл.______________________________

№	ЗНАНИЯ , УМЕНИЯ, НАВЫКИ	САМООЦЕНКА
		теория по данной теме. Я знаю «+»: Я не знаю (-)	Я умею решать задачи на эту тему (+), не умею (-)	План исправления недочетов
1	Формула площади треугольника по стороне и высоте опущенной к ней.
2	Формула площади треугольника по треугольника по двум сторонам и углу между ними
3	Формула площади треугольника по формуле Герона
4	Формула площади прямоугольник
5	Формула площади параллелограмма
6	Формула площади квадрата
7	Формула площади трапеции
8	Формула площади ромба
9	Формула площади круга
10	Формула площади кругового сектора

Я оцениваю свои знания и умения на оценку ___

Кластер.

П л о щ а д и
площади плоских фигур		площади стереометрических фигур

Математика подготовка к ЕГЭ | Материалы и рекомендации

Математика Подготовка к ЕГЭ. Готовитесь к экзамену? Вы попали куда нужно. Приветствую вас уважаемый посетитель! Меня зовут Александр, являюсь автором и администратором данного проекта.

Здесь для вас актуальная информация и практически всё необходимое для того, чтобы хорошо подготовиться и сдать экзамен на достойном уровне (как профильный, так и базовый). Посмотрите карту блога и вы увидите объём размещённых публикаций. Их структура такова: теория + практика с объяснениями. Регулярно добавляются новые задачи.

Важно! В структуре экзамена 2021 года по сравнению с 2020 никаких изменений не внесено. На сайте ФИПИ вы можете скачать документацию по математике и другим предметам.

Как известно, с 2015 года экзамен по математике разделён на базовый и профильный уровень. В содержании самих заданий, как правило, особых изменений не бывает — типы заданий остаются те же что были в предыдущие годы. Новых добавляется незначительное количество. Вполне можно использовать литературу и готовиться по сборникам опубликованным для выпускников прежних лет.

Профильный уровень.

Проф. уровень №1-19 (описание) ПОКАЗАТЬ/СКРЫТЬ

Экзамен включает в себя 19 задач. Они разделены на две части.

Часть 1. Состоит из 8 заданий, это задания 1-8, с кратким ответом. Процесс решения описывать здесь не требуется. Если вы владеете базовыми знаниями, то время на решение потратите немного, можно уложиться в 20-45 минут. Помните, что в ответе всегда должно получиться целое число или конечная десятичная дробь.

*Первая часть предназначена для проверки базовых знаний — эти задачи соответствуют уровню обычной средней школы без углубленного изучения математики.

Часть 2. Содержит 11 заданий по материалу курса средней школы. Это задания 9-19. Задания 9-12 повышенного уровня сложности с кратким ответом и задания 13-19 повышенного и высокого уровня сложности с развёрнутым ответом. В заданиях 13-19 необходимо привести грамотное и обоснованное решение.

*Вторая часть (9-19) подразумевает повышенный и высокий уровень знаний и навыков.

* * *

Задания 13 и 14 — никаких углублённых знаний математики не требуют. Важно грамотно оформить решение задачи.

Задачи 15 и 16 — это уже серьезный уровень. Но школьной программы также достаточно, чтобы их решить. Хорошие теоретические знания плюс навыки решения плюс умение делать выводы из начального условия — и задачи будут вами решены.

Задачи 17, 18 и 19 — самые сложные и нестандартные. Подвластны тем, кто не просто хорошо знает математику, а увлечён ей и постоянно совершенствуется. Требуется оригинальное, нестандартное мышление, смекалка, изобретательность. Само решение занимает на тетрадном листе немного места, но поразмыслить придётся.

На выполнение работы отводится 3 часа 55 минут. Калькулятором пользоваться запрещено. О его существовании советую забыть и в течение учебного года не использовать.

Базовый уровень.

Экзаменационная работа состоит из одной части, включающей 20 заданий с кратким ответом базового уровня сложности. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

Ответом к каждому из заданий 1–20 является целое число или конечная десятичная дробь, или последовательность цифр. Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов № 1 в той форме, которая предусмотрена инструкцией по выполнению задания.

Распределение заданий варианта КИМ по содержанию, видам умений и способам действий
В экзаменационной работе проверяется следующий учебный материал:
1. Математика, 5–6 классы;
2. Алгебра, 7–9 классы;
3. Алгебра и начала анализа, 10–11 классы;
4. Теория вероятностей и статистика, 7–9 классы;
5. Геометрия, 7–11 классы.

Много пишут о том, что − это ВЕЛИКОЕ испытание, стресс и прочее, такое «тяжко-неприятное» событие. В средствах массовой информации в 2011 году был сюжет о том, что какой-то школьник чуть не покончил с собой из-за не сданного экзамена. И, вообще, само озвучивание вслух слова «ЕГЭ» у многих учащихся вызывает негативную реакцию. ЗАБУДЬТЕ!!!

Забудьте о том, что это стресс, что это испытание и какое-то пороговое событие, которое изменит всю вашу жизнь в лучшую (при сдаче) или в худшею (при провале) сторону. Да! Экзамен важный, нужный и необходимый. Да, он влияет на многое. Но вы помните главное — в жизни тысячи путей и дорожек, которыми вы можете следовать. Вы молоды, даже если случится так, что экзамен не сдадите или сдадите на неожиданный для вас балл, это не приговор. Круто сданное ЕГЭ это не гарантия счастья и успеха )

Примеров успешных людей без высшего образования множество, и миллионерами становились. Просто у этих людей была в жизни цель — получить знания и навыки в каком-то направлении, достигнуть достатка, обеспечить себя и семью. И если у вас будет цель реализоваться, вы достигнете её, какой бы она ни была: хотите ли чему-то научится, получить высшее образование (пусть и не сразу после школы), организовать что-либо… Вы добьётесь этого!

Пусть на данный момент вашей целью, пока учитесь в школе, будет качественная подготовка к экзаменам и сдача его на высокий балл. Подробнее о постановке цели читайте в этой статье

Ещё обязательно посмотрите видео об одном Человеке, о нём должны знать все. Фильм разрывает мозг, понятия о ваших возможностях в этой жизни после просмотра изменятся. Что нам какие-то там школьные экзамены после этого? Кстати, он снялся в короткометражном фильме «Цирк бабочки» (вы легко найдёте его на ютубе).

Сосредоточьтесь на том, что у вас получается уже сейчас и отрабатывайте навыки. Затем постепенно разбирайтесь в том материале, по которому есть вопросы.

Вы не останетесь с экзаменом один на один. Есть множество способов и инструментов, которые вам помогут:

1. Учебники и сборники задач. Но не все учебники одинаково полезны. Поэтому внимательно изучайте книги перед покупкой.
2. Сайты и форумы. Инструмент становится все популярнее. В интернете можно найти решение практически любой задачи, а также много полезной информации. Хороших сайтов предостаточно.
3. Подготовительные курсы с небольшими группами или репетиторы. Обучение под руководством опытного педагога всегда эффективнее, чем самостоятельная работа.
4. Школа. Если в школе занятия математикой регулярны, учитель знает и любит своё дело, то вам повезло. Хороший школьный учитель даст вам многое, всё зависит от вашего интереса. Любому учителю приятно, когда ученик его проявляет.

Здесь хотелось бы сказать об организации вашего процесса обучения. Самый надежный способ сдать экзамен — это просто хорошо подготовиться. Звучит очевидно и банально ).

Основная проблема в том, что очень сложно себя заставить систематически и методично изучать теорию, повторять её и отрабатывать практике. Что ж … Как ни просто это звучит, но всё зависит именно от Вас, придётся потрудиться. Иначе никак. Если, конечно, у вас есть цель поступить на в выбранный вами ВУЗ. Даже если вы занимаетесь с репетитором, не возлагайте на него все свои надежды.

Сдавать экзамен вам, и вы должны обучаться самостоятельно. Репетитор не волшебник, это руководитель, который «активирует» вас и направляет. Знания в вашу голову он механически вставить не сможет, вы должны их осознать. Учитесь учиться!

Главное — это желание и цель. Без них никакой сайт, учитель и репетитор не поможет. Ставьте сами себе конкретные цели на конкретные сроки! Ваш высокий результат никому кроме вас самих и родителей не нужен.

!!! ВАЖНЫЙ МОМЕНТ >>>

Какой уровень знания математики у вас сейчас? Как вы его оцениваете? Обозначим некоторую точку отсчёта, относительно которой вы можете оценить свои знания и навыки. Перечислю моменты, которые не должны вызывать у вас затруднений:

1. Сложить в уме два трёхзначных числа, например 185 и 238.
2. Сложить, найти разность, умножить и разделить столбиком любые целые числа.
3. Произвести действия с дробями (сложение, вычитание, умножение, деление), сократить дробь.
4. Найти результат умножения (деления) положительных и отрицательных чисел (не потерять знак).
5. Выразить из равенства любую неизвестную величину.
6. Найти результат умножения многочленов.
7. Записать свойства корней и степеней по памяти.
8. Решить квадратное уравнение, неравенство.
9. Перечислить и построить графики основных функций.
10. Воспроизвести основные теоремы (Пифагора, косинусов, синусов, сумма углов треугольника и пр).
11. Назвать признаки равенства треугольников, подобия треугольников.
12. Озвучить определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике.
13. Воспроизвести формулы площадей (треугольник, квадрат, прямоугольник, параллелограмм, трапеция, круг, сектор круга).
14.Записать все формулы, связанные с координатной плоскостью (длина отрезка, координаты середины отрезка, координаты вектора, длина вектора, скалярное произведение).
15. Записать основные формулы тригонометрии.
16. Записать формулы сокращённого умножения.

Если вы смогли это сделать, то теоретическая база у вас отличная, если нет — учебники всегда готовы вам помочь, дело наживное. Какие бы изменения не произошли в будущем — добавят или исключат какие-либо части или задачи из состава экзамена — если у вас будет хорошая база знаний и навыков, то вы решите любую задачу.

Курс школьной математики статичен, сегодня изучают то, что и 10, 20, 30 лет назад. В будущем содержание будет тем же. Поэтому, если услышите о каких-то изменениях, не паникуйте, система (содержание) знаний останется.

Конечно, существуют небольшие нововведения, но они незначительны. Например, в 2012 добавились задачи по теории вероятностей, но посмотрев их, вы убедитесь что сложности они не представляют, большинство задач вычисляется устно.

Успеха вам во всех начинаниях!

С уважением, Александр Крутицких.

Основные математические формулы

Здесь вы найдете полный список основных математических формул, обычно используемых при выполнении основных математических вычислений.
Формула среднего значения:

Пусть a ₁, a ₂, a ₃, ……, a _n будет набором чисел, среднее значение = (a ₁ + a ₂ + a ₃, + …… + a _n) / n

Формулы дробей:

Преобразование неправильной дроби в смешанное число:

Формула пропорции:

В пропорции произведение крайностей (ad) равно произведению средних (bc),

Таким образом, ad = bc

Процент:

Процент на дробь: x% = x / 100

Формула процента: Ставка / 100 = Процент / база

Ставка: Процент.
База: сумма, от которой вы берете процент.
Процент: ответ, полученный путем умножения основания на коэффициент

Потребительские математические формулы:

Скидка = прейскурантная цена × ставка дисконтирования

Цена продажи = прейскурантная цена — скидка

Ставка дисконтирования = скидка ÷ прейскурантная цена

Налог с продаж = цена товара × ставка налога

Процент = основная сумма × ставка процентов × время

Чаевые = стоимость еды × ставка чаевых

Комиссия = стоимость услуги × ставка комиссии

Формулы геометрии:

Периметр :

Периметр квадрата : s + s + s + s
s: длина одной стороны

Периметр прямоугольника : l + w + l + w
l: длина
w: ширина

Периметр треугольника : a + b + c
a , b и c: длины трех сторон

Площадь:

Площадь квадрата : s × s
s: длина одной стороны

Площадь прямоугольника : l × w
l : длина
w: ширина

Площадь a треугольник : (b × h) / 2
b: длина основания
h: длина высоты

Площадь трапеции : (b ₁ + b ₂) × h / 2
b ₁ и b ₂: параллельные стороны или основания
h: длина высоты

объем:

Объем куба : s × s × s
s: длина одной стороны

Объем ящика : l × w × h
l: длина
w: ширина
h: высота

Объем шара : (4/3) × pi × r ³
pi: 3.14
r: радиус сферы

Объем треугольной призмы : площадь треугольника × высота = (1/2 основания × высота) × высота
основание: длина основания треугольника
высота: высота треугольника
Высота: высота треугольной призмы

Объем цилиндра : pi × r ² × Высота
pi: 3,14
r: радиус окружности основания
Высота: высота цилиндра

Имеются любые вопросы об основных математических формулах? Отправьте мне электронное письмо здесь и задавайте мне любые вопросы об этих основных математических формулах

Веселые математические головоломки
11 марта, 21 06:50
Множество забавных математических головоломок, которые дразнят ваш мозг и оттачивают ваши базовые математические навыки.
Подробнее

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

16 важнейших математических формул ACT Математические формулы, которые вам НЕОБХОДИМО знать

Давайте разберемся, из чего состоит математический раздел ACT. Всего 60 вопросов с множественным выбором из шести областей математики: предалгебра, элементарная алгебра, промежуточная алгебра, координатная геометрия, плоская геометрия и тригонометрия.Таким образом, подсчет очков и математические формулы, которые вам нужно знать, распределяются следующим образом:

Предалгебра / Элементарная алгебра: 24 вопроса, 24 балла
Промежуточная алгебра / координатная геометрия: 18 вопросов, 24 балла
Плоская геометрия / тригонометрия: 18 вопросов, 24 точки

В математическом разделе ACT есть особенность: даже после того, как вы прошли всю подготовку к тесту ACT, ACT не дает вам шпаргалки со всеми математическими формулами, записанными на них.Следовательно, вы должны их запомнить. Но некоторые важные математические формулы ACT требуются чаще, чем другие. Это то, что нужно знать. Хотя может показаться заманчивым просто предположить и уйти, лучше, если вы будете готовы с самого начала.

Давайте посмотрим на самые важные формулы в разделе.

Предалгебра / Элементарная алгебра

Эти формулы включают основы математики и алгебры. Другими словами, от ученика требуется найти неизвестную переменную.

1. Среднее арифметическое (среднее) = сумма значений / количество значений

Специально используется для вычисления среднего значения заданного набора чисел.

Например: (10 + 12 + 14 + 16) / 4 = 13

2. Вероятность = Целевые результаты / Общие результаты

Специально используется для расчета вероятности того, что что-то произойдет из набора возможных результатов.

Например: банка содержит пять синих шариков, пять красных шариков и десять белых шариков.Какова вероятность случайного выбора красного шарика?

5/20 = 0,25 или 25%

3. Квадратичная формула: x = −b ± √b²-4ac / 2a

Специально используется для определения точек пересечения по оси x квадратного (параболического) уравнения.

Например: A = 1, B = 4, C = 4

x = -4 ± √4² — 4 (1) (4) / 2 (1)
х = -4 ± √ 16-4 (4) / 2
х = -4 ± √16 — 16/2
х = -4 ± √ 0/2
х = -4 / 2
х = -2

Промежуточная алгебра / координатная геометрия

Эти формулы помогают вычислять расстояния, длины и свойства точек на плоскости, а также находить переменные в более сложных алгебраических выражениях.

4. Формула расстояния: d = √ (x₁ — x₂) ² + (y₁ — y₂) ²

Специально рассчитывает расстояние между двумя точками на координатной плоскости.

Например: Найдите расстояние между точками (6, 6) и (2, 3)

d = √ (6–2) ² + (6–3) ²
d = √ (4) ² + (3) ²
г = √16 + 3
d = √25
г = 5

5. Формула наклона: Наклон = y₂ — y₁ / x₂ — x₁

В частности, вычисляет наклон (угол) линии, соединяющей две точки на плоскости.

Например: Координаты = (-2, -1) (4, 3)

с = 3 — (-1) / 4 — (-2)
с = 4/6
с = 2/3

6. Пересечение наклона: y = mx + b

Формула, определяющая линию на плоскости с известным наклоном и точкой пересечения по оси Y.

Например: наклон = 2, точка пересечения (0,3)

7. Формула средней точки: (x₁ + x₂) / 2, (y₁ + y₂) / 2

В частности, вычисляет среднюю точку между точками на плоскости.

Например: Найдите середину между (-1, 2) и (3, -6)

(-1 + 3) / 2, (2 + -6) / 2
2/2, -4/2
Середина (1, -2)

Плоская геометрия

Формулы для вычисления атрибутов геометрических фигур на плоскости и решения для переменных на основе углов данной формы (тригонометрические тождества).

8. Площадь треугольника: площадь = (1/2) (основание) (высота)

В частности, вычисляет общую площадь треугольника на основе длин сторон.

Например: База = 5, Высота = 8

a = 1/2 (5) (8)
а = 1/2 (40)
а = 20

9. Теорема Пифагора: a² + b² = c²

Используется специально для вычисления длины неизвестной стороны прямоугольного треугольника, если известны две стороны.

Например: a = 3, b = 4

c² = 3² + 4²
c² = 9 + 16
c² = 25
с = √25
с = 5

10.Площадь прямоугольника: площадь = длина x ширина

Конкретно рассчитывает общую площадь прямоугольника.

Например: длина = 5, ширина = 2

11. Площадь параллелограмма: площадь = основание x высота

Специально рассчитывает общую площадь параллелограмма.

Например: основание = 6, высота = 12

12. Площадь круга: π * r²

Конкретно рассчитывает общую площадь круга.

Например: радиус = 4

a = π x 4²
а = π х 16
а = 50,24

13. Окружность круга: окружность = 2π * r

Вычисляет длину контура круга.

Например: радиус = 7

Тригонометрия

Продолжает работу с предыдущим геометрическим разделом плоскости.

14. Синус (SOH): Синус = противоположный / гипотенуза

Тригонометрическая идентичность, которая представляет относительные размеры сторон треугольника и может также использоваться для вычисления неизвестных сторон или углов треугольника.

Например: напротив = 2,8, гипотенуза = 4,9

15. Косинус (CAH): косинус = смежный / гипотенуза

Например: смежный = 11, гипотенуза = 13

16. Касательная (TOA): Касательная = противоположная / смежная

Например: напротив = 15, рядом = 8

Другие советы

Конечно, есть и другие формулы, которые могут появиться в ACT, но эти самые распространенные. Следовательно, они важнее всего. Запомните эти формулы, изучите, практикуйтесь, и все будет хорошо, когда наступит день экзамена.

Кроме того, убедитесь, что вы хорошо выспались ночью, и приготовьте то, что вам нужно, на ночь вместо утра. Также нет необходимости забивать накануне вечером; вместо этого расслабься! Зубки не работают, и это также лучший способ сделать передышку.

Удачи!

Проверьте, как ваши результаты ACT влияют на ваши шансы зачисления в College Raptor!

Математическая формула для конкурсных экзаменов

Математические формулы — одна из самых важных вещей на экзаменах. Время — главный фактор при проведении конкурсных экзаменов. Если вы будете распоряжаться своим временем, то сможете хорошо сдать эти экзамены. Большинство из нас пропускают эту часть. На этой странице ниже приведены несколько математических формул. Здесь представлены все типы математических формул.Мы просим всех посетителей внимательно прочитать все формулы. Эти математические формулы помогут вам очень легко выполнить экзамен по математике.

Несколько важных вещей, о которых следует помнить

Математический раздел на конкурсном экзамене — самая важная часть экзамена. Это не значит, что другие темы менее важны. Но если вам нужен хороший результат на экзамене, вы должны получить хороший результат по математике. Хорошая оценка приходит с практикой и практикой. Единственное, что вам нужно сделать, это правильно и вовремя решать свои математические задачи, а это можно сделать только с помощью трюков с горячими клавишами.Опять же, это не значит, что вы не можете заниматься математикой, не прибегая к трюкам. Вы можете решать математические задачи вовремя, не прибегая к каким-либо трюкам. У вас может быть такой потенциал.

Но многие другие люди могут не делать то же самое. Здесь мы подготовили для этих людей трюки с сокращенными математическими формулами. И на этой странице мы пытаемся применить все виды трюков с математической формулой. Но мы можем упустить некоторые из них. И, если вы знаете что-то еще, кроме этого, пожалуйста, поделитесь с нами.Ваша небольшая помощь поможет многим нуждающимся.

Зачем нужны математические формулы?

Конкурсные экзамены заполнены математикой, где вам нужны математические формулы. Итак, Математические формулы очень важны и необходимы для выполнения математических операций. Если вы выучите все математические формулы, вам будет очень легко сдать экзамен. И, не помня формулы, вы не сможете выжить в этом мире конкурсных экзаменов.

Итак, здесь, на этой странице, мы собрали все основные математические формулы.И эти формулы вам понадобятся на экзаменах. По сути, это основные формулы, которые вы все делали в школьные годы. Вы использовали эти формулы в классах 6, 7, 8, 9, 10. Во-первых, вам нужно очень внимательно запомнить эти математические формулы перед экзаменом. Чтобы вы могли правильно применять его на экзаменах. И, поверьте мне, это очень легко запомнить. Итак, здесь мы приводим несколько основных математических формул, которые помогут вам выполнять математические вычисления на конкурсных экзаменах.

ГеометрияТригонометрияУравненияАналитическая геометрияПроизводнаяИнтеграцияМатрицыСтатистикаПреобразование единиц

Все формулы алгебры:

Квадратные формулы

1.(a + b) ² = a ² + 2ab + b ²
2. (a — b) ² = a ² — 2ab + b ²
3. a ² + b ² = (a + b) ² — 2ab
4. a ² + b ² = (a — b) ² + 2ab
5. a ² + b ² = ½ {(a + b) ² + (a — b) ²}
6. a ² — b ² = (a + b) (a — b)

Формулы куба

1.(a + b) ³ = a ³ + b ³ + 3ab (a + b)
2. (a — b) ³ = a ³ — b ³ — 3ab ( a — b)
3. a ³ + b ³ = (a + b) ³ — 3ab (a + b)
4. a ³ — b ³ = (a — б) ³ + 3ab (a — b)
5. a ³ — b ³ = (a — b) (a ² + ab + b ²)
6. a ³ + b ³ = (a + b) (a ² — ab + b ²)

Все остальные формулы алгебры

a ⁴ — b ⁴ = (a ² — b ²) (a ² + b ²) = (a + b) (a — b) (a ² + b ²)
a ⁴ + b ⁴ = (a ² + b ²) ² — 2a ² b ² = (a ² + √2ab + b ²) (a ² — √2ab + b²)
a ⁵ + b ⁵ = (a + b) (a ⁴ — a ³ b + a ² b ² — ab ³ + b ⁴)
a ⁵ — b ⁵ = (a — b) (a ⁴ + a ³ b + a ² b ² + ab ³ + b ⁴)
a ⁿ — b ⁿ = (a — b) (a ^{n − 1} + a ^{n − 2} b + a ^{n − 3} b ² + ··· + b ^{n − 1} n − 1)
(a + b + c) ² = a ² + b ² + c ² + 2 (ab + bc + ca)
a ³ + b ³ + c ³ — 3abc = (a + b + c) (a ² + b ² + c ² — ab — bc — ca)
Если a + b + c = 0, то приведенное выше тождество сводится к ³ + b ³ + c ³ = 3abc

Несколько других математических формул: 90 248
Вот все остальные математические формулы, которые также не менее важны для ваших экзаменов.Мы знаем, что все эти формулы не требуются вместе для каких-либо конкурсных экзаменов. Но, поверьте, некоторые экзамены действительно включают математику, где вам нужны эти формулы.
Некоторые действительно сложные экзамены или некоторые вступительные экзамены часто добавляют математику, которая требует этих предварительных формул. Итак, если вы планируете сдавать эти экзамены, вы должны выучить эти формулы.
Итак, здесь, на этой странице, мы приводим несколько математических формул. А также посетите эту страницу, чтобы получать обновления о других математических трюках.Между тем, вы также можете проверить нашу страницу facebook, чтобы получать больше обновлений.
Теперь, если у вас есть какие-либо вопросы по этой теме, прокомментируйте, пожалуйста, раздел ниже. И вы также можете отправить нам сообщение на facebook.
31 критическая математическая формула ACT, которую вы ДОЛЖНЫ знать
Две самые большие проблемы ACT Math — это нехватка времени (тест по математике состоит из 60 вопросов за 60 минут!) И тот факт, что тест не дает вам никаких формул. Все формулы и математические знания для ACT основываются на том, что вы выучили и запомнили.
В этом полном списке критических формул, которые вам понадобятся для теста ACT, я изложу все формулы, которые вы, , должны запомнить до дня теста, а также объясню, как их использовать и что они означают. Я также покажу вам, какие формулы вам следует отдавать приоритет запоминанию (те, которые необходимы для нескольких вопросов), а какие — вы должны запоминать только тогда, когда у вас есть все остальное.
Уже чувствуете себя разбитым?
Заставляет ли вас запоминать кучу формул бежать в горы? Мы все были там, но пока не бросайте полотенце! Хорошая новость об экзамене ACT заключается в том, что он предназначен для того, чтобы дать всем участникам теста шанс добиться успеха.Многие из вас уже знакомы с большинством этих формул на уроках математики.
Формулы, которые чаще всего встречаются в тесте, также будут вам наиболее знакомы. Формулы, которые нужны только для одного или двух вопросов теста, будут вам менее всего знакомы. Например, уравнение круга и формулы логарифма всегда отображается как один вопрос в большинстве тестов по математике ACT. Если вы стремитесь к каждому пункту, запоминайте его. Но если вы чувствуете себя перегруженным списками формул, не беспокойтесь об этом — это только один вопрос.
Итак, давайте рассмотрим все формулы, которые вам обязательно нужно знать перед экзаменом (а также одну или две, которые вы можете вычислить самостоятельно, вместо того, чтобы запоминать еще одну формулу).
Алгебра
Линейные уравнения и функции
В каждом тесте ACT будет как минимум пять-шесть вопросов по линейным уравнениям и функциям, так что это очень важный раздел, который нужно знать.
Наклон

Наклон — это мера изменения линии.Это выражается как: изменение по оси Y / изменение по оси X или $ \ rise / \ run $.
Даны две точки, $ A (x_1, y_1) $, $ B (x_2, y_2) $, найдите наклон линии, соединяющей их:
$$ (y_2 — y_1) / (x_2 — x_1) $$
Форма пересечения уклона

Линейное уравнение записывается как $ y = mx + b $

м — это наклон, а b — точка пересечения с y (точка линии, пересекающей ось y)
Линия, проходящая через начало координат (ось Y в 0), записывается как $ y = mx $

Если вы получите уравнение, которое НЕ написано таким образом (т.2} $$
На самом деле вам не нужна эта формула, , поскольку вы можете просто изобразить свои точки, а затем построить из них прямоугольный треугольник. Расстояние будет гипотенузой, которую можно найти с помощью теоремы Пифагора
.
Логарифмы
Обычно в тесте с логарифмами задается только один вопрос. Если вы беспокоитесь о том, что вам придется запоминать слишком много формул, не беспокойтесь о журналах, если только вы не пытаетесь набрать наивысший балл.y = x $$
$$ log_bxy = log_bx + log_by $$
$$ log_b {x / y} = log_bx — log_by $$
Статистика и вероятность
Среднее значение
Среднее значение — это то же самое, что и среднее значение
Найдите среднее / среднее значение набора терминов (чисел)
$$ \ Mean = {\ sum \ of \ terms} / {\ the \ number (\ amount) \ of \ different \ terms} $$
$$ \ Speed = {\ total \ distance} / {\ total \ time} $$
Пусть шансы всегда будут в вашу пользу.
Вероятности
Вероятность — это вероятность того, что что-то произойдет. Вероятность 1 гарантирована. Вероятность 0 никогда не произойдет.
$$ {\ Вероятность‌ \ of‌ \ an‌ \ исход‌ \ событие} = {\ число‌ \ of‌ \ желаемое‌ \ results} / {\ total \ number \ of \ possible \ results} $$
Вероятность двух независимых исходов , когда произойдет , равна
$$ \ Вероятность‌ \ of‌ \ event‌ \ A * \ вероятность \ of‌ \ event \ B $$
e.g. Событие A имеет вероятность $ 1/4 $, а событие B имеет вероятность $ 1/8 $. Вероятность того, что оба события произойдут, равна: $ 1/4 * 1/8 = 1/32 $. Вероятность того, что произойдет как событий A, так и события B, составляет 1 из 32.
Комбинации
Возможное количество различных комбинаций ряда различных элементов
«Комбинация» означает, что порядок элементов не имеет значения (т. Е. Блюдо из рыбы и диетическая газировка — это то же самое, что и диетическая газировка и блюдо из рыбы)
Возможные комбинации = количество элементов A * количество элементов B * количество элементов C….
например В кафетерии есть 3 различных варианта десертов, 2 различных варианта закуски и 4 варианта напитков. Сколько различных комбинаций обеда возможно, используя один напиток, один десерт и одно блюдо?
Всего возможных комбинаций = 3 * 2 * 4 = 24
в процентах
Найти x процента заданного числа n
$$ n (x / 100) $$
Узнать, на сколько процентов число n принадлежит другому числу m
$$ (100n) / м $$
Узнайте, какое число n равно x процента от
$$ (100n) / x $$

ACT — это марафон.Не забывайте иногда делать перерыв и наслаждаться хорошими вещами в жизни. Щенки делают все лучше.
Геометрия
Прямоугольники

Площадь
$$ \ Area = lw $$
l — длина прямоугольника
w ширина прямоугольника
Периметр
$$ \ Периметр = 2l + 2w $$
Прямоугольный цельный

Объем
$$ \ Объем = л / ч $$
h — высота фигуры
Параллелограмм
Самый простой способ получить площадь параллелограмма — это опустить два прямых угла для высоты и преобразовать их в прямоугольник.
Затем решите относительно h , используя теорему Пифагора
Площадь
$$ \ Area = lh $$
(это то же самое, что прямоугольник lw . В этом случае высота эквивалентна ширине)
Треугольники

Площадь
$$ \ Area = {1/2} bh $$
b — длина основания треугольника (край одной стороны)
h — высота треугольника
Высота такая же, как сторона угла 90 градусов в прямоугольном треугольнике.2 $$
В прямоугольном треугольнике две меньшие стороны (a и b) возведены в квадрат. Их сумма равна квадрату гипотенузы (c, самая длинная сторона треугольника)
Свойства особого правого треугольника: равнобедренный треугольник
Равнобедренный треугольник имеет две стороны равной длины и два равных угла, противоположных этим сторонам.
Равнобедренный прямоугольный треугольник всегда имеет угол 90 градусов и два угла по 45 градусов.
Длины сторон определяются по формуле: x, x, x √2, причем длина гипотенузы (сторона, противоположная 90 градусам) равна одной из меньших сторон * √2.
Например, равнобедренный прямоугольный треугольник может иметь длину стороны 12, 12 и 12√2.
Свойства специального правого треугольника: треугольник под углом 30, 60, 90 градусов
Треугольник 30, 60, 90 описывает градусы трех его углов.
Длины сторон определяются по формуле: x , x √3 и 2 x .
Сторона, противоположная 30 градусам, является наименьшей, ее размер составляет x.
Сторона, противоположная 60 градусам, представляет собой среднюю длину с размером x √3.
Сторона, противоположная 90 градусам, представляет собой гипотенузу длиной 2 x.
Например, треугольник 30-60-90 может иметь длину стороны 5, 5√3 и 10.
Трапеции
Площадь
Возьмите среднее значение длины параллельных сторон и умножьте его на высоту.
$$ \ Area = [(\ parallel \ side \ a + \ parallel \ side \ b) / 2] h $$
Часто вам дают достаточно информации, чтобы выпустить два угла 90, чтобы получился прямоугольник и два прямоугольных треугольника. Это вам все равно понадобится для высоты, поэтому вы можете просто найти площади каждого треугольника и добавить их к площади прямоугольника, если вы не хотите запоминать формулу трапеции.
Трапеции и необходимость в формуле трапеции будет не более чем одним вопросом на тесте .2 $$
π — константа, которая для целей ACT может быть записана как 3,14 (или 3,14159)
Особенно полезно знать, если у вас нет калькулятора с функцией $ π $ или вы не используете калькулятор во время теста.
r — радиус круга (любая линия, проведенная от центральной точки прямо к краю круга).
Площадь сектора
Зная радиус и градус дуги от центра, найдите площадь этого сектора круга.2) (\ градус \ мера \ центра \ центра \ дуги / 360) $$
Окружность
$$ \ Окружность = 2πr $$
или
$$ \ Окружность = πd $$
d — диаметр круга. Это линия, которая делит круг пополам через середину и касается двух концов круга на противоположных сторонах. Это в два раза больше радиуса.
Длина дуги
По заданному радиусу и градусам дуги от центра найдите длину дуги.
Используйте формулу для длины окружности, умноженной на угол дуги, разделенный на общий угол круга (360).
$$ \ Окружность \ точки \ дуги = (2πr) (\ градус \ мера \ центр \ дуги / 360) $$
Пример: дуга в 60 градусов имеет 1/6 доллара от общей длины окружности, потому что 60/360 = 1/6
доллара.
Альтернативой запоминанию «формул» для дуг является просто остановиться и логически подумать об окружностях дуги и областях дуги.
Если вы знаете формулы для площади / длины окружности круга и знаете, сколько градусов в круге, сложите их вместе.
Если дуга охватывает 90 градусов окружности, она должна составлять $ 1/4 $ общей площади / длины окружности, потому что $ 360/90 = 4 $.
Если дуга расположена под углом 45 градусов, то это $ 1/8 $ окружности, потому что $ 360/45 = 8 $.
Концепция в точности такая же, как и у формулы, но она может помочь вам думать о ней именно так, а не как о «формуле» для запоминания.2 ч. $$
Тригонометрия
Почти всю тригонометрию на ACT можно свести к нескольким базовым концепциям
SOH, CAH, TOA
Синус, косинус и тангенс — функции графика
Синус, косинус или тангенс угла (тета, обозначаемый как Θ) находится по сторонам треугольника согласно мнемоническому устройству SOH, CAH, TOA.
Синус — SOH
$$ \ Sine‌ Θ = \ напротив / \ гипотенуза $$
Противоположная = сторона треугольника, прямо противоположная углу Θ
Гипотенуза = самая длинная сторона треугольника
Иногда ACT заставляет вас манипулировать этим уравнением, давая вам синус и гипотенузу, но не меру противоположной стороны.Управляйте им так же, как и любым алгебраическим уравнением:
$ Синус Θ = \ напротив / \ гипотенуза $ => $ \ гипотенуза * \ синус = \ напротив $
Косинус — CAH
$$ \ Косинус Θ = \ смежный / \ гипотенуза $$
Соседний = сторона треугольника, ближайшая к углу Θ (который создает угол), который не является гипотенузой
Гипотенуза = самая длинная сторона треугольника
Касательная — TOA
$$ \ Tangent‌ Θ = \ напротив / \ смежный $$
Противоположная = сторона треугольника, прямо противоположная углу Θ
Соседний = сторона треугольника, ближайшая к углу Θ (который образует угол), который не является гипотенузой
Косеканс, Секанс, Котангенс
Косеканс является обратной величиной синуса
$ \ Cosecant‌ Θ = \ hypotenuse / \ напротив $
Секанс обратен косинусу
$ \ Secant‌ Θ = \ hypotenuse / \ смежный $
Котангенс — величина, обратная касательной
$ \ Cotangent‌ Θ = \ смежный / \ напротив $
Полезные формулы, которые нужно знать
$$ \ Sin ^ 2Θ + \ Cos ^ 2Θ = 1 $$
$$ {\ Sin Θ} / {\ Cos Θ} = \ Tan Θ $$
Ура! Вы запомнили свои формулы.А теперь побалуй себя.
Но помните
Хотя это все формулы , которые вам следует запомнить, чтобы хорошо сдать математический раздел ACT, этот список никоим образом не охватывает все аспекты математических знаний, которые вам понадобятся на экзамене. Например, вам также необходимо знать свои правила экспоненты, как выполнять FOIL и как находить абсолютные значения. Чтобы узнать больше об общих математических вопросах, охватываемых тестом, прочитайте нашу статью о том, что на самом деле тестировалось в математическом разделе ACT.
Что дальше?
Теперь, когда вы знаете основные формулы для ACT, возможно, пришло время ознакомиться с нашей статьей о том, как набрать высший балл по математике ACT с помощью 36 ACT-Scorer.
Не знаете с чего начать? Посмотрите нашу статью о том, что считается хорошей, плохой или отличной оценкой ACT.
Хотите улучшить свой результат на 4+ балла? Наша полностью интерактивная и индивидуальная программа подготовки адаптируется к вашим сильным и слабым сторонам и потребностям. И мы гарантируем вам возврат денег , если вы не улучшите свой результат на 4 очка и более. Подпишитесь на бесплатную пробную версию сегодня.
Хотите улучшить свой результат ACT на 4 балла?
Посетите наши лучшие в своем классе онлайн-классы подготовки к ACT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат ACT на 4 или более балла.
Наши классы полностью онлайн, и их ведут эксперты ACT. Если вам понравилась эта статья, вам понравятся наши классы. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно. Мы также дадим вам пошаговую индивидуальную программу, которой вы будете следовать, чтобы вы никогда не запутались, что изучать дальше.
Попробуйте без риска сегодня:
28 важнейших математических формул SAT, которые вы ДОЛЖНЫ знать
Математический тест SAT не похож ни на один тест по математике, который вы проходили раньше.Он предназначен для того, чтобы взять концепции, к которым вы привыкли, и заставить вас применять их новыми (и часто странными) способами. Это сложно, но, уделяя внимание деталям и зная основные формулы и концепции, охватываемые тестом, вы можете улучшить свой результат.
Итак, какие формулы вам нужно запомнить для раздела SAT по математике до дня теста? В этом полном руководстве я рассмотрю каждую критическую формулу, которую вы ДОЛЖНЫ знать, прежде чем приступить к тесту. Я также объясню их, если вам нужно пробудить вашу память о том, как работает формула.Если вы понимаете каждую формулу в этом списке, вы сэкономите драгоценное время на тесте и, вероятно, правильно ответите на несколько дополнительных вопросов.
Формулы, данные на SAT, объяснены
Это именно то, что вы увидите в начале обоих математических разделов (калькулятор и без калькулятора). Легко не обращать внимания на это, поэтому ознакомьтесь с формулами сейчас, чтобы не тратить время зря в день тестирования.
Вам дается 12 формул самого теста и три закона геометрии.Запоминание приведенных формул может быть полезным и сэкономить ваше время и усилия, но в этом нет необходимости, , поскольку они приводятся в каждом разделе SAT по математике.
Вам даются только геометрические формулы, поэтому уделите первоочередное внимание запоминанию алгебр и тригонометрических формул перед экзаменом (мы рассмотрим их в следующем разделе). В любом случае вам следует сосредоточить большую часть своих усилий на изучении алгебры, потому что геометрия была уменьшена в новом SAT и теперь составляет только 10% (или меньше) вопросов в каждом тесте.2 $$
π — константа, которая для целей теста SAT может быть записана как 3,14 (или 3,14159)
r — радиус круга (любая линия, проведенная от центральной точки прямо к краю круга)
Окружность круга
$ C = 2πr $ (или $ C = πd $)
d — диаметр круга. Это линия, которая делит круг пополам через середину и касается двух концов круга на противоположных сторонах.Это в два раза больше радиуса.
Площадь прямоугольника
$$ A = lw $$
l — длина прямоугольника
w ширина прямоугольника
Площадь треугольника

$$ A = 1 / 2bh $$
b — длина основания треугольника (край одной стороны)
h — высота треугольника
В прямоугольном треугольнике высота равна стороне угла в 90 градусов.2 $$
В прямоугольном треугольнике две меньшие стороны ( a и b ) возведены в квадрат каждая. Их сумма равна квадрату гипотенузы (c, самая длинная сторона треугольника).
Свойства особого правого треугольника: равнобедренный треугольник
Равнобедренный треугольник имеет две стороны равной длины и два равных угла, противоположных этим сторонам.
Равнобедренный прямоугольный треугольник всегда имеет угол 90 градусов и два угла по 45 градусов.
Длины сторон определяются по формуле: $ x $, $ x $, $ x√2 $, при этом гипотенуза (сторона, противоположная 90 градусам) имеет длину одной из меньших сторон * $ √2 $.
Например, равнобедренный прямоугольный треугольник может иметь длину стороны 12 $, 12 $ и 12√2 $.
Свойства специального правого треугольника: треугольник под углом 30, 60, 90 градусов

Треугольник 30, 60, 90 описывает градусы трех углов треугольника.
Длины сторон определяются по формуле: $ x $, $ x√3 $ и $ 2x $
Сторона, противоположная 30 градусам, является наименьшей, ее размер составляет $ x $.
Сторона, противоположная 60 градусам, представляет собой среднюю длину с размером $ x√3 $.
Сторона, противоположная 90 градусам, — это гипотенуза (самая длинная сторона) с длиной $ 2x $.
Например, треугольник 30-60-90 может иметь длину стороны 5 долларов, 5√3 долларов и 10 долларов.
Объем прямоугольного твердого тела

$$ V = lwh $$
l — длина одной из сторон.2 ч. $$
$ r $ — радиус круговой стороны конуса.
$ h $ — высота заостренной части конуса (измеренная от центра круглой части конуса).
Объем пирамиды
$$ V = (1/3) л / ч $$
$ l $ — длина одного из ребер прямоугольной части пирамиды.
$ h $ — высота фигуры в пике (измеренная от центра прямоугольной части пирамиды).
$ w $ — ширина одного из краев прямоугольной части пирамиды.
Закон: количество градусов в окружности 360
Закон: число радианов в круге равно 2π $
Закон: количество градусов в треугольнике 180
Подготовьте этот мозг, потому что вот формулы, которые вам нужно запомнить.
Формулы, не указанные в тесте
Для большинства формул в этом списке вам просто нужно пристегнуться и запомнить их (извините).Некоторые из них, однако, может быть полезно знать, но в конечном итоге их не нужно запоминать, поскольку их результаты можно вычислить другими способами. (Тем не менее, это все еще полезно знать, поэтому относитесь к ним серьезно).
Мы разбили список на «Необходимо знать», и «Полезно знать», в зависимости от того, любите ли вы тестировать формулу или тестируете меньшее количество формул, тем лучше. 2 + bx + c $, найти x.2-4ac}} / {2a} $$
Примечание: Если вы знаете, как заполнить квадрат, то вам не нужно запоминать квадратное уравнение. Однако, если вам не совсем комфортно завершать квадрат, то относительно легко запомнить квадратную формулу и иметь ее наготове. Я рекомендую запоминать его на мелодию «Поп идет ласка» или «Греби, греби, греби своей лодкой».
Среднее значение
Нужно знать
Среднее значение — это то же самое, что и среднее значение
Найдите среднее значение набора чисел / терминов
$$ \ Mean = {\ sum \ of \ the \ terms} / {\ number \ of \ different \ terms} $$
$$ \ Speed = {\ total \ distance} / {\ total \ time} $$
Вероятности
Нужно знать
Вероятность — это вероятность того, что что-то произойдет.
$$ \ text «Вероятность исхода» = {\ text «количество желаемых результатов»} / {\ text «общее количество возможных исходов»} $$
Полезно знать
Вероятность 1 гарантирована. Вероятность 0 никогда не произойдет.
в процентах
Нужно знать
Найдите x процентов заданного числа n.
$$ n (x / 100) $$
Узнайте, какой процент число n принадлежит другому числу m.
$$ (n100) / м $$
Узнайте, какое число n составляет x процентов.
$$ (n100) / x $$
Тригонометрия
Тригонометрия — это новое дополнение к новому математическому разделу SAT 2016. Хотя это составляет менее 5% математических вопросов, вы не сможете ответить на вопросы по тригонометрии, не зная следующих формул.
Нужно знать
Найдите синус угла по размерам сторон треугольника.
$ sin (x) $ = Измерение стороны, противоположной углу / Измерение гипотенузы
На рисунке выше синус обозначенного угла будет $ a / h $.
Найдите косинус угла по размерам сторон треугольника.
$ cos (x) $ = Измерение стороны, прилегающей к углу / Измерение гипотенузы
На рисунке выше косинус обозначенного угла будет $ b / h $.
Найдите тангенс угла по размерам сторон треугольника.
$ tan (x) $ = Измерение стороны, противоположной углу / Измерение стороны, прилегающей к углу
На рисунке выше тангенс обозначенного угла будет $ a / b $.
Полезный трюк с памятью — это сокращение: SOHCAHTOA.
S ine равно O pposite over H ypotenuse
C осин равен A djacent выше H ypotenuse
T angent равен O pposite over A djacent
SAT Math: Помимо формул
Хотя это все формулы , которые вам понадобятся (те, которые вам даны, а также те, которые вам нужно запомнить), этот список не охватывает все аспекты SAT Math.Вам также необходимо понимать, как множить уравнения, как манипулировать абсолютными значениями и решать их, как манипулировать и использовать экспоненты и многое другое. Все эти темы рассмотрены здесь.
Еще одна важная вещь, которую следует помнить, — это то, что, хотя запоминание формул из этой статьи, которые вам не даны на тесте, важно, знание этого списка формул не означает, что вы готовы к SAT Math. Вам также необходимо попрактиковаться в применении этих формул, чтобы отвечать на вопросы, чтобы знать, когда есть смысл их использовать.
Например, если вас просят вычислить, насколько вероятно, что белый шарик будет извлечен из банки, содержащей три белых шарика и четыре черных шарика, достаточно легко понять, что вам нужно взять эту формулу вероятности:
$$ \ text «Вероятность исхода» = {\ text «количество желаемых результатов»} / {\ text «общее количество возможных исходов»} $$
и используйте его, чтобы найти ответ:
$ \ text «Вероятность белого шарика» = {\ text «количество белых шариков»} / {\ text «общее количество шариков»} $
$ \ text «Вероятность белого мрамора» = 3/7 $
Однако в математическом разделе SAT вы также столкнетесь с более сложными вопросами вероятности, такими как этот:
снов, вспомнившихся за одну неделю
Нет
от 1 до 4
5 и более
Всего
Группа X
15
28
57
100
Группа Y
21
11
68
100
Всего
36
39
125
200
Данные в таблице выше были получены исследователем сна, изучавшим количество снов, которые вспоминают люди, когда их просили записать свои сны в течение одной недели.Группа X состояла из 100 человек, которые наблюдали раннее время отхода ко сну, а группа Y состояла из 100 человек, которые наблюдали более позднее время отхода ко сну. Если человек выбирается случайным образом из тех, кто вспомнил хотя бы 1 сон, какова вероятность того, что этот человек принадлежал к группе Y?
A) 68 $ / 100 $
B) 79 $ / 100 $
C) 79 $ / 164 $
D) 164 долл. США / 200 долл. США
долл. США
В этом вопросе нужно обобщить много информации: таблица данных, объяснение таблицы, состоящее из двух предложений, и, наконец, то, что вам нужно решить.
Если вы не практиковали такого рода задачи, вы не обязательно поймете, что вам понадобится та формула вероятности, которую вы запомнили, и вам может потребоваться несколько минут, порываясь по таблице и ломая голову, чтобы выяснить, как чтобы получить ответ — 90 247 минут, которые вы теперь не можете использовать для решения других задач в разделе или для проверки своей работы.
Однако, если вы практиковались в вопросах такого рода, вы сможете быстро и эффективно применить эту заученную формулу вероятности и решить задачу:
Это вопрос вероятности, поэтому мне, вероятно, (ха) нужно будет использовать эту формулу:
$$ \ text «Вероятность исхода» = {\ text «количество желаемых результатов»} / {\ text «общее количество возможных исходов»} $$
Хорошо, количество желаемых результатов — это любой член группы Y, который вспомнил хотя бы один сон.Вот эти выделенные жирным шрифтом ячейки:
Нет
от 1 до 4
5 и более
Всего
Группа X
15
28
57
100
Группа Y
21
11
68
100
Всего
36
39
125
200
И тогда общее количество возможных исходов — это все люди, вспомнившие хотя бы один сон.Чтобы получить это, я должен вычесть количество людей, которые не вспомнили хотя бы один сон (36), из общего количества людей (200). Теперь я снова включу все это в уравнение:
$ \ text «Вероятность исхода» = {11 + 68} / {200-36} $
$ \ text «Вероятность исхода» = {79} / {164} $
Правильный ответ: C) 79 $ / 164 $
Вывод из этого примера: после того, как вы запомните эти математические формулы SAT, вам нужно узнать, когда и как их использовать , изучив практические вопросы.
Что дальше?
Теперь, когда вы знаете основные формулы для SAT, возможно, пришло время проверить полный список математических знаний и ноу-хау SAT, которые вам понадобятся перед экзаменом. А для тех из вас, кто забивает особо высокие баллы, ознакомьтесь с нашей статьей о том, как набрать 800 баллов по SAT Math с помощью идеального тестировщика SAT.
Сейчас средний балл по математике? Не ищите дальше нашей статьи о том, как улучшить свой результат, если вы сейчас набираете меньше 600 баллов.
Хотите улучшить свой результат SAT на 160 баллов?
Посетите наши лучшие в своем классе онлайн-классы подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой SAT на 160 или более баллов.
Наши классы полностью онлайн, и их ведут эксперты SAT. Если вам понравилась эта статья, вам понравятся наши классы. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно.Мы также дадим вам пошаговую индивидуальную программу, которой вы будете следовать, чтобы вы никогда не запутались, что изучать дальше.
Попробуйте без риска сегодня:
Шпаргалка по математическим формулам Praxis
### Объявление! По состоянию на сентябрь 2019 года содержание математического теста Praxis Core изменилось. Узнайте больше здесь. ###
Признаюсь, я испытываю определенную педагогическую амбивалентность по поводу предложения этого списка математических формул Праксиса для Праксис Ядро Математики.Совершенно верно, что для успешной сдачи теста Praxis Mathematics Test вы должны знать некоторые основные формулы; в этом ключе стоит поделиться этими формулами со студентами.
Однако будьте осторожны: одна из самых больших ошибок, которые могут совершить студенты-математики, — это принять знание формулы за подлинное математическое понимание . Знание всех формул — это удовольствие, когда вы знаете все правила движения фигур в шахматах: да, эти знания необходимы для игры, но овладение этими основными правилами — это только начало — одно только это знание не делает человека автоматически миром. мастер шахмат! В этом духе знайте эти формулы, но осознавайте, сколько еще нужно узнать, помимо них.
Номера и операции
Во-первых, несколько шаблонов, указанных в переменных: это не столько «формулы», сколько шаблоны, которые нужно распознать.
Коммутативное свойство добавления : A + B = B + A
Коммутативное свойство умножения : A × B = B × A
Ассоциативное свойство сложения : (A + B) + C = A + (B + C)
Ассоциативное свойство умножения : (A × B) × C = A × (B × C)
Распределительное свойство : A × (B + C) = AB + AC
Также важен образец дроби: Перекрестное умножение :

Наконец, правило процентов .
Алгебра
Проблемы с движением : D = RT
Это расстояние равно скорости, умноженной на время.
Проблемы с работой : A = RT
Эта сумма равна норме работы, умноженной на время.
Геометрия
Единицы измерения
1 фут = 12 дюймов
1 ярд = 3 фута
1 миля = 5280 футов = 1760 ярдов
1 метр = 100 см
1 км = 1000 метров
1 миля ≈ 1.6 км
1 дециметр = 10 см ≈ 4 дюйма
1 фунт = 16 «сухих» унций
1 короткая тонна = 2000 фунтов
1 кг = 1000 грамм
1 кг ≈ 2,2 фунта
1 чашка = 8 жидких унций
1 пинта = 2 чашки
1 кварта = 2 балла = 4 чашки
1 галлон = 4 кварты = 16 чашек
1 литр = 1000 мл
1 мл = 1 кубический сантиметр
1 литр ≈ 1 кварта (литр немного больше)
В координатной геометрии полезно знать
Форма пересечения наклона : y = mx + b
Вы должны понимать, что м — это наклон, а b — пересечение линии по оси Y.
Я также дам вам две формулы для наклона
Анализ данных
определение среднего (среднего) : среднее = (сумма терминов) / (количество терминов)
определение диапазона : диапазон = (максимальное значение) — (минимальное значение)
В Вероятность , вы должны знать формулу ожидаемого числа .
ожидаемое количество успехов = (вероятность) * (количество испытаний)
Вы также должны знать
0 ≤ P ≤ 1
P = 0 означает, что событие невозможно, гарантированно не произойдет
P = 1 означает, что событие обязательно, обязательно произойдет
Сводка математических формул Praxis
Это основные математические формулы Праксиса.Знайте их, но помните, что эти формулы — это далеко не вся история математического понимания. Посмотрите математические статьи в блоге и, конечно же, видеоуроки Magoosh Praxis Math, чтобы получить подробные объяснения всего, что вам нужно знать!
Кстати, подпишитесь на нашу 1-недельную бесплатную пробную версию, чтобы попробовать Magoosh Praxis Prep!
О Майке MᶜGarry
Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах.Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс.
32 математических формулы на ACT
{{Privy: Embed campaign = 1309544}}
В отличие от SAT, ACT не предоставляет вам список основных математических формул, на которые можно положиться в начале математического теста ACT. Это означает, что вам нужно будет запоминать математические формулы на ACT. Ниже вы найдете списки математических формул ACT, которые необходимо знать, формулы «Полезно знать» и формулы «Бонус», которые нужно сохранить в памяти для ACT! Выучите их все, а затем ознакомьтесь с нашим списком тем по математике ACT, чтобы приступить к их применению!
Необходимо знать математические формулы ACT
Хотя ACT проверяет разные концепции на каждом экзамене, есть популярные темы, которые возникают снова и снова.Этот список содержит лучшие математические формулы ACT, которые нужно знать. Чтобы больше попрактиковаться, попробуйте Magoosh ACT Prep.
Среднее значение
S / T (Среднее = Сумма / Количество вещей)
Строки
Форма пересечения откоса:
y = м x + b (где м — наклон, а b — пересечение по оси Y)
Наклон:
Треугольники
Площадь треугольника:
1/2 bh (1/2 основания × высота)
Теорема Пифагора:
a ² + b ² = c ²
Четырехугольники
Периметр прямоугольника:
2 l + 2 w (где l — длина, а w — ширина)
Площадь прямоугольника:
lw (длина × ширина)
Объем ящика:
л / ч (длина × ширина × высота)
Площадь прямоугольного твердого тела:
2 левый + 2 белый + 2 левый
Диагональ в сплошном прямоугольнике:
Примените теорему Пифагора дважды или l ² + w ² + h ² = d ²
Круги и сферы
Площадь круга:
πr ²
Окружность круга:
2 πr
Объем шара:
4/3 πr ³
Цилиндры
Объем цилиндра:
πr ² h
Тригонометрия
SOHCAHTOA:
sin x = противоположный / гипотенуза
cos x = смежный / гипотенуза
tan x = противоположный / смежный
Вы также должны знать свои квадранты и где синус, косинус и тангенс положительны или отрицательны:
Вероятность
Вероятность:
Количество желаемых результатов / общее количество результатов
Факториалы (например,грамм. 8!):
Чтобы найти факториал любого целого числа, умножьте его на каждое положительное целое число под ним, например:
8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
Бонус: математические формулы «Должен знать» в ACT также появляются на уроках математики в старшей школе. Итак, вы действительно учитесь сразу двум вещам. Хороший.
Бонусный бонус: посмотрите видео ниже, чтобы увидеть, как эксперт ACT Кристин более подробно обсуждает 6 обязательных математических формул ACT:

Полезные формулы ACT
Объем и площадь
Объем конуса:
V = 1/3 πr ² h
Объем пирамиды:
Площадь трапеции:

(Сложите основания, разделите на два, затем умножьте на высоту.)
Логарифмы
Определение:
Если log _a b = c , то a ^c = b
Изменение основного правила:
Треугольники
30-60-90 Передаточное число треугольника:
1:
: 2
45-45-90 Передаточное число треугольника:
1: 1:
Дополнительные формулы
Уравнение круга:
( x — h ) ² + ( y — k ) ² = r ² (где центр круга ( h , k ) )
Арифметические последовательности:
т _н = т ₁ + д ( н -1)
Геометрические последовательности:
т _n = т ₁ × r ^{( n — 1)}
Формула экспоненциального роста:
Где P = основная сумма (начальная стоимость), r = скорость роста, n = количество месяцев, t = время в годах и A = новая сумма.
Дополнительные сведения
Квадратное уравнение:
Часто для решения сложной алгебраической задачи лучше применить такую стратегию, как обратное решение, но если вам удобно квадратное уравнение, держите его в уме.
Перестановки:
Комбинации:
Важное примечание о математических формулах ACT
Иногда математическая задача ACT может полагаться на более сложную формулу, такую как площадь поверхности сферы.В таких случаях формула, которая вам нужна, обычно предоставляется в самом вопросе. Так что не нужно думать, что нужно все запоминать. Тем не менее, способность вспоминать основные формулы гарантирует, что вы сможете с уверенностью решать проблемы, не содержащие формулы! В приведенный ниже список включены формулы для концепций, которые ACT проверяет наиболее часто.
Важные математические формулы ACT (PDF)
Иногда легче запоминать формулы, каждый день изучая понемногу. Чтобы упростить задачу, мы создали PDF-файл с математическими формулами Magoosh ACT для печати. Вот ссылка, по которой вы можете получить копию.
{{Privy: Embed campaign = 1309544}}
Сообщите нам, если у вас есть какие-либо вопросы об этих формулах ACT. 🙂
Изображение предоставлено: hotmath.com и getmathhelp.jimdo.com
Популярные ресурсы
О Кристин Фраккиа
Доктор Кристин Фраккиа в настоящее время занимается подготовкой к экзаменам MCAT и LSAT, но она также имеет опыт проведения широкого спектра стандартизированных тестов, включая ACT, SAT, GRE и GMAT, а также приема в колледжи и аспирантуру.Имея докторскую степень в Калифорнийском университете в Ирвине и степень в области образования и английского языка, она работает в сфере образования с 2004 года.

Формулы для базового егэ по математике: задания, ответы, решения. Обучающая система Дмитрия Гущина.

Год до ЕГЭ по математике: как подготовиться? / TeachMePlease

Что выбрать: базовый экзамен или профильный

Как избежать ошибок

Как подготовиться

Базовый экзамен по математике

ЕГЭ математика 2020: все, что нужно знать

Что такое базовый уровень ЕГЭ по математике

Профильный уровень ЕГЭ по математике

Добавить комментарий

ЕГЭ по математике: материалы для подготовки

Курс подготовки к ЕГЭ по базовой (непрофильной) Математике

Цель и структура курс

Технология обучения

Особенности нашей технологии

«ПОДГОТОВКА К ЕГЭ. БАЗОВЫЙ УРОВЕНЬ.»

Математика подготовка к ЕГЭ | Материалы и рекомендации

Основные математические формулы

Веселые математические головоломки

16 важнейших математических формул ACT Математические формулы, которые вам НЕОБХОДИМО знать

Тригонометрия

Другие советы

Математическая формула для конкурсных экзаменов

Математическая формула для конкурсных экзаменов

Несколько важных вещей, о которых следует помнить

Зачем нужны математические формулы?

Квадратные формулы

Формулы куба

Все остальные формулы алгебры

31 критическая математическая формула ACT, которую вы ДОЛЖНЫ знать

Уже чувствуете себя разбитым?

Алгебра

Линейные уравнения и функции

Логарифмы

Статистика и вероятность

Среднее значение

Вероятности

Комбинации

в процентах

Геометрия

Прямоугольники

Параллелограмм

Треугольники

Трапеции

Тригонометрия

SOH, CAH, TOA

Но помните

Что дальше?

28 важнейших математических формул SAT, которые вы ДОЛЖНЫ знать

Формулы, данные на SAT, объяснены

Окружность круга

Площадь прямоугольника

Площадь треугольника

Свойства особого правого треугольника: равнобедренный треугольник

Свойства специального правого треугольника: треугольник под углом 30, 60, 90 градусов

Объем прямоугольного твердого тела

Объем пирамиды

Формулы, не указанные в тесте

Среднее значение

Нужно знать

Вероятности

Нужно знать

Полезно знать

в процентах

Нужно знать

Тригонометрия

Нужно знать

SAT Math: Помимо формул

Что дальше?

Шпаргалка по математическим формулам Praxis

Номера и операции

Алгебра

Геометрия

Анализ данных

Сводка математических формул Praxis

О Майке MᶜGarry

32 математических формулы на ACT

Необходимо знать математические формулы ACT

Среднее значение

Строки