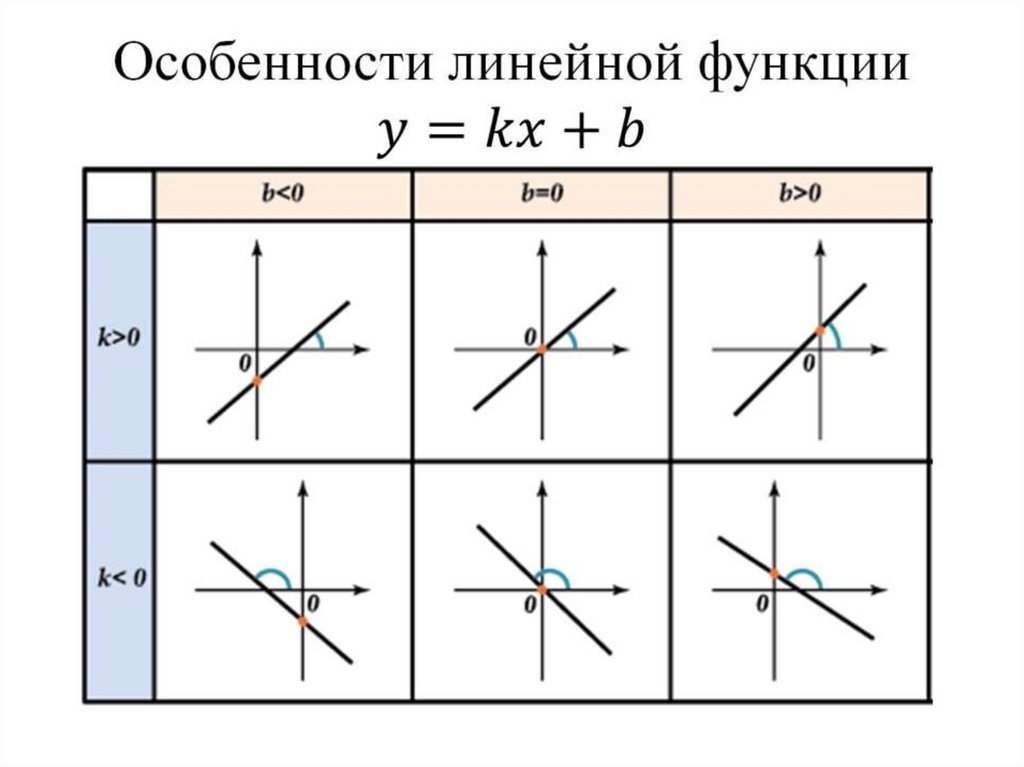
Линейная функция y=kx+b определение и её график
- Определение линейной функции
- График линейной функции
- Примеры
Определение линейной функции
Рассмотрим движение машины по прямой со скоростью 50 км/ч, но не из начальной точки. Допустим, что мы уже находимся на расстоянии 20 км от начала координат и будем удаляться. Тогда зависимость расстояния до начала координат от времени s = 50t+20. От прямой пропорциональности s = 50t эту формулу отличает дополнительное слагаемое, связанное с ненулевыми начальными условиями.
Если обобщить формулы, описывающие подобные зависимости, то получаем:
Прямая пропорциональность y = kx является частным случаем линейной функции y = kx+b, при k $\neq$ 0 и b = 0.
График линейной функции
Графиком линейной функции является прямая.
Согласно аксиоме планиметрии, через любые две точки можно провести прямую и притом только одну. Значит, положение прямой на плоскости полностью определяется двумя точками . Получаем:
Получаем:
Например: построим график функции y = 2x+1
$k = 2 \gt 0$ – функция возрастает
b=1 – функция пресекает ось Y в точке (0;1)
Примеры
Пример 1.Постройте графики линейных функций. Укажите, возрастает или убывает функция. Найдите точку её пересечения с осью Y.
а) y = x+2
$k = 1 \gt 0$ – функция возрастает
b = 2 точка пересечения с осью Y (0;2)
б) y = x-1
$k = 1 \gt 0$ – функция возрастает
b = -1 точка пересечения с осью Y (0;-1)
в) $y = \frac{1}{2} x+3$
$k = \frac{1}{2} \gt 0$ – функция возрастает
b = 3 точка пересечения с осью Y (0;3)
г) y = -x-1
$k = -1 \lt 0$ – функция убывает
b = -1 точка пересечения с осью Y (0;-1)
д) y = -2x+3
$k = -2 \lt 0$ – функция убывает
b = 3 точка пересечения с осью Y (0;3)
е) $y = — \frac{1}{3} x$
$k = -\frac{1}{3} \lt 0$ – функция убывает
b = 1 точка пересечения с осью Y (0;1)
ж) y = 1
Прямая, параллельная оси Х и проходящая через точку (0;1)
k = 0 функция постоянна
b = 1 точка пересечения с осью Y (0;1)
з) y = -5
Прямая, параллельная оси Х и проходящая через точку (0;-5)
k = 0 функция постоянна
b = -5 точка пересечения с осью Y (0;-5)
Пример 2.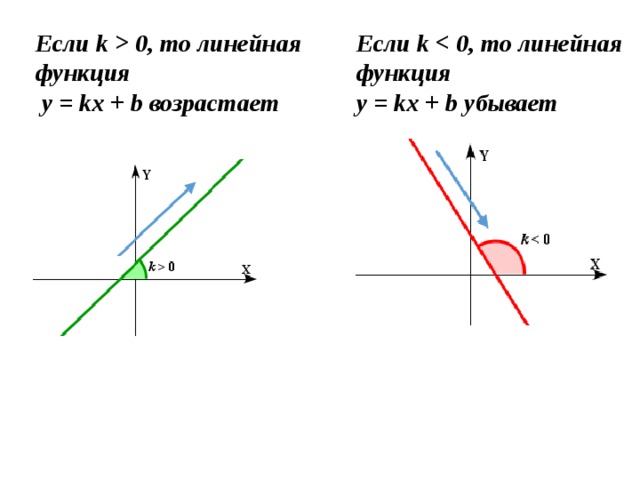 График линейной функции y=kx-3 проходит через точку A(-1;0,5). Найдите k.
График линейной функции y=kx-3 проходит через точку A(-1;0,5). Найдите k.
Подставляем в формулу функции координаты точки A:
$0,5 = k \cdot (-1)-3$
k=-0,5-3=-3,5
Ответ:-3,5
Пример 3*.Найдите уравнение прямой, проходящей через точки A(2;4)и B(-1;1)
Угловой коэффициент:
$$k = \frac{Y_B-Y_A}{X_B-X_A} = \frac{-1-2}{1-4} = 1$$
Уравнение имеет вид y = x+b.
Подставляем координаты A:
$$4 = 2+b \Rightarrow b = 2 $$
Искомое уравнение: y = x+2
Линейная функция — определение, основные свойства, график.
Если функция задана формулой , где и — некоторые числа, называется линейной функцией. Линейная функция областью определения имеет множество всех действительных чисел, потому что выражение имеет смысл при всех значениях . Все частные виды линейной функции можно записать общей формулой . Линейные функции изучаются в школьном курсе математики 7 класса. О том какие они бывают, как построить их графики мы поговорим в этой статье.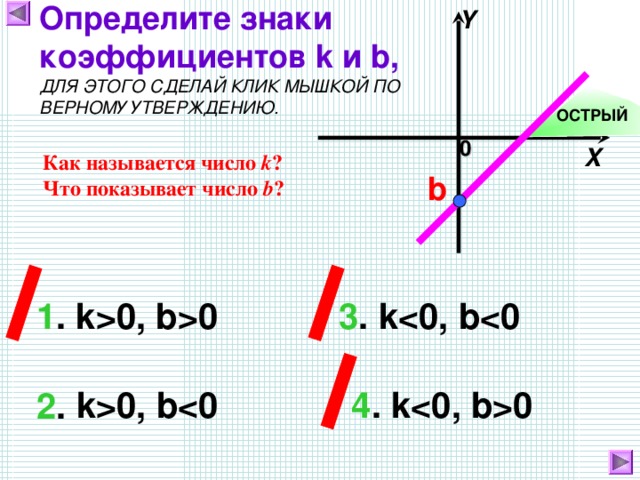 Вы получите все ответы на тему линейной функции, потому что мы с вами разберем примеры определения ее вида, построения графика и его анализа. Почитать о функции, что это такое и как ее можно задать можно здесь.
Вы получите все ответы на тему линейной функции, потому что мы с вами разберем примеры определения ее вида, построения графика и его анализа. Почитать о функции, что это такое и как ее можно задать можно здесь.
Содержание
Определение линейной функции
Вот так выглядит график линейной функции:
Линейная функция y=kx+b и ее график
Примеры линейных функций:
- ,
- ,
Обратите внимание, что уравнение — описывает общий вид, есть и частные виды, линейной функции, например, (когда ) и , когда .
Частный случай линейной функции y=b
Частный вид линейной функции y=kx
Стоит заметить, что уравнение задает прямую пропорциональность между значением и аргументом . Прямая пропорциональность — это зависимость вида , она изучается в курсе алгебры.
Для построения графика линейной функции достаточно двух точек.
Коэффициенты k и b
Коэффициент характеризует угол, который образует прямая с положительным направлением оси .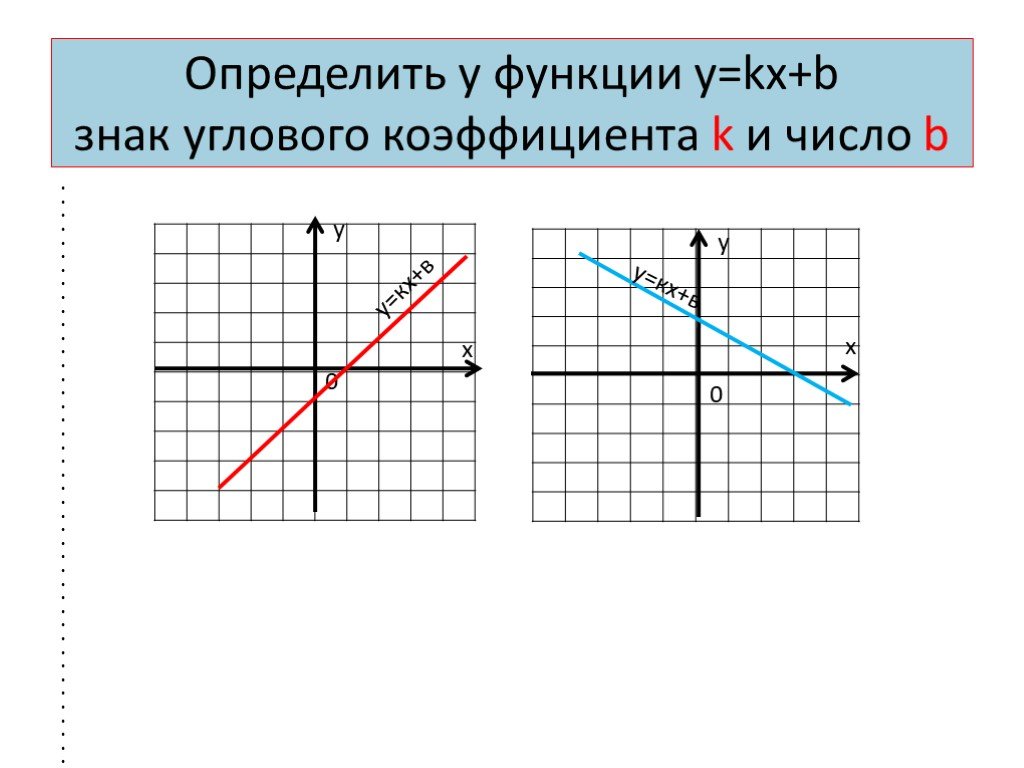 Поэтому коэффициент k линейной функции называется угловым коэффициентом.
Поэтому коэффициент k линейной функции называется угловым коэффициентом.
Частный случай линейной функции y=x
- Если , то угол между графиком линейной функции и осью острый.
- Если , то угол между графиком линейной функции и осью тупой.
- Если , то прямая совпадает с осью .
Коэффициент — показывает сдвиг графика вдоль оси .
У коэффициентов и есть геометрический смысл. Коэффициент показывает длину отрезка, которую прямая отсекает по оси , начало отрезка находится в точке . Геометрический смысл коэффициента — тангенс угла наклона прямой линии к положительному направлению оси . По данному коэффициенту можно определить угол наклона прямой линии, например, , это означает и . То есть угол наклона прямой к оси будет 450.
Примеры
Определите коэффициенты и функций и результаты запишите в таблицу.
| Линейная функция | Коэффициент | Коэффициент |
| 1 | 0 | |
| 3 | 5 | |
| 0 | 6 | |
| -1 | 3 | |
| 2 | -5 | |
| -3 | -1 |
Обратите внимание, что данная функция может быть задана и числом, например, , это означает, что угловой коэффициент равен нулю, то есть , а значит и прямая параллельна оси . Коэффициенты и могут принимать любые числовые значения, то есть могут быть и 0, и 1, и отрицательным числом.
Коэффициенты и могут принимать любые числовые значения, то есть могут быть и 0, и 1, и отрицательным числом.
Попробуем записать функцию y=kx+b, зная только значения коэффициентов.
Пример 1
Запишите линейную функцию, если известно, что , .
Решение: сначала запишем общий вид линейной функции: , теперь вместо и подставим указанные значения: . Упростим выражение и получим:
.
Ответ:
Пример 2
Запишите линейную функцию, если известны коэффициенты и .
Решение: .
Ответ: .
Область определения и область значений
Проанализируем и определим область определения линейной функции. Смотрим на уравнение, очевидно, что в это уравнение можно подставить любое значение . Это значит, что областью определения является вся числовая ось: .
Так как и может принимать любые значения, то мы можем говорить о том, что область значений линейной функции — все числа: .
График линейной функции
Если вы видите прямую линию — например, прямую дорогу или столб, дерево, то знайте — линии эти могут быть описаны с помощью функции, которая называется линейной.
Чтобы построить график функции необходимо и достаточно взять всего две точки. Построим таблицу координат точек:
| x | 0 | -b/k |
| y | b | 0 |
Таким образом, мы можем построить график любой линейной функции вида .
График прямой в общем виде
Примеры построения графика линейной функции
Пример 1
Построим график линейной функции .
Графиком функции является прямая линия. Для построения прямой достаточно взять две точки.
Возьмем точки и . Кстати, эти точки являются одновременно и точками пересечения графика с осями и соответственно.
Нарисуем координатные оси, покажем масштаб и отметим точки и , затем их соединим, получим прямую.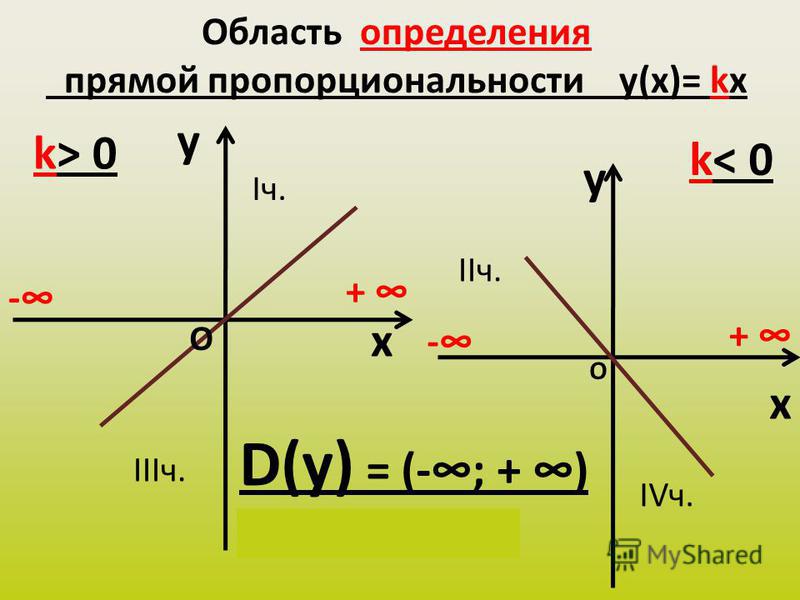 Эта прямая и будет графиком функции .
Эта прямая и будет графиком функции .
График функции y=2x+1
Итак, мы научились с вами строить график функции, зная ее уравнение. Алгоритм построения графика линейной функции прост:
- Найти координаты двух точек, удовлетворяющих данному уравнению прямой. Для этого берем произвольное значение аргумента и подставляем его в уравнение, вычисляем значение . Можно действовать и наоборот — задать определенное значение и решить уравнение относительно .
- Рисуем координатные оси, указываем их направление, определяем масштаб.
- Наносим найденные точки на координатную плоскость.
- Проводим прямую, через две эти точки.
Совет: если точки взяты близко друг к другу, то при продлении прямой можно получить погрешность рисования — отклонение на несколько градусов, поэтому старайтесь брать точки подальше друг от друга, или же возьмите пару контрольных точек, опираясь на уравнение прямой линии.
Пример 2
Построим новый график линейной функции.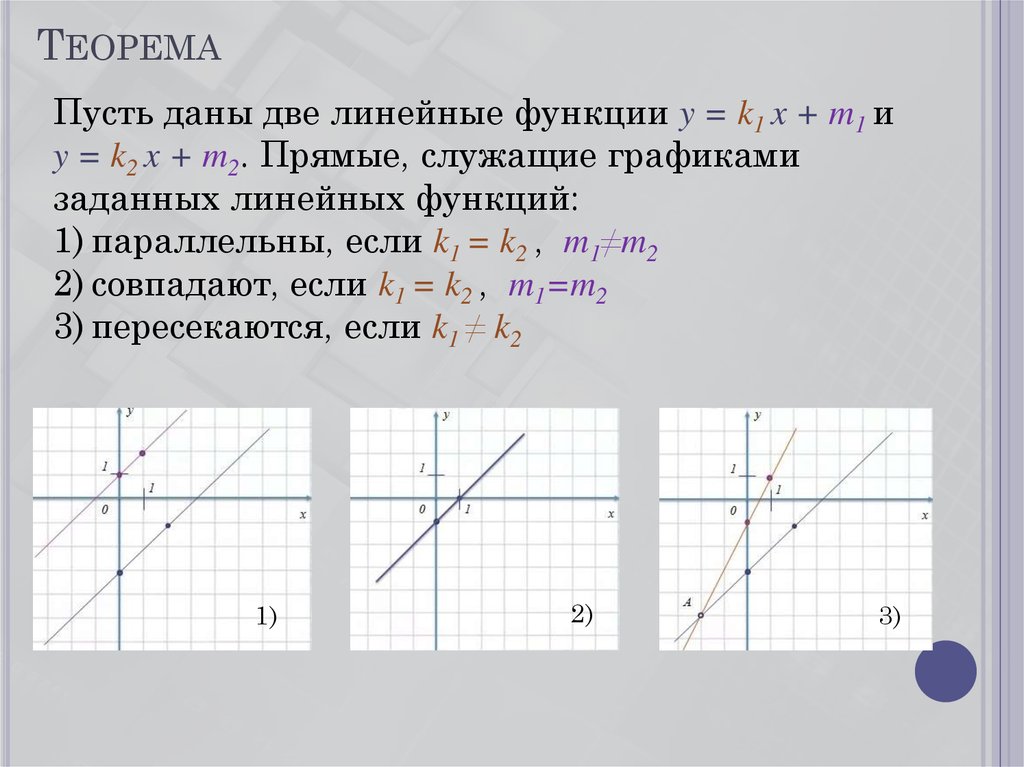 Пусть нам дано уравнение: .
Пусть нам дано уравнение: .
Находим две точки. Пусть , тогда подставим в формулу функции ноль вместо , получим: . Вторую точку возьмем немного подальше — пусть , тогда .
Итак, мы получили две точки: и . Построим график прямой.
График функции y=-x-2
Убывает или возрастает
Функция прямой является убывающей или возрастающей функцией? Вопрос не корректен. Все функции прямых разные, одни убывают, другие возрастают, надо обращать внимание при оценке убывания или возрастания функции на поведение ее при изменении аргумента. Существует такое правило:
Если при увеличении аргумента значение функции возрастает, то функция является возрастающей, если значение функции при возрастании аргумента уменьшается, то функция является убывающей. Давайте посмотрим как это выглядит на графике.
Перед вами два графика функции, — на каком графике функция убывает, а на каком возрастает, можно понять по тому увеличивается или уменьшается значение функции при движении в положительном направлении оси .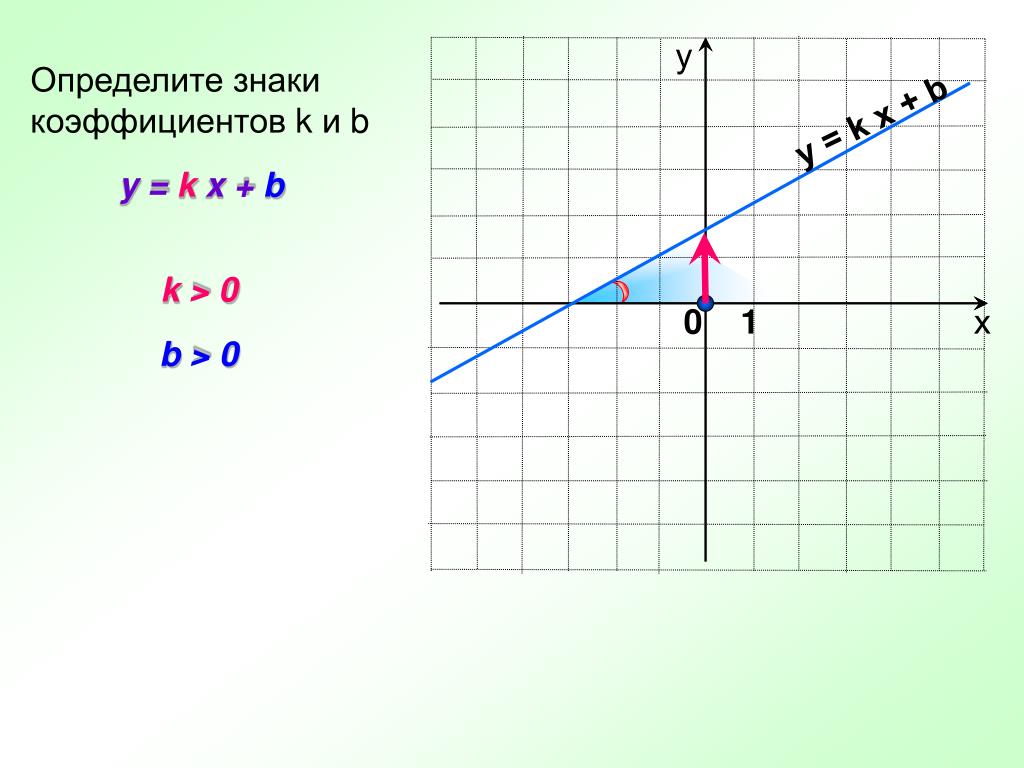
График возрастающей линейной функции
Теперь легко увидеть, почему ниже приведен график убывающей линейной функции:
График убывающей линейной функции
Как мы видим — при увеличении значения аргумента значение функции уменьшается.
Свойства линейной функции
Функция y = x называется линейной функцией, так как переменная x находится в первой степени. Графиком такой функции будет прямая.
Построение графика функции y = x
Для того, чтобы построить график линейной функции нам необходимо задать две точки. Берем их произвольно. Пусть , тогда . И вторая точка , тогда .
Отмечаем эти точки на координатной плоскости и проводим через них прямую. Это и есть график функции y = x.
Свойства функции
Выпишем свойства функции y = x:
- Функция y = x является линейной, непрерывной и монотонно возрастающей на всем протяжении координатной плоскости, со скоростью 1, так как производная функции равна 1.
- Любое значение переменной будет равно такому же значению функции.

- График функции проходит через начало координат.
- График функции располагается в первой и четвертой четвертях.
- Функция принимает отрицательные значения при отрицательных значениях переменной и положительные значения при положительных значениях переменной.
- Функция y = x является нечетной, так как (условие нечетности функции).
Обратная функция
Обратная функция совпадает с функцией y (x)=x и тоже записывается y = x.
Данная функция также является осью симметрии для всех обратных функций. Графики обратных функций симметричны относительно оси симметрии y=x.
y = mx + b
y = mx + b — форма пересечения наклона записи уравнения прямой линии. В уравнении «y = mx + b» «b» — это точка, в которой линия пересекает «ось y», а «m» обозначает наклон линии. Наклон или градиент линии описывает, насколько крута линия. Он может иметь как положительное, так и отрицательное значение. Когда стандартная форма линейного уравнения имеет форму Ax + By = C, где «x», «y» и «C» являются переменными, а «A», «B» являются константами, форма пересечения наклона представляет собой наиболее предпочтительный способ выражения прямой линии из-за его простоты, так как очень легко найти наклон и точку пересечения по оси y из данного уравнения.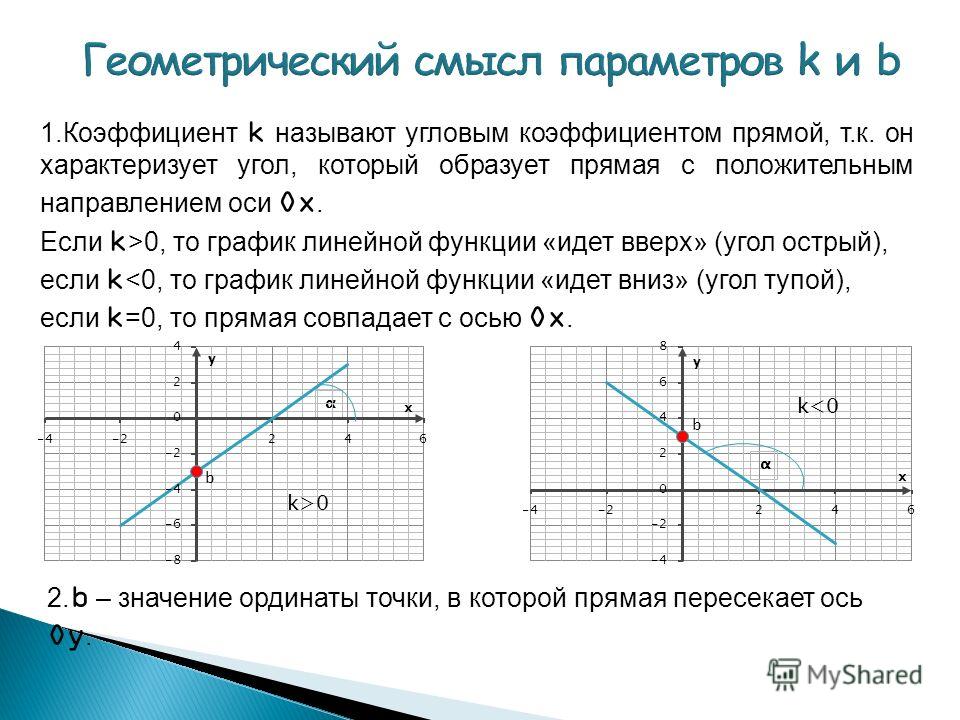
| 1. | Значение y = mx + b |
| 2. | Как найти y = mx + b? |
| 3. | Написание уравнения в форме пересечения наклона |
| 4. | Решенные примеры на y mx b |
| 5. | Практические вопросы по y mx b |
| 6. | Часто задаваемые вопросы по y mx b |
Значение y = mx + b
y = mx + b – форма наклона прямой линии. В уравнении y = mx + b для прямой линии m называется наклоном линии, а b — точкой пересечения линии по оси y. y = mx+b, где
y ⇒ насколько далеко вверх или вниз проходит линия,
x ⇒ как далеко проходит линия,
b ⇒ значение y при x = 0 и
3 м ⇒ насколько крута линия.
Определяется как m = (разница в координатах y)/ (разница в координатах x). Обратите внимание, что разница в координатах Y обозначается как подъем или спад, а разница в координатах X обозначается как пробег.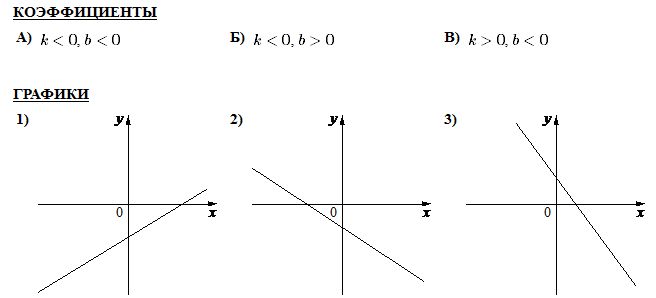
Как найти y = mx + b?
y = mx + b — это формула, используемая для нахождения уравнения прямой линии, когда мы знаем наклон (m) и точку пересечения с осью y (b) прямой. Для определения m применим формулу, основанную на расчетах. Давайте выведем эту формулу, используя уравнение для наклона линии. Давайте рассмотрим линию, наклон которой равен «m», а точка пересечения с осью y равна «b». Пусть (x,y) — любая другая случайная точка на прямой, координаты которой неизвестны. Получаем график следующим образом.
Мы знаем, что уравнение для наклона линии в форме пересечения наклона имеет вид y = mx+b
Переписывая это, мы получаем m = (y-b) / x
Таким образом, формула для нахождения m = изменение y/ изменение x
Выведем формулу для нахождения значения наклона, если две точки \((x_{1},y_{1})\) и \((x_{2 },y_{2})\) на прямой известны. Тогда мы имеем \(y_{1} = mx_{1} + b\) и \(y_{2} = mx_{2} + b\)
Мы знаем, что наклон = изменение y/ изменение x
Подставляя значения y 1 и y 2 , мы получаем \[\begin{align}\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}& = \dfrac{(mx_{2}+b) — (mx_{1}+b)}{x_{2}-x_{1}}\\\\&=\dfrac{mx_{2}-mx_{1 }}{x_{2}-x_{1}}\\\\&= \dfrac{m(x_{2}-x_{1})}{x_{2}-x_{1}}\\\\ &=m\end{align}\]
Таким образом, мы находим, что наклон (м) рассчитывается как (изменение y)/(изменение x)
m = (разница в координатах y)/(разница в координаты x)
Чтобы найти точку пересечения с осью y или b, подставьте значение x вместо 0 в уравнение прямой линии, которое имеет форму Ax + By + C = 0.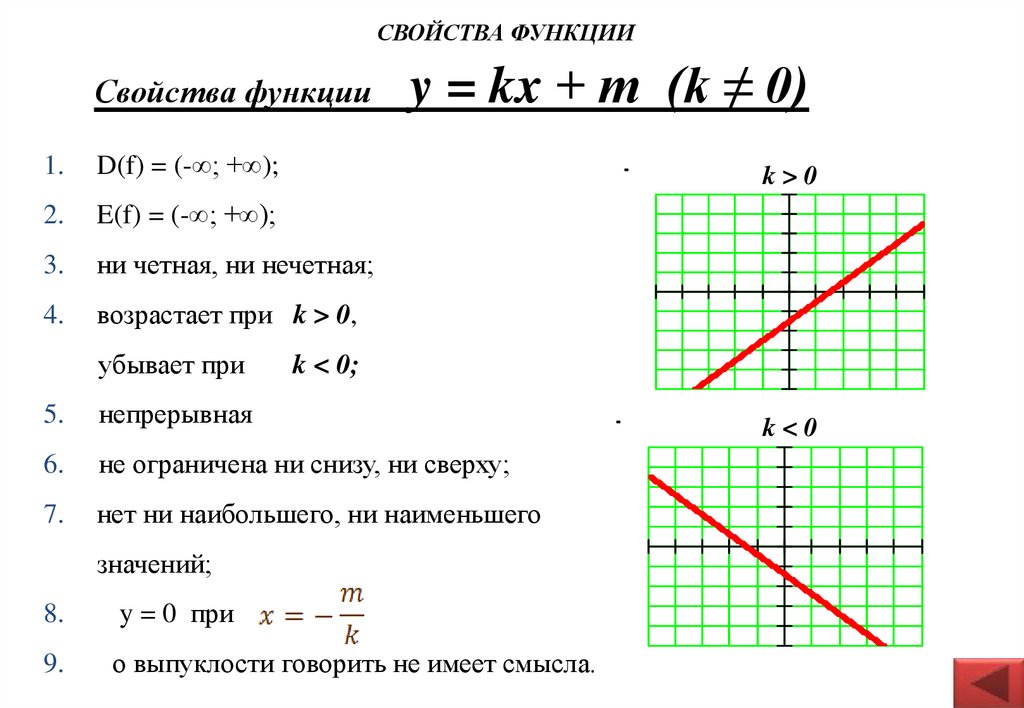 Рассмотрим уравнение прямой линии: 3x + 5y = 10. Чтобы найти точку пересечения с осью y, замените значение «x» на 0 в уравнении и найдите «y». Подставив «x = 0» в уравнение 3x + 5y = 10, мы получим 3 (0) + 5y = 10
Рассмотрим уравнение прямой линии: 3x + 5y = 10. Чтобы найти точку пересечения с осью y, замените значение «x» на 0 в уравнении и найдите «y». Подставив «x = 0» в уравнение 3x + 5y = 10, мы получим 3 (0) + 5y = 10
⇒ 5y = 10 и, следовательно, y = 10/5 ⇒ y = 2 или ‘b’ = 2.
Написание уравнения в форме пересечения наклона
Если заданы наклон ‘m’ и точка пересечения с осью ‘b’, то уравнение прямой может быть записано в виде ‘y = mx +b’. Например, если наклон (m) для линии равен 2, а точка пересечения с осью y равна -1, то уравнение прямой линии записывается как y = 2x – 1. Значение наклона может быть положительным или отрицательным. . Как мы обсуждали в предыдущих разделах, в y = mx + b «m» представляет наклон уравнения. Чтобы найти наклон линии, учитывая ее уравнение, мы должны преобразовать его члены в форму пересечения наклона y = mx + b. Здесь «m» обозначает наклон, а «b» — точку пересечения уравнения по оси Y.
Рассмотрим уравнение 2x + 3y = 6.
Перепишем стандартную форму уравнения линия к форме пересечения наклона y = mx + b.
2х + 3у = 6
3у = 2х + 6
y = (-2/3) x + 2
Сравнивая окончательное уравнение с y = mx + b, мы получаем, что наклон уравнения равен m = -2/3, а пересечение y уравнения равно, b = 2 или (0,2).
Важные примечания:
- Уравнение формы пересечения наклона линии с наклоном m и точкой пересечения по оси y b или (0,b) равно y = mx + b.
- Уравнение горизонтальной линии, проходящей через (a,b), имеет форму y = b.
- Уравнение вертикальной линии, проходящей через (a,b), имеет форму x = a.
- м рассчитывается по формуле подъем над пробегом или (изменение по y)/(изменение по x)
Темы, связанные с y = mx + b
Ознакомьтесь с некоторыми интересными статьями, связанными с y = mx + b.
- Формула линейного уравнения
- Уравнение прямой
- Линейные уравнения
- Линейные уравнения и полуплоскости
- Формула точки-наклона
- Двухточечная форма
Пример 1: Найдите уравнение прямой, график которой содержит точки (1,3) и (3,7)
Требуемое уравнение прямой: y = mx + b
Используя формулу для наклона, m = изменение y / изменение x = \(\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\) 90 103 = (7-3)/(3-1) = 4/2 ⇒ m = 2
Чтобы найти y-пересечение b, мы рассмотрим любую из координат.
Воспользуемся (1,3) и m = 2 и подставим значения в уравнение \(y_{1} = mx_{1} + b\)
3 = 2(1) + b ⇒ b = 3 — 2 = 1
Применяя m = 2 и b = 1 в уравнении прямой (y = mx + b), получаем y = 2x + 1 Таким образом, уравнение прямой имеет вид y = 2x + 1Пример 2: Найдите форму пересечения наклона линии с наклоном -2, которая проходит через точку (-1,4).
Решение :
.
Мы знаем, что форма пересечения наклона линии есть y = mx + b.
Дано, что наклон (m) = -2, а координаты, через которые проходит линия, равны (-1,4). Подставляя данные значения в уравнение формы пересечения наклона, мы получаем 4 = (-2) (-1) + b.
4 = 2 + b b = 4 — 2 = 2. 90 103 Форма пересечения наклона линии: y = — 2 x + 2,
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.
Часто задаваемые вопросы по y mx b
Что такое y = mx + b?
y = mx + b является представлением уравнения прямой линии. Это называется формой пересечения наклона. «m» относится к наклону линии, а «b» относится к «y-перехвату» линии.
Как найти наклон линии?
Для двух координат (x 1 ,y 1 ) и (x 2 , y 2 ) наклон линии представляет собой отношение разности между разницей между координатами y и разностью между координатами x, также известный как подъем над пробегом. Формула для нахождения наклона линии: m = (y 2 -y 1 )/(x 2 -x 1 )
Что такое форма пересечения наклона?
Уравнение прямой линии, имеющее вид y = mx + b, называется формой пересечения наклона. Здесь «m» — это наклон линии, а «b» — точка, в которой линия пересекает ось y.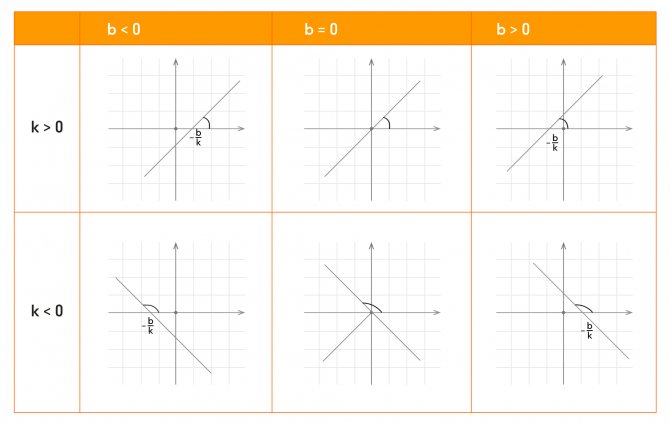 Пример уравнения формы пересечения наклона: y = 3x + 5
Пример уравнения формы пересечения наклона: y = 3x + 5
Что такое линия с отрицательным наклоном?
Линия, для которой говорят, что отрицательный наклон движется слева направо на графике. Наклон линии определяется отношением разности координат y к разнице координат x. Если это значение отрицательно для линии, то линия имеет отрицательный наклон.
Что означает наклон линии?
Направление линии определяется ее наклоном. Наклон может быть положительным или отрицательным, в зависимости от его направления. Отрицательный наклон движется вниз слева направо, а линия с положительным наклоном движется вверх справа налево.
Скачать БЕСПЛАТНЫЕ учебные материалы
Алгебра
Уравнение прямой
Уравнение прямой обычно записывается так:
у = мх + б
(или «y = mx + c» в Великобритании, см. ниже)
Что это означает?
| Наклон или Градиент | y значение, когда x=0 (см. 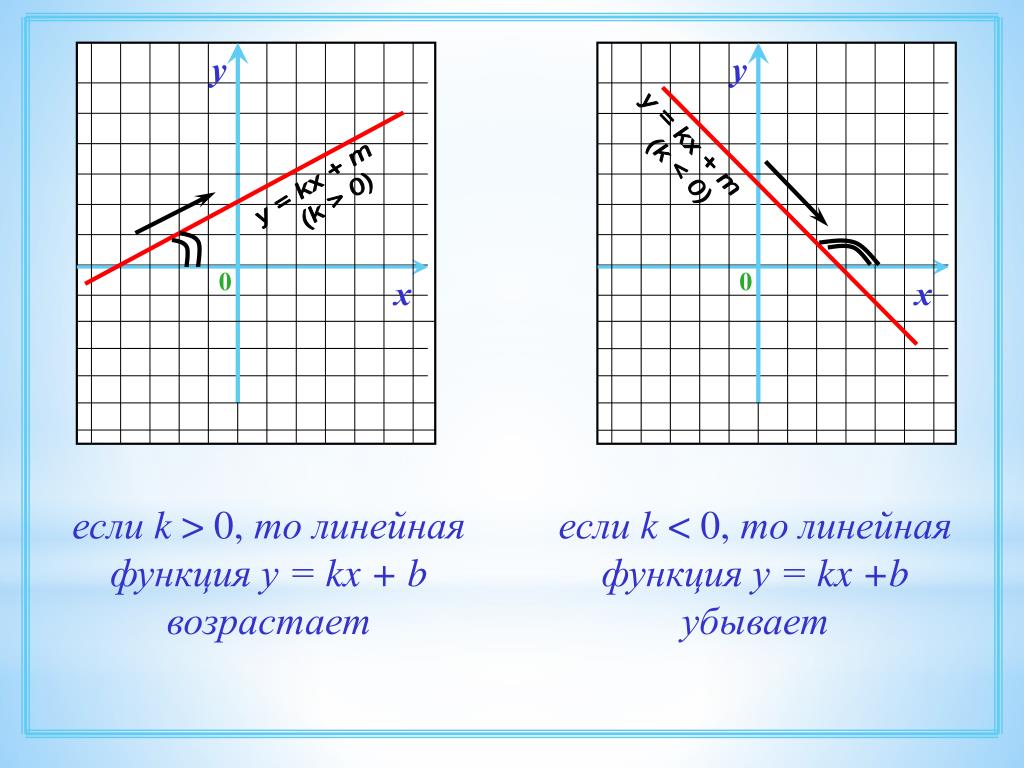 Пересечение Y) Пересечение Y) |
y = как далеко вверх
x = как далеко по
м = уклон или уклон (насколько крута линия)
b = значение y , когда x=0
Как найти «м» и «б»?
- b легко: просто посмотрите, где линия пересекает ось Y.
- м (Уклон) нуждается в подсчете:
м = Изменение Y Изменение X
Зная это, мы можем составить уравнение прямой линии:
Пример 1
м = 2 1 = 2
b = 1 (значение y при x=0)
Подставляя это в y = mx + b получаем:
y = 2x + 1
С помощью этого уравнения мы можем теперь …
… выбрать любое значение для x и найти соответствующее значение для y
Например, когда x равно 1:
y = 2× 1 + 1 = 3
Убедитесь сами, что x=1 и y=3 действительно находятся на прямой.
Или мы могли бы выбрать другое значение для x, например 7:
y = 2× 7 + 1 = 15
Таким образом, когда x=7, у вас будет y=15
Положительный или отрицательный наклон?
Двигаясь слева направо, велосипедист должен P проехать по положительному склону P :
Пример 2
м = −3 1 = −3
b = 0
Это дает нам:
y = −3x + 0
Нуль нам не нужен! Итак:
y = −3x
Пример 3: Вертикальная линия
Какое уравнение составляет вертикальная линия?
Наклон undefined … и где он пересекает ось Y?
На самом деле это частный случай , и мы используем другое уравнение, не « y =…», а вместо этого используем « x =…».
Вот так:
x = 1,5
Каждая точка на прямой имеет координату x 1,5 ,
поэтому ее уравнение x = 1,3
Вставай и беги
Иногда употребляются слова «вставать» и «бежать».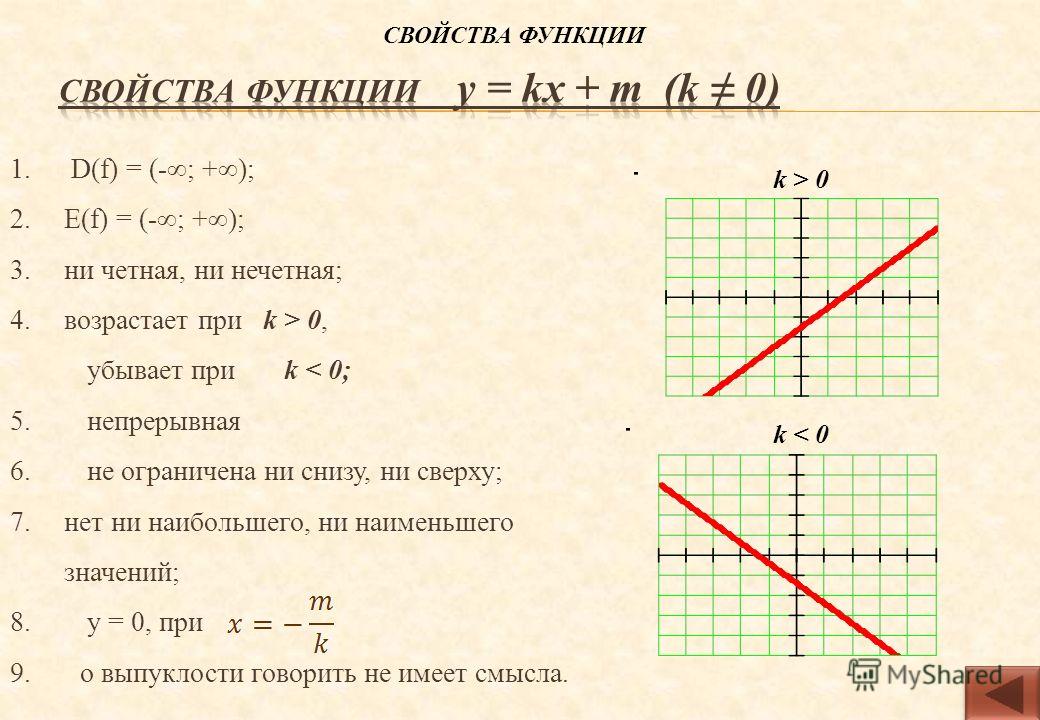


Leave A Comment