Y корень x 2 9: Mathway | Популярные задачи

2

Построение графика функции методом дифференциального исчисления

Существует способ построения графика функции, основанный на аналитическом исследовании функции. Исследование проводится по следующей примерной схеме:
1) выяснение области определения функции;
2) решается вопрос о четности или нечетности функции;
3) исследуется периодичность функции;
4) находят точки пересечения кривой с осями координат;
5) находят точки разрыва функции и определяют их характер;
6) проводят исследования на экстремум, находят экстремальные значения функции;
7) ищутся точки перегиба и интервалы выпуклости и вогнутости кривой;
8) отыскание асимптот кривой;
9) полученные результаты наносят на чертеж и получают график исследуемой функции.

Построить график без исследования функции (получить просто рисунок) можно с помощью этого сервиса.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Правила ввода функции

Примеры
≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)

Пример №1. Провести полное исследование функции  и построить ее график.

1) Функция определена всюду, кроме точек .

2) Функция нечетная, так как f(-x) = -f(x), и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.

3) Функция не периодическая.

4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.

5) Функция имеет разрыв второго рода в точке , причем , . Попутно отметим, что прямая  – вертикальная асимптота.

6) Находим  и приравниваем ее к нулю: , откуда x₁ = -3, x₂ = 0, x₃ = 3. На экстремум надо исследовать только точку x=3 (точку x₂=0 не исследуем, так как она является граничной точкой промежутка [0, +∞)).

В окрестности точки x₃=3 имеет: y’>0 при x<3 и y ’<0 при x>3, следовательно, в точке x₃ функция имеет максимум, y_max(3)=-9/2.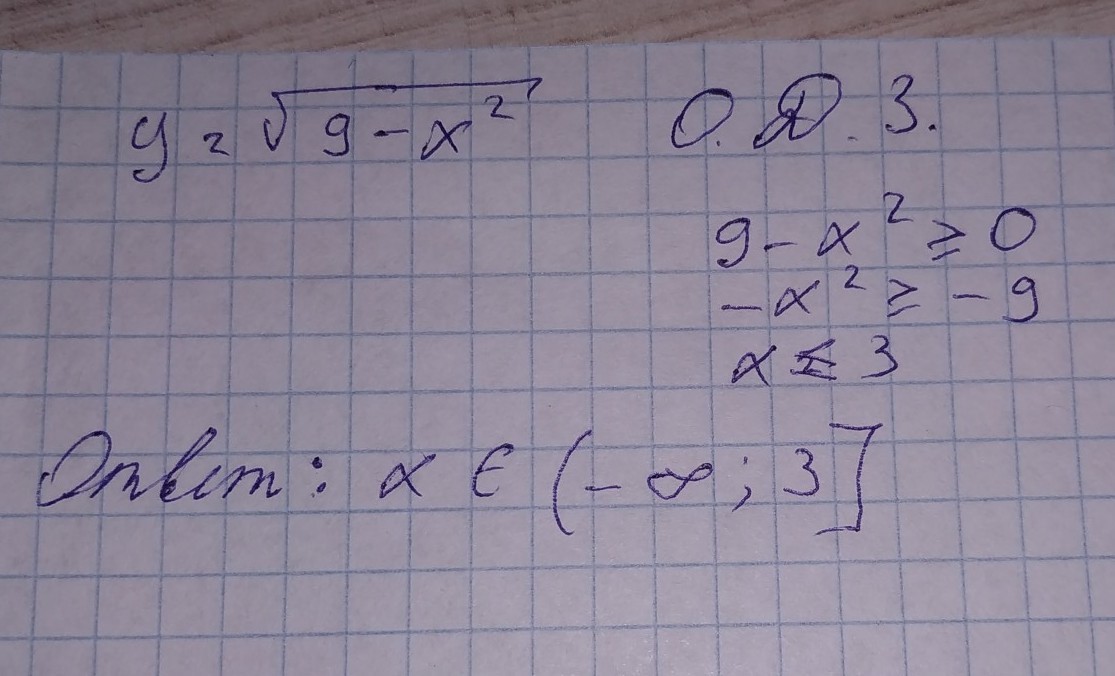

Найти первую производную функции

Для проверки правильности нахождения минимального и максимального значения.

7) Находим . Видим, что y’’=0 только при x=0, при этом y”<0 при x<0 и y”>0 при x>0, следовательно, в точке (0,0) кривая имеет перегиб. Иногда направление вогнутости может измениться при переходе через разрыв кривой, поэтому следует выяснить знак y” и около точек разрыва функции. В нашем случае y”>0 на промежутке (0, ) и y”<0 на (, +∞), следовательно, на (0, ) кривая вогнута и выпукла на (, ∞).

Найти вторую производную функции

8) Выясним вопрос об асимптотах.

Наличие вертикальной асимптоты  установлено выше. Ищем горизонтальные: , следовательно, горизонтальных асимптот нет.

Найдем наклонные асимптоты: , , следовательно, y=-x – наклонная двусторонняя асимптота.

9) Теперь, используя полученные данные, строим чертеж:

Построить график функции

Пример №2. Построить график функции .
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем
; .
4. Точки разрыва x=0, причем ; следовательно, x=0

является вертикальной асимптотой графика.
Найдем наклонные асимптоты:
;
.
Наклонная асимптота имеет уравнение y=x.
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем . Существует единственная критическая точка x=2. В промежутках x∈(-∞ ;0)∪(2; +∞) y’>0, следовательно, функция возрастает; в промежутке x∈(0;2) y'<0, функция убывает. Далее, находим ; y»(2)>0, следовательно, x=2 – точка минимума y_min=3.
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92+9)?

Математическая задача

Эшли В.

спросил 12.01.14

Я упростил это до этого, и я знаю, что вы все еще можете упростить еще больше, потому что это квадратный корень, но каков будет ответ? ПОЖАЛУЙСТА ПОЖАЛУЙСТА ПОМОГИТЕ!

Подписаться І 3

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСамыеСтарые

Варайя Р. ответил 12.01.14

Репетитор

5 (29)

Я был помещен на эту землю, чтобы вы, наконец, могли «получить» математику.

Смотрите таких репетиторов

Смотрите таких репетиторов

Я предполагаю, что все знаки верны. 92+9)=0 , а если x=-3, то у вас есть (0)(количество) или свойство нулевого продукта.

 

3 решения для x: -3, 3i и -3i

 

 

 

 

 

90 906  

Голосовать за 1 Понизить

Подробнее

Отчет

Уильям С. ответил 12.01.14

Репетитор

4.4 (10)

Опытный ученый, математик и преподаватель — Уильям

Смотрите таких репетиторов

Смотрите таких репетиторов

x ³ + 3x ² + 9x + 27 = 0

 

(x + 3)(x ² + 9) = 0

  90 907

Это все, что можно учесть Эшли. Они хотят, чтобы вы нашли нули? Если это так, то есть только одно: x = -3.

Голосовать за 0 Понизить

Подробнее

Отчет

Вивиан Л.

ответил 12.01.14

Репетитор

3 (1)

Microsoft Word/Excel/Outlook, составление эссе, математика; Я ЛЮБЛЮ УЧИТЬ

Смотрите таких репетиторов

Смотрите таких репетиторов

Привет, Эшли;

(x ³ +3x ² ) + (9x+27)= 0

Раскроем скобки…

x ³ +3x ^{2 9101 2 +9x+27= 0}

Для ФОЛЬГА…

ПЕРВАЯ должна быть (x ² )(x).

ВНЕШНИЙ должен быть (x ² )(3).

ВНУТРЕННЕЕ должно быть (9)(x).

ПОСЛЕДНИЙ должен быть (9)(3).

(x

2 +9)(x+3)=0

Давайте ФОЛЬГИРОВАНИЕ…

ПЕРВОЕ…(x ² )(x)=x ³

ВНЕШНИЙ…(x ² )(3)=3x ²

ВНУТРЕННИЙ…(9)(x)=9x

909 06 ПОСЛЕДНИЙ. ..(9)(3)=27

x ³ +3x ² +9x+27=0

(x ² +9)(x+3)=0

Одна или обе скобки уравнение(я) должно быть равно нулю.