Функция y = k/x — урок. Алгебра, 8 класс.
если x=−18, то \(y = -8\).
Короче говоря, мы составили следующую таблицу:
Построим найденные точки на координатной плоскости \(xOy\).
А теперь объединим два этапа в один, т. е. из двух рисунков сделаем один.
Это и есть график функции y=1x, его называют гиперболой.
Попробуем по чертежу описать геометрические свойства гиперболы.
Во-первых, замечаем, что эта линия выглядит так же красиво, как парабола, поскольку обладает симметрией. Любая прямая, проходящая через начало координат \(O\) и расположенная в первом и третьем координатных углах, пересекает гиперболу в двух точках, которые лежат на этой прямой по разные стороны от точки \(O\), но на равных расстояниях от неё. Это присуще, в частности, точкам \((1; 1)\) и \((- 1; — 1)\), 2;12 и −2;−12 и т. д.
Значит, \(O\) — центр симметрии гиперболы. Говорят также, что гипербола симметрична относительно начала координат.
Во-вторых, видим, что гипербола состоит из двух симметричных относительно начала координат частей; их обычно называют ветвями гиперболы.
В-третьих, замечаем, что каждая ветвь гиперболы в одном направлении подходит всё ближе и ближе к оси абсцисс, а в другом направлении — к оси ординат. В подобных случаях соответствующие прямые называют асимптотами.
Значит, график функции y=1x, т. е. гипербола, имеет две асимптоты: ось \(x\) и ось \(y\).
Если внимательно проанализировать построенный график, то можно обнаружить ещё одно геометрическое свойство, не такое очевидное, как три предыдущих (математики обычно говорят так: «более тонкое свойство»).
Обрати внимание!
У гиперболы имеется не только центр симметрии, но и оси симметрии.
В самом деле, построим прямую \(y = x\).
Теперь смотрите: точки 2;12 и 12;2 расположены по разные стороны от проведённой прямой, но на равных расстояниях от неё. Они симметричны относительно этой прямой. То же можно сказать о точках 4;14 и 14;4,8;18 и 18;8 и т. д. Значит, прямая \(y =x\) — ось симметрии гиперболы y=1x (равно как и \(y = -x\)).
То же можно сказать о точках 4;14 и 14;4,8;18 и 18;8 и т. д. Значит, прямая \(y =x\) — ось симметрии гиперболы y=1x (равно как и \(y = -x\)).
Построить график функции у=-x²+2x+8 (парабола) – решение и ответ
Формулировка задания: Построить график функции у = -x² + 2x + 8.
Решение:
Для построения графика параболы нужно построить таблицу значений x и y.
Для удобства начнем с точек, находящихся на осях Ox и Oy. Если точка лежит на оси Oy (x = 0), тогда:
x = 0 ⇒
y = -0² + 2 ⋅ 0 + 8 = 8
Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:
y = 0 ⇒
-x² + 2x + 8 = 0
a = -1, b = 2, c = 8
D = 2² – 4 ⋅ (-1) ⋅ 8 = 36
x1 = (-2 + 6) / (-2) = -2
x2 = (-2 – 6) / (-2) = 4
Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:
Заполняем ими таблицу:
Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:
x = 1 ⇒
y = -1² + 2 ⋅ 1 + 8 = 9
x = -1
y = -(-1)² + 2 ⋅ (-1) + 8 = 5
Таблица значений теперь выглядит следующим образом:
Отметим полученные точки на координатной плоскости:
Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними. Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):
(4 – (-2)) / 2 = 6 / 2 = 3
xв = -2 + 3 = 1
Точка с таким значением x уже есть в таблице значений. Осталось построить график:
Поделитесь статьей с одноклассниками «Построить график функции у=-x²+2x+8 (парабола) – решение и ответ».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Задание 20 (С5) из реального ЕГЭ по математике 4.06.2015
Найдите все значения параметра , при каждом из которых система
имеет более двух решений.
Решение.
Заметим, что первое уравнение системы не содержит параметр. Построим график этого уравнения:
Раскроем модуль, для этого приравняем подмодульное выражение к нулю: . Так как в левой части стоит выражение с двумя переменными, мы не можем найти значение каждой переменной, но можем выразить одну переменную через другую.
.
Если , то подмодульное выражение , и мы раскрываем модуль с противоположным знаком.
Если , то подмодульное выражение , и мы раскрываем модуль с тем же знаком.
Получаем:
(1)
(2)
Первое уравнение в каждой системе похоже на уравнение окружности.
Для первой системы:
Вернемся к системе (1).
— это часть окружности с центром в точке (8;-5), R=5, расположенная ниже прямой :
Аналогично выделяем полный квадрат в первом уравнении второй системы:
Вернемся к системе (2).
— это часть окружности с центром в точке (0;0), R=5, расположенная выше прямой :
Итак, мы построили график первого уравнения исходной системы.
Преобразуем второе уравнение:
При варьировании параметра мы получим семейство прямых, параллельных прямой . Нужно определить, при каких значениях эти прямые имеют более двух точек пересечения с графиком первого уравнения.
Заметим, что уравнение прямой , соединяющей центры окружностей и имеет вид . Так как окружности имеют равные радиусы, то их общая касательная параллельна прямой, проходящей через центры окружностей. Таким образом, прямые вида и общие касательные к окружностям параллельны прямой .
Двигая мысленно прямую (варьируя значения параметра) вдоль оси , мы получим области, внутри которых прямые имеют более двух точек пересечения с графиком первого уравнения исходной системы. Касательные к окружностям обозначены пунктирными линиями, так как они имеют 2 точки пересечения с графиком уравнения:
Осталось найти уравнения прямых, ограничивающих эти области.
Прямая вида проходит через точку (3;-4) если выполняется равенство:
, отсюда
Аналогично, прямая вида проходит через точку (5;0), если .
Найдем уравнения касательных. Прямая является касательной к окружности, если имеет с ней одну общую точку. Найдем уравнения касательных вида (или ) к окружности .
Мы ищем, при каком значении система
имеет единственное решение. Это произойдет в том случае, если уравнение
будет иметь единственное решение.
Квадратное уравнение имеет единственное решение, если
Итак, мы получили ограничения на параметр :
Ответ: (][)
И. В. Фельдман, репетитор по математике.
В. Фельдман, репетитор по математике.
Решить свойства прямой линии y = 8x − 2 Решатель алгебры тигра
Решить свойства прямой линии y = 8x − 2 Решатель алгебры тиграЭтот сайт лучше всего просматривать с помощью Javascript. Если вы не можете включить Javascript, нажмите здесь.
Введите уравнение или задачуВход камеры не распознается!
Мы думаем, что вы написали:
y = 8x − 2
Это касается свойств прямой линии.
Наклон = 16,000 / 2,000 = 8,000Наклон = 16,000 / 2,000 = 8.000
xi «ntercept = 2/8 = 1/4 = 0,25000xi» ntercept = 2/8 = 1/4 = 0,25000
yi «ntercept = -2 / 1 = -2,00000yi» ntercept = -2 / 1 = -2,00000
Пошаговое решение
Переставьте:
Переставьте уравнение, вычтя то, что находится справа от знака равенства из обеих частей уравнения:
y- (8 * x-2) = 0
Шаг 1:
Уравнение прямой
1.1 Решите y-8x + 2 = 0
Тигр понимает, что здесь у нас есть уравнение прямой. Такое уравнение обычно записывается как y = mx + b («y = mx + c» в Великобритании).
Такое уравнение обычно записывается как y = mx + b («y = mx + c» в Великобритании).
«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.
В этой формуле:
y указывает нам, как далеко идет линия.
x сообщает нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является точкой пересечения оси Y, т.е. Ось Y
Пересечения X и Y и уклон называются свойствами линии.Теперь мы построим график линии y-8x + 2 = 0 и вычислим ее свойства
График прямой линии:
Вычислите точку пересечения оси Y:
Обратите внимание, что когда x = 0, значение y равно -2 / 1, поэтому эта линия «разрезает» ось y в точке y = -2,00000
y-intercept = -2/1 = -2,00000
Вычислите точку пересечения X:
Когда y = 0, значение x равно 1 / 4 Наша линия поэтому «разрезает» ось x в точке x = 0,25000
x-intercept = 2/8 = 1/4 = 0.25000
Расчет наклона:
Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно -2,000, а для x = 2,000 значение y равно 14,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 14 000 — (-2 000) = 16 000 y. (Изменение y иногда называют «ПОДЪЕМ», а наклон m = RISE / RUN)
Наклон = 16,000 / 2,000 = 8,000
Геометрическая фигура: прямая линия
- Наклон = 16.000 / 2.000 = 8.000
- пересечение по оси x = 2/8 = 1/4 = 0,25000
- пересечение по оси y = -2/1 = -2,00000
Зачем это изучать
Термины и темы
Ссылки по теме
4x-y = 8 и x + 2y = 2 | Wyzant Спросите эксперта
Привет, Конни,
Давайте начнем с решения этой системы уравнений алгебраически, а затем покажем решение графически.
Алгебраическое решение:
1.Наша система уравнений:
Уравнение # 1: 4x — y = 8
Уравнение 2: x + 2y = 2
2.
Уравнение № 3: 8x — 2y = 16
3. Добавьте уравнение № 2 к уравнению № 3:
Уравнение 4: 9x = 18
4. Решите относительно x, используя уравнение № 4:
9x = 18
х = 2
5.Подставьте значение x обратно в уравнение 2 и решите
.для y:
х + 2у = 2
2 + 2у = 2
2y = 2–2
2y = 0
г = 0/2
у = 0
Теперь давайте проверим наши ответы, вставив их обратно в уравнение № 1 и посмотрим, равны ли обе стороны:
4x — у = 8
4 (2) — 0 = 8
8 — 0 = 8
8 = 8 (обе стороны равны)
Поскольку обе стороны равны, мы уверены, что наши ответы верны.
Теперь мы покажем графическое решение, дающее то же решение, что и наше алгебраическое решение выше. Сначала мы преобразуем каждое уравнение из стандартной формы в форму с пересечением наклона, чтобы было легко подставить значения для x и получить наши значения для y:
1.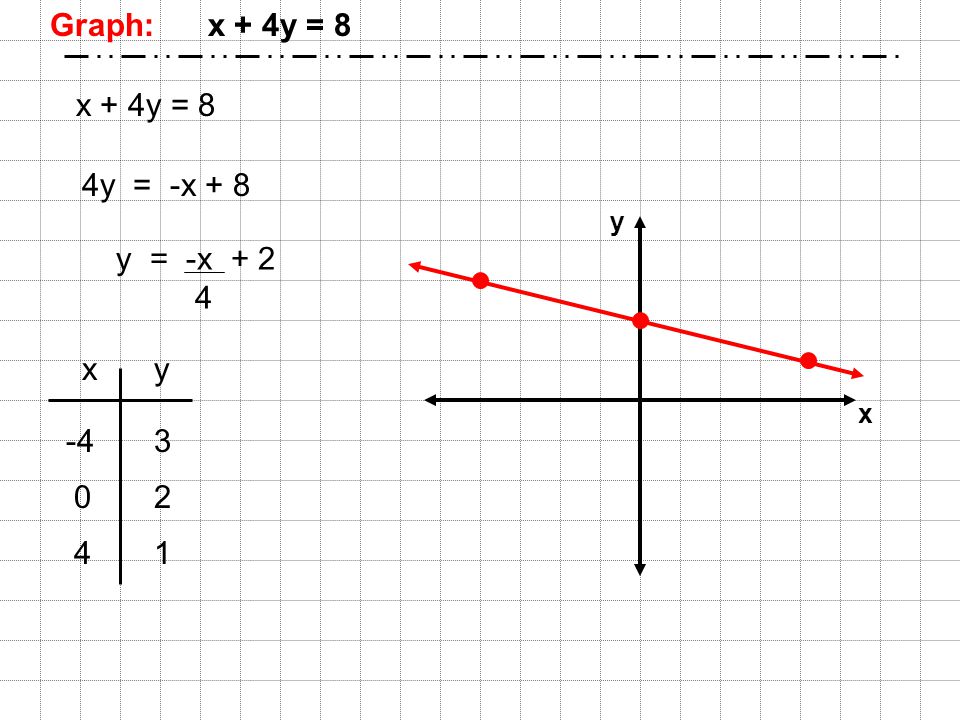 Уравнение № 1:
Уравнение № 1:
4x — y = 8 (стандартная форма)
-y = -4x + 8
(-1) (- y) = (-1) (- 4x) + (-1) (8)
y = 4x — 8 (форма пересечения наклона)
2.Уравнение # 2:
x + 2y = 2 (стандартная форма)
2у = -x + 2
у = -x / 2 + 2/2
y = -0,5x + 1 (форма пересечения наклона)
Ниже приведена ссылка на наши графики двух уравнений (в форме пересечения угла наклона), где синий график соответствует уравнению №1, красный график — уравнению №2, а координаты точки пересечения (розовый крест: x = 2 и y = 0) — наше графическое решение (такое же, как и наше алгебраическое решение выше):
https: // дл.dropbox.com/s/9bclzxn9uaohs6l/Graphical_Solution.png?raw=1
Спасибо за сообщение об этой проблеме и рад помочь.
Да благословит Бог, Иордания.
Системы линейных уравнений
Линейное уравнение — это уравнение для линии .
Линейное уравнение не всегда имеет вид y = 3,5 — 0,5x ,
Также может быть как y = 0.5 (7 — х)
Или как y + 0,5x = 3,5
Или как y + 0,5x — 3,5 = 0 и больше.
(Примечание: все это одно и то же линейное уравнение!)
A Система линейных уравнений — это когда у нас есть два или более линейных уравнения
Пример: Вот два линейных уравнения:
Вместе они представляют собой систему линейных уравнений.
Сможете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)
Попробуем построить и решить реальный пример:
Пример: вы против лошади
Это гонка!
Вы можете бегать 0,2 км каждую минуту.
Лошадь может бежать 0,5 км каждую минуту. Но оседлать лошадь нужно за 6 минут.
Как далеко вы можете уйти, прежде чем лошадь вас поймает?
Мы можем составить два уравнения ( d = расстояние в км, t = время в минутах)
- Вы работаете на 0.

- Лошадь бежит со скоростью 0,5 км в минуту, но мы берем на ее время 6: d = 0,5 (t − 6)
Итак, у нас есть система уравнений ( линейных ):
Решаем на графике:
Вы видите, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймают через 10 минут … Тебе всего 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Давайте продолжим узнавать о них больше ….
Решение
Существует множество способов решения линейных уравнений!
Давайте посмотрим на другой пример:
Пример: решите эти два уравнения:
На этом графике показаны два уравнения:
Наша задача — найти место пересечения двух линий.
Ну, мы видим, где они пересекаются, так что это уже решено графически.
А теперь давайте решим это с помощью алгебры!
Хммм .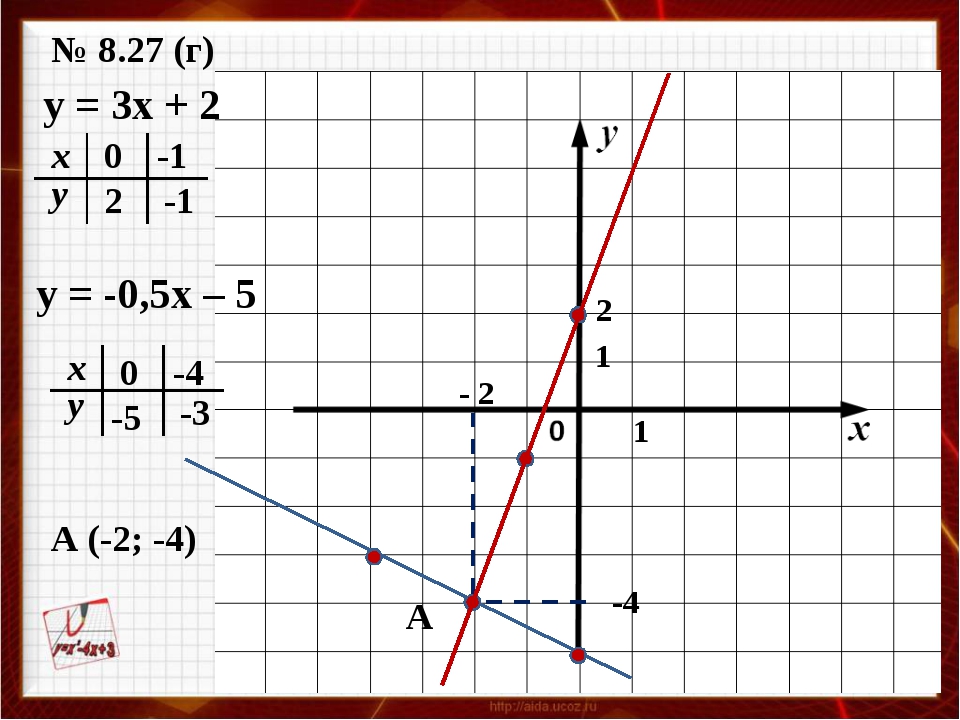 .. как это решить? Способов может быть много! В этом случае оба уравнения имеют «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
.. как это решить? Способов может быть много! В этом случае оба уравнения имеют «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
x + y — (−3x + y) = 6 — 2
А теперь упростим:
х + у + 3х — у = 6-2
4x = 4
х = 1
Итак, теперь мы знаем, что линии пересекаются в точке x = 1 .
И мы можем найти совпадающее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одинаковое значение при x = 1). Воспользуемся первым (второй можете попробовать сами):
х + у = 6
1 + у = 6
г = 5
И решение:
x = 1 и y = 5
И график показывает, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. Нет x 2 , y 3 , √x и т. Д. :
Линейное против нелинейного
Размеры
A Linear Equation может быть в 2 измерениях . .. .. (например, x и y ) | ||
| … или в 3-х измерениях … (делает самолет) | ||
| … или 4 размера … | ||
| … или больше! |
Общие переменные
Чтобы уравнения «работали вместе», они разделяют одну или несколько переменных:
Система уравнений содержит два или более уравнений в одну или несколько переменных
Множество переменных
Таким образом, Система уравнений может иметь множество, уравнений и множество переменных.
Пример: 3 уравнения с 3 переменными
| 2x | + | y | – | 2z | = | 3 |
| x | – | y | – | z | = | 0 |
| x | + | y | + | 3z | = | 12 |
Может быть любая комбинация:
- 2 уравнения с 3 переменными,
- 6 уравнений в 4 переменных,
- 9000 уравнений в 567 переменных,
- и др.

Решения
Когда количество уравнений равно , то же , что и количество переменных, , вероятно, будет решением. Не гарантировано, но вероятно.
На самом деле возможны только три случая:
- Нет раствор
- Одно решение
- Бесконечное множество решений
Когда нет решения , уравнения называются «несовместимыми» .
Один или бесконечно много решений называются «согласованными»
Вот диаграмма для 2 уравнения с 2 переменными :
Независимый
«Независимый» означает, что каждое уравнение дает новую информацию.
В противном случае они «Зависимые» .
Также называется «линейная независимость» и «линейная зависимость»
Пример:
Эти уравнения «Зависимые» , потому что они на самом деле являются тем же уравнением , только умноженным на 2.
Таким образом, второе уравнение не дало новой информации .
Где верны уравнения
Уловка состоит в том, чтобы найти, где все уравнения являются истинными одновременно .
Верно? Что это значит?
Пример: вы против лошади
Линия «ты» истинна по всей ее длине (но больше нигде).
В любом месте этой строки d равно 0.2т
- при t = 5 и d = 1 уравнение истинно (d = 0,2t? Да, поскольку 1 = 0,2 × 5 верно)
- при t = 5 и d = 3, уравнение не соответствует действительности (верно ли d = 0,2t? Нет, поскольку 3 = 0,2 × 5 неверно )
Точно так же линия «лошади» истинна по всей ее длине (но больше нигде).
Но только в точке, где они пересекают (при t = 10, d = 2), они оба являются истинными .
Значит, они должны быть правдой одновременно . ..
..
… поэтому некоторые люди называют их «Одновременные линейные уравнения»
Решить с помощью алгебры
Для их решения принято использовать алгебру.
Вот пример «Лошади», решенный с помощью алгебры:
Пример: вы против лошади
Система уравнений:
В этом случае кажется самым простым приравнять их друг к другу:
г = 0.2т = 0,5 (т − 6)
Начать с : 0,2t = 0,5 (t — 6)
Расширить 0,5 (t − 6) : 0,2t = 0,5t — 3
Вычтем 0,5t с обеих сторон: −0,3t = −3
Разделим обе части на −0,3 : t = −3 / −0,3 = 10 минуты
Теперь мы знаем , когда тебя поймают!
Зная t , мы можем вычислить d : d = 0,2t = 0,2 × 10 = 2 км
И наше решение:
t = 10 минут и d = 2 км
Алгебра и графики
Зачем использовать алгебру, если графики настолько просты? Потому что:
Более двух переменных невозможно решить с помощью простого графика.
Итак, алгебра приходит на помощь двумя популярными методами:
- Решение заменой
- Решение методом исключения
Мы увидим каждую с примерами по 2 переменным и 3 переменным. Вот и …
Решение заменой
Это шаги:
- Напишите одно из уравнений в стиле «переменная = …»
- Заменить (т.е. заменить) эту переменную в другое уравнение (а).
- Решите другое уравнение (а)
- (при необходимости повторить)
Вот пример 2 уравнения с 2 переменными :
Пример:
Мы можем начать с любого уравнения и любой переменной .
Воспользуемся вторым уравнением и переменной «y» (это выглядит как простейшее уравнение).
Напишите одно из уравнений в стиле «переменная =»… «:
Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 — x . Теперь наши уравнения выглядят так:
Теперь замените «y» на «8 — x» в другом уравнении:
- 3x + 2 (8 — x) = 19
- у = 8 — х
Решите, используя обычные методы алгебры:
Развернуть 2 (8 − x) :
- 3x + 16 — 2x = 19
- у = 8 — х
Тогда 3x − 2x = x :
И на последок 19-16 = 3
Теперь мы знаем, что такое x , мы можем поместить его в уравнение y = 8 — x :
И ответ:
х = 3
у = 5
Примечание: поскольку — это решение , уравнения «непротиворечивы»
Проверка: почему бы вам не проверить, работают ли x = 3 и y = 5 в обоих уравнениях?
Решение подстановкой: 3 уравнения с 3 переменными
ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .
Это несложно, сделать … просто нужно много времени !
Пример:
- х + г = 6
- г — 3у = 7
- 2x + y + 3z = 15
Мы должны аккуратно выровнять переменные, иначе мы потеряем из виду, что делаем:
| x | + | z | = | 6 | |||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 |
WeI может начать с любого уравнения и любой переменной. Воспользуемся первым уравнением и переменной «x».
Воспользуемся первым уравнением и переменной «x».
Напишите одно из уравнений в стиле «переменная = …»:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 | |||
Теперь замените «x» на «6 — z» в других уравнениях:
(К счастью, есть только одно уравнение с x в нем)
| х | = | 6 — z | ||||||||
| – | 3 года | + | z | = | 7 | |||||
| 2 (6-z) | + | y | + | 3z | = | 15 | ||||
Решите, используя обычные методы алгебры:
2 (6 − z) + y + 3z = 15 упрощается до y + z = 3 :
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| y | + | z | = | 3 | |||||
Хорошо. Мы достигли некоторого прогресса, но пока не достигли его.
Мы достигли некоторого прогресса, но пока не достигли его.
Теперь повторите процесс , но только для последних 2 уравнений.
Напишите одно из уравнений в стиле «переменная = …»:
Выберем последнее уравнение и переменную z:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| z | = | 3 — х лет | |||||||
Теперь замените «z» на «3 — y» в другом уравнении:
| x | = | 6 — z | |||||||
| – | 3 года | + | 3 — х лет | = | 7 | ||||
| z | = | 3-й год | |||||||
Решите, используя обычные методы алгебры:
−3y + (3 − y) = 7 упрощается до −4y = 4 , или другими словами y = −1
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 3-й год | |||||||
Почти готово!
Зная, что y = −1 , мы можем вычислить, что z = 3 − y = 4 :
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 4 | |||||||
И зная, что z = 4 , мы можем вычислить, что x = 6 − z = 2 :
| x | = | 2 | |||||||
| y | = | -1 | |||||||
| z | = | 4 |
И ответ:
х = 2
у = -1
г = 4
Проверка: проверьте сами.
Мы можем использовать этот метод для 4 или более уравнений и переменных … просто повторяйте одни и те же шаги снова и снова, пока не решите проблему.
Заключение: Замена работает нормально, но требует много времени.
Решение путем исключения
Уничтожение может быть быстрее … но должно быть аккуратным.
«Исключить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.
По идее, мы можем спокойно :
- умножить уравнение на константу (кроме нуля),
- добавить (или вычесть) уравнение к другому уравнению
Как в этих примерах:
ПОЧЕМУ мы можем складывать уравнения друг в друга?
Представьте себе два действительно простых уравнения:
х — 5 = 3
5 = 5
Мы можем добавить «5 = 5» к «x — 5 = 3»:
х — 5 + 5 = 3 + 5
х = 8
Попробуйте сами, но используйте 5 = 3 + 2 в качестве второго уравнения
Он по-прежнему будет работать нормально, потому что обе стороны равны (это то, для чего стоит знак =!)
Мы также можем поменять местами уравнения, чтобы первое могло стать вторым и т. д., если это поможет.
д., если это поможет.
Хорошо, время для полного примера. Давайте использовать предыдущий пример 2 уравнения с 2 переменными :
Пример:
Очень важно держать вещи в порядке:
| 3x | + | 2 года | = | 19 | |||
| x | + | y | = | 8 |
Сейчас…. наша цель — исключить переменную из уравнения.
Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.
Умножьте второе уравнение на 2:
| 3x | + | 2 года | = | 19 | |||
| 2 x | + | 2 л | = | 16 |
Вычтем второе уравнение из первого уравнения:
| x | = | 3 | |||||
| 2x | + | 2 года | = | 16 |
Ура! Теперь мы знаем, что такое x!
Затем мы видим, что во втором уравнении есть «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:
Умножьте второе уравнение на ½ (т. е. разделить на 2):
е. разделить на 2):
| x | = | 3 | |||||
| x | + | y | = | 8 |
Вычтем первое уравнение из второго уравнения:
| x | = | 3 | |||||
| y | = | 5 |
Готово!
И ответ:
x = 3 и y = 5
А вот график:
Синяя линия — это место, где 3x + 2y = 19 верно
Красная линия — это место, где x + y = 8 верно
При x = 3, y = 5 (где линии пересекаются) они равны , оба истинны. Это ответ.
Это ответ.
Вот еще один пример:
Пример:
- 2x — y = 4
- 6x — 3y = 3
Разложите аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 3 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 3 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 9 | |||
| 6x | – | 3 года | = | 3 |
0 — 0 = 9 ???
Что здесь происходит?
Проще говоря, решения нет.
| На самом деле это параллельные линии: |
И на последок:
Пример:
- 2x — y = 4
- 6x — 3y = 12
Аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 12 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 12 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 0 | |||
| 6x | – | 3 года | = | 3 |
0 — 0 = 0
Ну, это на самом деле ИСТИНА! Ноль действительно равен нулю. ..
..
… это потому, что на самом деле это одно и то же уравнение …
… значит существует бесконечное количество решений
| Это та же строка: |
Итак, теперь мы рассмотрели пример каждого из трех возможных случаев:
- Нет раствор
- Одно решение
- Бесконечное множество решений
Решение методом исключения: 3 уравнения с 3 переменными
Прежде чем мы начнем со следующего примера, давайте посмотрим на улучшенный способ решения задач.
Следуйте этому методу, и мы уменьшим вероятность ошибки.
Прежде всего удалите переменные в порядке :
- Сначала удалите x с (из уравнений 2 и 3, по порядку)
- , затем исключите y (из уравнения 3)
Вот как мы их устраняем:
У нас есть «форма треугольника»:
Теперь начните снизу и вернитесь к предыдущему результату. (так называемая «обратная подстановка»)
(так называемая «обратная подстановка»)
(введите z , чтобы найти y , затем z и y , чтобы найти x ):
И решаемся:
ТАКЖЕ, мы обнаружим, что проще выполнить некоторые вычислений в уме или на бумаге для заметок, чем всегда работать в рамках системы уравнений:
Пример:
- х + у + г = 6
- 2y + 5z = −4
- 2x + 5y — z = 27
Аккуратно написано:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 2x | + | 5лет | – | z | = | 27 |
Сначала удалите x из 2-го и 3-го уравнения.
Во втором уравнении нет x … переходите к третьему уравнению:
Вычтите 2 раза 1-е уравнение из 3-го уравнения (просто сделайте это в уме или на бумаге для заметок):
И получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 3 года | – | 3z | = | 15 |
Затем удалите y из 3-го уравнения.
Мы, , могли бы вычесть 1½ раза 2-е уравнение из 3-го (потому что 1½ раза 2 равно 3) …
… но мы можем избежать дробей , если мы:
- умножить третье уравнение на 2 и
- умножьте второе уравнение на 3
и , затем выполняют вычитание … вот так:
И в итоге получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| z | = | −2 |
Теперь у нас есть «треугольная форма»!
Теперь вернемся снова вверх «обратная замена»:
Мы знаем z , поэтому 2y + 5z = −4 становится 2y − 10 = −4 , затем 2y = 6 , поэтому y = 3 :
| x | + | y | + | z | = | 6 | |||
| y | = | 3 | |||||||
| z | = | −2 |
Тогда x + y + z = 6 становится x + 3−2 = 6 , поэтому x = 6−3 + 2 = 5
| x | = | 5 | |||||||
| y | = | 3 | |||||||
| z | = | −2 |
И ответ:
x = 5
y = 3
z = −2
Проверка: проверьте сами.
Общий совет
Как только вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто следуете инструкциям, и появляются ответы.
Но иногда замена может дать более быстрый результат.
- Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
- Устранение проще для больших ящиков
И всегда полезно сначала просмотреть уравнения, чтобы увидеть, есть ли простой ярлык… так что опыт помогает.
Wolfram | Alpha Примеры: Алгебра
Другие примеры
Решение уравненияРешите уравнения с одной или несколькими переменными как символически, так и численно.
Решите полиномиальное уравнение:
Решите систему линейных уравнений:
Решите уравнение с параметрами:
Другие примеры
Другие примеры
Полиномы Решайте, строите и находите альтернативные формы полиномиальных выражений от одной или нескольких переменных.
Вычислить свойства полинома от нескольких переменных:
Другие примеры
Другие примеры
Рациональные функции Вычислить разрывы и другие свойства рациональных функций.
Вычислить свойства рациональной функции:
Вычислить частичное разложение дроби:
Другие примеры
Другие примеры
Упрощение Упростите алгебраические функции и выражения.
Другие примеры
Другие примеры
МатрицыНайдите свойства и выполните вычисления с матрицами.
Выполните базовую арифметику с матрицами:
Вычислить собственные значения и собственные векторы матрицы:
Другие примеры
Другие примеры
Кватернионы Выполните вычисления в кватернионной системе счисления.
Получите информацию о кватернионе:
Проведите расчеты с кватернионами:
Другие примеры
Другие примеры
Конечные группы Откройте для себя свойства групп, содержащих конечное число элементов.
Получите информацию о конечной группе:
Спросите о собственности группы:
Сделайте алгебру с перестановками:
Другие примеры
Другие примеры
Конечные поля Откройте для себя свойства полей, содержащих конечное число элементов.
Вычислить свойства конечного поля:
Вычислить конкретное свойство:
Другие примеры
Другие примеры
Домен и диапазон Найдите область и диапазон математических функций.
Вычислить область определения функции:
Вычислить диапазон функции:
Другие примеры
Графическое решение — стр. 17d
ГРАФИЧЕСКОЕ РЕШЕНИЕ
Четвертый метод решения квадратного уравнения — это
построение графиков. При построении графиков линейных уравнений с использованием обеих осей в качестве эталона мы
При построении графиков линейных уравнений с использованием обеих осей в качестве эталона мы
Поскольку рассматриваемые нами квадраты содержат только одну переменную, как в уравнении
x 2 — 8x + 12 = 0
, мы не можем построить значения для уравнений в существующей форме
, используя оси x и y.А зависимая переменная y необходима.Если подумать о выражении
x 2 — 8x + 12
как функция, то можно считать, что эта функция имеет много возможных числовых значений,
в зависимости от того, какое значение мы присваиваем x. В конкретное значение или значения x, которые вызывают значение функции равным 0 являются решениями для уравнениеx 2 — 8x + 12 = 0
Для удобства мы можем позволить y
представлять функциюX2 — 8x + 12
Если числовые значения теперь присвоены x, можно вычислить
соответствующих значений y.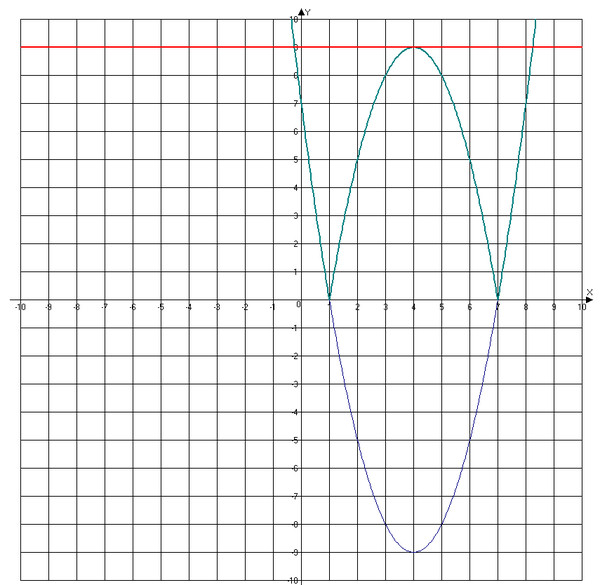 Когда эти пары соответствующих значений x
и y сведены в таблицу, итоговая таблица предоставляет информацию, необходимую для построения графика
график функции.
Когда эти пары соответствующих значений x
и y сведены в таблицу, итоговая таблица предоставляет информацию, необходимую для построения графика
график функции.ПРИМЕР: Постройте уравнение
х 2 + 2х — 8 = 0
и по графику запишите корни уравнения.
РЕШЕНИЕ:
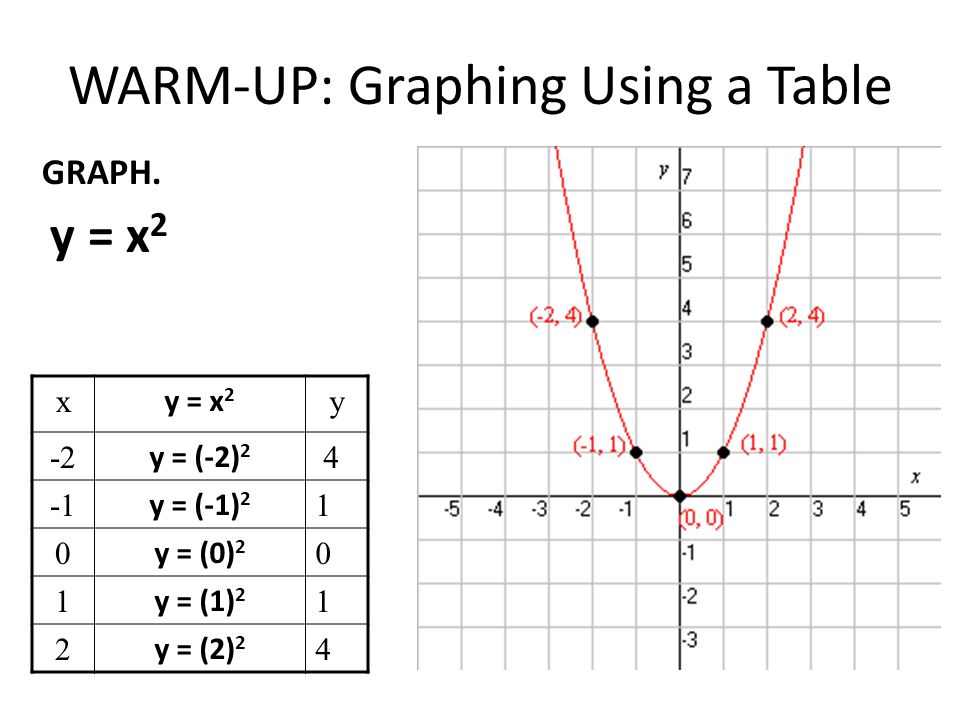
1. Пусть y = x 2 + 2x — 8.
2.
Сделать таблица значений y, соответствующих присвоенному значению x, как показано в таблице 16-1.Таблица 16-1.-Табулирование значений x и y для функции y = x 2 + 2x — 8.
3. Постройте пары значений x и y, которые появляются в таблице, как координаты точек на прямоугольная система координат, как на рисунке 16-1 (A).
4. Проведите плавную кривую через эти точки, как показано на рисунке 16-1 (B).
Обратите внимание, что эта кривая пересекает ось X в двух местах. Напомним также, что для любой точки
на оси X координата y равна нулю. Таким образом, на рисунке мы видим, что когда y равно нулю, x равно
-4 или +2. Кроме того, когда y равно нулю, мы имеем исходное уравнение
Таким образом, на рисунке мы видим, что когда y равно нулю, x равно
-4 или +2. Кроме того, когда y равно нулю, мы имеем исходное уравнение
Рисунок 16-1.-График уравнения y = x 2 + 2x — 8. (A) Нанесены точки; (B) кривая, проведенная через нанесенные точки.
х 2 + 2х — 8 = 0
Таким образом, значения x в этих точках, где график уравнения пересекает ось X (х = -4
или +2) являются решениями исходного уравнения.Мы можем проверить эти результаты, решив уравнение алгебраически. Таким образом,Кривая на рисунке 16-1 (B) называется ПАРАБОЛА. Всякая квадратичная формы ax 2 + bx + c = y будет иметь график этой общей формы. Кривая откроется вниз, если отрицательно, и вверх, если a положительно.
Графики предоставляют четвертый метод нахождения корней квадратичной функции от одной переменной. Когда
уравнение изображено на графике, корнями будут точки пересечения X (те значения x, где кривая
пересекает ось X).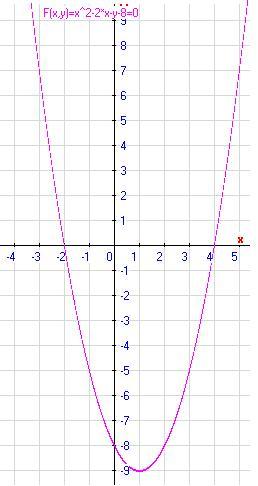 X точки пересечения — это точки, в которых y равно 0.
X точки пересечения — это точки, в которых y равно 0.
Практические задачи. Постройте график следующих квадратных уравнений и прочтите корни каждого уравнение из его графика
1. x 2 — 4x — 8 = 0
2. 6x — 5 — x 2 = 0
Ответы:
1. См. Рисунок 16-2. х = 5,5; х = -1,5
2. См. Рисунок 16-3. х = 1; х = 5
NCERT для математики класса 7 Глава 4
Страница № 81:
Вопрос 1:
Заполните последний столбец таблицы.
С. № | Уравнение | Значение | Скажите, удовлетворяется ли уравнение. (Да / Нет) |
(я) | х + 3 = 0 | x = 3 | – |
(ii) | х + 3 = 0 | х = 0 | – |
(iii) | х + 3 = 0 | x = — 3 | – |
(iv) | x — 7 = 1 | x = 7 | – |
(в) | x — 7 = 1 | х = 8 | – |
(vi) | 5 x = 25 | х = 0 | – |
(vii) | 5 x = 25 | х = 5 | – |
(viii) | 5 x = 25 | х = — 5 | – |
(ix) | м = — 6 | – | |
(х) | м = 0 | – | |
(xi) | м = 6 | – |
Ответ:
(i) x + 3 = 0
Л. H.S. = x + 3
H.S. = x + 3
Положив x = 3,
L.H.S. = 3 + 3 = 6 ≠ R.H.S.
∴ Нет, уравнение не выполняется.
(ii) x + 3 = 0
L.H.S. = x + 3
Положив x = 0,
L.H.S. = 0 + 3 = 3 ≠ R.H.S.
∴ Нет, уравнение не выполняется.
(iii) x + 3 = 0
L.H.S. = x + 3
Положив x = −3,
Л.H.S. = — 3 + 3 = 0 = R.H.S.
∴ Да, уравнение выполнено.
(iv) x — 7 = 1
L.H.S. = x — 7
Положив x = 7,
L.H.S. = 7-7 = 0 ≠ R.H.S.
∴ Нет, уравнение не выполняется.
(в) x — 7 = 1
L.H.S. = x — 7
Положив x = 8,
L.H.S. = 8-7 = 1 = R.H.S.
∴ Да, уравнение выполнено.
(vi) 5 x = 25
L.H.S. = 5 x
Положив x = 0,
L.H.S. = 5 × 0 = 0 ≠ R.H.S.
∴ Нет, уравнение не выполняется.
(vii) 5 x = 25
L.H.S. = 5 x
Положив x = 5,
L.H.S. = 5 × 5 = 25 = R.H.S.
∴ Да, уравнение выполнено.
(viii) 5 x = 25
L.H.С. = 5 х
Положив x = −5,
L.H.S. = 5 × (−5) = −25 ≠ R.H.S.
∴ Нет, уравнение не выполняется.
(ix) знак равно 2
L.H.S. знак равно
Положив м = −6,
Л. Х. С. = ≠ R.H.S.
∴Нет, уравнение не выполняется.
(х) знак равно 2
L.H.S. знак равно
Положив м = 0,
L.H.S. = ≠ R.H.S.
∴Нет, уравнение не выполняется.
(xi) знак равно 2
L.H.S. знак равно
Положив м = 6,
L.H.S. знак равно = R.H.S.
∴ Да, уравнение выполнено.
Страница № 81:
Вопрос 2:
Проверить является ли значение, указанное в скобках, решением данной уравнение или нет:
(а) н + 5 = 19 ( n = 1) (б) 7 n + 5 = 19 ( n = — 2)
(в) 7 n + 5 = 19 ( п = 2) (г) 4 п — 3 = 13 ( п = 1)
(e) 4 p — 3 = 13 ( p = — 4) (f) 4 p — 3 = 13 ( p = 0)
Ответ:
(а) н + 5 = 19 ( п = 1)
Положив n = 1 в L. Х.С.,
Х.С.,
n + 5 = 1 + 5 = 6 ≠ 19
Как сообщает L.H.S. ≠ R.H.S.,
Следовательно, n = 1 не является решением данного уравнения, n + 5 = 19.
(б) 7 н + 5 = 19 ( п = −2)
Положив n = −2 в L.H.S.,
7 n + 5 = 7 × (−2) + 5 = −14 + 5 = −9 ≠ 19
Как сообщает L.H.S. ≠ R.H.S.,
Следовательно, n = −2 не является решением данной уравнение, 7 n + 5 = 19.
(в) 7 n + 5 = 19 ( п = 2)
Положив n = 2 в L.H.S.,
7 n + 5 = 7 × (2) + 5 = 14 + 5 = 19 = R.H.S.
Как сообщает L.H.S. = R.H.S.,
Следовательно, n = 2 является решением данного уравнения, 7 n + 5 = 19.
(д) 4 п — 3 = 13 ( п = 1)
Положив p = 1 в L.Х.С.,
4 п — 3 = (4 × 1) — 3 = 1 ≠ 13
Как L.H.S ≠ R.H.S.,
Следовательно, p = 1 не является решением данного уравнения, 4 p — 3 = 13.
(e) 4 p — 3 = 13 ( п = −4)
Положим p = −4 в L.H.S.,
4 p — 3 = 4 × (−4) — 3 = — 16 — 3 = −19 ≠ 13
Как сообщает L.H.S. ≠ R.H.S.,
Следовательно, p = −4 не является решением данной уравнение, 4 p — 3 = 13.
(ж) 4 п — 3 = 13 ( п = 0)
Положив p = 0 в L.H.S.,
4 п — 3 = (4 × 0) — 3 = −3 ≠ 13
Как сообщает L.H.S. ≠ R.H.S.,
Следовательно, p = 0 не является решением данного уравнения, 4 p — 3 = 13.
Страница № 81:
Вопрос 3:
Решите следующие уравнения методом проб и ошибок:
(i) 5 п. + 2 = 17 (ii) 3 м — 14 = 4
Ответ:
(я) 5 п + 2 = 17
Положив p = 1 в L. Х.С.,
Х.С.,
(5 × 1) + 2 = 7 ≠ R.H.S.
Положим p = 2 в L.H.S.,
(5 × 2) + 2 = 10 + 2 = 12 ≠ R.H.S.
Положим p = 3 в L.H.S.,
(5 × 3) + 2 = 17 = R.H.S.
Следовательно, p = 3 является решением данного уравнения.
(ii) 3 м — 14 = 4
Положим м = 4,
(3 × 4) — 14 = −2 ≠ Р.H.S.
Положим м = 5,
(3 × 5) — 14 = 1 ≠ R.H.S.
Положим м = 6,
(3 × 6) — 14 = 18 — 14 = 4 = R.H.S.
Следовательно, м = 6 является решением данного уравнения.
Страница № 81:
Вопрос 4:
Напишите уравнения для следующих утверждений:
(i) Сумма чисел x и 4 равна 9.
(ii) 2 вычитается из y равно 8.
(iii) Десять раз , равно 70.
(iv) Число b разделенное на 5 дает 6.
(v) Три четверти от т — 15.
(vi) Семь раз м плюс 7 — 77.
(vii) Одна четвертая числа x минус 4 дает 4.
(viii) Если от 6 умножить на y , то получится 60.
(ix) Если вы прибавите 3 к одной трети от z , вы получите 30.
Ответ:
(i) x + 4 = 9
(ii) y — 2 = 8
(iii) 10 a = 70
(iv)
(в)
(vi) Семь раз по м равно 7 м .
7 м + 7 = 77
(vii) Четвертая часть числа x равна.
(viii) Шесть раз от до равно 6 y .
6 y — 6 = 60
(ix) Треть от z составляет.
Видео решение для простых уравнений (Страница: 81, Вопрос №: 4)
Решение NCERT для математики класса 7 — простые уравнения 81, вопрос 4
Страница № 81:
Вопрос 5:
Напишите следующие уравнения в формах отчетов:
(i) p + 4 = 15 (ii) m — 7 = 3
(iii) 2 м = 7 (iv)
(v) (vi) 3 p + 4 = 25
(vii) 4 п. — 2 = 18 (viii)
— 2 = 18 (viii)
Ответ:
(i) сумма p и 4 равно 15.
(ii) 7 вычтем из м равно 3.
(iii) Дважды из номера м — 7.
(iv) Одна пятая м это 3.
(v) Три пятых м это 6.
(vi) Три умноженное на число p , при добавлении к 4 дает 25.
(vii) Когда 2 вычитается из четырехкратного числа p , получается 18.
(viii) Когда 2 прибавляется к половине числа p , получается 8.
Страница № 82:
Вопрос 6:
Составьте уравнение в следующих случаях:
(i) Ирфан говорит, что у него есть 7 шариков больше, чем в пять раз больше шариков Пармита. У Ирфана 37 шариков. (Возьмите м как количество шариков Пармита.)
(ii) Отцу Лакшми 49 лет. Он на 4 года старше Лакшми в три раза. (Возьмем возраст Лакшми: и лет.)
(Возьмем возраст Лакшми: и лет.)
(iii) Учитель сообщает классу, что самые высокие оценки, полученные учеником в его классе, вдвое превышают самые низкие оценки плюс 7. Наивысший балл — 87. (Возьмите самый низкий балл, равный -1.)
(iv) В равнобедренном треугольнике угол при вершине вдвое больше угла основания. (Пусть базовый угол равен b в градусах. Помните, что сумма углов треугольника равна 180 градусам.)
Ответ:
(i) Let Parmit имеет м и мраморов.
5 × Количество шариков, которые есть у Пармита + 7 = Количество шариков Ирфана
5 × м + 7 = 37
5 м + 7 = 37
(ii) Пусть Лакшми будет y лет.
3 × возраст Лакшми + 4 = возраст отца Лакшми
3 × y + 4 = 49
3 y + 4 = 49
(iii) Пусть самые низкие оценки будут l .
2 × самые низкие оценки + 7 = самые высокие оценки
2 × л + 7 = 87
2 л + 7 = 87
(iv) Равнобедренный треугольник имеет два угла одинаковой меры.
Пусть базовый угол равен b .
Угол при вершине = 2 × Угол основания = 2 b
Сумма всех внутренних углов Δ = 180 °
b + b + 2 b = 180 °
4 b = 180 °
Видео решение для простых уравнений (Страница: 82, Q.No .: 6)
Решение NCERT для математики класса 7 — простые уравнения 82, вопрос 6
Стр. № 86:
Вопрос 1:
Дай первым шаг, который вы будете использовать для разделения переменной, а затем решите уравнение:
(а) x + 1 = 0 (б) x + 1 = 0 (в) x — 1 = 5
(г) x + 6 = 2 (д) y — 4 = — 7 (f) y — 4 = 4
(г) y + 4 = 4 (з) y + 4 = — 4
Ответ:
(а) x — 1 = 0
Добавляя 1 к обеим частям данного уравнения, получаем
х — 1 + 1 = 0 + 1
х = 1
(б) x + 1 = 0
Вычитая 1 из обеих частей данного уравнения, получаем
x + 1 — 1 = 0 — 1
х = -1
(в) x — 1 = 5
Добавляя 1 к обеим частям данного уравнения, получаем
х — 1 + 1 = 5 + 1
х = 6
(г) x + 6 = 2
Вычитая 6 из обеих частей данного уравнения, получаем
x + 6 — 6 = 2 — 6
х = −4
д y — 4 = −7
Добавляя 4 к обеим частям данного уравнения, получаем
y — 4 + 4 = — 7 + 4
y = −3
(ж) y — 4 = 4
Добавляя 4 к обеим частям данного уравнения, получаем
y — 4 + 4 = 4 + 4
y = 8
(г) y + 4 = 4
Вычитая 4 из обеих частей данного уравнения, получаем
y + 4 — 4 = 4 — 4
y = 0
(в) y + 4 = −4
Вычитая 4 из обеих частей данного уравнения, получаем
y + 4 — 4 = — 4 — 4
y = −8
Стр.
 № 86:
№ 86:Вопрос 2:
Дай первым шаг, который вы будете использовать для разделения переменной, а затем решите уравнение:
(а) 3 л = 42 (б) (в)
(г) 4 x = 25 (е) 8 y = 36 (е)
(г) (в) 20 т = — 10
Ответ:
(а) 3 л = 42
Разделив обе части данного уравнения на 3, получим
л = 14
(б)
Умножая обе части данного уравнения на 2, получаем
б = 12
(в)
Умножая обе части данного уравнения на 7, получаем
п = 28
(г) 4 x = 25
Разделив обе части данного уравнения на 4, получим
х =
(д) 8 y = 36
Разделив обе части данного уравнения на 8, получим
y =
(ж)
Умножая обе части данного уравнения на 3, получаем
(г)
Умножая обе части данного уравнения на 5, получаем
(в) 20 т = −10
Разделив обе части данного уравнения на 20, получим
Стр.
 № 86:
№ 86:Вопрос 3:
Укажите шаги, которые вы будете использовать для разделения переменной, а затем решите уравнение:
(а) 3 n — 2 = 46 (б) 5 м + 7 = 17 (в)
(г)
Ответ:
(a) 3 n — 2 = 46
Добавляя 2 к обеим частям данного уравнения, получаем
3 n — 2 + 2 = 46 + 2
3 n = 48
Разделив обе части данного уравнения на 3, получим
n = 16
(б) 5 м + 7 = 17
Вычитая 7 из обеих частей данного уравнения, получаем
5 м + 7-7 = 17-7
5 м = 10
Разделив обе части данного уравнения на 5, получим
(в)
Умножая обе части данного уравнения на 3, получаем
Разделив обе части данного уравнения на 20, получим
(г)
Умножая обе части данного уравнения на 10, получаем
Разделив обе части данного уравнения на 3, получим
п = 20
Стр.
 № 86:
№ 86:Вопрос 4:
Решите следующие уравнения:
(а) 10 п = 100 (б) 10 п + 10 = 100 (в)
(г) (д) (ж) 3 с = — 9
(г) 3 с + 12 = 0 (h) 3 с = 0 (i) 2 q = 6
(к) 2 к — 6 = 0 (k) 2 q + 6 = 0 (l) 2 q + 6 = 12
Ответ:
(а) 10 п = 100
(б) 10 п + 10 = 100
10 п + 10 — 10 = 100 — 10
10 п = 90
(в)
(г)
(д)
(ж) 3 с = −9
(г) 3 с + 12 = 0
3 с + 12 — 12 = 0 — 12
3 с = −12
(в) 3 с = 0
(i) 2 q = 6
(к) 2 к — 6 = 0
2 q — 6 + 6 = 0 + 6
2 q = 6
(к) 2 q + 6 = 0
2 q + 6-6 = 0-6
2 q = −6
(л) 2 q + 6 = 12
2 q + 6 — 6 = 12 — 6
2 q = 6
Стр.
 № 89:
№ 89:Ответ:
(а)
(Транспонирование к Р.H.S.)
Делим обе стороны на 2,
(б) 5 т + 28 = 10
5 t = 10 — 28 = −18 (перенос 28 на R.H.S.)
Делим обе стороны на 5,
(в)
(Транспонирование 3 к R.H.S.)
Умножение обеих сторон на 5,
a = −1 × 5 = −5
(г)
(Транспонирование 7 к Р.H.S.)
Умножение обеих сторон на 4,
q = −8
(д)
Умножение обеих сторон на 2,
5 x = −10 × 2 = −20
Делим обе стороны на 5,
(ж)
Умножение обеих сторон на 2,
Делим обе стороны на 5,
(г)
(Транспонирование к Р.H.S.)
Делим обе стороны на 7,
(высота) 6 z + 10 = −2
6 z = — 2 — 10 = −12 (транспонирование 10 в
R. H.S.)
H.S.)
Делим обе стороны на 6,
(я)
Умножение обеих сторон на 2,
Делим обе стороны на 3,
(к)
(Транспонирование От −5 до R.H.S.)
Умножение обеих сторон на 3,
2 b = 8 × 3 = 24
Делим обе стороны на 2,
б = знак равно 12
Стр. № 89:
Вопрос 2:
Решите следующие уравнения.
(а) 2 ( x + 4) = 12 (б) 3 ( n — 5) = 21
(в) 3 ( н. — 5) = — 21 (г) −4 (2 + x ) = 8
(е) 4 (2 — x ) = 8
Ответ:
(а) 2 ( x + 4) = 12
Делим обе стороны на 2,
x = 6 — 4 = 2 (транспонирование 4 в R.H.S.)
(б) 3 ( н — 5) = 21
Делим обе стороны на 3,
n = 7 + 5 = 12 (преобразование −5 в R. H.S.)
H.S.)
(в) 3 ( н. — 5) = −21
Делим обе стороны на 3,
n = — 7 + 5 = −2 (Преобразование −5 в R.H.S.)
(г) −4 (2 + x ) = 8
Делим обе части на −4,
x = — 2 — 2 = −4 (транспонирование 2 в R.H.S.)
(е) 4 (2 — x ) = 8
Делим обе стороны на 4,
2 — х = 2
— x = 2 — 2 (транспонирование 2 в R.H.S.)
— х = 0
х = 0
Стр. № 89:
Вопрос 3:
Решите следующие уравнения.
(а) 4 = 5 ( п — 2) (б) — 4 = 5 ( п — 2)
(в) 16 = 4 + 3 ( т + 2) (г) 4 + 5 ( п — 1) = 34
(д) 0 = 16 + 4 ( м — 6)
Ответ:
(а) 4 = 5 ( п. -2)
Делим обе стороны на 5,
(б) — 4 = 5 ( п -2)
Делим обе стороны на 5,
(в) 16 = 4 + 3 ( т + 2)
16-4 = 3 ( t + 2) (преобразование 4 в L.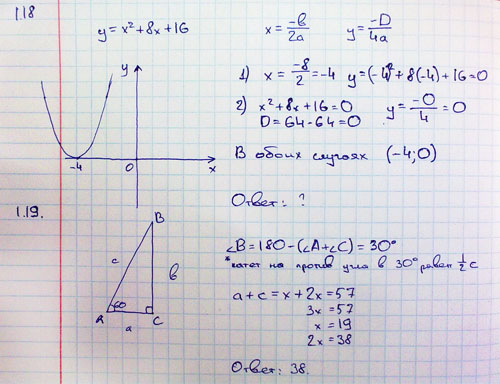 H.S.)
H.S.)
12 = 3 ( т + 2)
Делим обе стороны на 3,
4 = т + 2
4-2 = т (перенос 2 на L.H.S.)
2 = т
(д) 4 + 5 ( п — 1) = 34
5 ( п. — 1) = 34 — 4 = 30 (перенос 4 на R.H.S.)
Делим обе стороны на 5,
p = 6 + 1 = 7 (Транспонирование −1 в R.H.S.)
(д) 0 = 16 + 4 ( м -6)
0 = 16 + 4 м — 24
0 = −8 + 4 м
4 м = 8 (Транспонирование −8 в L.H.S)
Делим обе стороны на 4,
м = 2
Стр. № 89:
Вопрос 4:
(а) Конструкция 3 уравнения, начинающиеся с x = 2
(б) Конструкция 3 уравнения, начинающиеся с x = — 2
Ответ:
(а) x = 2
Умножение в обе стороны по 5,
5 x = 10 (я)
Вычитание 3 с двух сторон,
5 x — 3 = 10 — 3
5 x — 3 = 7 (ii)
Разделение обе стороны по 2,
(б) x = −2
Вычитание 2 с двух сторон,
x — 2 = — 2 — 2
x — 2 = −4 (я)
Опять же, х = −2
Умножение по 6,
6 × х = −2 × 6
6 x = −12
Вычитание 12 с двух сторон,
6 x — 12 = — 12 — 12
6 x — 12 = −24 (ii)
Добавление 24 в обе стороны,
6 x — 12 + 24 = — 24 + 24
6 x + 12 = 0 (iii)
Стр.
 № 91:
№ 91:Вопрос 1:
Составьте уравнения и решите их, чтобы найти неизвестные числа в следующие случаи:
а) прибавить от 4 до восьми число; вы получите 60.
(b) Одна пятая числа минус 4 дает 3.
(c) Если я возьму три четверти числа и прибавлю к нему 3, я получу 21.
(d) Когда я вычел 11 из двойного числа, результат был 15.
(e) Мунна вычитает трижды количество записных книжек, которые у него есть, из 50, он находит результат 8.
(е) Ибенхал придумывает число. Если она прибавит к нему 19 и разделит сумма на 5, она получит 8.
(g) Анвар придумывает число.Если он уберет 7 из из число, результат 23.
Ответ:
(a) Пусть число будет х .
8 умноженное на это число = 8 x
8 x + 4 = 60
8 x = 60 — 4 (перенос 4 на R.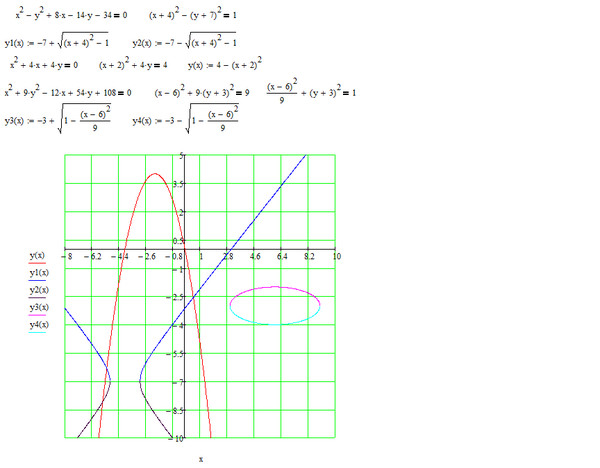 H.S.)
H.S.)
8 x = 56
Разделение обе стороны по 8,
(b) Пусть число будет х .
Одна пятая из этого числа =
(транспонирование От -4 до R.H.S.)
Умножение в обе стороны по 5,
(c) Пусть число будет х .
Три четверти из этого числа =
(транспонирование 3 к R.H.S.)
Умножение
с обеих сторон по 4,
Разделение обе стороны по 3,
(d) Пусть число будет х .
Дважды из этого числа = 2 x
2 x — 11 = 15
2 x = 15 + 11 (преобразование −11 в R.H.S.)
2 x = 26
Разделение обе стороны по 2,
x = 13
(e) Пусть количество книги быть x .
Трижды количество книг = 3 x
50 — 3 х = 8
—
3 x = 8 −50 (преобразование 50 в R. H.S.)
H.S.)
−3 х = -42
Разделение обе стороны на −3,
(f) Пусть число будет х .
Умножение в обе стороны по 5,
x + 19 = 40
x = 40 — 19 (перенос 19 на R.H.S.)
х = 21
(g) Пусть число будет х .
из этого числа =
Умножение обе стороны по 2,
Разделение в обе стороны по 5,
Стр. № 91:
Вопрос 2:
Решите следующие задачи:
(a) Учитель сообщает классу, что самые высокие оценки, полученные учеником в его классе, вдвое превышают самые низкие оценки плюс 7.Самый высокий балл — 87. Какой самый низкий балл?
(b) В равнобедренном треугольнике углы основания равны. Угол при вершине 40 °. Каковы углы основания треугольника? (Помните, сумма трех углов треугольника равна 180 °).
(c) Сачин забил вдвое больше пробежек, чем Рахул. Вместе их тиражи не достигли двух столетий. Сколько пробежек забил каждый?
Ответ:
(a) Пусть самая низкая оценка будет l .
2 × самые низкие оценки + 7 = самые высокие оценки
2 л + 7 = 87
2 л = 87 — 7 (перенос 7 на правое вращение)
2 л = 80
Делим обе стороны на 2,
Следовательно, наименьшая оценка — 40.
(b) Пусть базовые углы равны b .
Сумма всех внутренних углов треугольника составляет 180 °.
b + b + 40 ° = 180 °
2 b + 40 ° = 180 °
2 b = 180º — 40º = 140º (смещение 40º на R.H.S.)
Делим обе стороны на 2,
Следовательно, углы основания треугольника равны 70 °.
(c) Пусть оценка Рахула будет x .
Следовательно, оценка Сачина = 2 x
Оценка Рахула + оценка Сачина = 200–2
2 x + x = 198
3 x = 198
Делим обе стороны на 3,
x = 66
Оценка Рахула = 66
Оценка Сачина = 2 × 66 = 132
Видео Решение для простых уравнений (Страница: 91, В.№: 2)
Решение NCERT для математики класса 7 — простые уравнения 91, вопрос 2
Стр. № 91:
Вопрос 3:
Решите следующие задачи:
(i) Ирфан говорит, что у него есть 7 шариков больше, чем в пять раз больше шариков Пармита. У Ирфана 37 шариков. Сколько шариков у Пармита?
(ii) Отцу Лакшми 49 лет. Он на 4 года старше Лакшми в три раза.Сколько лет Лакшми?
(iii) Жители Сундарграма посадили деревья в саду деревни.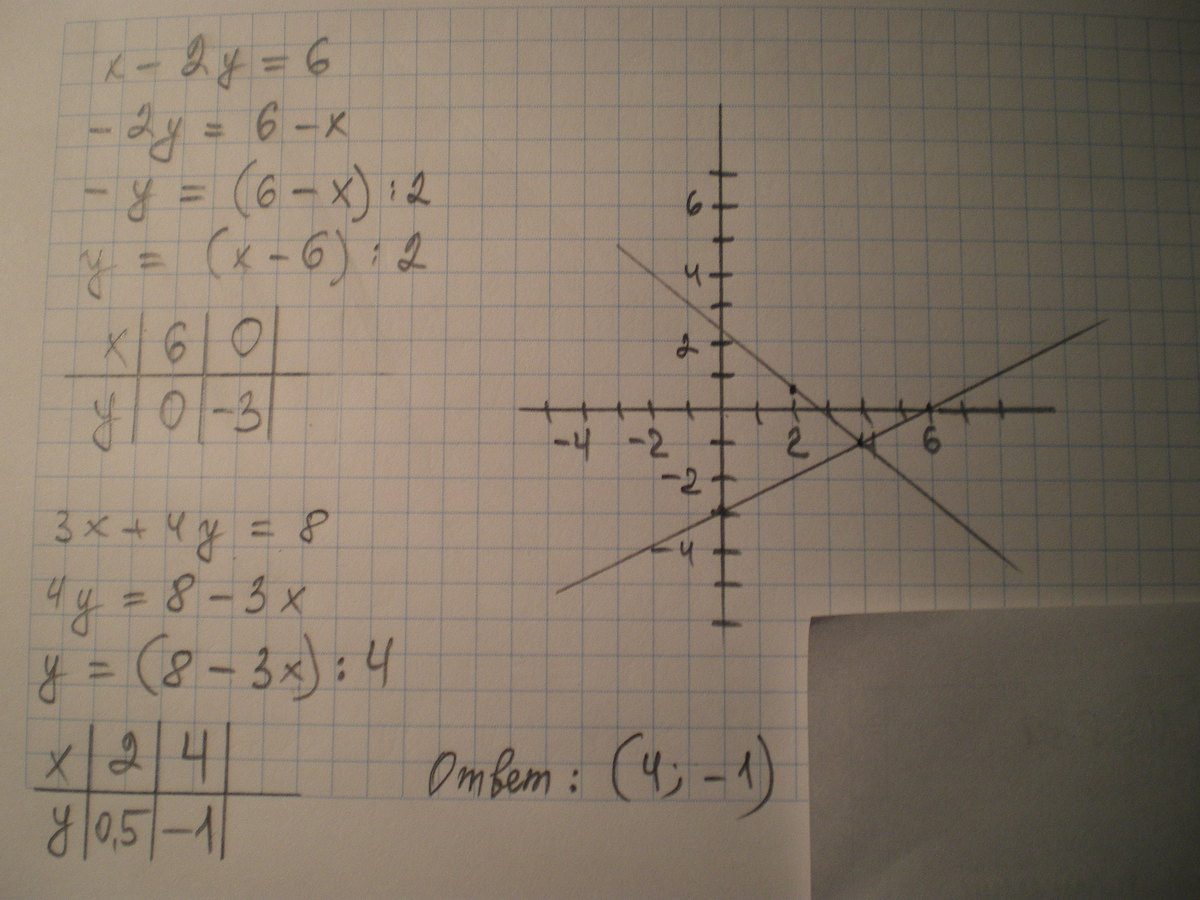 Некоторые деревья были фруктовыми. Количество неплодовых деревьев было в два раза больше, чем в три раза больше фруктовых деревьев. Сколько было посажено фруктовых деревьев, если было посажено 77 неплодородных деревьев?
Некоторые деревья были фруктовыми. Количество неплодовых деревьев было в два раза больше, чем в три раза больше фруктовых деревьев. Сколько было посажено фруктовых деревьев, если было посажено 77 неплодородных деревьев?
Ответ:
(i) Пусть размер мрамора Пармита равен x .
В 5 раз больше шариков у Пармита = 5 x
5 x + 7 = 37
5 x = 37 — 7 = 30 (перенос 7 на R.H.S.)
Делим обе стороны на 5,
Следовательно, у Пармита 6 шариков.
(ii) Пусть возраст Лакшми будет x лет.
3 × возраст Лакшми + 4 = возраст ее отца
3 x + 4 = 49
3 x = 49 — 4 (транспонирование 4 в правое положение)
3 x = 45
Делим обе стороны на 3,
x = 15
Следовательно, возраст Лакшми составляет 15 лет.
(iii) Пусть количество фруктовых деревьев будет x .
3 × Количество фруктовых деревьев + 2 = Количество неплодовых деревьев
3 x + 2 = 77
3 x = 77 — 2 (транспонирование 2 в правое положение)
3 x = 75
Разделив обе части уравнения на 3,
x = 25
Таким образом, количество фруктовых деревьев было 25.
Видео Решение для простых уравнений (Страница: 91, В.№: 3)
Решение NCERT для математики класса 7 — простые уравнения 91, вопрос 3
Стр. № 92:
Вопрос 4:
Решите следующая загадка:
Я номер,
Скажи мою личность!
Возьми меня в семь раз больше
И добавь пятьдесят!
Чтобы добраться до тройной век
Тебе еще нужно сорок!
Ответ:
Пусть
Номер должен быть x .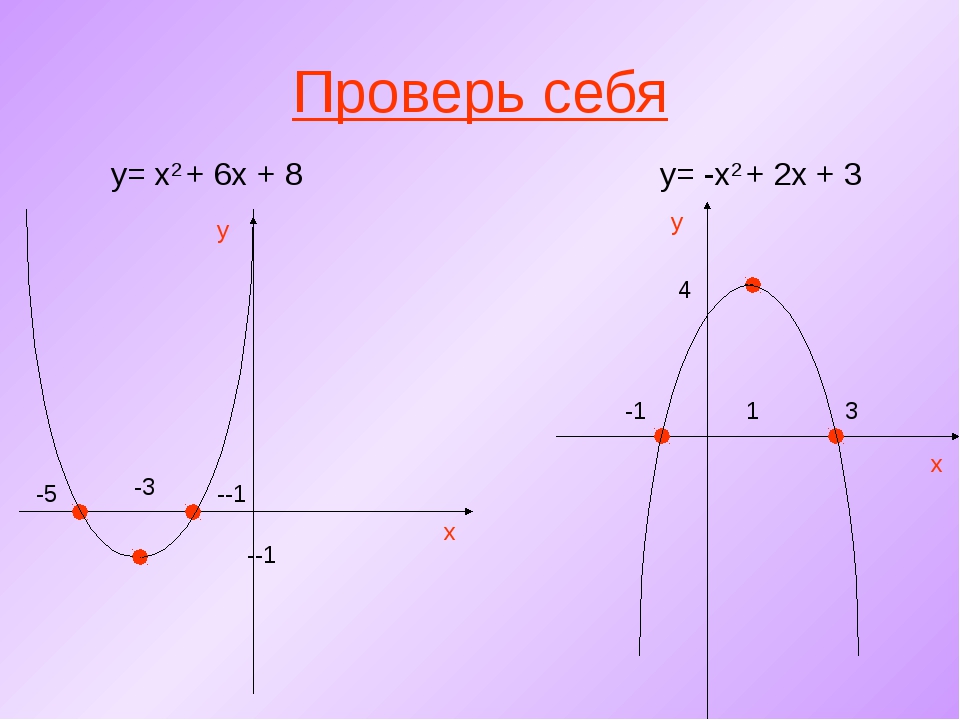
(7 x + 50) + 40 = 300
7 x + 90 = 300
7 x = 300 — 90 (перенос 90 на R.H.S.)
7 x = 210
Разделение обе стороны по 7,
х = 30
Следовательно, номер 30.
Посмотреть решения NCERT для всех глав класса 7
Различные способы исследования
Различные способы исследования Запись 2Различные способы проверки
ax 2 + bx + c = 0
по
Джеймс У.Wilson и Kyungsoon Jeon
Университет Джорджии
Сейчас это стало довольно стандартным упражнением с доступными технологиями для построить графики для рассмотрения уравнения
ах 2 + bx + c = 0и наложить несколько графиков
у = ах 2 + bx + с для разных значений a, b или c, поскольку два других остаются постоянными. Из этих графиков обсуждение шаблонов для корней топора 2 +
bx + c = 0 может следовать.
Из этих графиков обсуждение шаблонов для корней топора 2 +
bx + c = 0 может следовать.
Например, если мы установим y = x 2 + bx + 1 для b = -3, -2, -1, 0, 1, 2, 3, и наложив графики, получается следующая картина.
Мы можем обсудить «движение» параболы при изменении b. Парабола
всегда проходит через одну и ту же точку на оси Y (точка (0,1) с
это уравнение). При b <-2 парабола пересечет ось x в
две точки с положительными значениями x (т.е. исходное уравнение будет иметь два
настоящие корни, оба положительные).При b = -2 парабола касается
по оси x, поэтому исходное уравнение имеет один действительный положительный корень в точке
касания. При -1 2 парабола дважды пересекает ось абсцисс, показывая два отрицательных вещественных
корни для каждого б. Снова рассмотрим уравнение x 2 + bx + 1 =
0.
Теперь изобразите это отношение на плоскости xb. Получаем следующий график.
Если мы возьмем какое-либо конкретное значение b, скажем, b = 3, и наложим это Уравнение на графике добавляем линию, параллельную оси x. Если он пересекает кривой в плоскости xb точки пересечения соответствуют корням исходное уравнение для этого значения b. У нас есть следующий график.
Для каждого выбранного значения b мы получаем горизонтальную линию.Это ясно на один график, на котором мы получаем два отрицательных действительных корня исходного уравнения, когда b> 2, один отрицательный действительный корень, когда b = 2, нет реальных корней для -2
Здесь давайте посмотрим на корни. Одна из самых интересных вещей заключается в том, что
два корня уравнения x2 + bx +1 = 0 не имеют разных знаков. Корни
все положительные или все отрицательные.Итак, у нас есть следующий вопрос.
Есть ли другой способ оценить характеристики корней, их сумму или их продукт и их знаки?
Давайте рассмотрим y = x2 -8x +12 для явного понимания взаимосвязи между коэффициентом уравнения и его корнями. Легко узнать корни уравнения x2 -8x +12 = 0, потому что его можно разложить на множители как (x — 2) ( х — 6). Мы можем проверить это на графике y = x2 -8x +12.
Просто подумайте о знаке корней, сумме и произведении корней.Она имеет два положительных корня, x = 2 и x = 6. Какова сумма двух корней? Это 8. Что есть продукт двух корней? Это 12.
Сравните значения с коэффициентами уравнения x2 -8x +12 = 0. Что можешь найти? Сумма двух корней одинакова с отрицательным коэффициентом при x уравнения, а произведение двух корней совпадает с константой уравнения. Вы думаете, что мы можем обобщить это правило на всех уравнение?
Давайте подумаем о другом примере, y = 3×2 + 6x -9.Какие корни у 3х2 + 6х -9 = 0.
Как видно на графике, функция пересекает ось x в x = 1 и x = -3.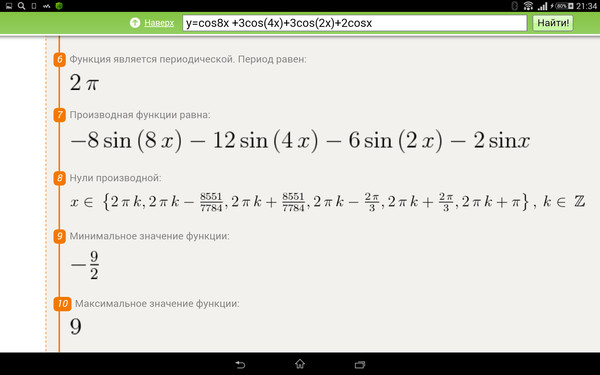 Какая сумма двух корней? Это -2. Что есть продукт двух корней? это
— 3. Посмотрите на коэффициенты 3×2 + 6x -9 = 0.
Какая сумма двух корней? Это -2. Что есть продукт двух корней? это
— 3. Посмотрите на коэффициенты 3×2 + 6x -9 = 0.
Он другой, поэтому мы не можем применить способ из предыдущего примера. Если мы следуем правилу, которое мы обобщили в предыдущем примере, сумма должна быть -6, а произведение должно быть -9.
Есть ли что-то другое, что привело к этим результатам? Да, это так.
Функция y = 3×2 + 6x -9 имеет коэффициент 3 перед x2. Если мы разделим примерные числа суммы и произведения на 3, то получаем правильные ответы на сумму и произведение двух корней.
Сделаем обобщение. Для данного ax2 + bx + c = 0 сумма двух корней уравнения — b / a, а произведение двух корней — c / a.
Здесь нам нужно сравнить два графика, y = 3×2 + 6x -9 и y = x2 + 2x -3.
Как показывают два графика, две функции пересекают ось x в одном и том же месте, но
их формы разные. У них разные у — перехваты, разные
наклон и так далее. Но мы можем узнать сумму и произведение двух корней только с помощью
две функции и их коэффициент.
Вернемся к x2 + bx + 1 = 0. Как мы говорили о горизонтальной прямой b для каждого значения b выбираем. Как насчет случая -2
Но мы можем сделать тот же расчет, чтобы получить сумму и произведение двух корней. без потери обобщения. Например, сумма — 1, а произведение — 1 для x2 + x + 1 = 0. Если учащимся известен определитель уравнения, ax2 + bx + c = 0, тогда мы получаем D = b2 -4ac = 12-4 * 1 * 1 = -3 <0. Так что это точно что уравнение не имеет действительных корней. Но мы все еще можем расширить свое мышление к мнимым корням уравнения. Уравнение x2 + x + 1 = 0 имеет два корня х = , и все же сумма двух корней равна -1, а произведение двух корней равно 1.
Для дальнейшего изучения связи между коэффициентами функции и характеристики корней уравнения, мы можем думать о следующем вопрос. Для данного уравнения x2 + 5x + c = c. Если c = 1, x2 + 5x + 1 = 0 имеет два отрицательных корня.
Сумма двух корней равна -5, а произведение двух корней равно 1. Вот еще один
образ мышления в соответствии с тем процессом, который мы делали до сих пор. мы уверены, что
тот факт, что уравнение имеет два отрицательных корня, хотя у нас нет
график y = x2 + 5x + 1.Поскольку произведение двух чисел положительно, 1,
а сумма двух чисел отрицательна, -5. Теперь проверим график.
Вот еще один
образ мышления в соответствии с тем процессом, который мы делали до сих пор. мы уверены, что
тот факт, что уравнение имеет два отрицательных корня, хотя у нас нет
график y = x2 + 5x + 1.Поскольку произведение двух чисел положительно, 1,
а сумма двух чисел отрицательна, -5. Теперь проверим график.
То, что мы сделали только что раньше, было противоположностью обычному процессу мышления. В общем, мы сначала строим график функции, а затем находим корни или получаем некоторую информацию о функция, такая как знак двух корней, сумма и произведение двух корни. Но мы также можем оценить форму функции с заданным функция и соотношение коэффициентов функции.
Действительно, алгебраическое понимание уравнения, функции и
исследование многих их характеристик было поставлено в одном из самых
важная учебная программа в средней школе. Я думаю, что
сочетание графического программного обеспечения и алгебраических знаний может ускорить
изучение математических понятий в классе.

 25000
25000 
Leave A Comment