1. Найти кооординаты центра масс (полагая распределение масс равномерным)
а) симметричного параболического сегмента с основанием $a$ и высоты $h$;
б) дуги окружности радиуса $R$, стягивающей центральный угол $\alpha $.
2. Найти момент инерции (полагая распределение масс равномерным)
а) полукруга радиуса $R$ относительно его диаметра;
б) конуса с радиусом основания $R$, высоты $H$, относительно его оси;
в) шара радиуса $R$ относительно его диаметра.
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько.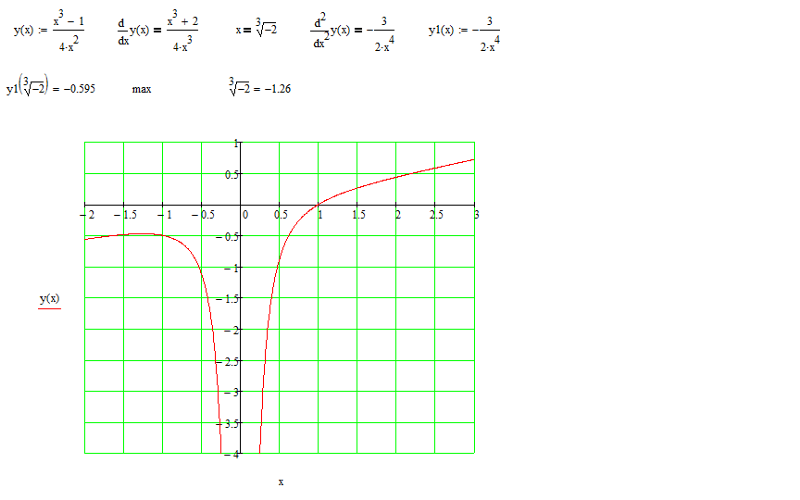 Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Постройте график функции y x2 4x 3. Квадратичная и кубическая функции. Основные свойства квадратичной функции
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3. Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно. {2}}}}
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
{2}}}}
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
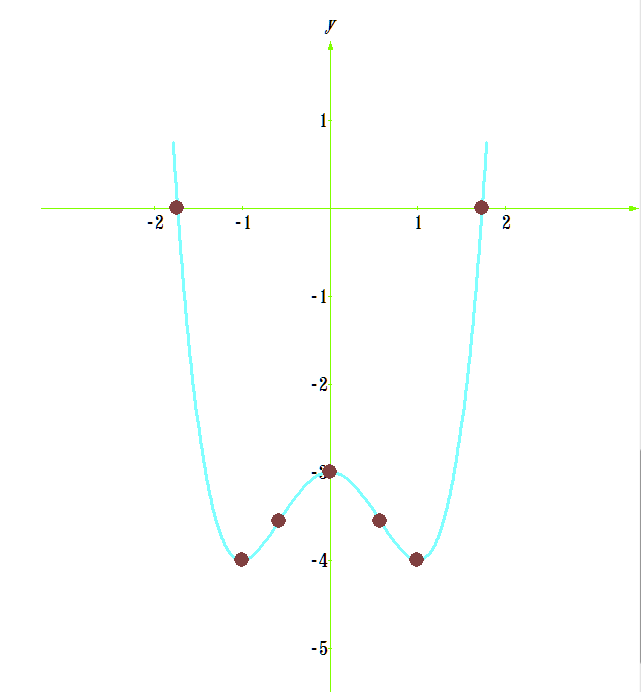
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Разложение многочленов на множители
Примеры комбинаций вынесения общего множителя, группировки слагаемых и формул сокращенного умножения для разложения многочленов на множители.
1) y3 + 16 – 4y – 4y2 = (y3 – 4y) + (16 — 4y2) = (y3 – 4y) – (4y2 – 16) = y(y2 – 4) – 4(y2 – 4) == (y2 – 4)(y — 4) = (y – 2)(y + 2)(y — 4).
2) (a – b)3 – a + b = (a – b)3 – (a – b) = (a – b)(( a – b)2 – 1) = (a – b)(a2 – 2ab + b2 — 1).
3) x2 – 6xy – 49 + 9y2 = (x2 – 6xy + 9y2) – 49 = (x – 3y)2 – 49 = (x – 3y – 7) (x – 3y +7).
4) c2 + 2c – d2 – 2d = (c2 – d2) + (2c – 2d) = (c – d)(c + d) + 2(c – d) = (c – d)( c + d + 2).
Примеры нестандартных разложений многочленов на множители.
Одно или несколько слагаемых представляется в виде суммы или разности, после чего можно применять группировку или формулы сокращенного умножения.Пример 1. Разложение многочлена на множители y2 – 14y + 40.
y2 – 14y + 40 = y2 – 14y + 49 – 9 = (y2 – 14y + 49) – 9 = (y – 7)2 – 32 = (y – 7 – 3)(y – 7 + 3) = (y – 10)(y – 4).
Пример 2. Разложение многочлена на множители x2 + 7x + 12.
x2 + 7x + 12 = x2 + 3x + 4x + 12 = (x2 + 3x) + (4x + 12) = x(x + 3) + 4(x + 3) = (x + 3)(x + 4).
Пример 3. Разложение многочлена на множители x2 + 8x +7.
x2 + 8x +7 = x2 + 7x + x + 7 = (x2 + 7x) + (x + 7) = x(x + 7) + (x + 7) = (x + 7)(x + 1).
Пример 4. Разложение многочлена x2 + x – 12 на множители.
x2 + x – 12 = x2 + 4x – 3x – 12 = (x2 + 4x) – (3x +12) = x(x + 4) – 3(x + 4) = (x + 4)(x – 3).
Пример 5. Разложение многочлена на множители x2 — 10x + 24.
x2 — 10x + 24 = x2 -2*5 x + 25 – 1 = (x2 — 2*5 x + 25) – 1 = (x – 5)2 – 1 = (x – 5 – 1)(x – 5 + 1) = (x – 6)(x – 4).
Пример 6. Разложение многочлена на множители x2 — 13x + 40.
x2 — 13x + 40 = x2 — 10x – 3x + 25 + 15 = (x2 — 10x + 25) – (3x – 15) = (x – 5)2 – 3(x – 5) =
= (x – 5)(x – 5 – 3) = (x – 5)(x – 8).
Пример 7. Разложим на множители многочлен x2 + 15x + 54.
x2 + 15x + 54 = x2 + (12x + 3x) + (36 + 18) = (x2 + 12x + 36) + (3x + 18) = (x + 6)2 + 3(x + 6) =
= (x + 6)(x + 6 + 3) = (x + 6 )(x + 9).
Пример 8. Разложение многочлена x4 + 3x2 + 4 на множители.
x4 + 3x2 + 4 = x4 + (4x2 – x2) + 4 = (x4 + 4x2 + 4) – x2 = (x2 + 2)2 – x2 = (x2 + 2 – x)( x2 + 2 + x) =
= (x2 – x + 2)( x2 + x + 2).
Пример 9. Разложение многочлена на множители x4 + x2 + 1.
x4 + x2 + 1 = x4 + (2x2 – x2) + 1 = (x4 + 2x2 + 1) – x2 = (x2 + 1)2 – x2 = (x2 + 1 – x)( x2 + 1 + x) =
= (x2 – x + 1)( x2 + x + 1).
Пример 10. Разложение многочлен x4 + 4 на множители. Данный многочлен представляет интересный пример выражения, когда на первый взгляд кажется, что его разложить на множители невозможно. Прибавим к нему 4x2 и вычтем 4x2, чтобы значение выражения не изменилось.
x4 + 4 = x4 + 4 + 4x2 – 4x2 = (x4 + 4x2 + 4) – 4x2 = (x2 + 2)2 – 4x2 = (x2 + 2 – 2x)( x2 + 2 + 2x) =
= (x2 – 2x + 2)( x2 + 2x + 2).
Графические уравнения и системы уравнений с пошаговым решением математических задач
ВВЕДЕНИЕ В КВАДРАТИКУ
Цели
В этом разделе вы будете складывать, вычитать, умножать и строить графики квадратов.
Словарь : Стандартный формат квадратного уравнения : y = ax 2 + bx + c ; a, b, c — постоянные; x — независимая переменная, а y — зависимая переменная. Квадраты также называют полиномами второй степени , потому что самый высокий показатель равен 2.Уравнение угла наклона-пересечения из второй главы y = mx + b называется полиномом первой степени , потому что наивысший показатель степени равен единице.
Зачем изучать квадратичность? Графики квадратных уравнений приводят к параболам (U-образные графики, открывающиеся вверх или вниз). Эта особенность квадратичности делает их хорошими моделями для описания пути объекта в воздухе или описания прибыли компании (примеры чего вы можете увидеть в конечной математике или в микроэкономике. )
)
Пример 1. Мальчик, лежащий на спине, выстрелом из пращи выстрелил в воздух камнем с начальной скоростью (силой, которую мальчик использует для выстрела камня) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, равно
.ч = -16т 2 + 64т.
а. Найдите высоту камня при t = 0.
В формуле h = -16t 2 + 64t, заменить t на 0.
h = -16 (0) 2 +64 (0)
h = 0
Камень находится на нулевом уровне в воздухе за 0 секунд.(Это момент прямо перед тем, как он стреляет камнем в воздух.)
г. Найдите высоту камня при t = 1.
В формуле h = -16t 2 + 64t, заменить t на 1.
Камень поднимается на высоту 48 футов за одну секунду.
Объяснение : Возводится в квадрат только «1». -16 умножается на 1 2
г. Найдите высоту камня при t = 2.
В формуле h = -16t 2 + 64t заменить t на 2.
Камень находится на высоте 64 фута за 2 секунды.
Объяснение : Порядок операций требует применения экспонент перед умножением.
г. Найдите высоту камня при t = 3.
В формуле h = -16t 2 + 64t, заменить t на 3.
Камень находится на высоте 48 футов за 3 секунды.
e. Найдите высоту камня при t = 4.
В формуле h = -16t 2 + 64t заменить t на 4.
Камень находится на нулевом уровне в воздухе за 4 секунды; то есть камень ударился о землю.
ф. Постройте график точек, полученных в частях от a до e.
Высота камня зависит от времени, поэтому h — зависимая переменная, а t — независимая переменная. Точки имеют вид (t, h).
Согласно графику, скала достигает максимальной высоты за 2 секунды. Максимальная высота — 64 фута. Точка максимума или минимума квадратичной называется вершиной.Вы узнаете, как найти вершину в Разделе 4.3, Квадратичные приложения и графики.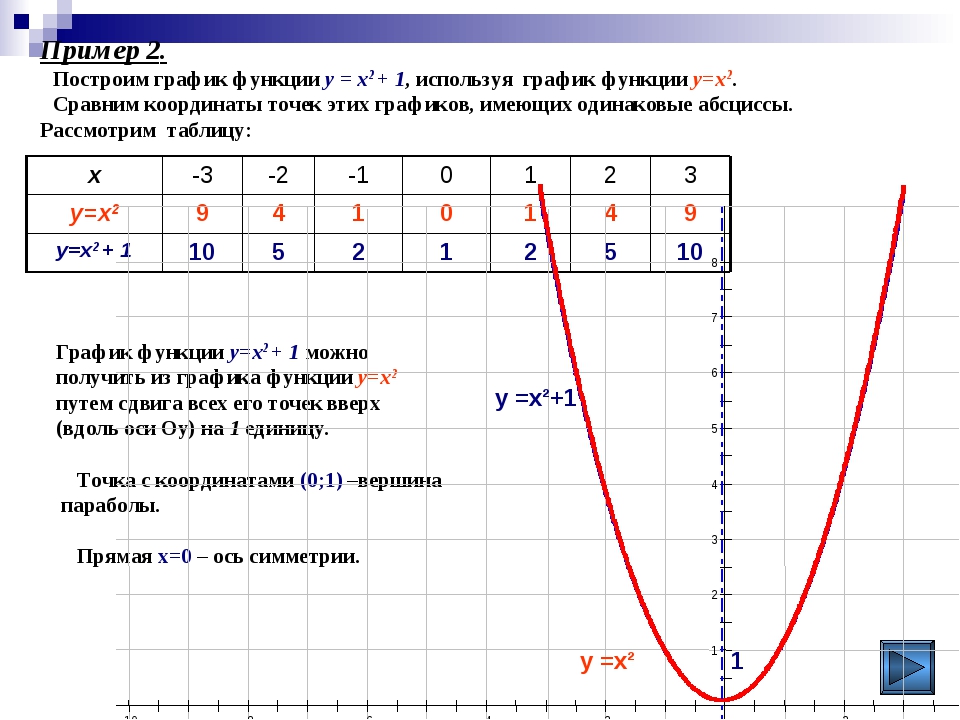
Согласно графику, камень оказывается на земле в 0 секунд (прямо перед тем, как мальчик стреляет в него) и в 4 секунды (когда камень приземляется). Эти точки являются отсечками времени. Вы узнаете, как их найти, в следующем разделе 4.2, «Применение квадратичной формулы».
Сложение и вычитание квадратичных:
Словарь : Чтобы добавить или вычесть квадратичные, объедините одинаковые термины. Подобные термины , первоначально представленные в Разделе 1.3, «Упрощение алгебраических выражений», имеют ту же переменную и одинаковый показатель степени. Например, 2x 2 и 5x 2 являются одинаковыми терминами, а 3x 2 и 7x — нет.
Коэффициент , первоначально представленный в Разделе 1.3, «Упрощение алгебраических выражений», является числом, умножающим переменную. Например, коэффициент 2x равен 2, а коэффициент -x 2 равен -1.
Правило: Чтобы объединить одинаковые термины, сложите их коэффициенты
Вспомните распределительное свойство : определение a (b + c) = ab + ac.
Не удалось объединить непохожие термины в скобках, поэтому мы использовали свойство распределения. После этого мы умножили 6x на 3, а затем -5 на 3.
Использовали свойство распределения и объединили похожие термины.
Пример 5. Уравнение прибыли: Прибыль = Выручка — Затраты
Если уравнение дохода для компании:
, а уравнение затрат:
найти уравнение прибыли для компании.
Подставил уравнения доходов и затрат в формулу для расчета прибыли. Необходимо использовать скобки.
Использовал свойство распределения и умножил уравнение доходов на 1 и уравнение затрат на -1.
Комбинированные одинаковые термины.
Подставил уравнения доходов и затрат в формулу прибыли. Необходимо использовать круглые скобки. Использовал распределительное свойство.
Умножил уравнение доходов на 1 и уравнение затрат на -1. Сочетание подобных терминов.
Сочетание подобных терминов.
Умножение двух биномов.
Словарь : У бинома есть два члена (точно так же, как у велосипеда есть два колеса).
Правило: Чтобы умножить два бинома, умножьте каждый член первого на каждый член второго.
Пример 7. Умножаем (x + 2) (5x + 3).
Умножить x на 5x и 3 и умножить 2 на 5x и 3.
Объединить похожие термины.
FOIL — это простая мнемоника, чтобы запомнить, как умножить два бинома.
Пример 8.Умножьте (8x + 6) (x + 7).
Совет для изучения: Напишите карточку с объяснением мнемонической ФОЛЬГИ. Часто просматривайте карту.
Сводка
Квадраты — важные уравнения в физике и микроэкономике. Техника сложения и вычитания квадратиков такая же, как и мы практикуем весь семестр; то есть складывать или вычитать похожие термины. Для умножения используйте свойство распределения или FOIL. Вершина квадратичной будет более подробно объяснена в разделе «Графики квадратичных вычислений и приложения».«Вершина — это точка максимума или минимума на квадратичном графике.
ПРИМЕНЕНИЕ КВАДРАТИЧЕСКОЙ ФОРМУЛЫ
Цель
В этом разделе показано, как решать квадратные уравнения.
Словарь : квадратное уравнение — это ax 2 + bx + c = 0. a, b и c — константы, а x — переменная.
Квадратичная формула ,, используется для решения квадратного уравнения.
Анализируем
Учебный совет: Напишите квадратное уравнение и квадратную формулу на карточках для заметок, чтобы вы могли ссылаться на них при выполнении домашнего задания.
Пример 1. Предположим, вы стоите на вершине утеса на высоте 375 футов над дном каньона и подбрасываете в воздух камень с начальной скоростью 82 фута в секунду. Уравнение, моделирующее высоту скалы над дном каньона:
ч = -16т 2 + 82т + 375.
Узнайте, сколько времени требуется камню, чтобы упасть на дно каньона.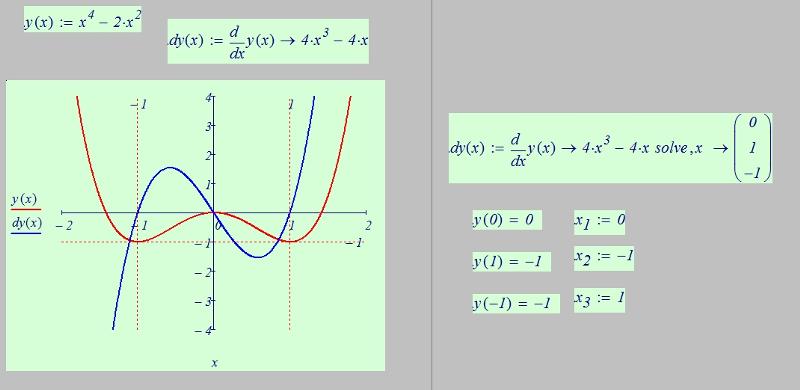
Найдите t, когда h = 0.
Решите 0 = -16t 2 + 82t + 375.
Определите константы a, b и c.
Объяснение : Одна часть квадратного уравнения должна быть равна нулю.
a = -16, b = 82, c = 375
Пояснение :
a — коэффициент переменной, возведенный в квадрат.
b — коэффициент переменной в первой степени.
c — постоянная.
Используйте формулу корней квадратного уравнения
с a = -16, b = 82 и c = 375.
T = -2,916 — бессмысленный ответ, поскольку t — это время, за которое камень ударится о дно каньона, и время не может быть отрицательным.
T = 8,041 секунды — это время, за которое камень ударится о дно каньона.
Камень ударится о дно каньона за 8,041 секунды.
Пример 2. У владельца ранчо есть 500 ярдов ограждения, чтобы ограждать два соседних загона для свиней, которые упираются в сарай. Если площадь двух ручек должна составлять 20 700 квадратных ярдов, каковы должны быть размеры ручек?
L — длина обоих ручек.
а. Воспользуйтесь таблицей, чтобы найти уравнение для площади ручек.
г. Упростите уравнение для площади.
г. Найдите W, когда A = 20700.
Ширина 76,67 или 90 ярдов.
г. Найдите длину ручек.
Из таблицы в Части а, L = 500 — 3Вт. Подставляем W = 76,67 и W = 90 в уравнение для длины, L = 500 — 3w.
Размеры загона для свиней, площадь которого составляет 20 700 квадратных ярдов, составляют 76,67 на 270 ярдов и 90 на 230 ярдов.
Пример 3. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,
T = 0,26 м 2 -4,1 м + 7,9
, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент. Определите, когда температура кислорода составляет 0 градусов Цельсия.
Задача просит вас найти m при T = 0.
Температура кислорода будет 0 градусов Цельсия через 2.246 минут 13,52 минуты.
Совет для исследования: Ключевая идея, продемонстрированная в примере 3, заключается в том, как обрабатывать отрицательное b в квадратном уравнении.
Сводка
В этом разделе показано, как решить новый тип уравнения — квадратное. У них есть важные приложения во многих областях, таких как бизнес, физика и инженерия. Учиться разница между квадратным уравнением и квадратной формулой.
Квадратное уравнение: ax 2 + bx + c = 0.
- Одна часть уравнения должна быть равна нулю.
- a — коэффициент при x.
- b — коэффициент при x.
- c — постоянный член.
Квадратичная формула решает квадратное уравнение.
- Формула дает два решения.
- Калькулятор используется для поиска ответов.
- Первым шагом в вычислении формулы является упрощение квадратного корня.
КВАДРАТИЧЕСКИЕ ПРИЛОЖЕНИЯ И ГРАФИКИ
Цели
В этом разделе исследуются дополнительные ключевые точки квадратичного графика, вершины и пересечений.Эти пункты будут интерпретированы в приложениях.
Пример 1. Мальчик, лежащий на спине, выстрелом из пращи выстрелил в воздух камнем с начальной скоростью (силой, которую мальчик использует, чтобы выстрелить в камень) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, равно
.ч = -16т 2 + 64т.
(Этот пример взят из Раздела 4.1 «Введение в квадратику», стр. 317.)
На странице 318 мы сгенерировали следующие значения:
Мы использовали точки, чтобы получить график ниже.Вершина и пересечения также отмечены на графике.
Объяснение : Точка (0, 0) — это время и высота пересечения.
Вершина , (2,64) представляет максимальную высоту скалы. Скала достигает максимальной высоты 64 фута за 2 секунды.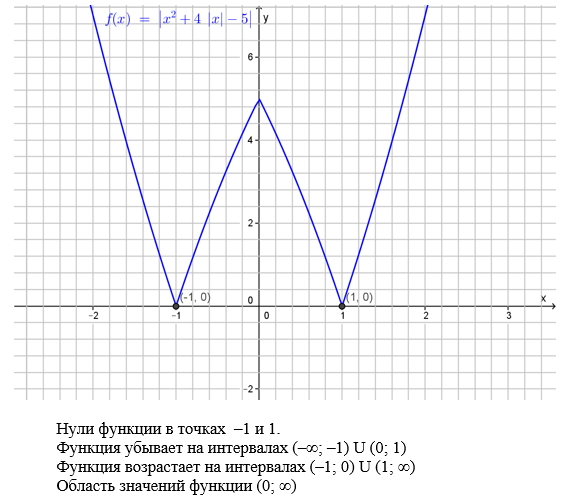
Временные точки , (0, 0) и (4, 0) представляют, когда камень находится на земле. Камень оказывается на земле за 0 секунд до выстрела (это Высота Intercept ) и через 4 секунды, когда он возвращается на землю.
Чтобы построить квадратичный график, указанный уравнением, y = ax 2 + bx + c, усвойте следующие термины:
Словарь : Вершина: Вершина — это максимальная или минимальная точка на графике. Чтобы найти вершину:
а. Найдите координату x:
b. Найдите координату y: подставьте значение x, полученное в части a, в формулу y = ax 2 + bx + c.
X intercept : установите y = 0 и решите 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения,
Пересечение Y : установите x = 0 и найдите y.y всегда будет c, константой.
Учебный совет: Напишите процедуру и определения на трех карточках для удобного использования.
Пример 2. Компания D +++ производит компьютерные игры. Стоимость создания g игр в месяц составляет C = 0,4g 2 — 32g + 625. Выручка от продажи игр g в месяц составляет R = -0,6g 2 + 52g. Единицы измерения g — сотни, C и R — тысячи долларов.
а. Найдите уравнение прибыли.
г.Найдите вершину и объясните, что эта вершина означает с точки зрения создания компьютерных игр.
Формула для координаты g:
Из уравнения прибыли a = -1, b = 84.
Вершина (42,1139). Если D +++ продаст 4200 игр, то они получат максимальную прибыль в размере 1 139 000 долларов США.
г. Найдите g перехватывает и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения g, установите P = 0.
Решить 0 = -g 2 + 84g — 625.
Используйте формулу корней квадратного уравнения, a = -1, b = 84, c = -625.
Перехваты g: (8. 251, 0) и (75.75, 0).
251, 0) и (75.75, 0).
Если они продадут 825 или 7 575 игр, они выйдут на уровень безубыточности.
г. Найдите P перехватчики и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения с P, установите g = 0.
P = -0 2 + 84 * 0-625
P = -625
Перехват по оси P равен (0, -625).
Стартовые затраты компании составляют 625 000 долларов.
e. Постройте график функции.
Постройте точки:
Вершина. (42, 1139).
Данный перехватывает. (8,251, 0) и (75,75, 0).
Перехват P. (0, -625).
Объяснение : Одно из объяснений того, что прибыль имеет две точки безубыточности, заключается в том, насколько эффективно компания производит продукт. Изготовление очень небольшого количества предметов обычно неэффективно. В какой-то момент фабрика становится очень эффективной в производстве продукта, но если фабрика пытается производить слишком много предметов, компания становится неэффективной в производстве своей продукции.
Помните, что единицы измерения g — сотни, а единицы P — тысячи.
Предположим, D +++ должен получать прибыль в размере 500 000 долларов (P = 500) в месяц. Нарисуйте эту линию на графике, полученном в Части b, и найдите, где линия пересекает график квадратичного. Напишите предложение, объясняющее, что означают ответы.
Эскиз P = 500 на предыдущем графике.
P = 500 — горизонтальная линия.
Если D +++ хочет получить прибыль в размере 500 000 долларов, им необходимо сделать и продать 1 672 или 6 728 игр.
Пояснение : График дает оценку того, где пересекаются горизонтальная линия P = 500 и уравнение прибыли P = -g 2 + 84g-625. Алгебра дает точную точку их пересечения.
г. Используя график и ответы к Части c, определите, сколько компьютерных игр необходимо сделать и продать, чтобы гарантировать прибыль, превышающую 500 000 долларов.
Компания получит прибыль более 500 000 долларов, если график прибыли находится выше горизонтальной линии P = 500.Эта проблема аналогична примеру 2d на стр. 203 в Разделе 2.9 «Приложения графиков».
Это происходит между точками g = 16,72 и g = 67,28 или
.16,72
Компания заработает более 500 000 долларов, если будет производить и продавать от 1 672 до 6 728 компьютерных игр.
Пример 3. Оператор питомника хочет поставить три соседние загоны для собак одинакового размера у стены. У него 96 метров забора.
а. Найдите формулу площади.
Объяснение : Самая трудная часть таблицы — найти значение длины.Если фермер использует 10 метров для ширины загона, а есть 4 ширины, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений осталось на эту длину, вычтите 40 из 96 — общего количества ограждений, доступных фермеру.
Формула площади загона для собак:
г. Найдите вершину и объясните, что это означает с точки зрения загонов для собак.
Формула для координаты W:
Из уравнения прибыли a = -4, b = 96.
Вершина равна (12, 576).
Вершина , (12, 576) представляет максимальную площадь трех загонов для собак. Когда W = 12, максимальная площадь будет 576. (Длина всех трех загонов будет 48 или длина одного загона для собак будет 16.) Будет три загона для собак, каждая размером 12 на 16 метров.
г. Найдите W перехватывает и объясните, что они означают в терминах загонов для собак.
Чтобы найти точку пересечения с W, установите A = 0.
Решить 0 = -4 Вт 2 + 96 Вт.
Используйте формулу корней квадратного уравнения, a = -4, b = 96, c = 0.
W-точки перехвата: (0, 0) и (24, 0).
Перемычки W, (0, 0) и (24, 0) представляют ширину загонов для собак, которые дадут нулевую площадь.
г. Найдите точку перехвата A и объясните, что это означает с точки зрения загонов для собак.
Чтобы найти точку пересечения A, установите W = 0.
Объяснение : Если ширина прямоугольника равна нулю, то площадь должна быть равна нулю.
Перехватчик A равен (0, 0).
Перехватчик A, (0, 0) — это область, когда W = 0.
e. Изобразите уравнение
Постройте точки:
Вершина. (12, 576).
W перехватывает. (0, 0) и (24, 0).
Перехват. (0, 0).
ф. Предположим, общая площадь должна быть 400 квадратных метров. На графике A = 400 найдите размеры загонов для собак.
Эскиз A = 400 на предыдущем графике.
A = 400 — горизонтальная линия.
Поскольку W, ширина, известна, длину L можно определить по формуле A = LW.
Решите относительно L, разделив обе части на W.
Размеры загона для собак, дающего площадь 400 квадратных метров, составляют 5,367 на 74,53 и 18,63 на 21,47.
Пример 4. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,
Т = 0.26 м 2 -4,1 м + 7,9
, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент. Постройте уравнение, найдя вершину и точки пересечения. Обозначьте эти точки на графике и объясните, что означают вершина и пересечения с точки зрения модели.
Вернуться назад: Это та же модель, что использовалась в примере 3 на стр. 332. Этот пример работал при нулевой температуре.
Найдите вершину из T = 0.26 м 2 — 4,1 м + 7,9.
Формула для координаты m вершины:
Вершина равна (7,885, -8,263).
Найдите точки пересечения м T = 0,26 м 2 -4,1 м + 7,9
Чтобы найти m точек пересечения, установите T = 0.
Решить 0 = 0,26 м 2 -4,1 м + 7,9.
Используйте формулу корней квадратного уравнения, a = 0,26, b = -4,1, c = 7,9.
M точек пересечения (13.52, 0) и (2.246, 0).
Найдите точки пересечения T T = 0,26 м 2 — 4,1 м + 7,9
Чтобы найти точку пересечения с Т, установите m = 0.
Т-образная точка пересечения (0, 7.9).
Vertex: Минимальная температура составляет 7,885 минут. Минимальная температура составит -8,263 градуса по Цельсию.
м пересекает: Температура будет ноль градусов Цельсия на отметках 2.246 и 13.52 мин.
T intercept: Температура в начале эксперимента составляла 7,9 градусов Цельсия.
Советы по изучению: Квадраты представляют собой U-образные графики. В некоторых случаях они имеют U-образную форму, как в примере выше, или форму, как в примерах с 1 по 3. Если a в уравнении, y = ax 2 + bx + c, положительно, тогда график имеет U-образную форму, что есть, открываясь. Если a отрицательно, график имеет форму, то есть раскрывается вниз. Этот факт следует записать на карточке для заметок.
Сводка
Графики квадратиков появляются по таким разнообразным предметам, как микроэкономика и физика. В этом разделе кратко излагаются основные идеи устройства.
Чтобы построить квадратичный график y = ax 2 + bx + c, вы должны найти:
- Вершина .
Формула для координаты x:
Чтобы найти координату y, подставьте свой ответ вместо координаты x в уравнение y = ax 2 + bx + c. - x перехватывает .Установите y = 0 и решите уравнение 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения
- Перехватчик y .
Установите x = 0 в уравнении, y = ax 2 + bx + c, и найдите y. Обратите внимание, когда x = 0, y = c. - Если a отрицательное , график обычно выглядит так:
- Если a положительное значение , обычно график выглядит следующим образом:
ФАКТОРИНГ
Цели
Факторинг — это алгебраический метод, используемый для разделения выражения на составные части. Когда составные части умножаются вместе, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг — важный навык в MAT 100, Intermediate Algebra.
Когда составные части умножаются вместе, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг — важный навык в MAT 100, Intermediate Algebra.
Словарь : алгебраическое выражение учитывается, если последней операцией при вычислении выражения является умножение.
Пример 1. Какое выражение разложено на множители , x 2 — 5x — 24 или (x — 8) (x + 3)?
Выберите значение x и подставьте его в выражение.
Пусть x = 3.
Поскольку последней операцией для (x — 8) (x + 3) было умножение, то факторизуется (x — 8) (x + 3).
Объяснение : Менее формально, алгебраическое выражение факторизуется, если оно заключено в круглые скобки.
Словарь : Распределительное свойство — это a (b + c) = ab + ac. Левая часть подвергается факторизации, и a является общим множителем.
У вас должна быть возможность проверить с помощью свойства distributive.
Объяснение : Хотя 8x 3 + 4x равно как 2x (4x 2 + 2), так и 4 (2x 3 + x), ни один из них не считается полностью разложенным, потому что в обоих случаях общее кратное 2, в 2x (4x 2 +2) и x в 4 (2x 3 + x) по-прежнему могут быть факторизованы из членов в скобках.
Факторинг трехчлена: (Трехчлен состоит из трех членов.) Чтобы разложить на множитель трехчлена, вспомните аббревиатуру FOIL.
Совет для изучения: Проверьте свои карточки для заметок на предмет определения ФОЛЬГИ.
Пример 4. Умножаем (x + 3) (x + 5).
(x + 3) (x + 5) учитывается, а x 2 + 8x +15 — нет. Чтобы разложить на множители трехчлены, вам нужно знать, как были вычислены 8x и 15. 8x произошло от сложения 5x и 3x, а 15 — от умножения 5 и 3.
Пример 5. Множитель x 2 + 8x +15. (Это из Примера 4.)
Нам нужны два числа, которые при сложении равны 8, а при умножении равны 15. 3 и 5 в сумме дают 8, а при умножении — 15.
3 и 5 в сумме дают 8, а при умножении — 15.
Таким образом, x 2 + 8x +15 = (x + 3) (x + 5)
Пример 6. Коэффициент x 2 -4x- 12.
Нам нужны два числа, которые при сложении равны -4, а при умножении равны -12. -6 и 2 в сумме дают -4, а при умножении -12.
Итак, x 2 -4x -12 = (x-6) (x + 2).
Пример 7. Коэффициент x 2 — 64.
Это не трехчлен, но он может стать одним, добавив 0x.
x 2 -64 = x 2 + 0x -64
Нам нужны два числа, которые при сложении равны 0, а при умножении равны -64.
-8 и 8 складываются в 0, а при умножении получается -64.
Итак, x 2 -64 = (x-8) (x + 8).
Этот пример называется факторизацией разности полных квадратов, и вы снова увидите это, если возьмете MAT 100, промежуточную алгебру.
Словарь : a 2 — b 2 — это разность полных квадратов .
Разность полных квадратов имеет специальную формулу факторизации: a 2 — b 2 = (a — b) (a + b)
Решение квадратных уравнений с помощью факторинга:
Если вы умножаете две величины и результат равен нулю, то вы знаете, что одна из величин должна быть равна нулю.В математической записи
, если a.b = 0, то a = 0 или b = 0.
Прежде чем вы подумаете, что разложение на множители для решения квадратичных уравнений намного проще, чем использование квадратичной формулы, вы должны знать, что разложение на множители не всегда работает. Рассмотрите возможность изменения примера 8 всего на единицу до x 2 — 11x + 31 = 0. Вы не можете найти два целых числа, которые при сложении равны -11, а при умножении равны 31. Чтобы множить x 2 — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как разложить на множители любое квадратное уравнение в Precalculus I, MAT 161.
Сводка
В этом модуле представлены два метода факторинга. Первый — это общие факторы, использующие свойство распределения, ab + ac = a (b + c). Другой — факторизация трехчленов. Чтобы разложить на множители трехчлены, вам нужно знать, как работает FOIL. Если вы возьмете MAT 100, промежуточную алгебру, вы увидите больше факторинга.
Первый — это общие факторы, использующие свойство распределения, ab + ac = a (b + c). Другой — факторизация трехчленов. Чтобы разложить на множители трехчлены, вам нужно знать, как работает FOIL. Если вы возьмете MAT 100, промежуточную алгебру, вы увидите больше факторинга.
ОБЗОР ГЛАВЫ 4
Эта глава познакомила вас с квадратиками. Две основные темы — это квадратичная формула и квадратичные графики.Эти темы имеют множество приложений в бизнесе, физике и геометрии. Факторинг — важная тема в MAT 100, Intermediate Algebra.
Раздел 4.1: Введение в квадратичность
Раздел 4.2: Приложения квадратичной формулы
Определение: ax 2 + bx + c = 0 — квадратное уравнение.
Определение: квадратная формула.
Пример 4. Фермер хочет ограждать два соседних курятника напротив сарая.У него 125 футов забора. Какие должны быть размеры, если он хочет, чтобы общая площадь составляла 700 квадратных футов.
а. Заполните таблицу, чтобы найти уравнение для площади.
г. Найдите W, когда A = 700.
Размеры курятника, который даст площадь 700 квадратных футов, составляют 35 на 20 футов и 6,667 на 105 футов.
(Чтобы получить длину, разделите 700 на 6,667 и 35.)
Раздел 4.3: Квадратичные приложения и графики
Для построения квадратичного графика y = ax 2 + bx + c необходимо найти:
- Вершина:
Координата x вычисляется по формуле
Координата y вычисляется путем подстановки координаты x в y = ax 2 + bx + c. - Пересечение x:
Установите y = 0 и решите 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения. - Пересечение оси y:
Замените x = 0 на y = ax 2 + bx + c. Обратите внимание, что когда x = 0, y = c.
Пример 5. Уравнение затрат на изготовление коробок для сока: C = 0,6B 2 — 24B + 36, а уравнение дохода — R = -0,4B 2 + 18B. B выражается в миллионах, а C и R — в тысячах долларов.
B выражается в миллионах, а C и R — в тысячах долларов.
а. Найдите уравнение прибыли.
г. Изобразите уравнение прибыли и объясните, что точки пересечения B и P означают с точки зрения проблемы.
Вершина — (21, 405).
Найдите точку пересечения B. Установите P = 0.
Перехваты B — это (0.875, 0) и (41.13, 0).
Найдите точку пересечения P. Установите B = 0.
Перехватчик P равен (0, -36).
г. Предположим, компании нужно заработать 200 000 долларов прибыли (P = 200).Изобразите линию P = 200 и найдите, сколько коробок из-под сока нужно сделать компании, чтобы заработать 200 000 долларов.
Чтобы получить прибыль в размере 200 000 долларов, компании необходимо произвести 6 682 или 35,32 миллиона ящиков для сока.
Вершина (21,405) представляет максимальную прибыль. Компания получит максимальную прибыль в размере 405 000 долларов, продав 21 миллион коробок сока.
Перехватчики B (0,875, 0) и (41,13, 0) говорят нам, что компания сломается, даже если они продадут.875 или 41,13 миллиона ящиков сока.
Перехват P (0–36) представляет начальные затраты компании в размере 36 000 долларов.
Раздел 4.4: Факторинг
Общие факторы:
Триномы:
Решение квадратных уравнений на множители.
Если a. b = 0, тогда a = 0 или b = 0
Советы по обучению:
- Практикуйте повторный тест, начиная со следующей страницы, поместив себя в реалистичные условия экзамена.
- Найдите тихое место и используйте таймер, чтобы смоделировать продолжительность урока.
- Запишите свои ответы в домашнюю тетрадь или сделайте копию теста. После этого вы можете повторно сдать экзамен для дополнительной практики.
- Проверьте свои ответы.
- Дополнительный экзамен доступен на веб-странице MAT 011.
 3.Не волнуйтесь, это точно такое же число: основание — это число слева, а степень — это число справа. В зависимости от типа используемого калькулятора — и особенно если вы используете калькулятор на своем телефоне или компьютере — вам может потребоваться ввести показатель степени таким образом, чтобы вычислить его.
3.Не волнуйтесь, это точно такое же число: основание — это число слева, а степень — это число справа. В зависимости от типа используемого калькулятора — и особенно если вы используете калькулятор на своем телефоне или компьютере — вам может потребоваться ввести показатель степени таким образом, чтобы вычислить его.Показатели в 1-й и 0-й степени
Как бы вы упростили эти показатели?
7 1 7 0
Не расстраивайтесь, если вы запутались. Даже если вы чувствуете себя комфортно с другими показателями, непонятно, как вычислить их со степенями 1 и 0.К счастью, эти экспоненты следуют простым правилам:
- Показатели степени 1
Любой показатель степени со степенью 1 равен основанию , поэтому 5 1 равно 5, 7 1 равно 7, а x 1 равно x . - Показатели степени 0
Любой показатель степени со степенью 0 равен 1 , поэтому 5 0 равно 1, а также 7 0 , x 0 и любой другой показатель степени со степенью 0 вы можете придумать.
Операции с показателями
Как бы вы решили эту проблему?
2 2 ⋅ 2 3
Если вы думаете, что вам нужно сначала решить экспоненты, а затем перемножить полученные числа, вы правы. (Если вы не уверены, ознакомьтесь с нашим уроком по порядку действий).
Как насчет этого?
х 3 / х 2
Или этот?
2x 2 + 2x 2
Хотя точно решить эти проблемы без дополнительной информации невозможно, можно упростить, их.В алгебре вас часто просят выполнить вычисления экспонент с переменными в качестве основы. К счастью, эти показатели легко складывать, вычитать, умножать и делить.
Сложение экспонент
Когда вы добавляете два показателя степени, вы не добавляете фактические полномочия — вы добавляете основания.
 Например, чтобы упростить это выражение, вы просто добавите переменные. У вас есть два xs, которые можно записать как 2x . Итак, x 2 + x 2 будет 2x 2 .
Например, чтобы упростить это выражение, вы просто добавите переменные. У вас есть два xs, которые можно записать как 2x . Итак, x 2 + x 2 будет 2x 2 .x 2 + x 2 = 2x 2
Как насчет этого выражения?
3 года 4 + 2 года 4
Вы добавляете 3y к 2y. Поскольку 3 + 2 равно 5, это означает, что 3y 4 + 2y 4 = 5y 4 .
3 года 4 + 2 года 4 = 5 лет 4
Вы могли заметить, что мы рассматривали только те задачи, в которых добавляемые показатели имели одинаковую переменную и мощность.Это потому, что вы можете складывать экспоненты только в том случае, если их основания и экспоненты точно такие же . Таким образом, вы можете добавить их ниже, потому что оба члена имеют одинаковую переменную ( r ) и одинаковую мощность (7):
4к 7 + 9к 7
Вы не можете никогда добавлять что-либо из них в том виде, в каком они написаны. В этом выражении есть переменные с двумя разными степенями:
4к 3 + 9к 8
У этого есть те же возможности, но разные переменные, поэтому вы также не можете добавить его:
4к 2 + 9с 2
Вычитание показателей
Вычитание экспонент работает так же, как их сложение.Например, вы можете придумать, как упростить это выражение?
5x 2 — 4x 2
5-4 равно 1, поэтому, если вы сказали 1 x 2 или просто x 2 , вы правы. Помните, что, как и при сложении показателей, вы можете вычитать только показатели с такой же степенью и основанием .
5x 2 — 4x 2 = x 2
Показатели умножения
Умножение экспонент — это просто, но способ, которым вы это делаете, может вас удивить.
 Чтобы умножить степень, сложите степени . Например, возьмите это выражение:
Чтобы умножить степень, сложите степени . Например, возьмите это выражение:x 3 ⋅ x 4
Мощности: 3 и 4 . Поскольку 3 + 4 равно 7, мы можем упростить это выражение до x 7 .
x 3 ⋅ x 4 = x 7
А как насчет этого выражения?
3x 2 ⋅ 2x 6
Степени равны 2 и 6 , поэтому наша упрощенная экспонента будет иметь степень 8.В этом случае нам также потребуется умножить коэффициенты. Коэффициенты равны 3 и 2. Нам нужно умножить их, как и любые другие числа. 3⋅2 равно 6 , поэтому наш упрощенный ответ: 6x 8 .
3x 2 ⋅ 2x 6 = 6x 8
Вы можете упростить умножение экспоненты только с той же переменной. Например, выражение 3x 2 ⋅2x 3 ⋅4y 2 будет упрощено до 24x 5 ⋅y 2 .Для получения дополнительной информации перейдите к нашему уроку «Упрощение выражений».
Показатели деления
Деление показателей аналогично их умножению. Вместо того, чтобы складывать степени, вы вычитаете их . Возьмите это выражение:
х 8 / х 2
Поскольку 8-2 равно 6, мы знаем, что x 8 / x 2 равно x 6 .
x 8 / x 2 = x 6
Что насчет этого?
10x 4 / 2x 2
Если вы думаете, что ответ — 5x 2 , вы правы! 10/2 дает нам коэффициент 5, а вычитание степеней ( 4-2 ) означает, что степень равна 2.
Возведение власти в степень
Иногда можно увидеть такое уравнение:
(х 5 ) 3
Показатель степени на другом показателе сначала может показаться запутанным, но у вас уже есть все навыки, необходимые для упрощения этого выражения.
 Помните, что показатель степени означает, что вы умножаете основание само на себя столько раз. Например, 2 3 равно 2⋅2⋅2. Это означает, что мы можем переписать (x 5 ) 3 как:
Помните, что показатель степени означает, что вы умножаете основание само на себя столько раз. Например, 2 3 равно 2⋅2⋅2. Это означает, что мы можем переписать (x 5 ) 3 как:x 5 ⋅x 5 ⋅x 5
Чтобы умножить показатель степени с одинаковым основанием, просто добавьте показателя степени.Следовательно, x 5 ⋅x 5 ⋅x 5 = x 5 + 5 + 5 = x 15 .
На самом деле есть еще более короткий способ упростить подобные выражения. Взгляните еще раз на это уравнение:
(x 5 ) 3 = x 15
Вы обратили внимание, что 5⋅3 тоже равно 15? Помните, умножение — это то же самое, что и добавление чего-либо более одного раза. Это означает, что мы можем думать о 5 + 5 + 5, как мы делали раньше, как о 5 умноженных на 3.Следовательно, когда вы возводите степень в степень , вы можете умножить степень .
Рассмотрим еще один пример:
(х 6 ) 4
Так как 6⋅4 = 24, (x 6 ) 4 = x 24
х 24
Рассмотрим еще один пример:
(3x 8 ) 4
Во-первых, мы можем переписать это как:
3x 8 ⋅3x 8 ⋅3x 8 ⋅3x 8
Помните, что при умножении порядок не имеет значения.Следовательно, мы можем переписать это снова как:
3⋅3⋅3⋅3⋅x 8 ⋅x 8 ⋅x 8 ⋅x 8
Поскольку 3⋅3⋅3⋅3 = 81 и x 8 ⋅x 8 ⋅x 8 ⋅x 8 = x 32 , наш ответ:
81x 32
Обратите внимание, это также было бы то же самое, что и 3 4 ⋅x 32 .
Все еще не знаете, как умножать, делить или возводить экспоненты в степень? Посмотрите видео ниже, чтобы узнать, как запомнить правила:
youtube.com/embed/8oLYEFGM0N0?rel=0&showinfo=0″ allowfullscreen=»» frameborder=»0″/>
/ ru / algebra-themes / negative-numbers / content /
BioMath: квадратичные функции
Завершение квадрата — это метод, который можно использовать для преобразования квадратного уравнения стандартной формы в форму вершины.Находясь в форме вершины, квадратное уравнение легко построить на графике или решить.
Метод завершения квадрата состоит из нескольких простых шагов. Основное упрощение, которое мы стремимся сделать, — это свернуть термин
.Другими словами, эти два члена равны друг другу, поэтому мы можем преобразовывать одно в другое.
Шаги для завершения квадрата можно резюмировать следующим образом:
1.Выделите все термины, включающие x .
2. Сделайте старший коэффициент равным 1, разделив или умножив обе части уравнения на соответствующую константу.
3. Возьмите половину коэффициента x , возведите его в квадрат и прибавьте к обеим частям уравнения.
4. Свернуть.
Мы проиллюстрируем каждый этап завершения квадрата на следующем примере:
.y = 2 x 2 -8 x + 10,
типичное квадратное уравнение в стандартной форме.
Чтобы завершить квадрат в этом уравнении, мы должны сначала выделить члены, включающие x as,
y — 10 = 2 x 2 — 8 x .
Затем мы получаем старший коэффициент 1 , разделив обе части уравнения на 2, как,
Теперь возьмем половину коэффициента x , возведем его в квадрат и прибавим к обеим сторонам как,
.
Обратите внимание, что у нас есть правая часть в форме,
где k = -4.У сворачиваем правую часть на
as,
x 2 — 4 x + 4 = ( x — 2) 2 .
Таким образом, имеем,
Решение для y дает,
Таким образом, мы преобразовали уравнение y = 2 x 2 -8 x + 10 в стандартной форме в форму вершины как,
y = 2 ( x -2) 2 + 2.Мы можем расширить уравнение y = 2 ( x -2) 2 + 2, чтобы проверить наше преобразование,
Завершение квадрата для решения квадратных уравнений.
Заполнение квадрата также можно использовать для решения квадратных уравнений. Например, предположим, что вас попросили решить уравнение
Решение вышеуказанного уравнения означает нахождение значений x , которые делают его истинным.Один из способов сделать это — завершить квадрат. Вы должны выполнить те же четыре шага, сначала выделив все термины, включающие x ,
.Затем мы делаем старший коэффициент 1, умножая обе части уравнения на 2, как,
x 2 + 6 x = 16.
Теперь возьмите половину коэффициента x , возведите его в квадрат и прибавьте к обеим сторонам уравнения как,
.Обратите внимание, что у нас есть левая часть формы,
Сворачиваем левую часть на
as,
( x + 3) 2 = 25.

Чтобы найти x , возьмем квадратный корень из обеих частей как,
Таким образом, мы находим решения нашего уравнения как,
x + = 5 — 3 = 2,
x — = −5 — 3 = −8.
Завершение квадрата для построения квадратичной функции
Любая квадратичная функция, не имеющая формы вершины, может быть преобразована в форму вершины, заполнив квадрат.Находясь в форме вершины, квадратное уравнение можно легко построить, вспомнив графические преобразования. Функция, задаваемая,
y ( x ) = a ( x — h ) 2 + k ,
можно построить, преобразовав базовую функцию f ( x ) = x 2 . Например,
г ( x ) = 3 ( x + 1) 2 -7
связан с графиком f ( x ) = x 2 посредством основных преобразований.В частности, график g ( x ) выглядит как график f ( x ), сдвинутый влево на 1 единицу, растянутый по вертикали в 3 раза и, наконец, сдвинутый вниз на 7.
Область всех квадратных уравнений состоит из всех действительных чисел. Зная, где находится вершина параболы, вы также можете определить диапазон этой квадратичной функции. В частности, если парабола открывается вверх, диапазон квадратичной функции f ( x ) = ax 2 + bx + c равен,
Если парабола открывается вниз, диапазон квадратичной функции f ( x ) составляет,
В качестве конкретного примера график функции f ( x ) = −2 x 2 -4 x + 1 имеет вершину,
Поскольку эта парабола открывается вниз (т.
 е. a <0), диапазон f ( x ) равен (-∞, 3].
е. a <0), диапазон f ( x ) равен (-∞, 3].*****
В следующем разделе мы введем квадратную формулу и узнаем, как найти корни ( x -перехваты) квадратных уравнений.
Корни квадратных уравнений
Теория и задачи линейных уравнений
Значение неизвестной величины, для которой из данного уравнения получаем истинное численное равенство, называется корнем этого уравнения.Два уравнения называются эквивалентными, если совпадают множества их корней, корни первого уравнения также являются корнями второго и наоборот. Действительны следующие правила:
1. Если в данном уравнении одно выражение заменяется другим тождественным, мы получаем уравнение, эквивалентное данному.
2. Если в данном уравнении какое-то выражение переносится с одной стороны на другую с противоположным знаком, мы получаем уравнение, эквивалентное данному.
3. Если мы умножим или разделим обе части данного уравнения на одно и то же число, отличное от нуля, мы получим уравнение, эквивалентное данному.
Уравнение вида $ ax + b = 0 $, где $ a, b $ — заданные числа, называется простое уравнение относительно неизвестной величины $ x $.Задача 1 Решите уравнение:
A) 16x + 10 — 32 = 35 — 10x — 5
B) $ y + \ frac {3} {2y} + 25 = \ frac {1} {2} y + \ frac {3} {4} y — \ frac {5} {2} y + y + 37 $
C) 7u — 9 — 3u + 5 = 11u — 6 — 4uРешение :
A) Мы выполняем некоторые из заданных действий и получаем
16x — 22 = 30 — 10x
. После использования правила 2 мы находим 16x + 10x = 30 + 22
. После сложения 26x = 52
Мы находим неизвестный множитель путем деления произведение на другой множитель.
Вот почему $ x = \ frac {52} {26} $
Следовательно, x = 2Б) По аналогии с А) находим:
$ y \ left (1 + \ frac {3} {2} \ right) + 25 = y \ left (\ frac {1} {2} + \ frac {3} {4} — \ frac {5} {2} + 1 \ right) + 37 \ Leftrightarrow $
$ \ frac {5} {2} y + 25 = — \ frac {1} {4} y + 37 \ Leftrightarrow \ frac {5} {2} y + \ frac {1} {4} y = 37 — 25 \ Leftrightarrow $
$ \ frac {11} {4} y = 12 \ Leftrightarrow y = \ frac {12. 4} {11 } \ Leftrightarrow y = \ frac {48} {11} $
4} {11 } \ Leftrightarrow y = \ frac {48} {11} $C) 4u — 4 = 7u — 6 6 — 4 = 7u — 4u 2 = 3u $ u = \ frac {2} {3} $
Задача 2 Решите уравнение:
A) 7 (3x — 6) + 5 (x — 3) — 2 (x — 7) = 5
B) (x -3) (x + 4) — 2 (3x — 2) = (x — 4) 2
C) (x + 1) 3 — (x — 1) 3 = 6 (x 2 + x + 1)Решение :
А) 21x — 42 + 5x — 15 — 2x + 14 = 5
21x + 5x — 2x = 5 + 42 + 15 — 14
24x = 48 x = 2B) x 2 + 4x — 3x — 12 — 6x + 4 = x 2 — 8x + 16
x 2 — 5x — x 2 + 8x = 16 + 12 — 4
3x = 24 x = 8C) x 3 + 3x 2 + 3x + 1 — (x 3 — 3x 2 + 3x — 1) = 6x 2 + 6x + 6
x 3 + 3x 2 + 3x + 1 — x 3 + 3x 2 + 1 = 6x 2 + 6x + 6
2 = 6x + 6 6x = -4 $ x = — \ frac {2} {3} $Задача 3 Решите уравнение:
A) $ \ frac {5x — 4} {2} = \ frac {0.5x + 1} {3}
$ B) $ 1 — \ frac {x — 3} {5} = \ frac {-3x + 3} {3}
$ C) $ \ frac {x + 1} {3} — \ frac {2x + 5} {2} = -3 $
D) $ \ frac {3 (x — 1)} {2} + \ frac {2 (x + 2)} {4} = \ frac { 3x + 4,5} {5} $Решение :
A) $ \ frac {5x — 4} {2} — \ frac {0.5x + 1} {3} \ Leftrightarrow $
3 (5x — 4) = 2 (0.5x + 1)
15x — 12 = x + 2
15x — x = 12 + 2
14x = 14 x = 1Б) $ 1 — \ frac {x — 3} {5} = \ frac {3 (1 — x)} {3} \ Leftrightarrow $
$ 1 — \ frac {x — 3} {5} = 1 — x \ Leftrightarrow $
-x + 3 = — 5x
5x — x = — 3
$ x = — \ frac {3} {4} $C) $ \ frac {3 (x — 1)} {2} + \ frac {2 (x + 2)} {4} = \ frac {3x + 4.5} {5} \ Leftrightarrow $
$ \ frac {2 (x + 1) — 3 (2x + 5)} {6} = — 3 \ Leftrightarrow $
$ \ frac {2x + 2 — 6x -15} { 6} = — 3 \ Leftrightarrow $
-4x — 13 = -18
-4x = -18 + 13
-4x = -5 $ x = \ frac {5} {4} $D) Мы приводим к общему знаменателю, который для 2, 4 и 5 равен 20
$ \ frac {3 (x — 1)} {2} + \ frac {2 (x + 2)} {4} = \ frac { 3x + 4. 2 = — 2x $
2 = — 2x $
-2x = -2x
-2x + 2x = 0
0.x = 0 Следовательно, каждое x является решением.C) 0.x = 26 — 2,13
0.x = 26 — 26
0.x = 0 каждый x является решением.D) -3x + 4x 2 = 5 (0,8x — 0,6) x
-3x + 4x 2 = (4x — 3) x
-3x + 4x 2 = 4x 2 — 3x
Следовательно каждый x является решением.Задача 5 Доказательство отсутствия корней уравнения:
A) 0.x = 34
B) 5 — 3x = 7 — 3x
C) $ \ frac {x — 3} {4} = \ frac {x + 5} {4}
долл. США D) 2 (3x — 1) — 3 (2x + 1) = 6Решение :
A) Для левой стороны мы получим значение 0 для каждого x, а для правой стороны — 34, т.е.е. число отличное от 0. Следовательно, не существует такого x, чтобы получить истинное числовое равенство;
Б) 5 — 3x = 7 — 3x 3x — 3x = 7 — 5 0. x = 2 0 = 2, что невозможно ни при каких x
C) $ \ frac {x — 3} {4} = \ frac {x + 5} {4} $ x — 3 = x + 5 x — x = 5 + 3 0 = 8 => нет решения;
D) 2 (3x — 1) — 3 (2x + 1) = 6 6x — 2 — 6x — 3 = 6 0.x = 6 + 5 0 = 11 нет решения.
Задача 6 Решите уравнение:
A) 2x 2 — 3 (1 — x) (x + 2) + (x — 4) (1 — 5x) + 58 = 0
B) 3.(x + 1) 2 — (3x + 5) .x = x + 3
C) x 2 — (x — 1). (x + 1) = 4
D) (x — 1). (x 2 + x + 1) = (x — 1) 3 + 3x (x — 1)
E) (3x — 1) 2 — x (15x + 7) = x (x + 1 ). (х — 1) — (х + 2) 3Решение :
A) 2x 2 — 3 (x + 2 — x 2 — 2x) + x — 5x 2 — 4 + 20x + 58 = 0
2x 2 — 3x — 6 + 3x 2 + 6x + x — 5x 2 — 4 + 20x + 58 = 0
0.х 2 + 24x + 48 = 0
24x = — 48 x = -2B) 3 (x 2 + 2x + 1) — 3x 2 — 5x = 3x 2 + 6x + 3 — 3x 2 -5x = x + 3
(3 — 3) x 2 + (6-5) . x — x = 3-3
x — x = 3-3
0 = 0 => каждый x является решениемC) x 2 — (x 2 -1) = 4
x 2 — x 2 + 1 = 4
0 = 3 => нет решенияD) x 3 + x 2 + x — x 2 — x — 1 = x 3 — 3x 2 + 3x — 1 + 3x 2 — 3x
0 = 0 => каждые x — решениеE) 9x 2 — 6x + 1 — 15x 2 — 7x = x 3 –x 2 + x 2 — x — x 3 — 6x 2 — 12x — 8
0 = 9 => нет решенияЗадача 7 Решите уравнение:
A) $ \ frac {6x — 1} {5} — \ frac {1 — 2x} {2} = \ frac {12x + 49} {10} $
B) $ \ гидроразрыв {x — 3} {2} + \ frac {2x — 2} {4} = \ frac {7x — 6} {3} $Решение :
А) Приводим к общему знаменателю и получаем:
12x — 2 — 5 + 10x = 12x + 49
22x — 12x = 49 + 7
10x = 56 x = 5.6Б) $ \ frac {x — 3} {2} + \ frac {2x — 2} {4} = \ frac {7x — 6} {3} $
$ \ frac {x -3 + x — 1} { 2} = \ frac {7x — 6} {3} $
3 (2x — 4) = 2 (7x — 6)
6x -12 = 14x — 12
8x = 0 x = 0Задача 8 Дана функция f (x) = x + 4. Решите уравнение:
$ \ frac {3f (x — 2)} {f (0)} + 4 = f (2x + 1) $Решение :
Вычисляем f (0), f (x -2), f (2x +1), а именно f (0) = 0 + 4 = 4;
f (x — 2) = x — 2 + 4 = x + 2;
f (2x + 1) = 2x + 1 + 4 = 2x + 5 Уравнение выглядит следующим образом
$ \ frac {3 (x + 2)} {4} + 4 = 2x + 5 $
3 (x + 2 ) +16 = 4 (2x + 5)
3x + 6 +16 = 8x + 20
22-20 = 8x — 3x
2 = 5x x = 0.4Задача 9 Решите уравнение:
(2x — 1) 2 — x (10x + 1) = x (1 — x) (1 + x) — (2 — x) 3Решение :
(2x — 1) 2 — x (10x + 1) = x (1 — x) (1 + x) — (2 — x) 3
4x 2 — 4x + 1 -10x 2 — x = x — x 3 — 8 + 12x — 6x 2 + x 3
18x = 9 $ x = \ frac {1} {2} $Задача 10 Решите уравнение:
(2x + 3) 2 –x (1 + 2x) (1 — 2x) = (2x — 1) 2 + 4x 3 — 1Решение :
(2x + 3) 2 — x (1 + 2x) (1-2x) = (2x — 1) 2 + 4x 3 -1
4x 2 + 12x + 9 — x (1 — 4x 2 ) = 4x 2 — 4x + 1 + 4x 3 — 1
12x + 9 — x + 4x 3 = — 4x + 4x 3
15x = -9 $ x = — \ гидроразрыв {3} {5} $Задача 11 Решите уравнение:
(2x — 1) 3 + 2x (2x — 3). 2} {3} = \ гидроразрыв {1} {5} \ left [5 — \ frac {20x — 43x} {3} \ right] $
2} {3} = \ гидроразрыв {1} {5} \ left [5 — \ frac {20x — 43x} {3} \ right] $Решение :
A) 4x 2 + 4x + 1 — x (1 — 4x 2 ) = 4x 2 — 4x + 1 + 4x 3 — 3
4x — x + 4x 3 = -4x + 4x 3 -3
3x + 4x = -3
7x = — 3 $ x = — \ frac {3} {7} $Б) 4x 2 — 4x + 1 + x 3 — 3x 2 .2 + 3x.2 2 — 8 = x 3 -2x 2 + 8x — 7
4x 2 — 6x 2 — 4x + 1 + 12x — 8 = — 2x 2 + 8x -7
-2x 2 + 8x — 7 = — 2x 2 + 8x — 7
0 = 0 => каждый x является решением;C) x 3 + 2x 2 — 2x 2 — 4x + 4x + 8 + x (1 — x 2 ) = x — 4
x 3 + 8 + x — x 3 = x — 4
8 = — 4, что невозможно. Следовательно, уравнение не имеет решения;D) $ \ frac {8x + 5} {4} — 1 + \ frac {3 — x} {6} = 2x + \ frac {5} {6} \ Leftrightarrow $
3 (8x + 5) — 12 + 2 (3 — х) = 24х + 2.2 — 43x} {15} \ Leftrightarrow $
3x — 5 (4x 2 -12x + 9) = 15 — 20x 2 + 43x
3x — 20x 2 + 60x — 45 = 15 — 20x 2 + 43x
63x — 43x = 15 + 45
20x = 60 x = 3Подробнее об уравнениях на математическом форуме
Регистрация на форуме
Использование FOIL — Бесплатная справка по математике
Вы уже знаете, как упростить выражение типа \ (7 (4x + 3) \), верно? Просто используйте распределительное свойство умножить 7 на 4x , а затем 7 на 3 .Это дает вам ответ \ (28x + 21 \). Довольно просто. Но что если у вас что-то вроде этого: \ ((4x + 6) (x + 2) \)? Вот где мы используем метод FOIL. ФОЛЬГА означает Первый , Снаружи , Внутри , Последний .
 2 + 14x + 12 \).2-13х + 20) \).
2 + 14x + 12 \).2-13х + 20) \).Освоить метод FOIL несложно, если вспомнить, что он означает. Просто повторите сначала, снаружи, внутри, в последнюю очередь, и вы это запомните. Помимо этого, нужно просто умножить каждый из этих шагов и сложить все вместе. Даже если числа действительно уродливые, с дробями и отрицательными знаками, просто следуйте инструкциям, и метод будет работать.
Если у вас есть дополнительные вопросы о FOIL, как всегда, не стесняйтесь обращаться за помощью на доску справочных сообщений по математике или воспользуйтесь калькулятором FOIL ниже.
Калькулятор ФОЛЬГИ
Алгебраных ошибок
Мы собрали здесь набор ошибок, которые довольно легко сделать.
Постарайтесь избежать этого!
Ошибка Исправление x 2 = 25, поэтому x = 5 x = 5 или x = −5 (x − 5) 2 = x 2 -25 = (x − 5) (x − 5) = x 2 — 10x + 25 √ (x 2 + y 2 ) = x + y √ (x 2 + y 2 ) как можно дальше x 2 x 4 = x 8 = x 6 (добавить экспоненты) (x 2 ) 4 = x 6 = x 8 (умножить показатели) 2x -1 = 1 / (2x) = 2 / х −5 2 = 25 = −25 (сделать показатель перед минусом) (-5) 2 = -25 = +25 (делать скобки перед показателем) 5 ½ = 1/5 2 = √5 журнал (a + b) = журнал (a) + журнал (b) лог (a + b) — это максимально возможное расстояние x (a / b) = xa / xb = xa / b x− (5 + a) = x − 5 + a = х-5-а И будьте осторожны с этими:
Упрощение дробей
x x + y = x x + x y Мы не можем это упростить!
Представьте, что x = 4 и y = 5:
4 4 + 5 = 4 9
Это определенно не равно 4 4 + 4 5 (что на самом деле больше 1)
Может быть, вы думали о такой дроби, которую мы можем упростить :
x + y x = x x + y x Корень квадратный из xy
√ (xy) = √x√y .
 .. но не всегда!
.. но не всегда!Пример: x = −5 и y = −2
√10 = √ (−5 × −2)
= √ (−5) √ (−2) (ошибка)
= i√5 × i√2
= я 2 √5√2
= −√10
Итак, √10 = −√10 ??? Думаю, нет!
√ (xy) = √x√y только тогда, когда x и y оба> = 0
Два равных одному
Пример:
Начать с: x = y
Умножаем обе стороны на x: x 2 = xy
Вычтем y 2 с обеих сторон: x 2 — y 2 = xy — y 2
Фактор: (x + y) (x − y) = y (x − y)
Разделим обе части на (x − y): x + y = y (ошибка)
Поскольку x = y, мы видим, что: 2y = y
Итак: 2 = 1
Подождите! Этого не может быть!
Что пошло не так? Глупые мы! Мы пробовали делить на ноль.
Когда мы сказали, что x = y, это означает, что (x − y) = 0 , поэтому переход от (x + y) (x − y) = y (x − y) к x + y = y — ошибка.
Факторинг
Пример: Решить x
2 — 5x = 2Начать с: x 2 — 5x = 2
Фактор x: x (x − 5) = 2
Итак: x = 2 или x − 5 = 2 (ошибка)
Итак: x = 2 или 7
Давайте проверим x = 2:
2 2 — 5 × 2 = 4−10 = −6 , но мы хотели x 2 — 5x = 2
Это работает только тогда, когда x (x − 5) = 0 (ноль), а не любое другое число
.
- Показатели степени 1

 3.Не волнуйтесь, это точно такое же число: основание — это число слева, а степень — это число справа. В зависимости от типа используемого калькулятора — и особенно если вы используете калькулятор на своем телефоне или компьютере — вам может потребоваться ввести показатель степени таким образом, чтобы вычислить его.
3.Не волнуйтесь, это точно такое же число: основание — это число слева, а степень — это число справа. В зависимости от типа используемого калькулятора — и особенно если вы используете калькулятор на своем телефоне или компьютере — вам может потребоваться ввести показатель степени таким образом, чтобы вычислить его. Например, чтобы упростить это выражение, вы просто добавите переменные. У вас есть два xs, которые можно записать как 2x . Итак, x 2 + x 2 будет 2x 2 .
Например, чтобы упростить это выражение, вы просто добавите переменные. У вас есть два xs, которые можно записать как 2x . Итак, x 2 + x 2 будет 2x 2 . Чтобы умножить степень, сложите степени . Например, возьмите это выражение:
Чтобы умножить степень, сложите степени . Например, возьмите это выражение: Помните, что показатель степени означает, что вы умножаете основание само на себя столько раз. Например, 2 3 равно 2⋅2⋅2. Это означает, что мы можем переписать (x 5 ) 3 как:
Помните, что показатель степени означает, что вы умножаете основание само на себя столько раз. Например, 2 3 равно 2⋅2⋅2. Это означает, что мы можем переписать (x 5 ) 3 как:

 е. a <0), диапазон f ( x ) равен (-∞, 3].
е. a <0), диапазон f ( x ) равен (-∞, 3]. 4} {11 } \ Leftrightarrow y = \ frac {48} {11} $
4} {11 } \ Leftrightarrow y = \ frac {48} {11} $ 2 = — 2x $
2 = — 2x $ 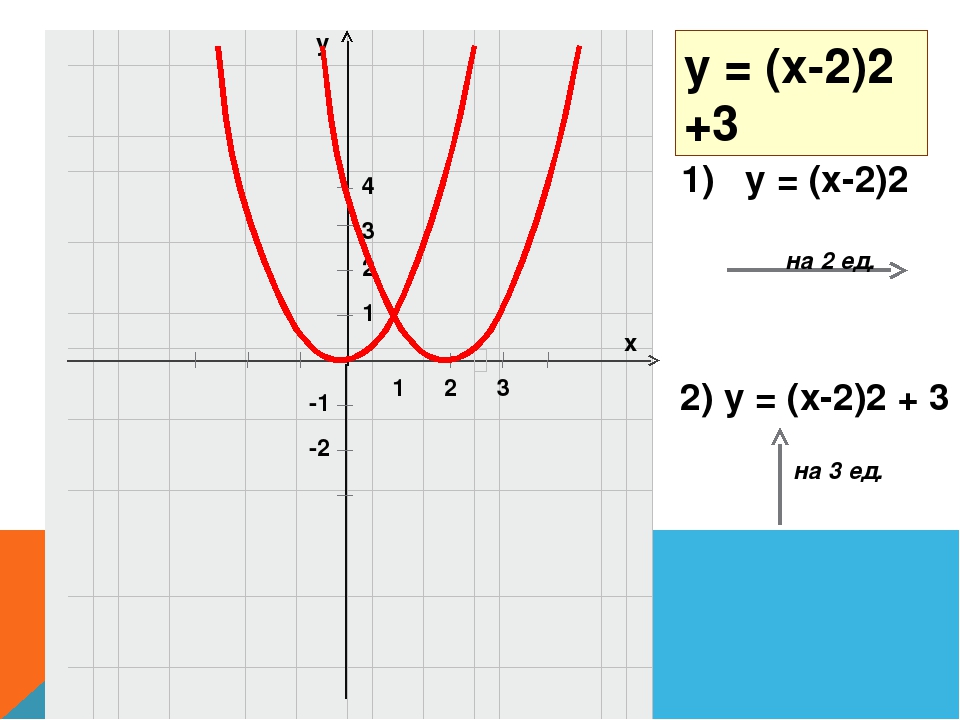 x — x = 3-3
x — x = 3-3  2} {3} = \ гидроразрыв {1} {5} \ left [5 — \ frac {20x — 43x} {3} \ right] $
2} {3} = \ гидроразрыв {1} {5} \ left [5 — \ frac {20x — 43x} {3} \ right] $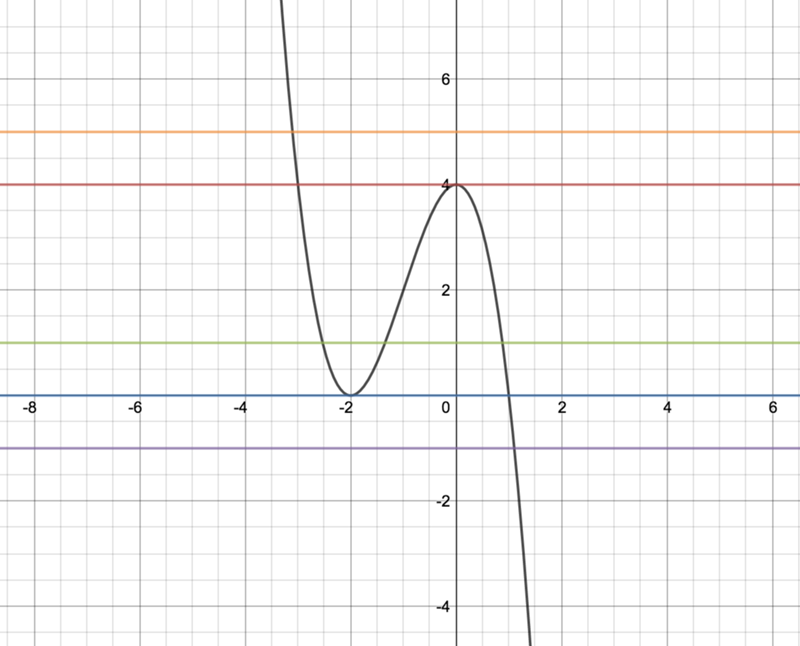 .. но не всегда!
.. но не всегда!
Leave A Comment