2. Графики

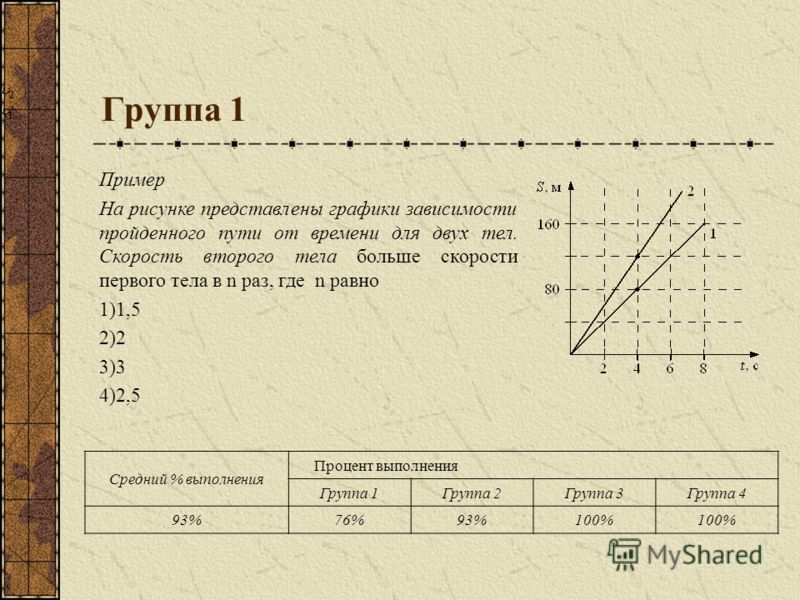
1. За­да­ние 1 № 101. Может ли гра­фик за­ви­си­мо­сти пути от вре­ме­ни иметь сле­ду­ю­щий вид?

 

 

1) да

2) нет

3) может, если тра­ек­то­рия пря­мо­ли­ней­ная

4) может, если тело воз­вра­ща­ет­ся в ис­ход­ную точку

Ре­ше­ние.

Путь — это фи­зи­че­ская ве­ли­чи­на, по­ка­зы­ва­ю­щая прой­ден­ное телом рас­сто­я­ние. Иначе го­во­ря, это длина прой­ден­но­го участ­ка тра­ек­то­рии. По опре­де­ле­нию, путь есть ве­ли­чи­на по­ло­жи­тель­ная, ко­то­рая может толь­ко воз­рас­тать со вре­ме­нем, так что пред­став­лен­ный гра­фик не может изоб­ра­жать за­ви­си­мость пути от вре­ме­ни.

Пра­виль­ный ответ: 2.

Ответ: 2

101

2

2. За­да­ние 1 № 102.

Мяч, бро­шен­ный вер­ти­каль­но вверх, па­да­ет на землю. Най­ди­те гра­фик за­ви­си­мо­сти от вре­ме­ни про­ек­ции ско­ро­сти на вер­ти­каль­ную ось, на­прав­лен­ную вверх.

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Мяч после брос­ка дви­жет­ся с по­сто­ян­ным уско­ре­ни­ем сво­бод­но­го па­де­ния, на­прав­лен­ным вниз. Сле­до­ва­тель­но, про­ек­ция ско­рости долж­на умень­шать­ся со вре­ме­нем по ли­ней­но­му за­ко­ну, , гра­фик за­ви­си­мо­сти её от вре­ме­ни пред­став­лен на ри­сун­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

102

2

3. За­да­ние 1 № 103. Мяч бро­шен с вер­ши­ны скалы без на­чаль­ной ско­ро­сти. Най­ди­те гра­фик за­ви­си­мо­сти мо­ду­ля пе­ре­ме­ще­ния от вре­ме­ни.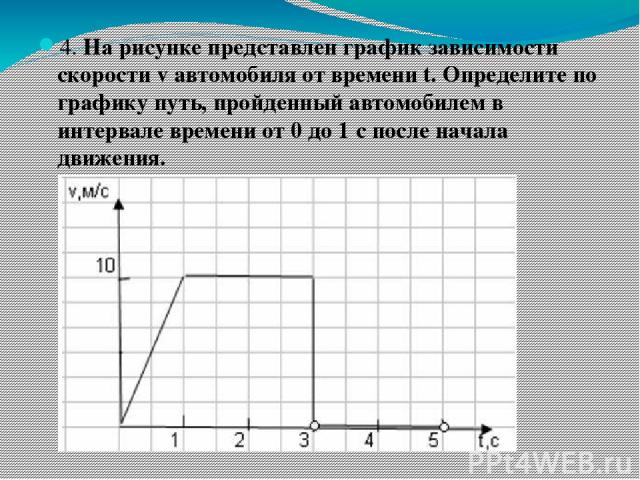 Со­про­тив­ле­ни­ем воз­ду­ха пре­не­бречь.

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

По­сколь­ку мяч бро­шен с вер­ши­ны скалы без на­чаль­ной ско­ро­сти, а со­про­тив­ле­ни­ем воз­ду­ха можно пре­не­бречь, за­ви­си­мость мо­ду­ля пе­ре­ме­ще­ния от вре­ме­ни долж­на иметь сле­ду­ю­щий вид:

.

Ис­ко­мая за­ви­си­мость пред­став­ле­на на ри­сун­ке 4. Кроме того, мо­дуль есть ве­ли­чи­на по­ло­жи­тель­ная, этому кри­те­рию также удо­вле­тво­ря­ет толь­ко гра­фик под но­ме­ром 4.

Пра­виль­ный ответ: 4.

Ответ: 4

103

4

4. За­да­ние 1 № 104. Ав­то­мо­биль дви­жет­ся по пря­мой улице. На гра­фи­ке пред­став­ле­на за­ви­си­мость ско­ро­сти ав­то­мо­би­ля от вре­ме­ни.

 

В каком ин­тер­ва­ле вре­ме­ни мак­си­ма­лен мо­дуль уско­ре­ния?

 

1) от 0 до 10 с

2) от 10 до 20 с

3) от 20 до 30 с

4) от 30 до 40 с

Ре­ше­ние.

На всех рас­смат­ри­ва­е­мых ин­тер­ва­лах вре­ме­ни ско­рость ав­то­мо­би­ля ме­ня­ет­ся рав­но­мер­но, сле­до­ва­тель­но уско­ре­ние на каж­дом ин­тер­ва­ле по­сто­ян­но. Все ис­сле­ду­е­мые ин­тер­ва­лы оди­на­ко­вы по дли­тель­но­сти, по­это­му мак­си­маль­но­му мо­ду­лю уско­ре­ния со­от­вет­ству­ет мак­си­маль­ный мо­дуль из­ме­не­ния ско­ро­сти в те­че­ние ин­тер­ва­ла (самый боль­шой угол на­кло­на). Из гра­фи­ка видно, что это ин­тер­вал от 10 до 20 с.

Пра­виль­ный ответ: 2.

Ответ: 2

104

2

5. За­да­ние 1 № 106.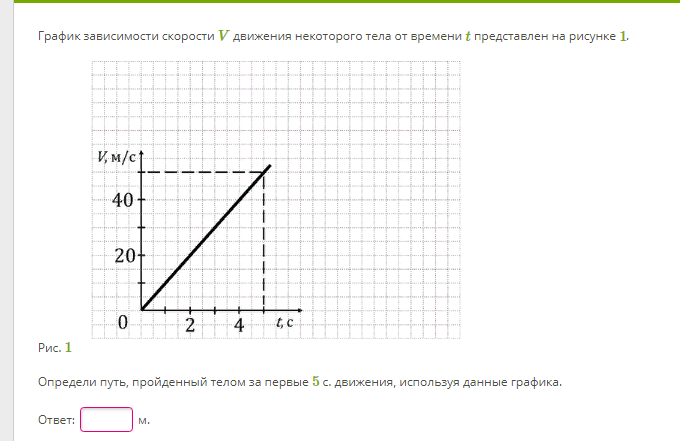 По гра­фи­ку за­ви­си­мо­сти мо­ду­ля ско­ро­сти тела от вре­ме­ни, пред­став­лен­но­го на ри­сун­ке, опре­де­ли­те путь, прой­ден­ный телом от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 2 с.

 

1) 1 м

2) 2 м

3) 3 м

4) 4 м

 

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). В ин­тер­ва­ле вре­ме­ни от 0 С до 2 с ав­то­мо­биль про­шел путь

.

При­ме­ча­ние: В прин­ци­пе, ин­те­ре­су­ю­щий нас уча­сток (от 0 до 2 с) не обя­за­тель­но раз­би­вать на два, пло­щадь под гра­фи­ком можно по­счи­тать, как пло­щадь тра­пе­ции:

.

Пра­виль­ный ответ: 3.

Ответ: 3

106

3

6. За­да­ние 1 № 107. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти ав­то­мо­би­ля от вре­ме­ни. Опре­де­ли­те по гра­фи­ку путь, прой­ден­ный ав­то­мо­би­лем в ин­тер­ва­ле от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с после на­ча­ла от­сче­та вре­ме­ни.

 

 

1) 6 м

2) 15 м

3) 17 м

4) 23 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный ав­то­мо­би­лем за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат).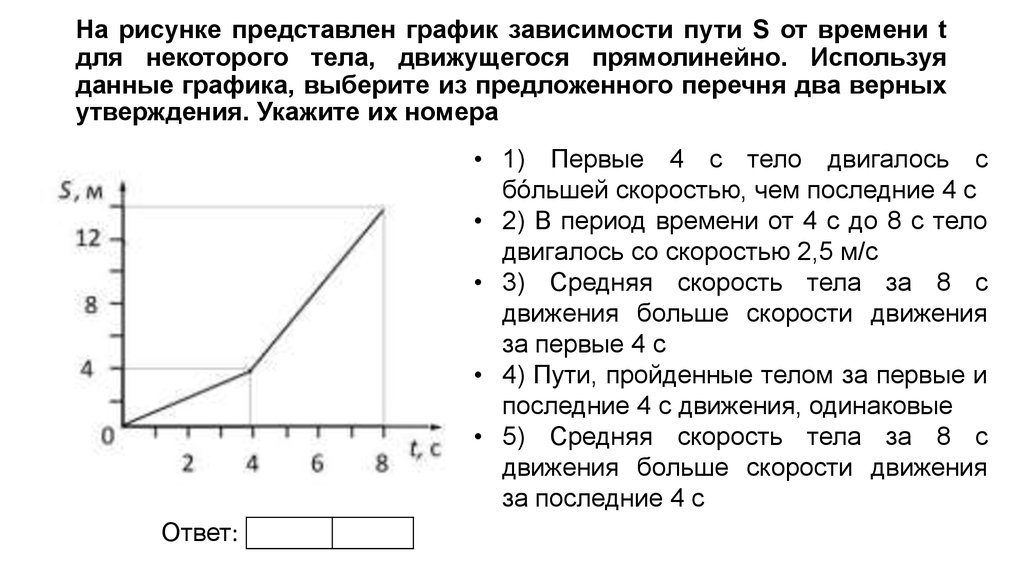 В ин­тер­ва­ле от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с после на­ча­ла дви­же­ния ав­то­мо­биль про­шел путь

 

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.

Пра­виль­ный ответ: 3.

Ответ: 3

107

3

7. За­да­ние 1 № 108. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти тела от вре­ме­ни.

 

Какой путь прой­ден телом за вто­рую се­кун­ду?

 

1) 0 м

2) 1 м

3) 2 м

4) 3 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). За вто­рую се­кун­ду ав­то­мо­биль про­шел путь

 

.

Пра­виль­ный ответ: 3.

Ответ: 3

108

3

8. За­да­ние 1 № 109. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти тела от вре­ме­ни.

 

Най­ди­те путь, прой­ден­ный телом за время от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с.

 

1) 0 м

2) 15 м

3) 20 м

4) 30 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). В ин­тер­ва­ле от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с после на­ча­ла дви­же­ния тело про­шло путь

 

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.

Пра­виль­ный ответ: 3.

Ответ: 3

109

3

9. За­да­ние 1 № 110. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти пути от вре­ме­ни.

 

Опре­де­ли­те по гра­фи­ку ско­рость дви­же­ния ве­ло­си­пе­ди­ста в ин­тер­ва­ле от мо­мен­та вре­ме­ни 1 с до мо­мен­та вре­ме­ни 3 с после на­ча­ла дви­же­ния.

 

1)

2)

3)

4)

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле от мо­мен­та вре­ме­ни 1 с до мо­мен­та вре­ме­ни 3 с после на­ча­ла дви­же­ния путь ве­ло­си­пе­ди­ста не из­ме­нял­ся. Сле­до­ва­тель­но на этом ин­тер­ва­ле вре­ме­ни ве­ло­си­пе­дист не дви­гал­ся, его ско­рость была равна нулю.

Пра­виль­ный ответ: 1.

Ответ: 1

110

1

10. За­да­ние 1 № 116. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком гра­фи­ке пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 10 до 20 с?

 

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 10 до 20 с про­ек­ция ско­ро­сти тела не из­ме­ня­лась, а зна­чит, про­ек­ция уско­ре­ния была равна нулю. Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

116

2

11. За­да­ние 1 № 117. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 0 до 6 с?

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что уско­ре­ние в ин­тер­ва­ле вре­ме­ни от 0 с до 10 с по­сто­ян­но. Зна­чит, на этом ин­тер­ва­ле ве­ре­ме­ни уско­ре­ние такое же, как и на ин­тер­ва­ле от 0 с до 6 с. Найдём это уско­ре­ние:

 

.

 

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 1.

 

Ответ: 1.

Ответ: 1

117

1

12. За­да­ние 1 № 118. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 20 до 26 с?

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 20 до 26 с про­ек­ция ско­ро­сти тела убы­ва­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 3.

Пра­виль­ный ответ: 3.

Ответ: 3

118

3

13. За­да­ние 1 № 119. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 54 до 60 с?

 

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 54 до 60 с про­ек­ция ско­ро­сти тела не из­ме­ня­лась, а зна­чит, про­ек­ция уско­ре­ния была равна нулю. Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

119

2

14. За­да­ние 1 № 120. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 42 до 48 с?

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 42 до 48 с (и даже на более боль­шом ин­тер­ва­ле от 40 с до 50 с) про­ек­ция ско­ро­сти тела воз­рас­та­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 4.

Пра­виль­ный ответ: 4.

 

Ответ: 4

120

4

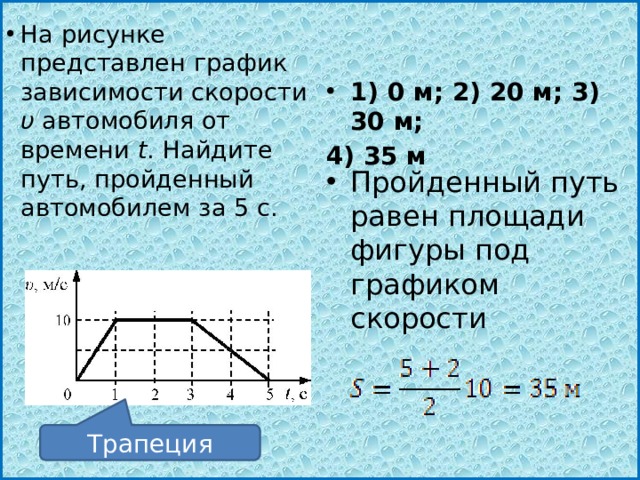
15. За­да­ние 1 № 121. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти ав­то­мо­би­ля от вре­ме­ни t.

 

Най­ди­те путь, прой­ден­ный ав­то­мо­би­лем за 5 c.

 

1) 0 м

2) 20 м

3) 30 м

4) 35 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом, не­об­хо­ди­мо вы­чис­лить пло­щадь под гра­фи­ком (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). За 5 c ав­то­мо­биль про­шел путь

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.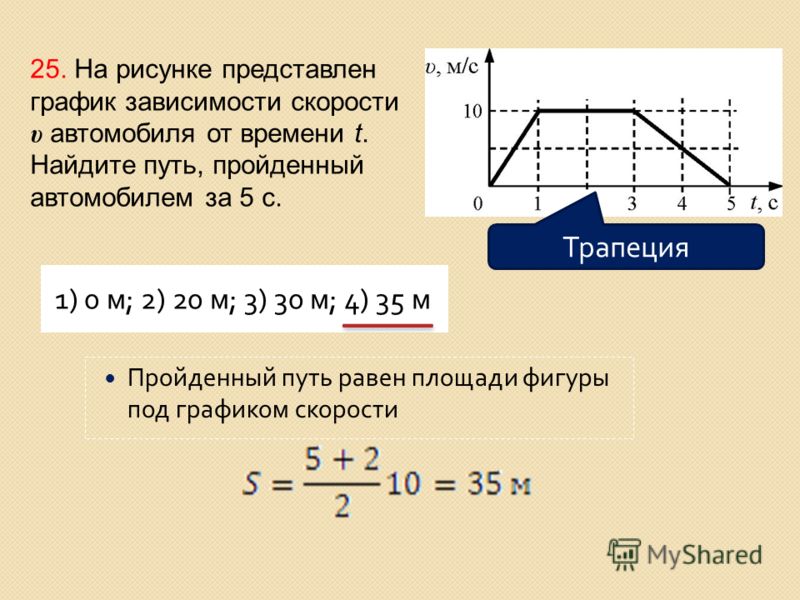

Пра­виль­ный ответ: 4.

Ответ: 4

121

4

16. За­да­ние 1 № 122. Ав­то­мо­биль дви­жет­ся по пря­мой улице. На гра­фи­ке пред­став­ле­на за­ви­си­мость его ско­ро­сти от вре­ме­ни.

 

На каком ин­тер­ва­ле вре­ме­ни мо­дуль уско­ре­ния ав­то­мо­би­ля мак­си­ма­лен?

 

1) от 0 с до 10 с

2) от 10 с до 20 с

3) от 20 с до 30 с

4) от 30 с до 40 с

Ре­ше­ние.

На всех рас­смат­ри­ва­е­мых ин­тер­ва­лах вре­ме­ни ско­рость ав­то­мо­би­ля ме­ня­ет­ся рав­но­мер­но, сле­до­ва­тель­но, уско­ре­ние на каж­дом ин­тер­ва­ле по­сто­ян­но. Все ис­сле­ду­е­мые ин­тер­ва­лы оди­на­ко­вы по дли­тель­но­сти, по­это­му мак­си­маль­но­му мо­ду­лю уско­ре­ния со­от­вет­ству­ет мак­си­маль­ный мо­дуль из­ме­не­ния ско­ро­сти в те­че­ние ин­тер­ва­ла: . Из гра­фи­ка видно, что это ин­тер­вал от 20 до 30 с

(в этом слу­чае , на дру­гих ин­тер­ва­лах мень­ше).

Пра­виль­ный ответ: 3.

Ответ: 3

122

3

17. За­да­ние 1 № 128. Тело дви­жет­ся по оси Ox. На гра­фи­ке по­ка­за­на за­ви­си­мость про­ек­ции ско­ро­сти тела на ось Ox от вре­ме­ни.

 

Каков путь, прой­ден­ный телом к мо­мен­ту вре­ме­ни

 

1) 6 м

2) 8 м

3) 4 м

4) 5 м

Ре­ше­ние.

На про­тя­же­нии всего ин­тер­ва­ла вре­ме­ни про­ек­ция ско­ро­сти тела на ось Ox по­ло­жи­тель­на. По­это­му, для того чтобы найти путь, прой­ден­ный телом, не­об­хо­ди­мо вы­чис­лить пло­щадь под гра­фи­ком (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). К мо­мен­ту вре­ме­ни тело про­шло путь

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.

Пра­виль­ный ответ: 1.

Ответ: 1

128

1

18. За­да­ние 1 № 130. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

С каким из гра­фи­ков сов­па­да­ет гра­фик за­ви­си­мо­сти от вре­ме­ни про­ек­ции уско­ре­ния этого тела в ин­тер­ва­ле вре­ме­ни от 10 до 15 с?

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 10 до 15 с про­ек­ция ско­ро­сти тела воз­рас­та­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 3.

Пра­виль­ный ответ: 3.

Ответ: 3

130

3

19. За­да­ние 1 № 132. Ав­то­мо­биль дви­жет­ся пря­мо­ли­ней­но. На гра­фи­ке пред­став­ле­на за­ви­си­мость ско­ро­сти ав­то­мо­би­ля от вре­ме­ни.

 

На каком ин­тер­ва­ле вре­ме­ни мо­дуль его уско­ре­ния ми­ни­ма­лен?

 

1) от 0 до 10 с

2) от 10 с до 20 с

3) от 20 с до 30 с

4) от 30 до 40 с

Ре­ше­ние.

На всех рас­смат­ри­ва­е­мых ин­тер­ва­лах вре­ме­ни ско­рость ав­то­мо­би­ля ме­ня­ет­ся рав­но­мер­но, сле­до­ва­тель­но уско­ре­ние на каж­дом ин­тер­ва­ле по­сто­ян­но. Все ис­сле­ду­е­мые ин­тер­ва­лы оди­на­ко­вы по дли­тель­но­сти, по­это­му ми­ни­маль­но­му мо­ду­лю уско­ре­ния со­от­вет­ству­ет ми­ни­маль­ный мо­дуль из­ме­не­ния ско­ро­сти в те­че­ние ин­тер­ва­ла. Из гра­фи­ка видно, что это ин­тер­вал от 0 до 10 с.

Пра­виль­ный ответ: 1.

Ответ: 1

132

1

20. За­да­ние 1 № 136. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 24 до 30 с?

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 24 до 30 с про­ек­ция ско­ро­сти тела убы­ва­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 3.

Пра­виль­ный ответ: 3.

Ответ: 3

136

3

21. За­да­ние 1 № 137. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 4 до 10 с?

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 0 до 6 с про­ек­ция ско­ро­сти тела воз­рас­та­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 1.

Пра­виль­ный ответ: 1.

Ответ: 1

137

1

22. За­да­ние 1 № 138. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком гра­фи­ке пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 30 до 40 с?

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 30 до 40 с про­ек­ция ско­ро­сти тела не из­ме­ня­лась, а зна­чит, про­ек­ция уско­ре­ния была равна нулю. Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

138

2

23. За­да­ние 1 № 140. Тело на­чи­на­ет дви­гать­ся из на­ча­ла ко­ор­ди­нат вдоль оси Ox, при­чем про­ек­ция ско­ро­сти ме­ня­ет­ся с те­че­ни­ем вре­ме­ни по за­ко­ну, при­ве­ден­но­му на гра­фи­ке.

 

Чему будет равна про­ек­ция уско­ре­ния тела через 2 c?

 

1)

2)

3)

4)

Ре­ше­ние.

Из гра­фи­ка видно, что про­ек­ция ско­ро­сти тела воз­рас­та­ла со вре­ме­нем по ли­ней­но­му за­ко­ну, это озна­ча­ет, что тело дви­га­лось с по­сто­ян­ным уско­ре­ни­ем вдоль оси Ox. Таким об­ра­зом, про­ек­ция уско­ре­ния тела через 2 c равна

 

.

Пра­виль­ный ответ: 2.

Ответ: 2

140

2

24. За­да­ние 1 № 3323. На гра­фи­ке при­ве­де­на за­ви­си­мость ско­ро­сти пря­мо­ли­ней­но­го дви­жу­ще­го­ся тела от вре­ме­ни. Опре­де­ли­те мо­дуль уско­ре­ния тела.

 

1)

2)

3)

4)

Ре­ше­ние.

Из гра­фи­ка видно, что ско­рость тела за­ви­сит ли­ней­но от вре­ме­ни, а зна­чит, его уско­ре­ние по­сто­ян­но. Для опре­де­ле­ния мо­ду­ля уско­ре­ния можно взять любые две точки на гра­фи­ке: .

 

Ответ: 1.

Ответ: 1

3323

1

25. За­да­ние 1 № 3324. Тело дви­жет­ся по оси х. По гра­фи­ку за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни t уста­но­ви­те, какой путь про­шло тело за время от до .

 

1) 10 м

2) 15 м

3) 45 м

4) 20 м

Ре­ше­ние.

Не­об­хо­ди­мо раз­ли­чать два по­ня­тия: путь и пе­ре­ме­ще­ние. Путь — ве­ли­чи­на стро­го по­ло­жи­тель­ная, это длина прой­ден­но­го телом участ­ка тра­ек­то­рии. Под пе­ре­ме­ще­ни­ем же тела по­ни­ма­ет­ся из­ме­не­ние его ко­ор­ди­на­ты, пе­ре­ме­ще­ние может быть от­ри­ца­тель­ным. Прой­ден­ный телом путь опре­де­ля­ет­ся за­ви­си­мо­стью от вре­ме­ни мо­ду­ля ско­ро­сти. Чтобы из гра­фи­ка за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни по­лу­чить гра­фик мо­ду­ля ско­ро­сти, не­об­хо­ди­мо зер­каль­но от­ра­зить от­но­си­тель­но го­ри­зон­таль­но оси все от­ри­ца­тель­ные участ­ки. В дан­ной за­да­че это не столь прин­ци­пи­аль­но, по­сколь­ку на рас­смат­ри­ва­ем ин­тер­ва­ле от до про­ек­ция ско­ро­сти тела оста­ет­ся по­ло­жи­тель­ной, но в общем слу­чае это может при­ве­сти к не­же­ла­тель­ной ошиб­ке.

Тест по теме «Механическое движение. Графики зависимости скорости, пути, координаты от времени». Вариант 2.

Новый сезон международных олимпиад стартовал! 165 олимпиад по 27 предметам, бесплатная викторина, результаты сразу

 

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Для закрепления темы «Механическое движени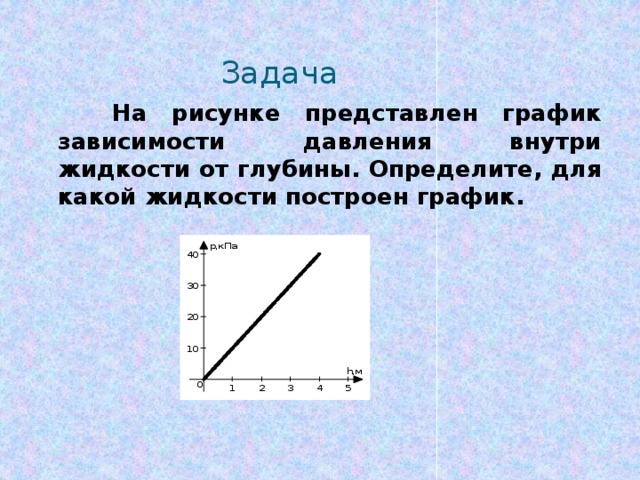е. Графики зависимости скорости, пути, координаты от времени» в 7 классе. Составлен из заданий из Открытого банка заданий ОГЭ по физике

Вопрос 1

На рисунке приведены графики зависимости пути и скорости тела от времени. Какой(-ие) график(-и) соответствует(-ют) равномерному движению?

1)

2)

3)

4)

Варианты ответов
  • 1
  • 2
  • 3
  • 4
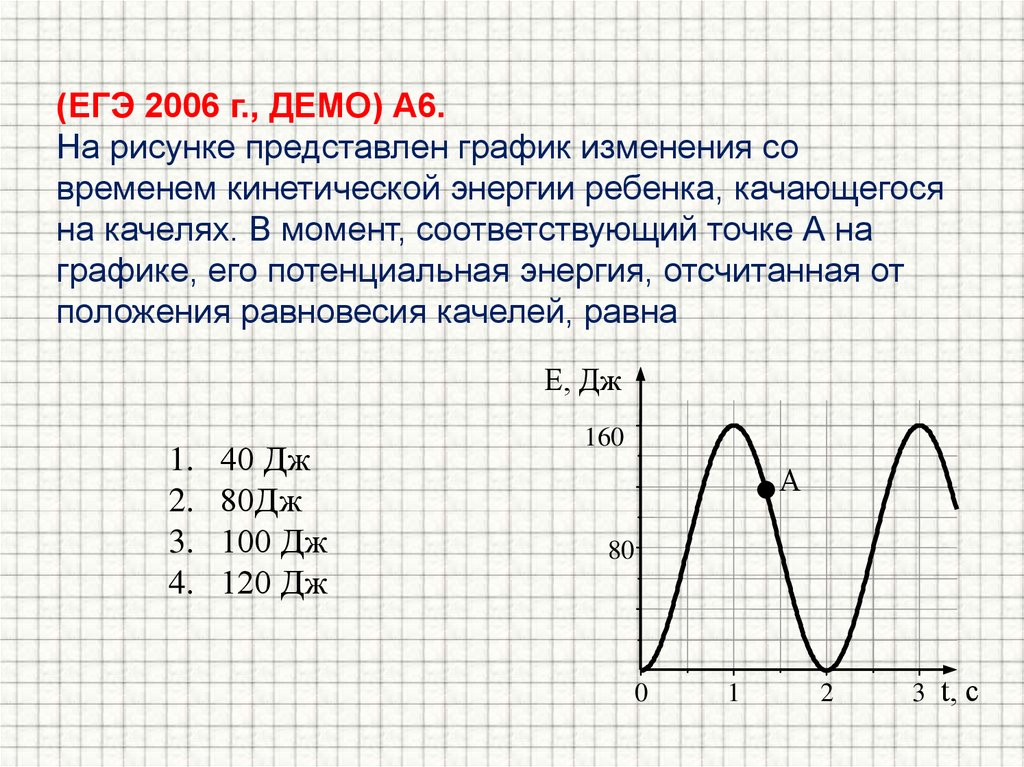
Вопрос 2

На рисунке представлен график зависимости модуля скорости υ от времени t для тела, движущегося прямолинейно.

Состоянию покоя тела соответствует(-ют) участок(-ки)

Варианты ответов
  • AB
  • DE
  • BC
  • BC и DE
Вопрос 3

5. Для каждого физического понятия из первого столбца подберите соответствующий пример из второго столбца. 

ФИЗИЧЕСКИЕ ПОНЯТИЯ

ПРИМЕРЫ

А)        физическая величина

Б)        единица физической величины

В)        физический прибор

 

1)         траектория

2)         средняя скорость

3)         литр

4)         измерительный цилиндр

5)         механическое движение

             

Запишите в таблицу выбранные цифры под соответствующими буквами.

А

Б

В

 

 

 

Варианты ответов
  • 423
  • 351
  • 154
  • 234
Вопрос 4

На рисунке представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси 0х.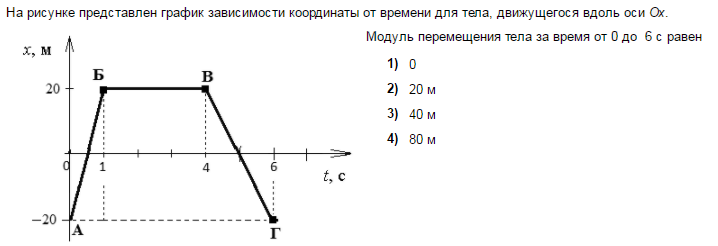 Какое из тел в момент времени t1 имеет наибольшую по модулю скорость?

Варианты ответов
  • 1
  • 2
  • 3
  • 4
Вопрос 5

На рисунке представлен график зависимости модуля скорости тела от времени. Путь равномерного движения тела составляет

Варианты ответов
  • 10 м
  • 30 м
  • 40 м
  • 60 м
Вопрос 6

На рисунке представлен график зависимости координаты x от времени t для четырёх тел (А, Б, В и Г), движущихся вдоль оси Ох.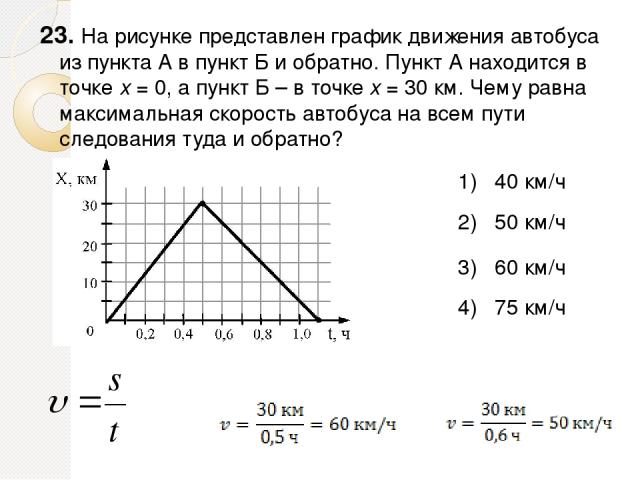

В отрицательном направлении оси движется(-утся)

Варианты ответов
  • только тело А
  • только тело Б
  • тела В и Г
  • тела А и Б
Вопрос 7

На рисунке приведены графики зависимости координат x двух тел от времени t при их движении по оси Ox. В момент времени t = 4 с

Варианты ответов
  • тела встретились
  • тела имели одинаковую скорость
  • тела имели одинаковое ускорение
  • тела остановились
Вопрос 8

На рисунке представлен график зависимости координаты от времени для тела, движущегося вдоль оси Ох.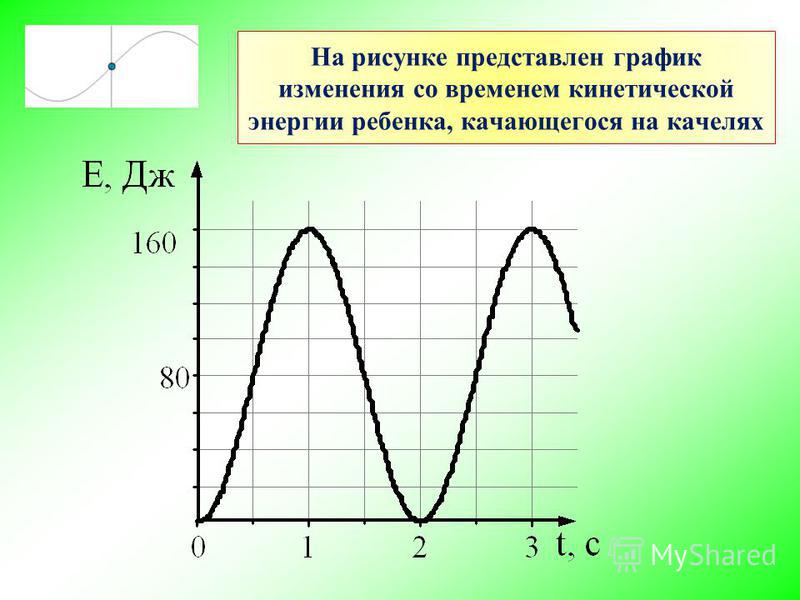

  

Путь тела за время от 0 до 8 с составил

Варианты ответов
  • 0
  • 10 м
  • 20 м
  • 30 м
Вопрос 9

На рисунке представлен график зависимости координаты от времени для тела, движущегося вдоль оси Ох.

  

Модуль перемещения тела за время от 0 до 8 с равен

  

Варианты ответов
  • 0
  • 10 м
  • 20 м
  • 40 м
Вопрос 10

На рисунке представлен график зависимости координаты x от времени t для четырёх тел (А, Б, В и Г), движущихся вдоль оси Ох.

  Модуль скорости равен 1 м/с

Варианты ответов
  • только у тела Б
  • только у тела В
  • у тел Б и Г
  • у тел А и Б
Вопрос 11

На рисунке точками на линейках показаны положения четырёх равномерно движущихся тел, причём для тел 1 и 2 положения отмечались через каждую секунду, а для тел 3 и 4 – через каждые 2 с.

 

Наименьшую скорость движения имеет тело

Варианты ответов
  • 1
  • 2
  • 3
  • 4
Вопрос 12

На рисунке представлен график зависимости координаты х от времени t для четырёх тел, движущихся вдоль оси Ох.

 

Равномерному движению с отличной от нуля скоростью соответствует график

Варианты ответов
  • 1
  • 2
  • 3
  • 4

Пройти тест

Сохранить у себя:

© 2019, Никифорова Наталья Владиленовна  1168

На рисунке показан график зависимости скорости от времени для частицы, движущейся вдоль оси x. Первоначально при t = 0 частица находится на расстоянии x = 3m. Найдите положение частицы в момент времени t = 2 с. (в м)

ДВИЖЕНИЕ-КИНЕМАТИКА-УПРАЖНЕНИЕ 1 ОБЪЕКТИВНЫЕ ЗАДАЧИ

20 видео

РЕКЛАМА

Аб Падхай каро бина адс ке

Хариэдо ДН Про и дехо сари видео бина киси ад ки рукаават ке!

Обновлено: 27 июня 2022 г.

Текстовое решение

Ответ

Правильный ответ A

Ответить

Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.

Видео по теме

На рисунке показан график зависимости скорости частицы от времени. Найти расстояние, пройденное частицей за время от t=0 до t=3с.

9515174

На рисунке показан график x-t частицы. Найдите время T, при котором средняя скорость частицы в период от 0 до T равна нулю.

9515256

Частица стартует из начала координат в момент времени t = 0 и движется вдоль положительной оси x. График зависимости скорости от времени показан на рисунке. Каково положение частицы в момент времени t = 5 с?

48250559

График ускорения частицы, движущейся по оси абсцисс, показан на рисунке. Если частица стартовала со скоростью 3 м/с в момент t = 0, найти скорость частицы в момент t = 4 с.

69127329

График зависимости положения (x) от времени (t) частицы показан на рисунке. Скорость равна нулю при?

291997486

График скорости (v) — время (t) для частицы, движущейся вдоль оси x, показан на рисунке. Соответствующее положение (x) — время (t) лучше всего представлено как

304589365

График ускорение-время для частицы, движущейся вдоль оси x, показан на рисунке. Если начальная скорость частицы равна −5 м/с, скорость в момент времени t = 8 с равна

304589405

На рисунке показан график зависимости скорости частицы от времени. Найти расстояние, пройденное частицей за время от t=0 до t=3с.

642594477

На рисунке показан график x-t частицы. Найдите время T так, чтобы средняя скорость частицы в течение периода от 0 до T была равна нулю.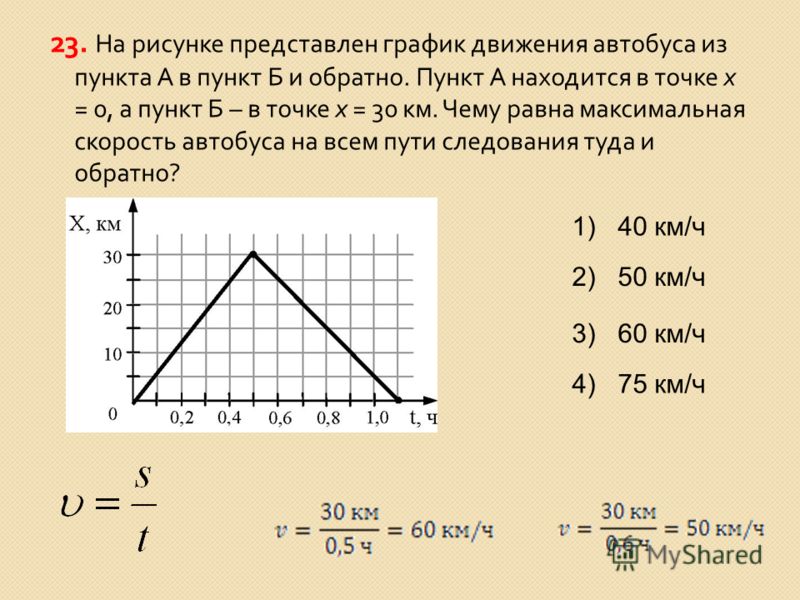

642594553

Частица стартует из начала координат в момент времени t = 0 и движется вдоль положительной оси x. График зависимости скорости от времени показан на рисунке. Каково положение частицы в момент времени t = 5 с?

642609428

Частица движется вдоль оси X как x=u(t−2)+a(t−2)2 9(2) а) начальная скорость частицы u б) ускорение частицы 2а в) в момент t=2с частица находится в начале координат

642728095

Текст Решение

по оси абсцисс показано на рисунке. Если частица стартовала со скоростью 3 м/с в момент t = 0, найти скорость частицы в момент t = 4 с.

644355916

График скорости (v) — время (t) для частицы, движущейся вдоль оси x, показан на рисунке. Соответствующая позиция (x) — время (t) лучше всего представлена ​​

644367967

График ускорение-время для частицы, движущейся вдоль оси абсцисс, показан на рисунке.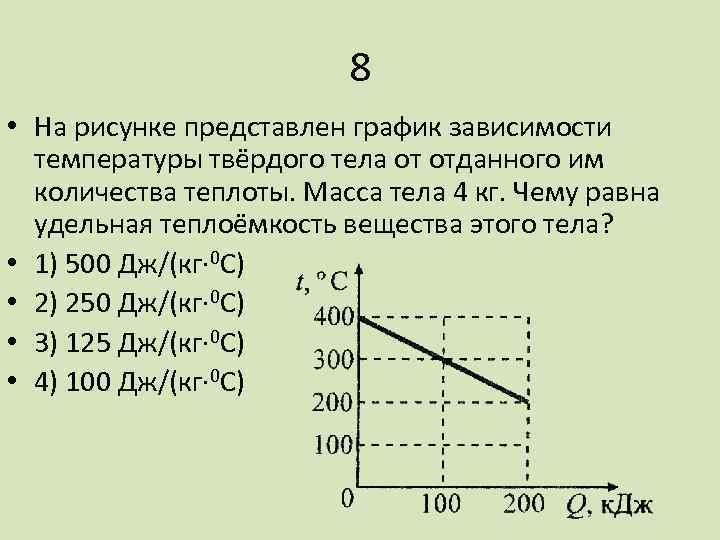 Если начальная скорость частицы равна −5 м/с, скорость в момент времени t = 8 с равна На рисунке показан график смещения во времени для четырех тел A B C и D. В каждом случае укажите, какая информация…

Перейти к

  • Упражнение 2А
  • Упражнение 2Б
  • Упражнение 2С
  • Глава 1 – Измерения и эксперименты
  • Глава 2. Движение в одном измерении
  • Глава 3 Законы движения
  • Глава 4 Давление в жидкостях и атмосферное давление
  • Глава 5. Аптраст в жидкости. Принцип Архимеда и плавучесть.
  • Глава 6 Тепло и энергия
  • Глава 7 Отражение света
  • Глава 8 Распространение звуковых волн
  • Глава 9 Текущее электричество
  • Глава 10 Магнетизм

Главная > Селина Солюшнс Класс 9 Физика > Глава 2 — Глава 2 Движение в одном измерении > Упражнение 2Б > Вопрос 14

Вопрос 14. Упражнение 2B

На рисунке показан график зависимости перемещения от времени для четырех тел A, B, C и D. В каждом случае состояние какую информацию вы получаете об ускорении (нулевое, положительное или отрицательное)?

Ответ:

Можно получить следующую информацию о ускорение:

A – Здесь наклон постоянен, поэтому скорость постоянна. ускорение равно 0.

B – Поскольку график B имеет постоянный наклон, ускорение 0.

C. На графике C показан наклон, уменьшающийся со временем. Следовательно, ускорение отрицательное, что называется замедлением.

D – На графике D показан наклон, увеличивающийся со временем. ускорение положительное.

Связанные вопросы

Как зависит пройденное расстояние от времени при движении с постоянной скоростью?

Какую информацию о движении тела можно получить из графика перемещение-время?

(a) Что представляет собой наклон графика смещения во времени? (b) Может ли зарисовка смещения во времени быть.