Mathway | Популярные задачи
Mathway | Популярные задачиПопулярные задачи
Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра ХимияЭтот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:
- число
- буква
- специальный символ: @$#!%*?&
Уравнения и неравенства с модулем
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что

Рассмотрим различные типы
Слева модуль, справа число
Это самый простой случай. Решим уравнение
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
или
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Ответ: 0; 5.
Переменная как под модулем, так и вне модуля
Здесь приходится раскрывать модуль по определению. . . или соображать!
1.
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.
2.
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения
Второй случай: x < 3. Снимаем модуль:
Число . больше, чем , и потому не удовлетворяет условию x < 3. Проверим :
Значит, . является корнем исходного уравнения.
Ответ:
3.
Снимать модуль по определению? Страшно даже подумать об этом, ведь дискриминант — не полный квадрат. Давайте лучше воспользуемся следующим соображением: уравнение вида |A| = B равносильно совокупности двух систем:

То же самое, но немного по-другому:
Иными словами, мы решаем два уравнения, A = B и A = −B, а потом отбираем корни, удовлетворяющие условию B ≥ 0.
Приступаем. Сначала решаем первое уравнение:
Затем решаем второе уравнение:
Теперь в каждом случае проверяем знак правой части:
Стало быть, годятся лишь и .
Ответ:
Квадратные уравнения с заменой |x| = t
Решим уравнение:
Поскольку , удобно сделать замену |x| = t. Получаем:

Ответ: ±1.
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Решим уравнение:
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Ответ: [1; 2] ∪ {5}.
Модуль в модуле
Решим уравнение:
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
2) x ≥ 3. Имеем:
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Ответ: 4.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Читайте также о том, как решать неравенства с модулем.
Решение уравнений с модулем
 Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x) < 0
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3<0.
Чтобы решить уравнение , содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля.
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x2+4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3<0, т.е. если х<3
2. Мы получили два числовых промежутка: х≥3 и х<3.
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
x-3=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
x2 -3х=0
и решим это уравнение.
Это уравнение имеет корни:
х1=0, х2=3
Внимание! поскольку уравнение x-3=-x2+4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х2=3.
Б) При x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:
3-x=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х<3!
Раскроем скобки, приведем подобные члены. Получим уравнение:
x2-5х+6=0
х1=2, х2=3
Внимание! поскольку уравнение 3-х=-x2+4x-3 существует только на промежутке x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х1=2.
Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.
Ответ: х=3, х=2
График функции y = (|2^x-1|)
Для того, чтобы найти экстремумы, нужно решить уравнение$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
$$2^{x} \log{\left (2 \right )} \operatorname{sign}{\left (2^{x} — 1 \right )} = 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = -66.1767600931$$
$$x_{2} = -100.176760093$$
$$x_{3} = -84.1767600931$$
$$x_{4} = -60.1767600931$$
$$x_{5} = -80.1767600931$$
$$x_{6} = -92.1767600931$$
$$x_{7} = -62.1767600931$$
$$x_{8} = -54.1767600931$$
$$x_{9} = -106.176760093$$
$$x_{10} = -40.1767600931$$
$$x_{11} = -128.176760093$$
$$x_{12} = -114.176760093$$
$$x_{13} = -56.1767600931$$
$$x_{14} = -116.176760093$$
$$x_{15} = -98.1767600931$$
$$x_{16} = -120.176760093$$
$$x_{17} = -50.1767600931$$
$$x_{18} = -78.1767600931$$
$$x_{19} = -126.176760093$$
$$x_{20} = -124.176760093$$
$$x_{21} = -42.1767600931$$
$$x_{22} = -44.1767600931$$
$$x_{23} = -52.1767600931$$
$$x_{24} = -96.1767600931$$
$$x_{25} = -90.1767600931$$
$$x_{26} = -110.176760093$$
$$x_{27} = -104.176760093$$
$$x_{28} = -88.1767600931$$
$$x_{29} = -102.176760093$$
$$x_{30} = -130.176760093$$
$$x_{31} = -82.1767600931$$
$$x_{32} = -58.1767600931$$
$$x_{33} = -74.1767600931$$
$$x_{34} = -68.1767600931$$
$$x_{35} = -64.1767600931$$
$$x_{36} = -48.1767600931$$
$$x_{37} = -118.176760093$$
$$x_{38} = -86.1767600931$$
$$x_{39} = -112.176760093$$
$$x_{40} = -72.1767600931$$
$$x_{41} = -108.176760093$$
$$x_{42} = -46.1767600931$$
$$x_{43} = -94.1767600931$$
$$x_{44} = -70.1767600931$$
$$x_{45} = 0$$
$$x_{46} = -76.1767600931$$
$$x_{47} = -122.176760093$$
Зн. экстремумы в точках:
(-66.1767600931, 1)
(-100.176760093, 1)
(-84.1767600931, 1)
(-60.1767600931, 1)
(-80.1767600931, 1)
(-92.1767600931, 1)
(-62.1767600931, 1)
(-54.1767600931, 1)
(-106.176760093, 1)
(-40.1767600931, 0.999999999999195)
(-128.176760093, 1)
(-114.176760093, 1)
(-56.1767600931, 1)
(-116.176760093, 1)
(-98.1767600931, 1)
(-120.176760093, 1)
(-50.1767600931, 0.999999999999999)
(-78.1767600931, 1)
(-126.176760093, 1)
(-124.176760093, 1)
(-42.1767600931, 0.999999999999799)
(-44.1767600931, 0.99999999999995)
(-52.1767600931, 1)
(-96.1767600931, 1)
(-90.1767600931, 1)
(-110.176760093, 1)
(-104.176760093, 1)
(-88.1767600931, 1)
(-102.176760093, 1)
(-130.176760093, 1)
(-82.1767600931, 1)
(-58.1767600931, 1)
(-74.1767600931, 1)
(-68.1767600931, 1)
(-64.1767600931, 1)
(-48.1767600931, 0.999999999999997)
(-118.176760093, 1)
(-86.1767600931, 1)
(-112.176760093, 1)
(-72.1767600931, 1)
(-108.176760093, 1)
(-46.1767600931, 0.999999999999987)
(-94.1767600931, 1)
(-70.1767600931, 1)
(0, 0)
(-76.1767600931, 1)
(-122.176760093, 1)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{47} = 0$$
Максимумов у функции нет
Убывает на промежутках
[0, oo)
Возрастает на промежутках
(-oo, 0]
Mathway | Популярные задачи
Mathway | Популярные задачиПопулярные задачи
Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра ХимияДля функционирования Mathway необходим javascript и современный браузер.
Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:
- число
- буква
- специальный символ: @$#!%*?&
Видеолекция 3. Построение графика функции, содержащей модуль.
ВИДЕОЛЕКЦИИОНЛАЙН КУРСЫУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМФУНКЦИИ И ГРАФИКИ
Содержание Видеолекции «Построение графика функции, содержащей модуль»:
1. График функции y=|x|.
2. Построение графика функции y=|x+3|+|2x+1|-x с помощью раскрытия модуля.
3. Построение графика функции y=|x+3|+|2x+1|-x по четырем точкам.
4. Преобразование функции f(x) -> f(|x|)
5. Построение графика функции 
6. Преобразование функции f(x) -> |f(|x|)|
7. Построение графика функции 
8. Построение графика функции 
9. Построение графика неравенства |y-2x-1|+2|x|≤3.
10. Решение задачи с параметром:
При каких значениях параметра а неравенство |х-2а-1|+2|а|≤3 не имеет решений.
Посмотрите видеолекцию:
И.В. Фельдман, репетитор по математике.


Модуль в модуле. Графический метод
Распространенными примерами с модулями является уравнение типа модуль в модуле. Двойной модуль можно записать в виде формулы
||a*x-b|-c|=k*x+m.
Если k=0 то такое уравнение с модулем легче решать графическим методом. Классическое раскрытия модулей в таких ситуациях громоздкое и не дает желаемого эффекта (экономии времени) на контрольных и тестах. Графический метод позволяет за короткое время выполнить построение модульных функций и найти количество корней уравнения.
Алгоритм построения двойного, тройного модуля достаточно прост и из приведенных ниже примеров понравится многим. Для закрепления методики внизу приведены примеры для самостоятельного вычисления.
Пример 1. Решить уравнение модуль в модуле ||x-3|-5|=3.
Решение: Решим уравнение с модулями классическим методом и графически. Найдем ноль внутреннего модуля
x-3=0 x=3.
В точке x=3 уравнения с модулем разделяется на 2. Кроме того, ноль внутреннего модуля является точкой симметрии графика модулей и если правая сторона уравнения равна постоянной, то корни лежат на одинаковом расстоянии от этой точки. То есть можно решить одно уравнение из двух, а остальные корней вычислить из этого условия.
Раскроем внутренний модуль для x>3
|x-3-5|=3; |x-8|=3.
Полученное уравнение при раскрытии модуля делится на 2
Под модульная функция >0
x-8=3; x=3+8=11;
и для значений < 0 получим
-(x-8)=3; x=8-3=5.
Оба корня уравнения удовлетворяют условию x>3, то есть являются решениями.
Учитывая записано выше правило симметрии решений уравнения с модулями, можно не искать корни уравнения для x< 3, которое имеет вид
|-(x-3)-5|=3; |-x-2|=3,
а вычислить их.
Значение симметрично относительно x=3 для x=11 равно
x=3-(11-3)=6-11=-5.
По той же формуле находим второе решение
x=3-(5-3)=6-5=1.
Заданное уравнение модуля в модуле имеет 4 решения
x=-5; x=1; x=5; x=11.
Теперь найдем решения уравнения с модулями графическим методом. С внутреннего модуля |x-3| следует что график стандартной модуль функции является смещен по оси Ох вправо на 3.
Дальше — отнять 5 означает что график необходимо опустить на 5 клеток по оси Oy. Чтобы получить модуль полученной функции симметрично отражаем все что находится ниже оси Ox.
И напоследок выполняем построение прямой y=3, параллельной оси Ox. Лучше всего для вычислений уравнений с модулями графически использовать тетрадь в клеточку, поскольку в ней удобно строить графики.
Окончательный вид графика модулей имеет вид
Точки пересечения модуль функции и прямой y=3 и является искомыми решениями x=-5;x=1; x=5;x=11.
Преимущество графического метода над раскрытием модулей для простых уравнений очевидно. Однако графически неудобно искать корни когда правая сторона имеет вид k*x+m, то есть является прямой наклоненной к оси абсцисс под углом.
Здесь таких уравнений рассматривать не будем.
Пример 2. Сколько корней имеет уравнение ||2x-3|-2|=2?
Решение: Правая сторона равна постоянной, поэтому скорее найти решение можно графическим методом. Внутренний модуль обращается в нуль
|2x-3|=0 x=3/2=1,5
в точке x=1,5.
Значит в эту точку смещаем график функции y=|2x|. Для того, чтобы его построить подставьте несколько точек и проведите через них прямые. От полученной функции вычитаем 2 то есть график опускаем на двойку вниз и, чтобы получить модуль переносим отрицательные значения (y< 0) симметрично относительно оси Ox.
Далее остается построить правую сторону (прямую y=2) и подсчитать количество точек пересечения. График модуль функции и прямой приведен ниже
Видим, что заданное уравнение имеет три решения.
Пример 3. При каком значении параметра a уравнение с модулем |||x+1|-2|-5|=a имеет 5 решений?
Решение: Имеем уравнение с тремя вложенными модулями. Найдем ответ с графического анализа. Начнем, как всегда, из внутреннего модуля. Он обращается в нуль
|x+1|=0 x=-1
в точке x=-1.
Строим график модуль функции в этой точке
Далее график опускаем вниз на двойку и отрицательные значения (y< 0) симметрично переносим вверх. Получим график функции
y=||x+1|-2|
Повторно выполним смещение графика модуль функции вниз на 5 и симметрично переносим отрицательные значения функции. В результате получим левую сторону уравнения с модулями
y=|||x+1|-2|-5|.
Параметр а соответствует значению параллельной прямой, которая должна пересечь график модуль функции в 5 точках. Сначала проводим такую прямую, далее ищем точку пересечения ее с осью Oy.
Это прямая y=3, то есть искомый параметр равен a=3.
Методом раскрытия модулей данную задачу можно было решать целый урок, если не больше. Здесь все свелось к нескольким графикам.
Ответ: a=3.
Пример 4. Сколько решений имеет уравнение |||3x-3|-2|-7|=x+5 ?
Решение: Раскроем внутренний модуль уравнения
|3x-3|=0 <=> x=3/3=1.
Строим график функции y=|3x-3|. Для этого на одну клетки изменения x от н
% PDF-1.4 % 772 0 объект > endobj Xref 772 130 0000000016 00000 н. 0000004174 00000 п. 0000004343 00000 п. 0000004626 00000 н. 0000004704 00000 н. 0000027458 00000 п. 0000045368 00000 п. 0000066902 00000 п. 0000095409 00000 п. 0000115081 00000 н. 0000136829 00000 н. 0000137402 00000 н. 0000138182 00000 н. 0000138663 00000 н. 0000148081 00000 н. 0000148674 00000 н. 0000149070 00000 н. 0000149402 00000 н. 0000157774 00000 н. 0000158236 00000 н. 0000158602 00000 н. 0000180023 00000 н. 0000203045 00000 н. 0000203103 00000 п. 0000203314 00000 н. 0000203483 00000 н. 0000203635 00000 н. 0000203813 00000 н. 0000203962 00000 н. 0000204077 00000 н. 0000204301 00000 н. 0000204465 00000 н. 0000204653 00000 н. 0000204794 00000 н. 0000204919 00000 н. 0000205083 00000 н. 0000205222 00000 н. 0000205411 00000 н. 0000205583 00000 н. 0000205722 00000 н. 0000205839 00000 н. 0000206009 00000 н. 0000206148 00000 н. 0000206317 00000 н. 0000206505 00000 н. 0000206654 00000 н. 0000206803 00000 н. 0000207105 00000 н. 0000207264 00000 н. 0000207473 00000 н. 0000207745 00000 н. 0000207904 00000 н. 0000208153 00000 н. 0000208315 00000 н. 0000208482 00000 н. 0000208645 00000 н. 0000208833 00000 н. 0000208952 00000 н. 0000209119 00000 н. 0000209308 00000 н. 0000209489 00000 н. 0000209621 00000 н. 0000209771 00000 н. 0000209931 00000 н. 0000210113 00000 п. 0000210264 00000 н. 0000210427 00000 н. 0000210601 00000 п. 0000210770 00000 н. 0000210949 00000 п. 0000211131 00000 п. 0000211301 00000 п. 0000211455 00000 н. 0000211628 00000 н. 0000211799 00000 н. 0000212035 00000 н. 0000212204 00000 н. 0000212377 00000 н. 0000212565 00000 н. 0000212737 00000 н. 0000212878 00000 н. 0000213053 00000 н. 0000213233 00000 н. 0000213360 00000 н. 0000213481 00000 н. 0000213663 00000 н. 0000213819 00000 н. 0000213999 00000 н. 0000214313 00000 п. 0000214653 00000 п. 0000214822 00000 н. 0000214995 00000 н. 0000215183 00000 п. 0000215374 00000 н. 0000215505 00000 н. 0000215687 00000 н. 0000215828 00000 н. 0000216003 00000 н. 0000216183 00000 п. 0000216300 00000 н. 0000216455 00000 н. 0000216621 00000 н. 0000216756 00000 н. 0000216955 00000 н. 0000217161 00000 п. 0000217351 00000 н. 0000217551 00000 н. 0000217693 00000 п. 0000217879 00000 н. 0000218065 00000 н. 0000218251 00000 н. 0000218379 00000 н. 0000218521 00000 н. 0000218653 00000 н. 0000218774 00000 п. 0000218897 00000 н. 0000219039 00000 н. 0000219172 00000 н. 0000219295 00000 н. 0000219460 00000 н. 0000219653 00000 п. 0000219830 00000 н. 0000220013 00000 н. 0000220181 00000 п. 0000220355 00000 н. 0000220477 00000 н. 0000220639 00000 н. 0000220783 00000 н. 0000220963 00000 н. 0000002896 00000 н. прицеп ] / Назад 5858002 >
Mathway | Популярные задачи
Mathway | Популярные проблемыMathway требует javascript и современного браузера.
Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство работы с ним.
Убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждое из следующих значений:
- номер
- письмо
- специальный символ: @ $ #!% *? &
Nand iMX6ull SOM imx6ulSOC Плата разработки i.MX6UL основная плата промышленный компьютер шлюз IOT Двойной Ethernet встроенный Linux | |
Описание пакета
Bundle_1: основной модуль CM6Y2 Dh2
(Спецификация: MCIMX6Y2DVM05, 256 МБ DDR3 / 256 МБ Nand, 100 Мбит / с PHY, 0 ° C ~ + 70 ° C)
Bundle_2: основной модуль CM6Y2 Ch2
(Спецификация: MCIMX6Y2CVM05, 256 МБ DDR3 / 256 МБ Nand, 100 Мбит / с PHY, -40 ° C ~ + 85 ° C)
Обзор
I.MX 6ULL - это семейство энергоэффективных и оптимизированных по стоимости процессоров для приложений, в которых используется усовершенствованная реализация одного ядра Arm Cortex-A7, работающего на частоте до 900 МГц. Процессор приложений i.MX 6ULL включает в себя интегрированный модуль управления питанием, который упрощает внешний источник питания и упрощает последовательность питания. Каждый процессор в этом семействе предоставляет различные интерфейсы памяти, включая 16-битный LPDDR2, DDR3, DDR3L, необработанную и управляемую флэш-память NAND, флэш-память NOR, eMMC, Quad SPI и широкий спектр других интерфейсов для подключения периферийных устройств, таких как WLAN, Bluetooth®, GPS, дисплеи и датчики камеры.

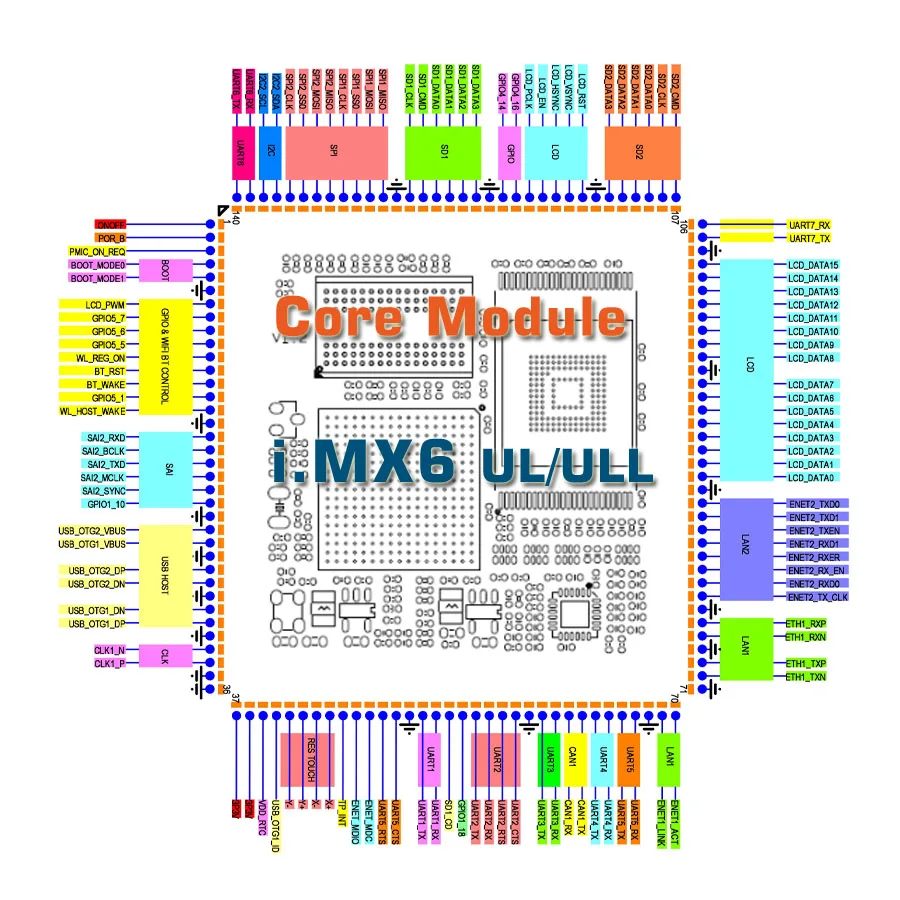
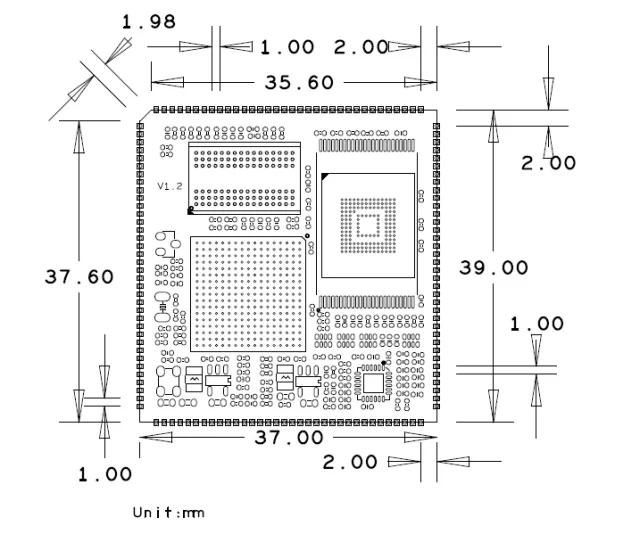
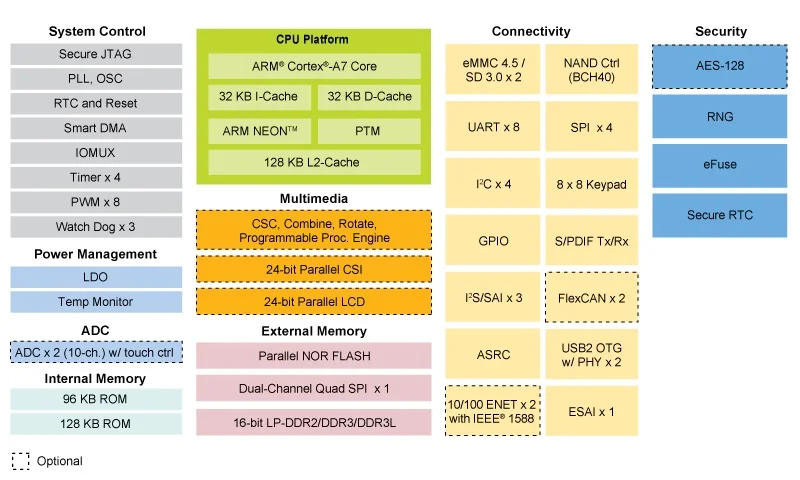
Дополнительные платы несущей, пожалуйста, свяжитесь с нами.

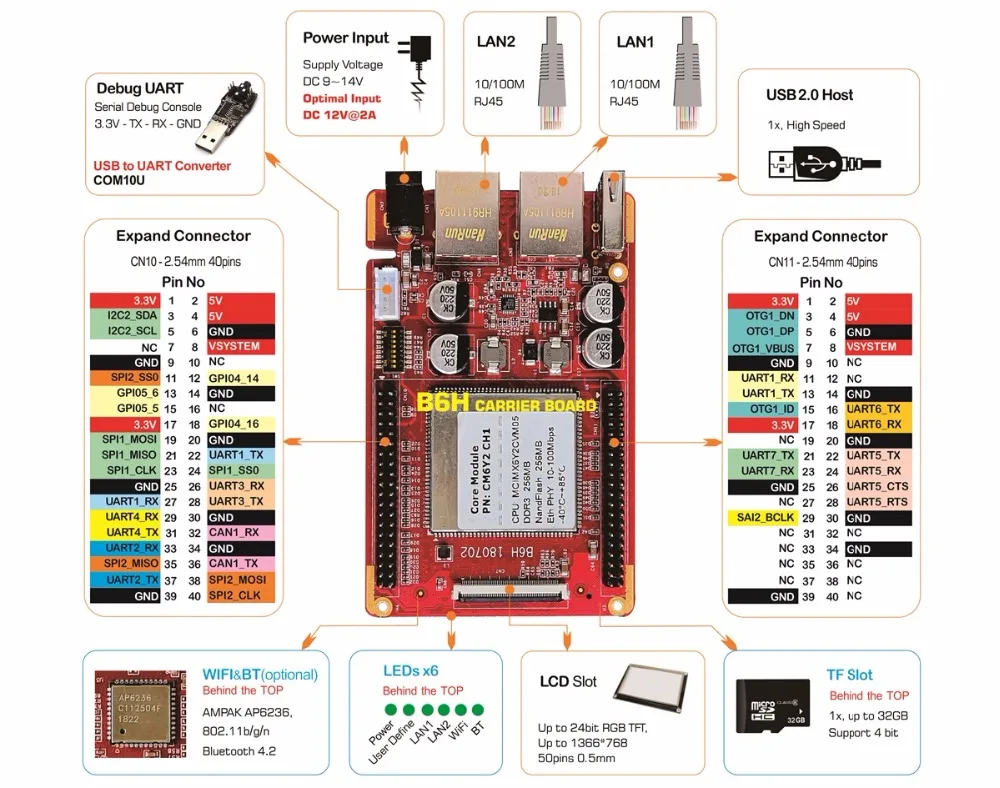 ,
,
Leave A Comment