В ведре находится смесь воды со льдом массой m=10 кг. Ведро внесли в комнату
Условие задачи:
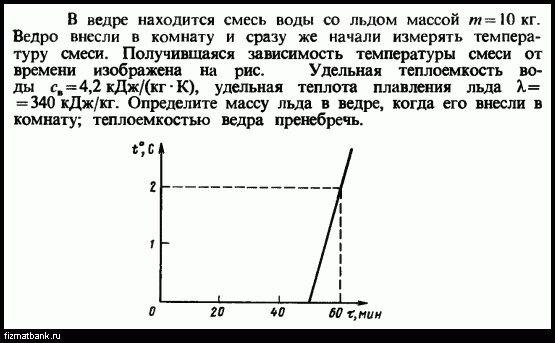
В ведре находится смесь воды со льдом массой \(m=10\) кг. Ведро внесли в комнату и сразу же начали измерять температуру смеси. Получившаяся зависимость температуры смеси от времени изображена на рисунке. Определить массу льда в ведре в момент внесения его в комнату.
Задача №5.2.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=10\) кг, \(\Delta m-?\)
Решение задачи:
Время плавления льда в смеси \(\tau_1\) равно 50 мин, время нагревания воды \(\tau_2\) равно 10 мин, температура \(t_1\) равна 0 °C, температура \(t_2\) равна 2 °C (смотрите схему).
Чтобы расплавить лёд массой \(\Delta m\), содержащийся в смеси, нужно количество теплоты \(Q_1\), которое можно определить по формуле:
\[{Q_1} = \lambda \Delta m\;\;\;\;(1)\]
Удельная теплота плавления льда \(\lambda\) равна 330 кДж/кг.
Для нагревания воды массой \(m\) (после расплавления льда) от температуры \(t_1\) до температуры \(t_2\) необходимо количество теплоты \(Q_2\), определяемое по формуле:
\[{Q_2} = cm\left( {{t_2} – {t_1}} \right)\;\;\;\;(2)\]
Удельная теплоёмкость воды \(c\) равна 4200 Дж/(кг·°C).
Вообще, смесь воды со льдом будет нагреваться, поскольку будет происходить теплообмен с воздухом комнаты. При этом нет причин полагать, что подводимая тепловая мощность \(N\) (от воздуха комнаты) меняется со временем. Так как количество теплоты равно произведению тепловой мощности на время, то можно получить такую систему:
\[\left\{ \begin{gathered}
{Q_1} = N{\tau _1} \hfill \\
{Q_2} = N{\tau _2} \hfill \\
\end{gathered} \right.\]
Учитывая формулы (1) и (2), система примет вид:
\[\left\{ \begin{gathered}
N{\tau _1} = cm\left( {{t_2} – {t_1}} \right) \hfill \\
N{\tau _2} = \lambda \Delta m \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда:
\[\frac{{\lambda \Delta m}}{{cm\left( {{t_2} – {t_1}} \right)}} = \frac{{{\tau _2}}}{{{\tau _1}}}\]
\[\Delta m = \frac{{cm\left( {{t_2} – {t_1}} \right){\tau _2}}}{{\lambda {\tau _1}}}\]
Переведём время \(\tau_1\) и \(\tau_2\) в систему СИ:
\[50\;мин = 3000\;с\]
\[10\;мин = 600\;с\]
Произведём вычисления:
\[\Delta m = \frac{{4200 \cdot 10 \cdot \left( {2 – 0} \right) \cdot 3000}}{{330 \cdot {{10}^3} \cdot 600}} = 1,27\;кг\]
Ответ: 1,27 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Что такое олимпиада по физике?
Интернет-олимпиада 2011-2012 уч. года
1-й этап
Физика, 8 класс
Дорогие ребята!
Уважаемые учителя!
Мы начинаем публикацию материалов, которые, надеемся, помогут школьникам, увлеченным физикой, попробовать себя в решении сложных, олимпиадных задач.
Что такое олимпиада по физике?
Это интеллектуальное соревнование! А значит, кроме прочных знаний по физике (и математике, конечно), требуется сообразительность и характер. Для чего нужны знания и сообразительность, наверное, каждому понятно. А вот зачем характер? Олимпиадную задачу быстро не решить. Приходится долго работать. Непривычно долго. Чем выше уровень олимпиады, тем тяжелее задачки. На одну задачу в среднем уходит один час! Для того чтобы не бросить все, нужно иметь характер…
Олимпиадное задание, как правило, составляется по всем изученным к этому моменту темам. Если речь идет об олимпиаде в 8 классе, то тогда сюда входит и изученное в 7 классе тоже (движение, плотность, силы, давление, простые механизмы, работа и энергия) и текущий материал (тепловые явления).
Здесь представлены задачи по темам «Тепловые явления», «Силы», «Правило моментов». Одни задачи полегче, другие – потяжелее. Многие задачи взяты из регионального этапа Всероссийской олимпиады школьников по физике. Отдельно приведены их решения. Сначала решения приведены очень подробные, в конце – достаточно конспективные, где для того, чтобы разобраться в решении, требуется поработать самому. Это сделано намеренно.
И, наконец, через некоторое время
вам, ребята, будет предложено олимпиадное
задание для самостоятельного решения.
Все ваши решения, присланные нам, будут проверены и оценены, а результаты (и решения) будут также размещены на этом сайте.
Можно решение набирать в любом текстовом редакторе, но можно и написать от руки, отсканировать, и послать в формате pdf, например. Главное, — чтобы ваша работа была читаемая!
Ну вот, вроде о главном и сказали. Если будут какие-то вопросы, задавайте, а мы постараемся на них ответить.
Ильин Александр Борисович,
преподаватель физики ЮФМЛИ,
ответственный за публикацию материалов по физике для учащихся 8 класса
Литература.
Всероссийские олимпиады по физике.1992-2001:Под ред. С.М.Козела, В.П.Слободянина. – М.: «Вербум-М», 2002. –392 с.
Всероссийские олимпиады по физике./Под ред. С.М.Козела. – М.: ЦентрКом, 1997. –240 с., илл.
Кабардин О.Ф. и др. Физика. Задачник. 9-11 кл.: Пособие для общеобразоват. учеб. заведений/ О.Ф.Кабардин, В.А.Орлов, А.Р.Зильберман. – М.: Дрофа, 1997. – 352 с.: илл.
Слободецкий И.Ш., Орлов. В.А. Всесоюзные олимпиады по физике: Пособие для учащихся 8-10 кл. сред. школы. – М.: Просвещение, 1982. – 256 с., илл.
Задачи московских физических олимпиад/ Под ред. С.С. Кротова. – М.: Наука. Гл. ред. Физ.-мат. лит., 1988. – 192 с. –(Б-чка «Квант». Вып. 60.)
Кабардин О.Ф., Орлов. В.А. Экспериментальные задания по физике. 9–11 классы: учебное пособие для учащихся общеобразовательных учреждений. – М.: Вербум-М, 2001. – 208 с.
Лукашик В.И. Сборник задач по физике. 7-9 кл.: Учеб. пособие для общеобразоват. учреждений/ В.
 И.Лукашик, Е.В.Иванова.
– М.: ООО «Издательский дом ОНИКС 21
век»: ООО «Издательство «Мир и
образование», 2003. – 288с: илл.
И.Лукашик, Е.В.Иванова.
– М.: ООО «Издательский дом ОНИКС 21
век»: ООО «Издательство «Мир и
образование», 2003. – 288с: илл.Задачник «Кванта»: Физика. Часть 1/ Под ред. А.Р. Зильбермана и А.И. Черноуцана. – М.: Бюро Квантум, 1997. – 128 с. (Прил. к журналу «Квант» №2/97)
Задачник «Кванта»: Физика. Часть 2/ Под ред. А.Р. Зильбермана и А.И. Черноуцана. – М.: Бюро Квантум, 1997. – 128 с. (Прил. к журналу «Квант» №4/97)
Задачник «Кванта»: Физика. Часть 3/ Под ред. А.Р. Зильбермана и А.И. Черноуцана. – М.: Бюро Квантум, 1997. – 128 с. (Прил. к журналу «Квант» №6/97)
Журнал «Квант».
Журнал «Физика в школе».
Гельфгат И.М., Гендельштейн Л.Э., Кирик Л.А. 1001 задача по физике с ответами, указаниями, решениями. – 5-е изд. – М.: «Илекса», 2001. – 352 с.
Шаскольская М.П., Эльцин И.А., Сборник избранных задач по физике. 3-е изд., стереотипное. – М.: Наука. Гл. ред. физ.-мат. лит., 1969. – 224 с.
Тренировочные задачи.
Тепловые явления. (8 кл.)
Если у воды, находящейся в калориметре, отнять 42 кДж теплоты, то ее температура понизится на 10°С. Если после этого еще раз отнять 42 кДж теплоты, то температура понизится только на 5°С. Найдите массу и начальную температуру воды.
Космонавт в скафандре выходит в отсек орбитальной станции, держа в руках сосуд с водой, масса которой равна m. Давление воздуха внутри отсека станции равно 0,01 Па, а температура равна 0°С. Какова будет масса образовавшегося льда? Удельная теплота парообразования воды при 0°С равна

В термос с водой, имеющей температуру t=40°С, опускают бутылочку с детским питанием. Там бутылочка нагревается до температуры t1=36°С, затем ее вынимают и в термос опускают другую точно такую же бутылочку. До какой температуры она нагреется? Перед погружением в термос обе бутылочки имели температуру t0=18°С.
В дне теплоизолированного сосуда (калориметра) имеется небольшое отверстие, через которое может вытекать вода. В сосуд поместили смесь воды и льда при температуре 0°C вместе с электрическим нагревателем мощностью P=600 Вт, и начали следить за изменением температуры содержимого калориметра в зависимости от времени. Экспериментальный график зависимости температуры t от времени τ представлен на рисунке.
Определите массу воды, оставшейся в калориметре к моменту окончания таяния льда.
Какая средняя масса воды вытекала из отверстия калориметра в течение 1 мин?
Сколько льда было в калориметре в начале эксперимента?
П
ринять
L=2260 кДж/кг; с=4,2 кДж/(кг·°C),
λ=340 кДж/кг.
Движение и силы. (7 кл.)
Динамометр показывает, что мраморный шарик, подвешенный к нему на тонкой нити, весит 1,62 Н. А если шарик погрузить в воду, то динамометр покажет 1,32 Н. Какова плотность мрамора? Плотность воды принять равной 1000кг/м3.
Из двух полушарий, сделанных из разных материалов, склеили шар. Массы половинок отличаются в два раза. Шар плавает в воде, погрузившись ровно наполовину. Найти плотность материала тяжелой половинки.
Стальной шарик плавает в ртути.
 Как
изменится объем погруженной в ртуть
части шарика, если сверху долить воды,
скрыв полностью весь шарик? Плотность
ртути 13600 кг/м3, стали –
7800 кг/м3, воды – 1000 кг/м3.
Как
изменится объем погруженной в ртуть
части шарика, если сверху долить воды,
скрыв полностью весь шарик? Плотность
ртути 13600 кг/м3, стали –
7800 кг/м3, воды – 1000 кг/м3.
Правило моментов. (7 кл.)
С
истема, состоящая из двух однородных стержней, трех невесомых нитей и блока, находится в равновесии. Трение в оси блока отсутствует. Все нити вертикальны. Масса верхнего стержня m1=0,5 кг. Найдите массу m2 нижнего стержня.Провода над железной дорогой, питающие то
ком электропоезда, натягиваются с помощью системы, показанной на рисунке. Она крепится к столбу и состоит из тросов, блоков с изоляторами и стального груза квадратного сечения со стороной a=20 см. Сила натяжения толстого троса, который идет от крайнего блока к держателю проводов, равна T=8 кН. Какова высота h стального груза? Плотность стали равна с=7800 кг/м3.Ко дну сосуда при помощи шарнира прикреплена за конец тонкая однородная палочка длиной L. В сосуд медленно наливают воду и отмечают, какая часть длины палочки
Решения тренировочных задач
Тепловые явления.
Задача №1.
Решение:
Во втором
опыте, отнимая то же самое количество
теплоты, получили иной результат.
Это означает, что вода отдала 21 кДж,
не изменяя своей температуры. Такое
возможно при изменении агрегатного
состояния вещества – в данном случае,
— кристаллизации воды в лед. Температура
плавления льда равна 0°C,
следовательно, начальная температура
воды 15°C. Для
охлаждения воды в первом опыте применим
известную формулу
,
где c – удельная
теплоемкость воды, равная 4200 Дж/(кг·°C).
Отсюда найдем массу воды:
.
Такое
возможно при изменении агрегатного
состояния вещества – в данном случае,
— кристаллизации воды в лед. Температура
плавления льда равна 0°C,
следовательно, начальная температура
воды 15°C. Для
охлаждения воды в первом опыте применим
известную формулу
,
где c – удельная
теплоемкость воды, равная 4200 Дж/(кг·°C).
Отсюда найдем массу воды:
.
Ответ: t0=15°C, m=1 кг.
Задача №2.
Решение:
Испарение жидкости идет при любой температуре. Очень низкое давление воздуха приведет к тому, что вылетающие из жидкости молекулы не будут возвращаться обратно – испарение будет происходить очень быстро. При испарении жидкость охлаждается. Но вода находится при температуре кристаллизации! Поэтому будет происходить не охлаждение, а кристаллизация воды. Запишем уравнение теплового баланса: .
Учтем, что .
Отсюда, решая систему уравнений, получим ответ: .
Ответ: .
Задача №3.
Решение:
Термос исключает теплообмен с окружающей средой, поэтому можно считать, что количество теплоты, отданное водой, равно количеству теплоты, полученному детским питанием. Запишем уравнение теплового баланса для каждого случая:
Здесь t2 — температура воды и детского питания
после установления теплового
равновесия во втором опыте, а с1, m1, с2, m2 –
соответственно удельная теплоемкость
и масса воды, находящейся в термосе и
удельная теплоемкость и масса детского
питания. Поделим второе уравнение на
первое. теплоемкости и массы сократятся,
останется одно уравнение с одной
неизвестной
. Решая его, получим
Решая его, получим
.
Ответ:
Задача №4.
Решение:
При плавлении кристаллических тел их температура не меняется. По графику видим, что плавление льда происходило в течение 5 минут. Отверстие в дне, а лед в воде плавает – он наверху, поэтому лед в отверстие не уходит. Все подведенное тепло идет на плавление льда, поэтому
Pτ1=λmл
Отсюда получим массу льда:
Теплообмена с окружающей средой нет, но вода в сосуде с 5-ой по 12-ю минуту нагревается все быстрее и быстрее. Как это можно объяснить? Тем, что вода вытекает, масса воды в сосуде уменьшается, а мощность нагревателя остается прежней! Если бы вода не вытекала, этот участок графика был бы прямолинейным. Проведем касательные к этому участку графика в начале и в конце.
По ним мы сможем рассчитать массу воды в сосуде в эти моменты времени. Поделив разницу найденных масс на время, в течение которого температура воды в калориметре изменялась, найдем расход жидкости.
П
ри
кипении идет интенсивный процесс
парообразования, а значит, масса воды
в калориметре уменьшается двумя путями
– вытекая через отверстие и превращаясь
в пар.
Вода в калориметре закончится еще до окончания эксперимента!
Ответ: a) ; b) ; c) mл=0,529 кг; d) m=0
Движение и силы. (7 кл.)
Задача №1
Решение:
В воздухе вес шарика
.
В воде вес шарика меньше на величину
силы Архимеда:
.
Сила Архимеда рассчитывается по формуле
.
Теперь легко найти плотность шарика –
для этого из первой формулы выразим его
массу, а из первых трех – его объем:
,
. Поделим массу на объем и получим плотность
шарика:
.
Поделим массу на объем и получим плотность
шарика:
.
Ответ: .
Задача №2.
Решение:
Обозначим массу легкой половинки , тогда масса тяжелой половинки . Шар плавает на поверхности воды – это значит, что сила тяжести, действующая на шар, уравновешивается силой Архимеда. Обозначим объем всего шара . Тогда .
Упрощая и преобразуя последнее уравнение, получим: , а значит
Ответ:
Задача №3.
Решение:
Поскольку шарик плавает, то сила тяжести уравновешивается силой Архимеда. В первом случае это можно записать так: . Во втором случае . Сократим каждое уравнение на и учтем, что .
Выразим, какая часть объема шарика была погружена в ртуть в каждом случае: и .
Таким образом, изменение объема погруженной в ртуть части шарика составляет всего объема шарика, или 3%.
Ответ: уменьшится на 3%.
Правило моментов. (7 кл.)
Задача №1.
Решение:
На верхний рычаг действуют четыре силы: слева – сила натяжения нити T1, справа – сила натяжения нити T2, в центре – сила тяжести m1g и – сила натяжения нити T3. Относительно оси вращения, находящейся в центре верхнего рычага, получаем, что плечи сил T1 иT2 одинаковы и равны L, а силы тяжести m1g и силы натяжения нити T3 равны нулю. Правило моментов в этом случае запишется так: . Отсюда получаем, что обе нити – и левая, и правая натянуты одинаково:
Такое же рассуждение про нижний рычаг
дает аналогичный вывод:
.
То есть все нити натянуты одинаково! Для простоты, обозначим эту силу T.
Для верхнего рычага сумма сил, действующих вертикально вверх уравновешивается суммой сил, действующих вертикально вниз: . Отсюда находим силу натяжения нити: .
То же самое для нижнего рычага дает . Значит .
Ответ: .
Задача №2.
Решение:
Подвижный блок дает двукратный выигрыш в силе. Если обозначить T1 первого троса, то тогда . Также со следующим блоком: и с последним блоком: .
На груз действует сила тяжести и сила натяжения третьего троса. Эти силы уравновешиваются, значит и .
Используя формулу плотности, найдем объем, а затем и высоту груза: .
.
Ответ: .
Задача №3.
Решение:
Слово «тонкая» означает, что не будь палочка прикреплена шарниром за один конец ко дну сосуда, то она при очень небольшом уровне воды в сосуде начала бы всплывать. Рассмотри эту ситуацию подробнее.
График показывает, что до какого-то уровня воды в сосуде длина погруженной в воду части палочки остается неизменной и равной .
При повышении уровня воды растет угол отклонения палочки от вертикали, и, когда она принимает вертикальное положение, длина погруженной в воду части палочки начинает расти.
Поэтому излом графика соответствует вертикальному положению палочки в воде. Запишем правило моментов относительно оси вращения, проходящей через шарнир в один из моментов времени, когда палочка находится еще в наклонном положении:
Если из точек приложения сил Архимеда
и тяжести опустить перпендикуляры на
горизонтальную линию, проходящую через
шарнир, мы получим два подобных
треугольника. В одном и катетом и гипотенузой прямоугольного
треугольника, в другом — и также катетом и гипотенузой. Сами
треугольники имеют общий угол – а
значит, подобны по двум углам.
В одном и катетом и гипотенузой прямоугольного
треугольника, в другом — и также катетом и гипотенузой. Сами
треугольники имеют общий угол – а
значит, подобны по двум углам.
Из подобия получаем: . Сократив на длину палочки L, получим
Выразим силу Архимеда через плотность воды и объем погруженной части палочки, силу тяжести – через плотность палочки и объем всей палочки и подставим в правило моментов, написанное выше: После упрощения получаем:
Ответ: .
Задачи интернет-олимпиады по физике за 8 класс 2010-2011 учебного годы (I тур)
Блиц-олимпиада.
Уважаемые восьмиклассники!
Вам предлагается решить несколько задач, где требуется проявить хорошее знание материала и сообразительность. Мы постарались подобрать не очень сложные задачи (но и не совсем уж простые!!), поэтому засчитываться они будут по ответу. В конце каждой задачи приведены варианты ответа. Только один из них является правильным. Решение присылать для этих задач не нужно, только назвать правильный ответ!
Задача №1.
На графике приведена зависимость температуры тела от количества теплоты, полученной телом для двух образцов массы 1 кг каждый. Определите по графику, во сколько раз отличаются удельные теплоемкости этих тел, когда они находятся в жидком состоянии.
Варианты ответа:
Задача №2.
В калориметр с водой, температура которой t0, бросили кусочек
льда, имевшего температуру 0°C.
После установления теплового равновесия
оказалось, что четверть льда не растаяло.
Считая известными массу воды M,
ее удельную теплоемкость c,
удельную теплоту плавления льда λ,
найдите начальную массу кусочка льда m.
Варианты ответа:
Задача №3.
Экспериментатор Глюк наблюдал за встречным движением скорого поезда и электрички. Оказалось, что каждый из поездов прошел мимо Глюка за одно и то же время t1=23 с. А в это время друг Глюка, теоретик Баг, ехал в электричке и определил, что скорый поезд прошел мимо него за t2=13 с. Во сколько раз отличаются длины поезда и электрички?
Варианты ответа:
А) скорый поезд короче ≈ в 1,77 раз | Б) они равны по длине | В) скорый поезд длиннее ≈ в 1,77 раз | Г) скорый поезд длиннее ≈ в 1,57 раза | Д) скорый поезд длиннее в 1,3 раза |
Задача №4.
Прямоугольная льдина длиной 5 м и шириной 2 м плавает в море. Высота льдины, выступающей над поверхностью воды, равна 1 м. Определите объем всей льдины. Плотность воды принять равной 1000 кг/м3, льда 900 кг/м3.
Варианты ответа:
А) 8 м3 | Б) 10 м3 | В) 90 м3 | Г) 100 м3 | Д) 108 м3 |
Задача №5.
В то утро
попугай Кешка, как обычно, собирался
сделать доклад о пользе банановодства
и бананоедства. Позавтракав 5 бананами,
он взял мегафон и полез на «трибуну» —
на верхушку пальмы высотой 20 м. На
полпути он почувствовал, что с мегафоном
ему не добраться до вершины. Тогда он
оставил мегафон и полез дальше без него.
Сумеет ли Кешка сделать доклад, если
для доклада нужен запас энергии в 200 Дж,
один съеденный банан позволяет совершить
работу в 200 Дж, масса попугая 3 кг,
масса мегафона 1 кг?
На
полпути он почувствовал, что с мегафоном
ему не добраться до вершины. Тогда он
оставил мегафон и полез дальше без него.
Сумеет ли Кешка сделать доклад, если
для доклада нужен запас энергии в 200 Дж,
один съеденный банан позволяет совершить
работу в 200 Дж, масса попугая 3 кг,
масса мегафона 1 кг?
Варианты ответа:
А) нет, ему не хватит энергии долезть до верхушки пальмы. | Б) нет, он залезет на верхушку пальмы, но не хватит энергии на доклад. | В) да, но в конце доклада он полностью потратит всю энергию | Г) да, и в конце доклада у него даже останется запас энергии | Д) да, он даже мог и не оставлять мегафон на полпути |
Олимпиадное задание №1. (8 кл.)
В калориметр с водой, температура которой t0, бросили кусочек льда, имевшего температуру 0°C. После установления теплового равновесия оказалось, что четверть льда не растаяло. Считая известными массу воды M, ее удельную теплоемкость c, удельную теплоту плавления льда λ, найдите начальную массу кусочка льда m.
В
ведре находится смесь воды со льдом общей массой M=10 кг. Ведро внесли в комнату и сразу же начали измерять температуру смеси. Получившаяся зависимость температуры от времени изображена на рисунке. Удельная теплоемкость воды с=4200 Дж/(кг·°С). Удельная теплота плавления льда λ=340000 Дж/кг. Определите массу льда в ведре, когда его внесли в комнату. Теплоемкостью ведра пренебречь.
Два малыша – Петя и Вася – решили устроить гонки на движущемся вниз эскалаторе. Начав одновременно, они побежали из одной точки, расположенной точно посередине эскалатора, в разные стороны: Петя – вниз, а Вася – вверх по эскалатору. Время, затраченное на дистанцию Васей, оказалось в 3 раза больше Петиного. С какой скоростью движется эскалатор, если друзья на последних соревнованиях показали одинаковый результат, пробежав такую же дистанцию со скоростью 2,1 м/с?
Колба из стекла плотностью 2,5 г/см3 вместимостью 1,5 л имеет массу 250 г. Груз какой массы надо поместить в колбу, чтобы она утонула в воде? Плотность воды 1 г/см3.
Н
евесомый рычаг AC установлен на упоре так, что BC в 2 раза больше AB. К рычагу с помощью ниток прикреплены невесомый блок и массивное неоднородное тело. Слева к блоку подвешивают груз так, что система находится в равновесии. Найти отношение массы груза к массе тела.
Решение задач «Блиц-олимпиады».
Задача №1.
На графике приведена зависимость температуры тела от количества теплоты, полученной телом для двух образцов массы 1 кг каждый. Определите по графику, во сколько раз отличаются удельные теплоемкости этих тел, когда они находятся в жидком состоянии.
Варианты ответа:
Решение:
На каждом графике есть два горизонтальных участка, когда тепло подводится к телу. а его температура не изменяется. эти участки соответствуют изменению агрегатного состояния вещества: первый (при более низкой температуре) – плавлению, второй – кипению. Наклонный участок между ними соответствует нагреванию жидкости.
Обозначим единичный отрезок по оси
количества теплоты Q0,
по оси температур – t0. Тогда, учитывая, что массы тел одинаковы,
можем записать:
Тогда, учитывая, что массы тел одинаковы,
можем записать:
Поделим первое уравнение на второе и получим, что правильный ответ В)
Ответ: В).
Задача №2.
В калориметр с водой, температура которой t0, бросили кусочек льда, имевшего температуру 0°C. После установления теплового равновесия оказалось, что четверть льда не растаяло. Считая известными массу воды M, ее удельную теплоемкость c, удельную теплоту плавления льда λ, найдите начальную массу кусочка льда m.
Варианты ответа:
Решение:
Поскольку не весь лед растаял, то после установления теплового равновесия в калориметре находится и вода и лед. Это возможно только при температуре плавления льда. Значит, конечная температура системы равна 0°C.
Четверть льда не растаяло, значит растаяло (расплавилось) три четверти льда.
Теплоту, необходимую для плавления, лед получил от воды, охладившейся до нуля градусов Цельсия. Запишем уравнение теплового баланса:
. Отсюда получим ответ Б) .
Ответ: Б).
Задача №3.
Экспериментатор Глюк наблюдал за встречным движением скорого поезда и электрички. Оказалось, что каждый из поездов прошел мимо Глюка за одно и то же время t1=23 с. А в это время друг Глюка, теоретик Баг, ехал в электричке и определил, что скорый поезд прошел мимо него за t2=13 с. Во сколько раз отличаются длины поезда и электрички?
Варианты ответа:
А) скорый поезд короче ≈ в 1,77 раз | Б) они равны по длине | В) скорый поезд длиннее ≈ в 1,77 раз | Г) скорый поезд длиннее ≈ в 1,57 раза | Д) скорый поезд длиннее в 1,3 раза |
Решение:
Пусть скорость скорого поезда будем
обозначать как v1,
а его длину – L1. Для электрички соответственно скорость v2, ее длина
– L2. Тогда:
Для электрички соответственно скорость v2, ее длина
– L2. Тогда:
Скорость сближения поезда и электрички равна сумме их скоростей. Поэтому:
.
Выразим из первого уравнения скорость поезда, из второго – скорость электрички и подставим в третье. Решая полученное уравнение, найдем отношение длин поезда и электрички:
.
Ответ: Д).
Задача №4.
Прямоугольная льдина длиной 5 м и шириной 2 м плавает в море. Высота льдины, выступающей над поверхностью воды, равна 1 м. Определите объем всей льдины. Плотность воды принять равной 1000 кг/м3, льда 900 кг/м3.
Варианты ответа:
А) 8 м3 | Б) 10 м3 | В) 90 м3 | Г) 100 м3 | Д) 108 м3 |
Решение:
Льдина плавает, это означает, что сила тяжести уравновешена силой Архимеда, действующей на погруженную в воду часть льдины. Обозначим весь объем льдины V, объем надводной части V1. Тогда объем погруженной части льдины равен V — V1 и
Сократив на g и преобразовав полученное равенство, найдем полный объем льдины:
Ответ: Г).
Задача №5.
В то утро попугай Кешка, как обычно, собирался сделать доклад о пользе банановодства и бананоедства. Позавтракав 5 бананами, он взял мегафон и полез на «трибуну» — на верхушку пальмы высотой 20 м. На полпути он почувствовал, что с мегафоном ему не добраться до вершины. Тогда он оставил мегафон и полез дальше без него. Сумеет ли Кешка сделать доклад, если для доклада нужен запас энергии в 200 Дж, один съеденный банан позволяет совершить работу в 200 Дж, масса попугая 3 кг, масса мегафона 1 кг?
Варианты ответа:
А) нет, ему не хватит энергии долезть до верхушки пальмы. | Б) нет, он залезет на верхушку пальмы, но не хватит энергии на доклад. | В) да, но в конце доклада он полностью потратит всю энергию | Г) да, и в конце доклада у него даже останется запас энергии | Д) да, он даже мог и не оставлять мегафон на полпути |
Решение:
Запас энергии, который дают пять съеденных бананов, равен .
Для того, чтобы попугаю Кешке забраться на пальму с мегафоном, потребовалось бы энергии.
После этого у него оставалось 200 Дж энергии на то, чтобы сделать доклад.
Варианты А) – В) неверные, Г) похож на правильный ответ, Д) – правильный ответ.
Ответ: Д).
Решение задач олимпиадного задания №1. (8 кл.)
В калориметр с водой, температура которой t0, бросили кусочек льда, имевшего температуру 0°C. После установления теплового равновесия оказалось, что четверть льда не растаяло.
 Считая известными
массу воды M, ее удельную
теплоемкость c, удельную теплоту
плавления льда λ, найдите
начальную массу кусочка льда m.
Считая известными
массу воды M, ее удельную
теплоемкость c, удельную теплоту
плавления льда λ, найдите
начальную массу кусочка льда m.
Решение:
Поскольку не весь лед растаял, то после установления теплового равновесия в калориметре находится и вода и лед. Это возможно только при температуре плавления льда. Значит, конечная температура системы равна 0°C.
Четверть льда не растаяло, значит, растаяло (расплавилось) три четверти льда.
Теплоту, необходимую для плавления, лед получил от воды, охладившейся до нуля градусов Цельсия. Запишем уравнение теплового баланса:
. Отсюда получим ответ .
Ответ:
В
ведре находится смесь воды со льдом общей массой M=10 кг. Ведро внесли в комнату и сразу же начали измерять температуру смеси. Получившаяся зависимость температуры от времени изображена на рисунке. Удельная теплоемкость воды с=4200 Дж/(кг·°С). Удельная теплота плавления льда λ=340000 Дж/кг. Определите массу льда в ведре, когда его внесли в комнату. Теплоемкостью ведра пренебречь.
Решение:
Температура смеси начала меняться, когда весь лед растаял и в ведре оказалась одна вода. За 10 минут (с 50-й по 60-ю) температура воды увеличилась на 2°C. Qв=cMΔt°.
Лед плавился 50 минут (с 0-й по 50-ю), а значит и тепла получил в 5 раз больше: Qл=5Qв.
Найдем массу льда, первоначально находившегося в ведре: .
Ответ: m=1,2 кг.
Два малыша – Петя и Вася – решили устроить гонки на движущемся вниз эскалаторе.
 Начав одновременно, они
побежали из одной точки, расположенной
точно посередине эскалатора, в разные
стороны: Петя – вниз, а Вася – вверх по
эскалатору. Время, затраченное на
дистанцию Васей, оказалось в 3 раза
больше Петиного. С какой скоростью
движется эскалатор, если друзья на
последних соревнованиях показали
одинаковый результат, пробежав такую
же дистанцию со скоростью 2,1 м/с?
Начав одновременно, они
побежали из одной точки, расположенной
точно посередине эскалатора, в разные
стороны: Петя – вниз, а Вася – вверх по
эскалатору. Время, затраченное на
дистанцию Васей, оказалось в 3 раза
больше Петиного. С какой скоростью
движется эскалатор, если друзья на
последних соревнованиях показали
одинаковый результат, пробежав такую
же дистанцию со скоростью 2,1 м/с?
Решение:
Петя и Вася пробежали равные пути, но за разное время. Из формулы скорости следует, что раз Петино время в 3 раза меньше, то его скорость в 3 раза больше Васиной.
Вася бежит вниз, эскалатор тоже движется вниз, поэтому его скорость относительно земли равна сумме этих скоростей:
Петя бежит вверх, а эскалатор движется вниз, поэтому его скорость равна разности этих скоростей:
Отсюда
Ответ: .
Колба из стекла плотностью 2,5 г/см3 вместимостью 1,5 л имеет массу 250 г. Груз какой массы надо поместить в колбу, чтобы она утонула в воде? Плотность воды 1 г/см3.
Решение:
Чтобы колба утонула в воде, необходимо, чтобы колба полностью погрузилась в воду. Объем колбы больше ее вместимости на объем стекла, из которого она изготовлена:
Сила Архимеда, действующая на колбу при полном погружении равна , а сила тяжести, действующая на эту же колбу с грузом, .
Приравняем правые части этих уравнений и сократим на g. Выразим массу груза:
Ответ: .
Н
евесомый рычаг AC установлен на упоре так, что BC в 2 раза больше AB. К рычагу
с помощью ниток прикреплены невесомый
блок и массивное неоднородное тело.
Слева к блоку подвешивают груз так, что
система находится в равновесии. Найти
отношение массы груза к массе тела.
К рычагу
с помощью ниток прикреплены невесомый
блок и массивное неоднородное тело.
Слева к блоку подвешивают груз так, что
система находится в равновесии. Найти
отношение массы груза к массе тела.
Решение:
На груз действует сила тяжести Mg и сила натяжения нити T1. Груз покоится, значит силы уравновешены: .
На блок действуют две силы натяжения T1, и сила натяжения верхней нити T2. Эти силы также уравновешивают друг друга. Блок невесомый, поэтому силу тяжести учитывать не нужно: .
На рычаг действуют две силы: слева – сила натяжения верхней нити T2 и справа – сила натяжения третьей нити T3. Плечо силы T3 в 2 раза больше, значит сама сила в 2 раза меньше: .
На тело действуют две нити с силами и вертикально вверх и сила тяжести mg вертикально вниз. Они также уравновешивают друг друга. Получаем и .
Ответ: . Масса груза к массе тела равна ½.
Задачник по физике — Белолипецкий С.Н. » СтудИзба
Описание файла
DJVU-файл из архива «Задачник по физике — Белолипецкий С.Н.», который расположен в категории «книги и методические указания». Всё это находится в предмете «физика» из четвёртого семестра, которые можно найти в файловом архиве МФТИ (ГУ). Не смотря на прямую связь этого архива с МФТИ (ГУ), его также можно найти и в других разделах. .
Просмотр DJVU-файла онлайн
Распознанный текст из DJVU-файла, 19 — страница
Определите расход М топлива с удельной теплотой сгорания >7 за время Ь1 работы двигателя, если уравнение адиаоаты для данного газа может быть записано в виде Тр( Рт = с>и>вг, где у известный показатель адиабаты газа. 2.10. Ъ’равнение теплового баланса Во всех задачах этого раздела принимайте удельнук> тепло- емкость воды равной с„=- 4, 2 кДж,,'(кг К), удельную теплоемкость льда с, — 2, 1 кДж!(кг К), удельную теплоту плавления л! да Л = О, 33 11Дж,’кг, удельнук> теплоту парообразования воды т = 2, 3 МДж,’кг.
2.10. Ъ’равнение теплового баланса Во всех задачах этого раздела принимайте удельнук> тепло- емкость воды равной с„=- 4, 2 кДж,,'(кг К), удельную теплоемкость льда с, — 2, 1 кДж!(кг К), удельную теплоту плавления л! да Л = О, 33 11Дж,’кг, удельнук> теплоту парообразования воды т = 2, 3 МДж,’кг.
2.135~. В сосуд, содержащий воду массы и>! = 2 кг при температуре ~! = 5’С, положили кусок льда массы тэ = 5 кг при температуре ~э =- — 40’С. Найдите температуру и объем смеси гло УРАВНВНИВ ТЕПЛОВОРО ВЛЛЛНСЛ 91 после установления равновесия. Плотность льда р, = 0,916 х х 100 кг/’мз. 2.136г. В калориметр.
где находятся т„„= 100 г льда при температуре 11 = 0’С, впускают водяной пар при температуре йг = 100’С. Какая масса, воды ш окажется в калориметре не~осредс~~е~но после того, как весь лед растает? ‘Теплоемкость калориметра считайте пренебрежимо малой. 2.137г. В калориметр, тегьчоемкость которого С = 209, 4 Дж~’К, содержащий шп = 500 г воды при температуре Т1 = 293 К, опу< кают тг = 100 г льда при температуре Тг =- = 253 К.
Определите установившуюся тегнпсратуру Т. 2.138г. В калориметр, содержащий ш1 = 250 г воды при температуре !и = 15 «С, бросили тг = 20 г мокрого снега. Температура в калориметре понизилась на,Ь1 = 5’С. Какая масса воды т„содсржвлась в спсгс? Теплосмкость калориметра считайте пренебрежимо малой. 2.139г. В медный сосуд, нагретый до температуры !и = 350 ‘С, положили т1 = 600 г льда при температуре !г = — 10 ‘С. В результате часть льда растаяла, масса оставшегося льда в сосуде оказалась равной тг = 550 г. Найдите массу гп сосуда, если удельная теплоемкость меди равна с = 420 Дж7′(кг.К).
2.140 . Некоторое количество воды медленно переохлаждаг ют, доведя температуру до 11 = — 10 ‘С. После этого вода быстро замерзает (без дальнейптего отвода теплоты). Температура при этом повьппается до !0 = 0’С. Какая часть воды в конце этого пропесса обрагцается в лед? 2.141г. В колбе находится вода прн ! = 0 «С.
Выкачивая из колбы воздух вместе с содержащимися в нем парами воды, воду в колбе замораживают. Какая часть воды Ь при этом испаряется? Удельная теплота парообразования воды при 1 = 0’С равна. г = 2, 5 Ь!Дж~’кп Почему с повы1пением температуры удельная теплота парообразования уменьшается’? 2.142г. В кастрюлю налили холодной воды (температура !„= 10’С) и поставили на плиту. Через время т; = 10 мин вода закипела. Через какое время т опа полностью испарится? 2.143 . В ведре находится смесь воды со льдом массы ЛХ = =- 10 кг. Ведро внесли в комнату.
Какая часть воды Ь при этом испаряется? Удельная теплота парообразования воды при 1 = 0’С равна. г = 2, 5 Ь!Дж~’кп Почему с повы1пением температуры удельная теплота парообразования уменьшается’? 2.142г. В кастрюлю налили холодной воды (температура !„= 10’С) и поставили на плиту. Через время т; = 10 мин вода закипела. Через какое время т опа полностью испарится? 2.143 . В ведре находится смесь воды со льдом массы ЛХ = =- 10 кг. Ведро внесли в комнату.
Лед растаял за т1 =- 50 мин, а еще за тг = 10 мин вода в ведре нагрелась на Ь! = 2 «С. Определите, какая масса льда т находилась в ведре, когда его внесли в комнату. Теплосмкостью ведра пренебречь. 2.144г. В калориметре находится лед. Определите теп.лоемкость калориметра, если для нагревания его вместе с содержимгям от Т1 = 270 К до Тг = 272 К требуется количество теплоты Я~ = 2, 1 кДж, а от Тг = 272 К до Тг = 274 К Дг = 69, 7 кДж. мОлекуляРнля Физикл и теРмОдинлмикл Гл. 3 2.145 . Какую массу ЛХ, аммиака, взятого прп температуре 2 кипения 1з = — 33,4’С, надо испарять и нагреть до Ее = 0’С в холодильной машине, чтобы за счет поглощенного количества теплоты получить т = 40 кг льда из воды, взятой при температуре 15 = 10’С? Удельная теплота парообразования аммиака г~ = 1,37 МДж/кг, удельная теплоех5кость аммиака с„= = 2, 1 кДж)'(кг.К).
2.11. Пары. Кипение Во всех задачах этого раздела считайте атмосферное давление равным ре = 1, 013. 10′ Па. Для определения давления насыщенных водяных паров пользуйтесь таблицей, приведенной в следуюп5ех5 разделе. 2.146~. В закрытом сосуде находятся воздух и капля воды массы т =- 0,5 г. Обьем сосуда Г =- 25 л., давление в пем р5 = 1,0 10 Па, температура Т = 300 К. Каким станет давление р в сосуде, когда капля испар55тс55? Температура остается неизменной.
2.147з. В откачанном герметически закрытом сосуде обьема 1г — 10 л находится открытая колбочка, содержащая ш = 10 г воды. Сосуд прогревают при температуре 1 = 100’С. Какая масса воды Ьгп испартлтгя? 2. 148~. В объеме 1г5 = 20 л содержатся насыщенные пары воды при температуре 1 = 100’С. Какую работу ЬА надо совершить, чтобы изотермическим сжатием уменьшить объем паров до 1в = 10 л? Обьемом воды., образовавпюйся при коншнсапии, пренебречь.
148~. В объеме 1г5 = 20 л содержатся насыщенные пары воды при температуре 1 = 100’С. Какую работу ЬА надо совершить, чтобы изотермическим сжатием уменьшить объем паров до 1в = 10 л? Обьемом воды., образовавпюйся при коншнсапии, пренебречь.
2.149~. Под колоколом насоса находится стакан, содержащий воду массы пэ = 200 г. 11асос откачивает воздух пз-под колокола со скоростьк> и = 50 л!мин. Через сколько времени вся вода испарится, если установившаяся под колоколом температура равна Т вЂ” 280 К? 2.150з. В запаянной трубке объема 1г = 0,40 л находится водяной пар под давлением р = 8,5. 10а Па при температуре Т = 423 К.
Какое количество росы выпадет на стенках трубки при охлаждении ее до температурьл Т’ =- 295 К? 2.151 . Сосуд объема 1г = 20 дх5З разделен тонкой подвижной перегородкой на две части. В левую часть помещена вода (и„= 1 моль). в правую — азот (Р, = 0,5 моль). Температура поддерживается равной Т = 373 К. Определите объем правой части сосуда Ъ;,. 2.152в.
Сосуд объема 1г = 120 дмв разделен тонкой подвижной перегородкой на две части. В левую помещена вода 93 2.11 нивы. Кипение 1))„= 2 моль), в праву)0 » азот ())~ = 1 моль). Температура поддерживается равной 7′ = 373 К. Определите объем правой части сосуда ))’„.
2.1532. Под поршнем цилиндра объема 1′ = 10 дма находится и) = 1,9 г газообразного аммиака. Цилиндр помещен в термостат при температуре 1 = — 57 «С. Какая масса аммиака Ь)п сконденсируется при сжатии газа поршнем до объема 1’/2? Давление насьпценного пара аммиака при 1 .= — 57’С составляет р = 26, 7 кПа. Молярная масса, газообразного аммиака 1( =- = 17 г,’моль. 2.154 .
Под невесомым поршнем в цилиндре находится )и = г = 1, 0 кг воды при температуре 1) = 0’С. В воду опускают кусок железа массы п)о = 1, 0 кг, нагретый до температуры 12 = = 1100’С. На каку)о высоту 6 поднимется поршень? Удельная тсплосмкость железа с = О, 5 кДж,)’1кг К). П:к>щадь поршня Я = 2 = 1000 см . Теплоемкостью цилиндра и потеряхп) тепла пренебречь.
2.155 . В цилиндре находятся гп = 18 г воды при темпсра- 2 туре 1 = 0’С; поршень се (ения Я = 100 смв н массы ЛХ = — 100 кг отделяет воду от атмосферы. Цилиндр нагревается до температуры 1 — 200 ‘С. На какую высоту 6 подниметгя поршень? 2.1562. В вертикально расположенном цилиндре под невесомым поршнем сечения Я = 100 см2 находится ьп = 18 г насьпценного водяного пара.
В цилиндр впрыскивают М = 18 г воды при температуре 1 = 0’С. На какую высоту (1)6 опустится поршень? 2.157 . В вертикально расположенном цилиндре под поршз нем массы М =- 10 кг находится некоторое количество воздуха,. воды и водяного пара при температуре 1 = 100’С.
В положении равновесия поршень находится на расстоянии 6 = 20 см от дна цилнндра. КОгда цилиндр ра( пОлО)кили горизонтально, поршень занял новос положение равновесия, сх(сстившись на (1)6 = = 3, 0 см от первоначального положения. Какая масса воды Ьгп была на дне сосуда? П:(ощадь поршня Я = 400 см2. 2.158~. В откачанный сосуд объема 1′ — 1,0 дма ввели водород до давления р) = 266 гПа при температуре 1 = 20’С. В другой такой жс сосуд вве.»ш кислород до давления рв = 133 гПа при той же температуре. Оба сосуда соединили, и, после завершения переходных процессов, гремучую смесь подожгли электрическим разрядом. Определите массу Ь)п воды, сконденспровавшейся на стенках сосуда после его охла)кдения до первоначальной температу ры. 2.1592.
Запаянный сосуд заполнен смесью водорода и кислорода прн температуре Т) = 300 К и давлении ро = 1, О. 10ь Па. 94 МОЛЕКУЛЯРНЛЯ ФИЗИКЛ И ТЕРМОДИНЛМИКЛ ГЛ. 2 Парциалье5ыс давлсеьия компонентов сыес55 одинаковы. В сосуде происходит взрыв. Определите давление р внутри сосуда после того, как температура продуктов реакции станет равной Хз = 373 К. 2.160 .
Запаянный сосуд заполнен смесью водорода и кис- 3 лорода при температуре Т1 = — 300 К и давлении ро = 1, 0 МТ1а. Парциальные давления компонентов смеси одинаковы. В сосуде происке,п5т взрыв. Определите давление р внутри сосуда после того, как температура прод ктов реакщп5 станет равной Т„= 373 К. 2.12. Влажность Абсолютной влажностью называют давление р (плотность р) водяного пара в атмосфере. Относительной влажностью называют отношение давления (плотностн) водяного пара в атхюсфере к давлению (плотности) нас5ященного водяного пара при данной температуре: — 100% = — 100%.
2.12. Влажность Абсолютной влажностью называют давление р (плотность р) водяного пара в атмосфере. Относительной влажностью называют отношение давления (плотностн) водяного пара в атхюсфере к давлению (плотности) нас5ященного водяного пара при данной температуре: — 100% = — 100%.
р Р р~.п Рн.п Нормальное атмосферное давление считайте равным ро = = 760,0 мм ртхт,= — 1,013 10′ Па; 1 мм рт. ст, = 133,3 Па. Для определения давления насьпценных водяных паров пользуйтесь приведенной ниже таблицей. 2.161~. Температура воздуха в комнате ~5 = 20’С.
Относительная влажность составляет 5′ = 60% . При какой температуре 12 воздуха за окном начнут запотевать оконные стекла? 2.162~. Относительная влажность воздуха в поме5ценни обьсма Ъ’ = 50 ма при температуре 1 = 20’С равна 75 = 0,6. Найдите изменение Ьт массы воды, содержащейся в воздухе комнаты, если значение относительной влажности станет равным ~’2 = О, 8.
Тема №8722 Расчетные задачи по физике 62
3. Расчетные задачи
52. В сосуд, содержащий 20 л воды при температуре 10 0С, опустили 50 кг свинца при температуре 310 0С. Какая температура установится в сосуде? Теплоемкостью сосуда пренебречь.
53. В сосуд, содержащий б кг машинного масла при температуре 300 К, опущена стальная деталь массой 200 г при температуре 800 К. Какая температура установится в сосуде после теплообмена, если удельная теплоемкость масла 2,3 кДж/(кгК)?
54. Сколько литров воды требуется пропустить по радиаторам, чтобы нагреть комнату размерами 8х6х4 м3 от 12 0С до 18 0С, если вода остывает от 60 0С до 50 0С? Теплоемкость воздуха принять равной 1 кДж//(кгК), плотность воздуха равна 1,3 кг/м3.
55. В сосуд, содержащий 500 г воды при 16 0С, впускают 75 г водяного пара при 100 0С, который обращается в воду. Какая температура установится в сосуде? Теплоемкостью сосуда пренебречь.
56. Ко льду массой m = 1 кг при температуре Т0 = 270 К подвели количество теплоты Q = 105 Дж. Определите температуру образовавшейся воды.
Определите температуру образовавшейся воды.
57. Горячее тело, температура которого 70 °С, приведено в соприкосновение с холодным телом с температурой 20 °С. В тепловом равновесии установилась температура 30 °С. Во сколько раз теплоемкость холодного тела больше теплоемкости горячего?
58. В калориметр, содержащий 200 г воды при температуре 80, погружают 300 г льда при температуре — 20 С. Какую температуру будет иметь содержимое калориметра после того, как установится тепловое равновесие?
59. В сосуд, содержащий 20 л воды при температуре 10 0С, опустили 50 кг свинца при температуре 310 0С. Какая температура установится в сосуде? Теплоемкостью сосуда пренебречь.
60. В сосуд, содержащий б кг машинного масла при температуре 300 К, опущена стальная деталь массой 200 г при температуре 800 К. Какая температура установится в сосуде после теплообмена, если удельная теплоемкость масла 2,3 кДж/(кгК)?
61. В калориметр с 1 кг льда при температуре 0 0С впускают 500 г водяного пара с температурой 100 °С. Какая температура установится после того, как произойдет теплообмен? Теплоемкостью калориметра пренебречь.
62. Какую работу нужно совершить, чтобы расплавить трением друг о друга два кусочка тающего льда массами по 5 г?
63. Температура медной гири массой 1 кг понизилась с 302 К до 19 0С. На сколько кДж при этом понизилась внутренняя энергия гири, если удельная теплоемкость меди 380 Дж/(кгК)?
64. Поезд массой 1000 т при торможении с ускорением -2 м/с2 остановился через 10 с. Какое количество теплоты выделилось при торможении?
65. Поезд массой 2000 т, шедший со скоростью 54 км/ч, начинает тормозить и останавливается. Какое количество теплоты выделяется при этом в его тормозах?
66. Определить КПД нагреватели, расходующего 80 г керосина на нагревание 3 л воды от 20 0С до кипения. Удельная теплота сгорания керосина 42 МДж/кг. Ответ выразить в процентах.
67. На плитке мощностью 700 Вт нагреваются 2 л воды от 20 °С до кипения за 20 минут. Определить коэффициент тепловой отдачи плитки
Определить коэффициент тепловой отдачи плитки
68. На газовой горелке 3 л воды нагреваются от 10 0С до кипения. При этом расходуется 60 л газа. Определить КПД газовой горелки, если удельная теплота сгорания газа 37,8 МДж/м3.
69. В сосуде нагревают 1 л воды и 50 г льда от 0 0С до кипения. Сколько минут длится нагревание на плитке мощностью 500 Вт, если КПД плитки 75 %.
70. На электроплитке мощностью 600 Вт, имеющей КПД 45 %, нагрелось 1,5 л воды от 10 0С до кипения, а 5 % ее обратилось в пар. Сколько минут длился этот процесс?
71. В сосуд, содержащий 500 г воды при 16 0С, впускают 75 г водяного пара при 100 0С, который обращается в воду. Какая температура установится в сосуде? Теплоемкостью сосуда пренебречь.
72. Кусок льда массой mЛ = 700 г поместили в калориметр с водой. Масса воды mB =2,5 кг, начальная температура воды t0 = 5 °С . Когда установилось тепловое равновесие, оказалось, что масса льда увеличилась на m = 64 г. Определите начальную температуру льда. Потерями тепла и теплоемкостью калориметра пренебречь.
73. В калориметр теплоемкостью 1254 Дж/К бросили 30 г мокрого снега, т.е. смеси снега с водой. Сколько было там собственно снега, если температура в калориметре понизилась от 24 °С до 16 0С?
74. В сосуд, содержащий 500 г воды при 35 0С, бросили 50 г мокрого снега при 0 °С. Температура в сосуде понизилась на 5 0С. Сколько воды было в снеге?
75. Для охлаждения до 40°С трех литров воды, имеющей температуру 80°С, в воду бросают некоторую массу льда, имеющего температуру 0°С. Какова должна быть при этом масса льда?
76. Внесенный с мороза в теплую комнату кусочек льда полностью растаял через 10 минут после начала таяния. Сколько времени он нагревался от -2 °С до -1 °С?
77. Санки массой 6 кг скатываются с горы, угол при основании которой 300. Пройдя по склону 40 м, санки приобретают скорость 10 м/с. Определить количество теплоты, выделившейся при трении полозьев о снег, если начальная скорость санок была равна 0.
78. На какую высоту можно было бы поднять груз в 1 т, если бы удалось использовать полностью энергию, освобождающуюся при остывании стакана чая емкостью 250 см3 от 100 0С до 20 0С?
79. Стальной шар, свободно падая с высоты 25 м, ударился о чугунную плиту и подскочил на высоту 2 м. Определить изменение температуры шара при ударе. Считать, что внутренняя энергия плиты при ударе изменяется. Удельная теплоемкость стали 460 Дж/(кгК).
80. На сколько градусов нагревается вода при падении с плотины высотой 280 м, если на нагревание идет 60 % всей энергии.
81. С какой высоты должен падать град с температурой 0 0С, чтобы градинки при ударе о землю расплавлялись?
82. Молот массой 2 т падает на стальную болванку массой 10 м с высоты 3 м. На сколько градусов нагревается болванка при ударе, если на надевание ее идет 50 % энергии молота?
83. Паровой молот массой 6,9 т кует стальную болванку массой 300 кг. Скорость молота при ударе 4 м/с. На сколько градусов нагреется болванка при ударе, если на нагревание ее идет 50 % энергии молота?
84. Паровой молот массой 9 т падает на стальную болванку массой 220 кг с высоты 2 м. Сколько раз он должен упасть, чтобы температура болванки повысилась на 50 К, если на нагревание ее идет 50 % энергии молота?
85. Пуля, летящая со скоростью 200 м/с, ударяется о препятствие и останавливается. На сколько градусов по шкале Цельсия повысится температура пули, если известно, что она выполнена из свинца и на нагревание ее идет 60 % выделившейся при ударе энергии7
86. Какова скорость свинцовой пули, если при внезапной ее остановке температура пули изменяется на 250 К? Считать, что на нагревание пули идет 60 % ее энергии.
87. В тающую льдину попадает пуля массой 10 г, летящая со скоростью 500 м/с. Определить количество растаявшего льда, если в теплоту превращается 50 % энергии пули.
88. Определить массу пороха, при сгорании которого пуля массой 10 г приобретает скорость 300 м/с, если удельная теплота сгорания пороха разна 4 МДж/кг, а КПД винтовки 30 %.
89. При выстреле 122-миллиметровой гаубицы сгорает 780 г пороха, в результате чего снаряд массой 26 кг приобретает скорость 300 м/с. Определить КПД гаубицы, если удельная теплота сгорания пороха равна 3 МДж/кг. Ответ выразить в процентах с точностью до целых.
90. С какой скоростью должна удариться о преграду свинцовая пуля. имеющая температуру 127 0С, чтобы при ударе расплавиться, если известно, что температура плавления свинца 600 К, а удельная теплота плавления свинца 25 кДж/кг.
91. Автомобиль мощностью 76,5 кВт с КПД двигателя 30 % при движении с постоянной скоростью расходует 68 кг бензина на 120 км пути. Определить скорость автомобиля, если известно, что удельная теплота сгорания бензина 45 МДж/кг.
92. Определить мощность двигателя автомобиля, если при КПД двигателя 25 % он расходует 15,4 кг бензина за 1 час Удельная теплота сгорании бензина 47 МДж/кг.
93. Определить расход бензина автомобиля «Запорожец» на пути 1 км при скорости движения 50 км/ч, если мощность мотора его 18 кВт, а КПД 30 %. Удельная теплота сгорания бензина равна 45 МДж/кг.
94. На сколько минут непрерывной работы двигателя мотоцикла «Восход» хватит 4 кг бензина, если мотоцикл движется но горизонтальной дороге с постоянной скоростью, мощность двигателя 7,5 кВт, а КПД его 25 %. Удельная теплота сгорания бензина 45 МДж/кг.
95. Определить массу бензина, израсходованного двигателями самолета, пролетевшего расстояние 500 км со скоростью 250 км/ч, если средняя мощность двигателей 2 МВт, а КПД их 25 %. Удельная теплота сгорания бензина 45 МДж/кг.
96. Определить массу кокса, сжигаемого при плавлении 1,5 г железного лома, взятого при температуре 303 К, если КПД вагранки 60 %, температура плавления железа 1803 К, удельная теплота плавления железа 270 кДж/кг, а удельная теплота сгорания кокса 30 МДж/кг.
97. При нормальном атмосферном давлении некоторую массу воды нагревают от 0 0С до температуры кипения, пропуская через нее пар при температуре 100 0С. Во сколько раз увеличится масса воды, когда она достигнет температуры кипения?
98. Для нагревания некоторой массы воды от 0 0С до кипения нагревателю потребовалось 15 минут. После этого потребовалось еще 80 минут, чтобы обратить всю воду в пар при тех же условиях. Определить по этим данным удельную теплоту парообразования воды.
Для нагревания некоторой массы воды от 0 0С до кипения нагревателю потребовалось 15 минут. После этого потребовалось еще 80 минут, чтобы обратить всю воду в пар при тех же условиях. Определить по этим данным удельную теплоту парообразования воды.
99. В чайник налили воду при 10 0С и поставили на нагреватель. Через 10 минут вода закипела. Через сколько минут от момента начала кипения вода полностью выкипит?
100. Холодильник за 20 минут работы охлаждает 1,5 л воды от 16 0С до 4 0С. Какое количество льда образовалось, если процесс охлаждения был продолжен еще на 60 минут при том же режиме?
101. Для приготовления льда в холодильнике в течение 1 часа из воды, взятой при 20 0С, затрачивают мощность 10 Вт. Какое количество льда можно получить за это время?
102. Сколько литров воды требуется пропустить по радиаторам, чтобы нагреть комнату размерами 8х6х4 м3 от 12 0С до 18 0С, если вода остывает от 60 0С до 50 0С? Теплоемкость воздуха принять равной 1 кДж//(кгК), плотность воздуха равна 1,3 кг/м3.
103. При включении нагревателя некоторое количество воды нагревается на 1 0С за 2 мин, а при отключении его эта же вода остывает на 1 0С за 1 мин. Определить массу нагреваемой воды, считая потери тепла пропорциональными времени.
104. На нагреватель поставили открытый сосуд с водой. Через 40 минут после начала кипения в сосуд добавили воду, масса которой равна массе выкипевшей воды. При неизменных, условиях вода закипела через 3 минуты. Определить начальную температуру добавленной воды.
105. Кастрюлю, в которую налит 1 л воды, никак не удается довести до кипения при помощи нагревателя мощностью 100 Вт. Определить, за сколько секунд вода остынет на 1 0С, если нагреватель отключить.
106. Хоккеист скользит по льду на одном коньке. Известно, что лед протаивает под коньком на глубину 0,03 мм. Ширина конька 2 мм. Найти силу трения между коньком и льдом, считая теплопроводность льда малой.
107. В сосуде находится лед. Для нагревания сосуда вместе со льдом от 270 К до 272 К требуется количество теплоты Q. Для дальнейшего нагревания от 272 К до 274 К требуется количество теплоты в 20 раз больше, чем Q. Определите массу льда в сосуде до нагревания. Потерями тепла пренебречь. Теплоемкость сосуда С = 600 Дж/ К, удельная теплоемкость льда 2100 Дж/(кг·К), удельная теплоемкость воды cB =4200 Дж/(кг·К), удельная теплота плавления льда λ= 340 кДж/кг.
Для дальнейшего нагревания от 272 К до 274 К требуется количество теплоты в 20 раз больше, чем Q. Определите массу льда в сосуде до нагревания. Потерями тепла пренебречь. Теплоемкость сосуда С = 600 Дж/ К, удельная теплоемкость льда 2100 Дж/(кг·К), удельная теплоемкость воды cB =4200 Дж/(кг·К), удельная теплота плавления льда λ= 340 кДж/кг.
108. Смесь, состоящую из 5 кг льда и 15 кг воды при общей температуре 0 0С, нужно нагреть до температуры 80 0С, впуская в нее водяной пар с температурой 100 0С. Определите необходимую для этого массу пара. Удельная теплоемкость льда 2100 Дж/(кг·0С), удельная теплоемкость воды 4200 Дж/(кг·°С), удельная теплота парообразования воды остается в смеси.
109. В ведре находится смесь воды со льдом общей массой m =10 кг. Какое количество льда было в смеси, если при добавлении V = 2 л горячей воды с температурой 80° С температура воды в ведре оказалась равной 100 С?
110. Температуры двух тел возрастают от начальной температуры 100° С до значений 3000 С и 200° С соответственно при сообщении им количества теплоты Q, достаточного для таяния 1,5 кг льда при 0° С. У какого из тел теплоемкость больше и во сколько раз? Чему равны теплоемкости тел? У какого тела удельная теплоемкость больше, если массы тел равны? У какого тела масса больше, если удельные теплоемкости тел равны?
111. В термос с горячей водой (t = 40 °С) опускают бутылочку с детским питанием. Она нагревается до температуры t1 = 36 °С. Эту бутылочку вынимают, и в термос опускают другую точно такую же. До какой температуры она нагреется? До погружения в термос обе бутылочки имели температуру t =18 °С.
112. В калориметр наливают ложку горячей воды, при этом его температура увеличивается на 5 градусов. После того как в него добавили еще одну ложку горячей воды, температура возросла еще на 3 градуса. На сколько еще градусов возрастет температура калориметра, если в него добавить еще 48 ложек горячей воды? Теплообменом с окружающей средой пренебречь.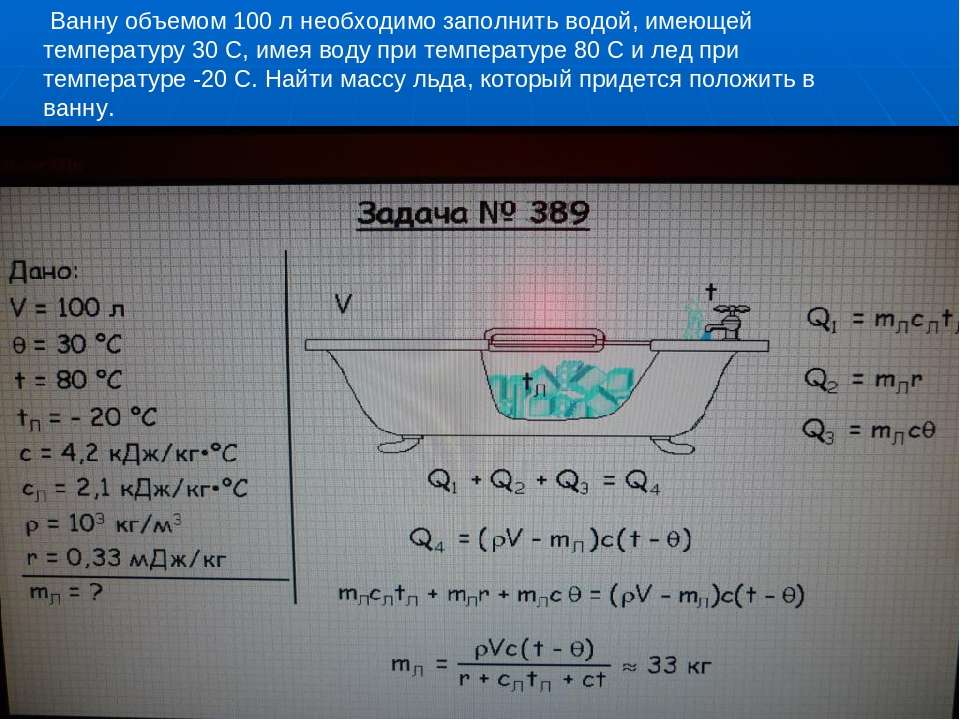
113. Брусок сливочного масла массой m= 500 г опустили в кастрюлю с горячим молоком. Найдите, на сколько изменится уровень жидкости в кастрюле, когда масло растает. Площадь сечения кастрюли S=200 см2. Плотность растопленного масла ρ1= 0,9 г/см3, молока ρ2 = 1,0 г/см3.
114. В ведре находится смесь воды со льдом. Масса смеси 10 кг. Ведро внесли в комнату и сразу же начали измерять температуру смеси. Получившийся график зависимости T(t) изображен на рисунке. Известны удельная теплоемкость воды с = 4200 Дж/(кг·К) и удельная теплота плавления льда λ=3,4·105 Дж/кг. Определите, сколько льда было в ведре, когда его внесли в комнату. Теплоемкостью ведра пренебречь.
Тепловые явления — презентация онлайн
Тепловые явленияКоличество теплоты — это энергия, переданная системе тел без совершения работы
в результате теплопередачи (конвекция, излучение, теплопроводность)
для нагревания и охлаждения
с – удельная теплоёмкость
t2 – конечная температура
t1 – начальная температура
будем считать количество теплоты положительной величиной
знак будет показывать на процесс:
тепло приходит : +
тепло уходит : —
Q3
Q1
Q2
Q
Дан кусок жидкого железа при температуре t1=12000C массой 1 кг с=500 Дж/(кг*К).
Необходимо найти сколько тепла выделилось при его остывании до 200 0С.
Qотд + Qполуч = 0
|Qотд| = |Qполуч |
«сферический конь в вукууме» …..
1.В калориметр с водой, имеющей температуру 200С кладут металлический
брусочек, имеющий температуру 400С. Через некоторое время в калориметре
устанавливается тепловое равновесие. Как в результате этого изменяются
следующие физические величины?
1)внутренняя энергия бруска
2)внутренняя энергия воды
3)суммарная внутренняя энергия системы.
L0
2. С использованием нагревателя известной мощности
исследовалась зависимость температуры 1 кг вещества от
количества теплоты, полученного от нагревателя.

Результаты измерений указаны на рисунке точками. Чему
примерно равна удельная теплоёмкость данного вещества?
(Ответ дайте в кДж/(кг*0С) с точностью до
0,5
кДж/(кг*0С) )
L0
3. Для нагревания 100 гр воды от 20 до 250С в неё бросили медный кубик с гранью
2 см. Какова должна была быть начальная температура кубика?
L0
4. До какой температуры надо нагреть железный кубик чтобы он полностью
погрузился в лед, будучи поставленным на него?
L0
5. В калориметр поместили лёд массой 100 гр при 00С. При пропускании пара
температура которого 1000С весь лёд растаял. Сколько воды при 00С окажется в
калориметре?
L0
ПЕРЕРЫВ
6. В медный калориметр массой 200 гр налили 150 гр воды и опустили кусок льда при
00С. Начальная температура калориметра с водой 250С. В момент времени, когда в
калориметре наступило тепловое равновесие, температура воды была 5 0С. Найдите
массу льда.
L1
7. В тонкий стаканчик с 200 гр воды при температуре 20 0С бросили лёд массой 50 гр
при температуре -400С. Найдите установившуюся температуру.
L2
8. В калориметр, содержащий 250 гр воды при температуре t1=150C бросили
m2=20гр мокрого снега. В результате температура понизилась на Dt=50C. Сколько
воды было в снеге?
L2
Если тело обладало механической энергией, то потом, в результате
неупругих процессов, эта механическая энергия может перейти во
внутреннюю.
В конечном итоге – тело нагреется.
9. Водопад имеет высоту h=807м. На сколько градусов могла бы повыситься
температура падающей воды, если считать, что на нагревание тратится 50% от
работы силы тяжести?
L2
10. Кусок льда при температуре 00С помещён в калориметр с нагревателем,
имеющим какую то мощность. Чтобы превратить этот лёд в воду с температурой
100С требуется количество теплоты 200кДж. Какая температура установится если
лёд получит 120кДж? Теплоёмкостью калориметра и потерями тепла пренебречь.

L2
ПЕРЕРЫВ
11.В ведре находится смесь воды со льдом массой
m=10 кг. Ведро внесли в комнату и сразу же начали
измерять температуру смеси. Получившаяся
зависимость температуры смеси от времени
изображена на рисунке. Определить массу льда в
ведре в момент внесения его в комнату.
L2
12. В калориметр с водой меланхолично бросают кусочки уныло тающего льда. В
некоторый момент кусочки льда перестают таять и к концу процесса масса воды
увеличилась на 84 гр. Какова начальная масса воды если её начальная температура
200С?
L2
13. При морозе в -130С каждый квадратный метр поверхности пруда отдаёт воздуху
220кДж тепла в час. Какой толщины ледяной покров образуется за одни сутки, если
температура воды 00С?
L3
14. Необходимо расплавить лёд, имеющий температуру 00С и массу 0,2кг.
Выполнимо ли это, если потребляемая мощность нагревательного элемента 400Вт,
потери составляют 30%, а время работы нагревателя не должно превышать 5 мин?
L3
15. В домике затопили печку. Когда печка топилась так, что её мощность была
равна N , то в домике была температура t1=100C. Печку отремонтировали и
увеличили её мощность втрое. Температура в домике стала t2=180C. Какая
температура была на улице?
L3
16. На скорости 100км/ч двигатель автомобиля мощностью 40кВт расходует 9л
бензина на 100 км пути. Найдите КПД двигателя в таком режиме.
L3
17. Луч лазера в экспериментальном двигателе направлен на кусок льда. Отверстие
в куске льда имеет площадь S. Мощность лазера N целиком идёт на испарение льда
без потерь. Удельная теплота плавления льда l. Плотность испаряющихся паров r.
Найдите силу тяги такого двигателя.
L3
18. Идеальная тепловая машина использует в качестве нагревателя и холодильника
два больших резервуара: с водяным паром tп = 1000С и льдом tл=00С.
Спустя некоторое время после начала работы выяснилось, что в холодном
резервуаре расплавилось m2=0,51кг льда.
 Какая масса пара m1 при этом
Какая масса пара m1 при этомсконденсировалась в горячем резервуаре? Теплообменом с окружающей средой
пренебречь.
L3
графические задачи на тепловой баланс, 8 класс.
В задачах на тепловой баланс иногда часть информации дана в виде графика, и нужно уметь эту информацию извлечь из такой графической формы и перевести в числовую, такую, которую можно использовать для расчетов.
Задача 1. В небольшой чайник налита доверху теплая вода при температуре С. Чайник остывает на С за время мин. Для того чтобы чайник не остыл, в него капают горячую воду с температурой С. Масса одной капли к г. На сколько градусов подогреется вода за одну минуту, если начать капать втрое чаще? Считать, что температура воды в чайнике выравнивается очень быстро. Лишняя вода выливается из носика. В чайник входит кг воды. Температура окружающего воздуха С. Ответ выразить в С, округлив до десятых.
Чайник за 300 с (5 минут) теряет тепла. Капли должны компенсировать эти потери. При этом горячая вода остынет на . Определим необходимую массу горячей воды:
Найдем, сколько это капель:
Эти капли должны попасть в чайник в течение 5 мин, следовательно, по 20 кап/мин. Капать втрое чаще – это по 60 кап/мин. Причем те же 20 будут покрывать потери тепла, и только добавочные – греть чайник. Тогда посчитаем, на сколько градусов нагреется чайник в этом случае:
Ответ: .
Задача 2. В ведре находится смесь воды со льдом. Масса смеси кг. Ведро внесли в комнату и сразу же начали измерять температуру смеси. Получившийся график зависимости температуры от времени изображён на рисунке. Известны удельная теплоёмкость воды Дж/кг С и теплота плавления льда кДж/кг. Определите, сколько льда было в ведре, когда его внесли в комнату. Теплоёмкостью ведра пренебречь. Ответ выразить в кг, округлив до десятых.
Рисунок 1
Температура не меняется, следовательно, лед тает. На это ушло 50 минут. На то, чтобы нагреть потом содержимое на , ушло 10 минут при той же мощности теплопередачи. Поэтому на плавление пошло впятеро больше энергии, нежели чем на нагрев 10 кг воды на , откуда
На это ушло 50 минут. На то, чтобы нагреть потом содержимое на , ушло 10 минут при той же мощности теплопередачи. Поэтому на плавление пошло впятеро больше энергии, нежели чем на нагрев 10 кг воды на , откуда
Или кг.
Ответ: 1,2 кг.
Задача 3. В сосуде с водой плавает кусок льда массой кг. Система находится в тепловом равновесии. Сколько тёплой воды при температуре С нужно добавить в сосуд, чтобы объём выступающей из воды части льда уменьшился в раза? Ответ выразить в кг, округлив до сотых.
Удельная теплоёмкость воды в Дж/кг С. Удельная теплота плавления льда кДж/кг.
Объем выступающей части всегда находится в одном и том же отношении к части подводной. Это следует из закона Архимеда. Поэтому то, что выступающая часть стала меньше в 2,4 раза, говорит о том, что весь объем уменьшился во столько же раз, а значит, и масса льда тоже сократилась в 2,4 раза. Тогда растаяло
На плавление такого количества льда нужно тепла
Ответ: кг.
Задача 4. На рисунке показано распределение температуры вдоль тонкого однородного теплоизолированного стержня длиной см в некоторый момент времени. Какая температура стержня установится через достаточно долгое время? Ответ выразить в C, округлив до целых.
Рисунок 2
Все количество теплоты, которым мы располагаем – это площадь под графиком (умноженная на некоторый коэффициент). Правая и левая части стержня будут остывать, отдавая тепло центральной части. При этом, если правая и левая остывают на градус, центральная должна нагреться на 2 градуса (теплообмена с окружающей средой нет, и тепло не теряется). Поэтому, чтобы не распределять теплоту «вручную», рискуя ошибиться, просто определим имеющееся тепло и разделим его на все три части поровну. Воспользуемся при этом методом “теплового банка” – охладим все части стержня до нуля, поместив тепло в такой “банк”, а потом раздадим “всем сестрам по серьгам” – поровну каждой части стержня:
Тогда
Ответ: 167 градусов.
Как найти время полного плавления. Удельная теплота плавления
Переход вещества из твердого кристаллического состояния в жидкое называется плавлением . Чтобы расплавить твердое кристаллическое тело, его нужно нагреть до определенной температуры, т. е. подвести тепло. Температура, при которой вещество плавится, называется температурой плавления вещества.
Обратный процесс — переход из жидкого состояния в твердое — происходит при понижении температуры, т. е. тепло отводится. Переход вещества из жидкого состояния в твердое называется отвердеванием, или кристал лизацией. Температура, при которой вещество кристаллизуется, называется температурой кристалли зации.
Опыт показывает, что любое вещество кристаллизуется и плавится при одной и той же температуре.
На рисунке представлен график зависимости температуры кристаллического тела (льда) от времени нагревания (от точки А до точки D) и времени охлаждения (от точки D до точки K ). На нем по горизонтальной оси отложено время, а по вертикальной — температура.
Из графика видно, что наблюдение за процессом началось с момента, когда температура льда была -40 °С, или, как принято говорить, температура в начальный момент времени t нач = -40 °С (точка А на графике). При дальнейшем нагревании температура льда растет (на графике это участок АВ ). Увеличение температуры происходит до 0 °С — температуры плавления льда. При 0°С лед начинает плавиться, а его температура перестает расти. В течение всего времени плавления (т.е. пока весь лед не расплавится) температура льда не меняется, хотя горелка продолжает го-реть и тепло, следовательно, подводится. Процессу плавления соответствует горизонтальный учас-ток графика ВС. Только после того как весь лед расплавится и превратится в воду , температура снова начинает подниматься (участок CD ). После того, как температура воды достигнет +40 °С, горелку гасят и воду начинают охлаждать, т. е. тепло отводят (для этого можно сосуд с водой по-местить в другой, больший сосуд со льдом). Температура воды начинает снижаться (участок DE ). При достижении температуры 0 °С температура воды перестает снижаться, несмотря на то, что тепло по-прежнему отводится. Это идет процесс кристаллизации воды — образования льда (гори-зонтальный участок EF ). Пока вся вода не превратится в лед, температура не изменится. Лишь после этого начинает уменьшаться температура льда (участок FK ).
После того, как температура воды достигнет +40 °С, горелку гасят и воду начинают охлаждать, т. е. тепло отводят (для этого можно сосуд с водой по-местить в другой, больший сосуд со льдом). Температура воды начинает снижаться (участок DE ). При достижении температуры 0 °С температура воды перестает снижаться, несмотря на то, что тепло по-прежнему отводится. Это идет процесс кристаллизации воды — образования льда (гори-зонтальный участок EF ). Пока вся вода не превратится в лед, температура не изменится. Лишь после этого начинает уменьшаться температура льда (участок FK ).
Вид рассмотренного графика объясняется следующим образом. На участке АВ благодаря подводимому теплу средняя кинетическая энергия молекул льда увеличивается, и температура его повышается. На участке ВС вся энергия, получаемая содержимым колбы, тратится на разрушение кристаллической решетки льда: упорядоченное пространственное расположение его молекул сменяется неупорядоченным, меняется расстояние между молекулами, т.е. происходит перестройка молекул таким образом, что вещество становится жидким. Средняя кинетическая энергия моле-кул при этом не меняется, поэтому неизменной остается и температура. Дальнейшее увеличение температуры расплавленного льда-воды (на участке CD ) означает увеличение кинетической энер-гии молекул воды вследствие подводимого горелкой тепла.
При охлаждении воды (участок DE ) часть энергии у нее отбирается, молекулы воды движутся с меньшими скоростями, их средняя кинетическая энергия падает — температура уменьшается, вода охлаждается. При 0°С (горизонтальный участок EF ) молекулы начинают выстраиваться в определенном порядке, образуя кристаллическую решетку. Пока этот процесс не завершится, температура вещества не изменится, несмотря на отводимое тепло, а это означает, что при отвер-девании жидкость (вода) выделяет энергию. Это как раз та энергия, которую поглотил лед, пре-вращаясь в жидкость (участок ВС ). Внутренняя энергия у жидкости больше, чем у твердого тела. При плавлении (и кристаллизации) внутренняя энергия тела меняется скачком.
Внутренняя энергия у жидкости больше, чем у твердого тела. При плавлении (и кристаллизации) внутренняя энергия тела меняется скачком.
Металлы, плавящиеся при температуре выше 1650 ºС, называют тугоплавкими (титан, хром , молибден и др.). Самая высокая температура плавления среди них у вольфрама — около 3400 °С . Тугоплавкие металлы и их соединения используют в качестве жаропрочных материалов в самолетостроении, ракетостроении и космической технике, атомной энергетике.
Подчеркнем еще раз, что при плавлении вещество поглощает энергию. При кристаллизации оно, наоборот, отдает ее в окружающую среду. Получая определенное количество теплоты, выделяющееся при кристаллизации, среда нагревается. Это хорошо известно многим птицам. Неда-ром их можно заметить зимой в морозную погоду сидящими на льду, который покрывает реки и озера. Из-за выделения энергии при образовании льда воздух над ним оказывается на несколько градусов теплее, чем в лесу на деревьях, и птицы этим пользуются.
Плавление аморфных веществ.
Наличие определенной точки плавления — это важный признак кристаллических веществ. Именно по этому признаку их можно легко отличить от аморфных тел, которые также относят к твердым телам. К ним, в частности, относятся стекла, очень вязкие смолы, пластмассы.
Аморфные вещества (в отличие от кристаллических) не имеют определенной температуры плавления — они не плавятся, а размягчаются. При нагревании кусок стекла, например, снача-ла становится из твердого мягким, его легко можно гнуть или растягивать; при более высокой температуре кусок начинает менять свою форму под действием собственной тяжести. По мере нагревания густая вязкая масса принимает форму того сосуда, в котором лежит. Эта масса сначала густая, как мед, затем — как сметана и, наконец, становится почти такой же маловязкой жидкостью, как вода. Однако указать определенную температуру перехода твердого тела в жидкое здесь невозможно, поскольку ее нет.
Причины этого лежат в коренном отличии строения аморфных тел от строения кристаллических. Атомы в аморфных телах расположены беспорядочно. Аморфные тела по своему строению напоминают жидкости. Уже в твердом стекле атомы расположены беспорядочно. Значит, повы-шение температуры стекла лишь увеличивает размах колебаний его молекул, дает им постепенно все большую и большую свободу перемещения. Поэтому стекло размягчается постепенно и не обнаруживает резкого перехода «твердое—жидкое», характерного для перехода от расположения молекул в строгом порядке к беспорядочному.
Атомы в аморфных телах расположены беспорядочно. Аморфные тела по своему строению напоминают жидкости. Уже в твердом стекле атомы расположены беспорядочно. Значит, повы-шение температуры стекла лишь увеличивает размах колебаний его молекул, дает им постепенно все большую и большую свободу перемещения. Поэтому стекло размягчается постепенно и не обнаруживает резкого перехода «твердое—жидкое», характерного для перехода от расположения молекул в строгом порядке к беспорядочному.
Теплота плавления.
Теплота плавления — это количество теплоты, которое необходимо сообщить веществу при постоянном давлении и постоянной температуре, равной температуре плавления, чтобы полностью перевести его из твердого кристаллического состояния в жидкое. Теплота плавления равна тому количеству теплоты , которое выделяется при кристалли-зации вещества из жидкого состояния. При плавлении вся подводимая к веществу теплота идет на увеличение потенциальной энер-гии его молекул. Кинетическая энергия не меняется, поскольку плавление идет при постоянной температуре.
Изучая на опыте плавление различных веществ одной и той же массы, можно заметить, что для превращения их в жидкость требуется разное количество теплоты. Например, для того чтобы расплавить один килограмм льда, нужно затратить 332 Дж энергии, а для того чтобы расплавить 1 кг свинца — 25 кДж .
Количество теплоты, выделяемое телом, считается отрицательным. Поэтому при расчете количества теплоты, выделяющегося при кристаллизации вещества массой m , следует пользоваться той же формулой, но со знаком «минус»:
Теплота сгорания.
Теплота сгорания (или теплотворная способность , калорийность ) — это количество теплоты, выделяющейся при полном сгорании топлива.
Для нагревания тел часто используют энергию, выделяющуюся при сгорании топлива. Обыч-ное топливо (уголь, нефть, бензин) содержит углерод . При горении атомы углерода соединяются с атомами кислорода , содержащегося в воздухе, в результате чего образуются молекулы углекислого газа . Кинетическая энергия этих молекул оказывается большей, чем у исходных частиц. Увеличение кинетической энергии молекул в процессе горения называют выделением энергии. Энергия, выделяющаяся при полном сгорании топлива, и есть теплота сгорания этого топлива.
Кинетическая энергия этих молекул оказывается большей, чем у исходных частиц. Увеличение кинетической энергии молекул в процессе горения называют выделением энергии. Энергия, выделяющаяся при полном сгорании топлива, и есть теплота сгорания этого топлива.
Теплота сгорания топлива зависит от вида топлива и его массы. Чем больше масса топлива, тем больше количество теплоты, выделяющейся при его полном сгорании.
Физическая величина , показывающая, какое количество теплоты выделяется при полном сгорании топлива массой 1 кг, называется удельной теплотой сгорания топлива. Удельную теплоту сгорания обозначают буквой q и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты Q , выделяющееся при сгорании m кг топлива, определяют по формуле:
Чтобы найти количество теплоты, выделяющееся при полном сгорании топлива произвольной массы, нужно удельную теплоту сгорания этого топлива умножить на его массу.
Что вещество может быть в одном из состояний — газообразном, жидком, твердом. И может переходить из одного в другое. Самый простой пример — кусок льда тает, превращается в жидкость и затем в пар. Во всем этом процессе превращения в пар очень интересен этап плавления и один из его параметров — удельная теплота плавления.
Если вспомнить, как проходит плавление, то можно выделить несколько этапов. Возьмем в качестве примера свинец. На первом этапе происходит нагрев свинца, температура поднимается до 327 (температура плавления). После того, как плавление началось, долгое время ничего не происходит.
Температура свинца, несмотря на подводимое к нему тепло, остается постоянной и держится такой, пока не закончится весь процесс. И только после этого при продолжающемся нагреве температура начинает опять повышаться. Из наблюдаемой картины следуют некоторые выводы. У твердого тела все молекулы находятся в определенном порядке и жестко связаны с соседними молекулами.
Для того чтобы они могли свободно перемещаться на другое место, связи с соседними молекулами надо разорвать, что и происходит в процессе плавления. Для этого телу надо передать определенную норму тепла, называемую теплотой плавления. Для каждого вещества потребуется разное количество тепла. Причина обусловлена таким свойством вещества, как удельная теплота плавления, которая определяется как количество тепла, затрачиваемое на расплавление одного килограмма вещества. Единицей измерения является Джоуль/килограмм.
Для этого телу надо передать определенную норму тепла, называемую теплотой плавления. Для каждого вещества потребуется разное количество тепла. Причина обусловлена таким свойством вещества, как удельная теплота плавления, которая определяется как количество тепла, затрачиваемое на расплавление одного килограмма вещества. Единицей измерения является Джоуль/килограмм.
Как уже упоминалась, для каждого материала эта величина своя. плавления свинца отличается от той же величины для льда. И здесь возникает очень любопытный момент. Удельная теплота плавления стали составляет в среднем 85 кДж/кг, а у воды (льда) тот же параметр составляет в среднем 335 кДж/кг. У льда высокое значение этого параметра можно считать большим подарком от природы.
Ведь благодаря этому весь снег, лед не тает мгновенно, а все происходит продолжительное время. В противном случае снег растаял бы очень быстро, и паводки были ли бы более многоводными и разрушительными. Кроме того, такие уникальные свойства воды способствуют стабилизации климата на планете.
Имеются таблицы с данными об удельной теплоте плавления отдельных материалов. Зная эту величину, рассчитывается, сколько тепла нужно для того, чтобы расплавить материал, и определить, сколько нужно топлива для проведения плавки. Если тело нагрето до температуры плавления, то теплота нужна только на плавление, а если его температура ниже температуры плавления, то теплота необходима на нагрев вещества до
Такие расчеты чрезвычайно полезны в промышленности для расчета затрат на производстве.
Кстати, при остывании расплавленного вещества происходит обратный плавлению процесс — кристаллизация. В этом случае при остывании вещества восстанавливаются разорванные связи между молекулами и выделяется тепло.
Рассматривая процесс плавления вещества и проходящие при этом явления, было определено такое понятие, как удельная теплота плавления. Проведено сравнение данного показателя для разных веществ, определено, каким образом высокое значение этого параметра у льда благотворно влияет на климат планеты.
На графике (рис. 198) очень наглядно показано, что, пока нафталин плавится, температура его не меняется. И лишь после того, как он весь расплавится, температура образовавшейся жидкости начинает повышаться. Но ведь и во время процесса плавления нафталин получает энергию от сгорающего в нагревателе топлива. А из закона сохранения энергии следует, что она не может исчезнуть. На что же расходуется энергия топлива во время процесса плавления?
На этот вопрос можно ответить, если вспомнить, что при плавлении происходит разрушение кристалла. На это и расходуется энергия.
Следовательно, энергия, которую получает кристаллическое тело, после того как оно уже нагрето до температуры плавления, расходуется на изменение его внутренней энергии при переходе в жидкое состояние.
Количество теплоты, необходимое для превращения при температуре плавления твердого кристаллического вещества массой 1 кг в жидкость, называют удельной теплотой плавления.
Удельную теплоту плавления измеряют в Дж/кг и обозначают буквой λ.
Определяют удельную теплоту плавления на опыте. Так, опытным путем было установлено, что удельная теплота плавления льда равна 3,4 10 5 Дж/кг. Это означает, что для превращения куска льда массой 1 кг, взятого при 0°С, в воду такой же температуры требуется затратить 3,4 10 5 Дж.
Следовательно, при температуре плавления внутренняя энергия вещества массой 1 кг в жидком состоянии больше внутренней энергии такой же массы вещества в твердом состоянии на удельную теплоту плавления.
Например, внутренняя энергия воды массой 1 кг при температуре 0°С на 3,4 10 5 Дж больше внутренней энергии льда массой 1 кг при той же температуре.
Пример. Для приготовления лая турист положил в котелок 2 кг льда, имеющего температуру 0°С. Какое количество теплоты необходимо для превращения этого льда в кипяток при температуре 100 °С?
Сколько теплоты понадобилось бы, если вместо льда турист взял из проруби 2 кг воды при температуре 0 °С?
Если бы вместо льда было взято 2 кг воды при 0°С, то понадобилось бы количество теплоты, необходимое только для ее нагревания от 0 до 100 °С, т. е. Q2= 8,4 10 5 Дж.
е. Q2= 8,4 10 5 Дж.
Вопросы. 1. Чем объяснить, что в течение всего времени процесса плавления кристаллического тела температура его не меняется? 2. На что расходуется энергия сгорающего в нагревателе топлива при плавлении кристаллического тела? 3. Что такое удельная теплота плавления? 4. В каких единицах выражают удельную теплоту плавления?
Упражнения. На рисунке 199 изображены графики зависимости изменения температуры от времени двух тел одинаковой массы. У какого из тел выше точка плавления? У какого больше теплота плавления ? Одинаковы ли удельные теплоемкости тел?
http://sernam. ru/book_phis_t1.php? id=272
§ 269. Удельная теплота плавления
Мы видели, что сосуд со льдом и водой, внесенный в теплую комнату, не нагревается до тех пор, пока весь лед не растает. При этом из льда при получается вода при той же температуре. В это время к смеси лед — вода притекает теплота и, следовательно, внутренняя энергия этой смеси увеличивается. Отсюда мы должны сделать вывод, что внутренняя энергия воды при больше, чем внутренняя энергия льда при той же температуре. Так как кинетическая энергия молекул, воды и льда при одна и та же, то приращение внутренней энергии при плавлении является приращением потенциальной энергии молекул
Опыт обнаруживает, что сказанное справедливо для всех кристаллов. При плавлении кристалла необходимо непрерывно увеличивать внутреннюю энергию системы, причем температура кристалла и расплава остается неизменной. Обычно увеличение внутренней энергии происходит при передаче кристаллу некоторого количества теплоты. Той же цели можно достигнуть и путем совершения работы, например трением. Итак, внутренняя энергия расплава всегда больше, чем внутренняя энергия такой же массы кристаллов при той же температуре. Это означает, что упорядоченное расположение частиц (в кристаллическом состоянии) соответствует меньшей энергии, чем неупорядоченное (в расплаве).
Количество теплоты, необходимое для перехода единицы массы кристалла в расплав той же температуры, называют удельной теплотой плавления кристалла. Она выражается в джоулях на килограмм .
Она выражается в джоулях на килограмм .
При затвердевании вещества теплота плавления выделяется и передается окружающим телам.
Определение удельной теплоты плавления тугоплавких тел (тел с высокой температурой плавления) представляет нелегкую задачу. Удельная теплота плавления такого легкоплавкого кристалла, как лед, может быть определена при помощи калориметра. Налив в калориметр, некоторое количество воды определенной температуры и бросив в нее известную массу льда, уже начавшего таять, т. е. имеющего температуру , выждем, пока весь лед не растает и температура воды в калориметре примет неизменяющееся значение. Пользуясь законом сохранения энергии, составим уравнение теплового баланса (§ 209), позволяющее определить удельную теплоту плавления льда.
Пусть масса воды (включая водяной эквивалент калориметра) равна масса льда — , удельная теплоемкость воды — , начальная температура воды — , конечная — , удельная теплота плавления льда — . Уравнение теплового баланса имеет вид
.
В табл. 16 приведены значения удельной теплоты плавления некоторых веществ. Обращает на себя внимание большая теплота плавления льда. Это обстоятельство очень важно, так как оно замедляет таяние льда в природе. Будь удельная теплота плавления значительно меньше, весенние паводки были бы во много раз сильнее. Зная удельную теплоту плавления, мы можем рассчитать, какое количество теплоты необходимо для расплавления какого-либо тела. Если тело уже нагрето до точки плавления, то надо затратить теплоту только на плавление его. Если же оно имеет температуру ниже точки плавления, то надо еще потратить теплоту на нагревание. Таблица 16.
269.1. В сосуд с водой, хорошо защищенный от притока теплоты извне, бросают кусочки льда при . Сколько можно бросить льда для того, чтобы он полностью растаял, если в сосуде имеется 500 г воды при ? Теплоемкость сосуда можно считать ничтожно малой по сравнению с теплоемкостью воды в нем. Удельная теплоемкость льда равна
http://earthz. ru/solves/Zadacha-po-fizike-641
ru/solves/Zadacha-po-fizike-641
2014-06-01 В ведре находится смесь воды со льдом массой m=10кг. Ведро внесли в комнату и сразу же начали измерять температуру смеси. Получившаяся зависимость температуры от времени T(ф) изображена на рис.. Удельная теплоемкость воды равна cв=4,2Дж/(кг⋅К), удельная теплота плавления льда л=340кДж/кг.
Определите массу mл льда в ведре, когда его внесли в комнату. Теплоемкостью ведра пренебречь. Решение: Как видно из графика, первые 50 минут температура смеси не менялась и оставалась равной 0∘C. Все это время теплота, получаемая смесью из комнаты, шла на таяние льда. Через 50 минут весь лед растаял и температура воды начала повышаться. За 10 минут (от ф1=50 до ф2=60мин) температура повысилась на ДT=2∘C. Теплота, поступившая к воде из комнаты за это время, равна q=cвmвДT=84кДж. Значит, за первые 50 минут к смеси из комнаты поступило количество теплоты Q=5q=420кДж. Эта теплота и пошла на таяние массы mл льда: Q=лmл. Таким образом, масса льда в ведре, внесенном в комнату, равна mл=Q/л≈1,2кг.
http://www.msuee.ru/html2/med_gidr/l3_4.html
Уде́льная теплота́ плавле́ния (также: энтальпия плавления ; также существует равнозначное понятие уде́льная теплота́ кристаллиза́ции ) — физическая величина, показывающая, какое количество теплоты необходимо сообщить одной единице массы кристаллического вещества в равновесном изобарно-изотермическом процессе, чтобы перевести его из твёрдого (кристаллического) состояния в жидкое при температуре плавления (то же количество теплоты выделяется при кристаллизации вещества).
Теплота плавления — частный случай теплоты фазового перехода I рода.
Различают удельную теплоту плавления (Дж /кг) и молярную (Дж /моль).
Удельная теплота плавления обозначается буквой \lambda (греческая буква лямбда ). Формула расчёта удельной теплоты плавления: \lambda=\frac{Q}{m}, где \lambda — удельная теплота плавления, Q — количество теплоты , полученное веществом при плавлении (или выделившееся при кристаллизации), m — масса плавящегося (кристаллизующегося) вещества.
| Вещество | Удельная теплота плавления (кДж/кг) |
|---|---|
| Алюминий | 390 |
| Железо | 277 |
| Золото | 66,2 |
| Лёд | 335 |
| Медь | 213 |
| Нафталин | 151 |
| Олово | 60,7 |
| Платина | 101 |
| 12 | |
| Свинец | 25 |
| Серебро | 105 |
| Цинк | 112 |
| Чугун (белый) | 140 |
| Чугун (серый) | 100 |
См.также
Напишите отзыв о статье «Удельная теплота плавления»
Литература
- Енохович А. С. Краткий справочник по физике. — М .: «Высшая школа», 1976. — С. 114. — 288 с.
Отрывок, характеризующий Удельная теплота плавления
Ночь была темная, теплая, осенняя. Шел дождик уже четвертый день. Два раза переменив лошадей и в полтора часа проскакав тридцать верст по грязной вязкой дороге, Болховитинов во втором часу ночи был в Леташевке. Слезши у избы, на плетневом заборе которой была вывеска: «Главный штаб», и бросив лошадь, он вошел в темные сени.– Дежурного генерала скорее! Очень важное! – проговорил он кому то, поднимавшемуся и сопевшему в темноте сеней.
– С вечера нездоровы очень были, третью ночь не спят, – заступнически прошептал денщицкий голос. – Уж вы капитана разбудите сначала.
– Очень важное, от генерала Дохтурова, – сказал Болховитинов, входя в ощупанную им растворенную дверь. Денщик прошел вперед его и стал будить кого то:
– Ваше благородие, ваше благородие – кульер.
– Что, что? от кого? – проговорил чей то сонный голос.
– От Дохтурова и от Алексея Петровича. Наполеон в Фоминском, – сказал Болховитинов, не видя в темноте того, кто спрашивал его, но по звуку голоса предполагая, что это был не Коновницын.
Разбуженный человек зевал и тянулся.

– Будить то мне его не хочется, – сказал он, ощупывая что то. – Больнёшенек! Может, так, слухи.
– Вот донесение, – сказал Болховитинов, – велено сейчас же передать дежурному генералу.
– Постойте, огня зажгу. Куда ты, проклятый, всегда засунешь? – обращаясь к денщику, сказал тянувшийся человек. Это был Щербинин, адъютант Коновницына. – Нашел, нашел, – прибавил он.
Денщик рубил огонь, Щербинин ощупывал подсвечник.
– Ах, мерзкие, – с отвращением сказал он.
При свете искр Болховитинов увидел молодое лицо Щербинина со свечой и в переднем углу еще спящего человека. Это был Коновницын.
РЕШЕНИЕ: Ковш из пенополистирола с незначительной массой…
Стенограмма видеозаписи
Хорошо, позвольте мне сначала обозначить проблему. Итак, у нас есть ведро со льдом и водой. Изначально жидкая вода составляет 1,75 кг, а льда — 0,45 кг. А потом добавляется немного глаз. Это отрицательное 15-градусное себя, вы. И наконец, количество глаз в ведре составляет 0,884 килограмма. И нам нужно найти хозяина того количества льда, которое мы добавили.Гм, мы также знаем, что скрытое тепловое излучение воды составляет 334 килограмма, убивает вашу конкретную марку и, ммм, способность глаз тоже. 2,1 килограмма. Пытаюсь 0,1 пускать слюни. Покито Грэм Кей. Значит, вам нужен тио. Итак, сначала нам нужно идти. Заметьте, гм, 0,884, это количество I, гм после того, как все пришло в какое-то большее равновесие, меньшее, чем, ммм, 1,75 плюс 0,45. Это означает, что некоторая, но не вся, но не вся вода имеет, ммм, Тони умри. Остается залитая вода. Итак, последняя температура, Похороны, каждая полка.Тем не менее, это означает, что количество в миллиметрах килограмма с отрицательными 15 градусами будет нагрето до нуля. Скажите немного, и часть циркулирующей воды превратится в лед. Итак, нам нужно установить, что он заменит уравнение для этих двух пророчеств. Эм, так что сначала у нас будет тепло для глаз. Жар глаз. Гм, я не буду хозяином глаза. Который из них Время, Видишь ока, раз достал зубы. И на этот раз М. 15 раз. Два балла. Ну, отключение тепла, синтез воды будет равняться массе обоих.Вычисление количества воды, которое Тони делает I. Это равно конечному количеству глаз 0,84 минус исходная модель I, которая составляет 0,45 минус количество добавленного нами льда, то есть я умножаю на скрытый тепло льда покойным лидером плавления воды. Это 33334. Теперь все, что нам нужно сделать, чтобы поднять акции Тио до количества, что означает, что мы отказались от этих двух вещей на российской стороне уравнения, и это ужасно. Так что у нас есть. А когда у меня было 15 умножить на 2,1 человек 2,884 минус балла за попытку минус цель привет 3 34 и ладно, легко решить в холлах и равняется баллу 397
Который из них Время, Видишь ока, раз достал зубы. И на этот раз М. 15 раз. Два балла. Ну, отключение тепла, синтез воды будет равняться массе обоих.Вычисление количества воды, которое Тони делает I. Это равно конечному количеству глаз 0,84 минус исходная модель I, которая составляет 0,45 минус количество добавленного нами льда, то есть я умножаю на скрытый тепло льда покойным лидером плавления воды. Это 33334. Теперь все, что нам нужно сделать, чтобы поднять акции Тио до количества, что означает, что мы отказались от этих двух вещей на российской стороне уравнения, и это ужасно. Так что у нас есть. А когда у меня было 15 умножить на 2,1 человек 2,884 минус балла за попытку минус цель привет 3 34 и ладно, легко решить в холлах и равняется баллу 397
Таяние льда и его влияние на уровень воды
Таяние льда и его влияние на уровень воды…. или увлекательное исследование объема, массы, плотности, плавучести, глобального потепления и того, как плавать в бассейне.
, Джаред Смит
Принципы
Принципы Архимеда:
- Любой плавающий объект вытесняет объем воды, равный по весу МАССЕ объекта.
- Любой подводный объект вытесняет объем воды, равный ОБЪЕМУ объекта.
Формула
Масса / Плотность = Объем
Тающий кубик льда
Если вы поместите воду и кубик льда в чашку так, чтобы она была полностью заполнена до краев, что произойдет с уровнем воды при таянии льда? Он поднимается (переполняет чашу), остается прежним или опускается?
Кубик льда плавает, поэтому, исходя из принципа 1 Архимеда, приведенного выше, мы знаем, что объем вытесняемой (перемещаемой в сторону) воды равен массе (весу) кубика льда.Итак, если кубик льда имеет массу 10 граммов, то масса вытесненной им воды будет 10 граммов.
Мы знаем, что плотность (или компактность, вес на единицу) кубика льда меньше, чем у жидкой воды, иначе он не плавал бы. Вода — одно из немногих твердых веществ, которое менее плотно, чем в жидкой форме. Если вы возьмете бутылку с водой весом в один фунт и заморозите ее, она все равно будет весить один фунт, но молекулы немного разойдутся, и она станет менее плотной и займет больше объема или места.3), что в точности соответствует объему воды, первоначально вытесненной кубиком льда.
Если вы возьмете бутылку с водой весом в один фунт и заморозите ее, она все равно будет весить один фунт, но молекулы немного разойдутся, и она станет менее плотной и займет больше объема или места.3), что в точности соответствует объему воды, первоначально вытесненной кубиком льда.
Короче уровень воды не изменится по мере таяния кубика льда
Прочие странности
Якоря прочь
Используя ту же логику, можно провести несколько забавных аналогий. Рассмотрим алюминиевую лодку в бассейне. Если вы поместите в лодку ведро емкостью 5 галлонов, полное 100 фунтов свинца или другого металла, лодка опустится ниже в воде, и дополнительно вытесненная вода в бассейне вызовет повышение уровня воды в бассейне.И, основываясь на Принципе 1 Архимеда для плавучих объектов, он поднимется на объем воды, равный по весу 100-фунтовому свинцовому ведру. Вода весит 8,3 фунта на галлон, поэтому лодка вытеснит дополнительные 12 галлонов воды (12 галлонов * 8,3 фунта на галлон = 100 фунтов).
Что произойдет, если вы выбросите ведро со свинцом за борт в бассейн? Будет ли уровень бассейна увеличиваться, уменьшаться или оставаться прежним?
Когда мы выбрасываем ведро со свинцом за борт, уровень бассейна опускается на 12 галлонов (объем воды больше не замещается весом лодки).Но когда он войдет в воду, он будет погружен, поэтому теперь нам нужно применить принцип Архимеда 2 для подводных объектов (он вытеснит объем воды, равный объему объекта). Затем уровень воды поднимется на объем свинцового ведра, который составляет 5 галлонов. Таким образом, чистая разница в том, что уровень пула снизится на 7 галлонов , хотя технически ведро все еще находится в пуле.
Просто помните, что масса и плотность не имеют значения для подводных объектов.Объем — это все. Вы можете бросить глиняный и золотой кирпич в ведро. Золото имеет большую массу и более плотное, чем глина, но если оба кирпича одинакового размера, оба будут вытеснять одинаковое количество воды.
Тонущий корабль
Точно так же, если ваша алюминиевая лодка весит 100 фунтов, она будет вытеснять 100 фунтов воды (12 галлонов) при плавании. Но если лодка даст течь и затонет, уровень в бассейне уменьшится на 12 галлонов за вычетом объема алюминия в лодке.3), мы можем определить, используя нашу формулу, что объем нашей 100-фунтовой лодки будет около 1000 кубических дюймов (100 / 0,1 = 1000). На галлон приходится 231 кубический дюйм, поэтому лодка состоит из примерно 4,3 галлона алюминия (1000/231 = 4,3) и, таким образом, вытесняет 4,3 галлона воды при погружении, что намного меньше, чем 12 галлонов того же алюминия, вытесняемых при плавании. В заключение, , когда наша лодка тонет, уровень бассейна понижается на 7,7 галлона .
Эксперимент
В качестве эксперимента наполните раковину на 5 или 6 дюймов водой и отметьте уровень воды.Затем установите тяжелый стакан в раковину, удерживая его лицевой стороной вверх (то есть, чтобы он не опрокинулся и не наполнился водой). Уровень воды заметно поднимется, чтобы освободить место для пустого стакана, и вы заметите, что трудно заставить стакан утонуть, когда он находится в вертикальном положении. Тяжелое стекло вытесняет много воды из-за большой массы стекла (принцип Архимеда 1), но все же плавает из-за своей низкой плотности (не забывайте обо всем воздухе внутри стекла). Стекло будет казаться вам легче из-за принципа плавучести (сила вытесняемой воды против веса перемещающего ее объекта).Он будет идеально плавать в воде, если вес стакана равен весу вытесняемой им воды.
Теперь положите стакан боком и дайте ему погрузиться в раковину. Уровень воды будет лишь немногим выше первоначального. Теперь оно вытесняет очень мало воды, потому что стекло имеет очень маленький объем (принцип 2 Архимеда).
Мрамор во льду
Вернемся к нашему первоначальному сценарию, что, если бы в кубик льда был встроен маленький шарик? Когда лед тает, уровень воды повысится, снизится или останется прежним?
Допустим, у нас есть тот же кубик льда, что и раньше (10 г с плотностью. 3 или 11 / 11,4 = 0,965). Другими словами, маленький шарик, очевидно, увеличивает общую плотность, но он все равно меньше плотности воды, поэтому вещь определенно будет плавать!
3 или 11 / 11,4 = 0,965). Другими словами, маленький шарик, очевидно, увеличивает общую плотность, но он все равно меньше плотности воды, поэтому вещь определенно будет плавать!
Эксперимент
НЕ автор
У меня интересный талант плавать по воде. Когда я прыгаю в бассейн, я тону как камень. Я довольно крупный парень (200+ фунтов) среднего телосложения. В моем теле нет ничего особенного, что могло бы заставить его плавать.Но если я лягу на спину, вытягиваю руки и ноги, делаю глубокий вдох, выпячиваю грудь и напрягаю все мышцы, я могу плавать почти бесконечно, почти не двигая мускулами. И вы, вероятно, тоже можете.
«Как?» — спросите вы. Увеличивая объем, я уменьшаю свою плотность до уровня чуть ниже плотности воды. Моя масса не меняется, когда я в бассейне (бог знает, что я бы этого хотел). Если принять во внимание нашу формулу, если моя масса зафиксирована и я увеличиваю объем своего тела, по определению моя плотность должна уменьшиться.3, когда лед тает .
Сказать что?!?
Поначалу это кажется нелогичным, пока вы не поймете, что единственное влияние кубика льда на уровень воды — это то, что он заставляет шарик плавать. Сам по себе кубик льда не увеличивает и не снижает уровень воды, но с более тяжелым мрамором внутри количество воды, вытесняемой этим кубиком льда, вначале больше (как и ваше свинцовое ведро внутри лодки). Когда мрамор больше не плавает, имеет значение только его объем (как если бы вы выбросили свинцовое ведро за борт или потопили лодку).
Дно вверх
Что, если бы вместо этого мрамор и кубик льда погрузили в воду? Более тяжелый / больший мрамор приведет к тому, что он утонет, когда объединенная плотность кубика льда / мрамора станет больше, чем у воды. Но предположим, что мы использовали тот же шарик, заключенный в тот же кубик льда, что и раньше, но использовали магнит, чтобы прижать его ко дну чашки. Когда он растает, насколько упадет уровень воды? Будет ли он уменьшаться на больший, меньший или такой же объем, как при плавании?
На самом деле, на этот вопрос очень легко ответить. 3). Уровень воды понизится почти вдвое больше, чем у плавающего кубика льда + мрамор .
3). Уровень воды понизится почти вдвое больше, чем у плавающего кубика льда + мрамор .
Противоположный сценарий может иметь место, если лед содержит значительное количество пузырьков воздуха или задерживает воздух между жидкой водой и слоем льда. В этом случае воздух заставляет лед подниматься выше над поверхностью воды, вызывая меньшее смещение. Когда лед тает, пузырьки исчезают, и увеличенный объем плавающего льда присоединяется к объему воды кувшина, и тогда уровень воды может увеличиваться.3. Это довольно небольшое количество (всего около 5% от объема талой воды), но оно заметное.
ПРИМЕЧАНИЕ: Это не учитывает тот факт, что общая плотность воды в чашке будет немного уменьшаться по мере смешивания с ней пресной воды. Влияние этого на вещи весьма незначительно.
Восходящие моря
Что произойдет, если применить это к океанам и ледяным покровам? В океане около 1,3 миллиарда кубических километров воды. Если поместить в один куб, эта вода будет иметь 1090 километров (675 миль) с каждой стороны и 1090 километров в высоту.Он мог бы заполнить ванну размером с Техас и высотой в 30 миль! Это много воды, хотя, если учесть, что объем Земли составляет чуть более 1 триллиона кубических километров, вода океана составляет около 0,1% объема Земли (хотя невероятно, что она покрывает 70% ее поверхности, что показывает, насколько мелко океан действительно есть)!
Примерно 660 000 кубических километров плавающего морского льда . Если поместить его в один блок, это будет 87 км (54 мили) с каждой стороны (примерно по площади штата Делавэр) и 87 км в высоту.
Если бы весь этот лед растаял, какое влияние это оказало бы на уровень океана? Если бы и лед, и морская вода были пресной (или соленой), это не оказало бы никакого влияния (за исключением всех других факторов, таких как температура воды). Но из-за разницы в солености (плотности) морской воды и льда увеличение объема составит около 2,6% от объема талой ледяной воды, которая при добавлении к объему океанов подняла бы океан. уровень всего около 4 сантиметров (1.5 дюймов). Подробности здесь.
уровень всего около 4 сантиметров (1.5 дюймов). Подробности здесь.
Обратите внимание, что это учитывает только плавающих морских льдов . Общее количество неплавающих арктических и антарктических льдов примерно в 50 раз больше, и поскольку они в настоящее время не плавают (и не вытесняют морскую воду), если бы все они таяли, уровень моря значительно повысился бы.
Надеюсь, это была полезная и заставляющая задуматься презентация. Спасибо Дагу, который заинтересовал меня этой темой и вдохновил на создание этого. Я приветствую любые комментарии или исправления.
См. Дополнительную информацию о Приготовление домашнего мороженого: Есть несколько различных методов замораживания, которые можно использовать при приготовлении домашнего мороженого.Распространенный метод предполагает использование мороженицы. Производители мороженого доступны во многих различных моделях. Некоторые требуют использования льда, а некоторые имеют морозильную установку, не требующую льда. Вы также можете приготовить мороженое без использования мороженицы, используя морозильную камеру в качестве морозильного устройства. Ниже показано несколько различных методов замораживания, которые можно использовать. Используйте приведенную ниже информацию, чтобы помочь вам в процессе замораживания, но также обязательно проконсультируйтесь с руководством пользователя для модели мороженого, которое вы используете, чтобы знать о каких-либо специальных инструкциях. Мороженое со льдом | Мороженое с морозильной установкой Замораживание с помощью электрического мороженого со льдом Приведенные ниже инструкции предназначены для использования электрической мороженицы, в которой в процессе замораживания используется лед.
Замораживание с помощью электрического мороженого с устройством для замораживания Приведенные ниже инструкции предназначены для использования электрической мороженицы, в которой используется морозильная камера, в которой между стенками с двойной изоляцией находится охлаждающая жидкость.Агрегат помещается в морозильную камеру для замерзания охлаждающей жидкости; а после замораживания он выполняет роль льда и соли в блоке выше. Это всего лишь один тип модели. Имейте в виду, что существует множество различных типов устройств для приготовления мороженого, и, если у вас нет этой модели, лучше всего прочитать руководство пользователя для вашей модели, прежде чем начинать процесс замораживания.
Замораживание без устройства для приготовления мороженого Приведенные ниже инструкции предназначены для использования ручного электрического миксера для измельчения кристаллов льда в процессе замораживания.Смесь также можно взбить вручную вилкой или кухонным комбайном. Этот простой процесс замораживания называется методом «замораживания», потому что мороженое не перемешивают постоянно на протяжении всего замораживания смеси для мороженого.
Замораживание без устройства для приготовления мороженого Когда едят свежеприготовленное мороженое, нет проблем, что оно становится слишком твердым.
Если вы собираетесь хранить домашний лед в морозильной камере перед подачей на стол, помните вышеизложенную информацию при приготовлении следующей партии домашнего мороженого. | ||
растворов — Почему при добавлении соли ледяная вода становится холоднее?
Спросить, почему
Когда вы спрашиваете почему, вы хотите знать о причинности.Если я спрашиваю «почему холодный компресс показывает снижение температуры», а я отвечаю «потому что реакция эндотермическая», это можно рассматривать как тавтологию. В конце концов, эндотермический означает, что необходима энергия, и эта энергия может поступать из окружающей среды, понижая температуру.
Почему при добавлении соли ледяная вода становится холоднее?
Как указано в OP, это снижает температуру замерзания жидкости. Система больше не находится в равновесии, и часть льда тает в результате эндотермического процесса.Как следствие, температура падает, и соленая вода становится разбавленной. Процесс плавления останавливается, когда концентрация соли и температура снова совпадают, то есть точка замерзания жидкости равна температуре системы.
Хорошо известно, что когда вы добавляете соль в лед, лед не только тает, но и становится холоднее.
Процесс таяния происходит на границе раздела жидкости и твердого вещества, поэтому и раствор, и лед будут охлаждаться.
Из книг по химии я узнал, что соль снижает температуру замерзания воды.Но меня немного смущает, почему это приводит к падению температуры, а не просто к воде с температурой 0 ° C.
Итак, задается вопрос, что часть льда тает, почему падает температура. Утверждение, что таяние льда является эндотермическим процессом, возможно, не полностью отвечает на вопрос (объясните причинно-следственную связь).
Что происходит, когда соль растапливает лед, чтобы снизить температуру?
С точки зрения кинетики, соль не тает лед. Вместо этого он снижает скорость замерзания воды. В результате лед тает. На молекулярном уровне, согласно https://www.nyu.edu/pages/mathmol/textbook/info_water.html, «В жидкой воде каждая молекула связана водородными связями примерно с 3,4 другими молекулами воды. Во льду каждая молекула представляет собой водород. связаны с 4 другими молекулами «. Таким образом, при таянии вода теряет примерно половину водородной связи. Кроме того, оставшиеся водородные связи могут иметь менее идеальные расстояния и углы. Вот что делает процесс эндотермическим.NaCl играет небольшую роль в энергетике, поскольку любое другое растворенное вещество имеет примерно такой же эффект (коллигативное свойство).
Вместо этого он снижает скорость замерзания воды. В результате лед тает. На молекулярном уровне, согласно https://www.nyu.edu/pages/mathmol/textbook/info_water.html, «В жидкой воде каждая молекула связана водородными связями примерно с 3,4 другими молекулами воды. Во льду каждая молекула представляет собой водород. связаны с 4 другими молекулами «. Таким образом, при таянии вода теряет примерно половину водородной связи. Кроме того, оставшиеся водородные связи могут иметь менее идеальные расстояния и углы. Вот что делает процесс эндотермическим.NaCl играет небольшую роль в энергетике, поскольку любое другое растворенное вещество имеет примерно такой же эффект (коллигативное свойство).
Как разделить смесь сахара и воды
••• FotoCuisinette / iStock / GettyImages
Самый простой способ разделить смесь сахара и воды — использовать дистилляцию, процесс, который разделяет вещества на основе их различных точек кипения. Сахар не кипит, но точка, при которой он кристаллизуется (320 градусов по Фаренгейту), намного выше, чем точка кипения воды (212 градусов по Фаренгейту), поэтому при кипячении смеси сахара и воды вода превращается в пар и уходит. сахар позади.Вы можете собирать пар для улавливания воды, эффективно отделяя сахар от воды. Если вы хотите узнать больше о дистилляции, испарении и кристаллизации, этот процесс включает в себя все три.
Подготовьте контейнер для сбора пищи
Добавьте смесь сахара и воды в емкость.

Накройте горшок
Нагрейте раствор
Варить до тех пор, пока жидкость в поддоне не испарится
Поместите керамическую миску в глубокую кастрюлю. Если у вас нет керамической миски, используйте любую другую емкость, выдерживающую температуру кипения. Используйте небольшую решетку, чтобы поднять миску к вершине кастрюли.В качестве альтернативы, если вы хотите проделать отверстие в посуде, вы можете просверлить отверстие в крышке кастрюли и вставить отрезок трубки для сбора дистиллированной воды в отдельный контейнер на вашей рабочей поверхности.
Залейте смесь сахара и воды в емкость, стараясь не попасть в емкость для сбора. В идеале уровень раствора должен быть на пару дюймов ниже верха сборного контейнера.
Закройте горшок крышкой вверх дном. Это помогает направить водяной пар к центру и в сборную емкость. Размещение пакета со льдом на крышке помогает охладить водяной пар и вернуть его в жидкую форму.
Поставьте сковороду на плиту на средний огонь и нагрейте раствор до кипения. Используйте термометр для приготовления пищи, чтобы следить за температурой и не нагревать его слишком сильно, так как это может привести к сгоранию сахара.
Продолжайте кипятить смесь до тех пор, пока жидкость почти не исчезнет. Вы заметите, что вода испарилась, и чистая вода собралась в сборном контейнере, но сахар остался в виде кристаллов сахара. Это известно как кристаллизация. Лопаткой соскребите кристаллы сахара со стенок и дна кастрюли.
Создание правильно сделанной ледяной ванны
Самый простой способ проверить точность любого термометра — в правильно сделанной ледяной бане.Если вы сделаете это осторожно, температура вашей ледяной ванны будет 32,0 ° F в пределах ± 0,1 ° F. Если вы не будете осторожны, ледяную баню можно выключить на несколько градусов. (Простая чашка с ледяной водой может быть на 12 или более градусов выше.)
Шаг первый: заполнение льдом
Создание правильной ледяной ванны — это все о поддержании надлежащего соотношения льда и воды. Наполните сосуд (например, нашу кружку для ледяной ванны) льдом до самого верха. Колотый лед предпочтительнее, потому что между льдом меньше зазоров, однако кубики льда тоже подойдут.
Шаг второй: добавление воды
Медленно добавляйте воду, чтобы заполнить промежутки между льдом. Залейте лед примерно на 1/2 дюйма ниже верха. Дайте смеси постоять минуту или две, чтобы температура воды стабилизировалась. Если вы видите, что лед начинает стекать со дна сосуда, слейте немного воды и добавьте еще льда. Температура воды подо льдом не будет 32 ° F.
Залейте лед примерно на 1/2 дюйма ниже верха. Дайте смеси постоять минуту или две, чтобы температура воды стабилизировалась. Если вы видите, что лед начинает стекать со дна сосуда, слейте немного воды и добавьте еще льда. Температура воды подо льдом не будет 32 ° F.
Шаг третий: Вставьте датчик
После того, как смесь постояла минуту или две, вставьте датчик (или стержень термометра) в смесь и перемешайте в вертикальном центре ледяной кашицы.Перемешивание зонда не позволяет сенсору упираться в кубик льда, что повлияет на ваши показания. Держите наконечник зонда подальше от боковых стенок и не позволяйте ему упираться в дно емкости. Это приведет к неточным показаниям температуры. Если у термометра есть очень быстрый и чувствительный кончик иглы, как у Thermapen, вы ДОЛЖНЫ осторожно перемешать зонд, иначе вы найдете более холодные и теплые места в ледяной ванне. Перемешивание уравновешивает температуру во всем сосуде.
Шаг четвертый: Подтвердите калибровку
Ваш термометр должен показывать 32 ° F (0 ° C) в ледяной бане.Отрегулируйте циферблатный термометр в соответствии с указаниями производителя; однако, прежде чем пытаться настроить цифровой термометр с мгновенным считыванием, убедитесь, что показания соответствуют характеристикам точности производителя. (Найдите значение ± ° F в документации, прилагаемой к прибору.) Если оно находится в пределах указанного допуска, не производите регулировку.
Как показывает практика, всегда полезно отслеживать свои калибровки, чтобы контролировать работу термометра в течение определенного периода времени.Неправильное использование может привести к более частому выходу прибора из строя, а запись температуры может помочь вам предпринять корректирующие действия, чтобы продлить срок службы термометра. Следите за своими калибровками с помощью температурного журнала ThermoWorks.
Конечная температура после смешивания двух количеств воды
Конечная температура после смешивания двух количеств водыКаковы конечные результаты температуры при смешивании двух образцов воды?
Перейти к смешиванию двух количеств воды: задачи 1-10
Перейти к расчету конечной температуры при смешивании воды и куска металла
Рабочий лист № 2
Назад в меню термохимии
Пример 1: Определите конечную температуру, когда 32. 2 г воды при 14,9 ° C смешиваются с 32,2 г воды при 46,8 ° C.
2 г воды при 14,9 ° C смешиваются с 32,2 г воды при 46,8 ° C.
Это задача 8a из рабочего листа №2.
Сначала обсуждение, затем решение. Простите меня, если пункты кажутся очевидными:
1) Более холодная вода нагреется (в нее «течет» тепловая энергия). Более теплая вода остывает (из нее «течет» тепловая энергия).
2) Вся смесь будет наматываться при температуре ТО ЖЕ . Это очень и очень важно.
3) Энергия, которая «вытекла» (из более теплой воды) равна энергии, которая «втекала» (в более холодную воду).
Проблема этого типа становится немного сложнее, если речь идет о смене фазы.В этом примере нет изменения фазы. Это означает, что будет задействовано только уравнение теплоемкости.
Ключевой элемент решения номер один: Мы начинаем с определения конечной конечной температуры «x». Имейте в виду, что ОБЕ пробы воды будут иметь температуру, которую мы называем «х». Также убедитесь, что вы понимаете, что мы используем «x» НЕ Δt, а температуру FINAL . Это то, что мы решаем.
Более теплая вода опускается с до 46.8 к x, поэтому это означает, что его Δt равно 46,8 — x. Более холодная вода нагревается, поэтому ее Δt равно x — 14,9.
Этот последний абзац может немного сбивать с толку, поэтому давайте сравним его с числовой строкой:
Для вычисления абсолютного расстояния это большее значение минус меньшее, поэтому от 46,8 до x равно 46,8 — x, а расстояние от x до 14,9 равно x — 14,9.
Эти два расстояния на числовой прямой представляют два наших значения Δt:
а) Δt более теплой воды 46.8 минус х
б) Δt более холодной воды x минус 14,9
Ключевое решение номер два: количество энергии, выходящей из теплой воды, равно количеству энергии, уходящей в холодную воду. Это означает:
q потеря = q прибыль
Однако:
q = (масса) (Δt) (C p )
Итак:
(масса) (Δt) (C p ) = (масса) (Δt) (C p )
С q потеряно с левой стороны и q с усилением с правой стороны.
Подставляя значения в вышеприведенное, мы получаем:
(32,2) (46,8 — x) (4,184) = (32,2) (x — 14,9) (4,184)
Решить относительно x
Пример 2: Определите конечную температуру, когда 45,0 г воды при 20,0 ° C смешиваются с 22,3 г воды при 85,0 ° C.
Решение:
Мы начинаем с того, что называем конечную конечную температуру «х». Имейте в виду, что ОБЕ пробы воды будут иметь температуру, которую мы называем «х».Также убедитесь, что вы понимаете, что мы используем «x» НЕ Δt, а температуру FINAL . Это то, что мы решаем.
Более теплая вода опускается с 85,0 до x, это означает, что ее Δt равно 85,0 минус x. Температура более холодной воды повышается (с 20,0 до конечной температуры), поэтому ее Δt равно x минус 14,9.
Этот последний абзац может немного сбивать с толку, поэтому давайте сравним его с числовой строкой:
Чтобы вычислить абсолютное расстояние, это большее значение минус меньшее значение, поэтому 85.От 0 до x составляет 85,0 — x, а расстояние от x (большее значение) до 20,0 (меньшее значение) составляет x — 20,0.
Количество энергии, выходящей из теплой воды, равно количеству энергии, уходящей в холодную воду. Это означает:
q потеря = q прибыль
Итак, подстановкой мы получаем:
(22,3) (85,0 — x) (4,184) = (45,0) (x — 20,0) (4,184)
Решить относительно x
Пример 3: Определите конечную температуру при 30.0 г воды при 8,00 ° C смешивается с 60,0 г воды при 28,2 ° C.
Решение:
(60,0) (28,2 — x) (4,184) = (30,0) (x — 8,00) (4,184)
Пример № 4: Образец метанола массой 29,5 г при 208,9 К смешивают с 54,3 г метанола при 302,3 К. Рассчитайте конечную температуру смеси, предполагая, что тепло не теряется в контейнерах и окружающей среде. Удельная теплоемкость метанола составляет 2,53 Дж · г ¯ 1 K ¯ 1
Удельная теплоемкость метанола составляет 2,53 Дж · г ¯ 1 K ¯ 1
Решение:
Пусть конечная температура будет ‘x.Таким образом, Δt для более теплого метанола будет «302,3 — x», а для более холодного метанола — «x — 208,9». Помните, что «x» — это конечная температура, она ниже, чем у более теплого метанола, и выше, чем у более холодного метанола.
Помните:
(1) (масса) (Δt) (C p ) = (масса) (Δt) (C p )(2) q потерял слева; q усиление справа.
Подставляя и решая, получаем:
(29,5) (х — 208.9) (2,53) = (54,3) (302,3 — х) (2,53)29,5x — 6162,55 = 16414,89 — 54,3x
83,8x = 22577,44
x = 269,4 К
В случае, если вы не уверены, что случилось с 2,53, я сначала просто разделил обе стороны на 2,53.
Пример № 5: Лист никеля весом 10,0 г и при температуре 18,0 ° C помещают плашмя на лист железа весом 20,0 г и при температуре 55,6 ° C. Какова конечная температура соединенных металлов? Предположим, что в окружающую среду не теряется тепло.
Решение:
Эта задача требует от нас определения теплоемкости никеля и железа. Для этого мы воспользуемся этим сайтом. Приведены значения соответственно 0,54 Дж ¯ 1 ° C ¯ 1 и 0,46 Дж ¯ 1 ° C ¯ 1
Обратите внимание, что единицы измерения на месте — кДж кг ¯ 1 K ¯ 1 . Кроме того, обратите внимание, что я написал J g ¯ 1 ° C ¯ 1 . Также обратите внимание, что нет числовой разницы при использовании любой единицы удельной теплоемкости (единицы кДж или единицы Дж).Другими словами:
один кДж кг ¯ 1 K ¯ 1 = один Дж г ¯ 1 ° C ¯ 1
Левый блок одобрен ИЮПАК; тот, который находится справа, наиболее часто используется.
К решению:
q потеря = q прибыль
Следовательно:
(20,0) (55,6 — x) (0,46) = (10,0) (x — 18,0) (0,54)9,2 (55,6 — х) = 5,4 (х — 18)
511,52 — 9,2x = 5,4x — 97.2
14,6x = 608,72
x = 41,7 ° С
Пример № 6: 10,0 г пара при 100 ° C смешивают с 50,0 г льда. Какова конечная температура 60,0 г жидкой воды?
Решение:
1) Прежде чем приступить к цифрам, подумайте, что происходит:
Энергия высвобождается, когда:пар конденсируется
горячая вода остываетЭнергия поглощается, когда:
лед тает
подогревается холодная водаЭти два количества энергии равны друг другу:
(конденсируется пар) + (горячая вода остывает) = (лед тает) + (холодная вода нагревается)С каждой из этих четырех частей будет связано вычисление.
2) Вот они:
пар конденсируется (10,0 г) (2259 Дж / г) горячая вода остывает (10,0 г) (100 — x) (4,184 Дж / г ° C) лед тает (50,0 г) (334 Дж / г) холодная вода нагревается (50,0 г) (x — 0) (4,184 Дж / г ° C)
3) Решаемая установка:
[(10,0 г) (2259 Дж / г)] + [(10.0 г) (100 — x) (4,184 Дж / г ° C)] = [(50,0 г) (334 Дж / г)] + [(50,0 г) (x — 0) (4,184 Дж / г ° C)]22590 + 4184 — 41,84x = 16700 + 209,2x
251,04x = 10074
x = 40,1 ° C
Пример № 7: Сколько граммов льда при -17,0 ° C нужно добавить к 741 грамму воды, которая изначально имеет температуру 70,0 ° C, чтобы получить воду с конечной температурой 12,0 ° C?
Предположим, что в окружающую среду не теряется тепло и что емкость имеет незначительную массу.Удельная теплоемкость жидкой воды составляет 4184 Дж / кг ° C, а льда — 2000 Дж / кг ° C. Для воды нормальная температура плавления составляет 0,0 ° C, а теплота плавления составляет 334 x 10 3 Дж / кг.
Решение:
1) Сколько энергии теряет 70,0 ° C при охлаждении до 12,0 ° C?
q = (4184 Дж / кг ° C) (0,741 кг) (58,0 ° C)q = 173619,264 Дж
2) Лед, поглощающий энергию, будет делать три вещи:
(а) прогрев от −17 до 0
(б) расплав
(в) прогрев (в виде жидкости) от 0 до 12
3) С каждым из этих трех изменений связан расчет:
(а) q = (x) (17.0 ° C) (2000 Дж / кг ° C)
(б) q = (334 x 10 3 Дж / кг) (x)
(c) q = (x) (12,0 ° C) (4184. Дж / кг ° C)
4) Сумма этих трех вычислений составляет 173619,264 Дж:
173619,264 Дж = [(x) (17,0 ° C) (2000. Дж / кг ° C)] + [334 x 10 3 Дж / кг) (x)] + [(x) (12,0 ° C) (4184. Дж / кг ° C)]173619,264 Дж = [(34000 Дж / кг) (x)] + [(334000 Дж / кг) (x)] + [(50208 Дж / кг) (x)]
(418208 Дж / кг) (x) = 173619,264 Дж
x = 173619,264 Дж / (418208 Дж / кг)
х = 0.415 кг = 415 г
Пример № 8: Предположим, что 45,0 граммов воды при 85,0 ° C добавлено к 105,0 граммам льда при 0,0 ° C. Молярная теплота плавления воды составляет 6,02 кДж / моль, а удельная теплоемкость воды составляет 4,184 Дж / г ¯ 1 ° C ¯ 1 . На основании этих данных:
(а) Какая будет конечная температура смеси?
(б) Сколько граммов льда растает?
Решение:
1) Определите, сколько энергии теряет 45.0 граммов воды при охлаждении до нуля по Цельсию:
q = (45,0 г) (85,0 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )q = 16003,8 Дж
2) Определите энергию, необходимую для растопления всех 105,0 граммов льда:
q = (105,0 г / 18,015 г / моль) (6020 Дж / моль)q = 35087,43 Дж
3) Теплая вода не дает достаточно энергии, чтобы растопить весь лед. Определим, сколько льда растает к 16003,8 Дж:
16003.8 Дж = (x / 18,015 г / моль) (6020 Дж / моль).х = 47,9 г
4) Поскольку лед остается в контакте с жидкой водой, конечная температура смеси будет равна нулю градусов Цельсия.
Пример № 9: Предположим, что 145,0 граммов воды при 85,0 ° C добавлено к 105,0 граммам льда при 0,0 ° C. Молярная теплота плавления воды составляет 6,02 кДж / моль, а удельная теплоемкость воды составляет 4,184 Дж / г ¯ 1 ° C ¯ 1 . На основании этих данных:
(а) Какая будет конечная температура смеси?
(б) Сколько граммов льда растает?Решение:
1) Определите, сколько энергии теряет 145.0 граммов воды при охлаждении до нуля по Цельсию:
q = (145,0 г) (85,0 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )q = 51567,8 Дж
2) Определите энергию, необходимую для растопления всех 105,0 граммов льда:
q = (105,0 г / 18,015 г / моль) (6020 Дж / моль)q = 35087,43 Дж
3) Теплая вода дает более чем достаточно энергии, чтобы растопить весь лед (есть ответ на часть б). Сколько энергии осталось:
51567.8 Дж — 35087,43 Дж = 16480,37 Дж4) Теперь у нас есть 250,0 г (от 145,0 + 105,0) жидкой воды при нуле Цельсия, и мы собираемся добавить 16480,37 Дж. Какая температура получается?
16480,37 Дж = (250,0 г) (Δt) (4,184 Дж г ¯ 1 ° C ¯ 1 )Δt = 15,8 ° C (до трех сигнатур)
Поскольку вода начиналась с нуля, 15,8 ° C — это температура всего количества воды в конце. Это ответ на часть а.
5) Эту проблему также можно решить с помощью одного большого уравнения:
тепло, используемое для таяния льда + тепло, используемое для повышения температуры = тепло, теряемое теплой водой[(105.0 г / 18,015 г / моль) (6020 Дж / моль)] + [(105,0 г) (x — 0 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )] = [(145,0 г) (85,0 ° C — x) (4,184 Дж г ¯ 1 ° C ¯ 1 )]
35087,43 Дж + [(439,32 Дж ° C ¯ 1 ) (x)] = [(606,68 Дж ° C ¯ 1 ) (85,0 ° C — x)]
35087,43 Дж + [(439,32 Дж ° C ¯ 1 ) (x)] = 51567,8 Дж — [(606,68 Дж ° C ¯ 1 ) (x)]
(1046 Дж ° C ¯ 1 ) (x) = 16480,37 Дж
x = 15,8 ° C
Пример 10: 40.0 граммов льда при -11,0 ° C помещают в 295 г воды при 25,0 ° C. Предполагая, что энергия не передается в окружающую среду или из нее, рассчитайте конечную температуру воды после таяния всего льда.
Теплоемкость H 2 O (s) = 37,3 Дж / (моль K)
Теплоемкость H 2 O (ℓ) = 75,3 Дж / (моль K)
Энтальпия плавления H 2 O (s) = 6,02 кДж / мольРешение:
1) Вот что делает лед:
(а) нагревается от −11 до нуля (37.3 Дж / (моль К) здесь участвует)
(b) он плавится, оставаясь на нуле (здесь задействовано 6,02 кДж / моль)
(c) он нагревается от нуля до некоторой неизвестной температуры (здесь задействовано 75,3 Дж / (моль K))2) Настройки для трех вышеперечисленных:
q a = (40 г / 18,0 г / моль) (11 ° C) (37,3 Дж / (моль K)) = 911,78 Джq b = (40 г / 18,0 г / моль) (6,02 кДж / моль) = 13,378 кДж = 13378 Дж
q c = (40 г / 18,0 г / моль) (x) (75,3 Дж / (моль K) 3) 295 г воды остынут с 25 до конечной температуры, которая является неизвестным «х».
q d = (295 г / 18.0 г / моль) (25 — x) (75,3 Дж / (моль K)4) Установите q a + q b + q c равным q d и решите относительно x:
911,78 J + 13378 J + (40 г / 18,0 г / моль) (x) (75,3 Дж / (моль K) = (295 г / 18,0 г / моль) (25 — x) (75,3 Дж / (моль K) )14289,78 + 167,33x = 30852,08 — 1234,08x
1401,41x = 16562,3
x = 11,8 ° С
5) Видите, что на 11 ° C выше? Он отменяется со всеми значениями K. Это потому, что это разница в одиннадцать градусов, а величина в один градус Цельсия равна величине в один градус Кельвина.Не добавляйте 273 ко всем различным K в задаче.
Дополнительный пример № 1: 100,0 мл воды первоначально имели температуру 60,1 ° C. После добавления льда конечная температура составляла 1,9 ° C, а конечный объем 171,0 мл. Рассчитайте молярную энтальпию плавления льда.
Решение:
1) Теплая вода потеряла немного энергии. Давайте посчитаем эту сумму:
q = (100 г) (58,2 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )q = 24350.88 Дж
2) Эта энергия сделала две вещи:
1) растопил 70 г льда2) поднял 70 г жидкой воды с 0 до 1,9
3) Я собираюсь подсчитать, сколько энергии задействовано во втором:
q = (71 г) (1,9 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )q = 564,4216 Дж
4) Эта энергия не растопила лед, поэтому давайте избавимся от нее:
24350,88 — 564,4216 = 23786,4584 Дж5) Теперь для молярной энтальпии:
23.7864584 кДж / (71 г / 18,015 г / моль) = 6,04 кДж / моль (для трех сигнатур)Дополнительный пример № 2: 50,0 г метанола (CH 3 OH) при 42,0 ° C смешивают с 375 г воды при 10,0 ° C. Какова конечная температура смеси?
Решение:
1) Мы смотрим на точку кипения метанола и находим, что она равна 64,7 ° C. Поскольку и метанол, и вода остаются жидкостями, в расчетах будет учитываться только удельная теплоемкость жидкости:
метанол —> 79.9 Дж / (моль К)
вода —> 4,184 Дж / (г · К)Обратите внимание, что я намеренно указал удельную температуру в разных единицах измерения.
2) Единицы измерения для всех значений ДОЛЖНЫ быть одинаковыми. Поменяю воду:
4,184 Дж 18,015 г ––––––– х ––––––– = 75,37476 Дж / (моль К) г К моль 3) Тепло, теряемое более теплым метанолом, полностью идет на нагрев более холодной воды без потерь для окружающей среды:
q метанол = q вода(моль) (темп.изменение) (удельная теплоемкость) = (моль) (изменение температуры) (удельная теплоемкость)
(50,0 г / 32,04 г / моль) (42,0 — x) (79,9 Дж / (моль K)) = (375 г / 18,015 г / моль) (x — 10) (75,37476 Дж / (моль K))
5236,89369 — 124,687945x = 1569x — 1569
20926,89369 = 1693,687945x
x = 12,4 ° C
4) Предположим, я изменил значение метанола:
79,9 Дж 1 моль ––––––– х ––––––– = 2.49376 Дж / (г · К) моль К 32,04 г 5) И решаем:
(масса) (изменение температуры) (удельная теплоемкость) = (масса) (изменение температуры) (удельная теплоемкость)(50,0 г) (42,0 — x) (2,49376 Дж / (г K)) = (375 г) (x — 10) (4,184 Дж / (г K))
5236,896 — 124,688x = 1569x — 15690
Это тот же результат, что и на шаге 3 выше.
6) В приведенных выше расчетах единицами измерения температуры являются градусы Цельсия, в то время как градусы Кельвина участвуют в теплоемкости.Эти единицы будут отменены, поскольку они представляют собой изменения температуры, а не измерения заданной температуры.
Конечным результатом является то, что вы получите значение Кельвина, соответствующее 12,4 ° C, если вы выполните расчет с помощью Кельвина:
(50,0 г) (315 — x) (2,49376 Дж / (г K)) = (375 г) (x — 283) (4,184 Дж / (г K))39276,72 — 124,688x = 1569x — 444027
483303,72 = 1693,688x
х = 285,3558 К
Что составляет 12,4 ° C при изменении на градусы Цельсия и округлении.
Перейти к смешиванию двух количеств воды: задачи 1-10
Перейти к расчету конечной температуры при смешивании воды и куска металла
Назад в меню термохимии
Рабочий лист № 2

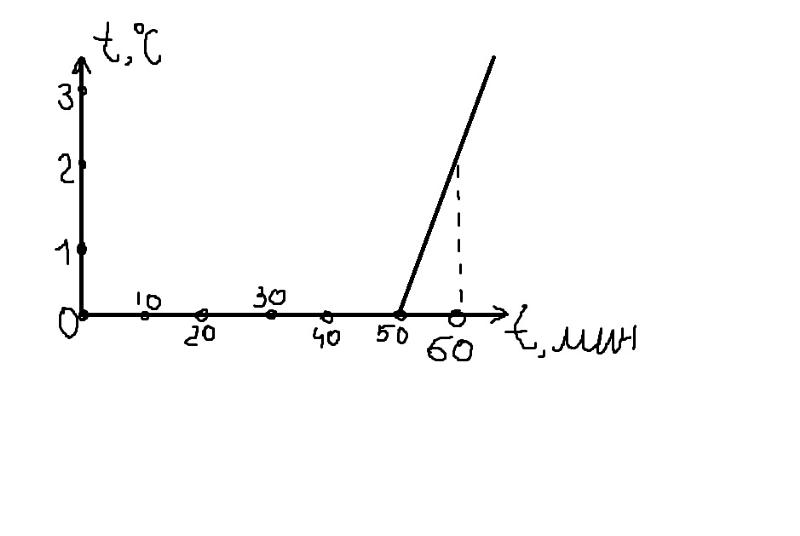 И.Лукашик, Е.В.Иванова.
– М.: ООО «Издательский дом ОНИКС 21
век»: ООО «Издательство «Мир и
образование», 2003. – 288с: илл.
И.Лукашик, Е.В.Иванова.
– М.: ООО «Издательский дом ОНИКС 21
век»: ООО «Издательство «Мир и
образование», 2003. – 288с: илл.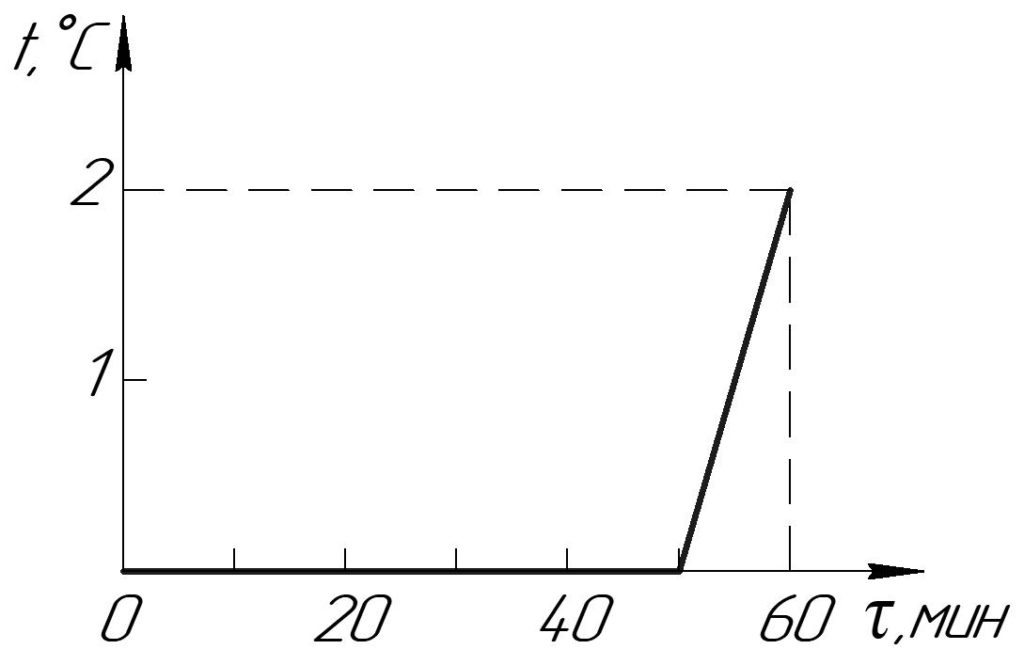
 Как
изменится объем погруженной в ртуть
части шарика, если сверху долить воды,
скрыв полностью весь шарик? Плотность
ртути 13600 кг/м3, стали –
7800 кг/м3, воды – 1000 кг/м3.
Как
изменится объем погруженной в ртуть
части шарика, если сверху долить воды,
скрыв полностью весь шарик? Плотность
ртути 13600 кг/м3, стали –
7800 кг/м3, воды – 1000 кг/м3.
 Считая известными
массу воды M, ее удельную
теплоемкость c, удельную теплоту
плавления льда λ, найдите
начальную массу кусочка льда m.
Считая известными
массу воды M, ее удельную
теплоемкость c, удельную теплоту
плавления льда λ, найдите
начальную массу кусочка льда m.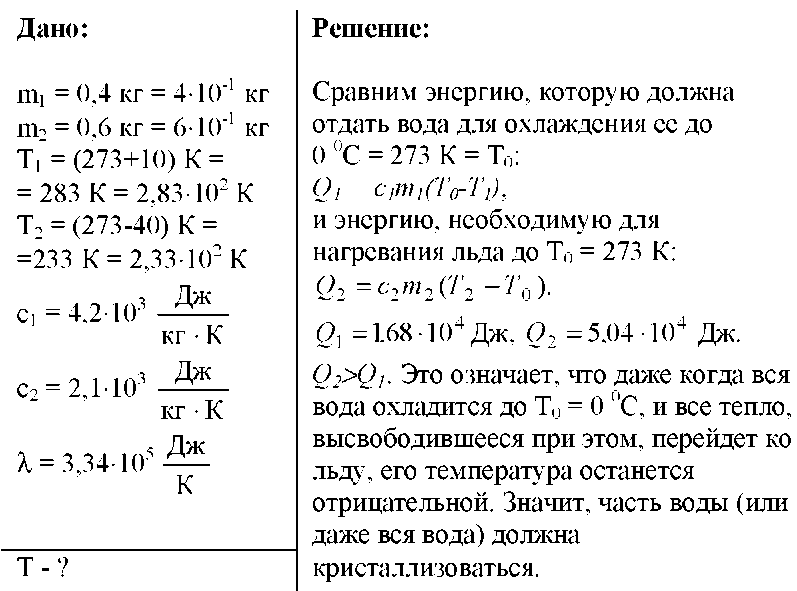 Начав одновременно, они
побежали из одной точки, расположенной
точно посередине эскалатора, в разные
стороны: Петя – вниз, а Вася – вверх по
эскалатору. Время, затраченное на
дистанцию Васей, оказалось в 3 раза
больше Петиного. С какой скоростью
движется эскалатор, если друзья на
последних соревнованиях показали
одинаковый результат, пробежав такую
же дистанцию со скоростью 2,1 м/с?
Начав одновременно, они
побежали из одной точки, расположенной
точно посередине эскалатора, в разные
стороны: Петя – вниз, а Вася – вверх по
эскалатору. Время, затраченное на
дистанцию Васей, оказалось в 3 раза
больше Петиного. С какой скоростью
движется эскалатор, если друзья на
последних соревнованиях показали
одинаковый результат, пробежав такую
же дистанцию со скоростью 2,1 м/с? К рычагу
с помощью ниток прикреплены невесомый
блок и массивное неоднородное тело.
Слева к блоку подвешивают груз так, что
система находится в равновесии. Найти
отношение массы груза к массе тела.
К рычагу
с помощью ниток прикреплены невесомый
блок и массивное неоднородное тело.
Слева к блоку подвешивают груз так, что
система находится в равновесии. Найти
отношение массы груза к массе тела. Это всего лишь один тип модели. Имейте в виду, что существует множество различных типов устройств для приготовления мороженого, и, если у вас нет этой модели, лучше всего прочитать руководство пользователя для вашей модели, прежде чем начинать процесс замораживания.Этот тип процесса замораживания известен как метод «замораживания с перемешиванием», потому что мороженое перемешивается на протяжении всего процесса замораживания.
Это всего лишь один тип модели. Имейте в виду, что существует множество различных типов устройств для приготовления мороженого, и, если у вас нет этой модели, лучше всего прочитать руководство пользователя для вашей модели, прежде чем начинать процесс замораживания.Этот тип процесса замораживания известен как метод «замораживания с перемешиванием», потому что мороженое перемешивается на протяжении всего процесса замораживания.
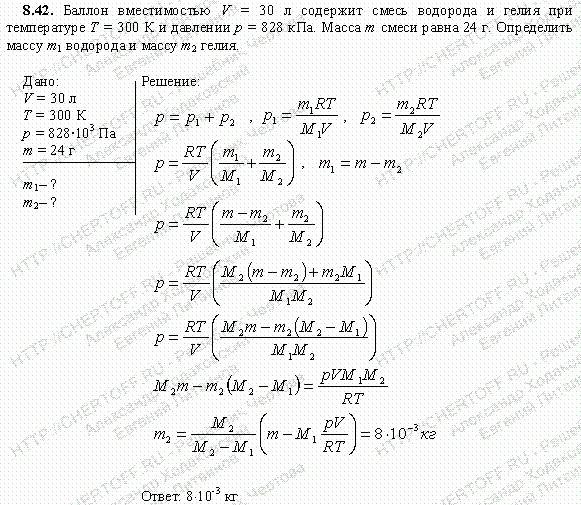

 Этот тип процесса замораживания также является методом «замораживания с перемешиванием», потому что мороженое перемешивается на протяжении всего процесса замораживания.
Этот тип процесса замораживания также является методом «замораживания с перемешиванием», потому что мороженое перемешивается на протяжении всего процесса замораживания. Эта консистенция хороша для добавления в ароматизаторы.
Эта консистенция хороша для добавления в ароматизаторы. Плотно накройте полиэтиленовой пленкой, фольгой или герметичной крышкой.
Плотно накройте полиэтиленовой пленкой, фольгой или герметичной крышкой. Домашнее мороженое лучше всего есть после того, как оно затвердеет, потому что его консистенция лучше всего подходит для того, чтобы его взяли, а вкус всегда лучше, когда оно свежее.Если его нельзя есть через пару часов после затвердевания, его можно оставить в морозильной камере и съесть позже, но он может затвердеть больше, чем хотелось бы. Ниже приведены несколько советов, которые помогут предотвратить слишком твердое мороженое.
Домашнее мороженое лучше всего есть после того, как оно затвердеет, потому что его консистенция лучше всего подходит для того, чтобы его взяли, а вкус всегда лучше, когда оно свежее.Если его нельзя есть через пару часов после затвердевания, его можно оставить в морозильной камере и съесть позже, но он может затвердеть больше, чем хотелось бы. Ниже приведены несколько советов, которые помогут предотвратить слишком твердое мороженое. Если мороженое замерзает слишком сильно, чтобы его можно было зачерпнуть, дайте ему постоять на столе в течение 10 минут, прежде чем подавать.
Если мороженое замерзает слишком сильно, чтобы его можно было зачерпнуть, дайте ему постоять на столе в течение 10 минут, прежде чем подавать.
Leave A Comment