2=64\)

 

\(a=\sqrt64=8\)

 

 

Найдем площадь заданного треугольника:

 

\(S={1\over2}*6*8=24\)

 

Ответ: 24.

 

 

Задача № 2

 

В треугольнике АВС угол С равен 90° (Рис. 2), угол B равен 58°, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

 

 

 

Решение

 

По условию задачи, CD — медиана в прямоугольном треугольнике. По свойству медианы имеем:

 

CD=AD=BD

 

Тогда треугольник ACD — равнобедренный, с основанием АС. И углы при его основании равны. Тогда получаем:

 

угол ACD=угол A=90°-58°=32°

 

 

Ответ: 32.

 

 

Задача № 3

 

Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. (Рис. 3). Ответ дайте в градусах.

 

 

 

Решение

 

Рассмотрим треугольник АОС. По условию задачи, угол САО равен половине угла САВ. А угол АСЕ равен половине угла АСВ. По свойству треугольников сумма углов равна 180°. Тогда получим:

 

угол AOC=180°-\(90°\over2\)-\(32°\over2\)=119°

 

 

Тогда угол АОЕ равен:

 

угол AOE=180°-119°=61°

 

Ответ: 61.

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Маргарита Руслановна Мередова

Репетитор по математике

Стаж (лет)

Образование:

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Елена Михайловна Глущенко

Репетитор по математике

Стаж (лет)

Образование:

Стерлитамакский государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Людмила Анатольевна Бочкарева

Репетитор по математике

Стаж (лет)

Образование:

Орский Государственный Педагогический Институт имени Т. Г.Шевченко

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

  • Математика
  • Репетитор по физике
  • Репетитор по химии
  • Репетитор по русскому языку
  • Репетитор по английскому языку
  • Репетитор по обществознанию
  • Репетитор по истории России
  • Репетитор по биологии
  • Репетитор по географии
  • Репетитор по информатике

Специализации

  • Подготовка к ЕГЭ по математике (базовый уровень)
  • Подготовка к олимпиадам по химии
  • Репетитор для подготовки к ЕГЭ по физике
  • Репетитор для подготовки к ОГЭ по физике
  • Подготовка к олимпиадам по физике
  • Английский язык для начинающих
  • Репетитор для подготовки к ОГЭ по истории
  • Репетитор для подготовки к ВПР по русскому языку
  • Репетитор для подготовки к ОГЭ по обществознанию
  • Репетитор по географии для подготовки к ОГЭ

Похожие статьи

  • Как легко разделить на 0,5
  • РУДН: прикладная математика и информатика (очно / заочно)
  • ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
  • ЕГЭ по математике, базовый уровень. Преобразование алгебраических выражений
  • Задачи на исследование функций
  • Топ-10 книг, которые нужно прочитать до окончания школы
  • Пищевые отравления: как защитить ребенка в лагере, деревне и городе
  • Зелень в рационе ребенка: когда и какую можно давать

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Система использования ключевых задач геометрии при обучении математике

Похожие презентации:

Деятельность пришкольного лагеря с дневным пребыванием детей «Дружба» МОУ школа № 71

Моя будущая профессия: юрист

Развитие интеллектуальной одаренности детей Новосибирской области с использованием дистанционных образовательных технологий

Элементы комбинаторики ( 9-11 классы)

Творческий проект «Планирование кухни-столовой»

Моя будущая профессия — военный

Кейсы (ситуации взаимодействия ребёнка и взрослого)

Творческий проект «мой профессиональный выбор»

Развитие связной речи у дошкольников

Технология В. А. Илюхиной «Письмо с открытыми правилами» для учащихся начальных классов

1. Система использования ключевых задач геометрии при обучении математике.

Учитель математики МБОУ г. Абакана «СОШ №1»
Ольга Ивановна Капарчук
В треугольнике ABC угол C равен
120°, AD и BE — биссектрисы,
пересекающиеся в точке O. Найдите
угол AOB. Ответ дайте в градусах.

3. В треугольнике ABC, CD – медиана, угол C  равен 90°, угол B равен 58°. Найдите угол  ACD . Ответ дайте в градусах.

В треугольнике ABC, CD – медиана,
угол C равен 90°, угол B равен 58°. Найдите
угол ACD . Ответ дайте в градусах.
Острые углы прямоугольного
треугольника равны 69° и 21° . Найдите
угол между биссектрисой СН и медианой
СD, проведёнными из вершины прямого
угла.
Ответ дайте в градусах.
С
В
D
H
А
В треугольнике
Найдите
.
угол
равен 90°,
.
.
Найдите площадь четырехугольника,
изображенного на клетчатой бумаге с
размером клетки 1 см 1 см (см. 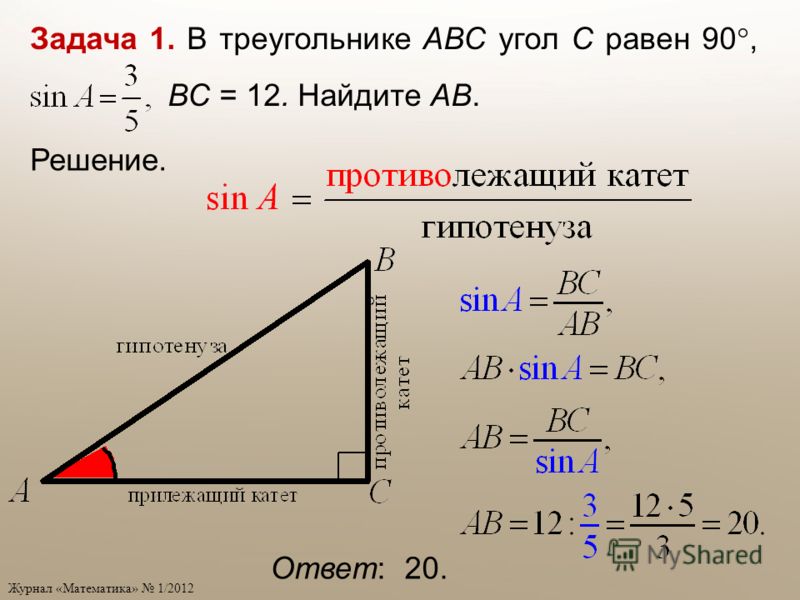рис.). Ответ
дайте в квадратных сантиметрах.

7. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

8. Хорда AB   стягивает дугу окружности в 92º . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через

Хорда AB стягивает дугу окружности в 92º . Найдите
угол ABC между этой хордой и касательной к окружности,
проведенной через точку B . Ответ дайте в градусах.
Гл.2 Тема:
Треугольники
№ задачи
114
Страница
37
(о равенстве медиан, проведенных к равным
сторонам)
128
41
(о равенстве биссектрис, проведенных к равным
сторонам)
133
42
(признак равнобедренного треугольника)
176
(еще один признак равенства треугольников)
52
Гл.3 Тема: Параллельные
прямые
№ задачи
211
(биссектрисы накрест лежащих
углов параллельны, биссектрисы
односторонних углов
перпендикулярны)
212
Страница
67
67
Гл. 4 Тема: Соотношение между сторонами и
углами треугольника
№ задачи
232
233
Страница
72
72
(биссектриса внешнего угла, при вершине
равнобедренного треугольника, параллельна
основанию)
239
74
( о медиане и высоте треугольника, проведённых из
одной вершины)
242
(о биссектрисе внешнего угла треугольника)
244
(о прямой проведенной через основание
биссектрисы параллельно другой стороне)
75
75
261
81
279
87
300
(расположение оснований высот в
тупоугольном треугольнике)
348
( об угле между медианой и высотой в
прямоугольном треугольнике)
349
90
(о медиане и высоте прямоугольного
треугольника)
94
94
Гл.5 Тема: Четырехугольники
№ задачи
Страница
374
(о биссектрисе угла параллелограмма)
385
(т. Фалеса)
388, 389
(свойства и признак равнобедренной трапеции)
404
(о медиане прямоугольного треугольника, проведенной к
гипотенузе)
424
104
105
106
113
115
(об углах выпуклого четырёхугольника)
428
439
(об отрезке, соединяющем середины сторон оснований трапеции)
115
116
Гл. 6 Тема: Площадь
№ задачи
474
(медиана треугольника делит его на два равновеликих)
476
(вывод формулы площади ромба, зная его диагонали)
478
Страница
128
129
129
(формула площади выпуклого четырёхугольника, диагонали
которого пересекаются под углом 90)
489
132
(S, равностороннего треугольника)
500
134
(сравнение площадей)
512
(о длине отрезка, параллельного основаниям трапеции и
делящего трапецию на две равновеликих)
135
519
(площадь трапеции с высотой h и
перпендикулярными диагоналями)
521
524
(формула Герона)
532
831
834
837
135
135
135
136
217
217
217
Гл.7 Тема: Подобные треугольники
№ задачи
Страница
535
(о делении биссектрисой треугольника противолежащей
стороны)
543
140
141
(об отношении сходственных сторон подобных
треугольников)
545
141
(об отношении площадей подобных треугольников)
547
(об отношении периметров подобных треугольников)
141
556
145
569
153
(об отрезке, соединяющих середины диагоналей трапеции)
574
(о высоте прямоугольного треугольника, проведенного из
вершины прямого угла)
154
Гл. 7 Тема: Подобные треугольники
№ задачи
598
Страница
154
(еще 2 формулы для вычисления площади
равнобедренного треугольника)
848
849
(об отрезках, соединяющих основания высот
остроугольного треугольника)
859
(признак параллелограмма)
862
866
868
219
219
220
220
221
221
Тема: Соотношение между сторонами и углами
прямоугольного треугольника
№ задачи
Страница
159
594,595
605
(о диагонали трапеции с известными основаниями)
609
(о свойстве биссектрисы угла треугольника)
615
(об отрезке трапеции, проходящем через точку
пересечения диагоналей параллельно основаниям )
619
(Свойство биссектрисы внешнего угла треугольника)
624
(о медианах треугольника)
626
161
161
162
162
163
163
Гл.8 Тема: Окружность
№ задачи
Страница
655
173
(вписанный и центральный угол, опирающиеся
на одну и туже дугу)
659
174
(градусные меры дуг, заключенные между
параллельными хордами)
664
174
668
175
670
(касательная и секущая, проведенные из одной
точки)
672
175
175
Гл. 8 Тема: Окружность
№ задачи
Страница
680
180
685
180
694
(о диаметре окружности, вписанной в
прямоугольный треугольник)
696
185
697
(формула площади описанного многоугольника)
704
(о вписанном прямоугольном треугольнике)
186
186
186
Гл.8 Тема: Окружность
№ задачи
Страница
186
709, 710
719
(о градусной мере угла между секущими)
189
724
189
725
(формула радиуса окружности, вписанного в
прямоугольную трапецию)
727
190
729
190
734
190
190
Гл.8 Тема: Окружность
№ задачи
Страница
735
190
887
(о биссектрисе угла треугольника)
223
890
223
892
(формула площади прямоугольной трапеции,
описанной около окружности)
893
(т. Птолемея)
894
(формула Эйлера, d²=R²-2Rr)
223
223
223
Гл.9 Тема: Векторы
№ задачи
Страница
797
805
808
817
(сумма трех медиан треугольника)
818
(дополнительное свойство диагоналей ромба)
821
831
834
837
213
214
215
216
216
216
217
217
217
Гл. 10 Тема: Метод координат
№ задачи
Страница
234
927
932
943
952
(Середина гипотенузы прямоугольного треугольника
равноудалена от всех его вершин)
958
972
981
991
(отработка понятия расстояния между двумя точками)
1008
1009 (формула для вычисления длины медианы
треугольника)
238
239
240
241
246
246
250
251
251
Гл.11 Тема: Соотношения между
сторонами и углами треугольника
№ задачи
Страница
1013,1015(нахождение синуса, косинуса, тангенса через
заданные тригонометрические функции)
1021(формула площади параллелограмма)
1033(об отношении стороны треугольника к синусу
противолежащего угла)
1054
255
1055
1059(формула вычисления площади выпуклого
четырехугольника)
1069(о нахождении угла между медианами в
равнобедренном треугольнике)
1075
1077
270
272
261
262
270
273
274
274
Гл.12 Тема: Длина окружности и площадь
круга
№ задачи
1096
(об отношениях площадей правильных многоугольников)
Страница
283
1097,1098
283
1102,1103
(об изменении длины окружности относительно радиуса)
287
1115,1116,1117
288
1132
(об отношении периметров правильных
многоугольников)
1140
290
1143
292
291

27.

ПАМЯТКА 1. Чтение условия задачи
2. Чертёж с буквенным обозначением
3. Краткая запись условия задачи
4. Перенос данных условия на чертёж,
выделение данных элементов
5. Запись требуемых формул и теорем
6. Вычерчивание отдельных деталей на
дополнительных чертежах
(«деталировка»)
7. Анализ данных задачи, привязка
искомых величин к элементам чертежа.
8. «Синтез» — алгоритм решения
9. Реализация данного алгоритма
10. Проверка правильности решения
11. Запись ответа

English     Русский Правила

геометрия — В $\треугольнике ABC$ $BD$ медиана, $\угол DAB=15$ и $\угол ABD=30$. Найдите $\угол ACB$.

$\begingroup$

Как следует из названия, цель состоит в том, чтобы найти величину недостающего угла на следующем рисунке. Хотя я решил это, что я покажу ниже в качестве ответа, я не совсем уверен, что мой ответ точен, поэтому я публикую это здесь, чтобы узнать, верен ли мой ответ и есть ли какие-либо альтернативные подходы.

Пожалуйста, опубликуйте свои собственные подходы к этому!

  • геометрия
  • тригонометрия
  • конкурс-математика
  • евклидова геометрия
  • треугольники

$\endgroup$

2

$\begingroup$

На рисунке $\Delta AED$ вместе с точкой $C$ составляют заданную цифру.

Построения:

(1) Равносторонний треугольник $BAC$,

90$

$\endgroup$

1

$\begingroup$

Это будет мой подход. Я также добавлю объяснение!

Вот как я это делаю:

1.) Обозначьте треугольник как $\triangle ABC$, где $BD$ — медиана с $AD=DC$. Поверните $\треугольник ABD$ по медиане $BD$ так, чтобы новый треугольник $\треугольник EBD$ был конгруэнтен $\треугольнику ABD$ с $AD=ED=DC$. Поскольку $\угол ABD=\угол EBD=30$, а отрезок $AB=EB$, можно сделать вывод, что $AB=EB=AE$, поэтому $\треугольник ABE$ равносторонний.

2.) Отсюда следует, что $\angle EAD=\angle AED=45$. Соедините точки $E$ и $C$ через $EC$. Заметим, что поскольку центр описанной окружности $\треугольника AEC$ лежит на $AC$, то $\треугольник AEC$ прямоугольный. Но, поскольку $\angle EAD=45$ и $\angle AEC=90$, отсюда следует, что $\angle ECA=45$, поэтому $\треугольник AEC$ является равнобедренным прямоугольным треугольником, а это означает, что $AB=AE= ЭБ=ЕС$.

3.) Из приведенного выше следует, что $E$ является центром описанной окружности $\треугольника ABC$ (поскольку $E$ равноудалено от всех вершин $\треугольника ABC$). Отсюда следует, что $\angle ACB$ составляет половину $\angle AEB$ (теорема о вписанном угле). Следовательно, $\угол ACB=30$.

$\endgroup$

6

$\begingroup$

Пусть $AD=DC=a$ и $DB=b$ согласно рисунку Гоку. Тогда по закону синусов в левом и прямоугольном треугольниках соответственно:

$\frac{a}{\sin30}=\frac{b}{sin15}$ и $\frac{a}{\sin(135-x)} =\frac{b}{sinx}$.

Исключая $a$ и $b$, получаем $\sin15\sin(135-x)=\sin30\sin x$.

После упрощений находим $\cot x=\frac{\sqrt{2}-\sqrt{2-\sqrt{3}}}{\sqrt{2-\sqrt{3}}}=\sqrt{ 3}$ и, таким образом, $x=30$.

$\endgroup$

2

$\begingroup$

Пусть $\color{blue}{l=(BD)}$ и $\color{blue}{s=s_l}$ симметрия.

$$s(\угол ABD)=\угол DBE=30°$$ $$s([AB])=[BE]\имеет \треугольник ABE \text{равнобедренный}$$ $$\угол ABE=60°\подразумевает \треугольник ABE\текст{равносторонний}\подразумевает \угол AEB=60°$$

Затем аргументы, предоставленные @Goku[Интересно, действительно ли я упростил :), но я люблю экзо ]

$\endgroup$

$\begingroup$

Мы можем выбрать систему координат, в которой $\D\$ лежит в начале координат с вершинами $\A\$ и $\C\$ в точках $\(-a\,\0)\$ и $ \ (а \ , \ 0 ) \ \ , \ $ соответственно. Несложно показать, что $ \ m(\угол BDC) \ = \ 45º \ \ . \ $ Vertex $ \ B \ $ тогда является пересечением прямой $ \ \overrightarrow{AB} \ \ , \ $ с уравнением $ \ y \ = \ -m·(x + a) \ \ $ (с $ \ m \ = \ \tan 15º \ ) \ $ , и линия $ \ \overrightarrow{DB} \ \ , \ $ с уравнением $ \ y \ = \ -x \ \ . \ $ Координаты $ \ B \ $ находятся из $$ -mx — ma \ \ = \ \ -x \ \ \Rightarrow \ \ x_B \ \ = \ \ a·\left(\frac{m}{1 — m} \right) \ \ = \ \ -y_B \ \ ; $$ этот результат разумен, поскольку $ \ 0 \ < \ m \ < \ 1 \ \ Rightarrow \ -y_B \ < \ 0 \ < \ x_B \ \ . $

Вершина $ \ B \ $ также лежит на прямой $ \ \overrightarrow{CB} \ $ неизвестного наклона $ \ M \ = \ \tan \theta \ $ через вершину $ \ C \ \ , \ $, поэтому ее уравнение $ \ y \ = \ M·(x-a) \ \ . \ $ Таким образом, мы определяем $$ -a·\left(\frac{m}{1 — m} \right) \ \ = \ \ M·\left( \ a·\left[\frac{m}{1 — m} \right] — a \right) \ \ \Rightarrow \ \ -ma \ \ = \ \ M · (ma \ — \ a \ + \ ma) $$ $$ \Rightarrow \ \ M \ \ = \ \ \frac{m}{1 \ — \ 2m} \ \ . 2 \ — \ 4m \ + \ 1) \ \ = \ \ 0 \ \ \Стрелка вправо \ \ m \ \ = \ \ 0 \ \ , \ \ 2 \ \pm \ \кв3\\ . \ ] $$ 9{\ круг} \end{выровнено} $$

$\endgroup$

Математическая задача: Треугольник ABC — вопрос № 3668, задачи на построение геометрии

Построить треугольник ABC по данным c = 60 мм hc = 40 мм и b = 48 мм
анализ
этапы процедуры
построение

Правильный ответ:

a =  52,154 мм

Пошаговое объяснение:

a=52,154=52,154 мм

Попробуйте рассчитать с помощью нашего калькулятора треугольников.


Вы нашли ошибку или неточность? Не стесняйтесь

пишите нам

. Спасибо!

Советы по использованию связанных онлайн-калькуляторов

См. также наш калькулятор тригонометрических треугольников.

Вам необходимо знать следующие знания для решения этой задачи по математике:

  • Planimetrics
  • ТРИУНГИ
Темы, темы:
  • Геометрия. 0166
    • Практика для 12-летних
    • Практика для 13-летних

     

    Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1

    • Построить 4129
      • Построить треугольники ABC, зная длины треугольников ABC. стороны c = 8 см, a = 5 см и длина Vc = 3,5 см. Проведите анализ, запишите процедуру проектирования, выполните ее и определите количество решений.
      • Треугольник SSA
        Построить треугольник ABC, если |AB| = 5 см v a = 3см, CAB = 50°. Это создание этапов анализа и построения.
      • Построить 25851
        A. Построить ∆ABC так, чтобы c = 55 мм, α = 45°, β = 60°. Б. Нарисуйте любой остроугольный треугольник и постройте его высоты.
      • Построение трапеции
        Построить трапецию, если b = 4 см, c = 7 см, d = 4,5 см, v = 3 см (Процедура, обсуждение, эскиз, анализ, построение)
      • Начертить треугольник
        Построить равнобедренный треугольник ABC, если AB = 7 см, размер угла ABC равен 47°, стороны | переменный ток | = | до нашей эры |. Измерьте размер стороны ВС в мм.
      • Построить
        Построить треугольник ABC, вписанная окружность имеет радиус r = 2 см, угол альфа = 50 градусов = 8 см. Сделайте эскиз, анализ, построение и описание.
      • Процедура 4578
        Я должен построить треугольник — процедура и решение сторона a = 7 см угол β = 40 медиана стороны c: tc = 5 см
      • Конструкция
        Постройте треугольник ABC, если вы знаете: размер стороны AC равен 6 см, величина угла ACB равна 60°, а расстояние центра тяжести T от вершины A равно 4 см. (Эскиз, анализ, обозначение построения, построение)
      • Гипотенуза 65744
        Постройте прямоугольный треугольник ABC с гипотенузой AB: а) | АБ | = 72 мм, | Британская Колумбия | = 51 мм б) | АБ | = 58 мм, | переменный ток | = 42 мм
      • Линейка и циркуль
        Используйте линейку и циркуль, чтобы построить треугольник ABC с AB 5см BAC 60° и ACB 45°.
      • Коэффициент 4872
        Выяснить, подобны ли треугольники ABC и A’B’C’, определить коэффициент подобия и записать сходство: a = 40 мм, b = 48 мм, c = 32 мм, a´ = 60 мм, b´ = 50 мм, c´ = 40 мм
      • Две высоты и сторона
        Постройте треугольник ABC, если сторона равна c = 7 см, высота до стороны a va = 5 см, а высота до стороны b: vb = 4 см.