Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°.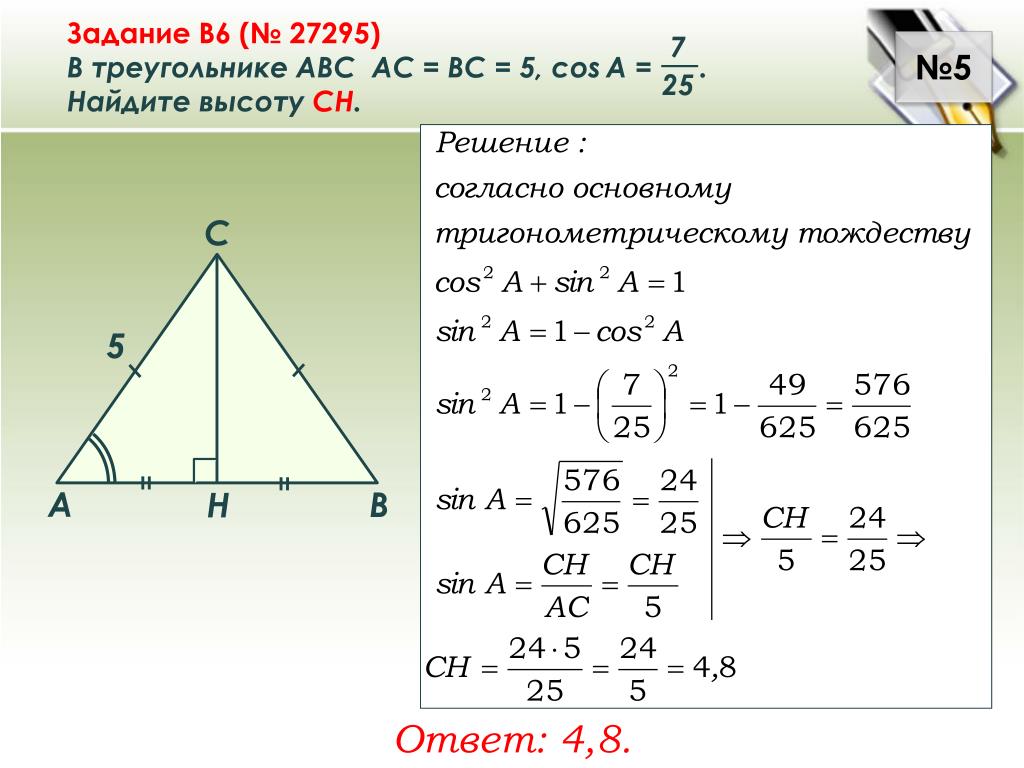 Найдите радиус описанной около этого треугольника окружность.
На пишите пожалуйста решение
Найдите радиус описанной около этого треугольника окружность.
На пишите пожалуйста решение
Тепловоз вёз много вагонов 7 с углем и 15 цестерн,сколько вагонов с лесом?с лесом чуть больше чем угля и чуть меньше цестерн
Эссе. На тему: Современный мир спасёт
Боковое ребро правильной треугольной призмы равно 9 см,а диагональ боковой грани равна 15 см. Найти площадь боковой и полной поверхности призмы
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Пользуйтесь нашим приложением
Главная → Видеоуроки → ЕГЭ по математике. Профильный уровень. Задание 7. Описание видеоурока: В видеоуроке показан процесс решения одного из заданий типа B8 по математике. Условие задачи: В треугольнике ABC AC=BC, AB=8, tgA=33/(4sqrt33). Найдите AC. 00:06:52 Валерий Волков 4 30.07.2014 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Примеры связанных вопросов
|
Важные вопросы для 10 класса Математика Глава 6 Треугольники
- Треугольники Класс 10 Mind Map
- Треугольники Класс 10 Ex 6.
 1
1 - Треугольники класса 10 Ex 6.1 на языке хинди средний
- Треугольники Класс 10 Ex 6.2
- Треугольники класса 10 Ex 6.2 на языке хинди средний
- Треугольники Класс 10 Ex 6.3
- Треугольники класса 10 Ex 6.3 на языке хинди средний
- Треугольники Класс 10 Ex 6.4
- Треугольники класса 10 Ex 6.4 на языке хинди средний
- Треугольники Класс 10 Ex 6.5
- Треугольники, класс 10, пример 6.5 на языке хинди, средний уровень
- Треугольники Класс 10 Ex 6.6
- Треугольники класса 10 Ex 6.6 на языке хинди средний
- Дополнительные вопросы для 10 класса Треугольники по математике
- Треугольники Класс 10 Заметки Математика Глава 6
- Образец NCERT, класс 10, математика, глава 6, треугольники
- Важные вопросы по математике для 10 класса Глава 6 Треугольники
Треугольники Класс 10 Важные вопросы Очень короткий ответ (1 балл)
Вопрос 1.
Если ∆ABC ~ ∆PQR, периметр ∆ABC = 32 см, периметр ∆PQR = 48 см и PR = 6 см, то найти длина АС. (2012)
(2012)
Решение:
∆ABC ~ ∆PQR …[Дано
Вопрос 2.
∆ABC ~ ∆DEF. Если AB = 4 см, BC = 3,5 см, CA = 2,5 см и DF = 7,5 см, найдите периметр ∆DEF. (2012, 2017D)
Решение:
∆ABC – ∆DEF …[Дано
Вопрос 3.
Если ∆ABC ~ ∆RPQ, AB = 3 см, BC = 5 см, AC = 6 см, RP = 6 см и PQ = 10, то найти QR. (2014)
Решение:
∆ABC ~ ∆RPQ …[Дано
∴ QR = 12 см
Вопрос 4.
В ∆DEW, AB || РЭБ. Если AD = 4 см, DE = 12 см и DW = 24 см, то найдите значение DB. (2015)
Решение:
Пусть BD = x см
тогда BW = (24 – x) см, AE = 12 – 4 = 8 см
In ∆DEW, AB || EW
Вопрос 5.
В ∆ABC, DE || до н.э., найдите значение х. (2015)
Решение:
In ∆ABC, DE || BC …[Дано
x(x + 5) = (x + 3)(x + 1)
x 2 + 5x = x 2 + 3x + x + 3
x 2 + 5x – x 2 – 3x – x = 3
∴ x = 3 см
Вопрос 6.
На данном рисунке, если DE || BC, AE = 8 см, EC = 2 см и BC = 6 см, затем найдите DE. (2014)
(2014)
Решение:
В ∆ADE и ∆ABC,
∠DAE = ∠BAC …Общее
∠ADE – ∠ABC … [Соответствующие углы
∆ADE – ∆ΑΒC …[AA следствие
Решение:
Пусть YR = x
\(\frac{\mathrm{PQ}}{\mathrm{XQ}}=\frac{\mathrm{PR}}{\mathrm{YR}}\) … [Теорема Фалеса
Вопрос 8.
Длины диагоналей ромба равны 24 см и 32 см. Вычислите длину высоты ромба. (2013)
Решение:
Диагонали ромба являются ⊥ биссектрисами друг друга.
∴ AC ⊥ BD,
OA = OC = \(\frac{A C}{2} \Rightarrow \frac{24}{2}\) = 12 см
OB = OD = \(\frac{B D}{2 } \Rightarrow \frac{32}{2}\) = 16 см
В rt. ∆BOC,
Вопрос 9.
Если PQR равносторонний треугольник и PX ⊥ QR, найдите значение PX 2 . (2013)
Решение:
Высота равностороннего треугольника ∆,
Класс треугольников 10 Важные вопросы Краткий ответ-I (2 балла)
Вопрос 10.
Стороны AB и AC и периметр P треугольника ∆ABC соответственно в три раза больше соответствующих сторон DE и DF и периметра P треугольника ∆DEF. Два треугольника подобны? Если да, найдите \(\frac { ar\left( \triangle ABC \right) }{ ar\left( \triangle DEF \right) } \) (2012)
Решение:
Дано: AB = 3DE и AC = 3DF
…[∵ Отношение площадей двух подобных ∆ равно отношению квадратов их соответствующих сторон
Вопрос 11.
На рисунке EF || AC, BC = 10 см, AB = 13 см и EC = 2 см, найти AF. (2014)
Решение:
BE = BC – EC = 10 – 2 = 8 см
Пусть AF = x см, тогда BF = (13 – x) см
In ∆ABC, EF || AC … [Дано
Вопрос 12.
X и Y — точки на сторонах AB и AC соответственно треугольника ABC, такие что \(\frac{\mathbf{A X}}{\mathbf{A B}}=\frac {1}{4}\), AY = 2 см и YC = 6 см. Найти, XY || БК или нет. (2015)
Решение:
Дано: \(\frac{A X}{A B}=\frac{1}{4}\)
AX = 1K, AB = 4K
∴ BX = AB – AX
= 4K – 1K = 3K
∴ XY || BC … [В силу обращения теоремы Фалеса
Вопрос 13.
На данном рисунке ∠A = 90°, AD ⊥ BC. Если BD = 2 см и CD = 8 см, найдите AD. (2012; 2017D)
Решение:
∆ADB ~ ∆CDA …[Если перпендикуляр провести из вершины прямого угла rt. ∆ на гипотенузу, то As по обе стороны от ⊥ подобны всему D и друг другу
∴ \(\frac{B D}{A D}=\frac{A D}{C D}\) …[∵ Стороны пропорциональный
AD 2 = BD , DC
AD 2 = (2) (8) = 16 ⇒ AD = 4 см
Вопрос 14.
В ∆ABC, ∠BAC = 90° и AD ⊥ BC. Докажите, что AD\frac{B D}{A D}=\frac{A D}{C D} = BD × DC. (2013)
Решение:
В 1т. ∆BDA, ∠1 + ∠5 = 90°
В рт. ∆BAC, ∠1 + ∠4 = 90° …(ii)
∠1 + ∠5 = ∠1 + ∠4 …[Из (i) и (ii)
.. ∠5 = ∠4 …(iii)
В ∆BDA и ∆ADC
∠5 = 24 … [Из (iii)
∠2 = ∠3 …[Каждые 90°
∴ ∆BDA ~ ∆ADC…[AA сходство
\(\frac{B D}{ A D}=\frac{A D}{C D}\)
… [In ~ Поскольку соответствующие стороны БА пропорциональны
∴ AD 2 = BD × DC
Вопрос 15.
Лестница длиной 6,5 м поставлена у стены так, что ее основание находится на расстоянии 2,5 м от стена. Найдите высоту стены в том месте, где ее касается вершина лестницы. (2015)
Найдите высоту стены в том месте, где ее касается вершина лестницы. (2015)
Решение:
Пусть AC — лестница, а AB — стена.
∴Требуемая высота, AB = 6 м
Вопрос 16.
На рисунке ABC и DBC два прямоугольных треугольника. Докажите, что AP × PC = BP × PD. (2013)
Решение:
В ∆APB и ∆DPC,
∠1 = ∠4 … [Каждый = 90°
∠2 = ∠3 …[Вертикально напротив. ∠s
∴ ∆APB ~ ∆DPC …[следствие AA
⇒ \(\frac{\mathrm{BP}}{\mathrm{PC}}=\frac{\mathrm{AP}}{\mathrm{PD}} \) … [Стороны пропорциональны
∴ AP × PC = BP × PD
Вопрос 17.
На данном рисунке QA ⊥ AB и PB ⊥ AB. Если AO = 20 см, BO = 12 см, PB = 18 см, найдите AQuestion (2017OD)
Решение:
В ∆OAQ и ∆OBP
∠OAQ = ∠OBP … [Каждый 90°
∠AOQ = ∠BOP … [вертикально противоположные углы
Треугольники Класс 10 Важные вопросы Краткий ответ-II (3 балла)
Вопрос 18.
На данном рисунке CD || Лос-Анджелес и Германия || переменного тока. Найдите длину CL, если BE = 4 см и EC = 2 см. (2012)
Найдите длину CL, если BE = 4 см и EC = 2 см. (2012)
Решение:
В ∆ABL, CD || LA
Вопрос 19.
Если отрезок пересекает стороны AB и AC ∆ABC в точках D и E соответственно и параллелен BC, докажите, что \(\frac{A D}{A B}=\frac{A E} {А С}\). (2013)
Решение:
Дано. В ∆ABC, DE || BC
Чтобы доказать. \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}\)
Доказательство.
В ∆ADE и ∆ABC
∠1 = ∠1 … Общий
∠2 = ∠3 … [Соответствующие углы
∆ADE ~ ∆ABC …[AA сходство
∴ \(\frac{\mathbf{A D}}{\ mathbf{A B}}=\frac{\mathbf{A} \mathbf{E}}{\mathbf{A C}}\)
…[In ~∆s соответствующие стороны пропорциональны
Вопрос 20.
В ∆ABC , Делавэр || BC с D на AB и E на AC. Если \(\frac{A D}{D B}=\frac{3}{4}\) , найдите \(\frac{\mathbf{B} C}{\mathbf{D} \mathbf{E}}\) . (2013)
Решение:
Дано: В ∆ABC, DE || BC с D на AB и E
на AC и \(\frac{A D}{D B}=\frac{3}{4}\)
Чтобы найти: \(\frac{\mathrm{BC}}{\mathrm {DE}}\)
Доказательство. Пусть AD = 3k,
Пусть AD = 3k,
DB = 4k
∴ AB = 3k + 4k = 7k
В ∆ADE и ∆ABC
∠1 = ∠1 …[Общий
∠2 = ∠3 … [Соответствующие углы
∴ADE ~ ∆ABC …[AA подобие
Вопрос 21.
На рисунке, если DE || ОБ и ЭФ || BC, то докажите, что DF || ОС. (2014)
Решение:
Дано. В ∆ABC, DE || ОБ и ЭФ || БК
Чтобы доказать. ДФ || ОС
Доказательство. В ∆AOB, DE || OB … [Дано
Вопрос 22.
Если периметры двух подобных треугольников ABC и DEF равны 50 см и 70 см соответственно и одна сторона ∆ABC = 20 см, то найдите соответствующую сторону ∆DEF. (2014)
Решение:
Дано. ∆ABC ~ ∆DEF,
Периметр(∆ABC) = 50 см
Периметр(∆DEF) = 70 см
Одна сторона ∆ABC = 20 см
Найти. Соответствующая сторона ∆DEF (т.е.) DE. ∆ABC ~ ∆DEF …[Дано
∴ Соответствующая сторона ADEF = 28 см
Вопрос 23.
Вертикальный столб длиной 8 м отбрасывает на землю тень длиной 6 см, а башня отбрасывает тень длиной 30 м.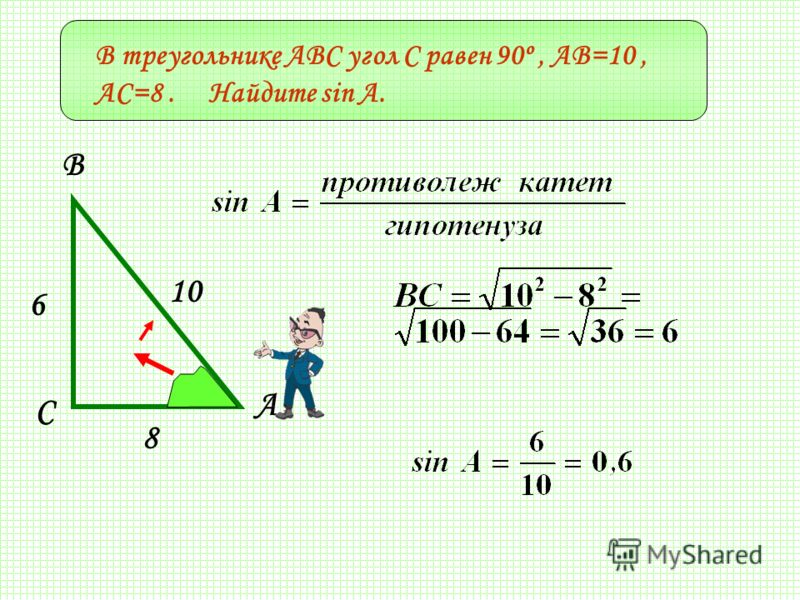 Найдите высоту башни. (2014)
Найдите высоту башни. (2014)
Решение:
Пусть BC будет полюсом, а EF будет башней Тень AB = 6 м и DE = 30 м.
В ∆ABC и ∆DEF,
∠2 = ∠4 … [каждые 90°
∠1 = ∠3 … [угол возвышения Солнца одновременно
∆ABC ~ ∆DEF …[AA сходство
\(\frac {A B}{D E}=\frac{B C}{E F}\) … [In -As соответствующие стороны пропорциональны
⇒ \(\frac{6}{30}=\frac{8}{\mathrm{EF}}\) ∴ EF = 40 м
Вопрос 24.
На данном рисунке EB ⊥ AC, BG ⊥ AE и CF ⊥ AE (2015)
Докажите, что:
(a) ∆ABG ~ ∆DCB
(b) \(\frac{\mathbf{B C}}{\mathbf{B D}}=\frac{\mathbf{B E} }{\mathbf{B A}}\)
Решение:
Дано: EB ⊥ AC, BG ⊥ AE и CF ⊥ AE.
Доказать: (a) ∆ABG – ∆DCB,
(b) \(\frac{B C}{B D}=\frac{B E}{BA}\)
Доказательство: (a) В ∆ABG и ∆DCB ,
∠2 = ∠5 … [каждые 90°
∠6 = ∠4 … [соответствующие углы
∴ ∆ABG ~ ∆DCB … [По подобию AA
(Следовательно доказано)
∴ ∠1 = ∠3 …(CPCT … [В ~∆s соответствующие углы равны
(b) В ∆ABE и ∆DBC,
∠1 = ∠3 … (доказано выше
∠ABE = ∠5 … [каждый равен 90°, EB ⊥ AC (Дано)
∆ABE ~ ∆DBC … [По подобию AA
\(\frac{B C}{B D }=\frac{B E}{B A}\)
… [В ~∆s соответствующие стороны пропорциональны
∴ \(\frac{B C}{B D}=\frac{B E}{BA}\) (Отсюда доказано )
Вопрос 25.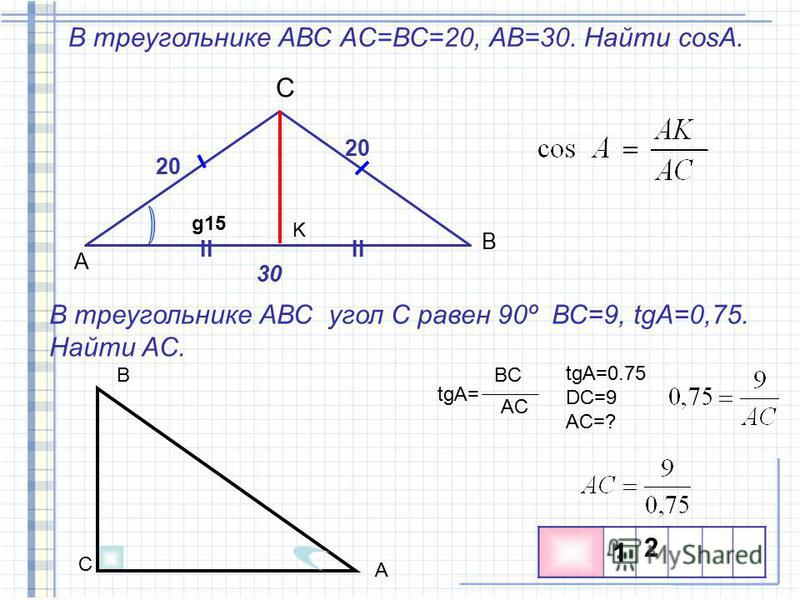
∆ABC ~ ∆PQR, AD — медиана BC, PM — медиана QR. Докажите, что \(\frac{\mathbf{A B}}{\mathbf{P Q}}=\frac {\mathbf{A D}}{\mathbf{P M}}\).(2017D)
Решение:
∆ABC ~ ∆PQR … [Дано
∠1 = ∠2 … [В ~∆s соответствующие углы равны
Вопрос 26.
Укажите, подобны ли данные пары треугольников или нет. В случае сходства укажите критерий. (2015)
Решение:
(b) В ∆PQR, ∠P + ∠Q + ∠ZR = 180° …[Свойство суммы углов ∆
45° + 78° + ∠R = 180°
∠ R = 180° – 45° – 78° = 57°
In ∆LMN, ∠L + ∠M + ∠N = 180° …[Свойство суммы углов ∆
57° + 45° + ∠N = 180°
∠N = 180° – 57 – 45° = 78°
∠P = ∠M … (каждый = 45°
∠Q = ∠N … (каждый = 78°
∠R = ∠L …(каждый = 57°
∴ ∆PQR – ∆MNL …[По теореме подобия ААА
Вопрос 27.
В фигуре ∆ABC D делит CA в отношении 4 : 3. Если DE || BC, то найти ar (BCDE) : ar (∆ABC).(2015)
Решение:
Дано:
D делит CA на 4 : 3
CD = 4K
DA = 3K
DE ||BC …[Дано
В ∆AED и ∠ABC,
∠ 1 = ∠1 …[общий
∠2 = ∠3 … соответствующие углы 9{ 2 } } =\frac { ar\left( \треугольник AED \right) }{ ar\left( \треугольник ABC \right) } =\frac { 9 }{ 49 } \)
Пусть ar(∆AED) = 9p
и ar(∆ABC) = 49p
ar(BCDE) = ar (∆ABC) – ar (∆ADE)
= 49p – 9p = 40p
∴ \(\frac { ar\left( BCDE \right) } { ar\left( \triangle ABC \right) } =\frac { 40p }{ 49p } \)
∴ ar (BCDE) : ar(AABC) = 40 : 49
Вопрос 28.
На данном рисунке DE || BC и AD : DB = 7 : 5, найти \frac { ar\left( \triangle DEF \right) }{ ar\left( \triangle CFB \right) } [/latex] (2017OD)
Решение:
Дано: In ∆ABC, DE || BC и AD : DB = 7 : 5.
Чтобы найти: \(\frac { ar\left( \triangle DEF \right) }{ ar\left( \triangle CFB \right) } \) = ?
Доказательство: Пусть AD = 7k
и BD = 5k, тогда
AB = 7k + 5k = 12k
В ∆ADE и ∆ABC
∠1 = ∠1 … (Общее
∠2 = ∠ABC … [Соответствующие углы 9001
Вопрос 29.
На данном рисунке отрезок XY параллелен стороне AC треугольника ∆ABC и делит треугольник на две равные по площади части.Найти отношение \(\frac{\mathbf{A} \ mathbf{X}}{\mathbf{A B}}\).(2017OD)
Решение:
У нас есть XY || AC … [Дано
Итак, ∠BXY = ∠A и ∠BYX = ∠C …[Соответствующие углы
∴ ∆ABC ~ ∆XBY …[AA критерий подобия
Вопрос 30.
На данном рисунке AD ⊥ BC и BD = \(\frac{1}{3}\)CD. Докажите, что 2AC 2 = 2AB 2 + BC 2 . (2012)
(2012)
Решение:
BC = BD + DC = BD + 3BD = 4BD
∴ \(\frac{\mathrm{BC}}{4}\) = BD
In rt. ∆ADB, AD 2 = AB 2 – BD 2 ….(ii)
В rt. ∆ADC, AD 2 = AC 2 – CD 2 …(iii)
Из (ii) и (iii) получаем
AC 2 – CD 2 = AB 2 – BD
2
AC 2 = AB 2 – BD 2 + CD 2
∴ 2AC 2 = 2AB 2 + BC 2 (Hence proved)
Question 31.
На данном рисунке ∆ABC прямоугольный в точке C и DE ⊥ AB. Докажите, что ∆ABC ~ ∆ADE, и, следовательно, найдите длины AE и DE. (2012, 2017Д)
Решение:
Дано: ∆ABC есть rt. ∠ed в C и DE ⊥ AB.
AD = 3 см, DC = 2 см, BC = 12 см
Доказать:
(i) ∆ABC ~ ∆ADE; (ii) АЭ = ? и ДЭ = ?
Доказательство. (i) В ∆ABC и ∆ADE,
∠ACB = ∠AED … [каждый 90°
∠BAC = ∠DAE …(общий .
∴ ∆ABC ~ ∆ADE …[критерий подобия AA
(ii) ∴ \ (\frac{A B}{A D}=\frac{B C}{D E}=\frac{A C}{A E}\) … [стороны пропорциональны
\(\frac{A B}{3}=\frac{12 }{D E}=\frac{3+2}{A E}\)
…..[In rt.∆ACB, … AB 2 = AC 2 + BC 2 (По теореме Пифагора)
= (5) 2 + (12) 2 = 169
∴ AB = 13 см
∆APB ~ ∆CPA
[Если из вершины прямого угла треугольника провести перпендикуляр к гипотенузе, то As по обе стороны перпендикуляра подобны всему треугольнику и друг другу.
∴ \(\frac{\mathrm{AP}}{\mathrm{CP}}=\frac{\mathrm{PB}}{\mathrm{PA}}\) … [В ~∆s соответствующие стороны пропорциональны
∴ ПА 2 = ПБ. CP (следовательно доказано)
Вопрос 33.
ABCD — ромб. Докажите, что AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2 . (2013)
(2013)
Решение:
Дано. В ромбе ABCD диагонали AC и BD пересекаются в точке O.
Чтобы доказать: AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD Pro9 из
∴ OA = OC и
OB = OD
In rt. ∆AOB,
AB 2 = OA 2 + OB 2 … [теорема Пифагора 9{2} \)
4ab 2 = AC 2 + BD 2
AB 2 + AB 2 + AB 2 + AB 2 + AB 2 + AB 2 + AB 2 + AB 2 + AB 2 + 2 + AB 2 + 2 + AB .
∴ AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2
. диагонали трапеции ABCD пересекаются в точке o. Если AB = 2CD, найти отношение площади ∆AOB к площади ∆COD. (2013)
Решение:
В ∆AOB и ∆COD, … [Альтерн.
 ∠s
∠s ∠1 = ∆3
∠2 = ∠4
Вопрос 35.
Диагонали четырехугольника ABCD пересекаются в точке O так, что \(\frac{A O}{B O}=\frac{ С О}{Д О}\). Докажите, что ABCD — трапеция. (2014)
Решение:
1-й способ.
Дано: четырехугольник ABCD, в котором
AC и BD пересекаются друг с другом в точке 0.
Такой, что \(\frac{A O}{B O}=\frac{C O}{DO}\)
Доказать: ABCD является трапецией
Пост.: Из O нарисуйте OE || CD.
Но это альтернативные внутренние углы
∴ AB || Квадрат постоянного тока. ABCD — трапеция.
Треугольники Класс 10 Важные вопросы Подробный ответ (4 балла).
Вопрос 36.
В прямоугольнике ABCD точка E — середина AD. Если AD = 40 м и AB = 48 м, то найти EB. (2014D)
Решение:
E — середина AD …[Дано
AE = \(\frac{40}{2}\) = 20 м
∠A = 90° …[Угол прямоугольника
В рт. ∆BAE,
EB 2 = AB 2 + AE 2 …[теорема Пифагора
= (48) 2 + (20) 2
= 2304 + 400 = 2704
∴ EB = \(\sqrt{2704}\) = 1047 м 90 90 Вопрос 37.
Пусть ABC — треугольник, а D и E — две точки на стороне AB такие, что AD = BE. Если ДП || БК и эквалайзер || AC, то докажите, что PQ || АБ. (2013)
Решение:
В ∆ABC,
DP || БК
и эквалайзер || AC … [Дано
Теперь, в ∆ABC, P и Q делят стороны CA и CB соответственно в том же отношении.
∴ ПК || АБ
Вопрос 38.
На рисунке ∠BED = ∠BDE & E делит BC в отношении 2 : 1.
Докажите, что AF × BE = 2 AD × CF. (2015)
Решение:
Построение:
Нарисуйте CG || DF
Доказательство: E делит
BC на 2 : 1.
\(\frac{B E}{E C}=\frac{2}{1}\) …(i)
Вопрос 39.
В данном фигура, AD = 3 см, AE = 5 см, BD = 4 см, CE = 4 см, CF = 2 см, BF = 2,5 см, затем найдите пару параллельных прямых и, следовательно, их длины. (2015)
Решение:
Вопрос 40.
Если стороны AB, BC и медиана AD AABC пропорциональны соответствующим сторонам PQ, QR и медиане PM PQR, покажите, что ∆ABC ~ ∆PQR.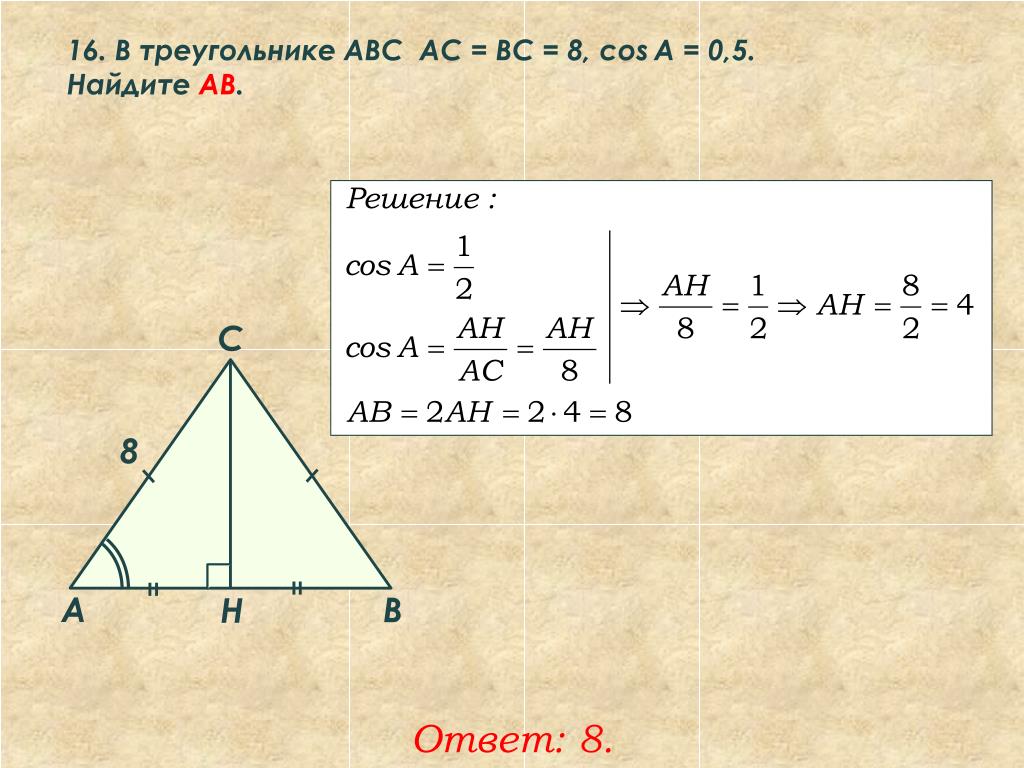 (2017OD)
(2017OD)
Решение:
Вопрос 41.
Докажите, что отношение площадей двух подобных треугольников равно отношению площадей их соответствующих сторон. (2012)
Решение:
Дано: ∆ABC ~ ∆DEF
Вопрос 42.
Сформулируйте и докажите обратную теорему Пифагора. Используя приведенную выше теорему, решите следующее: В ∆ABC, AB = 6\(\sqrt{3}\) см, BC = 6 см и AC = 12 см, найдите ∠B. (2015)
Решение:
Часть I:
Утверждение: Докажите, что в треугольнике, если квадрат одной стороны равен сумме квадратов двух других сторон, то угол, противолежащий первой стороне, прямой.
Чтобы доказать: ∠ABC = 90°
Const.: Нарисуйте прямой угол ∆DEF, в котором DE = BC и EF = AB.
Доказательство: В ст. ∆ABC,
AB 2 + BC 2 = AC 2 …(i) Дано
В rt. ∆DEF
DE 2 + EF 2 = DF 2 … [По теореме Пифагора
BC 2 + AB 2 = DF 2 …(ii)…[∵ DE = BC; EF = AB
Из (i) и (ii) получаем
AC 2 = DF 2 = AC = DF
Теперь DE = BC …[По построению
EF = AB …[По построению
DF = AC … [Доказано выше:
∴ ∆DEF = ∆ABC … (Конгруэнтность SSS:
∴ ∠DEF = ∠ABC …[c. p.c.t.
p.c.t.
∵ ∠DEF = 90° ∴ ∠ABC = 90°
Дано: В правом направлении, ∆ABC
AB 2 + BC 2 = AC 2
AB 2 + BC 2 = (6\(\sqrt{3}\)) 2 + (6) 2
= 108 + 36 = 144 = (12) 2
АВ 2 + ВС
9 = 2 АС 2 ∴ ∠B = 90° … [Выше теорема
Вопрос 43.
На данном рисунке BL и CM — медианы треугольника ABC с прямым углом в A. Докажите, что: 4(BL 2 + CM 2 ) = 5BC 2 (2012)
Решение:
Дано: BL и CM медианы ∆ABC, прямые в A.
Доказать: 4(BL 2 9{2}}{4}\)
4MC 2 = 4CA 2 + BA 2
Складывая (ii) и (iii), получаем
4BL 2 + 4MC 2 = 1 8BA 393 + CA 2 + 4CA 2 + BA 2 …[From (ii) & (iii)
4(BL 2 + MC 2 ) = 5BA 2 + 5CA 2
4(BL 2 + MC 2 ) = 5(BA 2 + CA 2 )
∴ 4(BL 2 + MC 2 ) = 185BC 2 9 00319 … [Используя (1)
Отсюда доказано.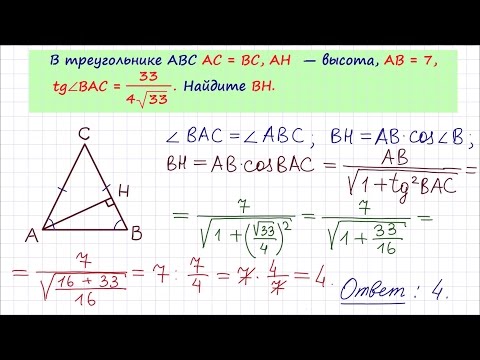
Вопрос 44.
На данном рисунке AD является медианой ∆ABC и AE ⊥ BC. (2013)
Докажите, что b 2 + c 2 = 2p 2 + \(\frac{1}{2}\) a 2 .
Решение:
Доказательство. Пусть ED = x
BD = DC = \(\frac{B C}{2}=\frac{a}{2}\) = …[∵ AD — медиана
In rt. ∆AEC, AC 2 = AE 2 + EC 2 …..[По теореме Пифагора
b 2 = h 2 9{2}}{4}\) …(ii)
In rt. ∆AEB, AB 2 = AE 2 + BE 2 … [По теореме Пифагора
Вопрос 45.
В ∆ABC перпендикуляр из A на сторону BC к AABC пересекает BC в точке D такой, что DB = 3 CD. Докажите, что 2 AB 2 = 2 AC 2 + BC 2 . (2013; 2017ОД)
Решение:
В рт. ∆ADB,
AD 2 = AB 2 – BD 2 …(i) [теорема Пифагора
In rt. ∆ADC,
г. н.э. 2 = AC 2 – DC 2 …(ii) [теорема Пифагора
Из (i) и (ii) получаем
AB 2 – BD 2 – AC
8 2 DC 2
AB 2 = AC 2 + BD 2 – DC 2
Теперь BC = BD + DC
= 3CD + CD = 40 CD …[∵ GBDiven = 3) ⇒ BC 2 = 16 CD 2 … (iv) [В квадрате
Сейчас, AB 2 = AC 2 + BD 2 – DC 2 9{2}}{2}\) … [Из (iv)
∴ 2AB 2 = 2AC 2 + BC 2 … [Доказано
Вопрос 46.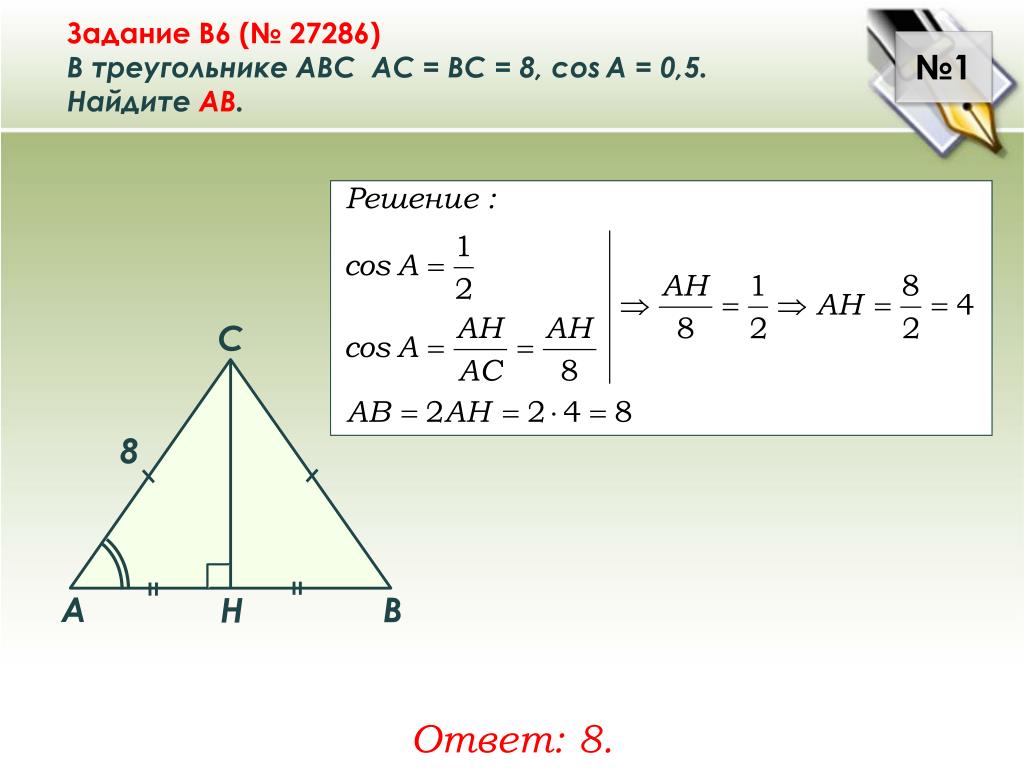
В ∆ABC высоты AD и CE пересекаются другое в точке P. Докажите, что: (2014)
(i) ∆APE ~ ∆CPD
(ii) AP × PD = CP × PE
(iii) ∆ADB ~ ∆CEB
(iv) AB × CE = BC × AD
Решение:
Дано. В ∆ABC AD ⊥ BC и CE ⊥ AB.
Чтобы доказать. (i) ∆APE ~ ∆CPD
(ii) AP × PD = CP × PE
(iii) ∆ADB ~ ∆CEB
(iv) AB × CE = BC × AD
Доказательство: (i) В ∆APE и ∆CPD
∠1 = ∠4 …[Каждые 90°
∠2 = ∠3 …[Вертикально противоположные углы
∴ ∆APE ~ ∆CPD …[AA-сходство
(ii) \(\frac{\mathrm{AP}}{\mathrm{CP}}=\frac{\mathrm{PE}}{\mathrm{PD}}\) … [In ~ ∆s соответствующие стороны пропорциональны
∴ AP × PD = CP × PE
(iii) В ∆ADB и ∆CEB,
∠5 = ∠7 …[Каждый 90°
∠6 = ∠6 …(Общий
∴ ∆ADB ~ ∆CEB …[AA сходство
( iv) ∴ \(\frac{A B}{C B}=\frac{A D}{C E}\) … [In ~ ∆s соответствующие стороны пропорциональны
∴ AB × CE = BC × AD
Вопрос 47.
На рисунке PQR и QST — два прямоугольных треугольника с прямыми углами R и T соответственно. Докажите, что QR × QS = QP × QT. (2014)
Докажите, что QR × QS = QP × QT. (2014)
Решение:
Дано: Два рт. PQR и QST ∆.
Чтобы доказать: QR × QS = QP × QT
Доказательство: В ∆PRQ и ∆STQ,
∠1 = ∠1 … [Общее
∠2 = ∠3 … [Каждый 90°
∆PRQ ~ ∆STO …( Сходство AA
∴ \(\frac{Q R}{Q T}=\frac{Q P}{Q S}\) ..[In -∆s соответствующие стороны пропорциональны
∴ QR × QS = QP × QT (отсюда доказано)
Вопрос 48.
На данном рисунке треугольники ABC и DBC имеют одно основание BC. Если AD пересекает BC в точке O, покажите, что \(\frac { ar\left( ABC \right) }{ ar\left( DBC \right) } =\frac { AO }{ DO } \). (2012)
Решение:
Дано: ABC и DBC — два As на одном основании BC. AD пересекает BC в точке O.
Доказать:
Вопрос 49.
Гипотенуза прямоугольного треугольника равна 25 см, а из оставшихся двух сторон одна длиннее другой на 5 см. Найдите длины остальных
две стороны. (2013)
Решение:
Пусть Основание, AB = x см
Тогда высота, BC = (x + 5) см
В rt.

 04.17
04.17 Урок будет полезен для самостоятельной подготовки учащихся к ЕГЭ.
Урок будет полезен для самостоятельной подготовки учащихся к ЕГЭ. 5 класс.
5 класс.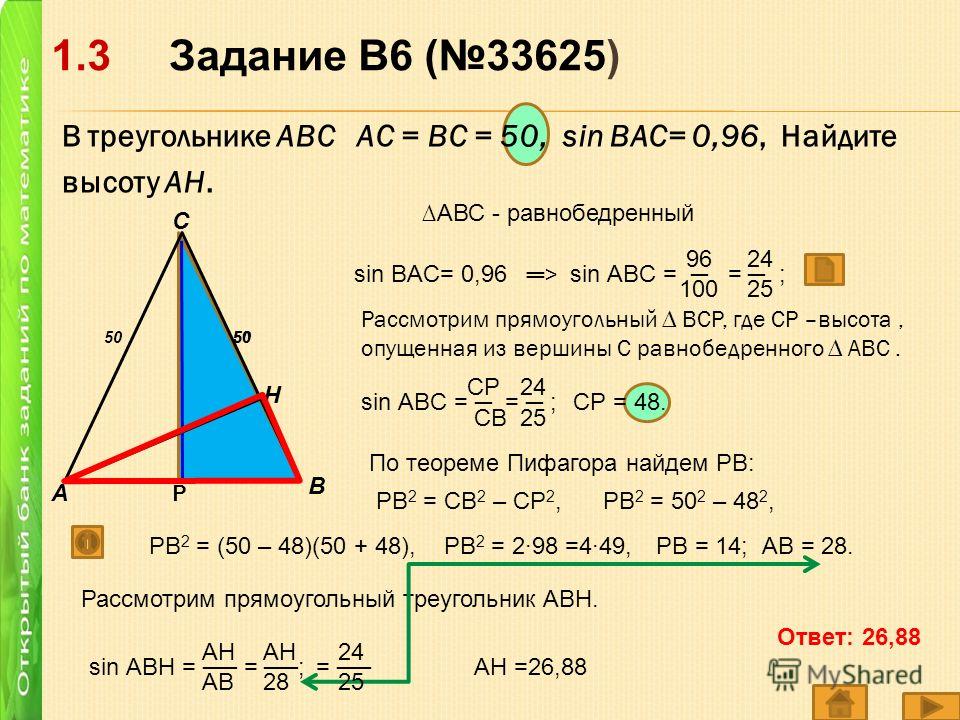 10 — 11 класс.
10 — 11 класс.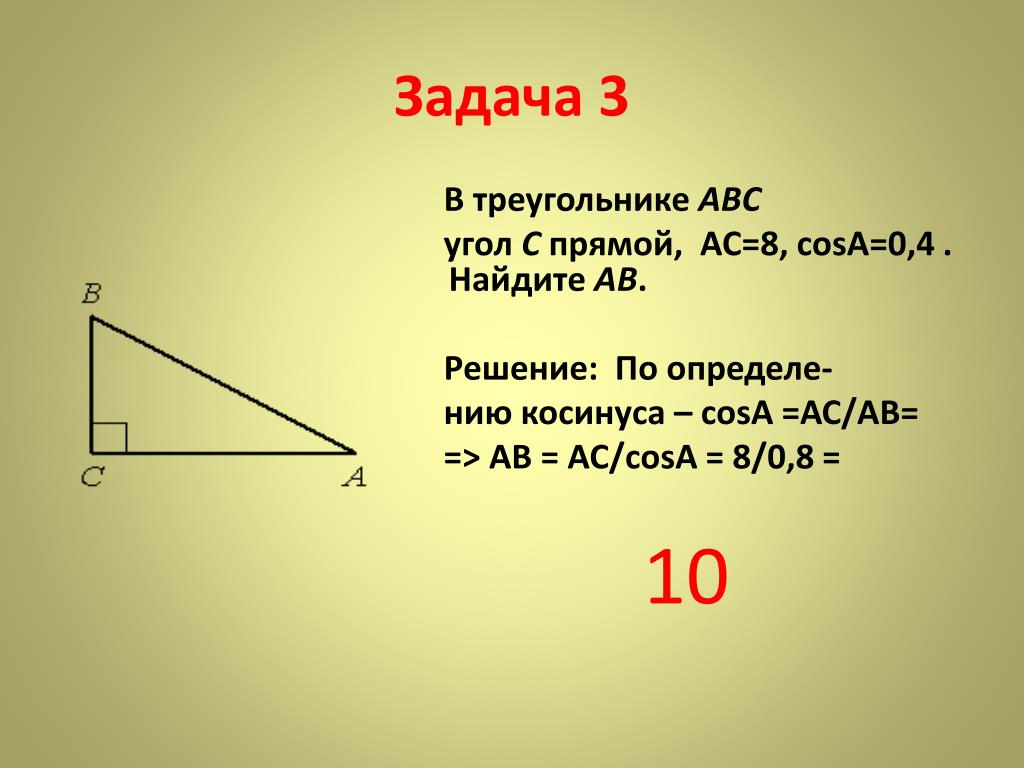
 Напишите sin C, cos A, tan C
Напишите sin C, cos A, tan C  Напишите sin C, cos A, tan C
Напишите sin C, cos A, tan C Напишите Cosec C, Sec A, Cot C
Напишите Cosec C, Sec A, Cot C 1
1
Leave A Comment