Тренировочные работы
1. Нахождение значений тригонометрических функций острых углов прямоугольного треугольника
1. В треугольнике ABC угол C равен 90о, AB = 10, BC = 6. Найдите cos A.
2. В треугольнике ABC угол C равен 90о, AB = 10, AC = 8. Найдите tg A.
3. В треугольнике ABC угол C равен 90о, cos A = 0,8. Найдите sin A.
4. В треугольнике ABC угол C равен 90о, cos A = 0,8. Найдите tg A.
5. В треугольнике ABC угол C равен 90о,
tg A = 0,75. Найдите sin A.
Найдите sin A.
7. В треугольнике ABC угол C равен 90о, cos A = 0,8. Найдите sin B.
8. В треугольнике ABC угол C равен 90о, CH – высота, AC = 10, AH = 8. Найдите cos B.
9. В треугольнике ABC угол C равен 90о, CH – высота, BC = 10,
2. Нахождение значений тригонометрических функций острых углов равнобедренного треугольника
1. В треугольнике ABC AC = BC = 10, AB = 12.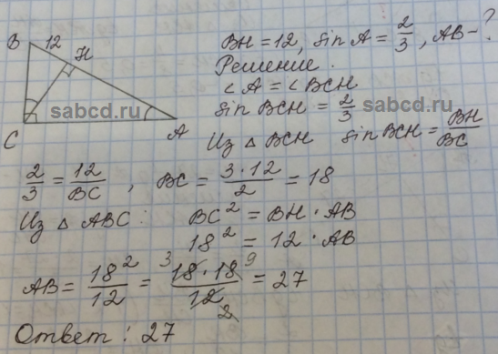 Найдите
cos A.
Найдите
cos A.
2. В треугольнике ABC AC = BC = 10, AB = 16. Найдите tg A.
3. В треугольнике ABC AC = BC = 10, AB = 16. Найдите sin A.
4. В треугольнике ABC
5. В треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите cos A.
6. В треугольнике ABC AC = BC, AB = 10, AH – высота, BH = 6. Найдите cos A.
7. В треугольнике ABC AC = BC, AH – высота, sin A = 0,8.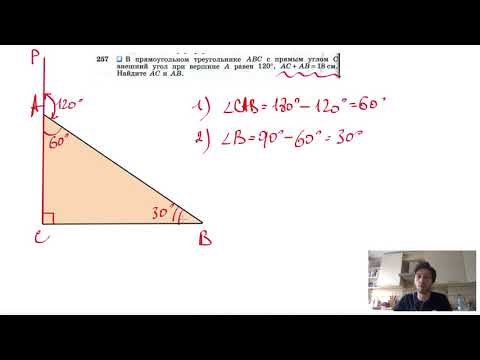 Найдите
косинус угла
Найдите
косинус угла
8. В треугольнике ABC AB = BC, AC = 16, высота CH равна 8. Найдите синус угла ACB.
9. В треугольнике ABC AB = BC, AC = 5, CH – высота, AH = 4. Найдите синус угла ACB.
3. Нахождение значений тригонометрических функций тупых углов
1. В треугольнике ABC угол C равен 90о, AB = 10, BC = 6. Найдите косинус внешнего угла при вершине A.
2. В треугольнике ABC
3. В треугольнике ABC угол C равен 90о,
cos B = 0,8.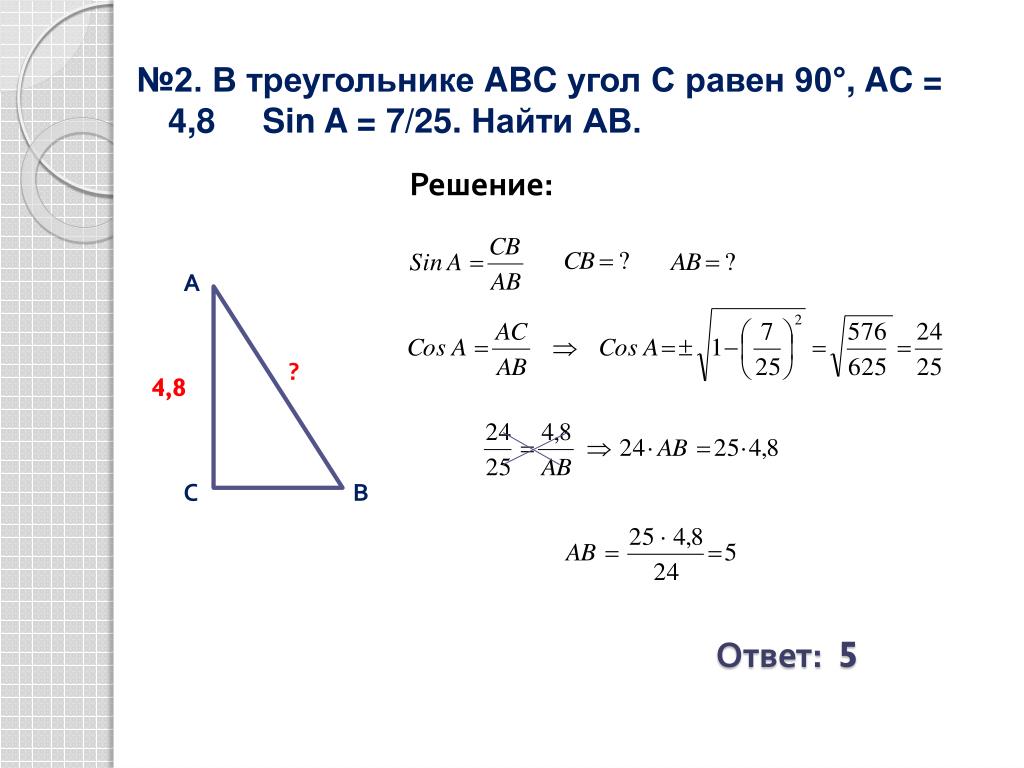 Найдите
косинус внешнего угла при вершине A.
Найдите
косинус внешнего угла при вершине A.
4. В треугольнике ABC угол C равен 90о, cos A = 0,8. Найдите синус внешнего угла при вершине A.
6. В треугольнике ABC угол C равен 90о, sin A = 0,6. Найдите косинус внешнего угла при вершине B.
7. В треугольнике ABC AC = BC = 10, AB = 12. Найдите синус внешнего угла при вершине B.
8. В треугольнике ABC AB = BC, AB = 10, высота CH
 Найдите косинус угла ABC.
Найдите косинус угла ABC.
9. В треугольнике ABC AB = BC, CH – высота, AB = 10, BH = 6. Найдите синус угла ABC.
4. Нахождение тригонометрических функций углов, изображенных на клетчатой бумаге
1. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
2. Найдите тангенс угла AOB.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .
4. Найдите тангенс угла
5. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .
6. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
7. Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
8. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .
9. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
подготовка к ЕГЭ, задание 9.
Задание 9 проверяет умения учащихся находить:
— углы треугольников, четырехугольников и углы, вписанные в окружность;
- значения тригонометрических функций углов по известным элементам геометрических фигур ;
- неизвестные элементы геометрических фигур по известным значениям тригонометрических функций.
Для успешного выполнения этого задания требуются знания теорем о сумме углов многоугольника и об угле, вписанном в окружность; определений тригонометрических функций, их свойств и значений для основных углов; умения работать с формулами, выполнять арифметические действия и преобразования числовых выражений.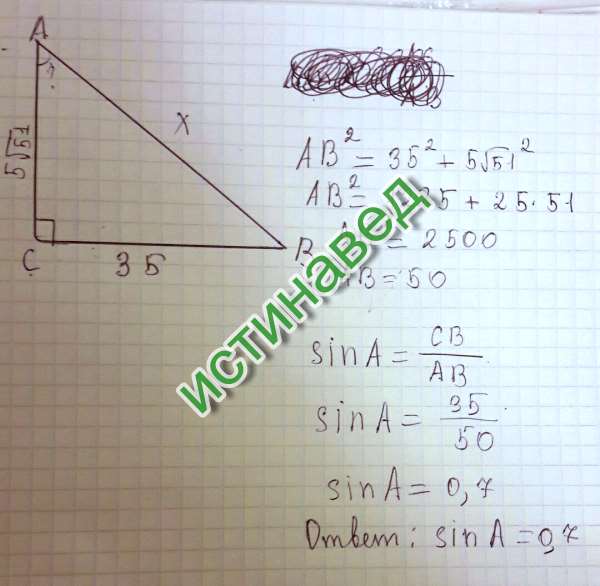
1. Один острый угол прямоугольного треугольника на 30 о больше другого. Найдите больший острый угол.
Решение. Пусть больший острый угол равен x . Тогда меньший острый угол равен x – 30 о . Так как сумма острых углов прямоугольного треугольника равна 90 о , имеем уравнение 2 x – 30 о = 90 о , из которого находим x = 60 о .
Ответ. 60 о .
2 . В треугольнике ABC AС = BC , угол C равен 50 o . Найдите внешний угол CBD .
Решение. Так как углы при основании равнобедренного треугольника равны и сумма углов треугольника равна 180 о , то углы
Ответ. 115 о .
3 . В треугольнике АВС AD – биссектриса, угол C равен 50 o , угол CAD равен 30 o .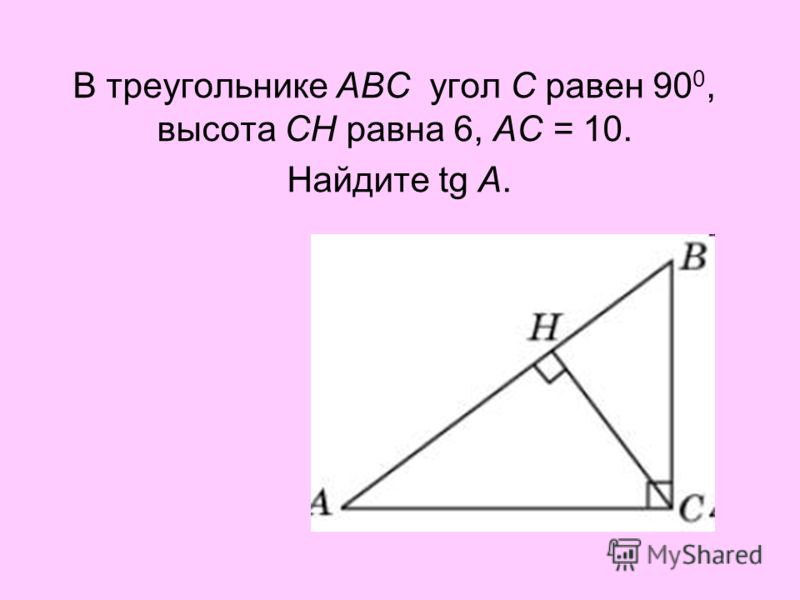 Найдите угол B .
Найдите угол B .
Ответ. 70 о .
4 . В треугольнике АВС CD – медиана, угол C равен 90 o , угол B равен 60 o . Найдите угол ACD .
Ответ. 30 о .
5 . В треугольнике АВС угол А равен 48 o , угол C равен 56 o . На продолжении стороны АB отложен отрезок BD = ВС . Найдите угол D треугольника BCD .
Ответ. 38 о .
6 . Сумма двух углов параллелограмма равна 80 о . Найдите один из оставшихся углов.
Ответ. 140 о .
7 . Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 60 о ?
Ответ. 120 о .
8 . Центральный угол на 3 5 о больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.
Ответ. 35 о .
9 . Найдите вписанный угол, опирающийся на дугу, которая составляет одну пятую окружности.
Ответ. 36 о .
10 . Точки А , В , С , расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1 : 3 : 5. Найдите больший угол треугольника АВС .
Ответ. 100 о .
1 1 . В треугольнике ABC угол C равен 90 о , AB = 10, AC = 8 . Найдите sin A .
Решение 1. В прямоугольном треугольнике ABC гипотенуза AB равна 10. Найдем катет BC . Используя теорему Пифагора, имеем BC = . Следовательно, sin A = 0,6.
Решение 2. Так как катет AC равен 8, а гипотенуза AB равна 10, то cos A = 0,8. Воспользуемся формулой , выражающей косинус через синус острого угла. Откуда sin A = 0,6.
Откуда sin A = 0,6.
Ответ. 0,6.
1 2. В треугольнике ABC угол C равен 90 о , высота CH равна 6, AC = 10. Найдите tg A .
Решение. В прямоугольном треугольнике ACH катет CH равен 6, гипотенуза AC равна 10. Используя теорему Пифагора, находим AH = 8. Следовательно, tg A = 0,75.
Ответ. 0,75.
13 . В треугольнике ABC AC = BC = 10, AB = 12. Найдите sin A .
Решение. Проведем высоту CH . В прямоугольном треугольнике ACH гипотенуза AC равна 10, катет AH равен 6. По теореме Пифагора находим CH = 8 и, следовательно, sin A = 0,8.
Ответ. 0,8.
14 . В треугольнике ABC AC = BC , AB = 10, высота AH равна 8. Найдите cos A .
Решение. В прямоугольном треугольнике ABH гипотенуза AB равна 10, катет AH равен 8.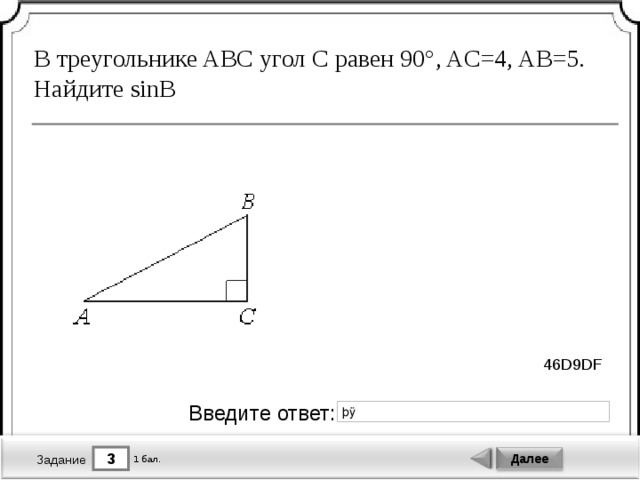 По теореме Пифагора находим BH = 6 и, следовательно, cos B = 0,6. Так как углы A и B треугольника ABC равны, то cos A = 0,6.
По теореме Пифагора находим BH = 6 и, следовательно, cos B = 0,6. Так как углы A и B треугольника ABC равны, то cos A = 0,6.
Ответ. 0,6.
15 . В треугольнике ABC AB = BC , высота CH равна 8, AC = . Найдите тангенс угла ACB .
Решение. По теореме Пифагора найдем катет AH прямоугольного треугольника ACH . Имеем AH = . Откуда tg A = 0,5. Так как углы A и C треугольника ABC равны, то тангенс угла ACB равен 0,5.
Ответ. 0,5.
16 . В треугольнике ABC угол C равен 90 о , AB = 10, BC = 6 . Найдите синус внешнего угла при вершине A .
Решение. Синус внешнего угла при вершине A треугольника ABC равен синусу угла A и, следовательно, равен 0,6.
Ответ. 0,6.
17 . В треугольнике ABC угол C равен 90 о , tg A = 0,75, AC = 8. Найдите AB .
В треугольнике ABC угол C равен 90 о , tg A = 0,75, AC = 8. Найдите AB .
Решение. Имеем BC = AC tg A = 8 0,75 = 6. По теореме Пифагора находим AB = 10.
Ответ. 10.
18 . В треугольнике ABC угол C равен 90 о , CH – высота, BC = 6, cos A = 0,8. Найдите CH .
Решение. Углы BCH и BAC равны, как острые углы с перпендикулярными сторонами, значит, cos BCH = 0,8. CH = BC cos BCH = 4,8.
Ответ. 4,8.
19 . В треугольнике ABC AC = BC = 10, sin A = 0,8. Найдите AB .
Решение. Проведем высоту CH . Имеем CH = AC sin A = 8. По теореме Пифагора находим AH = 6 и, следовательно, AB = 12.
Ответ. 12.
20 .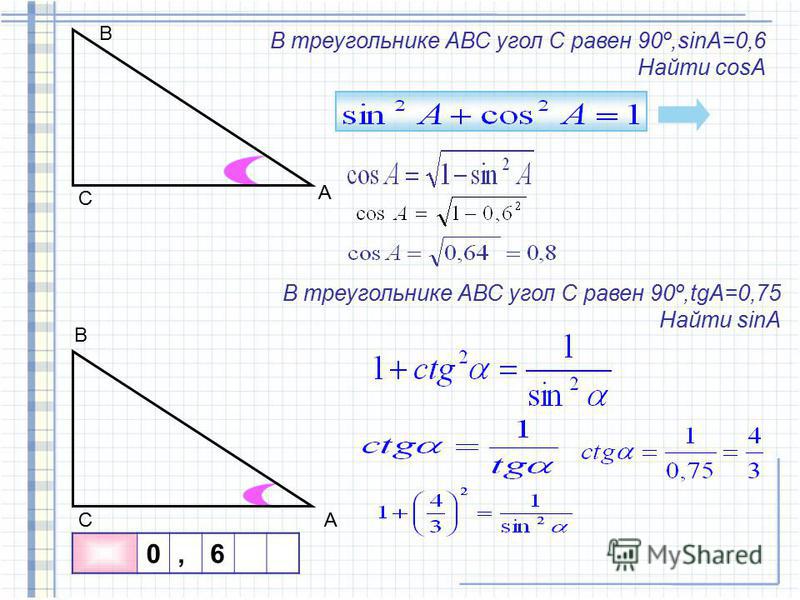 В треугольнике ABC AC = BC , AB = 10, cos A = 0,6. Найдите высоту AH .
В треугольнике ABC AC = BC , AB = 10, cos A = 0,6. Найдите высоту AH .
Решение. В равнобедренном треугольнике ABC угол A равен углу B , BH = AB cos B = 6. По теореме Пифагора находим AH = 8.
Ответ. 8.
21 . В треугольнике ABC AB = BC , высота CH равна 5, tg C = . Найдите AC .
Решение 1. В равнобедренном треугольнике ABC угол A равен углу C , значит, tg A = tg C и AH = . По теореме Пифагора находим AC = 10.
Решение 2. Так как tg C = , то угол C равен 30 о . Угол A равен углу C . Так как катет прямоугольного треугольника, лежащий против угла в 30 о , равен половине гипотенузы, то AC = 10.
Ответ. 10.
22 . Найдите косинус угла AOB . В ответе укажите значение косинуса, умноженное на .
Решение. Рассмотрим треугольник OBС . OC = BC = , OB = . Следовательно, треугольник OBC – прямоугольный, косинус угла AOB равен .
Ответ. 1.
Законы косинусов и синусов
Сначала опустите перпендикулярную линию AD от A вниз к основанию BC треугольник. Основание D этого перпендикуляра будет лежать на ребре BC треугольника, когда оба угла B и C являются острыми. Но если угол B тупой, то основание D будет лежать на BC , вытянутом в направлении B. Но если угол C тупой, то D будет линией на г. до н.э. простирается в направлении г. н.э. К счастью, Аргумент один и тот же во всех трех случаях.
Пусть ч обозначает длина этой линии н.э., то есть высота (или высота) треугольника.
Если угол B острый, то
sin B = h/c.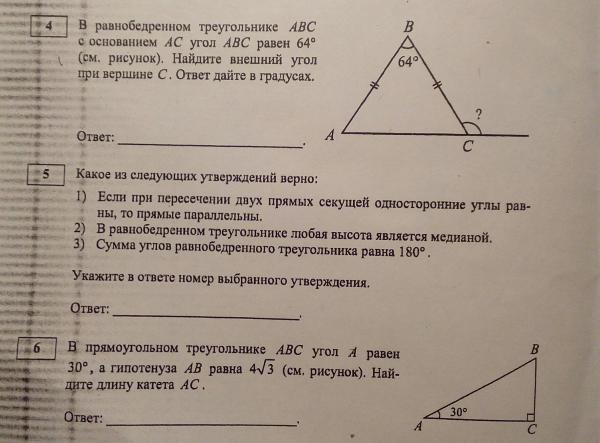 Но это верно и тогда, когда B — тупой угол, как на третьей диаграмме. Там,
угол ABC тупой. Но синус тупого угла равен
то же, что и синус его добавки. Это значит
sin ABC совпадает с sin ABD, , то есть они оба равны h/c.
Но это верно и тогда, когда B — тупой угол, как на третьей диаграмме. Там,
угол ABC тупой. Но синус тупого угла равен
то же, что и синус его добавки. Это значит
sin ABC совпадает с sin ABD, , то есть они оба равны h/c.
Точно так же не имеет значения, острый угол C или тупой, sin C = h/b в любом случае.
Эти два уравнения говорят нам, что h равно c sin B и b sin C. But из уравнения c sin B = b sin C, мы можем легко получить закон синусов:
Закон косинусов
Есть две другие версии закона косинусов,
и

Поскольку три версии отличаются только маркировкой треугольника, достаточно проверить только один из них. Будем рассматривать изложенную версию первый.
Чтобы понять, почему эти законы действуют, нам нужно рассмотреть три случая. Для случая 1 возьмем угол C быть тупым. В случае 2 угол C будет прямым. В случае 3, угол С будет острым.
| Случай 1. В этом случае мы принимаем угол C тупым. Этот случай имеет в нем морщина, так как косинус тупого угла отрицателен. Посмотрим, как это пойдет. | |||||||||||||
| Сначала опустите перпендикулярную линию AD от A вниз к основанию BC из
треугольник. В этом случае основание D этого перпендикуляра будет лежать вне
треугольник. Пусть h обозначает высоту треугольника, пусть d обозначает BD, и пусть e обозначает CD. Из рисунка можно вывести следующие уравнения:
В общем случае косинус тупого угла есть отрицание косинуса его дополнения. | |||||||||||||
Эти уравнения и простая алгебра завершают рассуждения следующим образом:
| с 2 | = | г 2 + ч 2 |
| = | ( a + e ) 2 + ч 2 | |
| = | a 2 + 2 ae + e 2 + h 2 | = | а 2 + б 2 + 2 ае |
| = | a 2 + b 2 – 2 ab cos C |
Таким образом, закон косинусов справедлив, когда C является тупым углом.
Случай 2. Теперь рассмотрим случай, когда угол при С прямой. Косинус прямого угла равен 0, поэтому закон косинусы, в 2 = а 2 + b 2 2 ab cos C, упрощается до пифагорейского тождества, в 2 = а 2 + б 2 , для прямоугольных треугольников, которое, как мы знаем, справедливо.
Случай 3. В этом случае мы предполагаем, что угол C является остроугольным треугольником. Бросьте перпендикулярная линия AD от A вниз к основанию г. до н.э. г. треугольника. Ступня D перпендикуляра будет (1) лежать на ребре BC , если угол B острый, (2) совпадают с точкой B , если угол B прямой, или (3) лежат на стороне B расширен, если угол B тупой.
Пусть h обозначает высоту треугольника, пусть d обозначают BD, и e обозначают CD.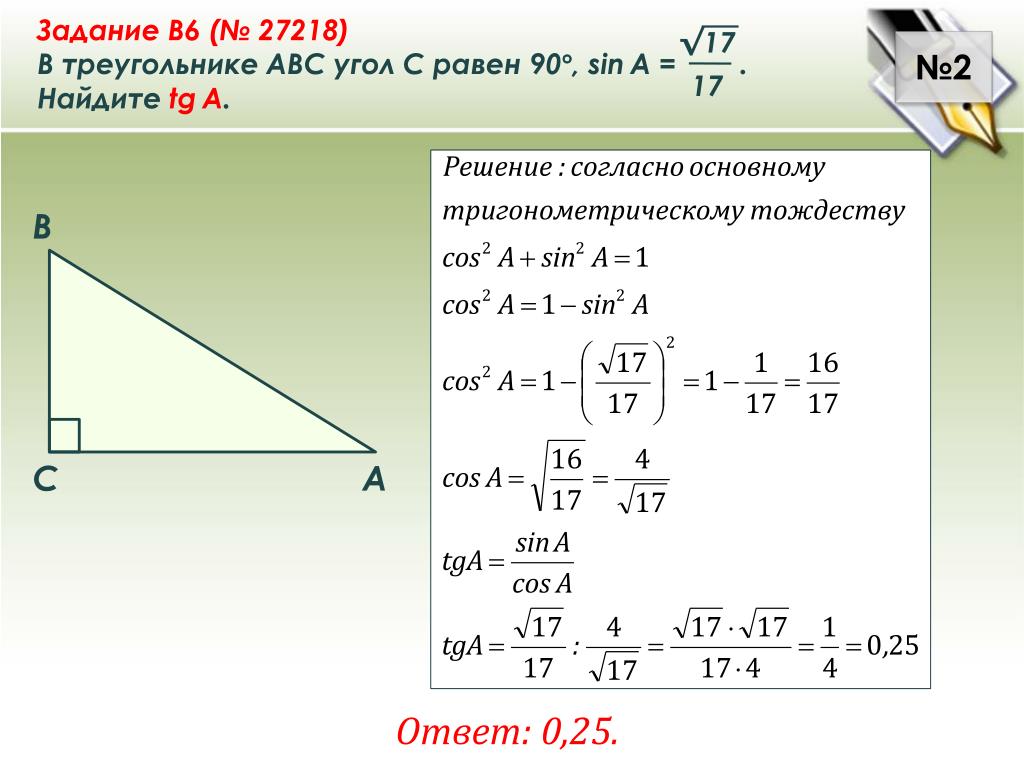
Тогда мы можем прочитать следующие отношения из диаграммы:
| с 2 | = | г 2 + ч 2 |
| б 2 | = | е 2 + ч 2 |
| соз С | = | е/б |
| д 2 | = | ( и и ) 2 |
Последнее уравнение требует пояснений. Если точка D лежит на стороне BC, тогда d = a – e, но если D лежит на BC расширенный, затем d = e – a. В любом случае d 2 = ( e – a ) 2 .
Эти уравнения и немного алгебры завершают доказательство следующим образом:
| с 2 | = | г 2 + ч 2 |
| = | d 2 – e 2 + b 2 | |
| = | ( d – e ) ( d + e ) + b 2 | |
| = | ( a – 2 e ) a + b 2 | |
| = | a 2 + b 2 – 2 ae | |
| = | A 2 + B 2 — 2 AB COS C |
Таким образом, теперь мы знаем, что закон Коснея действителен, когда оба угла C — ах мы закончили все три дела.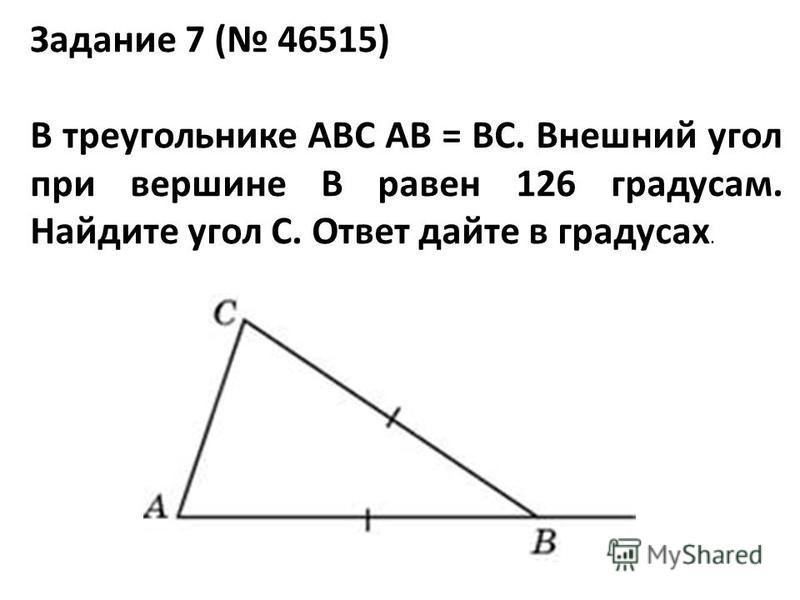
Между прочим, Евклид включил в свои элемента пару предложений, II.12 и II.13, это очень похоже на закон косинусов, но на самом деле это, конечно, не закон косинусов, поскольку тригонометрия не была развита во времена Евклида.
Калькулятор треугольника
Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным.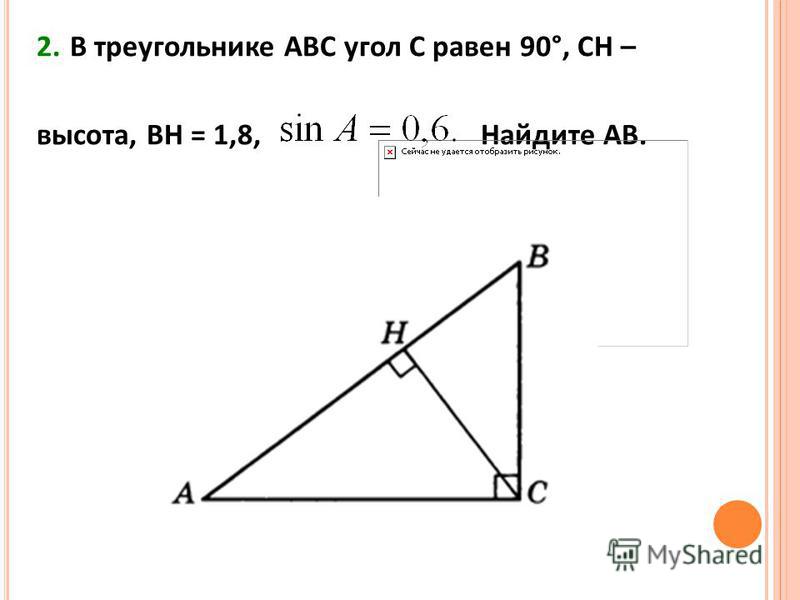 Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.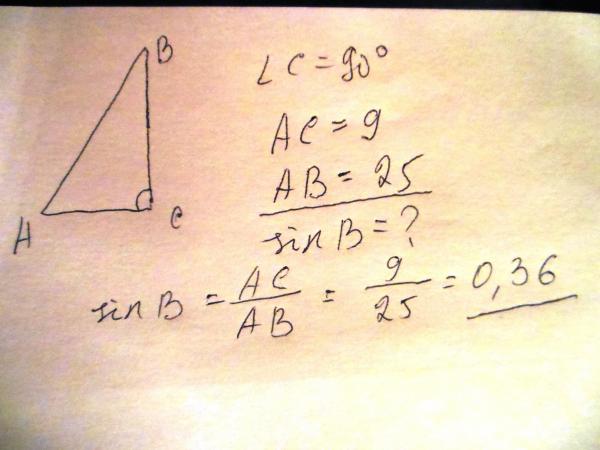
Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.
Факты, теоремы и законы треугольника
- Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.
Площадь треугольника
Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Учитывая а = 9, b = 7 и C = 30°:
Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний радиус и радиус описанной окружности
Медиана
Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Медианы треугольника представлены отрезками m a , m б и м с . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.
Например, учитывая, что a=2, b=3 и c=4, медиана m a может быть рассчитана следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Для целей данного калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:
| внутренний радиус = |
| с = |
|
где a, b и c — стороны треугольника
Радиус окружности
Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности.

 В данном случае это косинус
угол C, , то есть угол ACB, есть отрицание
косинус угла ACD. Поэтому в последнем уравнении стоит знак минус.
В данном случае это косинус
угол C, , то есть угол ACB, есть отрицание
косинус угла ACD. Поэтому в последнем уравнении стоит знак минус.
Leave A Comment