в равнобедренном треугольнике боковая сторона равна 10см ,а основание 12см.Найдите высоту проведеную к основанию.решение — Спрашивалка
Ол
Ольга
- сторона
- треугольник
- основание
- решение
- высота
Ма
Марал
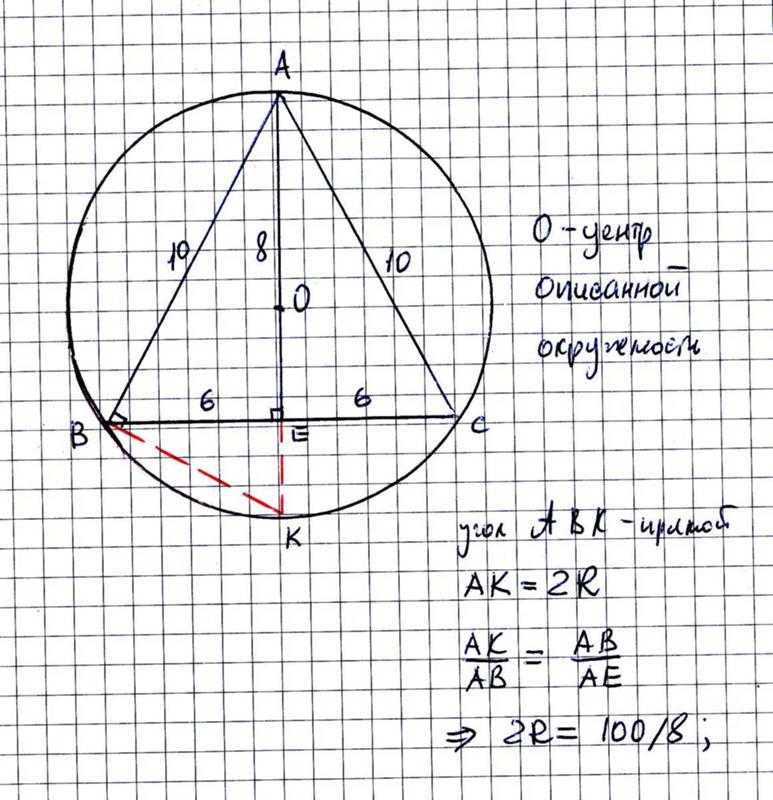
однако, раз присуствует Пифагорова тройка, я предложу свое, немного — совсем чуть-чуть — нестандартное.
Заданный равнобедренный треугольник можно разрезать на два Пифагоровых со сторонами (5,12,13), проведя медиану-высоту-биссектрису к основанию. Действительно, половина основания 5, высота 12, поэтому боковая сторона 13. При этом мы нашли — заодно — и синус угла при основании, он равен 12/13. Отсюда получаем для радиуса описанной окружности
2*R*12/13 = 13; R = 169/24.
Если такой способ не нравится (хотя не понятно, чем) — есть много способов получить эту величину. Например, можно провести препендикуляр к боковой стороне через вершину основания до пересечения с продолжением высоты-медианы-биссектрисы (то есть оси симметрии исходного треугольника). Расстояние между полученной точкой и вершиной треугольника (противолежащей основанию, отрезок оси симметрии) — это диаметр описанной окружности (поскольку вписанный прямой угол всегда опирается на диаметр). Поскольку при этом получился опять Пифагоров треугольник (точнее, ему подобный), то
Например, можно провести препендикуляр к боковой стороне через вершину основания до пересечения с продолжением высоты-медианы-биссектрисы (то есть оси симметрии исходного треугольника). Расстояние между полученной точкой и вершиной треугольника (противолежащей основанию, отрезок оси симметрии) — это диаметр описанной окружности (поскольку вписанный прямой угол всегда опирается на диаметр). Поскольку при этом получился опять Пифагоров треугольник (точнее, ему подобный), то
D/13 = 13/12, то есть ответ будет таким же.
Найдем теперь радиус вписанной окружности. Для этого из центра ВПИСАННОЙ окружности проведем препендикуляр к боковой стороне. Отрезок от вершины до центра вписаной окружности это 12 — r, и получившийся треугольник, в котором этот отрезок — гипотенуза, а проведеный радиус — катет, опять подобен пифагоровому (5,12,13) (ну, просто у них угол общий :))
Получается r/(12 — r) = 5/13; откуда найдем r = 10/3;
Опять таки, если такой элегантный способ не нравится, в нашем распоряжеии есть и тупой
Считаем периметр 13*2 + 10 = 36 и площадь 10*12/2 = 60, r = 2*60/36 = 10/3; так мы не потратим ни одной извилины, но получим результат
Миша
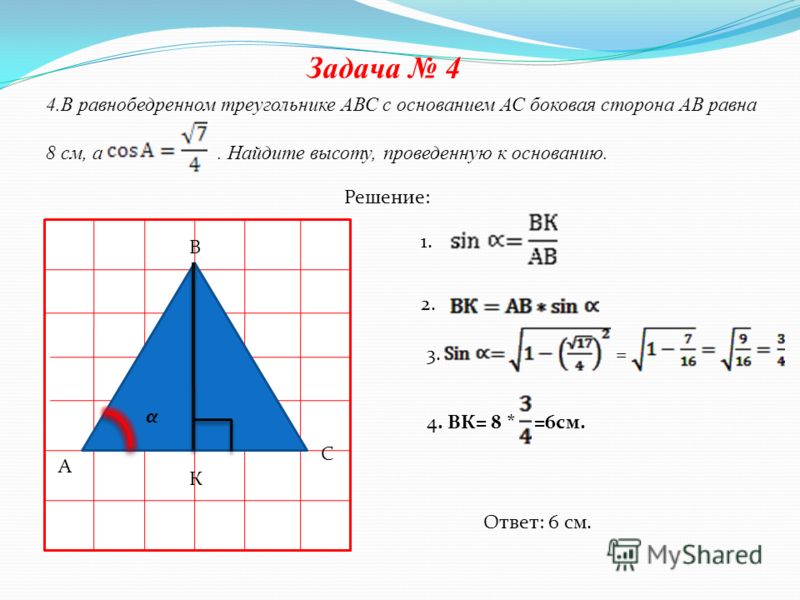
Треугольник АВС
АВ = ВС = 10 см
АС = 12 см
Проводим высоту ВК
АК = АС / 2 = 12 / 2 = 6 см
ВК = корень(AB^2 — AK^2) = корень(10^2 — 6^2) = 8 см
Похожие вопросы
как найти высоту проведенную к основанию равнобедренного треугольника если даны все стороны? по какой формуле?
В равнобедренном треугольнике основание равно 16,а высота проведенная к основанию 4.
высота равнобедренного треугольника равна 15.боковая сторона меньше основания на 15.найдите основание этого треугольника
Докажите, что в равнобедренном треугольнике высоты, проведенные из вершин основания, равны?
В равнобедренном треугольнике основание равно 24см, высота, проведённая к основанию, равна 16см, Найти боковую сторону.
в равнобедренном треугольнике боковая сторона равна 15 см высота проведенная к основанию равна 9, найдите а) основание,
может ли основание равнобедренного треугольника быть равным 8 м, если его боковая сторона равна
Боковая сторона равнобедренного треуголика равна 61см, а высота проведенная к основанию, 60см. Найти площадь треугольника
Боковая сторона равнобедренного треугольника равна 10см один из внешних углов 120градусов найти основание
основание равнобедреннго треугольника равно 12см, а боковая сторона 10см, Найти высоту треугольника
1. В равнобедренном треугольнике боковая сторона равна а, а угол.
 .. Самостоятельные работы. С-9. В-5. Геометрия 11 класс Зив Б.Г. ГДЗ. – Рамблер/класс 1. В равнобедренном треугольнике боковая сторона равна а, а угол… Самостоятельные работы. С-9. В-5. Геометрия 11 класс Зив Б.Г. ГДЗ. – Рамблер/класс
.. Самостоятельные работы. С-9. В-5. Геометрия 11 класс Зив Б.Г. ГДЗ. – Рамблер/класс 1. В равнобедренном треугольнике боковая сторона равна а, а угол… Самостоятельные работы. С-9. В-5. Геометрия 11 класс Зив Б.Г. ГДЗ. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
1.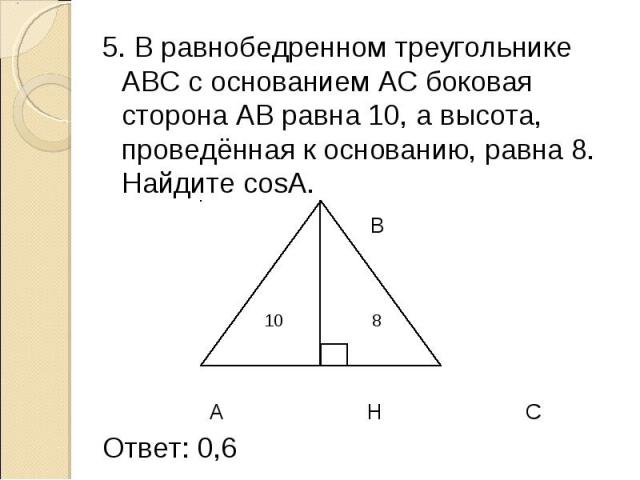 В равнобедренном треугольнике боковая сторона равна а,
В равнобедренном треугольнике боковая сторона равна а,
а угол при вершине равен 120°. Треугольник вращается
вокруг прямой, проходящей через вершину треугольника,
которая параллельна биссектрисе угла при основании.
Найдите площадь поверхности тела вращения.
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Юмор
Олимпиады
ЕГЭ
Компьютерные игры
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л. С.
С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
С чем связано окончание приема учащихся в Московский институт телевидения и радиовещания «Останкино»? (Подробнее…)
ВузыПоступление11 классНовости
Какой был проходной балл в вузы в 2017 году?
Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее. ..)
..)
Поступление11 классЕГЭНовости
Площадь равнобедренного треугольника – формула, определение, примеры, часто задаваемые вопросы
Площадь равнобедренного треугольника – это пространство, ограниченное сторонами треугольника. Общая формула нахождения площади равнобедренного треугольника определяется как половина произведения основания и высоты треугольника. Помимо этого, для нахождения площади треугольников используются различные формулы. Треугольники классифицируются в зависимости от их сторон, различные типы треугольников в зависимости от сторон приведены ниже:
Что такое равнобедренный треугольник?Равносторонний треугольник: Треугольник, у которого все три стороны равны.
Равнобедренный треугольник: Треугольник, у которого две стороны равны.
Разносторонний треугольник: Треугольник, все стороны которого не равны.
Равнобедренный треугольник — это треугольник с двумя равными сторонами.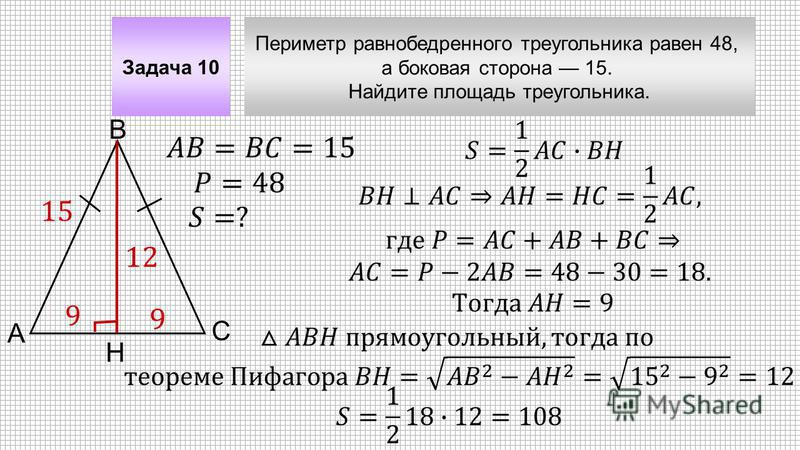 Два угла, противолежащие двум равным сторонам, также равны. Предположим, что в треугольнике △ABC, если стороны AB и AC равны, ABC является равнобедренным треугольником с ∠B = ∠C. Равнобедренный треугольник описывается теоремой «Если две стороны треугольника равны, то и угол, противолежащий им, также равен».
Два угла, противолежащие двум равным сторонам, также равны. Предположим, что в треугольнике △ABC, если стороны AB и AC равны, ABC является равнобедренным треугольником с ∠B = ∠C. Равнобедренный треугольник описывается теоремой «Если две стороны треугольника равны, то и угол, противолежащий им, также равен».
Какова площадь равнобедренного треугольника?
Полное пространство внутри границы равнобедренного треугольника называется его площадью. В равнобедренном треугольнике площадь легко вычислить, если известны высота и основание треугольника. Произведение половины на основание и высоту равнобедренного треугольника дает площадь равнобедренного треугольника.
Isocles Triangle FormulaПлощадь Isosceles Triangle приведена по формуле, перечисленной ниже:
Область = ½ × основание × рост
,
Площадь равнобедренного треугольника ФормулыPerimeter of Isoscel isosceles isosceles isosceles isoscel isoscel isoscel isoscel isoscel isoscel isosceles isoscel isosceles isosceles isoscel isoscel isoscel isoscel.
= 2a + b
Высота равнобедренного треугольника (h) = √(a 2 − b 2 /4), где a, b — стороны равнобедренного треугольника.
Для нахождения площади равнобедренного треугольника используются различные формулы. Некоторые из наиболее часто используемых формул для площади равнобедренного треугольника перечислены ниже:
- Если известны основание и высота A = ½ × b × h
- Если известны все три стороны A = ½[√( a 2 − b 2 ⁄4) × b]
- Если даны длины двух сторон и угол между ними A = ½ × b × c × sin(α)
- Если два угла а длина между ними равна A =
- Для равнобедренного прямоугольного треугольника A = ½ × a 2
треугольника, то высота треугольника также может быть рассчитана по данной формуле:
Высота равнобедренного треугольника = √(a 2 − b 2 /4)
Площадь равнобедренного треугольника Треугольник (если даны все стороны) = ½[√(a 2 − b 2 /4) × b]
где,
b = основание равнобедренного треугольника
a = длина двух равных сторон
Как найти площадь равнобедренного треугольника Равнобедренный треугольник?
Чтобы найти площадь равнобедренного треугольника, выполните следующие действия:
Шаг 1: Отметьте длину (l) и ширину (b) данного треугольника.
Шаг 2: Умножьте значения, полученные на шаге 1, и разделите их на 2.
Шаг 3: Полученный результат представляет собой искомую площадь, она измеряется в м 2
Вычисление площади равнобедренного треугольникаЕсли известны длины равных сторон и основания равнобедренного треугольника высота треугольника или высота могут быть вычислены. Формула для вычисления площади равнобедренного треугольника со сторонами выглядит следующим образом:
Площадь равнобедренного треугольника = ½[√(a 2 − b 2 /4) × b]
где,
b = основание равнобедренного треугольника
a = длина двух равных сторон
Площадь правой угловой азобель Прямоугольный треугольник Площадь = ½ × a 2равной длины)
BD = DC = ½ BC = ½ b (Перпендикуляр от угла при вершине ∠A делит основание BC пополам)
Используя теорему Пифагора об ΔABD,
a 2 = (b/2) 2 + (AD) 2
AD =
Высота равнобедренного треугольника =
Известно, что общая формула площади треугольника: Площадь = ½ × b × h
Подставляя значение высоты, получаем
Площадь равнобедренного треугольника = ½ [√ (A 2 — B 2 /4) × B]
Вывод:
Площадь равнобедренного треугольника (Площадь) = ½ × основание × высота
4 5 × высота 4 5 × 9 a0 = 0 5 × 9 a0 = 0 5 × 9 a0Площадь = ½ × основание × высота 2
Периметр равнобедренного прямоугольного треугольника P = (2+√2)a
Вывод:
Область Isosceles. ТригонометрияПериметр равнобедренного прямоугольного треугольника равен сумме всех сторон равнобедренного прямоугольного треугольника.
Пусть две равные стороны равны и . По теореме Пифагора неравная сторона равна a√2.
Периметр Isockeles Правой треугольник = a+a+a√2
= 2a+a√2
= a (2+√2)
= a (2+√2)
Когда даны длина двух сторон и угол между ними,
A = ½ × b × c × sin(α)
где,
b, c — стороны данного треугольника
α — угол между ними
Стороны между ними приведены,
9008 Солированные примеры на областях. Равнобедренный треугольникA =
, где
C — это стороны данного треугольника
α, β — угол, связанный с ними
Пример 1: Найдите площадь равнобедренного треугольника со стороной , равной стороне , равной 13 см, и основанием , равным 24 см.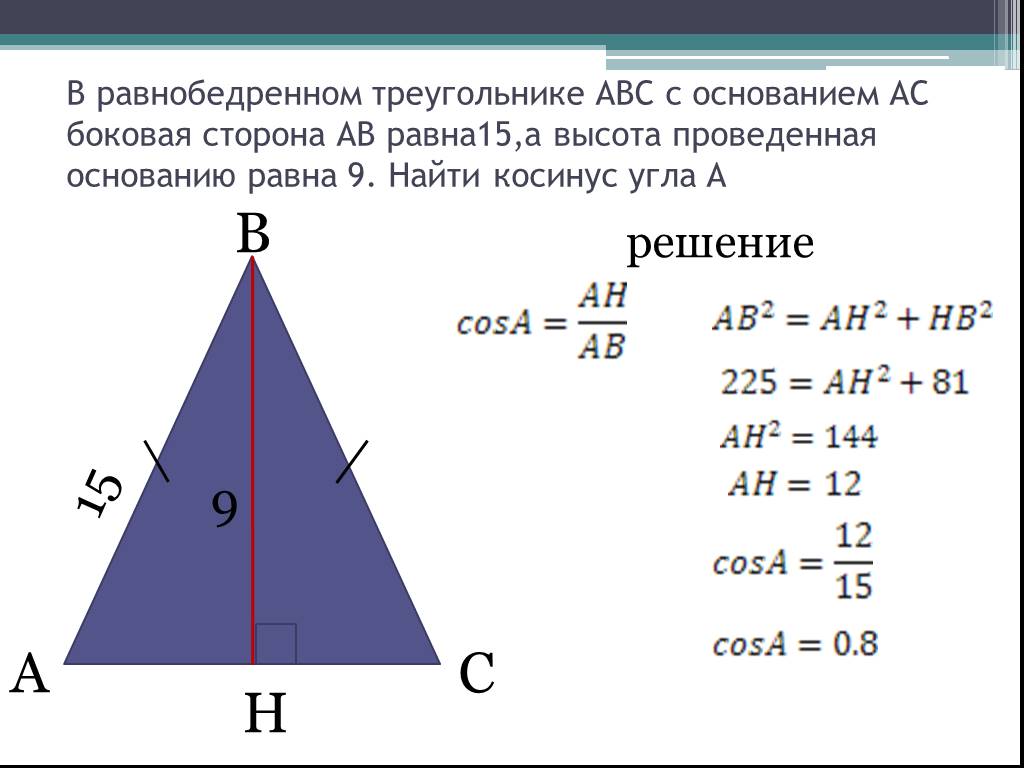
Решение:
У нас есть, A = 13 и B = 24.
Площадь Isockeles Triangle определяется,
A =
=
= 1/2 × 5 × 240003
. = 60 см 2
Пример 2: Найдите площадь равнобедренного треугольника с сторона равна 10 см и основание 12 см.
Решение:
У нас есть, a = 10 и B = 12.
Площадь Isockeles Triangle определяется,
A =
=
= 1/2 × 8 × 12
. = 48 см 2
Пример 3: Найдите площадь равнобедренного треугольника со стороной равной 5 см и основанием 6 см.
Решение:
У нас есть, A = 5 и B = 6.
Площадь Isockeles Triangle определяется,
A =
=
= 1/2 × 4 × 70003
.
= 12 см 2
Пример 4. Найдите площадь равнобедренного треугольника, сторона которого равна 15 см, а основание равно 24 см.
Решение:
равные стороны 17 см и основание 30 см.Имеем a = 15 и b = 24,
Площадь равнобедренного треугольника определяется как
Решение:
Имеем a = 17 и b = 30.0002 = 1/2 × 8 × 30
= 120 см 2
.
Решение:
У нас есть, a = 20 и B = 24.
Площадь Isockeles Triangle определяется,
A =
=
= 1/2 × 16 × 240003
. = 192 см 2
Пример 7: Найдите площадь равнобедренного треугольника с равные стороны 25 см и основание 30 см.
Решение:
Часто задаваемые вопросы о площади равнобедренного треугольникаУ нас есть, A = 25 и B = 30.
Площадь Isockeles Triangle определяется,
A =
=
= 1/2 × 20 × 300003
. = 300 см 2
Вопрос 1: Какова площадь равнобедренного треугольника?
Ответ:
Площадь фигуры – это пространство, ограниченное границами фигуры. Итак, площадь равнобедренного треугольника можно определить как пространство, занимаемое равнобедренным треугольником.
Вопрос 2: Что вы подразумеваете под равнобедренным треугольником?
Ответ:
Равнобедренный треугольник можно определить как треугольник, который имеет две равные стороны, также в равнобедренном треугольнике противоположные углы также равны. Некоторые из свойств равнобедренного треугольника:
- Две равные стороны равнобедренного треугольника равны, и угол между ними называется углом при вершине или углом при вершине.
- Сторона, противоположная углу при вершине, называется основанием, и в равнобедренном треугольнике углы при основании также равны.
Вопрос 3: Напишите формулу для нахождения площади равнобедренного треугольника.
Ответ:
Для вычисления площади равнобедренного треугольника используется следующая формула:
A = ½ × b × h
где
b — основание треугольника,
h — высота треугольника.
Вопрос 4 : Напишите формулу для нахождения периметра равнобедренного треугольника.
Ответ:
Для вычисления периметра равнобедренного треугольника используется следующая формула:
P = 2a + b
где0006 a, b — стороны равнобедренного треугольника.
Вопрос 5: Напишите формулу площади равнобедренного прямоугольного треугольника.
Ответ:
Для расчета площади правого углового треугольника используется следующая формула:
a = ½ × A 2
Где
A 9007 — The сторона треугольника,
Похожие статьи
- Площадь квадрата
- Площадь ромба
- Площадь прямоугольника
Q15 Найдите периметр i равностороннего треугольника со стороной 98 см ii равнобедренного треугольника с каждым…
Перейти к
- Система счисления (закрепление чувства числа)
- Оценка
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Номер строки
- HCF и LCM
- Игра с числами
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Десятичные дроби
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- четырехугольник
- Полигоны
- Круг
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
- Среднее и медиана
Главная >
Селина Солюшнс
Класс 6
Математика
>
Глава 32. Периметр и площадь плоских фигур.
>
Упражнение 32 (А)
>
Вопрос 15
Периметр и площадь плоских фигур.
>
Упражнение 32 (А)
>
Вопрос 15
Вопрос 15 Упражнение 32(A)
Q15) Найдите периметр : (i) равносторонний треугольник со стороной 9,8 см. (ii) равнобедренный треугольник, каждая сторона которого равна 13 см, а третья сторона = 10 см. (iii) правильный пятиугольник со стороной 8,2 см. (iv) правильный шестиугольник со стороной 6,5 см.
Ответ:
Решение 15:
(i) Периметр равностороннего треугольника = 3 x сторона = 3 х 9,8 см = 29,4 см (ii) Требуемый периметр = 13 см + 13 см + 10 см. = 36 см (iii) Периметр данного пятиугольника = 5 x сторона = 5 x 8,2 см. = 41 см (iv) Периметр данного шестиугольника = 6 x сторона = 6 x 6,5 см. = 39 см
Похожие вопросы
Q1) Что вы понимаете под плоской замкнутой фигурой?
Q2) Внутренняя часть фигуры называется областью фигуры. Верно ли это утверждение?
Q3) Найдите периметр каждой из следующих замкнутых фигур:
Q4) Найдите периметр прямоугольника, у которого: (i) длина = 40 см и ширина = 35 см (ii) длина = 10 м. ..
..
Q5) Если P обозначает периметр прямоугольника, l обозначает его длину, а b обозначает его ширину, найдите :(i)…
Q6) Найдите периметр квадрата, каждая сторона которого равна 1,6 м.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 32(А)
Упражнение 32(B)
Главы
Система счисления (закрепление смысла числа)
Оценка
Числа в Индии и международной системе (с сравнением)
Отрицательные числа и целые числа
Числовая строка
HCF и LCM
Игра с числами
Наборы
Соотношение
Пропорции (включая задачи со словами)
унитарный метод
Фракции
Десятичные фракции
процента (процент)
Идея скорости, расстояния и времени
Фундаментальные концепции (алгебра)
Фундаментальные операции (связанные с алгебрическими выражениями)
.

 = 2a + b
= 2a + b 
 = 12 см 2
= 12 см 2 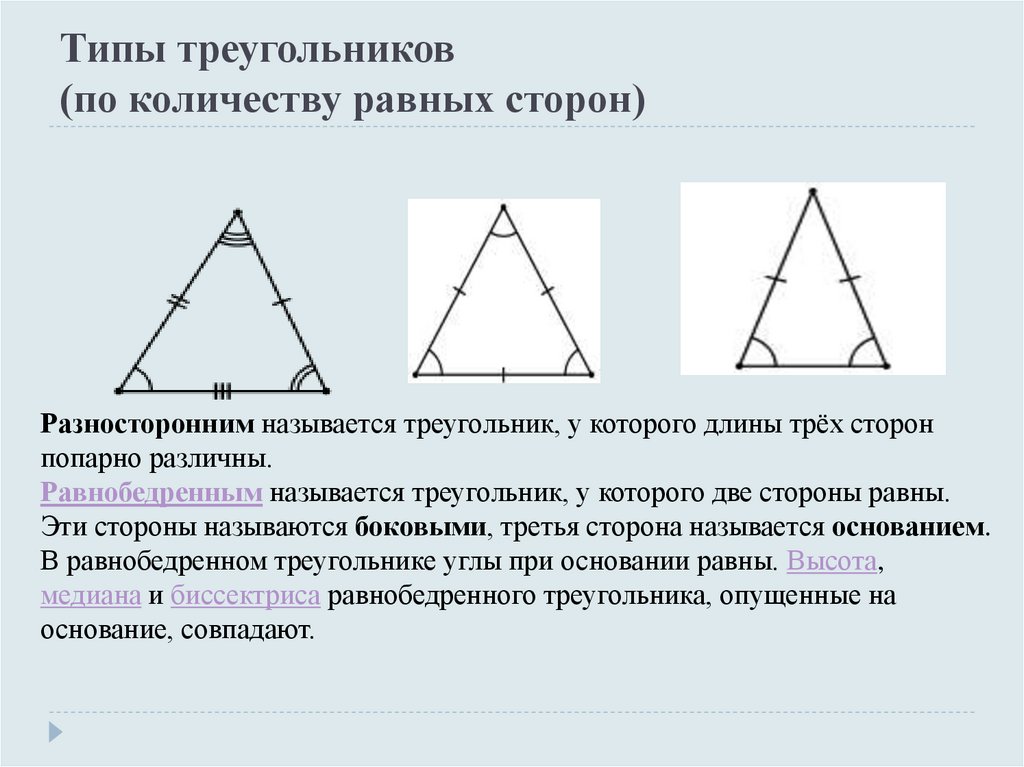
Leave A Comment