Задание № 1. Планиметрия. ЕГЭ. Математика. 1

1.  Планиметрия 

2.  Стереометрия 
3.  Начала теории вероятностей 

4.  Теория вероятностей

5.  Простейшие уравнения
6.  Преобразование выражений 
7.  Производная функции 
8.  Практические задачи 
9.  Текствые задачи 
10.  Графики функций 
11.  Исследование функций
12.  Уравнения 
13.  Стереометрия с доказ-вом
14.  Неравенства 
15.  Финансовая математика 
16.  Планиметрия с доказ-вом 
17.  Задачи с параметром 
18.  Задачи на логику 

      БАЗА ЗАДАНИЙ

Задание № 1. Планиметрия.

1. У треугольника со сторонами 12 и 15 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 10. Найдите длину высоты, проведенной ко второй стороне.

Ответ: 8

2. В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.

Ответ: 124°

3. В треугольнике ABC угол C равен 66°, биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах.

Ответ: 123°

4. Угол A прямоугольного треугольника равен 64°. Найдите угол

AOE, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Ответ: 77°

5. В треугольнике ABC AC=BC, AB=20, высота AH равна 8. Найдите синус угла BAC.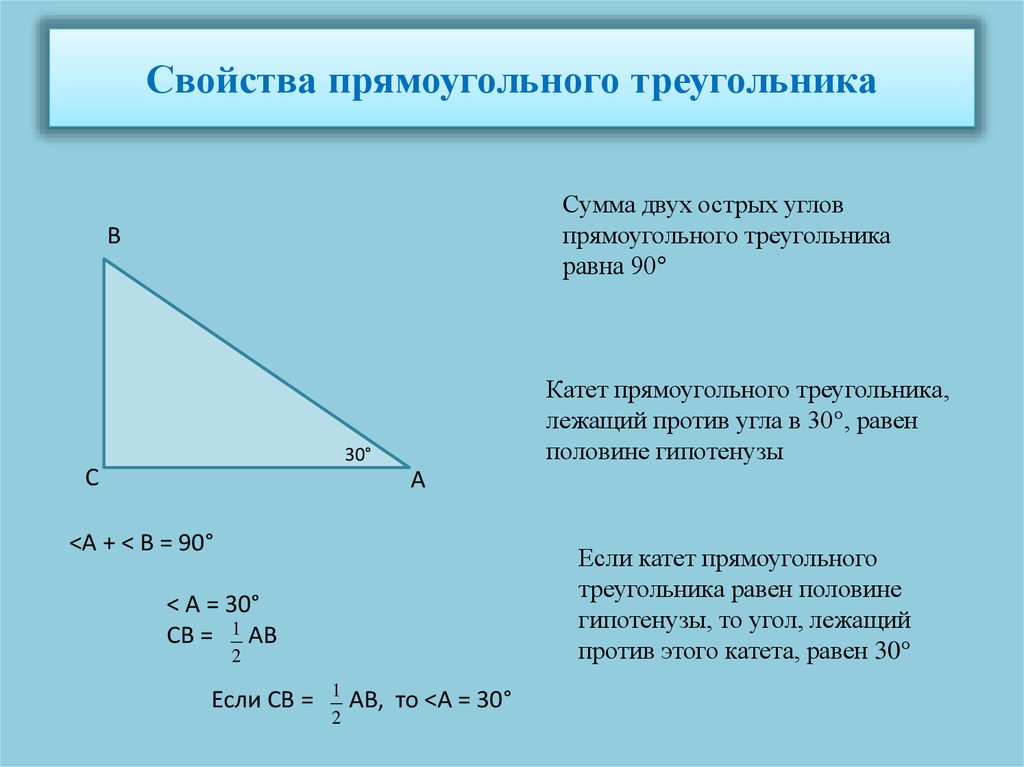

Ответ: 0,4

6. В треугольнике ABC AC = BC, AB = 8, sin∠BAC = 0,5. Найдите высоту AH.

Ответ: 4

7. В треугольнике ABC известно, что AC = BC, AH – высота, sin∠BAC=7/25. Найдите sin∠BAH.

Ответ: 0,96

8. В треугольнике ABC известно, что AC = BC, AH – высота, tg∠BAC=7/24. Найдите cos∠BAH.

Ответ: 0,28

9. В треугольнике ABC известно, что AC = BC=4√15, cos∠BAC=0,25. Найдите высоту AH.

Ответ: 7,5

10. В треугольнике ABC угол C равен 90°, AB=10, AC=√51. Найдите sin∠A.

Ответ: 0,7

11. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 11. Найдите площадь этого треугольника.

Ответ: 30,25

12.

В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

Ответ: 31°

13. Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Ответ: 78°

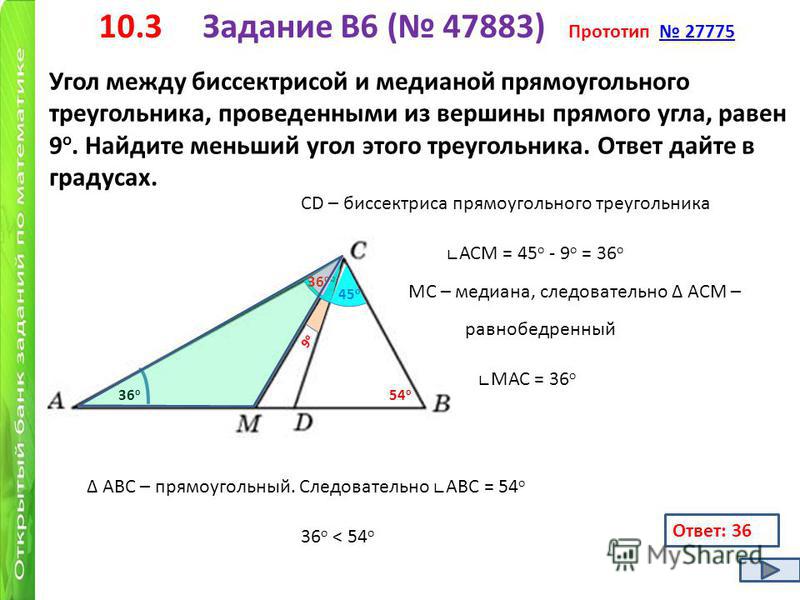
14. Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника.

Ответ: 31°

15. В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.

Ответ: 55°

16. В треугольнике ABC AC=BC=20, AB=28. Найдите косинус угла A.

Ответ: 0,7

17. В треугольнике ABC известно, что AC=BC=7, tg∠A= √33/4 .   Найдите AB.

Ответ: 8

18. В треугольнике ABC AC = BC = 5, sin∠A =0,8. Найдите АВ.

Ответ: 6

19. В равностороннем треугольнике ABC

высота CH равна 45√3. Найдите AB.

Ответ: 90

20. В треугольнике ABC известно, что AC = BC, AB = 1, cos∠A= √17/17.  Найдите высоту CH.

Ответ: 2

21. В треугольнике ABC известно, что AC = BC, AB = 16, tg∠A=0,5. Найдите высоту CH.

Ответ: 4

22. В треугольнике ABC известно, что AC = BC, AB = 4, высота CH=2√3. Найдите угол С.

Ответ: 60°

23. В треугольнике ABC угол C равен 90°, AC=6, tg∠A=√5/2. Найдите AB.

Ответ: 9

24. В треугольнике ABC стороны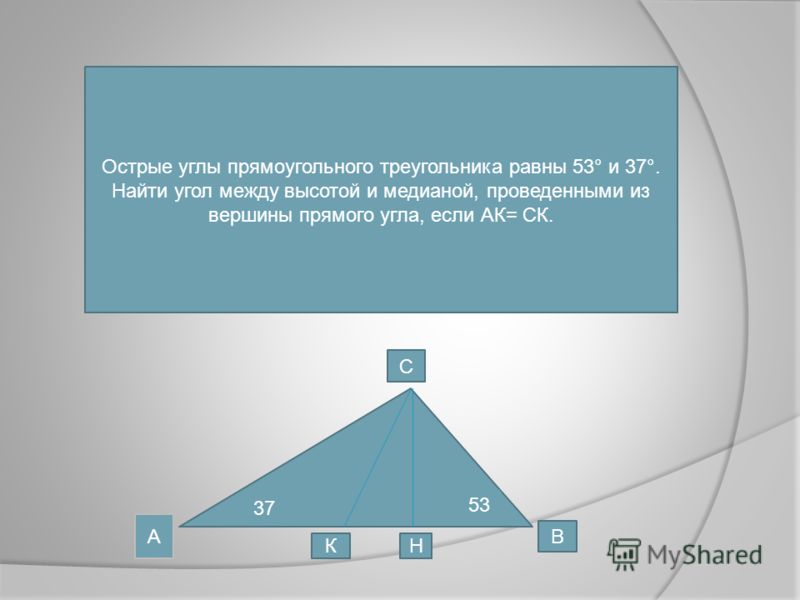

AC и BC равны, угол C равен 156°, угол CBD – внешний. Найдите угол CBD. Ответ дайте в градусах.

Ответ: 168°

25. В прямоугольном треугольнике АВС из вершины прямого угла проведена медиана CD, причем величины углов BDC и ADC относятся как 4:5. Найдите величину угла А в градусах.

Ответ: 40°

26. Высота AD треугольника АВС делит противоположную сторону на части: CD = 4, BD =1,5. Найдите длину стороны АC, если tg∠B = 2.

Ответ: 5

27. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sin∠A=0,5. Найдите BH.

Ответ: 4

28. В треугольнике ABC угол C равен 90°, AB = 5, cos∠A = 0,6. Найдите высоту CH.

Ответ: 2,4

29. В треугольнике ABC угол C равен 90°, угол A равен 30°, AB=2√3. Найдите высоту CH.

Ответ: 1,5

30. В треугольнике ABC

угол C равен 90°, CH — высота, BC = 3, cos∠A= √35/6. Найдите AH.

Ответ: 17,5

31. В треугольнике ABC угол C равен 90°, CH — высота, AB = 13, tg∠A = 1/5. Найдите AH.

Ответ: 12,5

32. В треугольнике ABC угол C равен 90°, AB = 13, tg∠A = 1/5. Найдите высоту CH.

Ответ: 2,5

33. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите cos∠A.

Ответ: 0,6

34. В тупоугольном треугольнике

ABC AC = BC=8, высота AH равна 4. Найдите sin∠ACB.

Ответ: 0,5

35. В тупоугольном треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите sin∠BAC.

Ответ: 0,8

36. В тупоугольном треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите cos∠BAC.

Ответ: 0,6

37. В треугольнике ABC угол C равен 90°, синус ∠В=7/25. Найдите синус внешнего угла при вершине А.

Ответ: 0,96

38. В треугольнике

ABC угол C равен 90°, косинус угла В=0,6. Найдите косинус внешнего угла при вершине А.

Ответ: -0,8

39. В треугольнике ABC угол C равен 90°, косинус внешнего угла при вершине A равен -0,1. Найдите синус ∠B.

Ответ: 0,1

40. В треугольнике ABC угол C равен 90°, тангенс внешнего угла при вершине A равен -2. Найдите тангенс ∠B.

Ответ: 0,5

41. В треугольнике ABC AC=BC=√17, AB=8. Найдите тангенс внешнего угла при вершине В.

Ответ: -0,25

42. В треугольнике ABC AC=BC=8, косинус внешнего угла при вершине В равен -0,5. Найдите AB.

Ответ: 8

43. Один из внешних углов треугольника равен 85°. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.

Ответ: 51°

44. В треугольнике ABC угол A равен 60°, угол B равен 70°, CH — высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.

Ответ: 10°

45. В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB.

Ответ дайте в градусах.

Ответ: 38°

46. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Ответ: 52°

1     2     3

Главная

Синус(sin), косинус(cos), тангенс(tg), котангенс(ctg) — как найти, отношение, формулы

Изучение тригонометрии мы начнем с прямоугольного треугольника.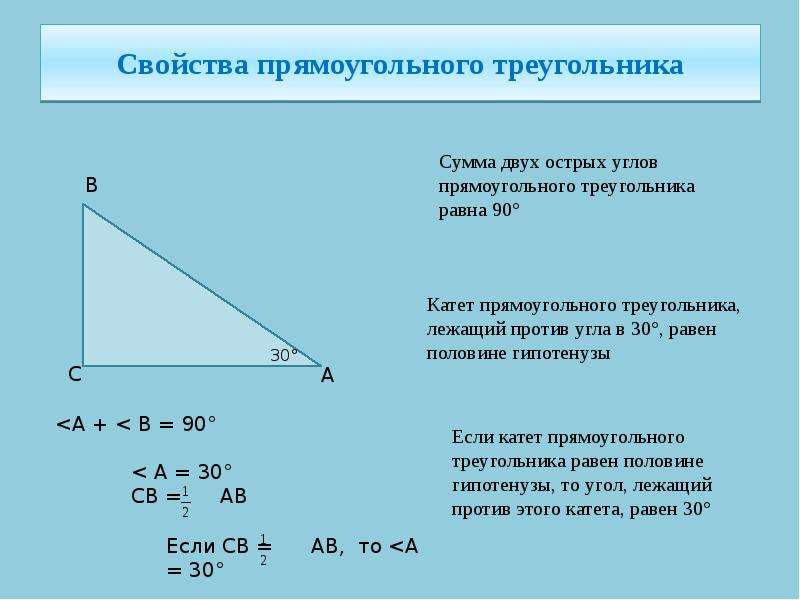 Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sinsincos
cos1+tgcos = sin
tg1+ctgsin = cos
ctgtg = ctg

Давайте докажем некоторые из них.

  1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
  2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, .
  3. Возьмем теорему Пифагора: . Поделим обе части на получаем то есть
    Мы получили основное тригонометрическое тождество.
  4. Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .

0
sin0
cos0
tg0−
ctg−0

Обратите внимание на два прочерка в таблице.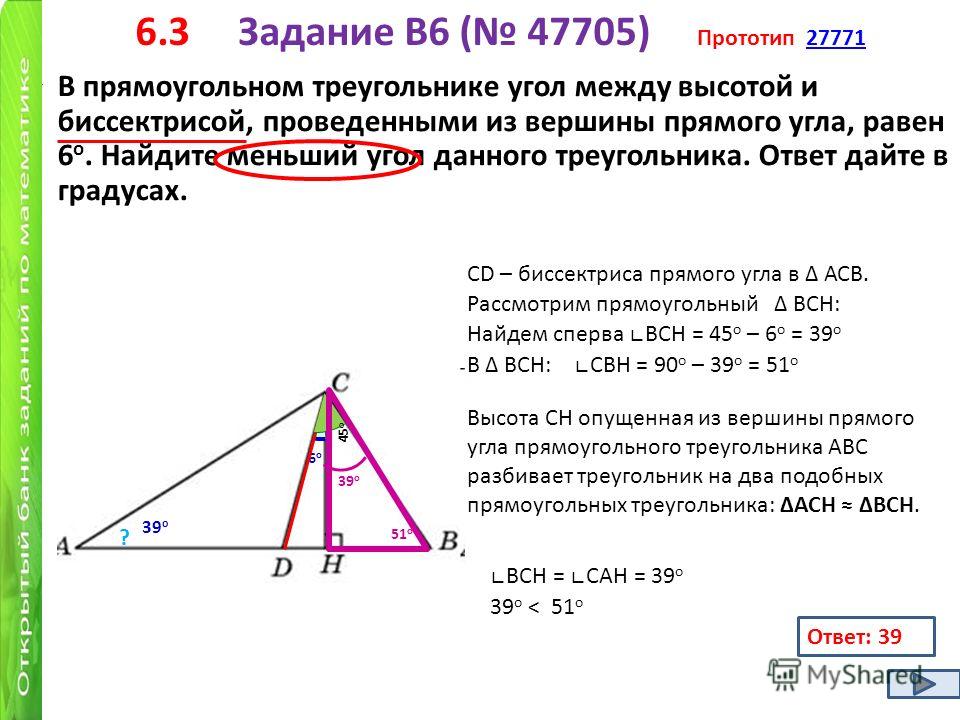 При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и и равными острыми углами А и

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому

Из этих равенств следует, что т. е. sin А = sin

Аналогично, т. е. cos А = cos и т. е. tg A = tg

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку , sin A = cos B = 0,1.

Задача 2. В треугольнике угол равен , , .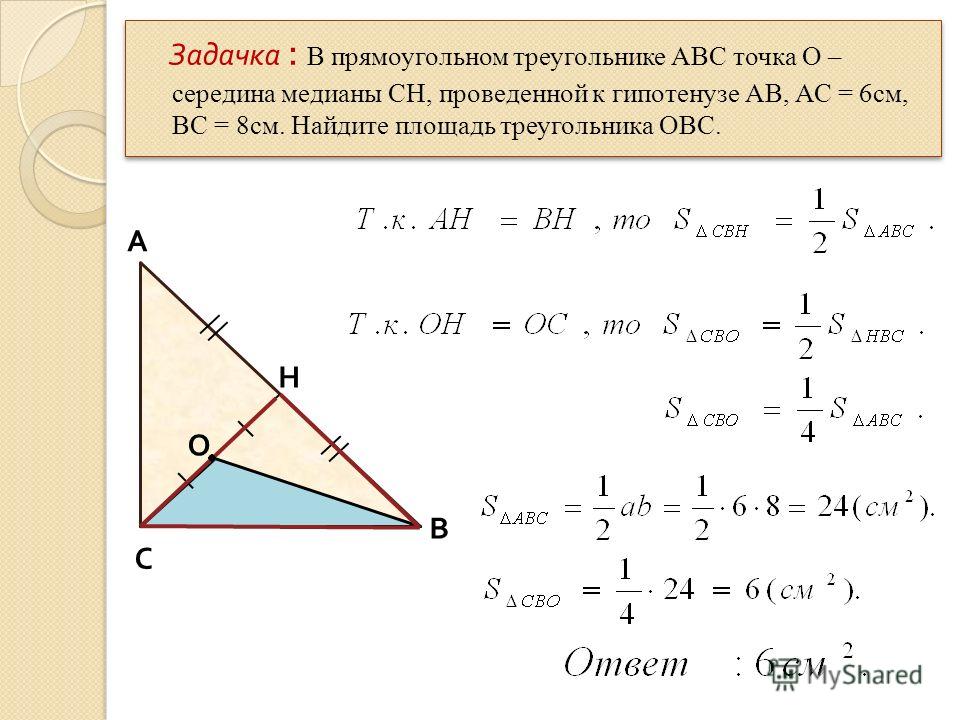

Найдите .

Решение:

Отсюда

Найдем AC по теореме Пифагора.

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A

Катет, прилежащий к – это катет АС, следовательно, cos⁡ А

Длину катета АС найдем по теореме Пифагора:

Тогда

cos⁡ А

tg A

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A

По теореме Пифагора получим

Ответ: 0,5.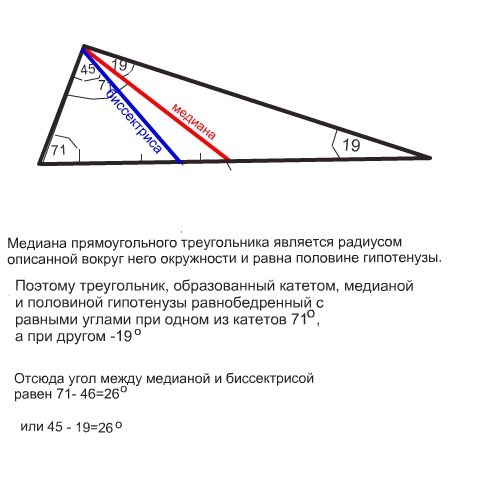

Задача 5. В треугольнике АВС угол С равен tg A = Найдите AB.

Решение:

AC = b = 4, tg A

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = Найдите AH.

Решение:

AВ = с = 13, tg A = тогда b = 5a.

По теореме Пифагора ABC:

тогда

(по двум углам), следовательно откуда

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A =

Найдите AH.

Решение:

Так как sin A = тогда c = АВ = 18.

sin A = = cos⁡ B =

Рассмотрим BHC:

= получим

тогда BH = = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =

Найдите АH.

Решение:

Так как для АВС: A = sin В =

а для ВНС: sin В = = , откуда СН =

По теореме Пифагора найдем ВН:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

тогда

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= = =

Рассмотрим BHC :

ВС найдем по теореме Пифагора:

ВС=

тогда а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = = = cos A = = =

тогда tg A = который найдем из BHC:

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A = Найдите АН.

Решение:

По определению tg A=

Для BHC: , значит СН =

Для АHC: tg A= то AH =

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A = Найдите АВ.

Решение:

Так как cos В = = sin A =

Из СВН имеем cos В = = тогда ВС =

В АВС имеем sinA = = тогда AВ =

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

sin В = =

Для АВС: cos A = получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора получим


х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит или

k = тогда АС = ; АВ =

3-й способ.

(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

=

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = =

cos C =

Для АВС: sin А = = cos C =

Для АНВ: sin А = = то = АВ =

Из основного тригонометрического тождества найдем

cos A =

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А =

значит = 14.

Второй катет найдем, используя теорему Пифагора:

Площадь прямоугольного треугольника равна S =

поэтому

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, ),

значит sin

Найдем АС по теореме Пифагора из САВ:

Тогда sin

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ =

Поскольку АСН — прямоугольный,

cos A = то есть АС =

По теореме Пифагора тогда

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 sin A = AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора

(14х- 11х)(14х + 11х) = 3 100;

учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством

cos A =

По определению cos A = значит

Так как АС=10 то откуда АВ = = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.

Решение:

Пусть ВАО =

Диагонали ромба делят его углы пополам, значит, =

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =

Поэтому tg откуда

Ответ:

Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 угол А равен 30 АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла имеем ВС = АВ =

В BHC: то следовательно, ВН = BC =

По теореме Пифагора найдем НС:

Ответ: 1,5.

Задача 21.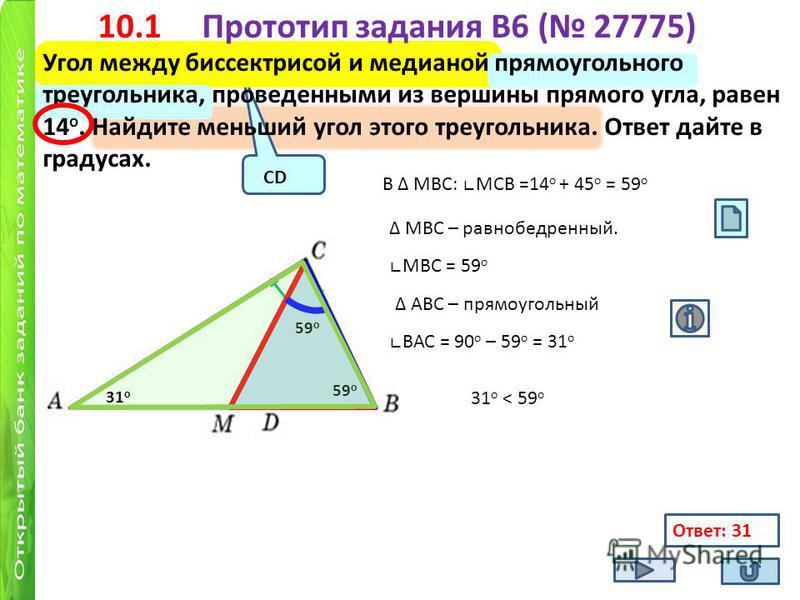

В треугольнике АВС угол С равен 90 CH — высота, АВ = 2, Найдите АH.

Решение:

Из АВС найдем ВС = АВ = 1 (по свойству катета, лежащего против угла 30),

то

Из ВСН: то следовательно,

ВН = ВС =

АН = АВ — НВ = 2 — = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

 

Спасибо за то, что пользуйтесь нашими публикациями.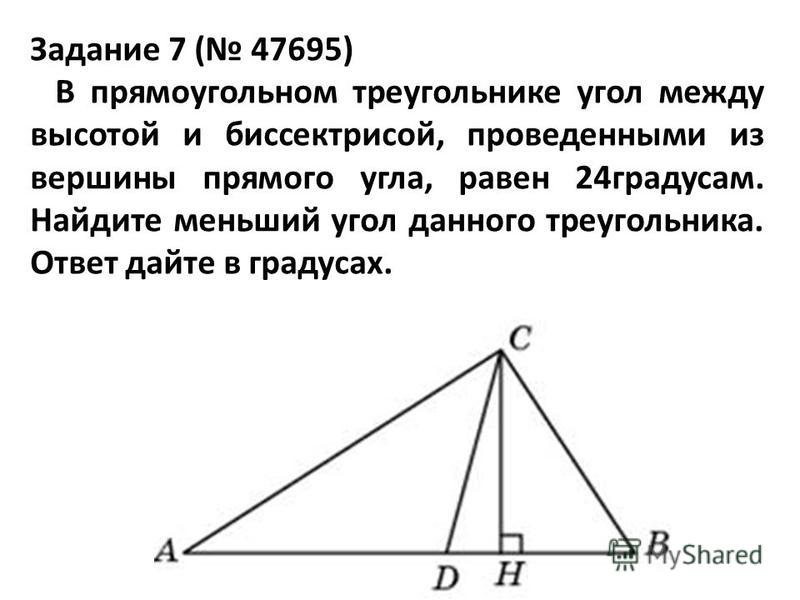 Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 07.02.2023

Калькулятор треугольника

Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.

Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.

Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.

Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.

Факты, теоремы и законы треугольника

  • Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.

Площадь треугольника

Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена ​​длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.

Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше.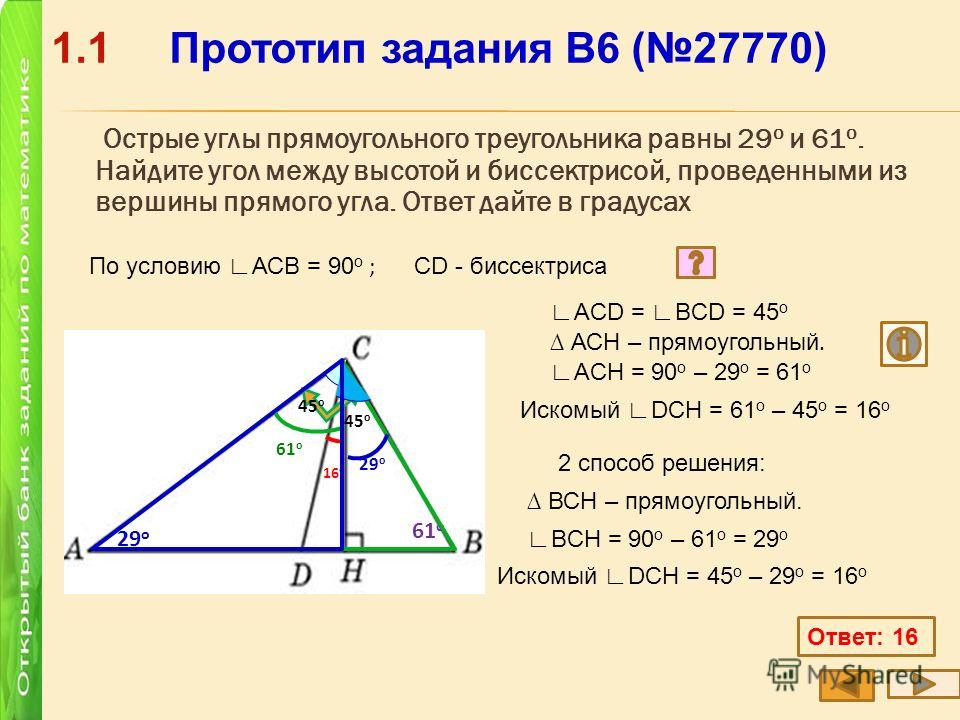 Учитывая а = 9, b = 7 и C = 30°:

Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:

Медиана, внутренний радиус и радиус описанной окружности

Медиана

Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.

Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:

Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.

Например, учитывая, что a=2, b=3 и c=4, медиана m a может быть рассчитана следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.

Для целей этого калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:

внутренний радиус =  
с =
а+б+в
2

где a, b и c — стороны треугольника

Радиус окружности

Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.

Для целей данного калькулятора радиус описанной окружности рассчитывается по следующей формуле:

радиус описанной окружности =  
а
2sin(A)

Где а — сторона треугольника, а А — угол, противоположный стороне а

Хотя сторона а и угол А используются, в формуле можно использовать любую из сторон и соответствующие им противоположные углы.

Прямоугольные треугольники

Прямоугольные треугольники

Давайте снова согласимся со стандартным правилом обозначения частей прямоугольного треугольника. Пусть прямой угол обозначен как C , а гипотенуза C. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им соответственно.

Решение прямоугольных треугольников
Мы можем использовать теорему Пифагора и свойства синусов, косинусов и тангенсов для решения треугольника, то есть для нахождения неизвестных частей через известные части.
  • Теорема Пифагора:   a 2  +  b 2  =  c 2 .
  • Синусы: sin A = a/c, sin B = b/c.
  • Косинусы:   cos  A  =  b/c, cos  B  =  a/c.
  • Касательные: tan A = a/b, tan B  = b/a.
Давайте сначала рассмотрим некоторые случаи, когда мы не знаем всех сторон. Предположим, мы не знаем гипотенузу, но знаем две другие стороны. Теорема Пифагора даст нам гипотенузу. Например, если a = 10 и B = 24, затем C 2 = A 2 + B 2 = 10 2 2 2 2 2 2

9 2

9 2 2 2 2 2 2 2 2 2 2 2

8 2 2 2+2 2 2

8. Квадратный корень из 676 равен 26, поэтому 90 148 c 90 149 = 26. (Приятно привести примеры, когда из квадратных корней получаются целые числа; в жизни это обычно не так.)

Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую. Например, если b  = 119 и C = 169, затем A 2 = C 2 — B 2 = 169 2 — 1199169 2 = 169 2 — 119169 2 = 169 2 — 119169 2 . равно 120, поэтому 90 148 a 90 149 = 120.

Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a  = 15 и угол A  = 41°, мы можем использовать синус и тангенс, чтобы найти гипотенузу и другую сторону. Поскольку грех A  = a/c, мы знаем c  = a /sin A  = 15/sin 41. Используя калькулятор, это 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.

Обратные триггерные функции: арксинус, арккосинус и арктангенс
Теперь давайте рассмотрим задачу нахождения углов, если известны стороны. Опять же, вы используете триггерные функции, но наоборот. Вот пример. Предположим a  = 12,3 и b  = 50,1. Тогда тангенс A = a/b = 12,3/50,1 = 0,2455. Раньше, когда люди использовали таблицы триггерных функций, они просто смотрели в таблицу тангенсов, чтобы увидеть, какой угол имеет тангенс 0,2455.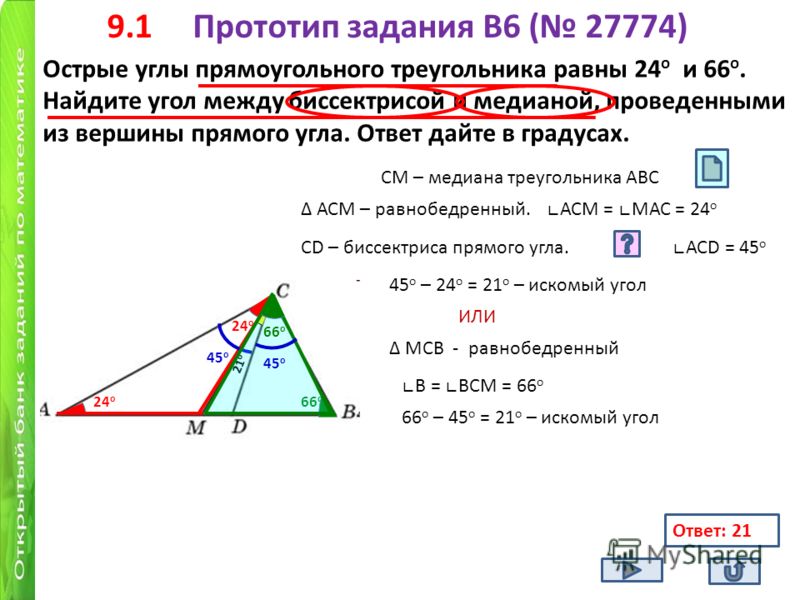 На калькуляторе мы используем обратные триггерные функции, называемые арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием соответствующей кнопки триггера. Арктангенс 0,2455 равен 13,79., поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.)

Вот и все.

Остальные три тригонометрические функции: котангенс, секанс и косеканс
Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса. Однако бывают случаи, когда нужны какие-то другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия. Есть шесть способов сделать отношения двух сторон прямоугольного треугольника, и это дает шесть функций:
    1. sin  A  =  a/c (opp/hyp)
    2. cos  A  =  b/c (adj/hyp)
    3. tan  A  =  a/b (opp/adj)
    4. детская кроватка A  =  b/a (adj/opp)
    5. сек  A  =  c/b (hyp/adj)
    6. csc  A  =  c/a (hyp/opp)
    Из листинга видно, что котангенс (сокращенно cot или иногда ctn) является величиной, обратной величине тангенса, секанс (сокращенно sec) является величиной, обратной величине косинуса, а косеканс (сокращенно csc или иногда cosec) является величиной, обратной величине синуса. Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A  = tan B, и косекансы являются секущими дополнительных углов, а это означает, что csc A  = sec  B.

    Эти три другие функции также можно интерпретировать с помощью единичной круговой диаграммы.

    Мы рассматриваем угол AOB. Напомним, что его касательной является прямая AC. По симметрии тангенсом угла FOB является линия FG, а FOB является дополнительным углом AOB, , следовательно, котангенс AOB равен FG.

    Далее, интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, so sec AOB = sec AOC  = hyp/adj = OC/OA  = OC. Итак, секанс — это линия, проведенная из центра круга к касательной AC. Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».

    Аналогично, косекансом угла АОВ является прямая ОГ , проведенная из центра окружности к линии котангенса ФГ.

    Упражнения
    Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначают гипотенузу, a и b для перпендикулярных сторон и A и B для углов, противоположных a и b соответственно.

    26. В каждом из следующих прямоугольных треугольников, две стороны которых заданы, вычислите sin, cos и тангенс углов A и B. Выразите результаты в виде обыкновенных дробей.
    (и). c  = 41, a  = 9.
    (ii). с  = 37, а  = 35.
    (iii). a  = 24, b  = 7.

    31. В прямоугольном треугольнике c  = 6 футов 3 дюйма и загар  B  = 1,2. Найдите а и б.

    34. a  = 1,2, b  = 2,3. Найти A и c.

    42. a  = 10,11, b  = 5,14. Найти B и c.

    В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя свои знания о прямоугольных треугольниках.

    61. В косом треугольнике ABC, A  = 30°, B  = 45°, а перпендикуляр из C в AB имеет длину 12 дюймов. Найдите длину АВ.

    67. Если сторона равностороннего треугольника равна а, найти высоту и радиусы описанной и вписанной окружностей.

    202. От вершины здания высотой 50 футов углы возвышения и углубления вершины и низа другого здания составляют 19° 41′ и 26° 34′ соответственно. Каковы высота и расстояние до второго здания.

    207. С вершины маяка высотой 175 футов углы наклона вершины и низа флагштока составляют 23° 17′ и 42° 38′ соответственно. Какой высоты столб?

    214. В двух точках на расстоянии 65 футов друг от друга на одной стороне дерева и на одной линии с ним углы возвышения вершины дерева составляют 21° 19′ и 16° 20′. Найдите высоту дерева.

    215. Когда воздушный шар проходит между двумя точками A, и B, находящимися на расстоянии 2 миль друг от друга, углы места воздушного шара в этих точках составляют 27° 19′ и 41° 45′ соответственно. Найдите высоту воздушного шара. Возьмите А и B на том же уровне.

    233. Верхняя часть маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится «на горизонте»? [Предположим, что Земля — это сфера радиусом 3956 миль.]

    234. На какой высоте должен находиться наблюдатель, чтобы он мог видеть объект на Земле на расстоянии тридцати миль? Предположим, что Земля представляет собой гладкий шар.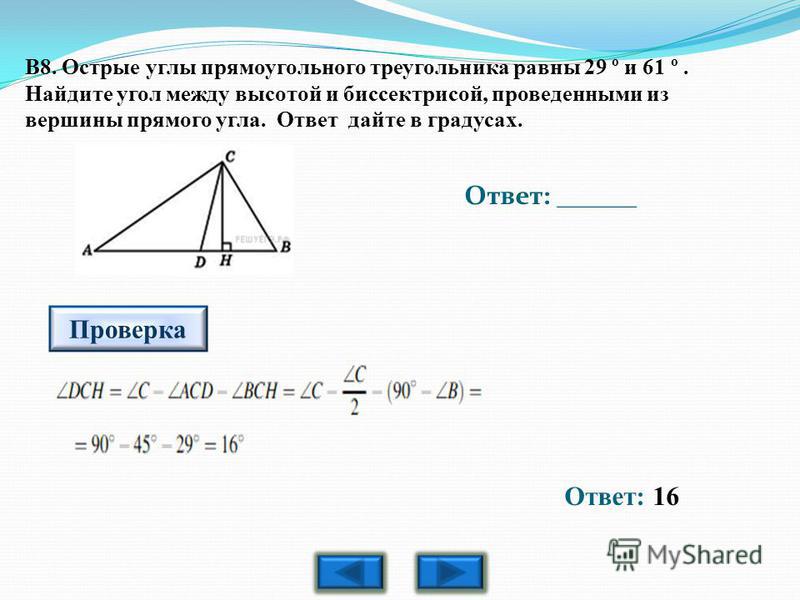

    В каждой из фигур, названных в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, , то есть радиус описанной окружности, (ii) по апофеме r, , то есть радиус вписанной окружности, и (iii) по стороне a.

    251. Равносторонний треугольник. [См. задачу 67 выше.]
    252. Квадрат.
    253. Правильный пятиугольник.
    254. Правильный шестигранник.
    255. Правильный восьмиугольник.

    Подсказки

    26. Вам нужны только sin, cos и тангенс углов A и B ; вам не нужны сами углы. Таким образом, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем взять отношения двух сторон.

    31. Вы знаете c и tan B. К сожалению, tan B — это отношение двух неизвестных вам сторон, а именно b/a. Есть несколько способов решить эту проблему. Вот два.

    Метод 1. Возьмем уравнение 1.2 = tan  B  =  b/a, , чтобы получить соотношение между a и b, , а именно b  = 1,2 a. Теорема Пифагора дает 6,25 2 = a 2 + 1,44 a 2 , из которых можно определить a,9 и затем найти b.

    Метод 2. Из тангенса B, можно определить угол B (используйте арктангенс). Отсюда вы можете найти cos B, и затем a, и вы можете найти sin B, и затем b.

    34. Поскольку у вас есть a и b, , вы можете использовать касательные, чтобы найти A , и теорему Пифагора, чтобы найти c.

    42. Найти B по касательной и c по теореме Пифагора.

    61. Начните с рисования фигуры. Хотя треугольник ABC не является прямоугольным, он распадается на два прямоугольных треугольника. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их вместе.

    67. Равносторонний треугольник ABC имеет три угла при вершине по 60°. Опустите перпендикуляр из одной вершины, скажем, вершины C, , и вы получите два конгруэнтных прямоугольных треугольника ACF и BCF, , и вы можете найти длину этого перпендикуляра, а это высота равностороннего треугольника. Описанная окружность — это та, которая проходит через три вершины, а вписанная окружность — это та, которая касается внутри трех сторон. Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и применяя тригонометрию к полученным маленьким треугольникам, можно найти радиусы этих двух окружностей.

    202. Поскольку вы знаете высоту своего здания и угол наклона к основанию другого здания, вы можете определить, как далеко оно находится. Тогда угол подъема на вершину другого здания скажет вам, насколько оно выше вашего.

    207. Подсказка похожа на 202. Смотрите, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!

    214. Это полезная задача. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота х дерева и расстояние х ближайшей точки к дереву. Дальнейшая точка — 90 148 x 90 149 + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить для определения y и x.

    215. Это похоже на 214, но в этой задаче шарик лежит между двумя точками. Нарисуйте фигуру. Определите свои переменные. Составьте уравнения и решите их.

    233. Очень интересная задача. Различные его обратные значения использовались на протяжении веков для вычисления радиуса Земли. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам нужно здесь, это теорема Пифагора. Одна сторона прямоугольного треугольника равна r, радиус Земли, а гипотенуза r + h , где h — высота маяка.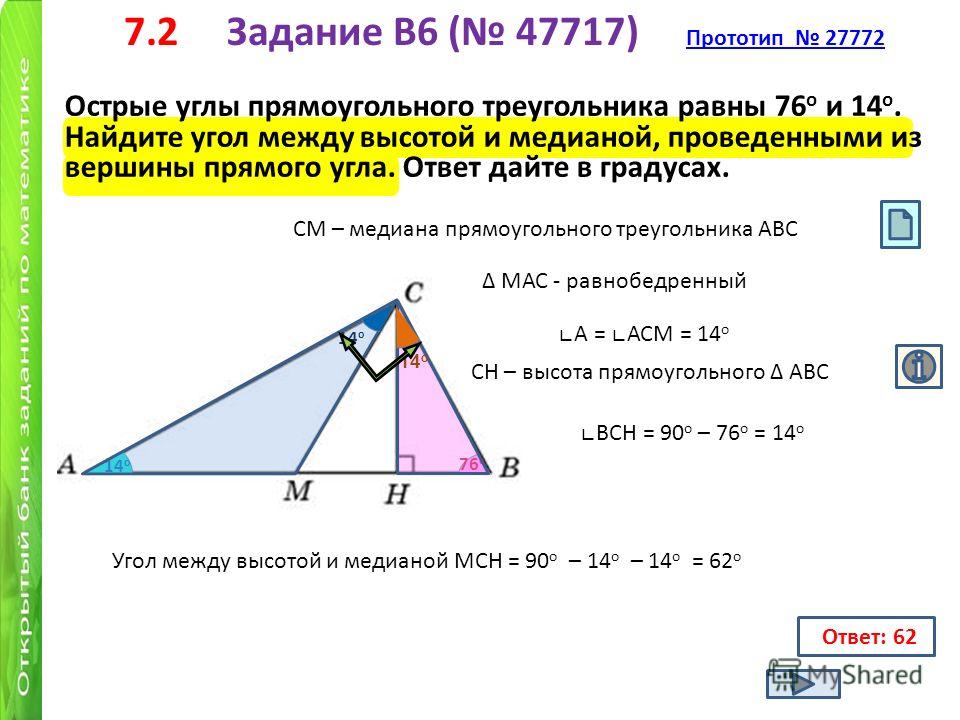 Теорема Пифагора третья сторона треугольника.

    234. Поставьте эту задачу аналогично 233, но известны другие переменные.

    251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и к серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, катетом р, и другая нога и /2. Угол в центре равен 360°/(2 n ) = 180°/ n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника по мере необходимости.

    Ответы
    26. (и). B = 40. SIN A = COS B = 9/41, COS A = SIN B = 40/41, TAN A = 9/40, TAN B = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149 = 40149. /9.
    (ii). B = 12. Итак, SIN A = COS B = 35/37, COS A = SIN B = 12/37, TAN A = 35/12, TAN B =     B     = B = B . /37.
    (iii). C = 25. Итак, SIN A = COS B = 24/25, COS A = SIN B = 7/25, TAN A = 24/7, TAN B = 7 = 7 = 7 = = 7 = = = 7 = a = 24/7, TAN B = a . /24.

    31. a  = 4 фута, b  = 4,8 фута, около 4 футов 10 дюймов.

    34. A  = 27,55°, около 28°. c  = 2,6.

    42. B  = 26,95° или 26°57′. c  = 11,3.

    61. AB = 12/тангенс A + 12/тангенс B = 12(√3 + 1) дюймов, примерно 33 дюйма.

    67. ( a √3)/2, ( a √3)/3 и ( a √3)/6 соответственно.

    202. Расстояние = 50/тангенс 26°34′ = 100 футов. Высота = 50 + 100 tan 19°41′ = 85,8′ = 85’9″.

    207. Расстояние = 175/тангенс 42°38′ = 190 футов. Рост = 175 — 190 тангенс 23°17′ = 93,23′ = 9’3″.

    214. Два уравнения

      0,293052 = тангенс 16°20′ = ч /(65 +  x ), и
      0,3 = тангенс 21°19′ = ч/х .
    где x — расстояние от ближайшей точки до основания дерева. Вы можете решить их одновременно за х и ч.
    Расстояние х = 196 футов. Высота ч = 76,5′.

    215. Если h — это высота воздушного шара, а x — это расстояние по земле от A до точки непосредственно под воздушным шаром, то два уравнения

      тангенс 27°19′ = ч/х и
      тангенс 41°45′ = ч / (2 –  x )
    Вы можете решить эту пару уравнений на х и ч.
    Высота = 0,654 мили = 3455 футов.

    233. Мелочь больше 18,5 миль.

    234. 600 футов.

    251–255. Площадь правильного n -угольника равна A = nra /2. Чтобы найти A через R, r, или a, , используйте соотношения

      cos 180°/ n = r/R, и
      тангенс 180°/ n = a /(2 r ).
    Затем
      (i) в пересчете на R, площадь A = nR 2  cos 180°/ n  sin 180°/ n ,
      (ii) в пересчете на r, площадь A = nr 2 tan 180&deg/ n , и
      (iii) по а, площади А = н/д 2 /(4tan 180&deg/ и ).
      Problem shape (i) R (ii) r (iii) a
      251 triangle (3 Р 2 √3)/4 3 р 2  √3 ( a 2 √3)/4
      252 квадратный 2 Р 2 4 р 2 a 2
      253 пятиугольник (5 R 2  sin 108°)/2 5 r 2 tan 36° (5 a 2 тангенс 54°)/4
      254 шестигранник (3 Р 2 √3)/2 2 р 2  √3 (3 a 2 √3)/2
      255 восьмиугольник 2 Р 2  √2 8 r 2 tan 22°30′ 2 a 2 tan 67°30′
    Отступление от троек Пифагора
    Это не имеет ничего общего с тригонометрией, но это интересно. Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как и в задаче 26, где все три прямоугольных треугольника имели целые числа в качестве сторон, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5.

    Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых являются целыми числами? Да и изучались они давно. Три числа a, b, и c такие, что a 2  +  b 2  =  c 2 образуют пифагорейскую тройку , в честь Пифагора. Он жил около 550 г. до н. э. и, вероятно, знаю немало из них. Но древние вавилоняне около 1800 г. до н. э. знали их все, и многие были известны в других древних цивилизациях, таких как Китай и Индия.