Задание №13. Стереометрия с доказательством. ЕГЭ. Математика. 1
1. Планиметрия
2. Стереометрия
3. Начала теории вероятностей
4. Теория вероятностей
5. Простейшие уравнения
6. Преобразование выражений
7. Производная функции
8. Практические задачи
9. Текствые задачи
10. Графики функций
11. Исследование функций
12. Уравнения
13. Стереометрия с доказ-вом
14. Неравенства
15. Финансовая математика
16. Планиметрия с доказ-вом
17. Задачи с параметром
18. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 13. Стереометрия с доказательством.
Стереометрия с доказательством.
1. В кубе ABCDA1B1C1D1 все рёбра равны 5. На его ребре BB1 отмечена точка K так, что KB=4. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.
а) Докажите, что A1P:PB1=3:1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
2. В кубе ABCDA1B1C

а) Докажите, что A1P:PB1=3:1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.
4. В правильной треугольной пирамиде SABC сторона основания
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Ответ: б) 8 + 2√2
5. В правильной треугольной пирамиде SABC сторона основания AB=60, а боковое ребро SA=37. Точки M и N — середины рёбер SA и SB соответственно.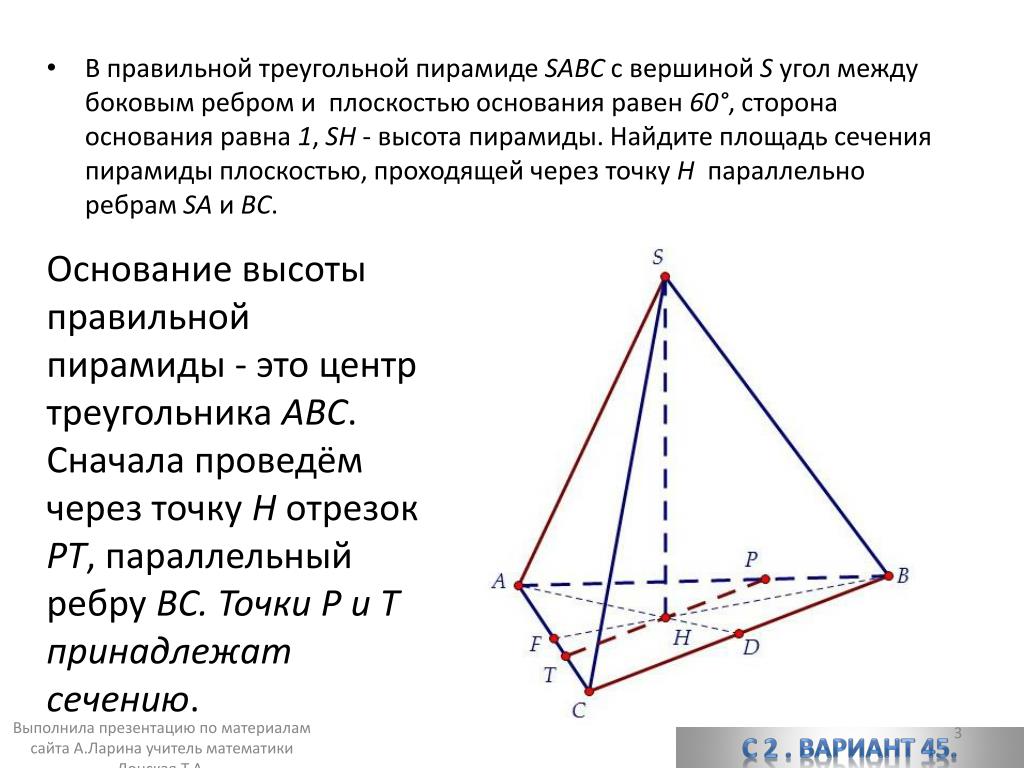
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите расстояние от вершины A до плоскости α.
Ответ: б) 5√3
7. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=6. Длины боковых рёбер пирамиды SA=3, SB=5, SD=3√5.
а) Докажите, что SA— высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
8. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6. Длины боковых рёбер пирамиды SA=√21, SB=√85, SD=√57.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.
9. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=5 и диагональю BD=9.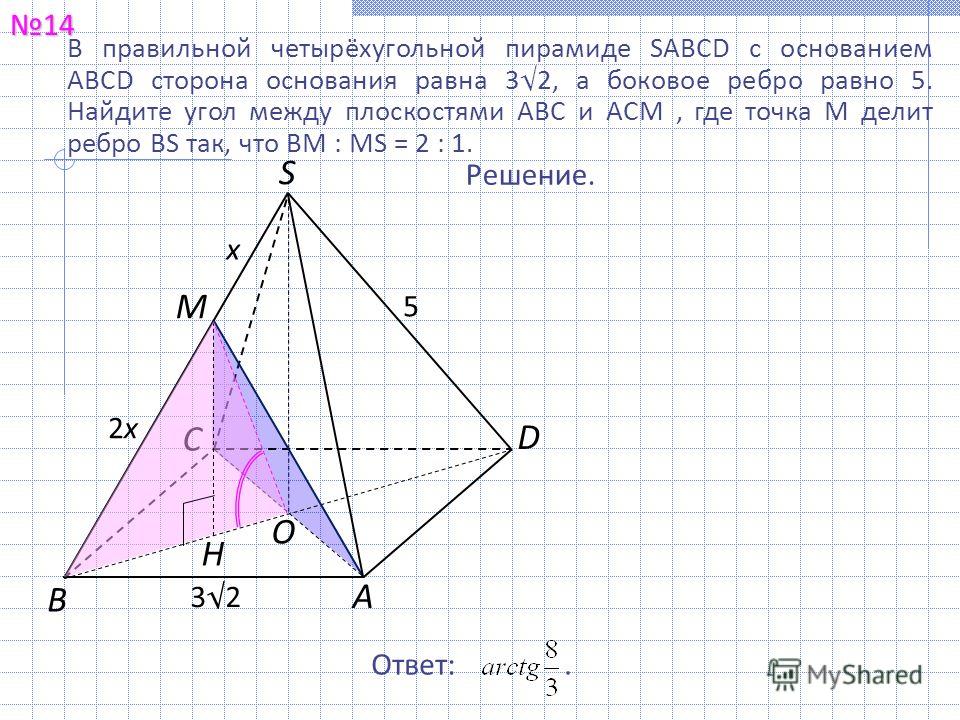 Все боковые рёбра пирамиды равны 5. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF=BE=4.
Все боковые рёбра пирамиды равны 5. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF=BE=4.
а) Докажите, что плоскость
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.
10. В правильной треугольной призме ABCA1B1C1 сторона основания AB равна 6, а боковое ребро AA1 равно 2√2. На рёбрах AB, A1B1 и B1C1 отмечены точки M, N и K соответственно, причём AM = B1N= C1K=2.
а) Пусть L — точка пересечения плоскости MNK
б) Найдите площадь сечения призмы плоскостью MNK.
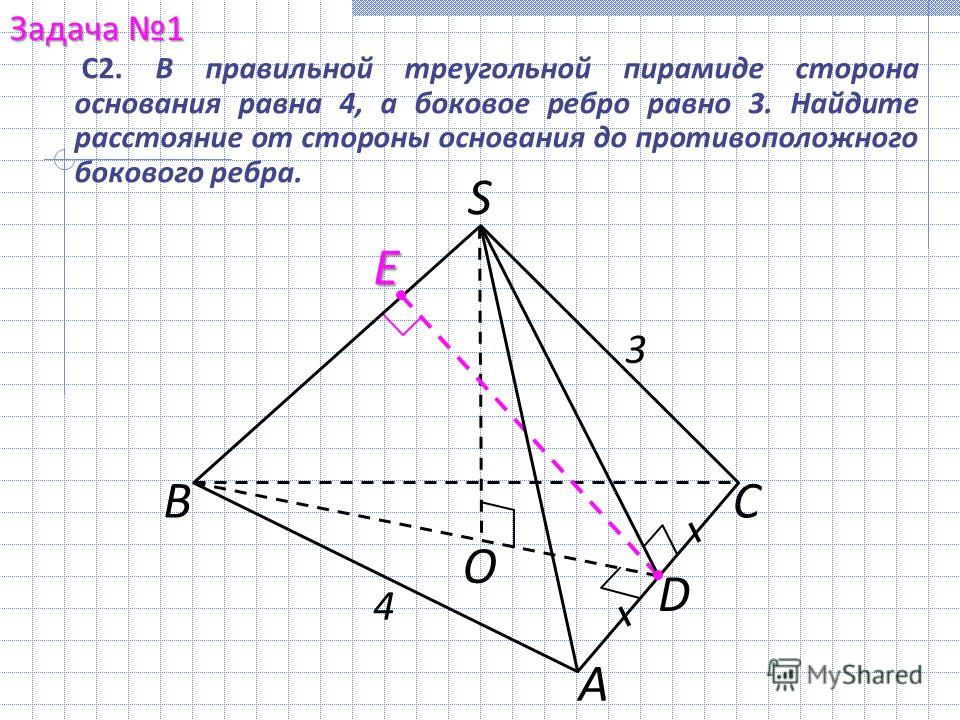
Ответ: б) 15
11. В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 6, а боковое ребро AA1=3. На ребре AB отмечена точка K так, что AK=1. Точки M и L— середины рёбер A1C1 и B1C1 соответственно. Плоскость γ параллельна прямой
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) 3/4
12. В правильной четырёхугольной призме ABCDA1B1C1D1 сторона AB основания равна 8, а боковое ребро AA1 равно 4√2. На рёбрах BC и C1D1 отмечены точки K и L соответственно, причём BK= C1L=2.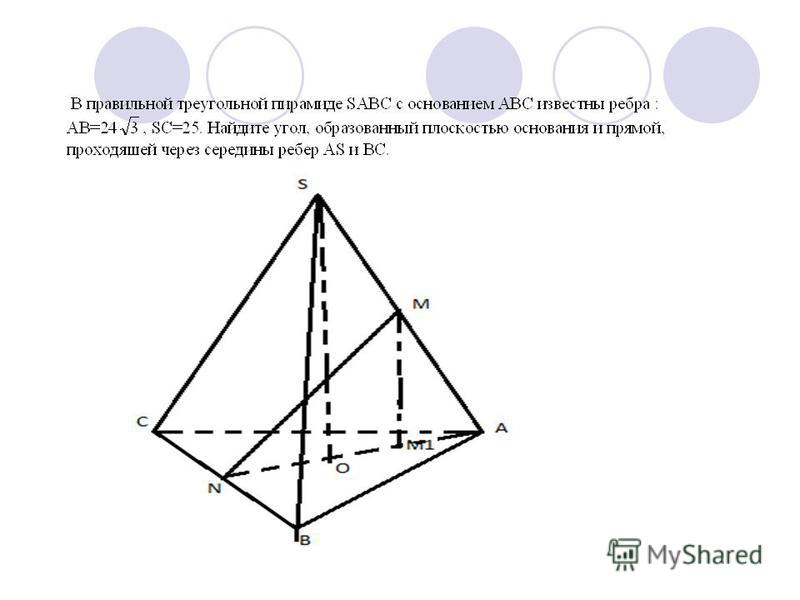
а) Докажите, что прямая A1C перпендикулярна плоскости γ.
б) Найдите расстояние от точки B до плоскости γ.
13. В основании прямой треугольной призмы ABCA1B1C1 лежит равнобедренный (AB=BC) треугольник ABC. Точка K— середина ребра A1B1, а точка M делит ребро AC в отношении AM:MC=1:3.
а) Докажите, что KM⊥AC.
б) Найдите угол между прямой KM и плоскостью ABB
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=2√2, AD=6, AA1=10. На рёбрах AA1 и BB1 отмечены точки E и F соответств.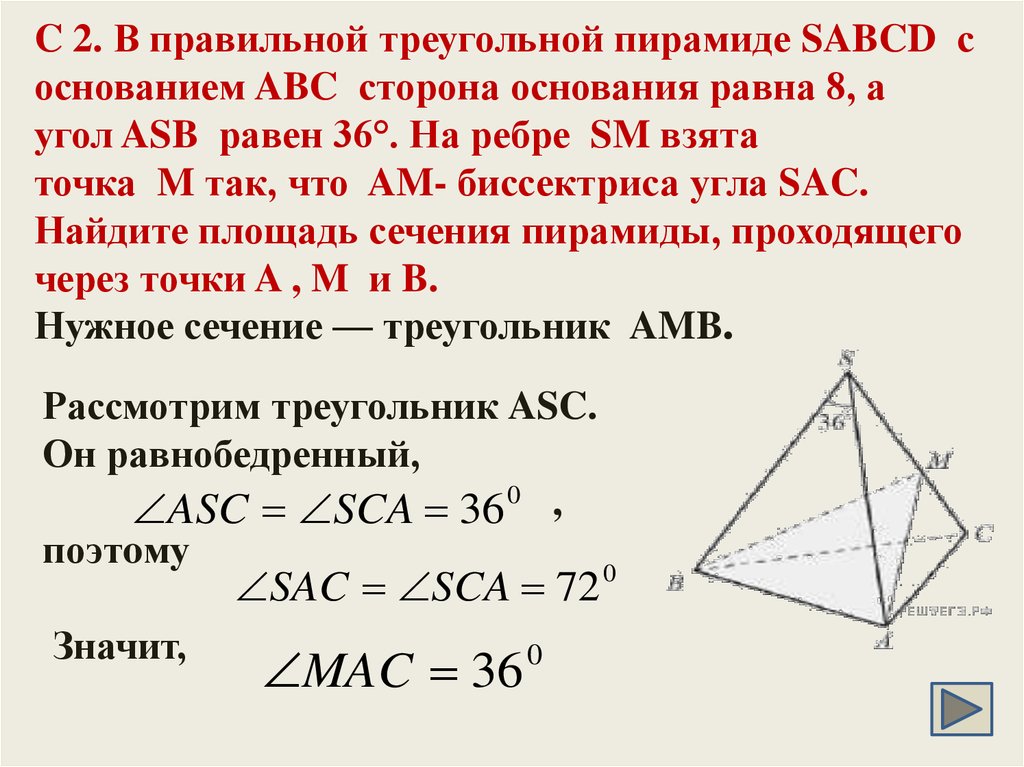 , причём A1E:EA =3:2 и B1F:FB=3:7. Точка T — середина ребра B1C1.
, причём A1E:EA =3:2 и B1F:FB=3:7. Точка T — середина ребра B1C1.
а) Докажите, что плоскость EFT проходит через точку
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Ответ: б) 22,5
15. На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E:EA=1:2, на ребре BB1 — точка F так, что B1F:FB=1:5 , а точка Т —середина ребра B1C1. Известно, что AB=2, AD=6, AA1=6.
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите угол между плоскостью 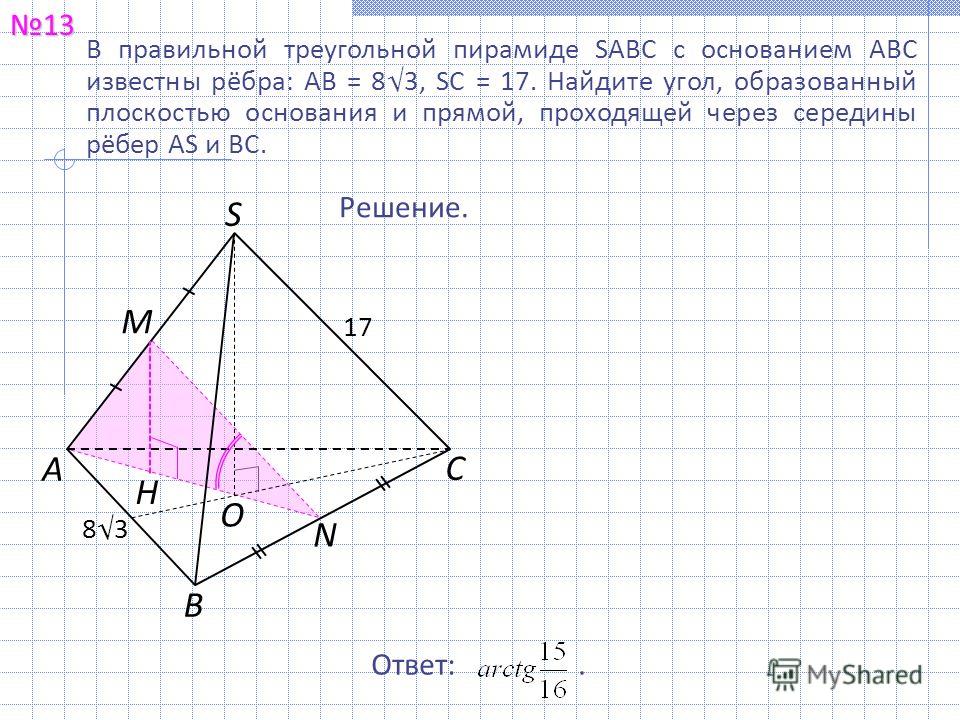
16. На ребрах CD и BB1 куба ABCDA1B1C1D1 c ребром 12 отмечены точки Р и Q соответственно, причем DP=4, а B1Q=3. Плоскость APQ пересекает ребро CC1 в точке М.
а) Докажите, что точка М является серединой ребра CC1.
б) Найдите расстояние от точки С до плоскости APQ.
17. В правильной четырехугольной пирамиде SABCD
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки К до плоскости SBC.
18. В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а высота равна 1. На ребрах АВ, АС и AS отмечены точки М, N и К соответственно, причем АМ=AN=3 и AK=7/4.
На ребрах АВ, АС и AS отмечены точки М, N и К соответственно, причем АМ=AN=3 и AK=7/4.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.
19. Основанием прямой четырехугольной призмы ABCDA1B1C1D1 является квадрат ABCD со стороной 4, высота призмы равна 6. Точка K делит ребро AA1 в соотношении AK:KA1=1:2. Через точки K и B проведена плоскость α, параллельная прямой AC и пересекающая ребро DD1 в точке M.
а) Докажите, что плоскость α делит ребро DD1 в отношении DM:MD1=2:1.
б) Найдите площадь сечения.
Ответ: б) 8√6
20. В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а боковое ребро AA1 равно 3√6. На ребрах AB и B1C1 отмечены точки K и L соответственно, причем AK=2, B1L=4. Точка M середина A1C1. Плоскость γ параллельна прямой AC и содержит точки K и L.
На ребрах AB и B1C1 отмечены точки K и L соответственно, причем AK=2, B1L=4. Точка M середина A1C1. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) √2
21. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=√5 и BC=2. Длины боковых рёбер пирамиды SA=√7, SB=2√3, SD=√11.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
Ответ: б) 30
22. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA=AQ=RC=2.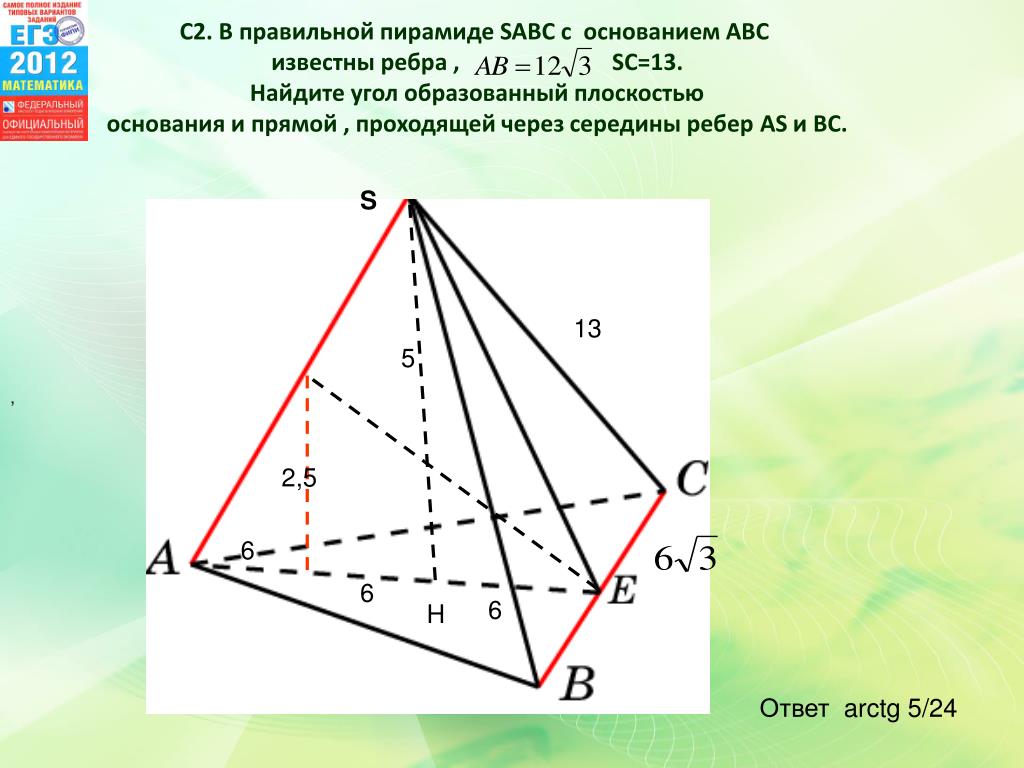
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Ответ: б) 7/2
23. В треугольной пирамиде PABC с основанием ABC известно, что AB=13, PB=15, cos PBA=48/65. Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Ответ: б) 90
24. Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Прямые CA1 и AB1 перпендикулярны.
а) Докажите, что AA1=AC.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 6, BC = 3.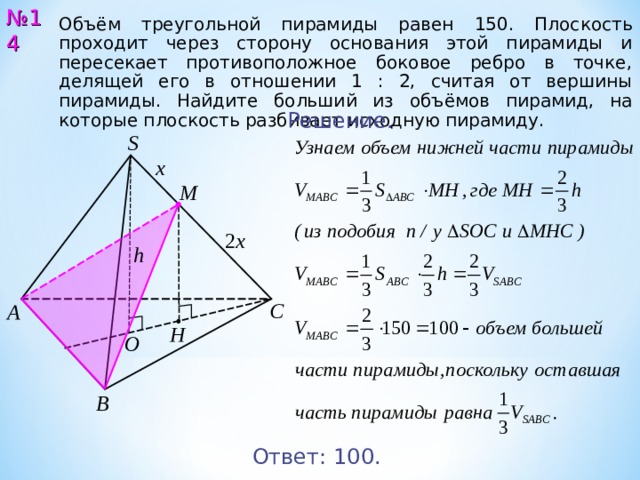
Ответ: б) √2
1 2 3
Главная
6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.
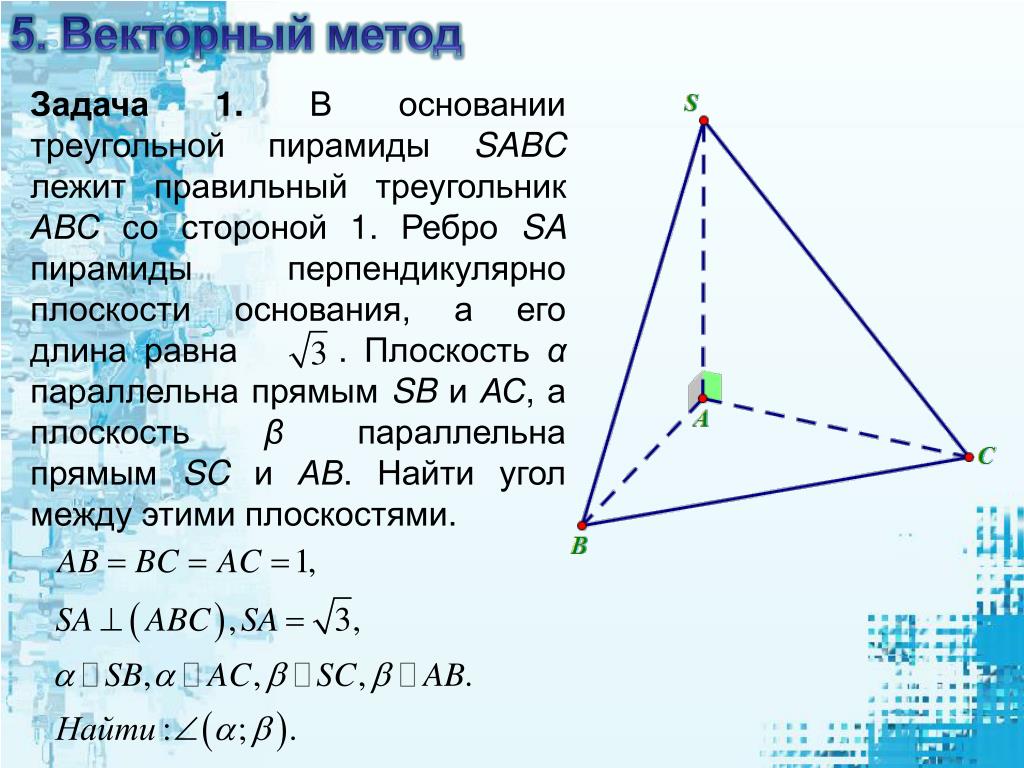
3. Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α, содержащей прямую BD1 и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD— квадрат.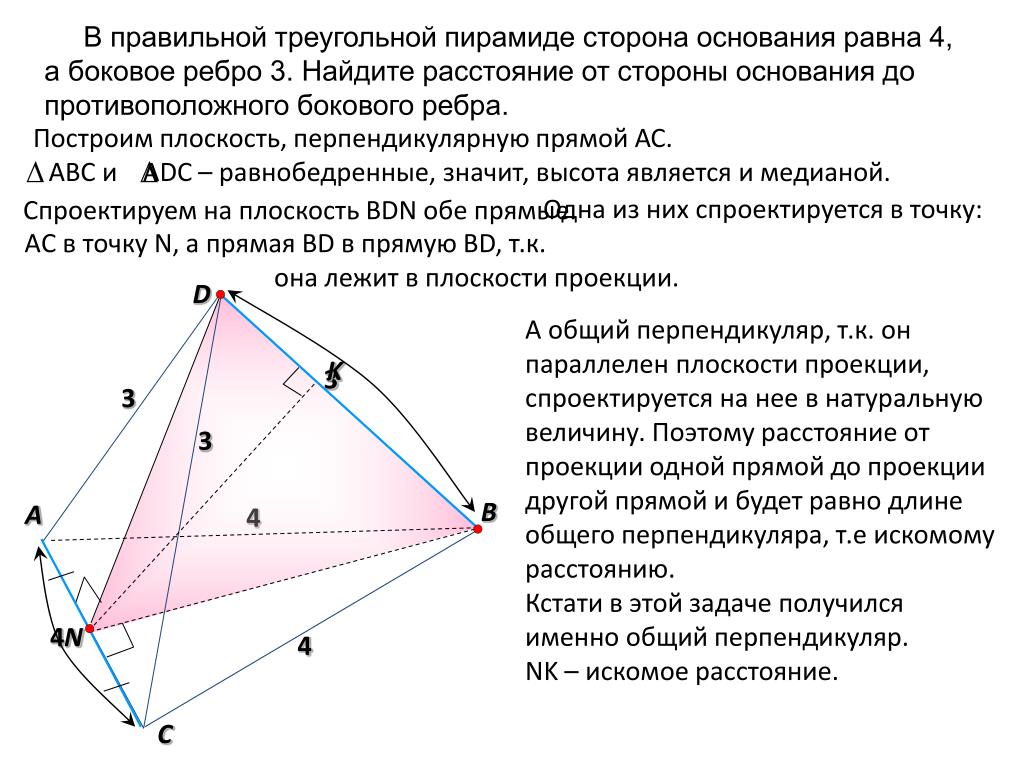
б) Найдите угол между плоскостями α и BCC1, если AA1=10, AB=12.
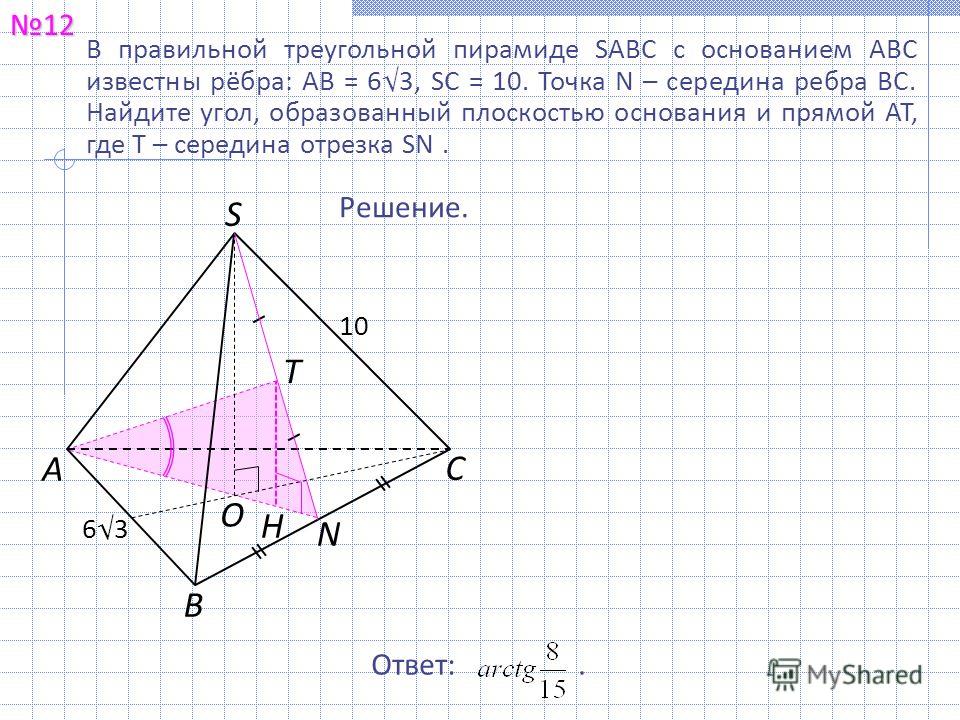
Решение №2312 Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА.
Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА. Плоскость, параллельная плоскости АВС, проходит через точку K и пересекает ребра SB и SC в точках Q и P соответственно.
а) Докажите, что площадь четырёхугольника BCPQ составляет \frac{3}{4} площади треугольника SBC
б) Найдите объем пирамиды KBCPQ.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
а) Доказать: SBCPQ = \frac{3}{4}·SΔSBC
Т.к. плоскость, параллельная плоскости АВС, проходит через точку K и пересекает ребра SB и SC в точках Q и P соответственно, то Q и P являются серединами рёбер SB и SC соответственно.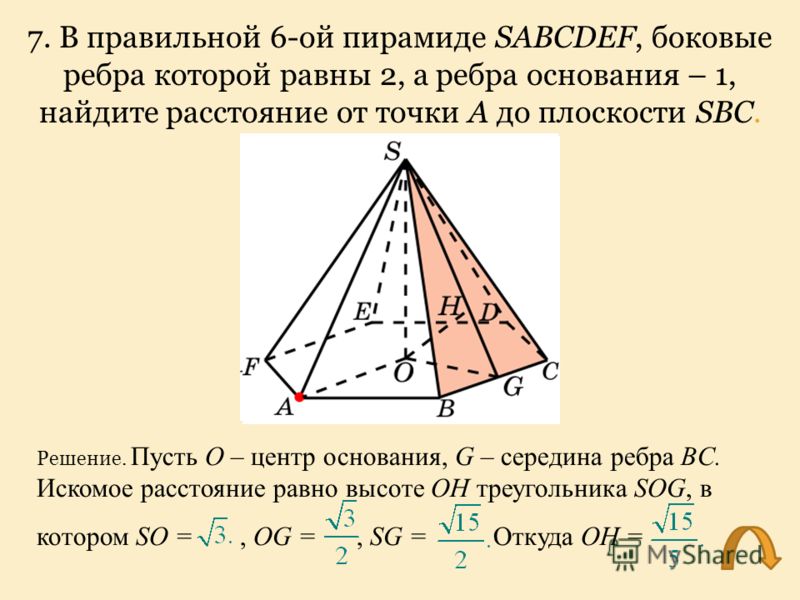 {2}\cdot \frac{\sqrt{3}}{4}\cdot 10=\frac{640\sqrt{3}}{3}
{2}\cdot \frac{\sqrt{3}}{4}\cdot 10=\frac{640\sqrt{3}}{3}
(площадь основания нашли по формуле площади равностороннего треугольника)
Высота пирамиды КBCPQ в два раза меньше высоты пирамиды SABC проведённой из вершины А (т.к. ΔАВС||ΔKQP, KQ, KP, QP – средние линии).
Площадь основания пирамиды КBCPQ составляет \frac{3}{4}·SΔSBC (площадь основания пирамиды SABC).
Найдём объём пирамиды КBCPQ:
V_{KBCPQ}=\frac{1}{2}\cdot \frac{3}{4}\cdot V_{SABC}=\frac{1}{2}\cdot \frac{3}{4}\cdot \frac{640\sqrt{3}}{3}=80\sqrt{3}
Ответ: 80\sqrt{3}.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.6 / 5. Количество оценок: 94
Оценок пока нет. Поставь оценку первым.
Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:15.10.2021
- Рубрика записи13. Стереометрическая задача
- Автор записи:Andrei Maniakin
Площадь поверхности треугольной пирамиды
Площадь поверхности треугольной пирамиды равна сумме площадей всех граней треугольной пирамиды. В основном треугольная пирамида имеет треугольное основание и ограничена тремя боковыми треугольными гранями, которые сходятся в одной вершине. У треугольной пирамиды все грани треугольники. Эта пирамида имеет 4 грани, 6 ребер и 4 угла или вершины. Ниже приведены несколько типов треугольных пирамид:
- Правильная треугольная пирамида — все грани представляют собой равносторонние треугольники и известны как тетраэдры.

- Прямоугольная пирамида — основанием является равносторонний треугольник, а остальные грани — равнобедренными треугольниками.
- Неправильная треугольная пирамида — основанием является разносторонний или равнобедренный треугольник.
| 1. | Какова площадь поверхности треугольной пирамиды? |
| 2. | Площадь поверхности треугольной пирамиды Формула |
| 3. | Как рассчитать площадь поверхности треугольных пирамид? |
| 4. | Площадь боковой поверхности треугольной пирамиды |
| 5. | Часто задаваемые вопросы о площади поверхности треугольной пирамиды Формула |
Какова площадь поверхности треугольной пирамиды?
Площадь поверхности любой трехмерной геометрической формы представляет собой сумму площадей всех граней или поверхностей этого замкнутого твердого тела.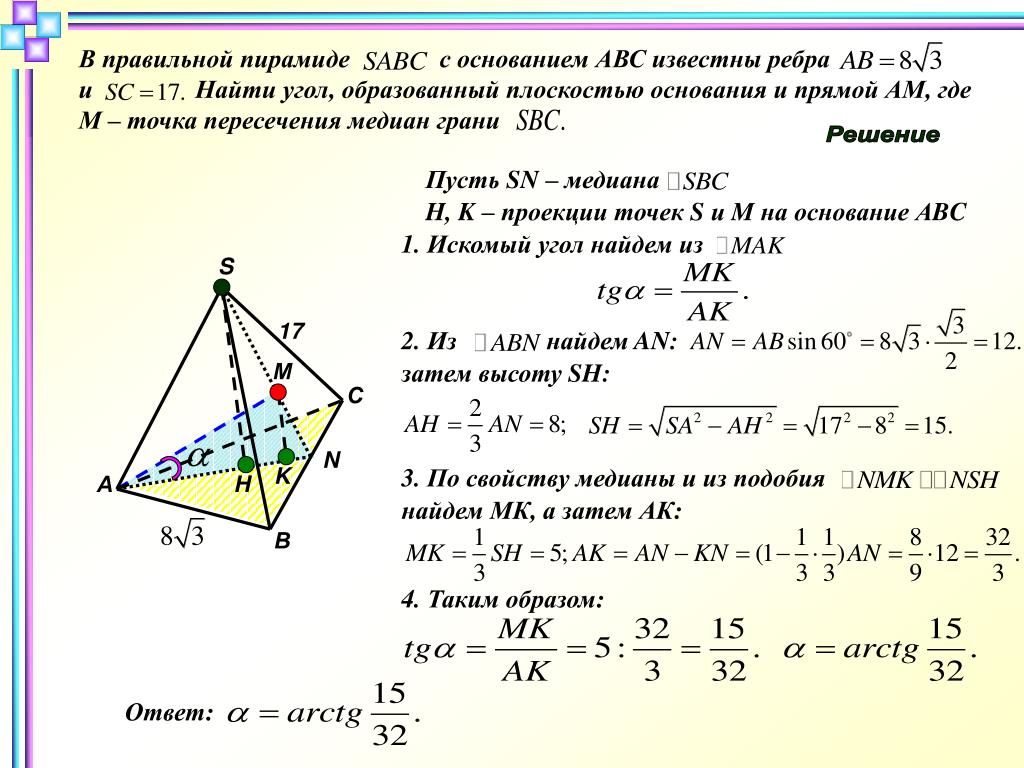 Треугольная пирамида имеет четыре треугольные грани. Таким образом, формула расчета площади поверхности треугольной пирамиды включает площадь основания, периметр основания и наклонную высоту любой стороны пирамиды. Площадь поверхности всегда измеряется в квадратных единицах, таких как см 2 , м 2 , фут 2 или локти 2 . Площадь поверхности треугольной пирамиды равна \(\begin{align} \text {Площадь основания}+\!\frac{1}{2} \text {(Периметр}\!\times\!\text {Наклонная высота} ) \end{выравнивание}\).
Треугольная пирамида имеет четыре треугольные грани. Таким образом, формула расчета площади поверхности треугольной пирамиды включает площадь основания, периметр основания и наклонную высоту любой стороны пирамиды. Площадь поверхности всегда измеряется в квадратных единицах, таких как см 2 , м 2 , фут 2 или локти 2 . Площадь поверхности треугольной пирамиды равна \(\begin{align} \text {Площадь основания}+\!\frac{1}{2} \text {(Периметр}\!\times\!\text {Наклонная высота} ) \end{выравнивание}\).
Площадь поверхности треугольной пирамиды Формула
Формула площади поверхности треугольной пирамиды рассчитывается путем сложения площадей всех треугольных граней пирамиды. Площадь поверхности прямоугольной пирамиды равна \(\begin{align} \text {Площадь основания}+\!\frac{1}{2} \text {(Периметр}\!\times\!\text {Наклон Высота}) \end{выравнивание}\).
После подстановки значений получаем выражение площади поверхности по формуле треугольной пирамиды как 1/2(a × b) + 3/2(b × s).
Где
- b — сторона треугольной пирамиды.
- а — высота основания треугольника
- с — наклонная высота треугольной пирамиды.
- 1⁄2(a × b) — площадь основания треугольных граней.
- 3⁄2(b × s) — это произведение периметра и наклонной высоты пирамиды.
Как рассчитать площадь поверхности треугольных пирамид?
Площадь поверхности треугольной пирамиды можно рассчитать, представив трехмерную фигуру в двумерную сеть, чтобы фигуры было легче увидеть. После расширения 3D-формы в 2D-форму мы получим четыре треугольника.
Следующие шаги используются для вычисления площади поверхности треугольной пирамиды:
- Шаг 1: Найдите площадь треугольников с основаниями: Площадь треугольников с основаниями равна (1/2 × основание треугольника × высота треугольника). треугольник), который становится основанием × высота.
- Шаг 2: Найдите периметр треугольных граней: периметр треугольника равен сумме всех сторон треугольника, которая равна \((сторона)_{1}\) + \((сторона)_{2} \) + \((сторона)_{3}\).

- Шаг 3: Найдите наклонную высоту треугольных граней: Наклонная высота треугольной пирамиды обычно обозначается буквой «s».
- Шаг 4: Сложите все области вместе. Таким образом, формула площади поверхности треугольной пирамиды равна 1/2 (a × b) + 3/2 (b × s) в квадратных единицах.
Площадь боковой поверхности треугольной пирамиды
Площадь боковой поверхности — это площадь неосновных граней, или можно сказать, что только площадь боковой поверхности любого объекта рассчитывается путем удаления базовой площади. Площадь боковой стороны треугольной пирамиды можно рассчитать, удалив площадь основания треугольника из произведения периметра основания и наклонной высоты пирамиды.
Таким образом, площадь боковой поверхности прямоугольной треугольной пирамиды составляет 1/2 (периметр основания × высота наклона), которая затем становится равной 3/2 (сторона × высота наклона).
Где
- b — сторона пирамиды.

- с – наклонная высота основания.
Примеры площади поверхности треугольной пирамиды Формула
Пример 1: Каждая сторона треугольной пирамиды имеет длину 3 единицы, высота треугольника с основанием равна 6, а высота наклона равна 5. Найдите общую площадь поверхности.
Решение
Площадь поверхности треугольной пирамиды со стороной а равна
Площадь поверхности = 1⁄2(a × b) + 3⁄2(b × s)
Подставляя значения, получаем,
Площадь поверхности = 1⁄2(6 × 3) + 3⁄2( 3 × 5)
Площадь поверхности = (9) + (22,5) = 31,5 ед.
Пример 2: Найдите площадь поверхности треугольной пирамиды, площадь основания которой равна 24 единицам 2 , периметр равен 12 единицам, а наклонная высота пирамиды равна 18.
Решение
Площадь поверхности треугольной пирамиды со стороной a равна
Площадь поверхности = 1/2(a × b) + 3⁄2(b × s)
Площадь поверхности треугольной пирамиды = \(\begin{align} \text {Площадь основания}+\!\frac{1}{2} \text {(Периметр}\! \times\!\text {Наклонная высота}) \end{align}\)
Подставляем значения в формулу,
Площадь поверхности треугольной пирамиды = \(\begin{align} \text {24}+ \!\frac{1}{2} \text {(12}\!\times\!\text {18}) \end{align}\)
= 132 кв.

Ответ: Площадь поверхности треугольной пирамиды 96 единиц 2 .
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Практические вопросы по площади поверхности треугольной пирамиды Формула
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности треугольной пирамиды Формула
Как найти площадь поверхности треугольной пирамиды?
Формула площади поверхности пирамиды рассчитывается путем сложения площадей всех треугольных граней пирамиды. что равно 1/2(a × b) + 3/2(b × s). Где b — сторона пирамиды, a — высота треугольника в основании, s — наклонная высота пирамиды.
Какова формула объема треугольной пирамиды?
Объем треугольной пирамиды можно найти по формуле 1/3 × площадь основания × высота.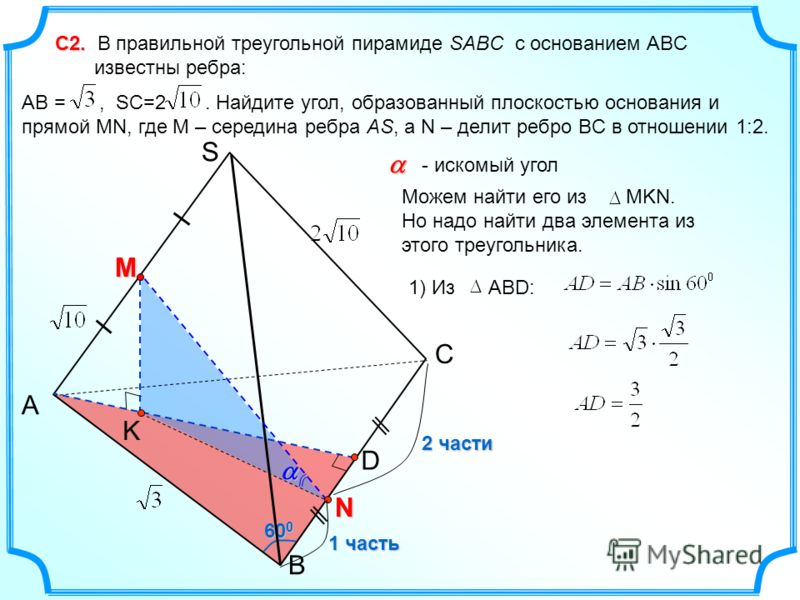
Как найти площадь основания прямоугольной пирамиды?
Площадь основания прямоугольной треугольной пирамиды равна 1/2 × высота треугольника с основанием × нижний край треугольника с основанием.
Что такое боковая поверхность треугольной пирамиды?
Боковая поверхность треугольной пирамиды рассчитывается по шагам, описанным ниже.
- Шаг 1: Найдите заданные параметры.
- Шаг 2: Умножьте 1/3 на периметр основания треугольника и наклонную высоту треугольной пирамиды.
- Шаг 3: Запишите результат в квадратах.
Как найти общую площадь поверхности треугольной пирамиды, зная площадь ее боковой поверхности и площадь основания?
Формула для расчета общей площади поверхности треугольной пирамиды: 1/2(a × b) + 3/2(b × s).
- Шаг 1: Проверьте заданные параметры.
- Шаг 2: Добавьте значение площади боковой поверхности и площади основания.
- Шаг 3: Запишите полученную сумму в квадратах.

Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист площади поверхности
Видео с вопросами: Определение высоты треугольной пирамиды
Стенограмма видео
𝑀𝐴𝐵𝐶 — это правильная пирамида, длина стороны которой равна 𝐴𝐵𝐶. Если длина ее бокового ребра равна 88 сантиметрам, найдите высоту пирамиды с точностью до сотых.
Давайте начнем с эскиза этой пирамиды 𝑀𝐴𝐵𝐶. Нам говорят, что 𝐴𝐵𝐶 — равносторонний треугольник, поэтому все его стороны будут иметь длину 32 сантиметра. Нам также говорят, что боковой край равен 88 сантиметрам. Так, например, мы могли бы сказать, что это означает, что длина 𝑀𝐴 составляет 88 сантиметров. Высота этой пирамиды — это перпендикулярное расстояние от вершины 𝑀 до центра тяжести основания. Давайте заметим, что мы могли создать этот прямоугольный треугольник внутри пирамиды. Мы хотим вычислить ℎ, перпендикулярную высоту. Мы знаем, что боковое ребро равно 88 сантиметрам. Итак, если бы мы могли определить эту длину от вершины 𝐴 до центроида основания, то мы смогли бы вычислить значение ℎ.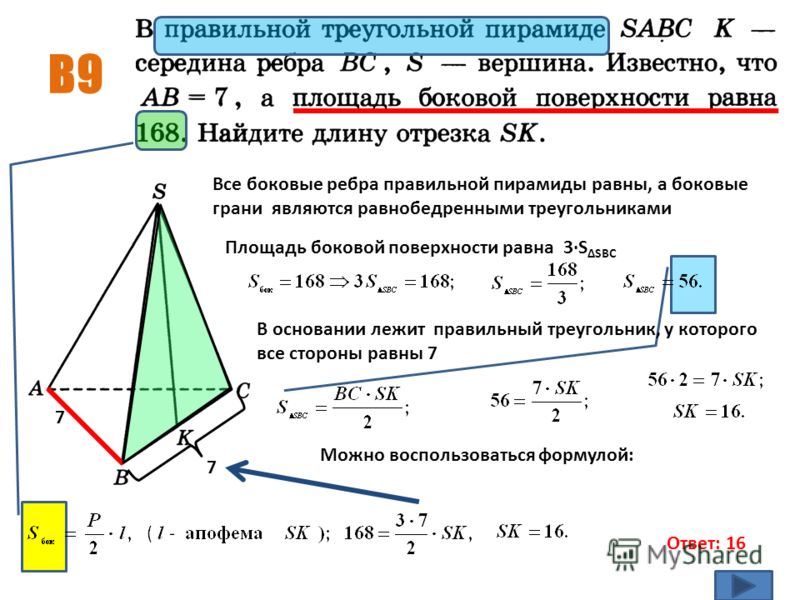 Итак, давайте рассмотрим, как мы можем рассчитать это расстояние от 𝐴 до центроида.
Итак, давайте рассмотрим, как мы можем рассчитать это расстояние от 𝐴 до центроида.
Создадим двухмерный рисунок основания пирамиды, который представляет собой равносторонний треугольник 𝐴𝐵𝐶. Определим это расстояние от вершины 𝐴 до центроида как 𝑥 сантиметров в пирамиде. Ну а в основании пирамиды, именно вот на этом равностороннем треугольнике. Если бы мы продолжили эту розовую линию, мы бы создали медиану равностороннего треугольника, потому что центр тяжести треугольника формируется в точке пересечения трех медиан треугольника. Итак, нам нужно сделать две вещи. Во-первых, нам нужно определить длину медианы, а затем нам нужно определить длину 𝑥.
Первое свойство, которое мы можем использовать и запомнить, состоит в том, что медиана равностороннего треугольника является серединным перпендикуляром. Итак, это означает, что 𝐵𝐶 разделена на две конгруэнтные части, и эта медиана пересекается с 𝐵𝐶 под прямым углом. Итак, учитывая, что мы знаем длину стороны этого равностороннего треугольника, у нас на самом деле достаточно информации, чтобы применить теорему Пифагора для определения длины медианы.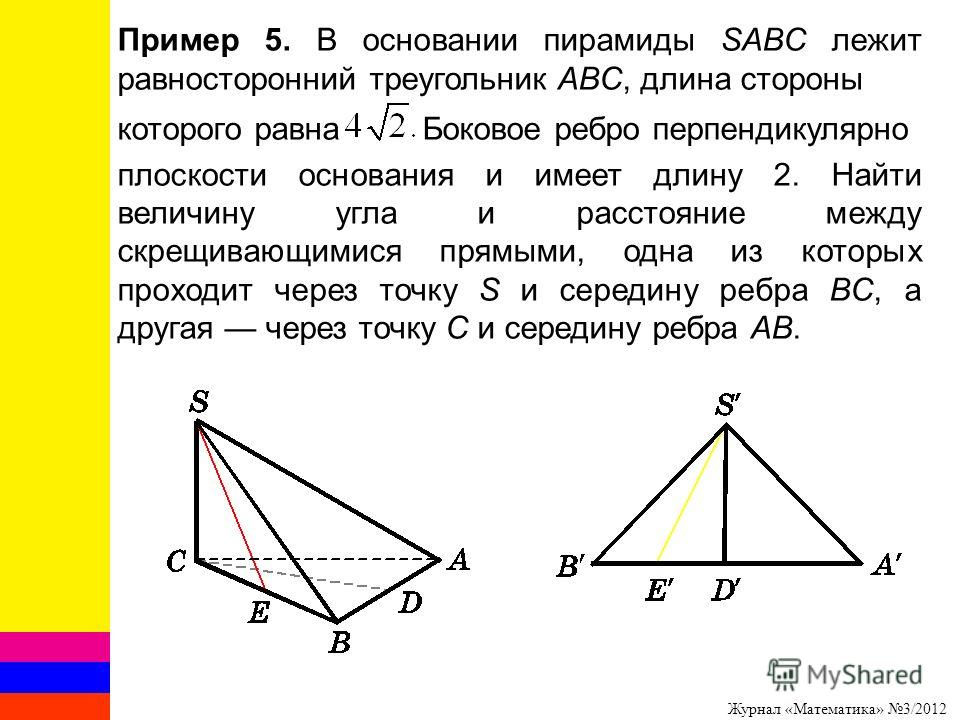 Поскольку длина стороны равностороннего треугольника равна 32 сантиметрам, то 𝐴𝐵 равно 32 сантиметрам. Длина от 𝐵 до середины 𝐵𝐶 должна составлять половину 32 сантиметров, то есть 16 сантиметров. Мы можем определить длину от 𝐴 до середины 𝐵𝐶 как 𝑚 сантиметров.
Поскольку длина стороны равностороннего треугольника равна 32 сантиметрам, то 𝐴𝐵 равно 32 сантиметрам. Длина от 𝐵 до середины 𝐵𝐶 должна составлять половину 32 сантиметров, то есть 16 сантиметров. Мы можем определить длину от 𝐴 до середины 𝐵𝐶 как 𝑚 сантиметров.
Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов двух других сторон. Итак, в этом треугольнике у нас есть две длины сторон 16 сантиметров и 𝑚 сантиметров, которые могут быть 𝑎 и 𝑏, а гипотенуза равна 32 сантиметрам. Подставляя эти значения в теорему Пифагора, мы получаем 16 в квадрате плюс 𝑚 в квадрате равно 32 в квадрате. Вычисляя квадраты, мы имеем 256 плюс 𝑚 в квадрате равно 1024. Переставляя это путем вычитания 256, мы получаем 𝑚 в квадрате равно 768. Взяв квадратный корень из обеих сторон, мы получаем, что 𝑚 равно квадратному корню из 768. Мы можно оставить как квадратный корень из 768 или еще больше упростить до 16 корня из трех. Если мы преобразуем это в десятичное число, то мы пока не будем его округлять, потому что нам нужно будет использовать его в следующих вычислениях.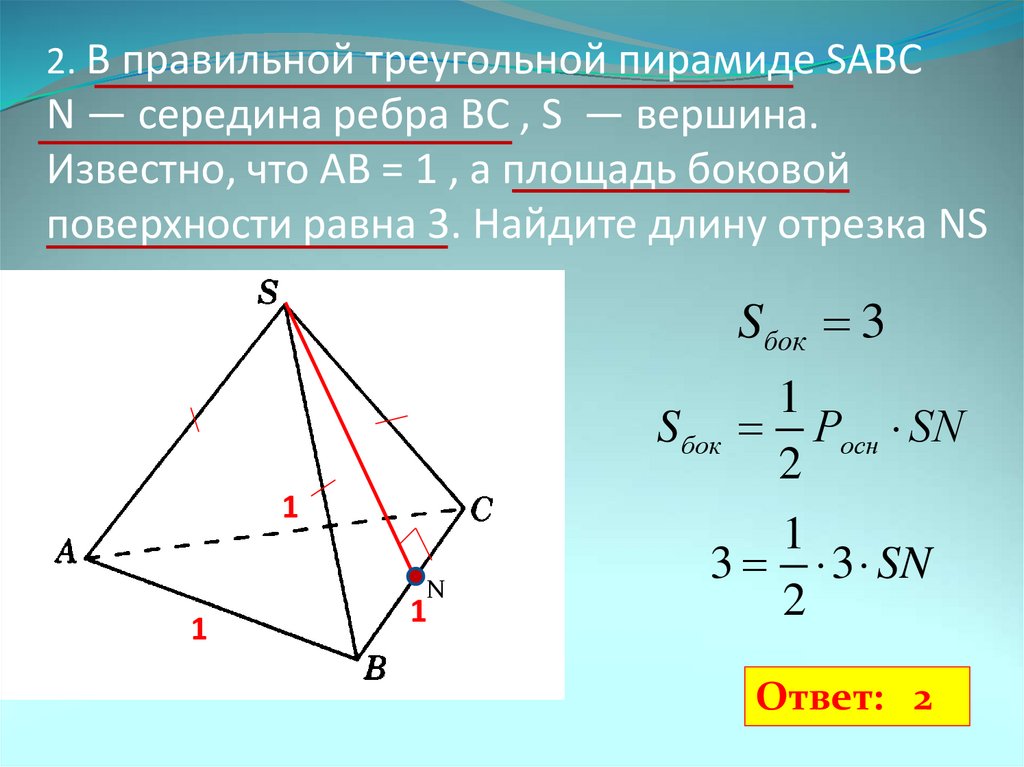
Итак, теперь мы подсчитали, что длина медианы составляет 16 корней из 3 сантиметров. Нам еще нужно вычислить это расстояние 𝑥, которое является долей медианы. И на самом деле именно теорема о центроиде говорит нам об этой пропорции. Эта теорема говорит нам, что расстояние от каждой вершины до центроида составляет две трети длины медианы от этой вершины. Итак, мы имеем здесь то, что 𝑥 — это две трети корня из 16 на три сантиметра. Затем мы можем умножить две трети и 16 корней из трех, и это даст нам 32 корня из трех на три сантиметра. Итак, наконец, мы выяснили, что 𝑥 — это корень 32 из трех на три сантиметра.
Когда мы вернемся к пирамиде, мы увидим, что внутри этой пирамиды у нас теперь есть прямоугольный треугольник, две длины которого нам известны, и мы можем вычислить высоту ℎ. Мы можем освободить место для этого вычисления. Может быть полезно нарисовать этот треугольник изнутри пирамиды. Итак, здесь у нас есть треугольник с гипотенузой 88 сантиметров, основанием из 32 корней три на три сантиметра и длиной стороны ℎ.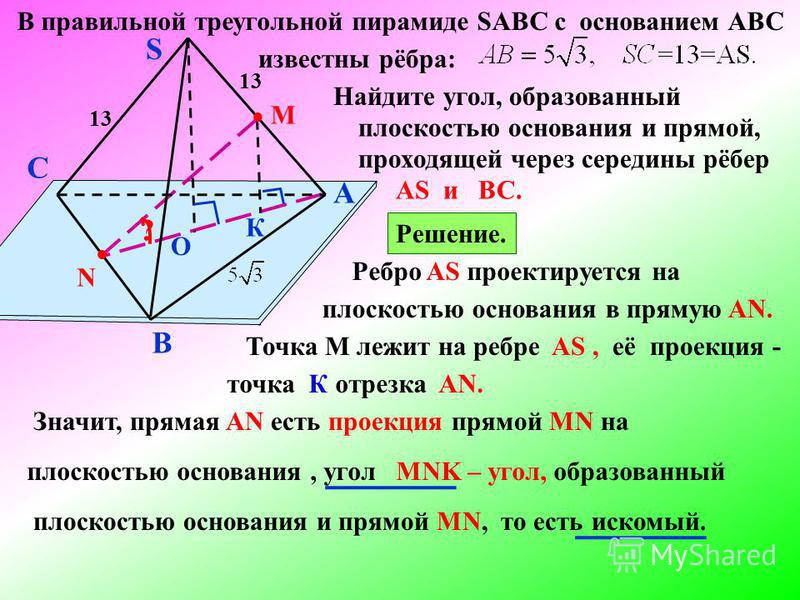 Применяя здесь теорему Пифагора, мы получим ℎ в квадрате плюс 32 корня из трех в квадрате равно 88 в квадрате. Когда мы возводим здесь значения в квадрат, если мы возьмем этот термин 32, корень три из трех и возведем его в квадрат, в числителе мы получим 32 в квадрате, умноженное на корень из трех в квадрате, что равно трем, деленным на три в квадрате.
Применяя здесь теорему Пифагора, мы получим ℎ в квадрате плюс 32 корня из трех в квадрате равно 88 в квадрате. Когда мы возводим здесь значения в квадрат, если мы возьмем этот термин 32, корень три из трех и возведем его в квадрат, в числителе мы получим 32 в квадрате, умноженное на корень из трех в квадрате, что равно трем, деленным на три в квадрате.
3072 более девяти на самом деле можно упростить до 1024 более трех. В правой части 88 в квадрате равно 7744. Затем мы переставляем, вычитая 1024 на три с обеих сторон, в результате чего ℎ в квадрате равно 22208 на три. Затем мы извлекаем квадратный корень из обеих сторон, что дает нам ℎ равно квадратному корню из 22208 на три. На этом этапе мы затем проверяем, как должен быть дан ответ. А так как нас просят дать ответ с точностью до сотой, то нам нужно найти десятичную аппроксимацию. Это будет 86,0387 и так далее сантиметров. Округлив это число до сотых, мы получим ответ, что высота этой пирамиды составляет 86,04 сантиметра с точностью до сотых.




Leave A Comment