Площадь круга равна 1 п найдите длину его окружности: Пло­щадь круга равна 1/пи . Най­ди­те длину его окруж­но­сти. — Спрашивалка

Длина окружности. Площадь круга (Вольфсон Г.И.) 6 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Как вы знаете, многие предметы имеют форму круга. Чем это обусловлено?

 

Возьмем, к примеру, колесо. Понятно, что круглое колесо катится гораздо лучше, чем, например, квадратное. Или, скажем, стакан круглой формы удобнее держать в руке, чем стакан прямоугольной формы. Поэтому в какой-то момент человечество стало использовать круглые предметы. Но если вы используете круглые предметы, нужно научиться их измерять. Например, вам нужно знать длину окружности стакана, чтобы понять, сколько материала пойдет на его изготовление, или вам нужно знать площадь колеса, чтобы, например, определять, какой должен быть объем исходных материалов, чтобы его сделать.

Поэтому сегодня мы обсудим, как же учились находить длину окружности и площадь круга, и решим некоторые задачи, связанные с этим.

 

Окружность и круг

 

 

Вначале вспомним, что такое окружность и круг.

 

Окружность – множество всех точек на плоскости, равноудаленных от данной точки.

Т. е. есть некоторая точка, мы задаем какое-то расстояние – радиус окружности – и берем все точки, которые находятся от исходной на данном расстоянии (см. Рис. 1).

Рис. 1. Окружность

А теперь вспомним еще два важных понятия (см. Рис. 2).

Хордой называется такой отрезок, которые соединяет любые две точки, лежащие на окружности.

Диаметр – это такая хорда, которая проходит через центр окружности. Соответственно, как следствие, нетрудно догадаться, что диаметр равен двум радиусам.

Рис. 2. Хорда и диаметр

Круг – это все точки на плоскости, которые лежат внутри окружности, а также сама окружность (см. Рис. 3).

Рис. 3. Круг

 

Длина окружности

 

 

Теперь, когда мы вспомнили все важные определения, мы можем подумать, как же нам измерить длину окружности.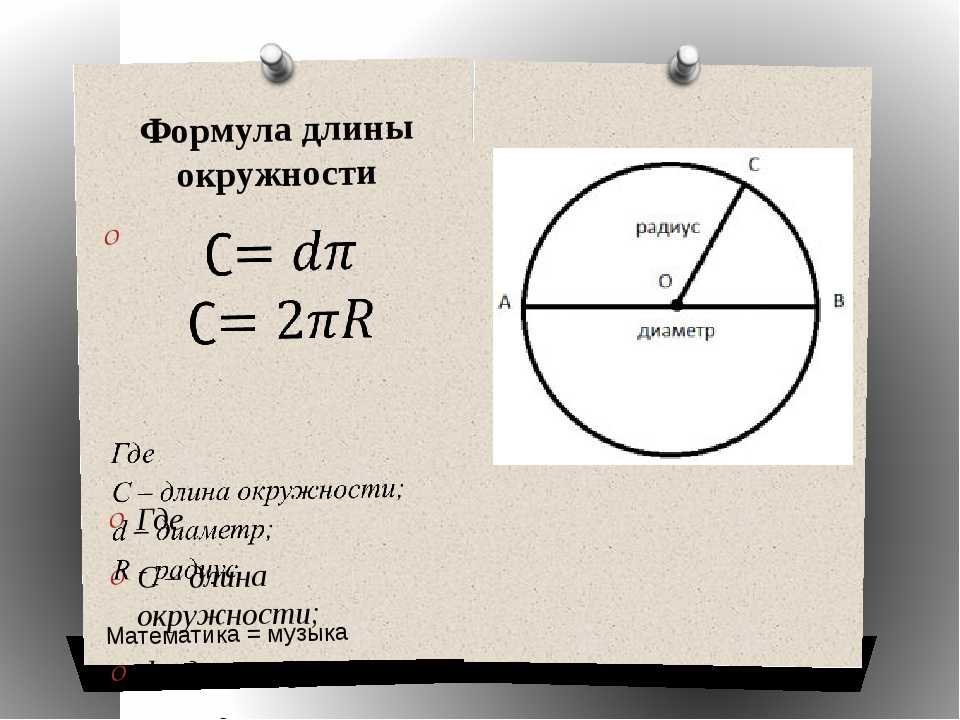

 

Один из способов, который был предложен, таков: возьмем, например, стакан, у которого дно будет круглой формы, и обмотаем нитку вокруг дна этого стакана. Теперь мы можем сделать засечку там, где конец нитки совпал с ее началом, затем размотать эту нитку и замерить ее длину линейкой. Естественно, измерение будет не совсем точным, оно будет зависеть от точности наших прикладываний, от точности линейки и т. п. Тем не менее мы примерно сможем измерить длину окружности (см. Рис. 4).

Рис. 4. Способ измерения длины окружности

Конечно же, чем дальше человечество продвигалось по своим научным взысканиям, тем более точно оно могло измерить эту самую длину окружности.

Еще в древности люди заметили, что если вы увеличите радиус окружности, например в два раза, то и длина этой окружности увеличится в два раза. Если уменьшить радиус в три раза, то и длина уменьшится в три раза. Иначе говоря: длина окружности и ее радиус пропорциональны друг другу. То есть их отношение – это постоянное число (см. Рис. 5).

Рис. 5. Иллюстрация пропорциональности длины окружности и радиуса

Так как отношение длины окружности к радиусу – постоянное число, то и отношение длины к диаметру – постоянное число.

Итак, пусть длина окружности , а диаметр окружности – . Так как отношение длины к диаметру всегда постоянное, то его можно примерно посчитать. Проделав это, вы примерно получите число  Так как число, которое равно отношению длины окружности к ее диаметру, не могли посчитать точно, его обозначили специальной буквой, буквой  (буква греческого алфавита).

На самом деле сейчас, когда в использование вошли мощные компьютеры, можно посчитать и тысячу, и даже миллионы знаков после запятой у числа . Это сделано, чтобы можно было более точно посчитать длину окружности. Для практических нужд нам достаточно знать первые несколько знаков: 3,14.

Кстати, есть специальные правила, которые позволяют запоминать число . Одно из правил – стихотворение:

Если очень постараться,

То запомнишь все как есть.

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Есть и другое довольно забавное правило, которое тоже позволяет запомнить первые несколько знаков от числа .

Это я знаю и помню прекрасно:

Пи многие знаки мне лишни, напрасны

 

Если посчитать количество букв в каждом слове, мы получим число 3,14159265358.

Таким образом, мы выписали еще более длинный ряд. На самом деле есть стихотворения еще более длинные, которые позволяют запоминать число π. Некоторые даже проводят соответствующее чемпионаты, есть, например, чемпионат мира по тому, кто больше запомнит знаков у числа π.

Вернемся к нашей теме.

Используя эту формулу, мы можем посчитать длину любой окружности практически точно, потому что диаметр мы можем просто измерить линейкой, и если мы умножим его число π, то мы получим длину. С другой стороны, число π мы знаем не совсем точно, но для наших приблизительных вычислений достаточно взять его с точностью до сотых или до тысячных, после чего, перемножив, получить искомое число длины.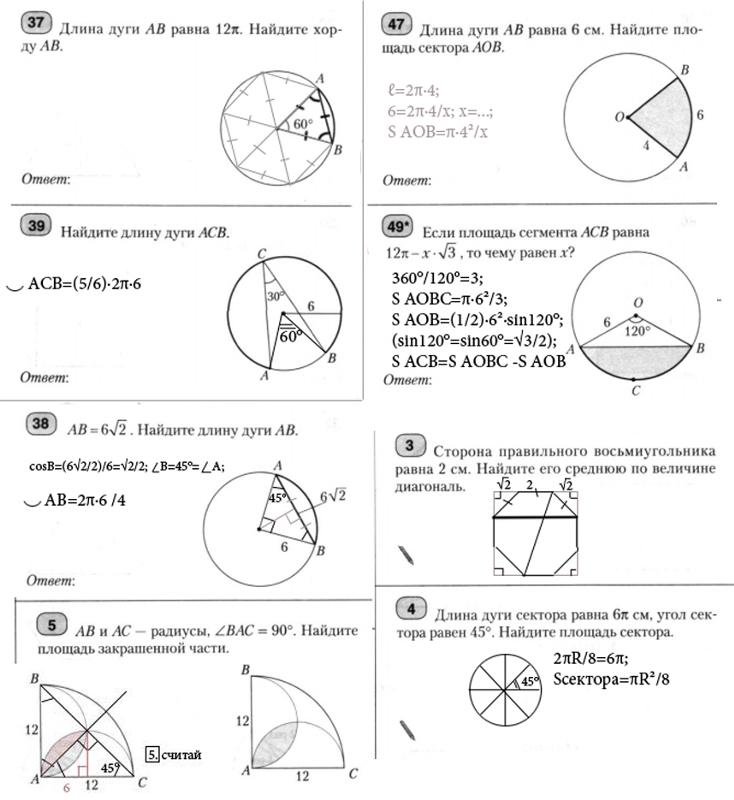 Не забывайте: если вы подставите вместо числа π, например, 3,14, или 3,1415, то длина у вас получится приблизительной, так что знак равенства в этом случае поставить не можем, а можем поставить лишь знак примерного равенства . Если же вы хотите точное равенство, то оставляйте в ответе букву π, это и будет правильным ответом.

Рассмотрим конкретные примеры, на которых это работает.

 

Примеры на вычисление длины окружности

 

 

Пример 1

 

Дана окружность с радиусом 2 сантиметра. Чему равна ее длина?

Решение:

Ответ: 12,56 см.

Как видите, тут мы использовали знак приблизительного равенства.

 

Пример 2

Диаметр окружности равен 3 см, чему равна длина этой окружности?

Решение:

Ответ: 9,42 см.

Можно было записать ответ в виде: .

В этом случае мы можем поставить знак равенства, ведь значение абсолютно точное. Другой вопрос, что для практических целей оно не совсем удобно. Но так как математика – точная наука, то точным ответом будет .

Между прочим, формулу  можно преобразовать. Если вспомнить, что диаметр – это удвоенный радиус, мы можем записать формулу в виде

Или:

.

 

Площадь круга

 

 

Разберемся, как наши предки искали площадь круга. Есть один метод для вычисления приблизительной площади.

 

Рассмотрим круг, заметим, что площадь этого круга, меньше, чем площадь квадрата, который описывает этот круг. Причем площадь этого квадрата мы легко можем посчитать – это квадрат его стороны.

С другой стороны, мы можем немного приблизить нашу фигуру к кругу, если вырезать квадратные уголки со сторон вершин квадрата. Остается фигура, которая по площади ближе к кругу. Аналогичным образом мы можем продолжать до бесконечности (см. Рис. 6).

Рис. 6. Приблизительное вычисление площади круга

Естественно, что точно так же мы можем сделать, если мы нарисуем квадрат внутри круга, после чего добавим такие прямоугольники со всех сторон и т. д., пока мы сколь угодно близко не приблизимся к площади искомого круга (см. Рис. 7).

Рис. 7. Приблизительное вычисление площади круга

Площадь круга мы можем оценить как сверху (площадь круга будем меньше, чем площадь фигуры, которая описывает круг), так и снизу (площадь круга больше, чем площадь фигуры, вписанной в эту окружность). Соответственно, если прямоугольников, которыми мы измеряем, будет довольно много, то мы сможем приблизительно оценить площадь круга.

В девятом классе вы докажете формулу, что на самом деле площадь круга  вычисляется так: .

 

Примеры на вычисление площади круга

 

 

Пример 1

 

Найдите площадь круга, если его радиус равен 1 см.

Решение:

Можно записать ответ в виде  либо же подставить число π и получить приблизительное значение.

Ответ: .

 

Пример 2

Найдите площадь круга, если диаметр круга равен 4 см.

Решение:

,

Или же можем записать этот ответ точно, через π.

Ответ:  .

 

Заключение

 

 

Сегодня мы вспомнили, что такое окружность и что такое круг. Поняли, как люди научились считать длину окружности и площадь круга хотя бы приблизительно. Узнали, по каким формулам можно найти длину окружности и площадь круга, и научились этими формулами пользоваться.

 

Обратите внимание, что можно решать и обратные задачи, то есть находить радиус (диаметр) по заданной длине окружности или площади круга.

 

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.

2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.

3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.

4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.

5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.

6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «Школьный помощник» (Источник)

2. Интернет-сайт math-prosto.ru (Источник)

3. Интернет-сайт «ЯКласс» (Источник)

 

Домашнее задание

1. Чему равна длина окружности, если ее радиус равен 31 дм, 200 см, 3200 мм. ()?

2. Окружность арены во всех цирках мира имеет длину 40,8 м. Найдите диаметр и площадь арены.

3. Останкинская телебашня в Москве опирается на площадку, имеющую форму кольца. Диаметр наружной окружности – 63 м, а внутренней – 14 м. Вычислить площадь фундамента башни.

 

Длина окружности. Решение задач на длину окружности и площадь круга

• Длина окружности
• Задачи на длину окружности
• Задачи на площадь круга

Длина окружности

Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в  3,14 раза.  Для обозначения этой величины используется маленькая (строчная) греческая буква  π  (пи):

C	= π.
D

Таким образом, длину окружности  (C)  можно вычислить, умножив константу  π  на диаметр  (D),  или умножив  π  на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

C = πD = 2πR,

где  C  — длина окружности,  π  — константа,  D  — диаметр окружности,  R  — радиус окружности.

Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.

Задачи на длину окружности

Задача 1. Найти длину окружности, если её диаметр равен  5 см.

Решение: Так как длина окружности равна  π  умноженное на диаметр, то длина окружности с диаметром  5 см  будет равна:

C ≈ 3,14 · 5 = 15,7 (см).

Ответ:  15,7 см.

Задача 2. Найти длину окружности, радиус которой равен  3,5 м.

Решение: Сначала найдём диаметр окружности, умножив длину радиуса на  2:

D = 3,5 · 2 = 7 (м),

теперь найдём длину окружности, умножив  π  на диаметр:

C ≈ 3,14 · 7 = 21,98 (м).

Ответ:  21,98 м.

Задача 3. Найти радиус окружности, длина которой равна  7,85 м.

Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на  2π:

R	=	C	,
		2π

следовательно, радиус будет равен:

R	≈	7,85	=	7,85	=  1,25 (м).
		2 · 3,14		6,28

Ответ:  1,25 м.

Задачи на площадь круга

Задача 1. Найти площадь круга, если его радиус равен  2 см.

Решение: Так как площадь круга равна  π  умноженное на радиус в квадрате, то площадь круга с радиусом  2 см  будет равна:

S ≈ 3,14 · 2² = 3,14 · 4 = 12,56 (см²).

Ответ:  12,56 см².

Задача 2. Найти площадь круга, если его диаметр равен  7 см.

Решение: Сначала найдём радиус круга, разделив его диаметр на  2:

7 : 2 = 3,5 (см),

теперь вычислим площадь круга по формуле:

S = πr² ≈ 3,14 · 3,5² = 3,14 · 12,25 = 38,465 (см²).

Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

S = π	D2	≈ 3,14 ·	72	= 3,14 ·	49	=
	4		4		4

=	153,86	=  38,465 (см2).
	4

Ответ:  38,465 см².

Задача 3. Найти радиус круга, если его площадь равна  12,56 м².

Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить  π,  а затем из полученного результата извлечь квадратный корень:

r = √S : π ,

следовательно, радиус будет равен:

r ≈ √12,56 : 3,14 = √4 = 2 (м).

Ответ:  2 м.

Калькулятор окружности и площади круга

Создано Luis Hoyos

Отзыв от Wojciech Sas, PhD

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Формула для расчета длины окружности и площади круга Как найти длину окружности и площадь круга?
• Другие удивительные калькуляторы Omni
• Часто задаваемые вопросы

Вас интересует вычисление площади и длины окружности и формула для этого? Это идеальный инструмент.

Круги присутствуют во многих местах . Монеты, пицца и виниловые диски являются примерами круглых объектов, и площадь является важным их аспектом.

Читайте дальше, если вам интересно:

• Как найти площадь и длину окружности.
• Как соотносятся длина окружности и площадь круга.
• Как найти площадь четверти круга.

💡 Знаете ли вы, что
Диаметр и, следовательно, площадь пиццы имеют решающее значение при определении оптимального размера пиццы для вашего бюджета и вкуса. На самом деле, у нас есть калькулятор сравнения стоимости пиццы для вашего удовольствия.

Формула для вычисления длины окружности и площади круга

Это формулы для вычисления длины окружности и площади круга:

c = 2πr
A = πr² = πd²/4

, где:

• c обозначает длину окружности;
• r для радиуса; и
• d для диаметра круга.

π — константа, приблизительно равная 3,14159265359 и, среди прочего, представляет отношение длины окружности к диаметру

любой окружности .

Как найти длину окружности и площадь круга?

Предположим, вы хотите узнать, как найти длину окружности и площадь круга с радиусом 8 см . В этом случае необходимо выполнить следующие шаги:

1. Используйте формулы для вычисления длины окружности и площади: c = 2πr и A = πr² .
2. Окружность должна равняться c = 2π × 8 см = 50,265 см .
3. Площадь должна равняться A = π × (8 см)² = 201,06 см² .
4. Чтобы проверить результаты , введите диаметр 8 см в калькулятор. Результаты также должны быть 50,265 см и 201,06 см².

Другие удивительные Omni-калькуляторы

Освоив процесс вычисления длины окружности и площади круга, вы можете посмотреть на эти другие инструменты и продолжать совершенствовать свои навыки:

• Расчет круга: найти c, d, a, r;
• Калькулятор измерения окружности;
• Калькулятор формулы круга;
• Калькулятор радиуса окружности;
• Калькулятор длины окружности;
• Окружность к диаметру;
• Калькулятор диаметра круга;
• Калькулятор периметра круга;
• Квадратные метры кругового калькулятора; и
• Квадратный дюйм калькулятора круга.

Часто задаваемые вопросы

Как связаны длина окружности и площадь круга?

Они связаны друг с другом следующей формулой: c = 2√(πA) . Уравнение говорит, что длина окружности пропорциональна квадратному корню из площади , поэтому чем больше размер окружности, тем больше длина окружности.

Какова площадь 9-дюймового круга?

63,617 дюйма² . Чтобы найти площадь любого круга, зная его диаметр:

1. Умножьте π (пи) на квадрат диаметра: π × (9 дюймов)² = 254,47 дюйма² .
2. Разделите полученный результат на четыре:
   254,47 дюйма²/4 = 63,617 дюйма² .
3. Теперь вы знаете, какова площадь 9-дюймового круга ✔️

Как найти площадь четверти круга?

Чтобы получить площадь четверти круга:

1. Возьмем формулу площади обычного круга: A = πr² .
2. Разделите эту формулу на четыре.
3. После выполнения этих шагов мы можем заметить, что площадь четверти круга равна A = πr²/4 .

Luis Hoyos

Радиус (R)

Диаметр (D)

Окружность (C)

Область (A)

Проверьте 23 Аналогичные 2D Геометрические калькуляторы 📏

Область области прямоугольной версии. 20 0003

Область Aredangearea из Строила… 200003

. подробнее

Калькулятор окружности круга

Радиус

Диаметр

Окружность

Расчет окружности Объяснение

1 Понимание того, что такое окружность200022 круга, и то, как его рассчитать, имеет решающее значение при переходе на более высокий уровень математики. В этой статье вы узнаете ответы на следующие вопросы.

• Какова длина окружности?
• Как рассчитать длину окружности?

Какова длина окружности?

Окружность окружности — это расстояние по внешней стороне окружности. Это как периметр других форм, таких как квадраты. Вы можете думать об этом как о линии, определяющей форму. Для фигур, состоящих из прямых краев, эта линия называется периметром , а для кругов эта определяющая линия называется окружностью.

На этом рисунке показана длина окружности.

На окружности есть два других важных расстояния: радиус (r) и диаметр (d). Радиус, диаметр и длина окружности являются тремя определяющими аспектами каждого круга. Зная радиус или диаметр и число пи, вы можете рассчитать длину окружности. Диаметр — это расстояние от одной стороны круга до другой в его самых широких точках. Диаметр всегда будет проходить через центр окружности. Радиус равен половине этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем.

На этой диаграмме показаны длина окружности, диаметр, центр и радиус окружности.

Как рассчитать длину окружности?

Если вы знаете диаметр или радиус круга, вы можете вычислить длину окружности. Для начала вспомним, что пи — иррациональное число, записываемое через символ π. π примерно равно 3,14.

Формула для вычисления длины окружности:

Длина окружности = π x Диаметр окружности

Обычно записывается как C = πd. Это говорит нам о том, что длина окружности в три «с небольшим» раза больше диаметра. Мы можем видеть это на графике ниже:

Вы также можете вычислить длину окружности, если знаете ее радиус. Помните, что диаметр в два раза больше длины радиуса. Мы уже знаем, что C = πd. Если r — радиус окружности, то d = 2r. Итак, C = 2πr.

Пример 1

Если диаметр круга 10 см, какова его окружность?

Ответ

Мы знаем, что C = πd. Поскольку диаметр равен 10 см, мы знаем, что C = π x 10 см = 31,42 см (с точностью до 2 знаков после запятой).

Пример 2

Если круг имеет радиус 3 м, какова его длина окружности?

Ответ

Мы знаем, что C = 2πr. Поскольку радиус равен 3 м, мы знаем, что C = π x 6 м  = C = 18,84 м (с точностью до 2 знаков после запятой).

Пример 3

Найдите недостающую длину (отмеченную знаком ?) на диаграмме ниже:

Ответ

Недостающая длина — это длина окружности. Зная, что диаметр на диаграмме равен 4,3 м, и зная, что C = πd, мы можем рассчитать длину окружности. Немного подумав, мы можем легко понять, что C = π x 4,3 м = 13,51 м (с точностью до 2 знаков после запятой). Недостающая длина составляет 13,51 м.

Как рассчитать окружность Земли

Задумывались ли вы, насколько велика Земля? Что ж, с помощью пи можно вычислить окружность Земли! Ученые установили, что диаметр Земли составляет 12 742 км. Учитывая эту информацию, какова окружность Земли? Возьмите лист бумаги и калькулятор и посмотрите, сможете ли вы решить это самостоятельно.

Опять же, мы знаем, что C = πd и что диаметр Земли равен 12 742 км. Используя эту информацию, мы можем рассчитать окружность Земли как C = π x 12 742 км = 40 030 км.