Угол между прямой и плоскостью (Задание 13)

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Задание 13.
Угол между прямой
и плоскостью
Повторение:
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на
плоскость.
М
перпендикуляр
А
проекция Н
Повторение:
Найти угол между наклонными и плоскостью
(описать алгоритм построения).


М
М
H
F
F
FМ
F
А
R
Н
К
FH
Повторение:
Угол между прямой m и плоскостью можно
вычислить:
1) Если этот угол удается включить в прямоугольный
треугольник в качестве одного из острых углов;
2) Используя векторный метод;
3) Используя координатно –векторный метод;
4) Используя ключевые задачи;
Устно:
Найдите тангенс угла между диагональю куба и
плоскостью одной из его граней.
D1
перпендикуляр
А1
А
С1
Подсказка
В1
М
D
В
перпендикуляр
С
А
Н
проекция
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на
№1
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между прямой АА1 и
плоскостью ВС1Д .
D1
С1 1) Прямая AА1 параллельна
1
А1
В1
1
2
2
D
О
А
1
В
прямой СС1, Угол между
прямой АА1 и плоскостью ВС1Д .
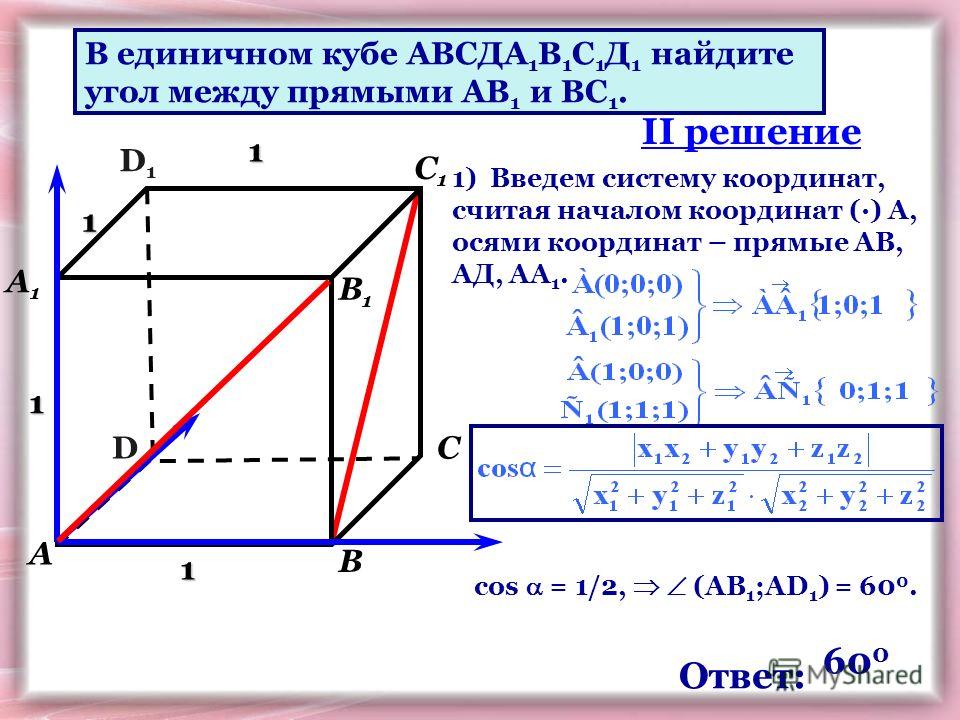
равен углу между СС1 и
плоскостью ВС1Д.
ВД ДВС1
1
ВД АС ДВС1 ОС1С
ВД СС1
С 2. Прямая СС проецируется на
1
плоскость ВС1Д в прямую ОС1.
Поэтому проекция точки С
лежит на отрезке ОС1. Значит,
прямая ОС1 является проекцией
прямой СС1, следовательно, угол
ОС1С искомый.
Ответ: 2
2
Критерии оценивания выполнения задания С2
баллы
Критерии оценивания
2
Правильный ход решения. Верно построен или
описан искомый угол. Получен верный ответ
1
1) Правильный ход решения. Получен верный
ответ, но имеется ошибка в построении и описании
искомого угла, не повлиявшая на ход решения
2) Правильный ход решения. Верно построен и
описан искомый угол, но имеется ошибка в одном
из
вычислений,
допущенная
из-за
невнимательности, в результате чего получен
неверный ответ
0
1) Ход решения правильный, но оно не доведено до
конца, или решение отсутствует. Нет ответа
2) Ход решения правильный, но имеются
существенные ошибки в вычислениях, приведшие
к неправильному ответу
3) Неправильный ход решения, приведший к
неверному ответу
4) Верный ответ получен случайно при неверном
№2
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла
между прямой АС1 и плоскостью ВСС1 .
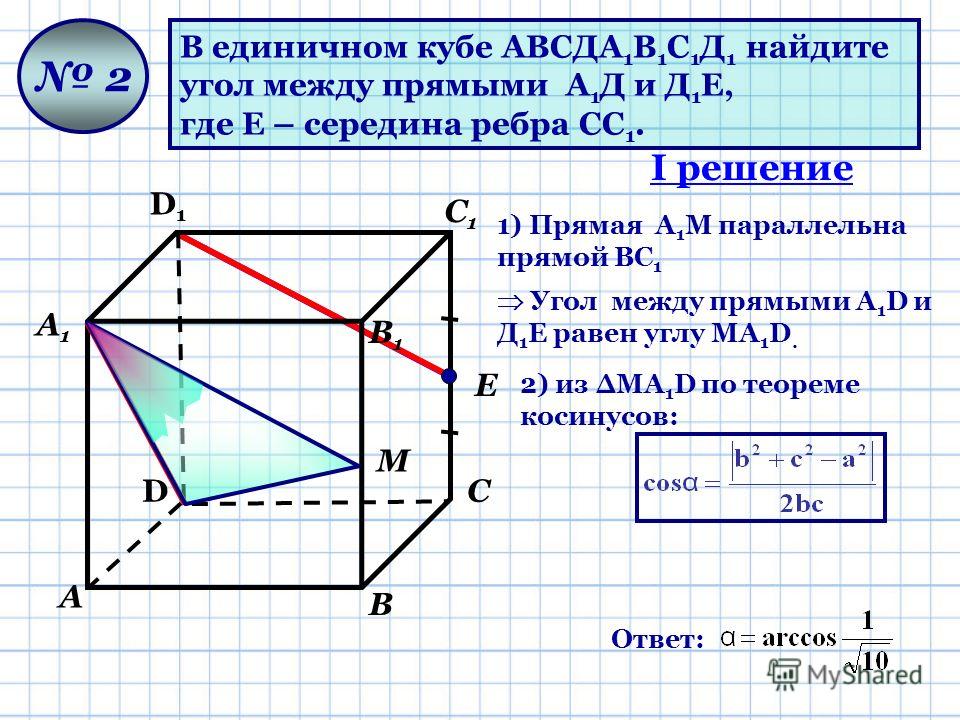
1) Построим плоскость AВС1,
С1
D1
1
В1
А1
2. Прямая АС1 проецируется на
плоскость ВСС1 в прямую ВС1.
следовательно, угол АС1В
искомый.
2
1
С
В
АВ АВС1
АВ ВС АВС1 ВВ1С1С
АВ ВВ1
D
1
А
Ответ: 2
2
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АА1 = 4, А1Д1 = 6, С1Д1 = 6, найдите тангенс
угла между плоскостью АДД1 и прямой ЕF,
проходящей через середины ребер АВ и В1С1.
№3
D1
С1 1) Угол между прямой EF и
6
6
плоскостью АDD1 равен углу
между EF и плоскостью ВСС1, т.к.
эти плоскости параллельны.
F
А1
В1
4
F F, Е В, ЕF ВF
угол EFB – искомый.
4
D
С
6
А
Е
6
В
Ответ: 0,6
№3
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите тангенс угла между прямой ВВ1 и
плоскостью АВ1С1.
С1
1
М1
А1
В1С1 АВ1С1
В1С1 ММ 1 АВ1С1 АМ 1М
1 В С АМ
1 1
1
1
С
А
1
1) Прямая ММ1 параллельна
прямой ВВ1, Угол между
прямой ВВ1 и плоскостью АВ1С1
В1 равен углу между ММ1 и
плоскостью АВ1С1.
угол АМ1М – искомый.
М
В
Ответ: 3
2
№4
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите угол между прямой АВ1 и
плоскостью АА1С1С.
С1
М
3
2
А1
1) Пусть М – середина А1С1, тогда
В1М – перпендикуляр к
плоскости АА1С1С, а М –
В1 проекция точки В1 на эту
плоскость,
угол МАВ1 – искомый.
2
1
С
1
1
А
1
В
Ответ: α arcsin
6
4
№5
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1. Найдите
синус угла между прямой ВД и плоскостью SВС.
S
Подсказка:
К
1
К
1
Д
О
А
1
1
2
С
D
1
В
3
2
В
О
2
2
Ответ: 3
3
№6
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
угол между прямой AА1 и плоскостью BCЕ1
Е1
D1
F1
С1
А1
В1
1
1
F
Е
D
С
3
А
1
В
1
Ответ: 600
№7
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите синус
угла между прямой BС1 и плоскостью АFF1
1
Е1
D1
F1
С1
А1
В1
1
Е
D
F
С
А
1
В
1
Ответ: 6
4
Домашнее задание
В единичном кубе АВСДА1В1С1Д1 точка Е – середина
ребра А1В1. Найдите синус угла между прямой АЕ и
плоскостью ВДД1.
10
10
Ответы :
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АВ = 4, ВС = 6, СС1 = 4, найдите тангенс
угла между плоскостью АВС и прямой ЕF,
проходящей через середины ребер АА1 и С1Д1.
Ответы :
1
10
В правильной шестиугольной призме
АВСДЕFА1В1С1Д1Е1F1, все ребра которой равны 1,
найдите угол между прямой СС1 и плоскостью BДЕ1 .
Ответы : 450
Литература
1. В.А. Смирнов ЕГЭ 2011. Математика.
Задача С2. Геометрия. Стереометрия. /
Под. редакцией А.Л. Семенова и И.В.
Ященко. – М.: МЦНМО, 2011.

English     Русский Правила

10А, 10Б | Образовательная социальная сеть

СПРАВОЧНЫЕ МАТЕРИАЛЫ ДЛЯ ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ

ЗАДАНИЯ 3 И 6: ПЛАНИМЕТРИЯ

ЭТО НАДО ЗНАТЬ: ТРЕУГОЛЬНИКИ

Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Треугольник называется равнобедренным, если две его стороны равны.

Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника. Вершина угла равнобедренного треугольника, лежащая напротив основания, называется вершиной равнобедренного треугольника. Высота, медиана и биссектриса равнобедренного треугольника, проведенные к его основанию, совпадают. Углы при основании равнобедренного треугольника равны. Высоты (медианы, биссектрисы), проведенные к боковым сторонам равнобедренного треугольника равны.

Равносторонний треугольник. Треугольник, все три стороны которого равны, называется правильным (равносторонним) треугольником.

Пусть a, h, S, R, r – соответственно длина стороны, высота, площадь, радиус описанной и радиус вписанной окружности правильного треугольника. Тогда имеют место следующие соотношения:

                       

                                                                   

Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника.

 Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине.

Три средние линии треугольника делят его на 4 равных треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Медианы треугольника пересекаются в одной точке, и точка пересечения делит каждую из них в отношении 2:1, считая от вершины.

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Биссектрисы треугольника пересекаются в одной точке (центре вписанной окружности).

Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Перпендикуляр, опущенный из вершины треугольника, на прямую, содержащую противоположную сторону, называется высотой треугольника.

Прямые, содержащие высоты треугольника, пересекаются в одной точке.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке (центре описанной окружности).

Квадрат стороны треугольника равен сумме квадратов двух других его сторон, уменьшенной на удвоенное произведение этих сторон на косинус угла между ними (теорема косинусов):                                    

ЭТО НАДО ЗНАТЬ: ЧЕТЫРЁХУГОЛЬНИКИ

Параллелограмм. Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Справедливы следующие утверждения.

– Две противоположные стороны четырехугольника равны и параллельны тогда и только тогда, когда этот четырехугольник — параллелограмм.

– Противоположные стороны четырехугольника попарно равны тогда и только тогда, когда этот четырехугольник —параллелограмм.

– Противоположные углы четырехугольника попарно равны тогда и только тогда, когда этот четырехугольник —параллелограмм.

– Диагонали четырехугольника пересекаются и точкой пересечения делятся пополам тогда и только тогда, когда этот четырехугольник — параллелограмм.

Прямоугольник. Прямоугольником называется параллелограмм, у которого все углы прямые.

Так как прямоугольник, по определению, является параллелограммом, то он обладает всеми свойствами параллелограмма.

Кроме того, прямоугольник обладает следующим характеристическим свойством.  Диагонали параллелограмма равны тогда и только тогда, когда этот параллелограмм — прямоугольник.

Ромб. Ромбом называется параллелограмм, все стороны которого равны. Так как ромб, по определению, является параллелограммом, то он обладает всеми свойствами параллелограмма.

Кроме того, ромб обладает следующими характеристическими свойствами.

1. Диагонали параллелограмма делят его углы пополам тогда и только тогда, когда этот параллелограмм — ромб.

2. Диагонали параллелограмма взаимно перпендикулярны тогда и только тогда, когда этот параллелограмм — ромб.

Параллелограмм Вариньона. Середины сторон произвольного (в том числе невыпуклого или даже пространственного) четырехугольника являются вершинами параллелограмма — параллелограмма Вариньона.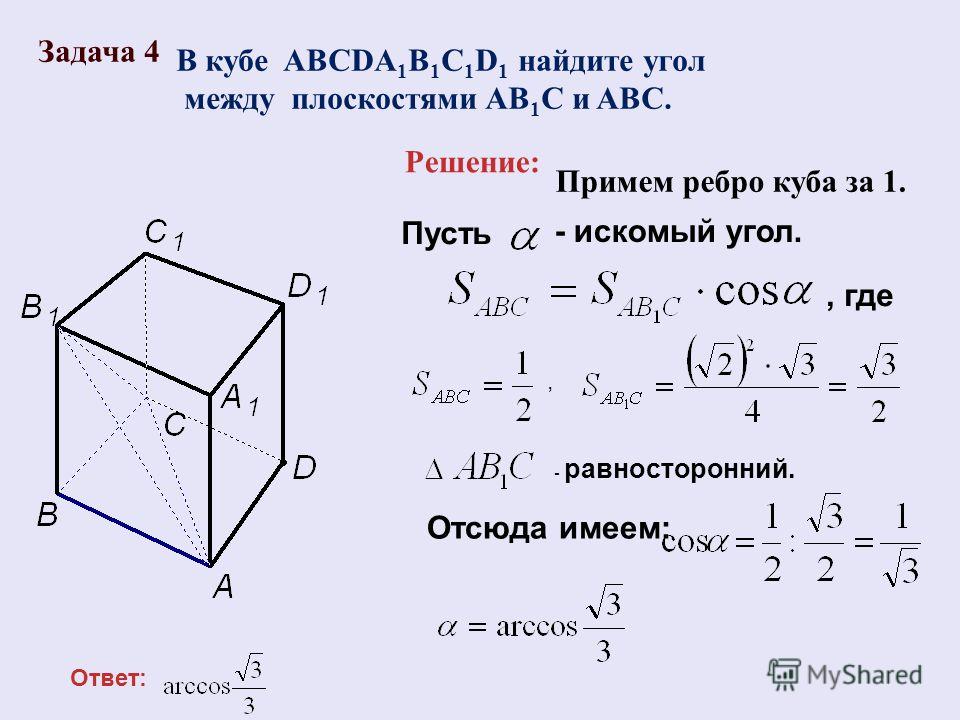

Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника.

Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.

Если исходный параллелограмм — прямоугольник, то параллелограмм Вариньона — ромб. Если исходный параллелограмм — ромб, то параллелограмм Вариньона — прямоугольник. Если исходный параллелограмм — квадрат, то параллелограмм Вариньона — квадрат.

Трапеция. Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.

Отрезок, соединяющий середины боковых сторон трапеции называется средней линией трапеции. Трапеция, боковые стороны которой равны, называется равнобедренной трапецией. Трапеция, один из углов которой прямой, называется прямоугольной трапецией.

Трапеция обладает следующими свойствами.

– Средняя линия трапеции параллельна ее основаниям и равна их полусумме.

– Отрезок, соединяющие середины диагоналей трапеции, равен полуразности большего и меньшего оснований.

– Диагонали трапеции равны тогда и только тогда, когда эта трапеция равнобедренная.

– Углы при каждом основании трапеции равны тогда и только тогда, когда эта трапеция равнобедренная.

– Сумма противолежащих углов в равнобедренной трапеции равна 180°.

– В равнобедренной трапеции расстояние от вершины одного основания до проекции противоположной вершины на прямую, содержащую это основание, равно средней линии.

ЭТО НАДО ЗНАТЬ: ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК

Правильный шестиугольник. Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.

– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

– Большая диагональ правильного шестиугольника является диметром описанной вокруг него окружности и равна двум его сторонам.

– Меньшая диагональ правильного шестиугольника в  раз больше его стороны.

– Угол между сторонами правильного шестиугольника равен 120°.

– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.

– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

ЭТО НАДО ЗНАТЬ: ПЛОЩАДИ МНОГОУГОЛЬНИКОВ

Теоремы о площадях многоугольников. Для вычисления площадей многоугольников применяют следующие теоремы.

– Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне или к ее продолжению.

– Площадь треугольника равна половине произведения сторон на синус угла между ними.

– Площадь квадрата равна квадрату его стороны.

– Площадь прямоугольника равна произведению его сторон.

– Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

– Площадь параллелограмма равна произведению сторон на синус угла между ними.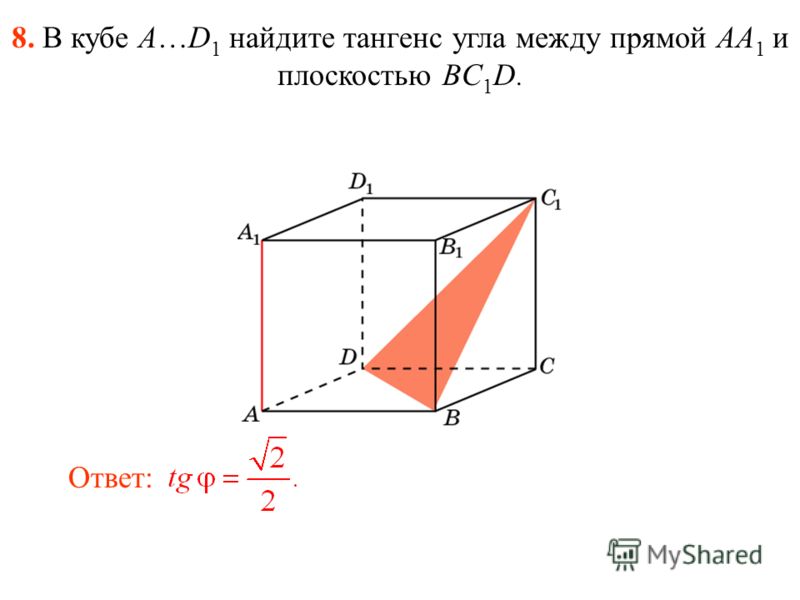

– Площадь ромба равна половине произведения его диагоналей.

– Площадь ромба равна произведению квадрата стороны на синус угла между сторонами.

– Площадь трапеции равна произведению полусуммы оснований на высоту.

– Площадь трапеции равна произведению средней линии на высоту.

– Площади подобных многоугольников относятся как квадрат коэффициента подобия.

– Формула ПИКА Площадь многоугольника, вершины которого лежат в узлах решетки, равна

ЭТО НАДО ЗНАТЬ: ОКРУЖНОСТИ

Окружность и ее элементы. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на данном расстоянии от данной точки.

Любые две точки окружности делят ее на две части, каждая из которых называется дугой окружности, а данные точки называются концами этих дуг.

Вписанный угол. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Справедливы следующие утверждения.

– Вписанный угол измеряется половиной дуги, на которую он опирается.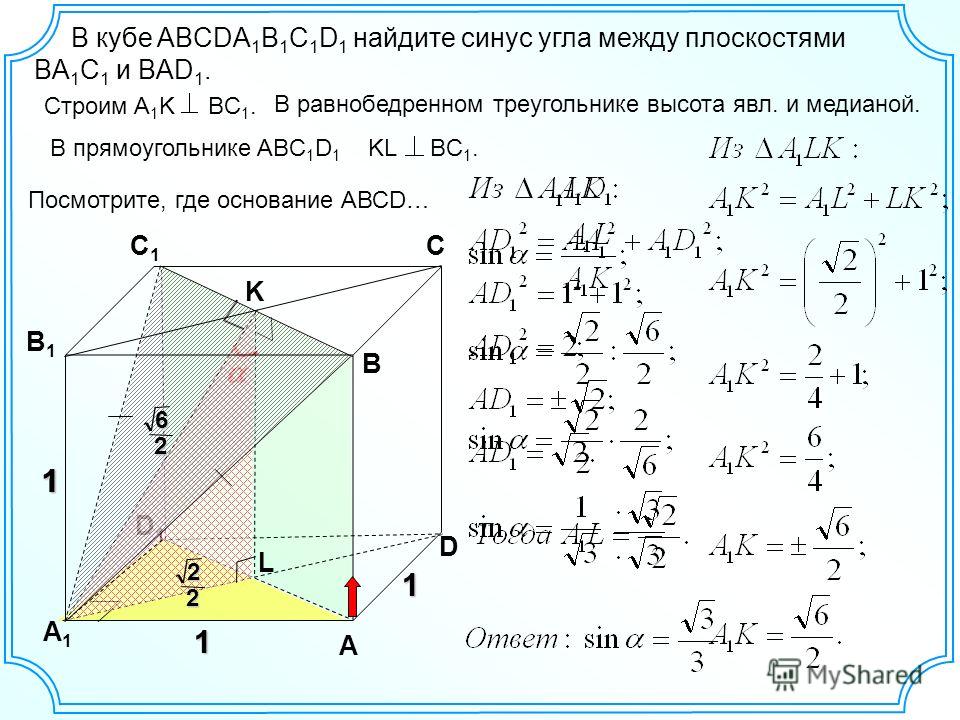

– Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

– Вписанные углы, опирающиеся на одну и ту же дугу, равны.

– Вписанный угол, опирающийся на полуокружность, — прямой.

– Отношение хорды к синусу вписанного угла, который на нее опирается, равно двум радиусам (теорема синусов).

Хорда. Отрезок, концы которого лежат на окружности, называется ее хордой. Справедливы следующие утверждения.

– Равные хорды стягивают равные дуги.

– Углы, опирающиеся на одну и ту же хорду, либо равны, либо в сумме дают 180.°

– Хорда, равная диаметру, из всех точек окружности видна под углом 90.°

– Радиус окружности, перпендикулярный хорде, делит ее пополам.

– Угол между двумя хордами равен полусумме высекаемых ими дуг:

– Произведение отрезков, на которые делится хорда данной точкой, есть для данной окружности величина постоянная и равная разности квадратов радиуса окружности и расстояния от точки пересечения хорд до центра окружности:

Касательная.  Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности. Справедливы следующие утверждения.

– Отрезки касательных к окружности, проведенные из одной точки, равны.

– Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

– Угол между касательной и хордой, проходящей через точку касания, равен половине заключенной между ними дуги.

– Угол между двумя касательными к окружности, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг.

Секущая. Прямая, имеющая с окружностью две общие точки, называется секущей. Справедливы следующие утверждения.

– Угол между касательной и секущей, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг:

Вписанная окружность. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Многоугольник в этом случае называется описанным около окружности.

Центр окружности, вписанной в многоугольник, есть точка, равноудаленная от всех сторон этого многоугольника, — точка пересечения биссектрис углов этого многоугольника.

В многоугольник можно вписать окружность и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В любой треугольник можно вписать окружность.

В правильный многоугольник можно вписать окружность.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.

Если окружность вписана в квадрат, то ее радиус равен половине стороны квадрата.

Описанная окружность.

 Определение. Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Центр окружности, описанной вокруг многоугольника, есть точка, равноудаленная от всех вершин этого многоугольника, — точка пересечения серединных перпендикуляров к сторонам этого многоугольника.