Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| Vulpeszg |
| ||
01/08/20 |
| ||
| |||
| Pphantom |
| ||
09/05/12 | |||
| |||
| Pphantom |
| |||||
09/05/12 |
| |||||
| ||||||
| Mihr |
| |||
18/09/14 |
| |||
| ||||
| Vulpeszg |
| ||
01/08/20 |
| ||
| |||
| Mihr |
| |||
18/09/14 |
| |||
| ||||
| Vulpeszg |
| ||
01/08/20 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
2.
 Динамика
Динамика2. Динамика
2.1. Локомотив на горизонтальном участке пути развивает постоянную силу тяги 350 кН. При этом на участке длиной 600 м скорость его возросла с 10 м/с до 20 м/с. Определить коэффициент трения, если масса поезда 1000 т. Ответ выразить с точностью до сотых. Ответ: 0,01. (1 балл)
2.2. Автомобиль массой 2 т, двигаясь из состояния покоя равноускоренно, через 10 с от начала движения достигает скорости 20 м/с. Коэффициент трения равен 0,1. Определить силу тяги двигателя. Ответ выразить в кН. Ответ: 6 кН. (1 балл)
2.3. Вагон массой 16 т, движущийся со скоростью 36 км/ч, начинает тормозить и останавливается, пройдя 500 м. Определить силу трения. Ответ выразить в кН с точностью до десятых. Ответ: 1,6 кН. (1 балл)
2.4. Тело массой 2
кг тянут по гладкой горизонтальной
поверхности с помощью пружины, которая
при движении растянулась на 1 см. Жесткость
пружины 100 Н/м. Определить ускорение;
с которым движется тело. Ответ: 0,5 м/с2 (1 балл)
Определить ускорение;
с которым движется тело. Ответ: 0,5 м/с2 (1 балл)
2.5. Груз массой 100 кг придавливается к стене силой 1 кН. Какую силу необходимо приложить, чтобы равномерно тянуть груз по стене вертикально вверх, если коэффициент трения равен 0,5? Ответ выразить в килоньютонах. Ответ: 1,5 кН. (1 балл)
2.6. Из орудия вылетает снаряд массой 10 кг со скоростью 600 м/c. Определить среднюю силу давления пороховых газов, если снаряд движется внутри ствола равноускоренно в течение 5 с. Ответ: 1,2 кН. (1 балл).
2.7. Тело массой 2 кг, имеющее скорость 25 м/с, ударяется о препятствие и упруго отскакивает от него без потери скорости. Направление удара перпендикулярно плоскости препятствия. Определить импульс, полученный стенкой при ударе. Ответ: 100 кг*м/с. (1 балл)
2.8. Шарик массой
100 г падает на горизонтальную плиту со
скоростью 50 м/с перпендикулярно к ее
поверхности и упруго отскакивает от
нее со скоростью 30 м/с. Определить
изменение импульса шарика. Ответ: 8
кг*м/с. (1 балл)
Определить
изменение импульса шарика. Ответ: 8
кг*м/с. (1 балл)
2.9. Определить вес груза массой 200 кг при вертикальном подъеме его с ускорением 5 м/с2. Ответ выразить в килоньютонах. Ответ: 3 кН. (1 балл)
2.10. Шахтная клеть весит в состоянии покоя 2,5 кН. С каким ускорением поднимается клеть, если вес ее стал равным 2 кН? Ответ: -2 м/с2. (1 балл).
2.11, Стальная проволока выдерживает силу натяжения 4400 Н. С каким наибольшим ускорением можно поднимать на ней груз массой 400 кг? Ответ: 1 м/с2. (1 балл)
2.12. Определить силу натяжения троса при равноускоренном подъеме кабины лифта массой 400 кг, если за 10 с она поднялась на 30 м. Ответ: 4240 Н. (1 балл)
2.13. При каком ускорении разорвется трос, прочность на разрыв которого 15 кН, а масса подвешенного груза 500 кг? Ответ: 20 м/с2. (1 балл)
2.14. Определить вес
человека в лифте, опускающемся вертикально
вниз равноускоренно, если масса человека
60 кг, а скорость лифта за 3 с возросла от
0 до 9 м/с. Ответ: 420 Н. (1 балл)
Ответ: 420 Н. (1 балл)
2.15. При каком коэффициенте трения автомобиль, движущийся со скоростью 72 км/ч, сможет сделать поворот радиусом 200 м на горизонтальной дороге без опасности заноса? Ответ: 0,2. (1 балл)
2.16. На какой скорости автомобиль сможет пройти закругление шоссе радиусом 200 м при коэффициенте трения между его колесами и покрытием дороги 0,2? Ответ выразить в единицах СИ. Ответ: 20 м/с. (1 балл)
2.17. Автомобиль массой 5 т движется по выпуклому мосту радиусом 100 м со скоростью 36 км/ч. Определить силу давления автомобиля на середину выпуклого моста. Ответ выразить в кН с точностью до целых. Ответ: 45 кН. (1 балл)
2.18. Шарик массой 20 г падает на стальную плиту с высоты 1,25 м и отскакивает в противоположном направлении до высоты 80 см. Определить силу удара, если длительность его 1О мс. Ответ: 18 Н. (2 балла)
2.19. На какое время
надо включить маршевый двигатель
космического корабля массой 1 т, чтобы
увеличить его скорость от 500 м/с до 2
км/с, если сила тяги двигателя 5 кН, а кпд
его 75 %? Ответ выразить в единицах СИ. (2
балла)
(2
балла)
2.20. Веревка выдерживает груз 90 кг при вертикальном подъеме с некоторым ускорением и груз 110 кг при спуске с таким же ускорением. Какой массы груз выдержит эта веревка при равномерном подъеме? Ответ выразить в единицах СИ с точностью до целых. Ответ: 100 кг. (2 балла)
2.21. Две гири массами 7 кг и 11 кг висят на концах нити, перекинутой через неподвижный блок. Вначале гири находились на одной высоте. Через сколько секунд после начала движения расстояние между ними станет равным 10 см? Ответ выразить в единицах СИ с точностью до сотых. Ответ: 0,21 с. (2 балла)
2.22. Два груза массами 3 кг и 7 кг висят на концах нити, перекинутой через неподвижный блок. Меньший груз находится на 1 м ниже большего. Грузы начинают двигаться без начальной скорости. Через сколько секунд они окажутся на одной высоте? Ответ выразить в единицах СИ с точностью до десятых. Ответ: 0,5 с. (2 балла)
2.23. Груз массой 10
кг перемещается равномерно по
горизонтальной поверхности под
действием силы, направленной под углом
300 к горизонту. Коэффициент трения равен
0,2. Определить значение действующей на
тело силы. Ответ выразить в единицах СИ
с точностью до целых. Ответ: 21 Н. (2 балла)
Коэффициент трения равен
0,2. Определить значение действующей на
тело силы. Ответ выразить в единицах СИ
с точностью до целых. Ответ: 21 Н. (2 балла)
2.24. Груз массой 50 кг перемещается по горизонтальной поверхности под действием силы 500 Н, направленной под углом 300 к горизонту. Коэффициент трения груза о плоскость равен 0,5. Определить ускорение груза. Ответ выразить в единицах СИ с точностью до десятых. Ответ: 6,2 м/с2 (2 балла)
2.25. Две книги лежат горизонтально одна на другой. Если нижнюю книгу приподнять за край, то верхняя равномерно соскользнет с нее при угле наклона 300 Чему равен коэффициент трения между книгами? Ответ дать с точностью до десятых. Ответ: 0,6. (2 балла)
2.26. При каком коэффициенте трения тело будет равномерно соскальзывать с наклонной плоскости, высота которой 2 м, а основание 4 м? Ответ: 0,5 (2 балла)
2.27. Автомобиль
поднимается в гору с углом при основании
300. Масса автомобиля 2 т. На участке пути 32
м скорость его возросла от 21,6 км/ч до 36
км/ч. Считая движение равноускоренным,
определить силу тяги двигателя, если
коэффициент трения равен 0,1. Ответ
выразить в килоньютонах. Ответ: 13,7 кН.
(2 балла)
Масса автомобиля 2 т. На участке пути 32
м скорость его возросла от 21,6 км/ч до 36
км/ч. Считая движение равноускоренным,
определить силу тяги двигателя, если
коэффициент трения равен 0,1. Ответ
выразить в килоньютонах. Ответ: 13,7 кН.
(2 балла)
2.28. По наклонной плоскости с углом при основании 300 соскальзывает тело в течение 2 с. Определить длину наклонной плоскости, если коэффициент трения равен 0,1. Ответ выразить в единицах СИ с точностью до сотых. Ответ: 8,26 м. (2 балла)
2.29. Автомобиль массой 2,5т движется по мосту со скоростью 36 км/ч. Сила давления автомобиля на середину моста равна 20 кН. Определить радиус кривизны моста. Ответ: 50 м. (2 балла)
2.30. Тело, привязанное к шнуру длиной 1 м, вращается а горизонтальной плоскости так, что шнур образует с вертикалью угол 600. Сколько оборотов в минуту делает тело? Ответ выразить с точностью до целых. Ответ: 43 об/мин. (2 балла)
2. 31. Определить вес
летчика массой 80 кг в верхней точке
петли Нестерова радиусом 200
м при скорости
самолета 360 км/ч. Ответ выразить в
килоньютонах. Ответ: 3,2 кН. (2 балла)
31. Определить вес
летчика массой 80 кг в верхней точке
петли Нестерова радиусом 200
м при скорости
самолета 360 км/ч. Ответ выразить в
килоньютонах. Ответ: 3,2 кН. (2 балла)
2.32. Диск вращается в горизонтальной плоскости со скоростью 4 об/мин. На расстоянии 20 см от оси вращения лежит тело. Каким должен был коэффициент трения, чтобы тело не было сброшено с диска? Ответ выразить с точностью до десятых. Ответ: 0,2. (2 балла)
2.33. Человек находится на краю круглой горизонтальной платформы радиусом 3 м. Сколько оборотов в минуту должна делать платформа, чтобы человек не мог удержаться на ней при коэффициенте трения 0,12? Считать, что ось платформы вертикальна. Ответ выразить с точностью до целых. Ответ: более 6 об/мин.(2 балла)
2.34. Определить ускорение свободного падения на высоте 6400 км над поверхностью Земли. Ответ: 2,5 м/с2. (2 балла)
2.35. Тело массой 12
кг поднято над Землей на высоту, 1/3
земного радиуса. Определить силу
тяжести тела. Ответ: 67,5 Н. (2 балла)
Определить силу
тяжести тела. Ответ: 67,5 Н. (2 балла)
2.36. Определить ускорение свободного падения на высоте, равной двум земным радиусам над поверхностью Земли. Ответ выразить в единицах СИ с точностью до десятых. Ответ: 1,1 м/с2. (2 балла)
2.37. На какой высоте над поверхностью Земли сила тяжести тела в 2 раза меньше, чем на поверхности Земли? Ответ: 2560 км. (2 балла)
2.38. На какой высоте над поверхностью Земли ускорение свободного падения в 4 раза меньше, чем на поверхности Земли? Ответ: 6400 км. (2 балла)
2.39. Определить первую космическую скорость для Луны. Ответ выразить в километрах в секунду. Ответ: 1,67 км/с. (2 балла)
2.40. Расстояние
между центрами Земли и Луны равно 60
земным радиусам, а масса Луны в 81 раз
меньше массы Земли. На каком расстоянии
от Земли тело будет притягиваться Землей
и Луной одинаково? Ответ выразить целым
числом радиусов Земли. Ответ: 54. (2 балла)
Ответ: 54. (2 балла)
2.41. Вес тела, измеренный пружинными весами, на экваторе некоторой планеты оказался на 10 % меньше, чем на полюсе. Определить среднюю плотность планеты, если продолжительность суток на ней 8 часов. Ответ выразить в единицах СИ. Ответ: 1700 кг/мЗ. (3 балла)
2.42. При какой продолжительности суток тела на экваторе Земли весили бы в 2 раза меньше, чем на полюсе? Ответ выразить в часах с точностью до целых. Ответ: 2 ч. (3 балла)
2.43. Определить период вращения Земли в минутах, при котором тела на экваторе находились бы в состоянии невесомости. Ответ: 84 мин. (3 балла)
2.44. Горизонтальный
диск радиуса 10 м вращается вокруг своей
оси со скоростью 2 об/мин. Вдоль края
диска навстречу вращению едет мотоциклист
со скоростью 30 км/ч относительно диска.
При каком минимальном коэффициенте
трения мотоцикл будет удерживаться на
диске? Ответ выразить с точностью до
десятых. Ответ: 0,4. (3 балла)
(3 балла)
2.45. Сила 60 Н прикладывается к санкам массой 40 кг под углом 300 к горизонту один раз вверх, другой раз — вниз. Во сколько раз ускорение санок в первом случае больше, чем во втором, если коэффициент трения равен 0,1? Ответ выразить с точностью до десятых. Ответ: 1,7. (3 балла)
2.46. Два бруска по 100 г каждый, связанные нитью, соскальзывают с наклонной плоскости с углом при основании 300. Коэффициент трения нижнего бруска о плоскость равен 0,2, а верхнего — 0,5. Определить силу натяжения нити, связывающей бруски. Ответ выразить в миллиньютонах с точностью до целых. Ответ: 130 мН. (3 балла)
2.47. С какой
горизонтальной силой надо действовать
на брусок массой 2 кг, находящийся на
наклонной плоскости с углом при
основании 300,
чтобы он двигался вверх по плоскости
равномерно? Коэффициент трения бруска
о плоскость равен 0,3. Ответ выразить
в единицах СИ с точностью до целых. Ответ: 21 Н. (3 балла)
Ответ: 21 Н. (3 балла)
2.48. Для равномерного поднятия груза массой 100 кг по наклонной плоскости с углом при основании 300, надо приложить силу 600 Н С каким ускорением будет скользить груз по этой плоскости, если его отпустить? Ответ: 4 м/с2 (3 балла)
2.49. Цепь длиной 1 м лежит на столе так, что ее конец свешивается со стола. При какой длине свешивающейся со стола части цепи вся цепь начнет скользить по столу, если коэффициент трения цепи о стол равен 0,33? Ответ дать в сантиметрах с точностью до целых. Ответ: 25 см. (3 балла)
2.50. За сколько секунд тяжелое тело спустится с горы высотой 2 м и углом при основании 450, если предельный угол, при котором тело может покоиться на этой плоскости, равен 300 ? Ответ дать с точностью до десятых. Ответ: 1,4 с. (3 балла)
2.51. Тело массой 10
кг находится на наклонной плоскости,
составляющей с горизонтом угол 300. Коэффициент трения о плоскость равен
0,6. Какая горизонтальная сила обеспечит
телу перемещение вниз по плоскости с
ускорением 1,63 м/с2?
Ответ выразить в единицах СИ с точностью
до десятых. Ответ: 15,8 Н. (3 балла)
Коэффициент трения о плоскость равен
0,6. Какая горизонтальная сила обеспечит
телу перемещение вниз по плоскости с
ускорением 1,63 м/с2?
Ответ выразить в единицах СИ с точностью
до десятых. Ответ: 15,8 Н. (3 балла)
2.52. Брусок массой 200 г находится на гладкой поверхности наклонной плоскости с углом при основании 300 и удерживается на ней с помощью невесомой и нерастяжимой нити, параллельной плоскости и закрепленной у ее верхнего края. Определить силу давления груза на наклонную плоскость, если она движется вертикально вверх с ускорением 2,2 м/с2. Ответ выразить в единицах СИ с точностью до целых. Ответ: 2 Н. (4 балла)
2.54. Тонкий обруч радиусом 10 см раскрутили вокруг его оси до угловой скорости 5,6 с-1 и положили на горизонтальный стол. Через сколько секунд обруч остановится, если коэффициент трения между ним и столом равен 0,01. Ответ дать с точностью до десятых. Ответ: 5,6 с. (4 балла)
2. 55. В цирковом
аттракционе мотоциклист едет по
внутренней поверхности вертикального
цилиндра радиусом 10 м. При какой скорости
мотоцикла это возможно, если коэффициент
трения между колесами мотоцикла и
поверхностью цилиндра равен 0,5? Размерами
мотоциклиста можно пренебречь. Ответ
выразить в единицах СИ с точностью до
десятых. Ответ: 14,1 м/с. (4 балла)
55. В цирковом
аттракционе мотоциклист едет по
внутренней поверхности вертикального
цилиндра радиусом 10 м. При какой скорости
мотоцикла это возможно, если коэффициент
трения между колесами мотоцикла и
поверхностью цилиндра равен 0,5? Размерами
мотоциклиста можно пренебречь. Ответ
выразить в единицах СИ с точностью до
десятых. Ответ: 14,1 м/с. (4 балла)
2.56. Тело соскальзывает без трения с наклонной плоскости. Определить угол наклона плоскости к горизонту, если средняя скорость тела за первые 0,5с на 2,5 м/с меньше, чем средняя скорость за первые 1,5 с. Ответ: 300 (4 балла)
2.57. Арбуз взвешивают
в салоне самолета на пружинных весах
дважды: один раз перед взлетом, а другой
— во время полета самолета вдоль меридиана.
Какой должна была быть скорость самолета,
чтобы показания весов в полете уменьшились
на 4 % по сравнению с показаниями их перед
взлетом? Вращением Земли вокруг своей
оси и высотой самолета по сравнению с
радиусом Земли пренебречь. Ответ выразить
в километрах в секунду с точностью до
десятых. Ответ: 1,6 км/с. (4 балла)
Ответ выразить
в километрах в секунду с точностью до
десятых. Ответ: 1,6 км/с. (4 балла)
2.58. Тележка массой 20 кг может катиться без трения по горизонтальном пути. У заднего края тележки лежит брусок массой 2 кг (края бруска и тележки совпадают). Коэффициент трения между бруском и тележкой равен 0,25. К бруску приложена горизонтальная сила 20 Н. Через какое время брусок упадет с тележки, если его длина 1 м? Ответ выразить в единицах СИ с точностью до сотых. Ответ: 0,36 с. (4 балла)
2.59. На гладком блоке радиусом 10 см висит однородный гибкий канат массой 12 кг и длиной 5 м. Определить максимальную силу натяжения каната. Ответ выразить в единицах СИ с точностью до десятых. Ответ: 58,6 Н. (4 балла)
2.60. Направленная
горизонтальная струя из брандспойта
бьет в вертикальную стенку со скоростью
60 л/мин. Площадь поперечного сечения
струи 1,5 см2.
Определить силу удара струи о стенку.
Ответ выразить в единицах СИ с точностью
до десятых. Ответ: 6,7 Н. (4 балла)
Ответ: 6,7 Н. (4 балла)
Работа
РаботаРабота, совершаемая постоянной силой
Предположим, вы поднимаете предмет массой 20 кг с земли на высоту. 1,5 м. Предположим, что вы прилагаете постоянную силу в восходящем направлении. направление и что вы перемещаете объект вверх с постоянной скоростью. результирующая сила, действующая на объект, равна нулю. Сила, которую вы прилагаете, равна по величине и противоположно по направлению силе тяжести. Пока вы поднимаетесь объект, над которым вы работаете.
Работа Вт, совершаемая над объектом постоянной силой, определяется как W = Ф · д . Он равен величине силы, умноженной на расстояние до объекта.
движется в направлении действия силы.
В примере выше F = мг = (20 кг) (9,8 м/с 2 ) = 196 Н, W = (196
Н)(1,5 м) = 294 Нм.
Работа — это скаляр, число с единицами измерения. Единица работы СИ Нм = Джоуль (Дж).
Работа » скалярное произведение » или « скалярное произведение »
силы и вектора смещения. Скалярное произведение двух векторов A и B — скалярная величина (число с единицами), равная
произведение величин двух векторов и косинуса наименьшего
угол между ними.
Скалярное произведение двух векторов A и B — скалярная величина (число с единицами), равная
произведение величин двух векторов и косинуса наименьшего
угол между ними.
А · В = ABcosθ.
В терминах декартовых компонент векторов А и Б скалярное произведение записывается как
А · В = А х В х + А у В у + А z Б z .
Работа, совершаемая силой, может быть положительной или отрицательной. Если составляющая силы в
направление перемещения положительное, то работа положительна, а если
составляющая силы в направлении перемещения отрицательна, то
произведение отрицательное.
В одном измерении скалярное произведение положительно, если два вектора
параллельны друг другу, и отрицательно, если два вектора антипараллельны
друг к другу, т. е. если они направлены в противоположные стороны.
Пример:
Предположим, вы забыли установить парковочный тормоз, и ваша машина начала катиться. вниз по холму. Вы тщетно пытаетесь остановить его, дергая изо всех сил.
бампер, но машина продолжает двигаться вперед. Вы прилагаете силу к
автомобиль против направления движения. Расстояние, пройденное в
направление силы отрицательное, вы совершаете с автомобилем отрицательную работу. Но
автомобиль тянет вас по ходу движения с силой, равной
величины (третий закон Ньютона). Машина производит на вас положительное впечатление.
вниз по холму. Вы тщетно пытаетесь остановить его, дергая изо всех сил.
бампер, но машина продолжает двигаться вперед. Вы прилагаете силу к
автомобиль против направления движения. Расстояние, пройденное в
направление силы отрицательное, вы совершаете с автомобилем отрицательную работу. Но
автомобиль тянет вас по ходу движения с силой, равной
величины (третий закон Ньютона). Машина производит на вас положительное впечатление.
Схема свободного тела объекта, поднимаемого с постоянная скорость на расстоянии d показано справа.
Суммарная сила, действующая на объект, равна нулю, F a + F г = 0.
Вектор смещения направлен вверх.
Работа, совершенная приложенной силой F a , W = F a · d = F a д = мгд , положительный.
Работа силы тяжести F g ,
W = F г ·d = -F г d = -mgd , отрицательно.
Чистая работа всех сил, действующих на объект, W net = F net ·d равна нулю.
Проблема:
Для А = 3 i + дж — к , Б = — я + 2 я + 5 к , и С = 2 j — 3 k , найти С ·( А — В ).
Решение:
- Обоснование:
Оцените скалярное произведение двух векторов. - Детали расчета:
A = 3 i + j — k . B = — i + 2 j + 5 k . А — В = 4 я — к — 6 к . С = 2 j — 3 k . С ·( А — В ) = -2 + 18 = 16.
Проблема:
Объясните, почему работа силы трения скольжения отрицательна. когда объект испытывает смещение на шероховатой поверхности?
Решение:
- Обоснование:
Сила трения скольжения всегда направлена в сторону, противоположную скорости v = d r /dt. Поэтому он указывает в направлении, противоположном направлению
рабочий объем d r . dW = F f · d r = -F f др.
Поэтому он указывает в направлении, противоположном направлению
рабочий объем d r . dW = F f · d r = -F f др.
Проблема:
При движении частицы по окружности на нее действует сила, направленная центр вращения. Почему эта сила не действует на частицу?
Решение:
- Обоснование:
Так как в любой точке окружности центростремительная сила перпендикулярна скорости v и, следовательно, к смещению d r скалярное произведение dW = F· d r это ноль.
Проблема:
Во время стрижки газона мальчик толкает газонокосилку на расстояние 350 м. траву с силой 90 Н, направленной по горизонтали. Какую работу выполнил мальчик?
Решение:
- Обоснование:
Работа, совершаемая над объектом постоянной силой, определяется как W = F · d = Fdcosθ.
Здесь F и d указывают в одном направлении, θ = 0, cosθ = 1, - Детали расчета:
Вт = F · d = 90 Н * 350 м = 31500 Дж.
Проблема:
Покупатель в супермаркете толкает тележку с силой 35 Н. направлена под углом 25 o вниз от горизонтали. Найдите работу, выполненную покупателем, когда он проходит по проходу длиной 50 м. длина.
Решение:
- Обоснование:
Работа, совершаемая над объектом постоянной силой, определяется как W = F · d = F x ∆x + F y ∆y + F z ∆z.
Тележка движется в направлении x, ∆y = ∆z = 0,
X-компонента сила F x = Fcosθ = (35 Н)cos(25 o ).
Работает только х-компонента силы, так как нет смещение тележки в направлении Y. - Детали расчета:
Работа, совершаемая покупателем, равна W = F x ∆x = (35 Н)cos(25 o )(50 м) = 1586 Дж.
Рампы
Предположим, вы хотите поднять свой мотоцикл на
свой пикап. Вероятно, вы будете использовать рампу. Вы выберете
длинная доска. Один конец доски будет опираться на кузов грузовика, а
другой конец будет лежать на земле. Вы закатите свой мотоцикл
эта рампа.
Вы выберете
длинная доска. Один конец доски будет опираться на кузов грузовика, а
другой конец будет лежать на земле. Вы закатите свой мотоцикл
эта рампа.
Вы прикладываете силу F a равную по величине и противоположное по направлению компоненту гравитационной силы параллельно рампе. Величина F a равна mgsinθ. Ты переместите мотоцикл на расстояние h/sinθ в направлении действия силы. Работа, которую вы совершаете, равна W = F·d = mgh, где mg — вес вашего мотоцикл и h высота кровати. Если бы вы подняли мотоцикл прямо, вы бы приложили силу, равную его весу. через расстояние ч. Когда вы катите его по рампе, вы должны нажать на это через гораздо большее расстояние. Чтобы выполнить ту же работу, вы, следовательно, нужна гораздо меньшая сила. Рампа обеспечивает механическое преимущество .
Работа = большая сила × малое расстояние = малая сила × большое расстояние .
Работа переменной силы в одном измерении
Если вы не знакомы с интегралами, пожалуйста, перейдите по этой ссылке, прежде чем продолжить.
Краткий обзор определенных интегралов
Работа, совершаемая переменной силой
F только с x-компонентой определяется как
W = ∫ х хf F(x)dx = lim ∆x—>0 Σ xi xf Ф(х)∆х.
(Символ Σ обозначает сумму.
Σ xi xf F∆x представляет собой сумму произведений F∆x из
от начального до конечного положения с шагом ∆x.)
Мы можем построить составляющую силы F
воздействуя на объект в положении x по сравнению с положением x.
Работа силы равна площади под кривой.
График для постоянной силы, действующей от x i до x f показано справа.
Работа силы
W = F(x f — x i ).
Работа, совершаемая переменной силой в трех измерениях
В трех измерениях работа, совершаемая переменной силой, равна W = ∫ r i r f F ·dr = lim ∆ r —>0 Σ r i r f F ·∆ r .
Здесь d r — бесконечно малый отрезок пути от начального
в конечное положение. По компонентам F и д р the integral can be written as
∫ path F ·d r = ∫ path F x dx + ∫ path F y dy + ∫ путь F z dz.
Подъем объекта вблизи поверхности Земли
Чтобы поднять предмет массой m так, чтобы его высота увеличилась на
расстояние h, вы должны приложить среднюю силу mg на расстоянии h.
Работа, которую нужно выполнить, чтобы поднять предмет, равна W = mgh.
Проблема:
Ящик на 100 Н стоит на земле и крепится к одному концу веревки.
Человек на балконе тянет веревку с постоянной силой 100 Н,
подъем ящика на расстояние 3 м.
а) Какой объем работы выполняет человек?
б) Какую работу совершает сила тяжести?
Решение:
- Обоснование:
Человек подтягивается, и ящик движется вверх в направлении действия силы.
Работа, совершаемая человеком, положительна, W = Fd = mgd = (100 Н)d.
Сила тяжести 100 Н направлена вниз, в то время как ящик движется вверх. Гравитация совершает отрицательную работу. - Детали расчета:
(a) Работа, выполненная человеком, равна W = (100 Н) * (3 м) = 300 Дж.
(б) Гравитация совершает 300 Дж отрицательной работы.
Проблема:
(a) Рассчитайте работу, выполненную на кабине лифта массой 1500 кг
его трос, чтобы поднять его на 40 м с постоянной скоростью, при условии, что сила трения усредняется
100 Н.
б) Какую работу совершает над кабиной лифта
гравитационная сила в этом процессе?
Решение:
- Рассуждение:
Кабина лифта весит 1500*9,8 Н = 14700 Н. Чтобы заставить кабину двигаться со постоянной скорости, результирующая сила, действующая на него, должна быть равна нулю. Сила кабеля воздействующая на автомобиль должна иметь величину 14800 Н, чтобы компенсировать вес и сила трения 100 Н направлена в противоположном направлении. 2$ в течение 3,00 с. Каково натяжение троса при торможении? г) На какую высоту поднялся лифт над исходной точкой и какова его конечная скорость? 9{3}$. Рабочие, скриншоты калькулятора и прочее правильные, просто показатель степени в итоговом ответе неверный.
2$ в течение 3,00 с. Каково натяжение троса при торможении? г) На какую высоту поднялся лифт над исходной точкой и какова его конечная скорость? 9{3}$. Рабочие, скриншоты калькулятора и прочее правильные, просто показатель степени в итоговом ответе неверный.Видеорешение
Зарегистрируйтесь для просмотра видеорешения!
Начать бесплатную неделю
Trustpilot
Рейтинг
ПлохоНе так уж плохоСреднеХорошоОчень хорошо
8 голосов со средней оценкой 2,2.
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. Этот лифт и люди внутри него имеют массу 1700 кг, и существует сила натяжения из-за троса, идущего вверх, и силы тяжести, падающей вниз. Здесь имеются три различных интервала движения, в течение которых существуют различные ускорения. Итак, в части А у нас есть ускорение вверх 1,2 метра в секунду в квадрате и за время 1,5 секунды. Наш вопрос заключается в том, какова сила натяжения кабеля.
 Ну, чистая сила — это все силы вверх за вычетом всех сил вниз. Итак, это сила натяжения вверх минус сила тяжести вниз, и это равно массе, умноженной на ускорение. Затем мы можем добавить силу тяжести к обеим сторонам. Я также сделал замену мг вместо фг . Тогда мы имеем силу натяжения мА плюс мг , и мы можем вынести из общего множителя м , и он равен м , умноженный на скобки a плюс г . Таким образом, 1700 кг умножить на 1,2 метра в секунду в квадрате ускорения вверх, плюс ускорение под действием силы тяжести 9,8, что дает 1,87 умножить на десять в трех ньютонах — это сила натяжения троса на этом участке его движения, когда он ускоряется вверх на 1,2 метра. за секунду в квадрате. Затем лифт движется с постоянной скоростью, то есть ускорение равно нулю в течение 8,5 секунд. Таким образом, результирующая сила остается той же картиной, но теперь ускорение равно нулю, и поэтому, когда мы добавляем силу гравитации к обеим сторонам, мы получаем силу гравитации саму по себе.
Ну, чистая сила — это все силы вверх за вычетом всех сил вниз. Итак, это сила натяжения вверх минус сила тяжести вниз, и это равно массе, умноженной на ускорение. Затем мы можем добавить силу тяжести к обеим сторонам. Я также сделал замену мг вместо фг . Тогда мы имеем силу натяжения мА плюс мг , и мы можем вынести из общего множителя м , и он равен м , умноженный на скобки a плюс г . Таким образом, 1700 кг умножить на 1,2 метра в секунду в квадрате ускорения вверх, плюс ускорение под действием силы тяжести 9,8, что дает 1,87 умножить на десять в трех ньютонах — это сила натяжения троса на этом участке его движения, когда он ускоряется вверх на 1,2 метра. за секунду в квадрате. Затем лифт движется с постоянной скоростью, то есть ускорение равно нулю в течение 8,5 секунд. Таким образом, результирующая сила остается той же картиной, но теперь ускорение равно нулю, и поэтому, когда мы добавляем силу гравитации к обеим сторонам, мы получаем силу гравитации саму по себе. Таким образом, сила натяжения равна силе тяжести. Мы заменили мг там и так сила натяжения 1700 кг умножить на напряженность гравитационного поля 9,8 метра на килограмм, что дает нам 1,67 умножить на десять в четырех ньютонах. Затем в части C лифт замедляется, что означает, что его ускорение направлено вниз, поэтому оно составляет минус 0,6 метра в секунду в квадрате в течение трех секунд. Затем сила натяжения, мы используем формулу, которую мы вычислили здесь, это масса, умноженная на ускорение плюс ускорение под действием силы тяжести. Получается 1700 кг, умноженное на минус 0,6 метра в секунду в квадрате, плюс 9.0,8, что дает 1,56 умножить на десять на четыре ньютона. Затем в части D нас просят выяснить окончательное положение лифта по вертикали. Таким образом, предположим, что он начинается с нулевой позиции, y ноль равен нулю, затем он перейдет в позицию y один в течение временного интервала delta t один , что составляет 1,5 секунды, и в течение этого интервала он имеет ускорение a one 1,2 метра в секунду в квадрате.
Таким образом, сила натяжения равна силе тяжести. Мы заменили мг там и так сила натяжения 1700 кг умножить на напряженность гравитационного поля 9,8 метра на килограмм, что дает нам 1,67 умножить на десять в четырех ньютонах. Затем в части C лифт замедляется, что означает, что его ускорение направлено вниз, поэтому оно составляет минус 0,6 метра в секунду в квадрате в течение трех секунд. Затем сила натяжения, мы используем формулу, которую мы вычислили здесь, это масса, умноженная на ускорение плюс ускорение под действием силы тяжести. Получается 1700 кг, умноженное на минус 0,6 метра в секунду в квадрате, плюс 9.0,8, что дает 1,56 умножить на десять на четыре ньютона. Затем в части D нас просят выяснить окончательное положение лифта по вертикали. Таким образом, предположим, что он начинается с нулевой позиции, y ноль равен нулю, затем он перейдет в позицию y один в течение временного интервала delta t один , что составляет 1,5 секунды, и в течение этого интервала он имеет ускорение a one 1,2 метра в секунду в квадрате. Затем он переходит в положение и два на интервал времени 8,5 секунд без ускорения, а затем, наконец, в положение 9.0524 и три , что мы и хотим найти. Во время этого интервала движения мы имеем ускорение три отрицательное 0,6 метра в секунду в квадрате за время дельта t три трех секунд. Таким образом, конечная позиция y 3 будет позицией перед ней, y 2 плюс начальная скорость в начале этого интервала, то есть скорость в позиции y 2 , и я обозначил это y two . , умноженное на временной интервал перехода от двух к трем, что равно дельта т три . Затем добавьте к этому половину ускорения в течение интервала три, умноженное на интервал времени дельта t три в квадрате. На самом деле мы не можем решить это, потому что мы не знаем некоторых вещей, которые входят в эту формулу. Мы еще не знаем и два , и мы не знаем и два . Итак, мы должны выяснить это. Теперь против двух будет равно против одного , потому что здесь нет ускорения и поэтому скорость постоянна.
Затем он переходит в положение и два на интервал времени 8,5 секунд без ускорения, а затем, наконец, в положение 9.0524 и три , что мы и хотим найти. Во время этого интервала движения мы имеем ускорение три отрицательное 0,6 метра в секунду в квадрате за время дельта t три трех секунд. Таким образом, конечная позиция y 3 будет позицией перед ней, y 2 плюс начальная скорость в начале этого интервала, то есть скорость в позиции y 2 , и я обозначил это y two . , умноженное на временной интервал перехода от двух к трем, что равно дельта т три . Затем добавьте к этому половину ускорения в течение интервала три, умноженное на интервал времени дельта t три в квадрате. На самом деле мы не можем решить это, потому что мы не знаем некоторых вещей, которые входят в эту формулу. Мы еще не знаем и два , и мы не знаем и два . Итак, мы должны выяснить это. Теперь против двух будет равно против одного , потому что здесь нет ускорения и поэтому скорость постоянна. Итак, независимо от скорости в также будет скоростью и два . Таким образом, это будет скорость в точке и ноль плюс ускорение в течение этого интервала здесь, плюс время этого интервала дельта t один . Итак, 1,2 метра в секунду в квадрате, умноженные на 1,5 секунды, что составляет 1,8 метра в секунду. Это дает нам часть нашей формулы для 90 524 y трех 90 525 . Теперь мы знаем, что такое против двух , это 1,8 метра в секунду. Нам еще нужно выяснить, что такое у два есть. Теперь умножить на два будет позицией перед ним, умножить на один плюс на два умножить на дельта t два плюс половина на два умножить на дельта t два . Но нет ускорения а двух , оно равно нулю. Таким образом, это сводится к этой формуле y один плюс постоянная скорость v два умножить на дельта t два . Мы не можем решить и это, потому что не знаем, что такое и . Так что разбираемся сейчас.
Итак, независимо от скорости в также будет скоростью и два . Таким образом, это будет скорость в точке и ноль плюс ускорение в течение этого интервала здесь, плюс время этого интервала дельта t один . Итак, 1,2 метра в секунду в квадрате, умноженные на 1,5 секунды, что составляет 1,8 метра в секунду. Это дает нам часть нашей формулы для 90 524 y трех 90 525 . Теперь мы знаем, что такое против двух , это 1,8 метра в секунду. Нам еще нужно выяснить, что такое у два есть. Теперь умножить на два будет позицией перед ним, умножить на один плюс на два умножить на дельта t два плюс половина на два умножить на дельта t два . Но нет ускорения а двух , оно равно нулю. Таким образом, это сводится к этой формуле y один плюс постоянная скорость v два умножить на дельта t два . Мы не можем решить и это, потому что не знаем, что такое и . Так что разбираемся сейчас. Так y один равен y ноль , который равен нулю, мы приняли его за опорный уровень, плюс v ноль умножить на дельта t один , также этот член равен нулю, потому что изначально нет скорости, плюс половина умножить на на единицу на на дельта т на единицу на в квадрате. Таким образом, это сводится только к этому термину: половина на единицу , умноженная на дельта t на единицу в квадрате. Таким образом, это половина, умноженная на 1,2 метра в секунду в квадрате, умноженная на 1,5 секунды в квадрате, и это дает 1,35 метра, которые мы затем можем подставить в 9.0524 и два . Таким образом, у нас есть 1,35 метра плюс 1,8 метра в секунду, умноженное на дельту t два , 8,5 секунды, что составляет 16,65 метра, и, в свою очередь, мы можем, наконец, подставить y два в формулу для y три . Таким образом, это 16,65 метра плюс 1,8 метра в секунду, умноженное на три секунды, это временной интервал дельта t три , плюс одна половина, умноженная на минус 0,6 метра в секунду в квадрате, умноженное на 3 секунды в квадрате, что дает нам 19,4 метра — окончательную высоту лифт.
Так y один равен y ноль , который равен нулю, мы приняли его за опорный уровень, плюс v ноль умножить на дельта t один , также этот член равен нулю, потому что изначально нет скорости, плюс половина умножить на на единицу на на дельта т на единицу на в квадрате. Таким образом, это сводится только к этому термину: половина на единицу , умноженная на дельта t на единицу в квадрате. Таким образом, это половина, умноженная на 1,2 метра в секунду в квадрате, умноженная на 1,5 секунды в квадрате, и это дает 1,35 метра, которые мы затем можем подставить в 9.0524 и два . Таким образом, у нас есть 1,35 метра плюс 1,8 метра в секунду, умноженное на дельту t два , 8,5 секунды, что составляет 16,65 метра, и, в свою очередь, мы можем, наконец, подставить y два в формулу для y три . Таким образом, это 16,65 метра плюс 1,8 метра в секунду, умноженное на три секунды, это временной интервал дельта t три , плюс одна половина, умноженная на минус 0,6 метра в секунду в квадрате, умноженное на 3 секунды в квадрате, что дает нам 19,4 метра — окончательную высоту лифт.


 08.2020, 02:43
08.2020, 02:43  08.2020, 07:13
08.2020, 07:13  08.2020, 15:31
08.2020, 15:31 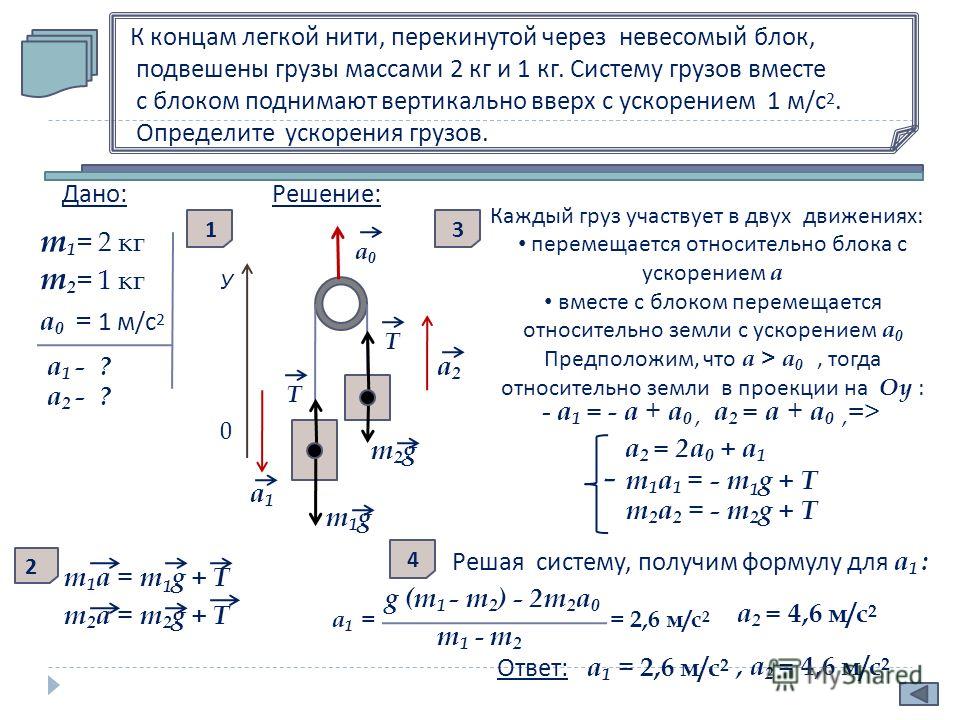 08.2020, 15:36
08.2020, 15:36  08.2020, 17:37
08.2020, 17:37 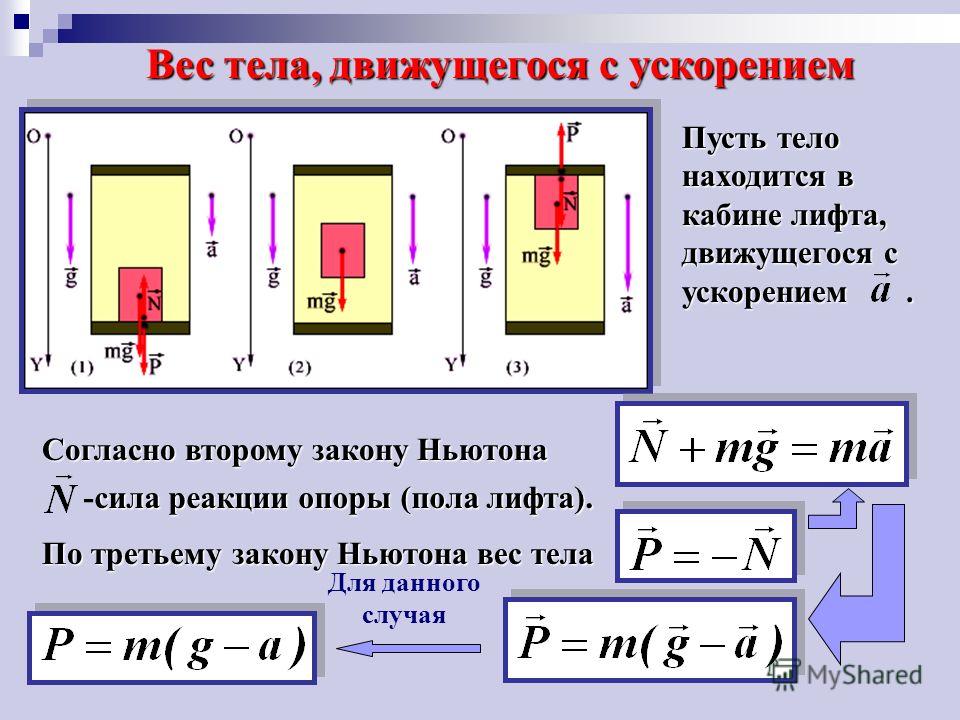 Поэтому он указывает в направлении, противоположном направлению
рабочий объем d r . dW = F f · d r = -F f др.
Поэтому он указывает в направлении, противоположном направлению
рабочий объем d r . dW = F f · d r = -F f др.

 2$ в течение 3,00 с. Каково натяжение троса при торможении? г) На какую высоту поднялся лифт над исходной точкой и какова его конечная скорость? 9{3}$. Рабочие, скриншоты калькулятора и прочее правильные, просто показатель степени в итоговом ответе неверный.
2$ в течение 3,00 с. Каково натяжение троса при торможении? г) На какую высоту поднялся лифт над исходной точкой и какова его конечная скорость? 9{3}$. Рабочие, скриншоты калькулятора и прочее правильные, просто показатель степени в итоговом ответе неверный. Ну, чистая сила — это все силы вверх за вычетом всех сил вниз. Итак, это сила натяжения вверх минус сила тяжести вниз, и это равно массе, умноженной на ускорение. Затем мы можем добавить силу тяжести к обеим сторонам. Я также сделал замену мг вместо фг . Тогда мы имеем силу натяжения мА плюс мг , и мы можем вынести из общего множителя м , и он равен м , умноженный на скобки a плюс г . Таким образом, 1700 кг умножить на 1,2 метра в секунду в квадрате ускорения вверх, плюс ускорение под действием силы тяжести 9,8, что дает 1,87 умножить на десять в трех ньютонах — это сила натяжения троса на этом участке его движения, когда он ускоряется вверх на 1,2 метра. за секунду в квадрате. Затем лифт движется с постоянной скоростью, то есть ускорение равно нулю в течение 8,5 секунд. Таким образом, результирующая сила остается той же картиной, но теперь ускорение равно нулю, и поэтому, когда мы добавляем силу гравитации к обеим сторонам, мы получаем силу гравитации саму по себе.
Ну, чистая сила — это все силы вверх за вычетом всех сил вниз. Итак, это сила натяжения вверх минус сила тяжести вниз, и это равно массе, умноженной на ускорение. Затем мы можем добавить силу тяжести к обеим сторонам. Я также сделал замену мг вместо фг . Тогда мы имеем силу натяжения мА плюс мг , и мы можем вынести из общего множителя м , и он равен м , умноженный на скобки a плюс г . Таким образом, 1700 кг умножить на 1,2 метра в секунду в квадрате ускорения вверх, плюс ускорение под действием силы тяжести 9,8, что дает 1,87 умножить на десять в трех ньютонах — это сила натяжения троса на этом участке его движения, когда он ускоряется вверх на 1,2 метра. за секунду в квадрате. Затем лифт движется с постоянной скоростью, то есть ускорение равно нулю в течение 8,5 секунд. Таким образом, результирующая сила остается той же картиной, но теперь ускорение равно нулю, и поэтому, когда мы добавляем силу гравитации к обеим сторонам, мы получаем силу гравитации саму по себе.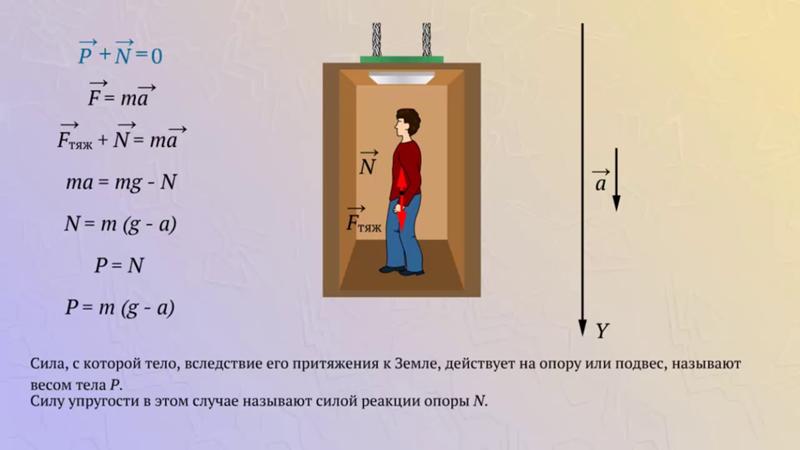 Таким образом, сила натяжения равна силе тяжести. Мы заменили мг там и так сила натяжения 1700 кг умножить на напряженность гравитационного поля 9,8 метра на килограмм, что дает нам 1,67 умножить на десять в четырех ньютонах. Затем в части C лифт замедляется, что означает, что его ускорение направлено вниз, поэтому оно составляет минус 0,6 метра в секунду в квадрате в течение трех секунд. Затем сила натяжения, мы используем формулу, которую мы вычислили здесь, это масса, умноженная на ускорение плюс ускорение под действием силы тяжести. Получается 1700 кг, умноженное на минус 0,6 метра в секунду в квадрате, плюс 9.0,8, что дает 1,56 умножить на десять на четыре ньютона. Затем в части D нас просят выяснить окончательное положение лифта по вертикали. Таким образом, предположим, что он начинается с нулевой позиции, y ноль равен нулю, затем он перейдет в позицию y один в течение временного интервала delta t один , что составляет 1,5 секунды, и в течение этого интервала он имеет ускорение a one 1,2 метра в секунду в квадрате.
Таким образом, сила натяжения равна силе тяжести. Мы заменили мг там и так сила натяжения 1700 кг умножить на напряженность гравитационного поля 9,8 метра на килограмм, что дает нам 1,67 умножить на десять в четырех ньютонах. Затем в части C лифт замедляется, что означает, что его ускорение направлено вниз, поэтому оно составляет минус 0,6 метра в секунду в квадрате в течение трех секунд. Затем сила натяжения, мы используем формулу, которую мы вычислили здесь, это масса, умноженная на ускорение плюс ускорение под действием силы тяжести. Получается 1700 кг, умноженное на минус 0,6 метра в секунду в квадрате, плюс 9.0,8, что дает 1,56 умножить на десять на четыре ньютона. Затем в части D нас просят выяснить окончательное положение лифта по вертикали. Таким образом, предположим, что он начинается с нулевой позиции, y ноль равен нулю, затем он перейдет в позицию y один в течение временного интервала delta t один , что составляет 1,5 секунды, и в течение этого интервала он имеет ускорение a one 1,2 метра в секунду в квадрате. Затем он переходит в положение и два на интервал времени 8,5 секунд без ускорения, а затем, наконец, в положение 9.0524 и три , что мы и хотим найти. Во время этого интервала движения мы имеем ускорение три отрицательное 0,6 метра в секунду в квадрате за время дельта t три трех секунд. Таким образом, конечная позиция y 3 будет позицией перед ней, y 2 плюс начальная скорость в начале этого интервала, то есть скорость в позиции y 2 , и я обозначил это y two . , умноженное на временной интервал перехода от двух к трем, что равно дельта т три . Затем добавьте к этому половину ускорения в течение интервала три, умноженное на интервал времени дельта t три в квадрате. На самом деле мы не можем решить это, потому что мы не знаем некоторых вещей, которые входят в эту формулу. Мы еще не знаем и два , и мы не знаем и два . Итак, мы должны выяснить это. Теперь против двух будет равно против одного , потому что здесь нет ускорения и поэтому скорость постоянна.
Затем он переходит в положение и два на интервал времени 8,5 секунд без ускорения, а затем, наконец, в положение 9.0524 и три , что мы и хотим найти. Во время этого интервала движения мы имеем ускорение три отрицательное 0,6 метра в секунду в квадрате за время дельта t три трех секунд. Таким образом, конечная позиция y 3 будет позицией перед ней, y 2 плюс начальная скорость в начале этого интервала, то есть скорость в позиции y 2 , и я обозначил это y two . , умноженное на временной интервал перехода от двух к трем, что равно дельта т три . Затем добавьте к этому половину ускорения в течение интервала три, умноженное на интервал времени дельта t три в квадрате. На самом деле мы не можем решить это, потому что мы не знаем некоторых вещей, которые входят в эту формулу. Мы еще не знаем и два , и мы не знаем и два . Итак, мы должны выяснить это. Теперь против двух будет равно против одного , потому что здесь нет ускорения и поэтому скорость постоянна. Итак, независимо от скорости в также будет скоростью и два . Таким образом, это будет скорость в точке и ноль плюс ускорение в течение этого интервала здесь, плюс время этого интервала дельта t один . Итак, 1,2 метра в секунду в квадрате, умноженные на 1,5 секунды, что составляет 1,8 метра в секунду. Это дает нам часть нашей формулы для 90 524 y трех 90 525 . Теперь мы знаем, что такое против двух , это 1,8 метра в секунду. Нам еще нужно выяснить, что такое у два есть. Теперь умножить на два будет позицией перед ним, умножить на один плюс на два умножить на дельта t два плюс половина на два умножить на дельта t два . Но нет ускорения а двух , оно равно нулю. Таким образом, это сводится к этой формуле y один плюс постоянная скорость v два умножить на дельта t два . Мы не можем решить и это, потому что не знаем, что такое и . Так что разбираемся сейчас.
Итак, независимо от скорости в также будет скоростью и два . Таким образом, это будет скорость в точке и ноль плюс ускорение в течение этого интервала здесь, плюс время этого интервала дельта t один . Итак, 1,2 метра в секунду в квадрате, умноженные на 1,5 секунды, что составляет 1,8 метра в секунду. Это дает нам часть нашей формулы для 90 524 y трех 90 525 . Теперь мы знаем, что такое против двух , это 1,8 метра в секунду. Нам еще нужно выяснить, что такое у два есть. Теперь умножить на два будет позицией перед ним, умножить на один плюс на два умножить на дельта t два плюс половина на два умножить на дельта t два . Но нет ускорения а двух , оно равно нулю. Таким образом, это сводится к этой формуле y один плюс постоянная скорость v два умножить на дельта t два . Мы не можем решить и это, потому что не знаем, что такое и . Так что разбираемся сейчас. Так y один равен y ноль , который равен нулю, мы приняли его за опорный уровень, плюс v ноль умножить на дельта t один , также этот член равен нулю, потому что изначально нет скорости, плюс половина умножить на на единицу на на дельта т на единицу на в квадрате. Таким образом, это сводится только к этому термину: половина на единицу , умноженная на дельта t на единицу в квадрате. Таким образом, это половина, умноженная на 1,2 метра в секунду в квадрате, умноженная на 1,5 секунды в квадрате, и это дает 1,35 метра, которые мы затем можем подставить в 9.0524 и два . Таким образом, у нас есть 1,35 метра плюс 1,8 метра в секунду, умноженное на дельту t два , 8,5 секунды, что составляет 16,65 метра, и, в свою очередь, мы можем, наконец, подставить y два в формулу для y три . Таким образом, это 16,65 метра плюс 1,8 метра в секунду, умноженное на три секунды, это временной интервал дельта t три , плюс одна половина, умноженная на минус 0,6 метра в секунду в квадрате, умноженное на 3 секунды в квадрате, что дает нам 19,4 метра — окончательную высоту лифт.
Так y один равен y ноль , который равен нулю, мы приняли его за опорный уровень, плюс v ноль умножить на дельта t один , также этот член равен нулю, потому что изначально нет скорости, плюс половина умножить на на единицу на на дельта т на единицу на в квадрате. Таким образом, это сводится только к этому термину: половина на единицу , умноженная на дельта t на единицу в квадрате. Таким образом, это половина, умноженная на 1,2 метра в секунду в квадрате, умноженная на 1,5 секунды в квадрате, и это дает 1,35 метра, которые мы затем можем подставить в 9.0524 и два . Таким образом, у нас есть 1,35 метра плюс 1,8 метра в секунду, умноженное на дельту t два , 8,5 секунды, что составляет 16,65 метра, и, в свою очередь, мы можем, наконец, подставить y два в формулу для y три . Таким образом, это 16,65 метра плюс 1,8 метра в секунду, умноженное на три секунды, это временной интервал дельта t три , плюс одна половина, умноженная на минус 0,6 метра в секунду в квадрате, умноженное на 3 секунды в квадрате, что дает нам 19,4 метра — окончательную высоту лифт.
Leave A Comment