В двух шахтах добывают алюминий и никель в первой шахте имеется 80 рабочих – Задача 18 — две шахты

Вопросы»В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день.|Поступи в ВУЗ

В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день.

создана: 26.01.2018 в 19:16
…………………………………………

liliana :

В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля.

Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля.

Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава.

Сколько килограммов сплава при таких условиях ежедневно может произвести завод?

Решение.

Т.к. не оговорено, что каждый рабочий занимается добычей только одного вида металла, то нельзя говорить, что х рабочих выплавляют только AL, а остальные только Ni.

Используем понятие «человеко-часы» — количество человек, умноженное на количество часов работы каждого (все рабочие работают одинаковое время).
Человеко-час — единица учёта рабочего времени, соответствует часу работы одного человека.

Первая шахта.  100 рабочих* 5 часов=500 человеко-часов.

Пусть х человеко-часов уходит на добычу AL, тогда 500-х человеко-часов  — на добычу Ni.

Добыча составит: х кг Al,   3(500-х) кг Ni.

Вторая шахта.

300*5=1500 человеко-часов.

Пусть у человеко-часов уходит на добычу Al, тогда 1500-у  — на добычу Ni.

Добыча составит: 3у кг Al,  (1500-у) кг Ni.

Всего:      (х+3у) кг   Al,   (3000-3x-y) кг Ni.

Т.к. Al в 2 раза больше, то составим уравнение: х+3у=2(3000-3х-у)  —>  у=1200-1,4х

Cоставим ф-цию выпуска металла. 

F(x,y)=x+3y+3000-3x-y=3000+2y-2x

F(x)=3000+2(1200-1,4x)-2x=5400-4,8x

Заметим, что хС[0;500].

F(x) — линейная, убывающая, значит наибольшее значение принимает при х=0 (на левом конце отрезка [0;100] ).  

F(0)=5400.

Ответ: 5400.

www.postupivuz.ru

Решение задания 17, вариант 29, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике: 2017, 2018

В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 1 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля.

Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Похожие варианты: 15, 19, 24, 31, 35

Первая шахта : всего 300 человеко-часов
Пусть M — число человеко-часов, потраченных на добычу алюминия в 1й области
Тогда (300-M) — число человеко-часов, потраченных на добычу никеля в 1й области
Тогда 2*M — число добытых килограмм алюминия в 1й области за сутки

Тогда 1*(300-M) — число добытых килограмм никеля в 1й области за сутки
2я область: всего 500 человеко-часов
Пусть N — число человеко-часов, потраченных на добычу алюминия в 2й области
Тогда (500-N) — число человеко-часов, потраченных на добычу никеля в 2й области
Тогда 1*N — число добытых килограмм алюминия в 2й области за сутки
Тогда 2*(500-N) — число добытых килограмм никеля в 2й области за сутки

Масса добытого в сумме в двух областях алюминия за сутки:

   

Масса добытого в сумме в двух областях никеля за сутки:

   

Поскольку у нас в сплаве на 2 кг алюминия должно приходится 1 кг никеля, то у нас есть условие 2:1 , количество кг одного должно

равняться удвоенному количеству килограмм другого, это задает строгую связь между и , например 100 кг алюминия = 2 * 50 кг никеля (на 100 кг алюминия приходится 50 кг никеля):

(1)  

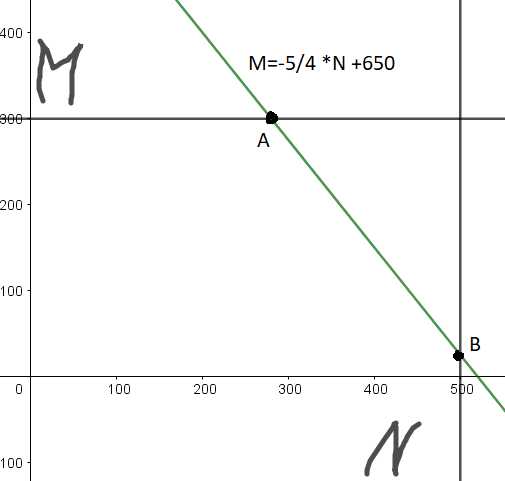
Это задает уравнение линии на плоскости :

(2)  

Полная масса сплава из никеля и алюминия за сутки как функция двух переменных :

(3)  

Полная масса сплава зависит и от , и от . Это задает поверхность над координатами (3).
Нам нужен максимум этой функции, максимум поверхности, но при этом на линии, задаваемой уравнением (2) и в рамках прямоугольника 300×500.

Для этого надо взять производную, но у нас две переменных , поэтому выразим через (уравнение (2)) и подставим это в (уравнение (3)). Получим зависимость , т.е. только от одной переменной :

   

   

Т.к. производная отрицательна, то функция максимальна на левом конце отрезка. Но фишка в том, что у нас на самом деле находится не в пределах [0,500], а в пределах [280,500] — это хорошо видно на рисунке — наши границы — это не весь прямоугольник, а мы живем на линии ограничения 2:1, поэтому мы живем между точками A и B, и нам нужно найти левую границу — координаты точки A. Они легко находятся, если подставить в наше ограничение 2:1 (уравнение (2) ) значение граничное . Отсюда и точка A имеет координаты
Подставляем координаты точки A в функцию F(M,N) и получаем ответ:

   

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Приходи на мой новый (2019) бесплатный тренинг-вебинар
по решению 12х,13х,14х,15х,16х,17х,18х задач:
«7 шагов скоростной подготовки к ЕГЭ по математике. »

Записаться бесплатный на тренинг. Заходи!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru

ege-resheniya.ru

2-ЕГЭ 2017. И.В. Ященко. Математика. 30 вариантов. Вариант 17. Задание 17. — Integrallo

Тип задания: 17 (Экономическая задача).

Id-2. Задание № 17. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод.

Решение:

1 шахта:

	Количество рабочих	Произведено за 1 час (кг)	Произведено за 5 часов (кг)
Алюминий	x	1\cdot x	5\cdot x
Никель	100-x	3\cdot (100-x)	5\cdot 3\cdot (100-x)

2 шахта:

	Количество рабочих	Произведено за 1 час (кг)	Произведено за 5 часов (кг)
Алюминий	y	3\cdot y	5\cdot 3\cdot y
Никель	300-y	1\cdot (300-y)	5\cdot (300-y)

5x+5\cdot 3y=2\cdot (5\cdot 3\cdot(100 — x)+5\cdot(300-y)) 5(x+3y)=5\cdot 2(3(100-x)+(300-y)) x+3y=2(300-3x+300-y) x+3y=2(600-3x-y) x+3y=1200-6x-2y 5y=1200-7x y=\frac{1200}{5}-\frac{7}{5}x y=240-\frac{7}{5}x

y\to max при x=0.

При x=0, \ y=240.

Тогда масса сплава = 5\cdot 0+5\cdot 3(100-0)+5\cdot 3\cdot 240+ 5\cdot (300-240)=
=5\cdot 3\cdot 100+5\cdot 3 \cdot 240+5\cdot 60=5400

Ответ: 5400.

Источник: ЕГЭ 2017. Математика. Профильный уровень. 30 вариантов типовых тестовых заданий и 800 заданий части 2/ под. ред. И.В. Ященко. — М.: Издательство «Экзамен», издательство МЦНМО, 2017. -215 с. (Серия «ЕГЭ. 30 вариантов. Типовые тестовые задания»). Вариант 17. Задание 17.

integrallo.ru