2. Трапеция ABCD (AD и ВС — основания) и треугольник AED имеют общую сторону… Геометрия Зив Б.Г. 10 класс. Контрольные работы. Вариант 3
2. Трапеция ABCD (AD и ВС — основания) и треугольник AED имеют общую сторону… Геометрия Зив Б.Г. 10 класс. Контрольные работы. Вариант 3 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
2.
Трапеция ABCD (AD и ВС — основания) и треугольник AED имеют общую сторону AD и лежат в разных плоскостях. Точка М лежит на стороне АЕ, а точка Р — на стороне DE, причем МР параллельна плоскости трапеции.
1) Докажите, что МР ║ ВС.
2) Каково взаимное расположение прямых МР и А В? Чему равен угол между этими прямыми, если
= 110°? Поясните.
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
похожие вопросы 5
Вариант 1. С-51. № 1. ГДЗ Алгебра 7 класс Звавич. помогите найти значения алгебраических дробей
Найдите значения алгебраических дробей при соответствующих значениях х и заполните таблицу: (Подробнее. ..)
..)
ГДЗАлгебра7 классЗвавич Л.И.
1. Перечислите свойства ромба, которые сохраняются при параллельном… Геометрия Зив Б.Г. 10 класс. Доп. Самостоятельные работы 1. Вариант 4
1. Перечислите свойства ромба, которые сохраняются при параллельном проектировании.
ГДЗГеометрияЗив Б. Г.10 класс
2. Изобразите квадрат ABCD с перпендикуляром, опущенным из вершины С… Зив Б.Г. 10 класс Геометрия. Доп. Самостоятельные работы 1. Вариант 5
2. Изобразите квадрат ABCD с перпендикуляром, опущенным из вершины С на отрезок BE, где Е — середина AD.
ГДЗГеометрияЗив Б. Г.10 класс
Помогите ответить! Вариант 4. Часть 2. Задание 22. ЕГЭ 5 вариантов ответов по Обществознанию 11 класс Королькова.
Взаимодействие каких сфер жизни общества раскрывает автор на
примере семьи? Каков, на взгляд автора, характер этого взаимо-
(Подробнее…)
ГДЗОбществознаниеЕГЭ11 классКоролькова Е.
1. Точки А, С, М и Р лежат в плоскости а, а точка B ¢ α (рис. 66). Постройте… Геометрия 10 класс Зив Б.Г. Контрольные работы. Вариант 1
1. Точки А, С, М и Р лежат в плоскости а, а точка B ¢ α (рис. 66). Постройте точку пересечения прямой МР с плоскостью АВС. (Подробнее…)
ГДЗГеометрияЗив Б. Г.10 класс
В трапеции abcd ab равен cd. Трапеция на ЕГЭ
Задание 11. В трапеции ABCD известно, что AB = CD, угол BDA = 54° и угол BDC = 33°. Найдите угол ABD. Ответ дайте в градусах.
Решение.
Теперь рассмотрим треугольник ABD, в котором известны углы A и BDA, и так как сумма всех углов в треугольнике равна 180 градусов, находим третий угол ABD:
Ответ: 39.
Задание 12. На клетчатой бумаге с размером клетки 1×1 отмечены три точки: А, В и С. Найдите расстояние от точки А до прямой ВС.
Решение.
Расстояние от точки A до прямой BC – это нормаль, опущенная из точки A на сторону BC (красная линия на рисунке). Длина этой нормали составляет 3 клетки, то есть 3 единицы.
Ответ: 3.
Задание 13. Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
Решение.
1) Верно. Площадь треугольника равна произведению высоты на половину основания треугольника, а все эти величины меньше длин любых двух его сторон.
Теорема 1 (теорема Фалеса ). Параллельные прямые высекают на пересекающих их прямых пропорциональные отрезки (рис.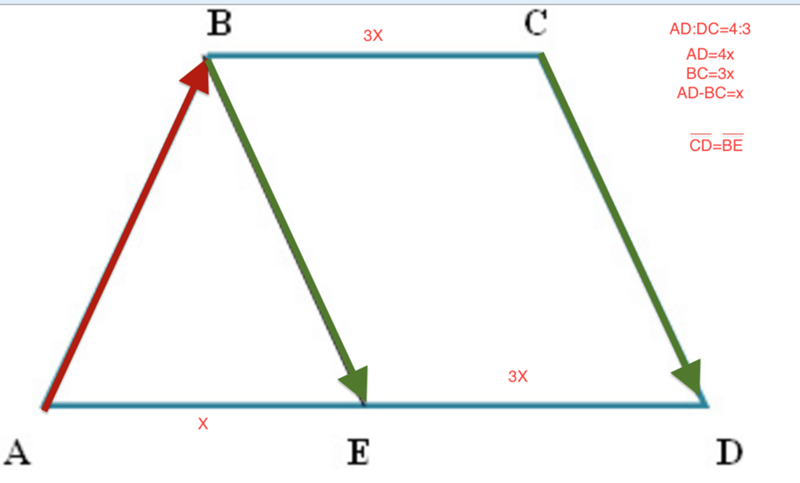
Определение 1 . Два треугольника (рис. 2) называются подобными, если соответствующие стороны у них пропорциональны.
Теорема 2 (первый признак подобия ). Если угол первого треугольника равен углу второго треугольника, а прилежащие к этим углам стороны треугольников пропорциональны, то такие треугольники подобны (см. рис. 2).
Теорема 3 (второй признак подобия ). Если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис. 3).
Теорема 4 (теорема Менелая ). Если некоторая прямая пересекает стороны AB и BC треугольника ABC в точках X и Y соответственно, а продолжение стороны AC — в точке Z (рис. 4), то
Теорема 5 . Пусть в остроугольном треугольнике ABC проведены высоты AA1 и CC1 (рис. 5). Тогда треугольники A1 BC1 и ABC подобны, причем коэффициент подобия равен cos ∠B.
Лемма 1 . Если стороны AC и DF треугольников ABC и DEF лежат на одной прямой или на параллельных прямых (рис. 6), то
6), то
Лемма 2 . Если два треугольника имеют общую сторону AC (рис. 7), то
Лемма 3 . Если треугольники ABC и AB1
C1
имеют общий угол A, то
Лемма 4 . Площади подобных треугольников относятся как квадрат коэффициента подобия.
Доказательства некоторых теорем
Доказательство теоремы 4 . Проведем через точку C прямую, параллельную прямой AB, до пересечения с прямой XZ в точке K (рис. 9). Надо доказать, что
Рассмотрим две пары подобных треугольников:
Перемножив почленно эти равенства, получим:
что и требовалось доказать.
Доказательство теоремы 5.
Но это следует из того, что из прямоугольного треугольника ABA1
, а из прямоугольного треугольника CBC1
. Попутно доказана и вторая часть теоремы.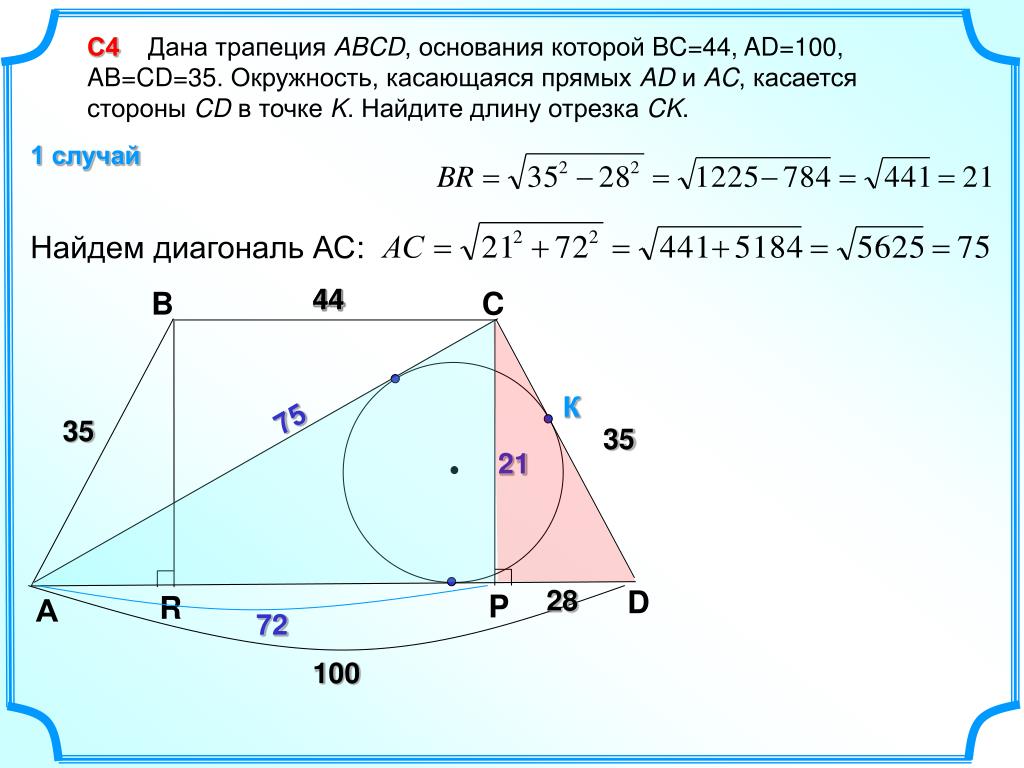
Решения задач
Задача 1 . Дана трапеция ABCD, причем известно, что BC = a и AD = b. Параллельно ее основаниям BC и AD проведена прямая, пересекающая сторону AB в точке P, диагональ AC в точке L, диагональ BD в точке R и сторону CD в точке Q (рис. 10). Известно, что PL = LR. Найти PQ.
Решение
Согласно теореме Фалеса имеем:
Обозначим теперь PL = LR = RQ = x и рассмотрим снова две пары подобных треугольников:
Имеем далее:
Значит,
Ответ :
Задача 2 . В треугольнике ABC угол A равен 45°, а угол C — острый. Из середины N стороны BC опущен перпендикуляр NM на сторону AC (рис. 11). Площади треугольников NMC и ABC относятся соответственно как 1: 8. Найти углы треугольника ABC.
Решение. Пусть BH — высота, опущенная из вершины B на сторону AC.
Так как NM — средняя линия треугольника BHC, то S∆BHC
= 4S∆NMC
.
Но, согласно условию задачи, S∆ABC = 8S∆NMC .
Следовательно, S∆ABC = 2S∆BHC , поэтому S∆ABH = S∆BHC . Значит, AH = HC,
откуда ∠CAB = ∠ACB = 45°, ∠ABC = 90°.
Ответ: ∠CAB = ∠ACB = 45°, ∠ABC = 90°.
Задача 3 . Дан треугольник ABC, в котором угол B равен 30°, AB = 4 и BC = 6. Биссектриса угла B пересекает сторону AC в точке D (рис. 12). Определить площадь треугольника ABD.
Решение . Применим к треугольнику ABC теорему о биссектрисе внутреннего угла:
Значит,
Ответ :
Статья опубликована при поддержке компании «Мир цветов». Оптово-розничный склад свадебных и ритуальных товаров, искусственных цветов в Краснодаре. Свадебные аксессуары — свечи, плакаты, бокалы, ленты, приглашения и многое другое. Ритуальные товары — ткани, одежда, фурнитура. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты Вы сможете на сайте, который располагается по адресу: flowersworld.su .
Задача 4 . Через середину M стороны BC параллелограмма ABCD, площадь которого равна 1, и вершину A проведена прямая, пересекающая диагональ BD в точке O (рис. 13). Найти площадь четырехугольника OMCD.
13). Найти площадь четырехугольника OMCD.
Решение . Площадь четырехугольника OMCD будем искать как разность площадей треугольников BCD и BOM. Площадь треугольника BCD равна половине площади параллелограмма ABCD и равна Найдем площадь треугольника BOM. Имеем:
∆
BOM ∼ ∆
AOD ⇒
Далее:
Значит,
Ответ :
Задача 5 . В прямоугольный равнобедренный треугольник ABC с прямым углом при вершине B вписан прямоугольный треугольник MNC так, что угол MNC прямой, точка N лежит на AC, а точка M на стороне AB (рис. 14). В каком отношении точка N должна делить гипотенузу AC, чтобы площадь треугольника MNC составляла от площади треугольника ABC?
Решение . Можно считать, что AB = 1. Обозначим AM = x, 0
Имеем:
Ответ :
Задача 6 . В трапеции ABCD диагональ AC перпендикулярна боковой стороне CD, а диагональ DB перпендикулярна боковой стороне AB. Продолжения боковых сторон AB и DC пересекаются в точке K, образуя треугольник AKD с углом 45° при вершине K (рис.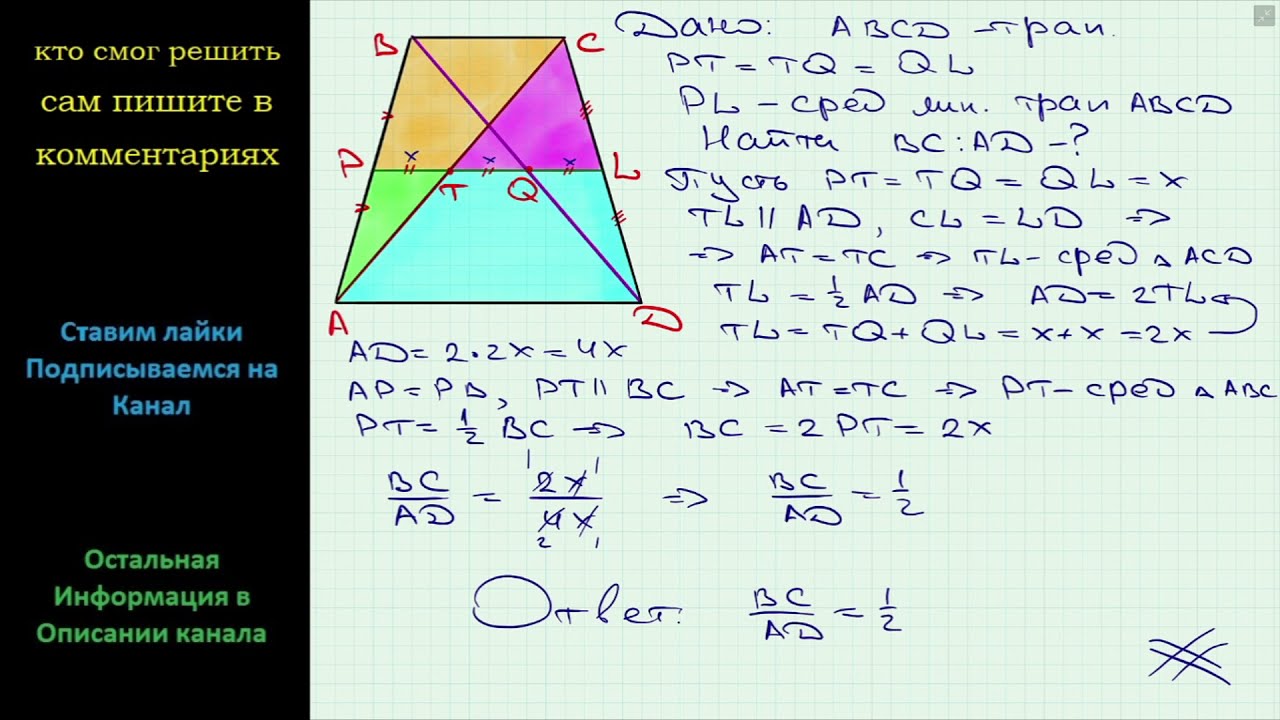 15). Площадь трапеции ABCD равна S. Найти площадь треугольника AKD.
15). Площадь трапеции ABCD равна S. Найти площадь треугольника AKD.
Решение . Согласно теореме 5, треугольник BKC подобен треугольнику AKD с коэффициентом подобия Следовательно, площади этих треугольников относятся как 1: 2, а это значит, что площадь трапеции ABCD равна площади треугольника BKC. Поэтому площадь треугольника AKD равна 2S.
Ответ : 2S.
Задача 7 . В треугольнике ABC на стороне AB взята точка K так, что AK: KB = 1: 2, а на стороне BC взята точка L так, что CL: LB = 2: 1. Пусть Q — точка пересечения прямых AL и CK (рис. 16). Найти площадь треугольника ABC, зная, что площадь треугольника BQC равна 1.
Решение . Пусть AK = x, BL = y. Тогда KB = 2x,
LC = 2y, значит, AB = 3x и BC = 3y. Применим к треугольнику ABL и секущей KQ теорему Менелая:
Задача 8 . Из точки M, которая расположена внутри остроугольного треугольника ABC, опущены перпендикуляры на стороны (рис. 17). Длины сторон и опущенных на них перпендикуляров соответственно равны a и k, b и m, c и n. Вычислить отношение площади треугольника ABC к площади треугольника, вершинами которого служат основания перпендикуляров.
Вычислить отношение площади треугольника ABC к площади треугольника, вершинами которого служат основания перпендикуляров.
Решение . Введем стандартные обозначения, то есть обозначим длины сторон треугольника ABC: BC = a , CA = b, AB = c; величины углов: ∠BAC = α,
∠ABC = β, ∠ACB = γ. Основания перпендикуляров, опущенных из точки M на стороны BC, CA и AB, обозначим соответственно через D, E и F. Тогда, согласно условию задачи, MD = k, ME = m, MF = n. Очевидно, что угол EMF равен π – α, угол DMF равен π – β, угол DME равен π – γ и точка M расположена внутри треугольника DEF. Площадь треугольника DEF равна:
Площадь треугольника ABC равна:
Найдем отношение площадей треугольников DEF и ABC:
Следовательно,
Ответ :
Задача 9 . Точки P и Q расположены на стороне BC треугольника ABC так, что BP: PQ: QC = 1: 2: 3.
Точка R делит сторону AC этого треугольника таким образом, что AR: RC = 1: 2 (рис. 18). Чему равно отношение площади четырехугольника PQST к площади треугольника ABC, где S и T — точки пересечения прямой BR с прямыми AQ и AP соответственно?
18). Чему равно отношение площади четырехугольника PQST к площади треугольника ABC, где S и T — точки пересечения прямой BR с прямыми AQ и AP соответственно?
Решение . Обозначим BP = x, AR = y; тогда
PQ = 2x, QC = 3x, RC = 2y. Вычислим, какую часть площадь четырехугольника PQST составляет от площади треугольника APQ, а значит, и от площади треугольника ABC. Для этого нам понадобятся отношения, в которых точки S и T делят прямые AQ и AP соответственно. Применим к треугольнику ACQ и секущей SR теорему Менелая:
Аналогично, применив теорему Менелая к треугольнику ACP и секущей TR, получим:
Далее:
С другой стороны, применив лемму о площадях к треугольникам APQ и ABC, получим, что
Ответ :
Задача 10 . В треугольнике ABC длина высоты BD равна 6, длина медианы CE равна 5, расстояние от точки пересечения BD с CE до стороны AC равно 1 (рис. 19). Найти длину стороны AB.
Решение . Пусть точка O — точка пересечения прямых BD и CE. Расстояние от точки O до стороны AC (равное по условию единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая:
Расстояние от точки O до стороны AC (равное по условию единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая:
Применив теперь теорему Менелая к треугольнику ACE и секущей OD, получим, что
откуда OE = 2CO, и с учетом OE + CO = CE = 5
получаем, что К прямоугольному треугольнику CDO применим теорему Пифагора:
Значит, Наконец, рассмотрим прямоугольный треугольник ABD, в нем также воспользуемся теоремой Пифагора:
Ответ :
Задача 11 . На отрезке AB лежат точки C и D, причем точка C находится между точками A и D. Точка M взята так, что прямые AM и MD перпендикулярны, и прямые CM и MB тоже перпендикулярны (рис. 20). Найти площадь треугольника AMB, если известно, что величина угла CMD равна α, а площади треугольников AMD и CMB равны S1 и S2 соответственно.
Решение . Обозначим площади треугольников AMB и CMD соответственно через
x и y (x > y). Заметим, что x + y = S1
+ S2
. Покажем теперь, что xy = S 1 S 2 sin 2 α. Действительно,
Покажем теперь, что xy = S 1 S 2 sin 2 α. Действительно,
Аналогично,
Так как ∠AMB = ∠AMC + ∠CMD + ∠DMB =
= 90° – α + α + 90° – α = 180° – α, и sin ∠AMB =
= sin α. Значит:
Таким образом, числа x и y являются корнями квадратного уравнения
t2
– (S1
+ S2
)t + S1
S2
sin2
α = 0.
Больший корень этого уравнения:
Ответ :
Задачи для самостоятельного решения
С-1. В треугольнике ABC, площадь которого равна S, проведена биссектриса CE и медиана BD, пересекающиеся в точке O. Найдите площадь четырехугольника ADOE, зная, что BC = a , AC = b.
С-2 . В равнобедренный треугольник ABC вписан квадрат так, что две его вершины лежат на основании BC, а две другие — на боковых сторонах треугольника. Сторона квадрата относится к радиусу круга, вписанного в треугольник, как
8: 5. Найдите углы треугольника.
С-3 . В параллелограмме ABCD со сторонами AD = 5 и AB = 4 проведен отрезок EF, соединяющий точку E стороны BC с точкой F стороны CD. Точки E и F выбраны так, что
Точки E и F выбраны так, что
BE: EC = 1: 2, CF: FE = 1: 5. Известно, что точка M пересечения диагонали AC с отрезком FE удовлетворяет условию MF: ME = 1: 4. Найдите диагонали параллелограмма.
С-4. Площадь трапеции ABCD равна 6. Пусть E — точка пересечения продолжений боковых сторон этой трапеции. Через точку E и точку пересечения диагоналей трапеции проведена прямая, которая пересекает меньшее основание BC в точке P, большее основание AD — в точке Q. Точка F лежит на отрезке EC, причем EF: FC = EP: EQ = 1: 3.
Найдите площадь треугольника EPF.
С-5. В остроугольном треугольнике ABC (где AB > BC) проведены высоты AM и CN, точка O — центр описанной около треугольника ABC окружности. Известно, что величина угла ABC равна β, а площадь четырехугольника NOMB равна S. Найдите длину стороны AC.
С-6 . В треугольнике ABC точка K на стороне AB и точка M на стороне AC расположены так, что выполняются соотношения AK: KB = 3: 2 и AM: MC = 4: 5. В каком отношении точка пересечения прямых KC и BM делит отрезок BM?
С-7 . Внутри прямоугольного треугольника ABC (угол B прямой) взята точка D так, что площади треугольников ABD и BDC соответственно в три и четыре раза меньше площади треугольника ABC. Длины отрезков AD и DC равны соответственно a и c. Найдите длину отрезка BD.
Внутри прямоугольного треугольника ABC (угол B прямой) взята точка D так, что площади треугольников ABD и BDC соответственно в три и четыре раза меньше площади треугольника ABC. Длины отрезков AD и DC равны соответственно a и c. Найдите длину отрезка BD.
С-8 . В выпуклом четырехугольнике ABCD на стороне CD взята точка E так, что отрезок AE делит четырехугольник ABCD на ромб и равнобедренный треугольник, отношение площадей которых равно Найдите величину угла BAD.
С-9 . Высота трапеции ABCD равна 7, а длины оснований AD и BC равны соответственно 8 и 6. Через точку E, лежащую на стороне CD, проведена прямая BE, которая делит диагональ AC в точке O в отношении AO: OC = 3: 2. Найдите площадь треугольника OEC.
С-10 . Точки K, L, M делят стороны выпуклого четырехугольника ABCD в отношении AK: BK = CL: BL = CM: DM = 1: 2. Известно, что радиус описанной около треугольника KLM окружности равен KL = 4, LM = 3 и KM С-11 . Продолжения сторон AD и BC выпуклого четырехугольника ABCD пересекаются в точке M, а продолжения сторон AB и CD — в точке O. Отрезок MO перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольников AOD и BOC, если OA = 6, OD = 4, CD = 1.
Отрезок MO перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольников AOD и BOC, если OA = 6, OD = 4, CD = 1.
С-12 . В треугольнике ABC угол при вершине A равен 30°, а высоты BD и CE пересекаются в точке O. Найдите отношение радиусов окружностей, описанных около треугольников DEO и ABC.
С-13 . Отрезки, соединяющие основания высот остроугольного треугольника, равны 5, 12 и 13. Найдите радиус описанной около треугольника окружности.
С-14 . В остроугольном треугольнике ABC на высоте AD взята точка M, а на высоте BP — точка N так, что углы BMC и ANC — прямые. Расстояние между точками M и N равно а ∠MCN = 30°.
Найдите биссектрису CL треугольника CMN.
С-15 . На сторонах AB, BC и AC треугольника ABC взяты точки D, E и F соответственно. Отрезки AE и DF проходят через центр вписанной в треугольник ABC окружности, а прямые DF и BC параллельны. Найдите длину отрезка BE и периметр треугольника ABC, если BC = 15, BD = 6, CF = 4.
С-16 . В треугольнике ABC биссектриса BB» пересекает медиану AA» в точке O.
В треугольнике ABC биссектриса BB» пересекает медиану AA» в точке O.
Найдите отношение площади треугольника BOA» к площади треугольника AOB», если AB: AC = 1: 4.
С-17 . В треугольнике ABC точка D лежит на AC, причем AD = 2DC. Точка E лежит на BC. Площадь треугольника ABD равна 3, площадь треугольника AED равна 1. Отрезки AE и BD пересекаются в точке O. Найдите отношение площадей треугольников ABO и OED.
С-18 . В параллелограмме ABCD точки E и F лежат соответственно на сторонах AB и BC, M — точка пересечения прямых AF и DE, причем AE = 2BE, а BF = 3CF. Найдите отношение AM: MF.
С-19 . В прямоугольнике ABCD на сторонах
AB и AD выбраны соответственно точки E и F так, что AE: EB = 3: 1, AF: FD = 1: 2. Найдите EO: OD, где O — точка пересечения отрезков
DE и CF.
С-20 . На стороне PQ треугольника PQR взята точка N, а на стороне PR — точка L, причем
NQ = LR. Точка пересечения отрезков QL и NR делит отрезок QL в отношении m: n, считая от точки Q. Найдите отношение PN: PR.
Найдите отношение PN: PR.
С-21 . На сторонах острого угла с вершиной O взяты точки A и B. На луче OB взята точка M на расстоянии 3OA от прямой OA, а на луче OA — точка N на расстоянии 3OB от прямой OB. Радиус окружности, описанной около треугольника AOB, равен 3. Найдите MN.
С-22 . В выпуклом пятиугольнике ABCDE диагонали BE и CE являются биссектрисами углов при вершинах B и C соответственно, ∠A = 35°, ∠D = 145°, S∆BCE
= 11. Найдите площадь пятиугольника ABCDE.
С-23 . На основаниях AD и BC трапеции ABCD построены квадраты ADEF и BCGH, расположенные вне трапеции. Диагонали трапеции пересекаются в точке O. Найдите длину отрезка AD, если BC = 2, GO = 7, а GF = 18.
С-24 . В треугольнике ABC известно, что AB = BC, а угол BAC равен 45°. Прямая MN пересекает сторону AC в точке M, а сторону BC — в точке N, причем AM = 2MC, а ∠NMC = 60°. Найдите отношение площади треугольника MNC к площади четырехугольника ABNM.
С-25 . В треугольнике ABC взяты точка N на стороне AB, а точка M — на стороне AC. Отрезки CN и BM пересекаются в точке O, AN: NB = 2: 3,
Отрезки CN и BM пересекаются в точке O, AN: NB = 2: 3,
BO: OM = 5: 2. Найдите CO: ON.
Трапеция на ЕГЭ. Базовый уровень.
Задачи из открытого банка заданий ФИПИ.
Задача 1. В трапеции ABCD известно, что AB=CD, ∠ BDA=54° и ∠ BDC=23°. Найдите угол ABD. Ответ дайте в градусах.
Решение. В данной трапеции угол А DC при нижнем основании равен сумме углов А D В и В DC , равен 54 + 23 =77 градусам. Поскольку трапеция равнобедренная, то углы при нижнем основании равны и угол ВА D тоже равен 77 градусам. Сумма углов ВА D и АВ D равна 180 градусам (односторонние при параллельных прямых А D и ВС и секущей АВ). Значит угол АВС равен 180 – 77 =103 градусам.
Далее используем равенство углов А D В и D ВС (накрестлежащие при параллельных прямых А D и ВС и секущей В D ). Значит угол АВ D равен 103 – 54 =49 градусам.
Ответ 49.
Задача 2. Основания равнобедренной трапеции
равны 10 и 24, боковая сторона равна 25. Найдите высоту трапеции.
Найдите высоту трапеции.
Решение. В данной трапеции верхнее основание ВС равно 10, нижнее А D =24. Из вершин В и С опустим высоты на нижнее основание. В получившемся прямоугольнике НВСК НК=ВС=10. Треугольники АВН и К DC DC ), значит АН=К D =(24-10):2=7. По теореме Пифагора в треугольнике АВН квадрат катета ВН равен разности квадрата гипотенузы АВ и квадрата катета АН. То есть ВН 2 = 625 – 49 = 576. ВН = 24.
Ответ 24.
Задача 3. В равнобедренной трапеции одно из
оснований
равно 3, а другое — 7. Высота трапеции равна 4. Найдите тангенс
острого угла трапеции.
Решение. В данной трапеции верхнее основание
ВС равно 3, нижнее А
D
=7. Из вершин В и С опустим высоты на нижнее
основание. В получившемся прямоугольнике НВСК НК=ВС=3. Треугольники АВН и К
DC
равны (они
прямоугольные, ВН=СК, АВ =
DC
), значит АН=К
D
=(7-3):2=2. Тангенс
острого угла ВАН в прямоугольном треугольнике АВН равен отношению
противолежащего катета ВН к прилежащему катету АН, то есть 4:2=2.
Ответ 2.
Задача 4. Основания трапеции равны 8 и 16, боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
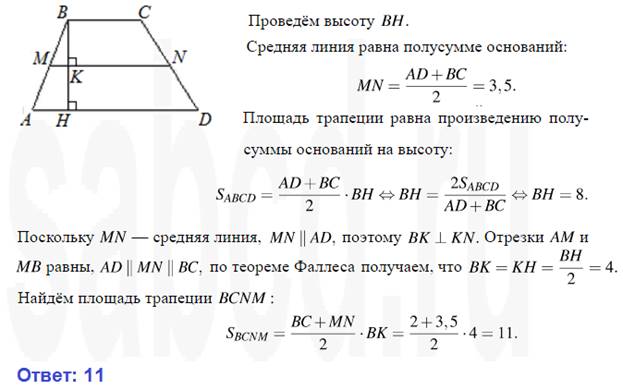
Решение. Пусть в трапеции на рисунке основания ВС=8, AD =16, боковая сторона АВ=6, а угол АВС равен 150 градусам. Мы знаем, что площадь трапеции равна произведению полусуммы оснований на высоту. Основания известны. Найдём высоту ВН. В прямоугольном треугольнике АВН угол АВН равен 150 – 90 =60 градусам. Значит угол ВАН равен 90 – 60 =30 градусам. А в прямоугольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Значит ВН=3.
Осталось вычислить площадь трапеции. Полусумма оснований равна (8+16):2=12. Площадь равна 12*3=36.
Ответ 36.
Задача 5. В прямоугольной трапеции АВС D с основаниями ВС и А D угол В AD прямой, АВ =3, ВС =CD =5. Найдите среднюю линию
трапеции.
Решение. Средняя линия трапеции равна полусумме оснований.В данной трапеции верхнее основание ВС равно 5, нижнее А D неизвестно. Из вершины С опустим высоту на нижнее основание. В получившемся прямоугольнике НВСК АН=ВС=5, СН=АВ=3. Треугольник Н DC прямоугольный. По теореме Пифагора квадрат катета Н D равен разности квадрата гипотенузы DC и квадрата катета СН. То есть Н D 2 = 65 –9 = 16. Н D = 4. Значит нижнее основание А D =АН+Н D =5+4=9. Средняя линия трапеции равна (5+9):2=7.
Ответ 7.
Задача 6. В прямоугольной трапеции основания равны 4 и 7, а один из углов равен 135°. Найдите меньшую боковую сторону.
Решение. Воспользуемся чертежом к предыдущей
задаче.В данной трапеции верхнее
основание ВС равно 4, нижнее А
D
=7. Угол ВС
D
равен 135 градусам. Из вершины С
опустим высоту на нижнее основание. Тогда Н
D
=7-4=3. В получившемся прямоугольном
треугольнике Н
DC
угол НС
D
равен 135-90=45 градусам. Значит и
угол Н
DC
тоже 45
градусов. Катеты СН= Н
D
=3.
Катеты СН= Н
D
=3.
Ответ 3.
Задачи для самостоятельного решения.
- ∠ BDA=40° и ∠ BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
- В трапеции ABCD известно, что AB =CD , ∠ BDA =45° и ∠ BDC =23°. Найдите угол ABD . Ответ дайте в градусах.
- В трапеции ABCD известно, что AB=CD, ∠ BDA=49° и ∠ BDC=31°. Найдите угол ABD. Ответ дайте в градусах.
- Основания равнобедренной трапеции равны 7 и 13, боковая сторона равна 5. Найдите высоту трапеции.
- Основания равнобедренной трапеции равны 11 и 21, боковая сторона равна 13. Найдите высоту трапеции.
- Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
- В равнобедренной трапеции одно из оснований равно 5, а другое — 9. Высота трапеции равна 6. Найдите тангенс острого угла трапеции.
- В прямоугольной трапеции АВС D с основаниями ВС и А D угол В AD прямой, АВ =8, ВС =CD =10.
 Найдите среднюю линию
трапеции.
Найдите среднюю линию
трапеции. - В прямоугольной трапеции АВС D с основаниями ВС и А D угол В AD прямой, АВ = 15 , ВС = CD = 17 . Найдите среднюю линию трапеции.
- В прямоугольной трапеции основания равны 3 и 5, а один из углов равен 135°. Найдите меньшую боковую сторону.
На рисунке A B C D — трапеция с AB||DC . Если /\ A E D подобен /\ B E C , докажите, что A D = B C .
RD SHARMA ENGLISH-TRIANGLES-Все вопросы
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Расшифровка
вопрос в том что на рисунке ABCD есть трапеция с ab параллельным dc если треугольник ABC подобен треугольнику BC то ad равен BC это наша диаграмма показывающая данный сценарий в треугольнике abc и треугольнике abc угол 1 равен углу , потому что они являются противоположными углами, угол 3 равен углу 4, они также являются противоположными углами, угол C равен углу abe, они являются противоположными углами по вертикали, поэтому на
a Критерий треугольника ABC подобен треугольнику ABC, в котором подразумевается, что bhai ab равен купить, а это подразумевает, что AC равен ab bi последний вызов, это уравнение номер один, теперь дано, что треугольник ABC подобен треугольнику ABC поэтому на AC равно 1 на 2 равно 1 на bc и ac номер вопроса 22 из уравнения 1 и 2
мы получаем би би равно, что подразумевает, что квадрат равен квадрату, а это означает, что ГБ равен к a теперь, помещая a b равно в нашем уравнении номер один, мы получаем a равно add, из чего следует, что ad by BC равно 1, что подразумевает, что a d равно BC, поэтому, наконец, доказано, что ad равно BC I надеюсь, вы хотите назначения спасибо
Похожие видео
На рисунке показано, что AB=BC
и AD=EC
. Докажите, что ABE≅CBD
Докажите, что ABE≅CBD
На рисунке показано, что AE=AD
и BD=СЕ.
Докажите, что AEB≅ADC
На рисунке ABCD
это
трапеция, в которой AB∣∣DC, DC
производится
палец на ноге
такой, что CE=AB,
докажите, что ar(ABD)=ar (BCE).
Конструкция: Нарисуйте ДМ
на бакалавриате
произведено
и BN⊥DC
1414820
Если A={a,b},B={c,d},C={d,e}, то {(a,c),(a,d)(a, д), (б, в), (б, г), (б, д)}=
8989256
Если A={a,b},B={c,d},C={d,e}, то: {(a,c),(a,d),(a,e), (b,c),(b,d),(b,e)} равно :
412659309
На рисунке дано, что AB=BC и AD=EC . Докажите, что ABE≅CBD
642564878
На рисунке показано, что AE=AD и BD=СЕ. Докажите, что △AEB≅△ADC
642564883
На рисунке DEAC и ДКэп. Докажите, что BEEC=BCCP
642565918
На рисунке DE∣∣AC и DF∣∣AE . Докажите, что EFBF=ECBE .
642565971
На рис.
4.31, если ADDC=BEEC
и ∠CDE=∠CED
, доказывать
что CAB
является
равнобедренный. (РИСУНОК)
(РИСУНОК)
642569340
В ABC, BD и СЕ являются высоты. Докажите, что АБР и АЭК являются похожий. CDB~BEC ?
642569400
На рисунке, если △ABE≅△ACD , доказывать что △ADE~△ABC .
642569411
На рисунке дано что AE=AD и BD=CE. Докажите, что AEB ≅ADC
642572010
На рисунке AC=AE, AB=AD и ∠BAD=∠EAC. Докажите, что BC=DE
642572021
На рисунке дано что AB=BC и AD=EC. Докажи это (i) АБЭ ≅ КБД (ii) BD=BE
642572055
ABCD — трапеция с параллельными сторонами AD и BC. E — точка на BC. Отношение площади трапеции ABCD к площади треугольника AED равно: E,BC पर एक बिंदु है। квадрат ABCD और треугольник AED के क्षेत्रफल का अनुपात क्या होगा?
ПУБЛИКАЦИЯ CHAMPION-2013 TIER-II PAPER(20)-УПРАЖНЕНИЕ
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки rukaavat ке!
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
На рис.4.123 ABCD — трапеция с AB||DC. Если дельта AED аналогична дельта BEC, докажите, что AD=BC .
174844
На рис. 4.116, АВСD это трапеция с ABDC . Если дирхам ОАЭ похож в БЭК , доказывать что AD=BC . (РИСУНОК)
1410184
समलम्ब ABCD की भुजा AD तथा BC समानान्तर हैंत ABCD तथा AED के क्षेत्रफल का अनुपात ज्ञात करें?
25789993
दी गई आकृति आकृति (चित्र 7,79) में, ABCD एक समलम्ब चतु выполнение है तथ तथ ab∣dc यदि △ aed तथ तथ सम सम सम है सिद सिद कीजिए कीजिए कि कि कि कि कि कि कि यदि यदि यदि यदि यदि यदि यदि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कि कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए कीजिए सिद कीजिए सिद सिद सिद सिद सिद सिद सिद सिद सिद सिदfrूप तो तो सिद. , где AD параллельно BC (см. рисунок). E — точка между A и D, где BE — высота ABCD, а E — середина AD.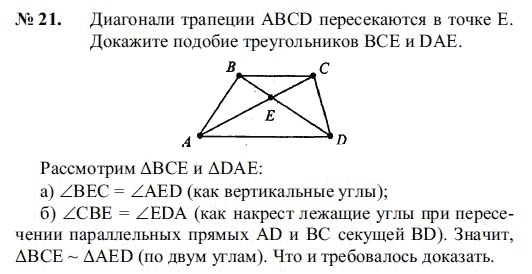 Чему равна площадь треугольника ABCD, если площадь треугольника ABE равна 12,5 квадратных дюймов?
Чему равна площадь треугольника ABCD, если площадь треугольника ABE равна 12,5 квадратных дюймов?
243136539
ABCD — трапеция с AB || ОКРУГ КОЛУМБИЯ. Диагонали AC и BD пересекаются в точке E . Если ΔAED~ΔBEC. Докажите, что AD = BC.
402411230
В трапеции ABCD параллель AB параллельна CD. BD перпендикулярно AD. АС перпендикулярен ВС. Если ad = bc = 15cmandab = 25 см, то площадь трапеции:
449930428
ABCD ఒక సమలంబ చతుర్భుజం (ట్రెపీజియం) లో ab∣dc రెండు కర్ణాలు ac మరియు bd లు e వద్ద ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ఖండించుకుంటాయి ΔAED మరియు ΔBEC సరూపాలు అయిన AD = BC అని చూపుము.
469254059
ABCD ট্রাপিজিয়ামের AD∣BC এবং ϪBC = ↑BCD, প্রমাণ করো যে ABCD একটি ট্রাপিজিয়াম ট্রাপিজিয়াম |
6428886410
ABCD एक चक्रीय समलम्ब चतुर्भुज है जिससे ad ДО Н.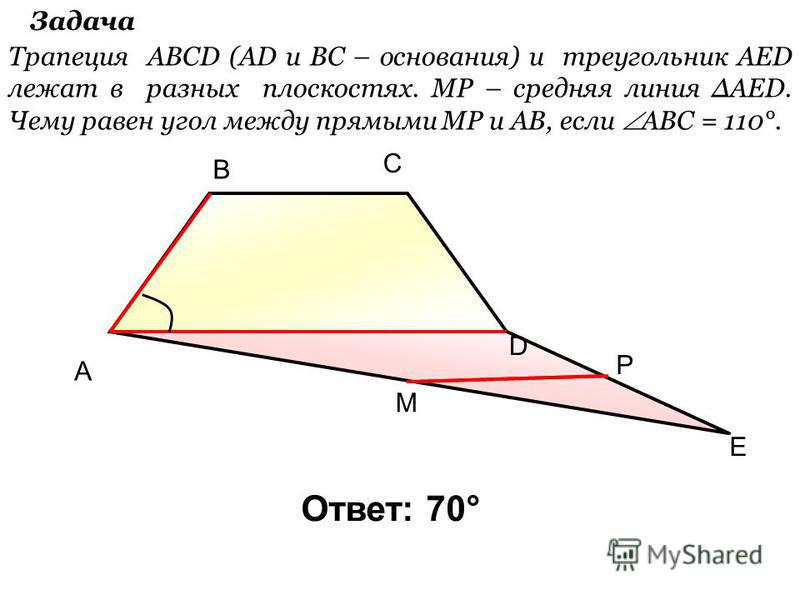 Э. AD = 5см, ВС = 9см. Если площадь ABCD 35 кв.см, то CD равна:
Э. AD = 5см, ВС = 9см. Если площадь ABCD 35 кв.см, то CD равна:
643373056
В трапеции ABCD, если AD/BC, то она представлена ……….
644203441
В △ABC ,D и E точки на сторонах AB и AC соответственно такие, что DE || ДО Н.Э. Если ad /bd = 3/4, то соотношение площади трапеции декабря к области △ ABC:
त्रिभुज ABC में, D तथा e भुजा ab और ac पर स्थित ऐसे बिंदु कि de || до н.э. और AD/BD = 3/4 है | समलम्ब decb के क्षेत्रफल और त्रिभुज abc के क्षेत्रफल में अनुपात ज्ञात करें।।।
645734196
В треугольнике ABC точки D и E лежат на сторонах AB и AC соответственно так, что DE || BC и AD/BD =3/4. Отношение площади △ABC к площади трапеции DECB равно:
त्रिभुज ABC में,D और E क्रमशः
भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्र फल
अनुपात ज्ञात करें |
645734204
В треугольнике ABC точки D и E лежат на сторонах AB и AC соответственно так, что DE || BC и AD/BD = 5/6.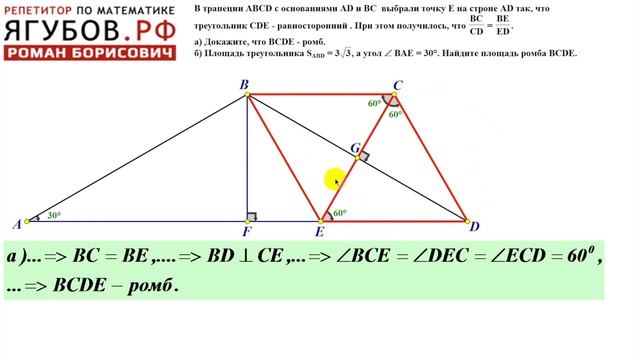

 Найдите среднюю линию
трапеции.
Найдите среднюю линию
трапеции.
Leave A Comment