Дан правильный тетраэдр DABC с ребром a. При симметрии относительно плоскости ABC точка D перешла в точку D1. Найти DD1. — Знания.site
Ответы 1
Всё решаем по формуле…
Знаешь ответ? Добавь его сюда!
Последние вопросы
Математика
22 часов назад
24.02.2022?
Ділянку прямокутної форми що має розміри 250м на 80м, засіяли кукурудзою. Скільки зерна було використано для цього, якщо на 10000м потрібно 18 кг?Математика
1 день назад
32) найдите область определение функции z = (1/x) + (1/y)Математика
1 день назад
33) найдите область определение функции z = (y — 1) / (x² + y²)1 день назад
31) найдите область определение функции z = 1 / (x-y)Геометрия
1 день назад
100 баллов таму кто поможетАнглийский язык
1 день назад
Subjunctive Mood
Test
I.
 Choose the right form:
Choose the right form:1. Jack doesn’t speak English. If he (spoke/ had spoken

II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.
- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал

Английский язык
1 день назад
Subjunctive Mood
Test
I. Choose the right form:
1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon
 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment.II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.

- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.
Литература
1 день назад
А где почему это напряжоный момент
Биология
1 день назад
У голонасінних рослин уперше з’являєтся:
Математика
1 день назад
Математика третий класс запиши все возможные значения длины и ширины по известному периметру прямоугольника периметр 98 м 120 м 140
Алгебра
2 дня назад
Решите графически системы уравнений (выражая у через х) 1 система {х+2у=6 х-4у=0} 2 система{3у-х=3 х-4у=1}
Физика
2 дня назад
Електричний нагрівник за 7 хв доводить до кипіння 10 кг води, початкова температура якої дорівнює 20 °С.
 Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.Физика
2 дня назад
Тело движется вдоль оси Ох. График зависимости проекции его скорости Vх от времени t изображён на рисунке. Найди путь S, пройденный телом за рассмотренный промежуток времени. Результат вырази в метрах, округлив до целого числа.
Українська мова
2 дня назад
Допоможіть будь ласка! Написати твір — роздум за алгоритмом.
Українська мова
2 дня назад
ДОПОМОЖІТЬ БУДЬ ЛАСКА! НАПИСАТИ ТВІР — РОЗДУМ ЗА АЛГОРИТМОМ ( ПРИКЛАД З ЛІТЕРАТУРИ).
 — Так, у творі… — Не можна не згадати… — Говорячи про…, не можна не згадати… — Яскравим прикладом цього може слугувати ситуація, описана в … — Проілюструвати наведене вище твердження може ситуація, зображена…
— Так, у творі… — Не можна не згадати… — Говорячи про…, не можна не згадати… — Яскравим прикладом цього може слугувати ситуація, описана в … — Проілюструвати наведене вище твердження може ситуація, зображена…
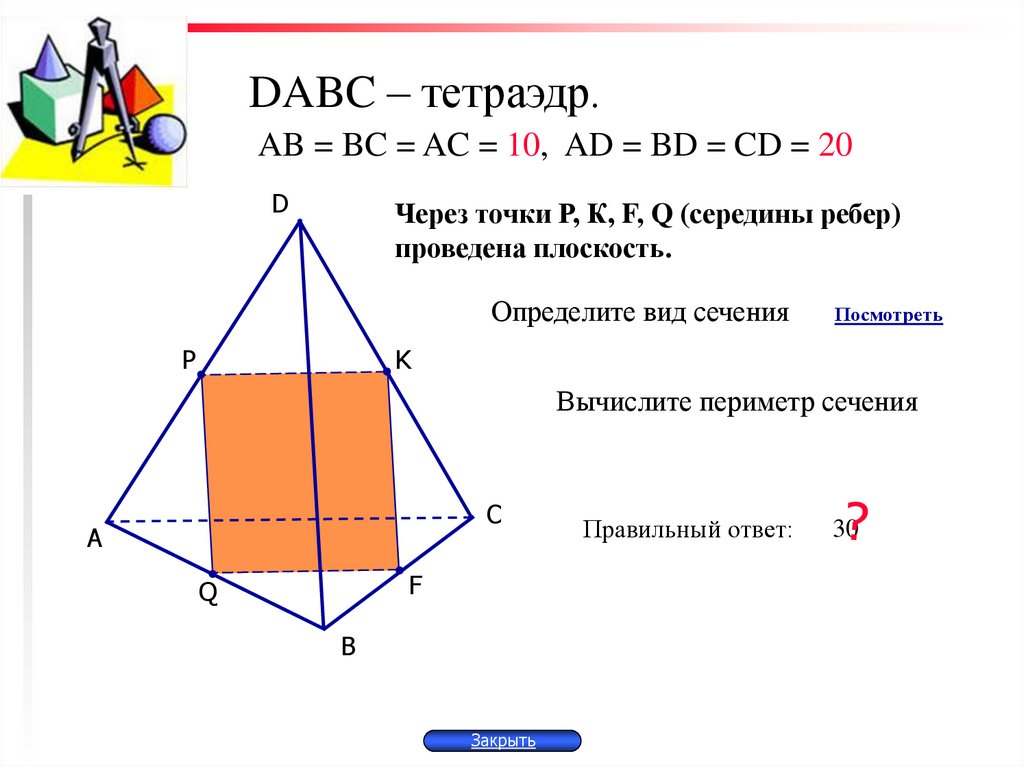
Контрольная работа № 1
Административная контрольная работа по геометрии
Вариант 1
| |=10, | | = 2, ( ) = 60°. Найти:
а) • ;
б) значение n, при котором векторы и {3; n; 3} перпендикулярны.
Найдите косинус угла между векторами и , если А (3, 4, 1), В (6, 6, 2), С (4, 2, 3) и D (3, 4, 6).
Дан правильный тетраэдр DABC с ребром 3. При симметрии относительно плоскости АВС точка D перешла в точку D1. Найдите DD1.
Административная контрольная работа по геометрии
Вариант 2
| |=5, | | = 3, ( ) = 45°.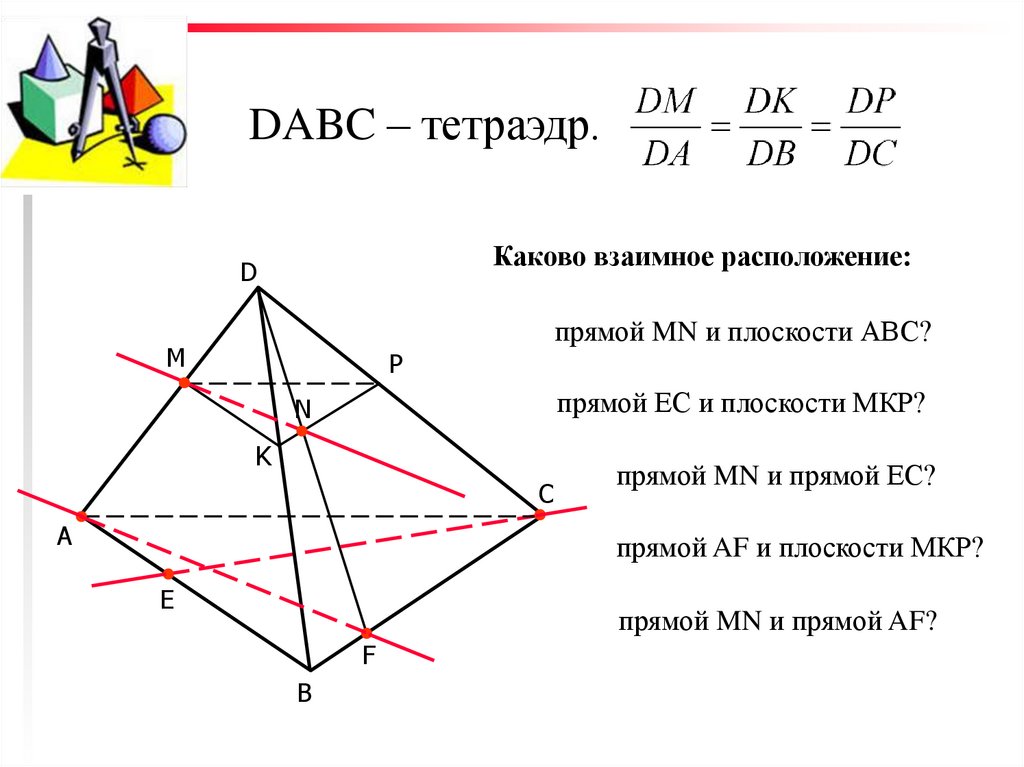 Найдите:
Найдите:
а) • ;
б) значение n, при котором векторы и {-3, 8, n} перпендикулярны.
Найдите угол между векторами и , если А(1, 2,1), В(4,-4,1), С(2, 1, 0) и D(-1, 2, 0).
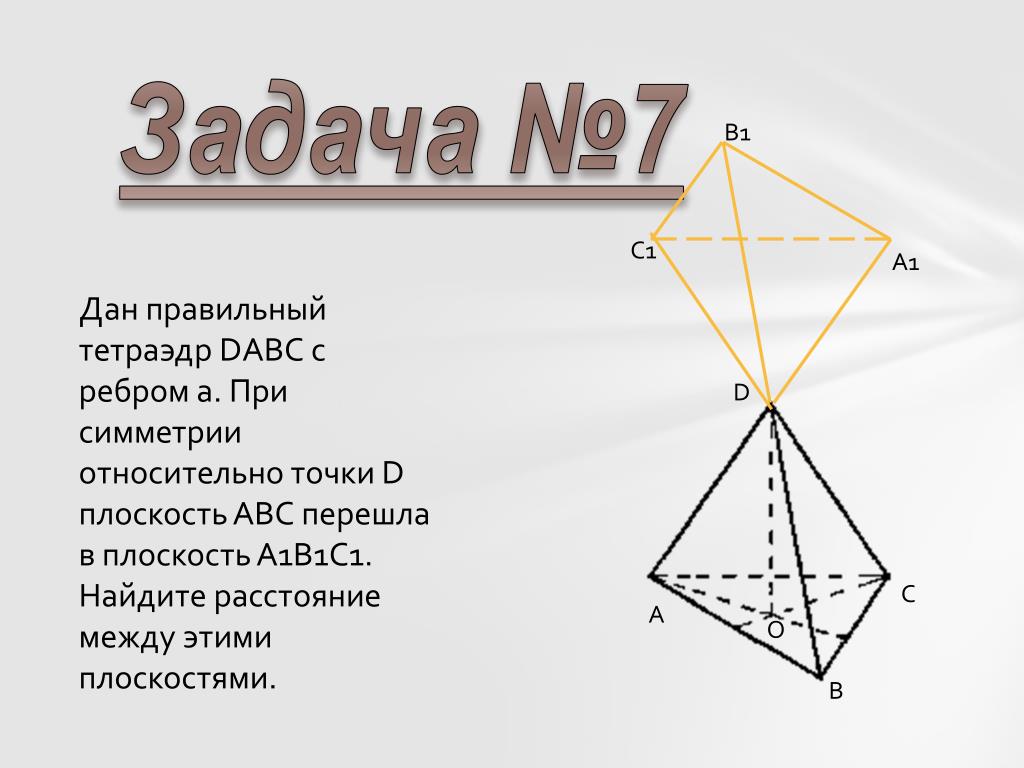
Дан правильный тетраэдр DABC с ребром 1. При симметрии относительно точки D плоскость АВС перешла в плоскость А1В1С1. Найдите расстояние между этими плоскостями.
Административная контрольная работа по геометрии
Вариант 1
| |=10, | | = 2, ( ) = 60°. Найти:
а) • ;
б) значение n, при котором векторы и {3; n; 3} перпендикулярны.
2. Найдите косинус угла между векторами и , если А(3,4,1), В (6, 6, 2), С (4, 2, 3) и D (3, 4, 6).
3. Дан правильный тетраэдр DABC с ребром 3. При симметрии относительно плоскости АВС точка D перешла в точку D1.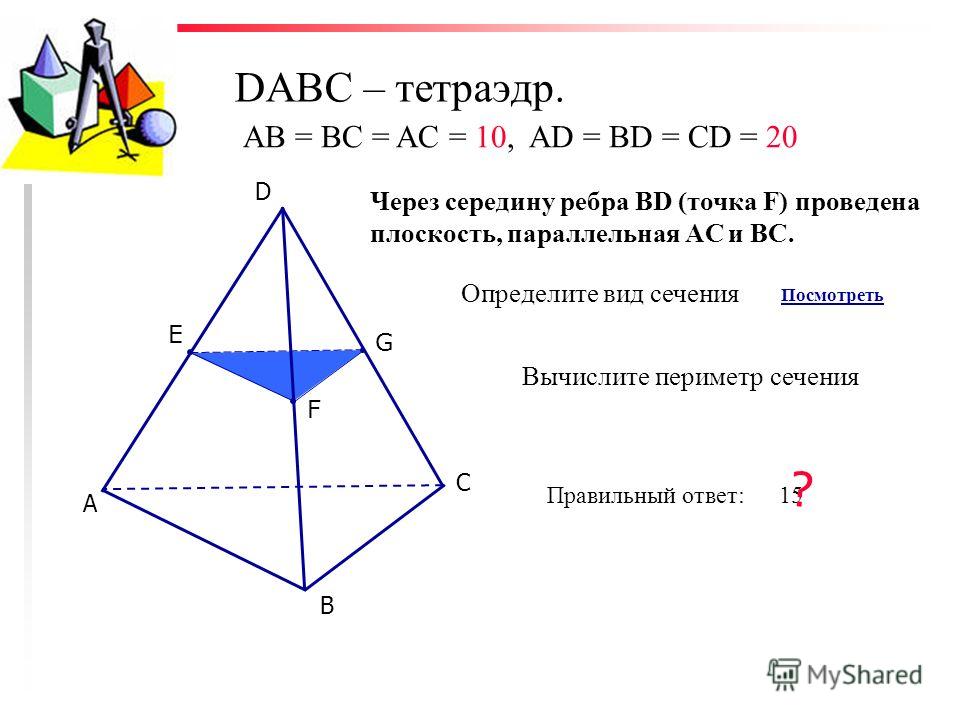 Найдите DD1.
Найдите DD1.
Административная контрольная работа по геометрии
Вариант 2
1. | |=5, | | = 3, ( ) = 45°. Найдите:
а) • ;
б) значение n, при котором векторы и {-3, 8, n} перпендикулярны.
Найдите угол между векторами и , если А(1,2,1),
В (4, — 4,1), С(2, 1, 0) и D(-1, 2, 0).
3. Дан правильный тетраэдр DABC с ребром 1. При симметрии относительно точки D плоскость АВС перешла в плоскость А1В1С1. Найдите расстояние между этими плоскостями.
Административная контрольная работа по геометрии
Вариант 1
Вычислите косинус угла между векторами и , если = + 2 – , = 2 – , где , ,
В кубе ABCDA1B1C1D1 с ребром равным 1 найдите с помощью векторов угол между прямыми CD1 и ВМ, где M – середина ребра DD1.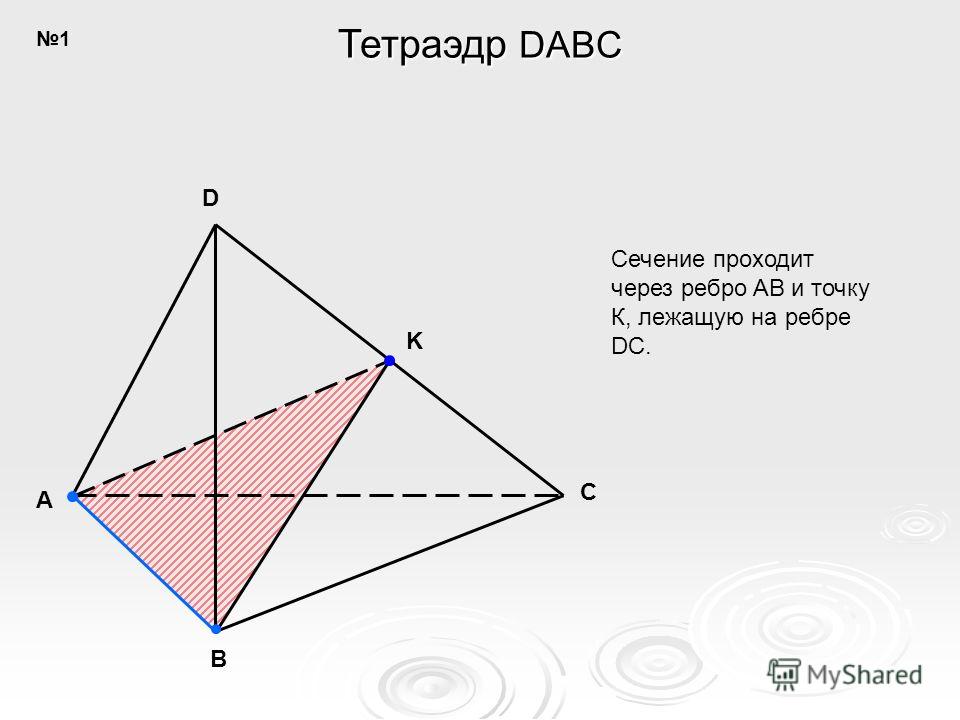
В кубе ABCDA1B1C1D1 с ребром а при симметрии относительно прямой CC1 точка A1 перешла в точку A2. Найдите длину вектора .
Административная контрольная работа по геометрии
Вариант 2
Вычислите косинус угла между векторами и , если = 2 – + , = – 2, где , ,
В кубе ABCDA1B1C1D1 с ребром равным 1 найдите с помощью векторов угол между прямыми AС и DM, где M – середина ребра AA1.
В куб ABCDA1B1C1D1 с ребром а при симметрии относительно прямой A1D1 точка B1 перешла в точку B2. Найдите длину вектора 2.
Административная контрольная работа по геометрии
Вариант 1
Вычислите косинус угла между векторами и , если = + 2 – , = 2 – , где , ,
В кубе ABCDA1B1C1D1 с ребром равным 1 найдите с помощью векторов угол между прямыми CD1 и ВМ, где M – середина ребра DD1.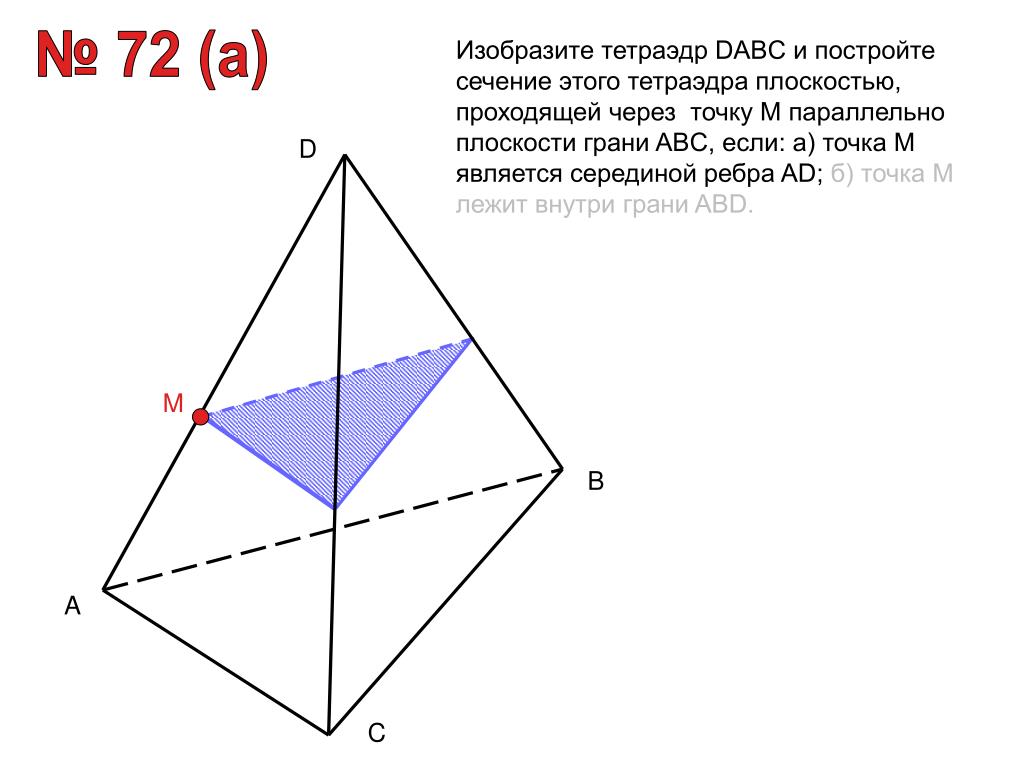
В кубе ABCDA1B1C1D1 с ребром а при симметрии относительно прямой CC1 точка A1 перешла в точку A2. Найдите длину вектора .
Административная контрольная работа по геометрии
Вариант 2
Вычислите косинус угла между векторами и , если = 2 – + , = – 2, где , ,
В кубе ABCDA1B1C1D1 с ребром равным 1 найдите с помощью векторов угол между прямыми AС и DM, где M – середина ребра AA1.
В куб ABCDA1B1C1D1 с ребром а при симметрии относительно прямой A1D1 точка B1 перешла в точку B2. Найдите длину вектора 2.
Административная контрольная работа по геометрии
Вариант 1
Даны векторы и , при чем =6, =3, ( ) =120 .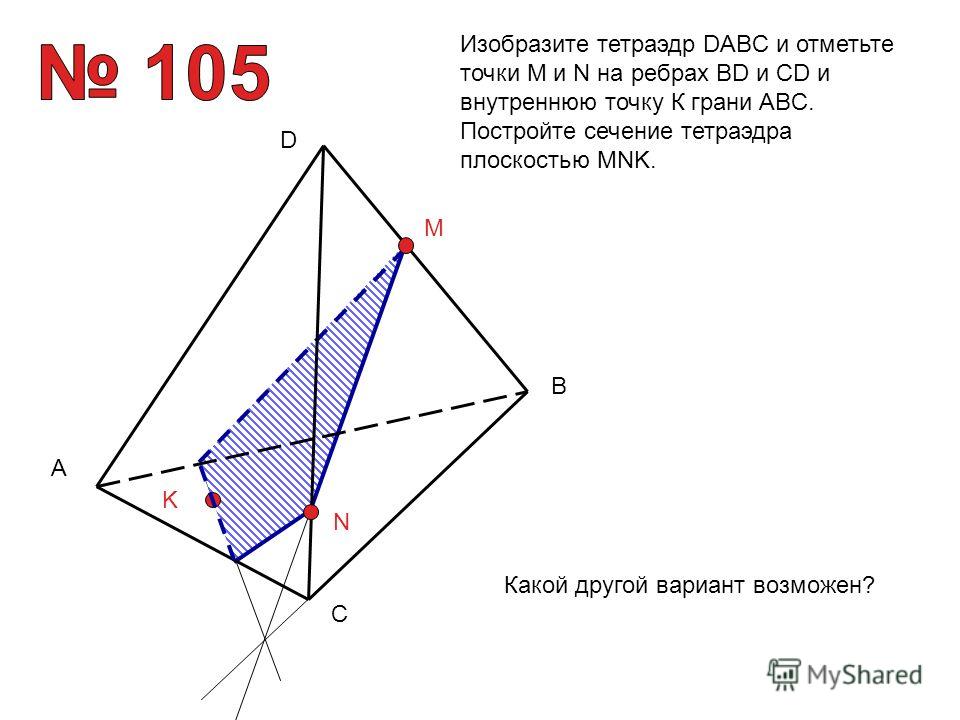 Найдите .
Найдите .
В тетраэдре DABC ребра DA, DB и DC взаимно перпендикулярны и равны a. Используя векторы, найдите угол между плоскостями DAB и ABC.
Основанием прямой призмы ABCDA1B1C1D1 является квадрат ABCD со стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1, причём BE = 1. Найдите угол между плоскостью сечения A1C1E и плоскостью ABC.
Административная контрольная работа по геометрии
Вариант 2
Даны векторы и , при чем =7, = , ( ) =135 . Найдите .
В тетраэдре DABC ребра DA, DB и DC взаимно перпендикулярны и равны a. Используя векторы, найдите угол между прямой DA и плоскостью ABC.
В правильной треугольной призме ABCA1B1C1 стороны основания равны 4, боковые рёбра равны 7, точка D — середина ребра BB1. Найдите угол между плоскостями ABC и ADC1.
Найдите угол между плоскостями ABC и ADC1.
Административная контрольная работа по геометрии
Вариант 1
Даны векторы и , при чем =6, =3, ( ) =120 . Найдите .
В тетраэдре DABC ребра DA, DB и DC взаимно перпендикулярны и равны a. Используя векторы, найдите угол между плоскостями DAB и ABC.
Основанием прямой призмы ABCDA1B1C1D1 является квадрат ABCD со стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1, причём BE = 1. Найдите угол между плоскостью сечения A1C1E и плоскостью ABC.
Административная контрольная работа по геометрии
Вариант 2
Даны векторы и , при чем =7, = , ( ) =135 .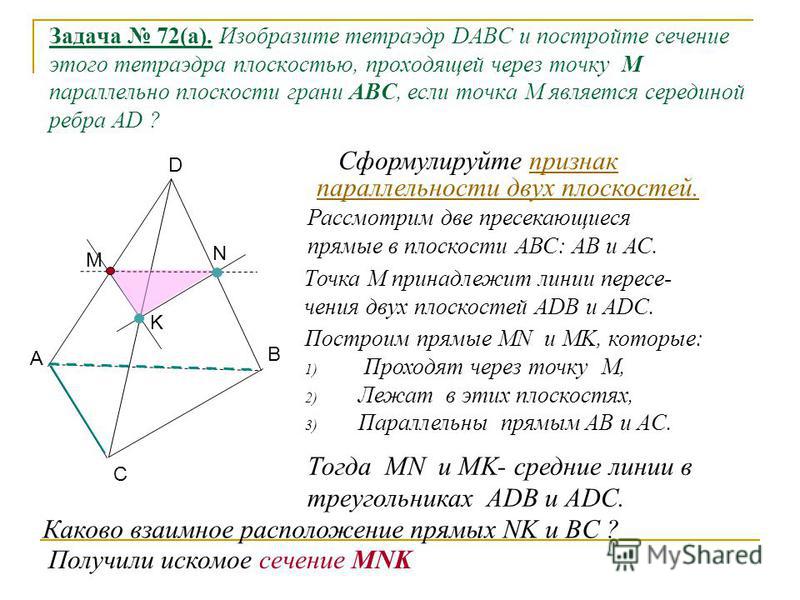 Найдите .
Найдите .
В тетраэдре DABC ребра DA, DB и DC взаимно перпендикулярны и равны a. Используя векторы, найдите угол между прямой DA и плоскостью ABC.
В правильной треугольной призме ABCA1B1C1 стороны основания равны 4, боковые рёбра равны 7, точка D — середина ребра BB1. Найдите угол между плоскостями ABC и ADC1.
Назначение 7
Назначение 7Упражнение 12 (выполняется в пятницу, 12 ноября)
Модели должны быть тщательно изготовлены из манильской папки других картон, на котором можно писать.
E 12.1 — Вложение тетраэдра в куб.
- Постройте куб со стороной 3 дюйма и одной стороной, открывающейся в виде коробка.
- Начертите на кубе сегменты, соединяющие 4 вершины, так, чтобы сегменты, которые вы рисуете, образуют правильный тетраэдр.
- Постройте из картона правильный тетраэдр, точно вписывающийся внутрь
поле, соответствующее сегментам, которые вы нарисовали.

E 12.2 — Поперечные сечения
Используйте те же модели, но другой цвет ручки или карандаша. сегменты выше.
- Нарисуйте сегменты, чтобы показать плоское поперечное сечение куба, правильный шестигранник.
- Нарисуйте сегменты, чтобы показать плоское поперечное сечение правильного тетраэдра то есть квадрат.
Задание 7. Понедельник, 15 ноября. (75 баллов)
Чтение
Начните читать Брауна. Читать с начала через введение для линий отражений и вращений.
Вам настоятельно рекомендуется сделать модели, чтобы помочь с раздел о многогранниках.
7.1 Тетраэдр (20 точек)
Плоскость симметрии правильного тетраэдра делит многогранник на две конгруэнтные части.
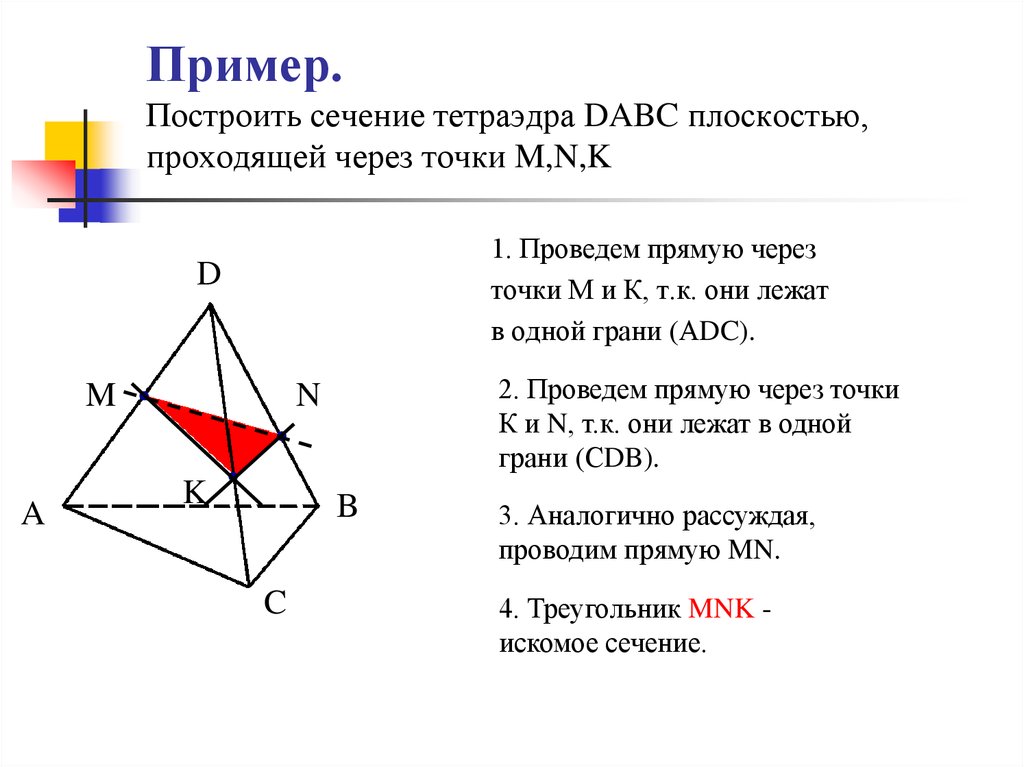
7.2 Куб (15 точек)
7.3 Подобные треугольники с общий угол. (15 баллов)
Предположим, у нас есть две линии, AB и AC. Пусть X — точка на прямой AB и Y быть точкой на линии AC.- Предположим, что треугольник ABC подобен треугольнику AXY.
 Покажите, что существует
постоянная k, так что AX/AB = k и AY/AC = k. Рассмотрите возможность того, что
отношения могут быть как отрицательными, так и положительными.
Покажите, что существует
постоянная k, так что AX/AB = k и AY/AC = k. Рассмотрите возможность того, что
отношения могут быть как отрицательными, так и положительными. - Покажите, что в этом случае прямая BC параллельна прямой XY. Мы называем эта фигура (параллельная) фигура Фалеса.
- Предположим, что треугольник ABC подобен треугольнику AYX. Покажите, что существует постоянная k, так что AX*AB = AY*AC = k. Рассмотрим возможность того, что k может быть отрицательным, если A находится между B и X и т. д.
- Покажите, что в этом случае прямая BC параллельна отражению прямой XY в биссектрисе угла BAC. Мы можем назвать этот случай «антипараллельный» или «антифалесовский».
7.4 Отражения двойной линии в параллельные линии. (15 баллов)
Пусть на плоскости (x,y) линия m задана уравнением x = a. Также пусть
линия n имеет уравнение x = b, а линия p имеет уравнение x = c. Пусть М. Н,
P обозначают преобразования отражения по m, n и p
соответственно.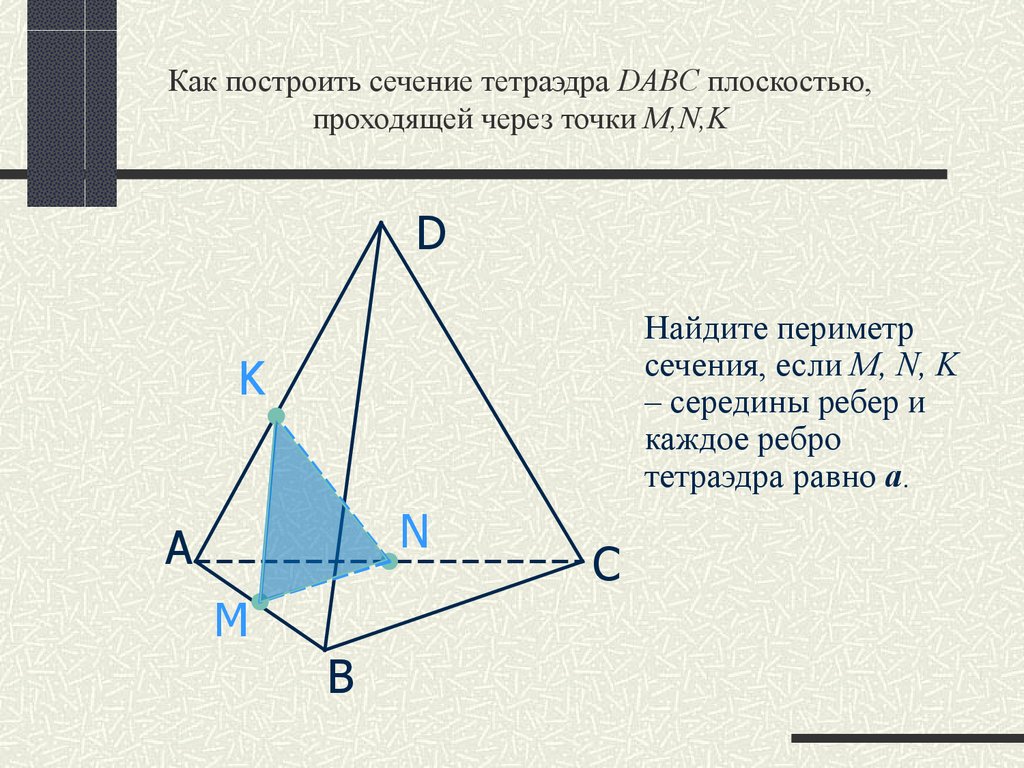
- Если Q = (x,y), найдите формулу Q’ = отражение Q в линия м.
- Продолжая с Q’, найдите формулу для Q» = отражение Q’ в строке м. Тогда Q» = N(Q’) = NM(Q), так что теперь у вас есть формула для НМ. Используйте эту формулу, чтобы сделать вывод, что NM является переводом. Что вектор перевода этого перевода?
- Используйте аналогичные рассуждения, чтобы найти формулу для MN. Что вектор перевода для этого перевода? Что является обратным MN?
- Теперь пусть Q»’ будет отражением Q» в p, так что Q»’ = PNM(Q). Напишите формулу для PNM(Q), когда Q=(x,y). Что это за изометрия? (А именно из списка видов изометрий мы знаем, что это такое?)
7.5 Отражения двойной линии в пересекающиеся линии. (10 баллов)
Учитывая, что m = линия AB и n = линия AC, отразите точку Q в m, чтобы получить Q’. Затем отразите Q’ в n, чтобы получить Q». Таким образом, Q» = NM(Q).
- Докажите, что угол QAQ» одинаков при любом значении Q (линии остаются фиксированными).
 и вдвое больше угла BAC. (Подсказка: с этим было бы сложно
координаты, поэтому попробуйте использовать треугольники. Что за треугольник QAQ’,
Q’AQ» и т.д.?
и вдвое больше угла BAC. (Подсказка: с этим было бы сложно
координаты, поэтому попробуйте использовать треугольники. Что за треугольник QAQ’,
Q’AQ» и т.д.?
Назад на домашнюю страницу Math 444
Длина ребра правильного тетраэдра DABC равна «a». Точки E и F взяты на ребрах AD и BD соответственно так, что E делит −−→DA и F делит −−→BD в отношении 2:1 каждое. Найдите площадь треугольника CEF.
Вопрос
Обновлено: 26/04/2023
Текст Решение
Ответ
Правильный ответ: 5a212√3 кв.ед.
ДВИЖЕНИЕ-ВЕКТОР -УПРАЖНЕНИЕ — 3
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Видео по теме
Длина ребра правильного тетраэдра D-ABC равна ‘a’. Точки E и F взяты на ребрах AD и BD соответственно так, что E делит vec [DA] и F делит vec [BD] в отношении 2:1 каждая.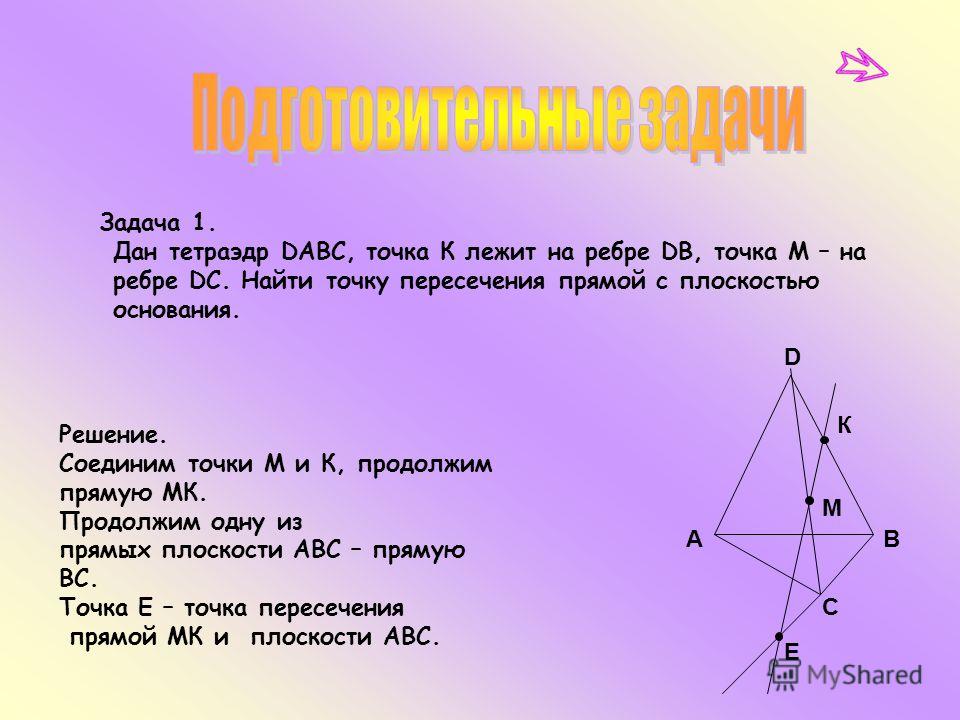 Затем найдите площадь треугольника CEF.
Затем найдите площадь треугольника CEF.
Если АВСD является четырехугольником и EandF являются серединами AC и BD соответственно, докажите, что →AB+→AD +→ЦБ +→CD =4 →ЭФ.
Если D, E, F являются серединами сторон BC, CA и АБ соответственно треугольника ABC, запишите значение →AD+→BE+→CF.
1486871
ΔABC में, बिंदु D तथा E, भुजा AB तथा AC पर इस प ्रकार है की DE∣∣BC तथा DE, ΔABC क्षेत्रफल को दो बराबर भागो में बाटता है। AD तथा BD का अनुपात ज्ञात करे?
23273321
Если A, B, C, D — любые четыре точки, а E и F — средние точки AC и BD соответственно, то A→B+C→B+C→D+−−→AD равно
53805696
Если D, E, F являются соответственно серединами AB, AC и BC соответственно в ΔABC, то −−→BE+−−→AF=
53805771
ABCD एक स मांतर चतुर्भुज है। E और F क्रमशः CD और DA के मध्य बिंदु हैं −−→BE और −−→BF को −−→BA और −−→BC
−−→ БЭ+—→БФ=32 −−→BD
67607813
ABCD एक समान्तर चतुर्भुज है। E तथा F क्रमशः DA और CD के मध्य बिन्दु है। −−→BE तथा −−→BF को −−→BA तथा −−→BC के पदों में व्यक्त कीजिये तथा सिद्ध कीजिये कि −−→BE+−−→BF=32−−→BD
92142151
Длина ребра правильного тетраэдра ABCD равна «a».

 Choose the right form:
Choose the right form:
 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment.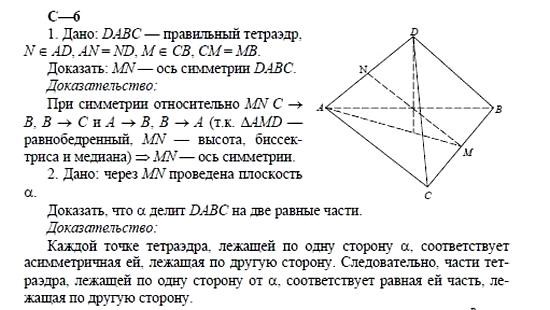
 Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %. — Так, у творі… — Не можна не згадати… — Говорячи про…, не можна не згадати… — Яскравим прикладом цього може слугувати ситуація, описана в … — Проілюструвати наведене вище твердження може ситуація, зображена…
— Так, у творі… — Не можна не згадати… — Говорячи про…, не можна не згадати… — Яскравим прикладом цього може слугувати ситуація, описана в … — Проілюструвати наведене вище твердження може ситуація, зображена…
 Покажите, что существует
постоянная k, так что AX/AB = k и AY/AC = k. Рассмотрите возможность того, что
отношения могут быть как отрицательными, так и положительными.
Покажите, что существует
постоянная k, так что AX/AB = k и AY/AC = k. Рассмотрите возможность того, что
отношения могут быть как отрицательными, так и положительными. и вдвое больше угла BAC. (Подсказка: с этим было бы сложно
координаты, поэтому попробуйте использовать треугольники. Что за треугольник QAQ’,
Q’AQ» и т.д.?
и вдвое больше угла BAC. (Подсказка: с этим было бы сложно
координаты, поэтому попробуйте использовать треугольники. Что за треугольник QAQ’,
Q’AQ» и т.д.?
Leave A Comment