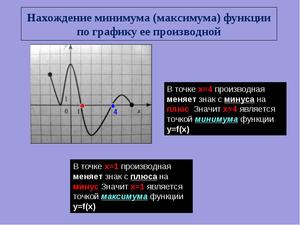
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки \(-13\), \(-11\), \(-9\),\(-7\) и \(3\). Количество точек экстремума функции – \(5\).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).
.
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).
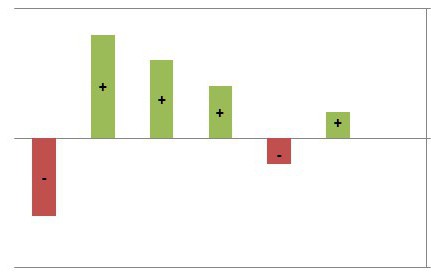
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
Начнем с \(-13\): до \(-13\) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что \(-13\) – точка максимума.
\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.
\(- 9\): функция возрастает, а потом убывает – максимум.
\(-7\): минимум.
\(3\): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции \(f'(x)\).
- Найдите корни уравнения \(f'(x)=0\).
- Нарисуйте ось \(x\) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью \(f'(x)\), а под осью \(f(x)\).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если \(f’(x)\) изменила знак с «\(+\)» на «\(-\)», то \(x_1\) – точка максимума;
— если \(f’(x)\) изменила знак с «\(-\)» на «\(+\)», то \(x_3\) – точка минимума;
— если \(f’(x)\) не изменила знак, то \(x_2\) – может быть точкой перегиба.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:
\(15x^4-60x^2=0\) \(|:15\)
\(x^4-4x^2=0\)
\(x^2 (x^2-4)=0\)
\(x=0\) \(x^2-4=0\)
\(x=±2\)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является \(-2\).
Ответ. \(-2\).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Исследование графика функции. Минимум и максимум
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Значения функции и точки максимума и минимума
Значения функции и точки максимума и минимума
 Наибольшее значение функции
Наибольшее значение функции
Наменьшее значение функции
Точки max
Точки min
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Найти точку максимума / минимума
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
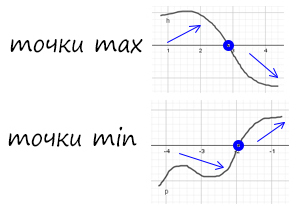
Задания с ЕГЭ:
Найдите точку максимума функции
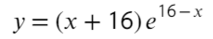
- Берем производную:
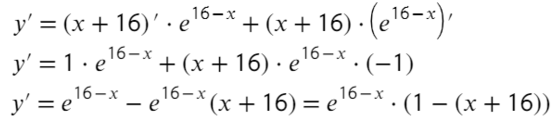
- Приравняем ее к нулю:

- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):
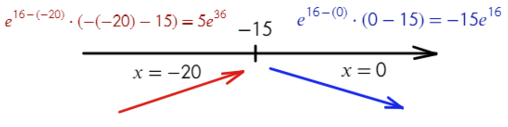
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15
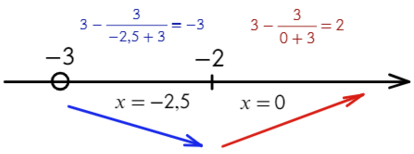
Найдите точку минимума функции
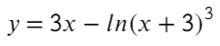
- Преобразуем и возьмем производную:
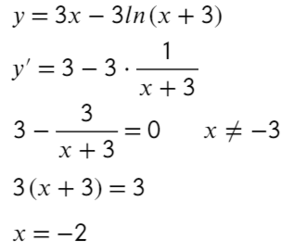
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]
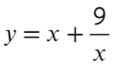
- Преобразуем и возьмем производную:

- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
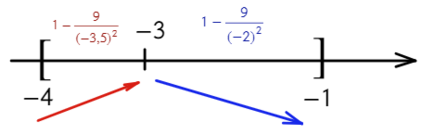
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:

Ответ: −6
Найдите наибольшее значение функции на отрезке [0; 1,5π]
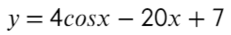
- Берем производную:

- Находим, чему равняется sin(x):

- Но такое невозможно! Sin(x)…

- Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:
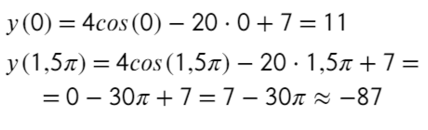
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
Будь в курсе новых статеек, видео и легкого математического юмора.
Максимальное и минимальное значения функций на интервале.
Доброго времени суток всем моим уважаемым читателям!
В этой статье мы попробуем научиться определять максимальное и минимальное значения различных функций, простых и посложнее, находить точки экстремумов, определять, является ли экстремум минимумом или максимумом функции, и даже отличать перегиб функции от экстремума.
Действовать мы будем так:
1. Определим производную функции.
2. Приравняем производную к нулю, чтобы определить, имеет ли функция экстремумы (если полученное уравнение имеет корни). Определим, принадлежат ли данные экстремумы заданному промежутку.
3. Если функция имеет экстремум на заданном промежутке, определим, максимум ли это или минимум.
4. Если функция не имеет экстремума (нет корней у уравнения, полученного путем приравнивания производной к нулю), определяем знак производной. Это покажет нам, является ли функция возрастающей или убывающей. Далее действуем по условию задачи: если функция возрастает, то максимальное значение справа, а минимальное – слева. Если убывает – то наоборот. Решение задач поможет нам все разложить по полочкам, и с помощью картинок мы постараемся не оставить непонятных мест в решении подобных задач.
Задача 1. Необходимо определить наибольшее значение функции:
Действуем по алгоритму: сначала определяем производную. Здесь мы имеем сумму функций, поэтому определяем производную от каждой в отдельности и складываем, после чего приравняем производную к нулю:

Решаем полученное уравнение. Если корни будут – значит, возможно, экстремумы есть (точка, где производная равна нулю, может быть и не экстремумом, а точкой перегиба).
Видим – корень есть:
В этой точке наша функция имеет экстремум. Важно, что эта точка принадлежит заданному интервалу. Выясним, максимум это или минимум.Для этого нужно определить знак производной в окрестности этой точки, то есть справа и слева от нее. Например, здесь можно взять точку – она будет располагаться слева, и точку – она будет справа. Тогда:

Понятно, что функция имеет наибольшее значение в точке максимума.Найдем это значение так: подставим найденную точку экстремума в уравнение функции:

Ответ: наибольшее значение функции на данном интервале равно 10.
2.Найти наименьшее значение функции на заданном интервале:
Точно так же, как и в первый раз, берем производную и приравниваем к нулю:
Уже видно, что это уравнение будет иметь корни:
В точке функция имеет экстремум. Максимум это или минимум? Найдем значение производной справа и слева от точки . Снова возьмем точку – она будет располагаться слева, и точку – она будет справа. Тогда:
Наименьшее значение функция принимает в точке минимума, найдем его:
Ответ: наименьшее значение функции на данном интервале равно 1.
Решим следующую задачу:
3. Определить наибольшее значение функции на отрезке:
Сначала, как всегда, производная:
Это как раз случай, когда экстремумов у функции на данном интервале нет: у уравнения выше нет корней. Это означает, что функция монотонная: либо убывает, либо возрастает. Мы можем определить это по знаку производной: если производная положительна – функция возрастает, если отрицательна – убывает. Зачем нам знать, убывает или возрастает функция? Дело в том, что если функция возрастает, то ее значение будет всегда больше на правом конце интервала, а если убывает – на левом.

У нас, какой бы угол мы ни взяли, косинус его не превышает 1, поэтому производная положительна, а значит, функция растет. Таким образом, своего наибольшего значения она достигнет в точке 0:
Ответ: наибольшее значение функции на данном интервале – 3.
4. Определить наименьшее значение функции на отрезке:

Определим производную и приравняем к нулю:

Уже видно, что функция монотонная (нет корней у получившегося уравнения):

Так как производная отрицательна, то делаем вывод, что функция убывает. Тогда ее наименьшее значение – на правом конце отрезка, то есть в 0:

Ответ: наименьшее значение функции на данном отрезке – 19.
5. Найдите наименьшее значение функции на отрезке:
Берем производную, приравниваем к нулю и решаем полученное уравнение:

Казалось бы – уравнение имеет корни, значит, функция будет иметь экстремум на данном отрезке (второй корень данному отрезку не принадлежит, поэтому не рассмотрен). Определим, максимум это или минимум. Значение 1 для косинуса – максимальное, то есть, какую точку ни возьми около нуля – значение косинуса – абсциссы – будет меньше, чем в точке ноль. Однако! Производная в точке ноль знака не меняет! Она положительна в окрестности нуля, и значит, функция возрастает как до нуля, так и после. Значит, функция в точке ноль имеет не экстремум, а перегиб.
Поэтому, чтобы определить наименьшее значение, надо брать левый конец отрезка и считать значение функции в этой точке. По счастливой случайности, это точка ноль. Однако, это могла бы быть и другая точка, отличная от нуля, и тогда можно было бы ошибиться, посчитав точку ноль экстремумом и определив значение функции в ней. Итак, значение функции:
Ответ: наименьшее значение функции на данном отрезке – 8.
6. Найдите точку максимума функции:

Алгоритм выполнения таких заданий тот же самый. Первым делом – производная. Здесь имеем произведение двух функций, поэтому брать производную будем по правилу взятия производной от произведения функций:

Далее приравняем полученное выражение к нулю. Понятно, что экспонента всегда неотрицательна, в какую степень ни возведи, поэтому корень “спрятан” во втором сомножителе:

Убедимся, что данный экстремум – максимум. Действительно, в этой точке производная знак меняет, и меняет с положительного на отрицательный, то есть до этой точки функция возрастает, а после – убывает.
 Таким образом, найденная нами точка – максимум. Ответ: точка х=-7.
Таким образом, найденная нами точка – максимум. Ответ: точка х=-7.
7. Найдите наименьшее значение функции на отрезке:

Нам предстоит, как обычно, найти производную данной функции, а это функция сложная: под знаком логарифма выражение в степени (причем степень – четная! Если выносить ее за знак логарифма, то нужно ставить знак модуля, чтобы не сузить область определения функции). Поэтому, чтобы не раскрывать модуль, можем воспользоваться правилом взятия производной от сложной функции:


Полученное выражение приравняем к нулю:

Отметим, что в точке (-3) производная не определена. Тем не менее в этой точке производная поменяет знак. Точка (-2) – минимум функции, так как в ней производная меняет знак с отрицательного на положительный. Значит, в этой точке у функции минимальное значение. Найдем его:

Ответ: наименьшее значение функции на данном отрезке – 8.
8. Найдите точку максимума функции:

Определяем производную сложной функции. Найденную производную приравняем к нулю:


Имеем две точки экстремумов. Одна из них – максимум, другая – минимум.
 Максимум функция имеет в точке 8.
Максимум функция имеет в точке 8.

Ответ: точка х=8.
9. Найдите точку минимума функции:

Определяем производную произведения, кроме того, экспонента является сложной функцией (здесь производная степени, в которую возведена экспонента, равна 1). Найденную производную приравняем к нулю:


Точкой минимума функции является точка 11. В этом можно убедиться: производная в ней меняет знак с минуса на плюс.
Ответ: точка х=11.
10. Найдите точки минимума и максимума функции:

Определяем производную сложной функции. Найденную производную приравняем к нулю:


Производная этой функции меняет знак с отрицательного на положительный в точке 2 (минимум), и с положительного на отрицательный – в точке 17 (максимум).
11. Найти наименьшее значение функции на отрезке:

Обратим внимание на то, что выражение, стоящее под знаком логарифма, больше нуля. Тогда Найдем производную и приравняем к нулю:

В точке 2 производная знак меняет, значит, это экстремум. Знак она меняет с отрицательного на положительный, поэтому данная точка – точка минимума. В ней функция принимает наименьшее значение:

Ответ: наименьшее значение функции на данном отрезке – 8.
12. Найти наименьшее значение функции на отрезке:

Найдем производную и приравняем к нулю:

Можем отметить, что область определения функции – положительные значения х (так как выражение под знаком логарифма больше ноля), и что производная в точке 0 не определена.Получим квадратное уравнение, у которого сумма коэффициентов равна 0 (a+b+c=0). В таком уравнении один корень равен 1, а второй c/a:

Заданному отрезку принадлежит лишь одна точка – 1. Производная здесь меняет знак с отрицательного на положительный, и значит, это минимум. Определим значение функции в этой точке:

13. Найдите наименьшее значение функции на отрезке:

Заметим, что функция не определена в точке 0.
Берем производную дроби:

Приравниваем производную к нулю и отыскиваем корни:
Один из корней нас не интересует, так как промежутку не принадлежит, а во второй точке производная меняет знак с отрицательного на положительный.То есть функция имеет минимум в данной точке. Определим ее минимальное значение:

Надеюсь, эта статья и, главное, приведенные примеры помогут вам справиться с заданием B15. Необходимо только помнить правила взятия производной, и особенно от сложных функций.
Как найти экстремум (точки минимума и максимума) функции
Простой алгоритм нахождения экстремумов. Учимся находить с bugaga.net.ru.- Находим производную функции
- Приравниваем эту производную к нулю
- Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)
- Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум
- Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.
Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.
Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.
https://bugaga.net.ru/ege/math/ekstremum.html bugaga.net.ru
Рассмотрим примерНаходим производную и приравниваем её к нулю:
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2 , а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума.
Смотрите также:
Еще больше материалов для подготовки к ЕГЭ
Как найти точки минимума и максимума функции: особенности, способы и примеры
Функция и исследование ее особенностей занимает одно из ключевых глав в современной математике. Главная составляющая любой функции — это графики, изображающие не только ее свойства, но также и параметры производной данной функции. Давайте разберемся в этой непростой теме. Итак, как лучше искать точки максимума и минимума функции?
Функция: определение
Любая переменная, которая каким-то образом зависит от значений другой величины, может называться функцией. Например, функция f(x2) является квадратичной и определяет значения для всего множества х. Допустим, что х = 9, тогда значение нашей функции будет равно 92= 81.
Функции бывают самых разных видов: логические, векторные, логарифмические, тригонометрические, числовые и другие. Их изучением занимались такие выдающиеся умы, как Лакруа, Лагранж, Лейбниц и Бернулли. Их труды служат оплотом в современных способах изучения функций. Перед тем как найти точки минимума, очень важно понять сам смысл функции и ее производной.
Производная и ее роль
Все функции находятся в зависимости от их переменных величин, а это значит, что они могут в любой момент изменить свое значение. На графике это будет изображаться как кривая, которая то опускается, то поднимается по оси ординат (это все множество чисел «y» по вертикали графика). Так вот определение точки максимума и минимума функции как раз связано с этими «колебаниями». Объясним, в чем эта взаимосвязь.
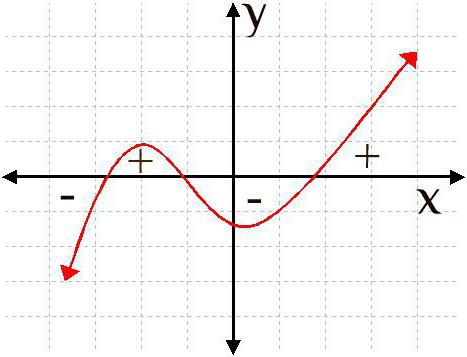
Производная любой функции изображается на графике с целью изучить ее основные характеристики и вычислить, как быстро изменяется функция (т.е. меняет свое значение в зависимости от переменной «x»). В тот момент, когда функция увеличивается, график ее производной будет также возрастать, но в любую секунду функция может начать уменьшаться, и тогда график производной будет убывать. Те точки, в которых производная переходит со знака минуса на плюс, называются точками минимума. Для того чтобы знать, как найти точки минимума, следует лучше разобраться с понятием производной.
Как вычислять производную?
Определение и вычисление производной функции подразумевает под собой несколько понятий из дифференциального исчисления. Вообще, само определение производной можно выразить следующим образом: это та величина, которая показывает скорость изменения функции.

Математический способ ее определения для многих учеников кажется сложным, однако на самом деле все гораздо проще. Необходимо лишь следовать стандартному плану нахождения производной любой функции. Ниже описано, как можно найти точку минимума функции, не применяя правила дифференцирования и не заучивая таблицу производных.
- Вычислить производную функции можно с помощью графика. Для этого необходимо изобразить саму функцию, затем взять на ней одну точку (точка А на рис.) Вертикально вниз провести линию к оси абсцисс (точка х0), а в точке А провести касательную к графику функции. Ось абсцисс и касательная образуют некий угол а. Для вычисления значения того, насколько быстро возрастает функция, необходимо вычислить тангенс этого угла а.
- Получается, что тангенс угла между касательной и направлением оси х является производной функции на маленьком участке с точкой А. Данный метод считается геометрическим способом определения производной.
Способы исследования функции
В школьной программе математики возможно нахождение точки минимума функции двумя способами. Первый метод с помощью графика мы уже разобрали, а как же определить численное значение производной? Для этого потребуется выучить несколько формул, которые описывают свойства производной и помогают преобразовать переменные величины типа «х» в числа. Следующий метод является универсальным, поэтому его можно применять практически ко всем видам функций (как к геометрическим, так и логарифмическим).
- Необходимо приравнять функцию к функции производной, а затем упростить выражение, используя правила дифференцирования.
- В некоторых случаях, когда дана функция, в которой переменная «х» стоит в делителе, необходимо определить область допустимых значений, исключив из нее точку «0» (по простой причине того, что в математике ни в коем случае нельзя делить на ноль).
- После этого следует преобразовать изначальный вид функции в простое уравнение, приравняв все выражение к нулю. Например, если функция выглядела так: f(x) = 2x3+38x, то по правилам дифференцирования ее производная равна f'(x) = 3x2+1. Тогда преобразуем это выражение в уравнение следующего вида: 3x2+1 = 0.
- После решения уравнения и нахождения точек «х», следует изобразить их на оси абсцисс и определить, является ли производная в этих участках между отмеченными точками положительной или отрицательной. После обозначения станет ясно, в какой точке функция начинает убывать, то есть меняет знак с минуса на противоположный. Именно таким способом можно найти как точки минимума, так и максимума.
Правила дифференцирования
Самая основная составляющая в изучении функции и ее производной — это знание правил дифференцирования. Только с их помощью можно преобразовывать громоздкие выражения и большие сложные функции. Давайте ознакомимся с ними, их достаточно много, но все они весьма просты благодаря закономерным свойствам как степенных, так и логарифмических функций.
- Производная любой константы равна нулю (f(х) = 0). То есть производная f(х) = x5+ х — 160 примет такой вид: f’ (х) = 5x4+1.
- Производная суммы двух слагаемых: (f+w)’ = f’w + fw’.
- Производная логарифмической функции: (logad)’ = d/ln a*d. Эта формула применима ко всем видам логарифмов.
- Производная степени: (xn)’= n*xn-1. Например,(9x2)’ = 9*2x = 18x.
- Производная синусоидальной функции: (sin a)’ = cos a. Если sin угла а равен 0,5, то ее производная равна √3/2.
Точки экстремума
Мы уже разобрали, как найти точки минимума, однако существует понятие и точек максимума функции. Если минимум обозначает те точки, в которых функция переходит со знака минуса на плюс, то точками максимума являются те точки на оси абсцисс, на которых производная функции меняется с плюса на противоположный — минус.
Находить точки максимума можно по вышеописанному способу, только следует учесть, что они обозначают те участки, на которых функция начинает убывать, то есть производная будет меньше нуля.
В математике принято обобщать оба понятия, заменяя их словосочетанием «точки экстремумов». Когда в задании просят определить эти точки, это значит, что необходимо вычислить производную данной функции и найти точки минимума и максимума.
Как найти точку максимума функции?
 Поиск точки максимума и минимума функции — довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом «экстремум» подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.
Поиск точки максимума и минимума функции — довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом «экстремум» подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.
Глобальный и локальный максимум
Максимум бывает локальным или глобальным. Точка локального максимума — это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.
Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.
Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:
- экстремума, если она попадает в указанный отрезок,
- разрыва,
- ограничивающей заданный отрезок.
Исследование
Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):
 Найти область допустимых аргументов и пересечения этой области с областью исследования.
Найти область допустимых аргументов и пересечения этой области с областью исследования.- Выявить асимптоты. Они равны пределу при стремлении аргумента к точкам разрыва.
- Определить первую производную и вычислить экстремальные точки и выяснить поведение функции в окрестности этих точек.
- Рассчитать значение f(x) в точках, ограничивающих область исследования.
- Сравнить экстремум со значением функции в точках разрыва и на концах интервала. Определить среди них наибольшее.
Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.
Область допустимых аргументов
Область допустимых аргументов — это те x, при подстановке которых в f(x) она не престаёт существовать.Область допустимых аргументов ещё называют областью определения. Например, y = x^2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.
Асимптоты
 Асимптота — это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.
Асимптота — это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.
Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.
Производная и экстремумы
 Производная — это предел изменения функции при стремящемся к нулю изменении аргумента. Что это значит? Возьмём небольшой участок из области допустимых аргументов и посмотрим как изменится здесь f(x), а потом уменьшим этот участок до бесконечно малого размера, в этом случае f(x) станет изменяться так же, как и некая более простая функция, которая именуется производной.
Производная — это предел изменения функции при стремящемся к нулю изменении аргумента. Что это значит? Возьмём небольшой участок из области допустимых аргументов и посмотрим как изменится здесь f(x), а потом уменьшим этот участок до бесконечно малого размера, в этом случае f(x) станет изменяться так же, как и некая более простая функция, которая именуется производной.
Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.
1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент «0», и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной.
После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).
Концы интервала и сравнение результатов
При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.
Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.
Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.
Видео
Как найти минимальные и максимальные точки на графике
- Education
- Графические калькуляторы
- Как найти минимальные и максимальные точки на графике
Джефф МакКалла, К. С. Эдвардс
Определение точки максимума или минимума на графике калькулятора TI-84 Plus имеет множество полезных приложений. Например, точка максимума на графике функции прибыли говорит вам не только о максимальной прибыли (координата y ), но и о том, сколько единиц продукции (координата x ) компания должна произвести, чтобы получить эту прибыль. ,Чтобы найти минимальное или максимальное значение функции, выполните следующие действия:
Постройте график функции в окне просмотра, которое содержит минимальное и / или максимальное значения функции.
Нажмите [2nd] [TRACE], чтобы войти в меню расчетов.
Нажмите [3], чтобы найти минимум, или нажмите [4], чтобы найти максимум.
При необходимости несколько раз нажмите клавиши со стрелками вверх и вниз, пока соответствующая функция не появится в рамке в верхней части экрана.
Установите левую границу минимальной или максимальной точки.
Для этого с помощью клавиш со стрелками влево и вправо поместите курсор на график немного левее точки минимума или максимума, а затем нажмите [ENTER]. На экране появляется Левый Ограниченный индикатор (пунктирная линия с треугольным индикатором, показанная на первом экране).
Установите правую границу нуля.
Для этого с помощью клавиш со стрелками влево и вправо поместите курсор на график немного правее точки минимума или максимума, а затем нажмите [ENTER].На экране появится индикатор Right Bound (крайняя правая пунктирная линия с треугольным индикатором на втором экране).
Сообщите калькулятору, где, по вашему мнению, находится минимум или максимум.
Для этого используйте клавиши со стрелками влево и вправо, чтобы поместить курсор на график как можно ближе к положению точки минимума или максимума, а затем нажмите [ENTER]. Координаты минимальной или максимальной точки отображаются в рамке в нижней части экрана (как показано на третьем экране).
Об авторе книги
Джефф МакКалла — учитель математики в епископальной школе Святой Марии в Мемфисе, штат Теннесси. Он стал соучредителем группы TI-Nspire SuperUser и получил президентскую награду за выдающиеся достижения в преподавании естественных наук и математики. C.C. Эдвардс — педагог, который провел множество семинаров по использованию калькуляторов TI.
,Максимальные и минимальные значения — подход к исчислению
10
Поворотные точки графика
МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) на больше , чем любое значение, непосредственно предшествующее или последующее.
Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше , чем любое значение, непосредственно предшествующее или последующее.
Опять же, другие значения функции могут быть меньше. С таким пониманием мы откажемся от термина «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производной при оценке на уровне a или b — равен 0.
f ‘ ( x ) = 0.
Более того, в точках непосредственно от слева от максимума — в точке C — наклон касательной положительный: f ‘ ( x )> 0.В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
Другими словами, максимальное значение f ‘ ( x ) меняет знак с + на -.
Как минимум, f ‘ ( x ) меняет знак с — на +. Мы видим, что в точках E и F .
Также можно заметить, что максимум на A график вогнутый вниз.(Тема 14 Precalculus.) Хотя как минимум, на B , он вогнутый вверх.
Значение x , при котором функция имеет максимум или минимум, называется критическим значением. На рисунке —
— критические значения x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x .Критические значения — если таковые имеются — будут для решений от до f ‘ ( x ) = 0.
Пример 1. Пусть f ( x ) = x 2 — 6 x + 5.
Есть ли критические значения — какие-то поворотные моменты? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x — 6 = 0 подразумевает x = 3. (Урок 9 алгебры)
x = 3 — единственное критическое значение. Это x — точка поворота. Чтобы определить y -coordinate, оцените f при этом критическом значении — оцените f (3):
| f ( x ) | = | x 2 — 6 x + 5 |
| ф (3) | = | 3 2 — 6 · 3 + 5 |
| = | −4. | |
Крайнее значение -4. Чтобы увидеть, является ли он максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — парабола, и мы видим, что точка поворота минимальна.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).
Но мы не всегда сможем посмотреть на график.Алгебраическим условием минимума является то, что f ‘ ( x ) меняет знак с — на +. Мы видим это в точках E , B , F выше. Величина наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9), которая представляет собой скорость изменения наклона, равна положительному значению .
Опять же, вот f ( x ):
| f ( x ) | = | x 2 — 6 x + 5. |
| f ‘ ( x ) | = | 2 x — 6. |
| f ‘ ( x ) | = | 2. |
f » оценивается при критическом значении 3 — f » (3) = 2 — положительно.Это алгебраически говорит нам, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение x = a , если f ‘ ( a ) = 0,
и f’ ‘ ( a ) = положительное число.
Функция имеет максимальное значение при x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = отрицательное число.
В случае максимума наклон касательной составляет с уменьшением, — от положительного к отрицательному. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3.
Есть ли крайние значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
| Решение . f ‘ ( x ) = 6 x 2 — 18 x + 12 | = | 6 ( x 2 — 3 x + 2) |
| = | 6 ( x — 1) ( x — 2) | |
| = | 0 | |
означает:
x = 1 или x = 2.
(Урок алгебры 37.)
Это критические значения. Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.
| f ‘ ( x ) | = | 6 x 2 — 18 x + 12. |
| f ‘ ( x ) | = | 12 x — 18. |
| f ‘ (1) | = | 12 — 18 = −6. |
Вторая производная отрицательна. Следовательно, функция имеет максимум x = 1.
Чтобы найти y -coördinate — крайнее значение — на этом максимуме мы оцениваем f (1):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3 |
| ф (1) | = | 2–9 + 12–3 |
| = | 2. | |
Максимум приходится на точку (1, 2).
Затем, x = 2 определяет максимум или минимум?
| f ‘ ( x ) | = | 12 900 10 x — 18. |
| f ‘ (2) | = | 24 — 18 = 6. |
Вторая производная положительна. Поэтому функция имеет минимум x = 2.
Чтобы найти y -coördinate — экстремальное значение — при этом минимуме, мы оцениваем f (2):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3. |
| ф (2) | = | 16–36 + 24–3 |
| = | 1. | |
Минимум приходится на точку (2, 1).
Вот собственно график f ( x ):
Решения для f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . y » = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 , а не максимум или минимум ,
Другой пример: y = sin x . Решения для y » = 0 — это умножения π, которые являются точками перегиба.
Задача 1. Найти координаты вершины параболы,
y = x 2 — 8 x + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему самостоятельно!
y ‘ = 2 x — 8 = 0.
Это подразумевает x = 4. Это x -кординация вершины. Чтобы найти y -coördinate, оцените y при x = 4:
y = 4 2 — 8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2. Проверьте каждую функцию на наличие максимумов и минимумов.
a) y = x 3 — 3 x 2 + 2.
y ‘ = 3 x 2 — 6 x = 3 x ( x -2) = 0 означает
x = 0 или x = 2.
y ‘ ( x ) = 6 x — 6.
у » (0) = −6.
Вторая производная отрицательна. Это означает, что существует максимум x = 0. Это максимальное значение составляет
.y (0) = 2.
Далее,
y ‘ (2) = 12 — 6 = 6.
Вторая производная положительна. Это означает, что существует минимум x = 2.Это минимальное значение
.y (2) = 2 3 -3 · 2 2 + 2 = 8-12 + 2 = −2.
б) y = −2 x 3 — 3 x 2 + 12 x + 10.
При x = 1 получается максимум y = 17.
При x = −2 минимум y = −10.
c) y = 2 x 3 + 3 x 2 + 12 x — 4.
Поскольку f ‘ ( x ) = 0 не имеет реальных решений, нет никаких экстремальных значений.
d) x = 3 x 4 — 4 x 3 — 12 x 2 + 2.
При x = 0 максимальное значение y = 2.
При x = −1 минимум y = −3.
При x = 2 минимум y = −30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2020 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
,
Нахождение максимумов и минимумов с использованием производных
Где функция в верхней или нижней точке? Исчисление может помочь!
Максимум — это высшая точка, а минимум — это низкая точка:
В плавно меняющейся функции максимум или минимум всегда там, где функция выравнивает (за исключением седловой точки ).
Где расплющивается? Где наклон равен нулю .
Где нулевой наклон? Производная говорит нам!
Давайте сразу рассмотрим пример:
Пример: в воздух подброшен мяч.Его высота в любой момент времени t определяется как:
ч = 3 + 14т — 5т 2
Какова его максимальная высота?
Используя производные, мы можем найти наклон этой функции:
h = 0 + 14-5 (2т)
= 14-10т
(См. Ниже этот пример, чтобы узнать, как мы нашли эту производную.)
Теперь найдите, когда наклон равен нулю :
14 — 10 т = 0
10т = 14
t = 14/10 = 1.4
Наклон равен нулю при t = 1,4 секунды
А высота на тот момент:
h = 3 + 14 × 1,4 — 5 × 1,4 2
ч = 3 + 19,6 — 9,8 = 12,8
А так:
Максимальная высота 12,8 м (при t = 1,4 с)
Краткое руководство по производным финансовым инструментам
Производная определяет наклон функции.
В предыдущем примере мы взяли это:
ч = 3 + 14т — 5т 2
и придумал эту производную:
h = 0 + 14-5 (2т)
= 14-10т
Что сообщает нам наклон функции в любое время t
Мы использовали эти производные правила:
- Наклон постоянного значения (например, 3) составляет 0
- Наклон линии , такой как 2x, равен 2, поэтому 14t имеет наклон 14
- Квадрат Функция, такая как t 2 , имеет наклон 2t, поэтому 5t 2 имеет наклон 5 (2t)
- И затем мы сложили их: 0 + 14 — 5 (2t)
Как узнать, что это максимум (или минимум)?
Мы видели это на графике! Но иначе… деривативы снова приходят на помощь.
Возьмем производную от наклона (вторая производная исходной функции):
Производная от 14 до 10t равна −10
Это означает, что наклон постоянно уменьшается (-10): при движении слева направо наклон сначала положительный (функция возрастает), затем проходит через ноль (плоская точка), а затем наклон становится отрицательным (функция падает). :
Уклон, который становится меньше (и идет через 0), означает максимум.
Это называется тестом второй производной
На графике выше я показал наклон до и после, но на практике мы проводим тест в точке, где наклон равен нулю :
Тест второй производной
Когда наклон функции равен нулю при x , а вторая производная при x составляет:
- меньше 0, это локальный максимум
- больше 0, это локальный минимум
- равно 0, тогда тест не пройден (хотя могут быть и другие способы выяснить)
«Вторая производная: меньше 0 — максимум, больше 0 — минимум»
Пример: Найдите максимумы и минимумы для:
y = 5x 3 + 2x 2 — 3x
Производная (наклон):
y = 15x 2 + 4x — 3
Квадратичная с нулями в:
Могут ли они быть максимальными или минимальными? (Не смотрите пока на график!)
Вторая производная: y » = 30x + 4
При x = −3/5:
у » = 30 (−3/5) + 4 = −14
меньше 0, поэтому −3/5 — это локальный максимум
При x = +1/3:
г ‘= 30 (+1/3) + 4 = +14
больше 0, поэтому +1/3 — это локальный минимум
(Теперь вы можете посмотреть на график.)
слов
Высшая точка называется максимумом (во множественном числе максимума ).
Нижняя точка называется минимум (во множественном числе минимум ).
Общее слово для максимума или минимума — экстремум ( экстремумов во множественном числе).
Мы говорим локальный максимум (или минимум), когда могут быть более высокие (или более низкие) точки в другом месте, но не поблизости.
Еще один пример
Пример: Найдите максимумы и минимумы для:
y = x 3 — 6x 2 + 12x — 5
Производная:
y = 3x 2 — 12x + 12
Которая квадратична с одним нулем при x = 2
Это максимум или минимум?
Вторая производная: y » = 6x — 12
При x = 2:
у » = 6 (2) — 12 = 0
это 0, поэтому тест не проходит
И вот почему:
Это седловина … наклон действительно становится нулевым, но он не является ни максимальным, ни минимальным.
Должен быть дифференцируемым
И еще важный технический момент:
Функция должна быть дифференцируемой (производная должна существовать в каждой точке своего домена).
Пример: Как насчет функции f (x) = | x | (абсолютная величина) ?
| | x | выглядит так: |
При x = 0 он имеет очень резкое изменение!
Фактически, это не дифференцируемое место (как показано на дифференцируемой странице).
Итак, мы не можем использовать этот метод для функции абсолютного значения.
Функция также должна быть непрерывной, но любая дифференцируемая функция также является непрерывной, поэтому об этом не нужно беспокоиться.
,Исчисление III — относительные минимумы и максимумы
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Вектор градиента, касательные плоскости и нормальные линии
- Абсолютные минимумы и максимумы
- Разделы
- Частные производные
- Несколько интегралов
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Параболы
- Отборочные

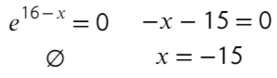
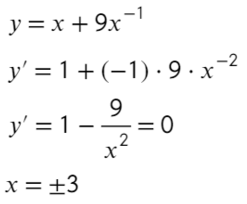
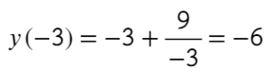
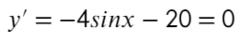
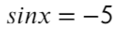
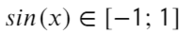
 Найти область допустимых аргументов и пересечения этой области с областью исследования.
Найти область допустимых аргументов и пересечения этой области с областью исследования.
Leave A Comment