Точка минимума функции как найти по уравнению: Как найти экстремум (точки минимума и максимума) функции

Найдите точку минимума функции

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2014-07-13

В этой статье мы рассмотрим несколько примеров на нахождение точек максимума (минимума) иррациональной функции. Алгоритм решения был уже неоднократно изложен в статьях с подобными заданиями, посмотрите его в одной из прошлых статей. 

У вас может возникнуть вопрос – а чем рациональная функция отличается от иррациональной? У иррациональной функции, говоря простыми словами, аргумент находится под корнем, или степень у него это дробное число (несокращаемая дробь). Другой вопрос —  в чём отличия в нахождении их точек максимума (минимума)? Да ни в чём. 

Сам принцип и алгоритм решения заданий на определения точек максимума (минимума) един. Просто для удобства и систематизации материала я разбил его на несколько статей – отдельно рассмотрел рациональные, логарифмические, тригонометрические и прочие, осталось ещё несколько примеров на нахождение наибольшего (наименьшего) значения иррациональной функции на отрезке. Их мы тоже рассмотрим.

Традиционно рекомендую ознакомится со статьёй «Исследование функций. Это нужно знать!», там же имеется таблица производных элементарных функций.

Давайте здесь подробно опишу нахождение производной, когда у аргумента имеется степень, во всех примерах ниже это используется.

Сама формула:

То есть, если у нас аргумент стоит в некоторой степени и требуется найти производную, то мы записывает это значение степени, умножаем его на аргумент, а его степень будет на единицу меньше, например:

Если же степень дробное число, то всё тоже самое:

Следующий момент! Конечно же, вы должны помнить свойства корней и степеней, а именно:

То есть, если в примере вы увидите, например, выражение (или подобное с корнем):

То при решении, чтобы вычислить производную, его необходимо представить как х в степени, будет так:

Остальные табличные производные и правила дифференцирования вы должны знать!!!

Правила  дифференцирования:

Рассмотрим примеры:

77451. Найдите точку минимума функции y = x^3/2 – 3x + 1

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 4, производная меняет знак с отрицательного на положительный, это означает, что данная точка является точкой минимума.

Ответ: 4

 

77455. Найдите точку максимума функции

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 4, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.

Ответ: 4

 

77457. Найдите точку максимума функции

Найдём производную заданной функции:

Найдем нули производной:

Решая уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 9, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.

Ответ: 9

 

77461. Найдите точку минимума функции

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 4, производная меняет знак с отрицательного на положительный, это означает, что данная точка является точкой минимума.

Ответ: 4

 

77463. Найдите точку максимума функции 

Посмотреть решение

На этом все. Успеха вам!

С уважением, Александр Крутиких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Функции MAX MIN | ЕГЭ-№11

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Значения функции и точки максимума и минимума

Назад к списку

Значения функции и точки максимума и минимума

Наибольшее значение функции 

Наменьшее значение функции 

Точки max 

Точки min

 

---

Как говорил крестный отец: «Ничего личного». Только производные!

Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.

12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.

12 задание бывает двух видов:

1. Найти точку максимума / минимума (просят найти значения «x»).
   
2. Найти наибольшее / наименьшее значение функции (просят найти значения «y»).

Как же действовать в этих случаях?

Найти точку максимума / минимума

1. Взять производную от предложенной функции.
2. Приравнять ее к нулю.
3. Найденный или найденные «х» и будут являться точками минимума или максимума.
4. Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.

Задания с ЕГЭ: 

Найдите точку максимума функции 

• Берем производную:

• Приравняем ее к нулю:
• Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):

Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15

Найдите точку минимума функции

• Преобразуем и возьмем производную: 

• Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

• Отлично! Сначала функция убывает, затем возрасает — это точка минимума!

Ответ: −2

Найти наибольшее / наименьшее значение функции

1. Взять производную от предложенной функции.
   
2. Приравнять ее к нулю.
   
3. Найденный «х» и будет являться точкой минимума или максимума.
   
4. Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
5. В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
6. Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции. 

Задания с ЕГЭ: 

Найдите наибольшее значение функции на отрезке [−4; −1] 

• Преобразуем и возьмем производную: 
• «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?

• Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:

Ответ: −6

Найдите наибольшее значение функции на отрезке [0; 1,5π]

• Берем производную:
• Находим, чему равняется sin(x):
• Но такое невозможно! Sin(x)…
• Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:

• Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
  

Ответ: 11

Выводы:

1. 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
   
2. Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
3. Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
4. В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
5. А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.

Будь в курсе новых статеек, видео и легкого математического юмора.

Как найти локальные минимальные графические функции кривых

Все ресурсы исчисления 1

10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Исчисление 1 Помощь » Функции » Графические функции » Кривые » Местный минимум » Как найти локальные минимальные графические функции кривых

Используя производные, найти относительный экстремум параболы, описываемой выражением f(x) = 4x ²  – 5x + 20

Возможные ответы:

(2, 8)

(5/8, 295/16)

Ни один из других ответов

5

(90 0 094) (90 0 094) /3, 25/7)

Правильный ответ:

(5/8, 295/16)

Пояснение:

Сначала мы должны найти первую производную f(x).

Это просто:

f'(x) = 8x – 5

Теперь относительный экстремум находится в точке, где производная равна 0. Поэтому положим f'(x) = 0:

0 = 8x – 5; 8х = 5; x = 5/8

Теперь подставьте это в исходное уравнение:

f(5/8) = 4(5/8) ²  – 5(5/8) + 20 = (100/64) – (25/8) + 20 = (100 – 200)/64 + 20 = (–100/64) + 20 = (1280 – 100)/64 = 1180/64 = 295/16

Сообщить об ошибке

Рассмотреть функция . Если минимум этой функции расположен в точке , то каковы значения и ?

Возможные ответы:

Ни один из других вариантов ответа не является правильным.

Правильный ответ:

Объяснение:

Возьмите производную функции по отношению к :

Подставьте точку и найдите :

Теперь функция .

Чтобы найти , подключитесь к исходной функции и решите для :

Сообщить об ошибке

Найдите локальный минимум следующей функции в диапазоне .

Возможные ответы:

Правильный ответ:

Объяснение:

Локальный минимум возникает, когда значение  изменяется с отрицательного на положительное. Первый шаг — найти.

Далее находим критические точки (когда  или undefined).

Последним шагом является проверка того, на каких интервалах  отрицательное и положительное значение, чтобы определить, при каком из этих значений происходит минимум. Обратите внимание, что первое значение  выходит за пределы области, указанной в задаче.

Проверяемые регионы  и .

Чтобы проверить регионы, выберите значение в этом регионе и вставьте его в  , чтобы увидеть, положительное оно или отрицательное.

 отрицательно в первой области и положительно во второй области, поэтому минимум приходится на  .

Чтобы найти соответствующее значение  , подставьте его в исходную функцию, получив значение .

Сообщить об ошибке

Пусть

Найти все локальные максимумы.

Возможные ответы:

Правильный ответ:

Объяснение:

Если в какой-то момент, то может быть локальный максимум.

Таким образом, возможные решения:

Чтобы определить, являются ли эти точки максимумами (или минимумами), нам нужно определить, является ли функция вогнутой вверх (минимум) или вогнутой вниз (максимум) в этих точках. Для этого нам понадобится вторая производная.

Взяв вторую производную от нашей функции, получим: 

Подставляя значения x, которые мы хотим исследовать, мы видим следующее.

максимумы

минимумы

Следовательно, единственные локальные максимумы находятся в точке 

Сообщить об ошибке

Учитывая уравнение графика, найдите координаты локального минимума(ов), если таковые имеются.

Возможные ответы:

Локальный минимум отсутствует

Правильный ответ:

Объяснение:

Чтобы найти локальный минимум любого графика, вы должны сначала взять производную уравнения графика, приравнять ее к нулю и найти . Чтобы получить производную от этого уравнения, мы должны использовать правило степени

.

Мы также должны помнить, что производная константы равна 0. Беря производную уравнения графика, мы получаем уравнение наклона. Решая для x, когда уравнение установлено в 0, мы получаем .

Чтобы  было локальным минимумом, наклон должен увеличиваться по мере прохождения 2 слева. Подставляя 1 и 3 в уравнение наклона, мы обнаруживаем, что наклон на самом деле увеличивается от -4 до 4, поэтому  является локальным минимумом.

Подключив обратно к исходному уравнению графика для решения для , мы находим координаты локального минимума для этого графика на самом деле .

Сообщить об ошибке

Найти любые локальные максимумы или минимумы  на интервале .

Возможные ответы:

Global Minimum AT:

Глобальный максимум AT:

Глобальный минимальный AT:

Глобальный максимум:

Правильный ответ:

. :

Объяснение:

Найдите любые локальные максимумы или минимумы f(x) на интервале [-10,10]

Чтобы начать нахождение локальных минимумов и максимумов, нам нужно взять первую производную указанной выше функции.

Локальный минимум и максимум встречаются везде, где первая производная равна 0. 

 

Найдите координату y через:

Итак, первый бит нашего ответа:

4 Но это максимум

4 минимум?

Чтобы найти это, нам нужно знать, является ли функция вогнутой вверх или вогнутой вниз в точке.

Для проверки вогнутости нам нужна вторая производная:

Вторая производная везде положительна, поэтому эта функция везде вогнута, что делает ее локальным минимумом.

Сообщить об ошибке

Найти локальный максимум функции .

Возможные ответы:

Нет.

Правильный ответ:

Объяснение:

Сначала найдите производную функции.

.

Затем мы находим, что точки, в которых производная равна 0, находятся в  и . Затем выбираем точки на интервалах между этими критическими точками и вставляем их в производную. Если результаты отрицательные, функция убывает. Там, где они положительны, функция возрастает.

С помощью этого метода мы видим, что на интервале функция возрастает. На  функция убывает. Функция возрастает. Поскольку функция возрастает слева от  и убывает справа,  является локальным максимумом.

Подключив его к функции, мы можем найти значение y.

Сообщить об ошибке

Найти локальный минимум функции .

Возможные ответы:

Нет.

Правильный ответ:

Объяснение:

Сначала найдите производную функции.

.

Затем мы находим, что точки, в которых производная равна 0, находятся в  и . Затем выбираем точки на интервалах между этими критическими точками и вставляем их в производную. Если результаты отрицательные, функция убывает.

Там, где они положительные, функция возрастает. Используя этот метод, мы видим, что на интервале функция возрастает. Вкл функция убывает. Функция возрастает. Поскольку функция убывает слева и возрастает справа, это локальный минимум. Подключив его к функции, мы можем найти значение y.

Сообщить об ошибке

Каково наименьшее значение функции?

Возможные ответы:

Правильный ответ:

Объяснение:

 Чтобы найти наименьшее значение y, мы должны сначала найти, где находится минимум функции. Это достигается путем нахождения производной и последующего тестирования значений. Производная этой функции равна

Затем нам нужно разложить это на множители и установить равным 0, что дает нам .

Затем мы устанавливаем каждое выражение равным 0, чтобы получить наши критические точки.

Это дает нам критические точки в . Затем мы устанавливаем числовую линию и проверяем значения с каждой стороны значений. Слева от , вы можете выбрать  и подставить его в производную. Получаем положительное значение. Между двумя критическими точками можно выбрать , что дает нам отрицательное значение. Справа от , вы можете выбрать , что дает положительное значение. Чтобы найти минимум, нужно найти точку, в которой знак меняется с отрицательного на положительный. Это происходит в . Это x-значение минимума.

Чтобы найти значение y, вы должны подставить это значение x в исходную функцию: 

.

Сообщить об ошибке

По заданному графику с уравнением найдите локальный минимум (минимумы), если таковые имеются.

Возможные ответы:

Нет локальных минимумов.

Правильный ответ:

Нет локальных минимумов.

Объяснение:

Чтобы решить это уравнение, мы должны сначала понять, что, взяв производную уравнения графика и приравняв ее к нулю, мы можем найти значения  , где есть критические точки. Критические точки — это либо локальные максимумы, либо минимумы, чтобы выяснить, какие из них вы просто подставляете числа до и после этого значения, чтобы увидеть, увеличивается/уменьшается ли наклон по мере приближения или ухода от этого значения.

Чтобы найти производную уравнения, необходимо применить правило степени, . Взяв производную уравнения графика, находим, что это так.

Приравняв уравнение к нулю и решив для , мы находим, что критические точки для этого графика присутствуют в . Теперь мы должны определить, являются ли эти критические точки локальными минимумами или максимумами.

 

Чтобы определить, являются ли они локальными минимумами/максимумами, мы должны определить поведение наклона графика вокруг этих точек. Если наклон положительный к критической точке и отрицательный от этой критической точки, эта критическая точка является локальным максимумом. Наоборот для локальных минимумов. составляет примерно 1,38. составляет примерно -1,38. Поэтому мы можем подставить -2,0,2 в уравнение наклона, чтобы определить поведение наклона вокруг этих точек.

 

Подставляя производную к уравнению графика, мы находим, что наклон положителен.

Подставив производную к уравнению графика, мы находим, что наклон также положительный.

Подставив производную к уравнению графика, мы находим, что наклон положителен.

 

Поскольку наклон всегда увеличивается, это означает, что на этом графике нет локальных минимумов.

 

Сообщить об ошибке

← Предыдущий 1 2 3 Следующий →

Уведомление об авторских правах

Все ресурсы исчисления 1

10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept

Самый простой способ найти точку минимума?

Минимальный балл по алгебре колледжа

Гейтс Б.

спросил 01.08.16

Я пытаюсь найти самый простой способ найти точку минимума: 92+20х+12

Подписаться І 5

Подробнее

Отчет

5 ответов от опытных наставников

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСамыеСтарые

Кеннет С. ответил 01.08.16

Репетитор

4,8 (62)

Algebra II EXPERT поможет вам выжить и преуспеть

Смотрите таких репетиторов

Смотрите таких репетиторов

САМЫЙ ПРОСТОЙ способ — признать, что график представляет собой график параболы, и он открывается вверх, так что его минимум находится в его вершине. Формула для координаты x вершины: x _{вершина} = -b/(2a)  для  y = ax ² +bx+c. Минимум приходится на x этой вычисленной вершины, а минимум — это y, вычисленный для этого x.

Голосовать за 1 Понизить

Подробнее

Отчет

Нил Д. ответил 01.08.16

Репетитор

4.9 (1417)

Образование стало понятным

Смотрите таких репетиторов

Смотрите таких репетиторов

Математика CPM также учит учащихся изменять квадратичную форму из стандартной формы

в форму графика: Узость или ширина графика

Изменение квадратичного:

Y = 2x ² + 20x +12 Завершите квадрат, используя X-Terms

Y = 2 (x ² + + 10x) + 12

 

y = 2 (x -5 ) ² дает постоянный член 50 ≠ 12, поэтому используйте -38 для константы

начертить его графиком!

 

y = 2( x-5) ² -38   Это графическая форма того же квадратного уравнения,

 

Голосовать за 0 Понизить

Подробнее

Отчет

Дэвид Ф.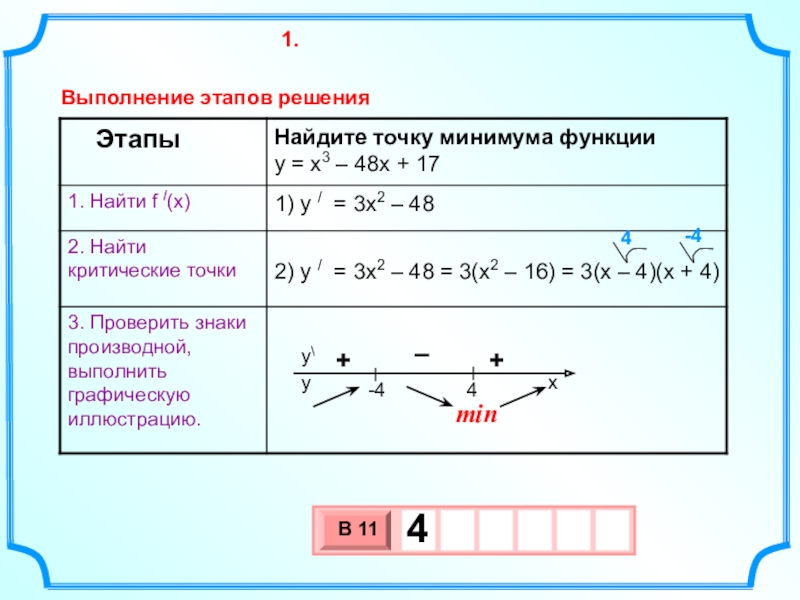 ответил 01.08.16

Репетитор

5 (2)

Math Wiz из Массачусетского технологического института

Смотрите таких репетиторов

Смотрите таких репетиторов

Привет Гейтс,

Хорошее время, чтобы задать вопрос!

Теперь Марк, отличный репетитор, дал подход с использованием алгебры.

и Бэм, еще один замечательный наставник, предложили подход с использованием исчисления.

 

Дэвид Ф

Голосовать за 0 Понизить

Подробнее

Отчет

Марк М. ответил 01.08.16

Репетитор

5,0 (265)

Учитель математики – высококвалифицированный специалист NCLB

Об этом репетиторе ›

Об этом репетиторе ›

В f(x) = ax ² + bx + c mas/min происходит при -b/2a

В приведенной функции -20/(2), -20/4, -5

Минимум происходит при x = -5

Теперь можно подставить и определить минимальное значение.

Голосовать за 0 Понизить

Подробнее

Отчет

Бам К. ответил 01.08.16

Репетитор

4,5 (12)

Многопрофильный, увлеченный и сострадательный наставник

Смотрите таких наставников

Смотрите таких репетиторов

Самый простой способ, если использовать первую производную. f'(x) = 0 в минимуме. Следовательно, 4x + 20 = 0 ⇒ x = -5 и изображение f(x) = 50 — 100 + 12 = -38 ;

Минимальная точка находится в точке (-5 ; -38) на декартовой плоскости.

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.