| |||||||||||
| Специальный поиск | |||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
||||||||||
тело брошено под углом Задача 13099 Тело брошено под углом α = 45° к горизонту со скоростью v0 = 15 м/с Используя закон сохранения энергии, определите скорость v тела в высшей точке его траектории.
Задача 19915 Тело брошено под углом 45° к горизонту.
Задача 20257 На какую наибольшую высоту h поднимется тело, брошенное под углом α к горизонту, если время полета тела равно t = 2 с.
Задача 11027 Тело брошено под углом α = 30° к горизонту. Найти тангенциальное аτ и нормальное аn ускорения в начальный момент движения.
Задача 13651 Тело, брошенное под углом α = 60° к горизонту (см. рис.), через время τ = 4 с после начала движения имело вертикальную составляющую скорости vy = 10 м/с. Требуется: 1) написать кинематические уравнения движения тела; 2) вывести уравнение траектории тела; 3) определить дальность L полета тела; 4) найти максимальную высоту Нmax подъема.
Задача 15246 Тело брошено под углом 60° к горизонту с начальной скоростью 20 м/с. Определить координаты точек на траектории тела, в которых нормальное ускорение равно тангенциальному.
Задача 20366 Тело брошено под углом α = 30° к горизонту. За время Δt = 5 с полета модуль изменения импульса тела равен Δр = 200 кг·м/с. Сопротивление воздуха не учитывать. Масса этого тела равна … кг.
Задача 22037 Тело бросают под углом 30° к горизонту с начальной скоростью 14 м/с. На расстоянии 11 м от точки бросания тело упруго ударяется о вертикальную стенку. На каком расстоянии от стенки оно упадет на землю?
Задача 23422 Тело, брошенное под углом α = 60° к горизонту, через время t = 4,0 с после начала движения имело вертикальную проекцию скорости ау = 9,8 м/с.
Задача 23604 Тело, брошенное под углом α к горизонту, пролетает за первые 3 с движения расстояние 25 м. Определить угол α, под которым бросили тело, модуль вектора начальной скорости, если наибольшая высота поднятия тела 26,8 м?
Задача 23669 Два тела брошены под углами α1 и α2 к горизонту из одной точки. Каково отношение сообщенных им начальных скоростей, если они упали на землю в одном и том же месте?
| |||||||||||
Тело рассматривать как материальную точку и принять g = 10 м/с2.
Найти расстояние S между местом бросания и местом падения.Примеры решенных задач по физике на тему «Свободное движение тела, брошенного под углом к горизонту»
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии.
Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Принцип решения этих задач заключается в разложении скорости свободно падающего тела на две составляющие — горизонтальную и вертикальную. Горизонтальная составляющая скорости постоянна, вертикальное движение происходит с ускорением свободного падения g=9.8 м/с2. Также может применяться закон сохранения механической энергии, согласно которому сумма потенциальной и кинетической энерги тела в данном случае постоянна.
Материальная точка брошена под углом к горизонту с начальной скоростью 15 м/с. Начальная кинетическая энергия в 3 раза больше кинетической энергии точки в верхней точке траектории. На какую высоту поднималась точка?
Тело брошено под углом 40 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние, которое пролетит тело до падения, высоту подъема в верхней точке траектории и время в полете.
Тело брошено с башни высотой H вниз, под углом α к горизонту, с начальной скоростью v. Найти расстояние от башни до места падения тела.
Тело массой 0,5 кг брошено с поверхност Земли под углом 30 градусов к горизонту, с начальной скоростью 10 м/с. Найти потенциальную и кинетическую энергии тела через 0,4 с.
Материальная точка брошена вверх с поверхности Земли под углом к горизонту с начальной скоростью 10 м/с. Определить скорость точки на высоте 3 м.
Тело брошено вверх с поверхности Земли под углом 60 градусов с начальной скоростью 10 м/с. Найти расстояние до точки падения, скорость тела в точке падения и время в полете.
Тело брошено вверх под углом к горизонту с начальной скоростю 20 м/с. Расстояние до точки падения в 4 раза больше максимальной высоты подъема. Найти угол, под которым брошено тело.
Тело брошено с высоты 5 м под углом 30 градусов к горизонту с начальной скоростью 22 м/с. Найти дальность полета тела и время полета тела.
Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью 30 м/с. Найти тангенциальное и нормальное ускорения тела через 1с после броска.
Тело брошено с поверхности Зесли под углом 30 градусов к горизонту с начальной скоростью 14,7 м/с. Найти тангенциальное и нормальное ускорения тела через 1,25с после броска.
Тело брошено под углом 60 градусов к горизонту с начальной скоростью 20 м/с. Через какое время угол между скоростью и горизонтом станет равным 45 градусов?
Мяч, брошенный в спортзале под углом к горизонту, с начальной скоростью 20 м/с, в верхней точке траектории коснулся потолка на высоте 8м и упал на некотором расстоянии от места броска. Найти это расстояние и угол, под которым брошено тело.
Тело, брошеное с поверхности Земли под углом к горизонту, упало через 2,2с. Найти максимальную высоту подъема тела.
Камень брошен под углом 30 градусов к горизонту. На некоторой высоте камень побывал дважды — через время 1с и 3 с после броска.
Найти эту высоту и начальную скорость камня.
Камень брошен под углом 30 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние от точки бросания до камня через 4 с.
Снаряд выпущен в момент, когда самолет пролетает над орудием, под углом к горизонту с начальной скоростью 500 м/с. Снаряд поразил самолет на высоте 3,5 км через 10с после выстрела. Какова скорость самолета?
Ядро массой 5 кг брошено с поверхности Земли под углом 60 градусов к горизонту. На разгон гири потрачена энергия 500Дж. Определить дальность полета и время в полете.
Тело брошено с высоты 100м вниз под углом 30 градусов к горизонту с начальной скоростью 5 м/с. Найти дальность полета тела.
Тело массой 200г, брошеное с поверхности Земли под углом к горизонту, упало на расстоянии 5м через время 1,2с. Найти работу по броску тела.
Ниже предлагаем вам посмотреть видеоуроки по данной теме:
com/embed/rscPxlPHTPU»> Компоненты начальной скорости
Уже было сказано и подробно обсуждено, что горизонтальное и вертикальное движения снаряда независимы друг от друга.
горизонтальная . Перпендикулярные составляющие движения не зависят друг от друга. Таким образом, анализ движения снаряда требует, чтобы две составляющие движения анализировались независимо друг от друга, стараясь не смешивать информацию о горизонтальном движении с информацией о вертикальном движении. То есть, если анализировать движение для определения вертикального смещения, можно использовать кинематические уравнения с параметрами вертикального движения (начальная вертикальная скорость, конечная вертикальная скорость, вертикальное ускорение), а не с параметрами горизонтального движения (начальная горизонтальная скорость, конечная горизонтальная скорость, горизонтальное ускорение).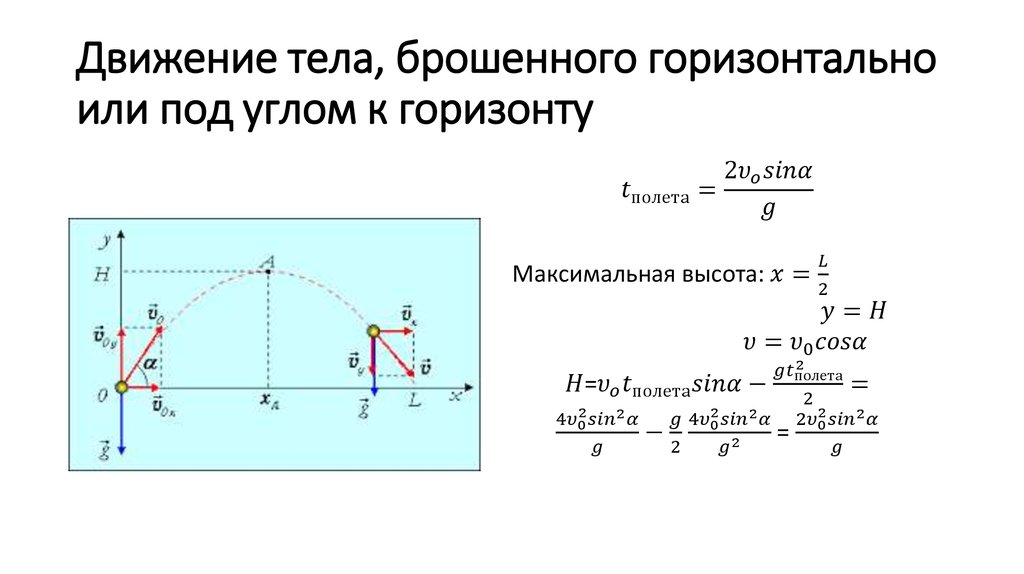
Определение компонентов вектора скорости
Ранее в этом разделе обсуждался метод векторного разрешения. Векторное разрешение — это метод взятия одного вектора под углом и разделения его на две перпендикулярные части. Две части вектора называются компонентами и описывают влияние этого вектора в одном направлении. Если снаряд пущен под углом к горизонту, то начальная скорость снаряда имеет как горизонтальную, так и вертикальную составляющие. Горизонтальная составляющая скорости ( 
Рассмотрим снаряд, запущенный с начальной скоростью 50 м/с под углом 60 градусов к горизонту. Такой снаряд начинает свое движение с горизонтальной скоростью 25 м/с и вертикальной скоростью 43 м/с. Они известны как горизонтальная и вертикальная составляющие начальной скорости. Эти числовые значения были определены путем построения эскиза вектора скорости с заданным направлением, а затем с использованием тригонометрических функций для определения сторон скорость треугольник. Эскиз показан справа, а использование тригонометрических функций для определения величин показано ниже. (При необходимости просмотрите этот метод на предыдущей странице этого модуля.)
Все проблемы с векторным разрешением могут быть решены аналогичным образом. В качестве проверки вашего понимания используйте тригонометрические функции для определения горизонтальной и вертикальной составляющих следующих значений начальной скорости. Когда закончите, нажмите кнопку, чтобы проверить свои ответы.
Практика A: Воздушный шар с водой запускается со скоростью 40 м/с под углом 60 градусов к горизонтали.
Практика B: Мотоциклист-каскадер, движущийся со скоростью 70 миль в час, прыгает с трапа под углом 35 градусов к горизонтали.
Практика C: прыгун с трамплина прыгает со скоростью 10 м/с под углом 80 градусов к горизонту.
Попробуйте еще!
Нужно больше практики? Используйте виджет Компоненты скорости для снаряда , чтобы решить некоторые дополнительные задачи. Введите любую величину скорости и угол относительно горизонтали. Используйте свой калькулятор, чтобы определить значения v x и v y .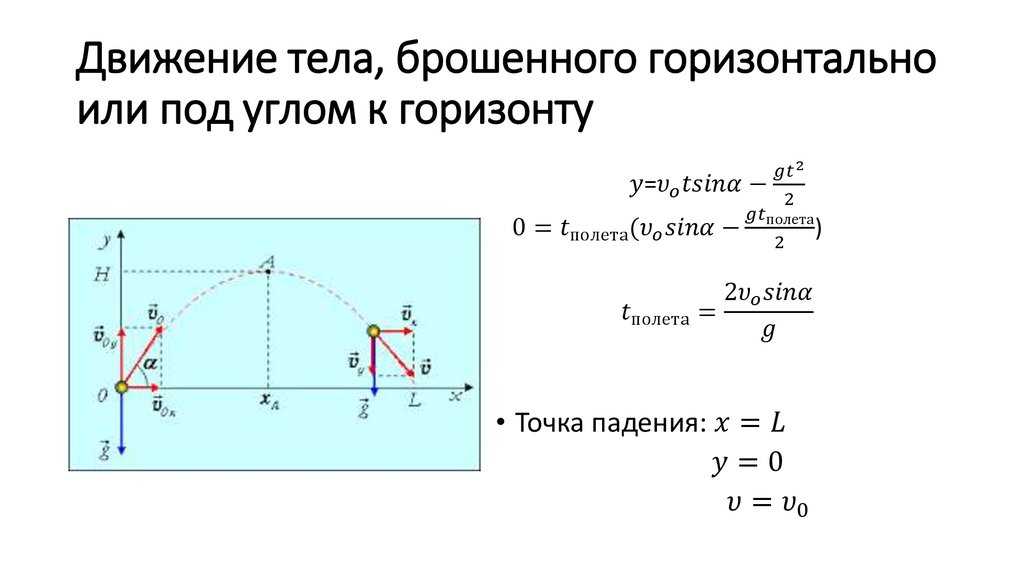
Затем нажмите
Как упоминалось выше, смысл разложения вектора начальной скорости на две его составляющие состоит в том, чтобы использовать значения этих двух составляющих для анализа движения снаряда и определения таких параметров, как горизонтальное смещение, вертикальное смещение, конечная вертикальная скорость, время достижения пика траектории, время падения на землю и т. д. Этот процесс продемонстрирован на оставшейся части этой страницы. Начнем с определения времени.
Время вертикального подъема снаряда до пика (а также время падения с пика) зависит от параметров вертикального движения. Процесс вертикального подъема на вершину траектории представляет собой вертикальное движение и, таким образом, зависит от начальной вертикальной скорости и вертикального ускорения (g = 9,8 м/с/с, вниз).
Зная время подъема на вершину траектории, можно определить общее время полета. Для снаряда, приземлившегося на той же высоте, на которой он стартовал, общее время полета в два раза превышает время подъема на пик. Вспомним из последнего раздела Урока 2, что траектория снаряда симметрична относительно вершины. То есть, если подъем на вершину занимает 4 секунды, то и падение с вершины займет 4 секунды; общее время полета 8 секунд. Время полета снаряда вдвое превышает время подъема на пик.
Определение горизонтального смещения
Горизонтальное смещение снаряда зависит от горизонтальной составляющей начальной скорости. Как обсуждалось в предыдущей части этого урока, горизонтальное перемещение снаряда можно определить с помощью уравнения
скорость 20 м/с, то горизонтальное перемещение 160 метров (20 м/с • 8 с).
Если снаряд имеет время полета 8 секунд и горизонтальную скорость 34 м/с, то снаряд имеет горизонтальное перемещение 272 метра (34 м/с • 8 с). Горизонтальное смещение зависит от единственного горизонтального параметра, существующего для снарядов, — горизонтальной скорости ( v ix ).
Определение высоты пика
Негоризонтально запущенный снаряд с начальной вертикальной скоростью 39,2 м/с достигнет пика за 4 секунды. Процесс подъема на пик является вертикальным движением и опять-таки зависит от параметров вертикального движения (начальной вертикальной скорости и вертикального ускорения). Высота снаряда в этом пиковом положении может быть определена с помощью уравнения
где v iy — начальная вертикальная скорость в м/с, g — ускорение силы тяжести 9,8 м/с/с), а t — время в секундах, необходимое для достижения пика.
Это уравнение может быть успешно использовано для определения вертикального смещения снаряда на первой половине его траектории (т. Е. Высота пика) при условии, что алгебра выполнена правильно и заданные переменные заменены правильными значениями. Особое внимание следует уделить тому факту, что t в уравнении представляет собой время до пика, а g имеет отрицательное значение -9,8 м/с/с.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора движения снарядов. Вы можете найти его в разделе Physics Interactives на нашем сайте. Симулятор позволяет исследовать концепции движения снаряда в интерактивном режиме. Измените высоту, измените угол, измените скорость и запустите снаряд.
Посетите: Симулятор движения снаряда
Ответьте на следующие вопросы и нажмите кнопку, чтобы увидеть ответы.
1. Аарон Эйгин разлагает векторы скорости на горизонтальную и вертикальную составляющие. В каждом случае оцените, правильные или неправильные диаграммы Аарона. Если неверно, объясните проблему или внесите поправку.
2. Используйте тригонометрические функции, чтобы разложить следующие векторы скорости на горизонтальную и вертикальную составляющие. Затем используйте кинематические уравнения для расчета других параметров движения. Будьте осторожны с уравнениями; руководствоваться принципом, что «перпендикулярные составляющие движения независимы друг от друга».
3.
Используйте кинематические уравнения и концепции движения снаряда, чтобы заполнить пробелы в следующих таблицах.
Следующий раздел:
Перейти к следующему уроку:
5.3 Движение снаряда — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать свойства движения снаряда
- Применение кинематических уравнений и векторов для решения задач, связанных с движением снаряда
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением в двух измерениях, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях с помощью уравнений.
- (C) анализировать и описывать ускоренное движение в двух измерениях с помощью уравнений.
Кроме того, руководство по физике для средней школы обращается к содержанию этого раздела лабораторной работы под названием «Движение в двух измерениях», а также к следующим стандартам:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
Основные термины раздела
| сопротивление воздуха | максимальная высота (снаряда) | снаряд |
| движение снаряда | диапазон | траектория |
Свойства движения снаряда
Движение снаряда — это движение предмета, брошенного (выброшенного) в воздух, когда после начальной силы, подбрасывающей предмет, сопротивление воздуха пренебрежимо мало и единственной другой силой, с которой действует предмет, является сила тяжести.
Объект называется снарядом, а его путь называется его траекторией. Сопротивление воздуха — это сила трения, которая замедляет его движение и может существенно изменить траекторию движения. Из-за сложности расчета во вводной физике рассматриваются только ситуации, в которых отклонение от движения снаряда незначительно и сопротивлением воздуха можно пренебречь. Такое приближение часто бывает достаточно точным.
Поддержка учителей
Поддержка учителей
[BL][OL] Проверьте добавление векторов графически и аналитически.
[BL][OL][AL] Объясните термин движение снаряда. Попросите учащихся угадать, от чего может зависеть движение снаряда? Важна ли начальная скорость? Важен ли угол? Как эти вещи повлияют на его высоту и расстояние, которое он покроет? Ввести понятие сопротивления воздуха. Просмотрите кинематические уравнения.
Наиболее важной концепцией движения снаряда является то, что если пренебречь сопротивлением воздуха, горизонтальные и вертикальные движения независимы , то есть они не влияют друг на друга.
На рис. 5.27 пушечное ядро в свободном падении (обозначено синим цветом) сравнивается с пушечным ядром, выпущенным горизонтально при движении снаряда (обозначено красным). Вы можете видеть, что пушечное ядро в свободном падении падает с той же скоростью, что и пушечное ядро в движении снаряда. Имейте в виду, что если бы пушка запускала шар с любой вертикальной составляющей скорости, вертикальные смещения не совпадали бы идеально.
Поскольку вертикальные и горизонтальные движения независимы, мы можем анализировать их отдельно, вдоль перпендикулярных осей. Для этого мы разделим движение снаряда на две составляющие его движения, одну по горизонтальной оси, а другую по вертикальной.
Рисунок 5.27 На диаграмме показано движение снаряда пушечного ядра, выпущенного под горизонтальным углом, по сравнению с ядром, брошенным без горизонтальной скорости. Обратите внимание, что оба ядра имеют одинаковое вертикальное положение с течением времени.
Мы назовем горизонтальную ось осью x , а вертикальную ось осью y .
Для обозначения d — полное перемещение, а х и y — его составляющие по горизонтальной и вертикальной осям. Величины этих векторов равны x и y , как показано на рис. 5.28.
Рисунок 5,28 Мальчик пинает мяч под углом θ , и он перемещается на расстояние с по своей траектории.
Как обычно, мы используем скорость, ускорение и перемещение для описания движения. Мы также должны найти компоненты этих переменных по осям x и y . Тогда компоненты ускорения очень просты: a y = – g = –9,80 м/с 2 . Обратите внимание, что это определение определяет направление вверх как положительное. Поскольку гравитация вертикальна, a x = 0. Оба ускорения постоянны, поэтому мы можем использовать кинематические уравнения.
Для обзора кинематические уравнения из предыдущей главы сведены в Таблицу 5.1.
| x=x0+vavgtx=x0+vavgt (когда a=constanta=константа) |
| vavg=v0+v2vavg=v0+v2 (когда a=0a=0 ) |
| v=v0+atv=v0+at |
| х=х0+v0t+12at2x=x0+v0t+12at2 |
| v2=v02+2a(x−x0)v2=v02+2a(x−x0) |
Стол 5.1 Сводка кинематических уравнений (константа а)
Где x — положение, x 0 — исходное положение, v — скорость, v avg — средняя скорость, t — время, a — ускорение.
Решение проблем, связанных с движением снаряда
Следующие шаги используются для анализа движения снаряда:
- Разделите движение на горизонтальную и вертикальную составляющие по осям x и y. Эти оси перпендикулярны, поэтому используются Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ. Величины смещения ss по осям x и y называются xx и y.y. Величины компонентов скорости vv равны vx=vcosθvx=vcosθ и vy=vsinθvy=vsinθ, где vv – модуль скорости, а θθ – ее направление. Начальные значения обозначены нижним индексом 0,
- Рассматривайте движение как два независимых одномерных движения, одно по горизонтали, а другое по вертикали. Кинематические уравнения для горизонтального и вертикального движения принимают следующий вид
Горизонтальное движение(ax=0)x=x0+vxtvx=v0x=vx=velocity – это константа. Horizontal Motion(ax=0)x=x0+vxtvx=v0x=vx=velocity – это константа.
Вертикальное движение (при положительном значении вверх ay=-g=-9,80 м/с2ay=-g=-9,80 м/с2)y=y0+12(v0y+vy)tvy=v0y-gty=y0+v0yt-12gt2vy2=v0y2-2g(y-y0)y=y0+12(v0y+vy)tvy=v0y-gty=y0+v0yt −12gt2vy2=v0y2−2g(y−y0)
- Найдите неизвестные для двух отдельных движений (горизонтального и вертикального). Обратите внимание, что единственной общей переменной между движениями является время tt. Процедуры решения задач здесь такие же, как и для одномерной кинематики.
- Объедините два движения, чтобы найти полное перемещение ss и скорость vv. Мы можем использовать аналитический метод сложения векторов, который использует A=Ax2+Ay2A=Ax2+Ay2 и θ=tan−1(Ay/Ax)θ=tan−1(Ay/Ax), чтобы найти величину и направление полное перемещение и скорость.
Смещениеd=x2+y2θ=tan−1(y/x)Скоростьv=vx2+vy2θv=tan−1(vy/vx)Смещениеd=x2+y2θ=tan−1(y/x)Скоростьv=vx2+vy2θv=tan −1(vy/vx)
θθ — направление смещения dd, θvθv — направление скорости vv. (См. рис. 5.29.Рисунок 5.29 (а) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения вдоль вертикальной и горизонтальной осей. (b) Горизонтальное движение простое, потому что ах=0 ах=0 и, таким образом, vx vx постоянна. в) скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта; в самой высокой точке вертикальная скорость равна нулю.
Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (г) x — и y -движений рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории.
Эти оси перпендикулярны, поэтому используются Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ. Величины смещения ss по осям x и y называются xx и y.y. Величины компонентов скорости vv равны vx=vcosθvx=vcosθ и vy=vsinθvy=vsinθ, где vv – модуль скорости, а θθ – ее направление. Начальные значения обозначены нижним индексом 0,
Обратите внимание, что единственной общей переменной между движениями является время tt. Процедуры решения задач здесь такие же, как и для одномерной кинематики.Поддержка учителей
Поддержка учителей
Демонстрация учителя
Продемонстрируйте путь снаряда, выполнив простую демонстрацию. Бросьте темный мешок с фасолью перед белой доской, чтобы учащиеся могли хорошо рассмотреть траекторию снаряда. Меняйте углы броска, чтобы отображались разные пути. Эту демонстрацию можно расширить, используя цифровую фотографию. Нарисуйте контрольную сетку на доске, затем подбрасывайте сумку под разными углами, снимая видео. Воспроизведите это в замедленном темпе, чтобы наблюдать и сравнивать высоты и траектории.
Советы для успеха
Для задач о движении снаряда важно настроить систему координат.
Первый шаг — выбрать начальную позицию для xx и yy. Обычно проще всего установить начальное положение объекта так, чтобы x0=0x0=0 и y0=0y0=0 .
Смотреть физику
Снаряд под углом
В этом видео представлен пример нахождения смещения (или дальности) снаряда, запущенного под углом. Он также рассматривает основы тригонометрии для нахождения синуса, косинуса и тангенса угла.
Предположим, что поверхность ровная. Если горизонтальную составляющую скорости снаряда удвоить, а вертикальную не изменить, как это повлияет на время полета?
Время достижения земли останется прежним, поскольку вертикальная составляющая не изменится.
Время достижения земли останется прежним, так как вертикальная составляющая скорости также удвоится.
Время достижения земли сократилось бы вдвое, так как горизонтальная составляющая скорости удвоилась.
Время достижения земли удвоится, так как горизонтальная составляющая скорости удвоится.
Рабочий пример
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка, подобного показанному на рис. 5.30, в воздух выстреливается снаряд с начальной скоростью 70,0 м/с под углом 75° над горизонтом. Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей высшей точки над землей. а) Вычислите высоту взрыва снаряда. б) Сколько времени прошло между пуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве?
Рисунок
5. 30
На схеме показана траектория снаряда фейерверка.
Стратегия
Движение можно разбить на горизонтальное и вертикальное, в которых ax=0ax=0 и ay=g ay=g . Затем мы можем определить x0x0 и y0y0 равными нулю и найти максимальную высоту.
Решение для (a)
Под высотой мы подразумеваем высоту или положение по вертикали yy над начальной точкой. Наивысшая точка любой траектории, максимальная высота, достигается, когда vy=0 vy=0; это момент, когда вертикальная скорость переключается с положительной (вверх) на отрицательную (вниз). Поскольку мы знаем начальную скорость, начальное положение и значение v y , когда фейерверк достигает максимальной высоты, мы используем следующее уравнение, чтобы найти yy
vy2=v0y2−2g(y−y0).vy2=v0y2−2g(y−y0).
Поскольку y0y0 и vyvy равны нулю, уравнение упрощается до
0=v0y2−2gy.0=v0y2−2gy.
Нахождение yy дает
y=v0y22g.y=v0y22g.
Теперь мы должны найти v0yv0y, составляющую начальной скорости в y -направлении. Она определяется выражением v0y=v0sinθv0y=v0sinθ, где v0yv0y — начальная скорость 70,0 м/с, а θ=75∘θ=75∘ — начальный угол. Таким образом,
v0y=v0sinθ0=(70,0 м/с)(sin75∘)=67,6 м/sv0y=v0sinθ0=(70,0 м/с)(sin75∘)=67,6 м/с
и yy равно
y=(67,6 м/с)22(9,80 м/с2),y=(67,6 м/с)22(9,80 м/с2),
, так что
y=233 м.у=233 м.
Обсуждение для (a)
Поскольку up положителен, начальная скорость и максимальная высота положительны, но ускорение свободного падения отрицательно. Максимальная высота зависит только от вертикальной составляющей начальной скорости. Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом.
Решение для (b)
Существует несколько способов решения для времени до высшей точки. В этом случае проще всего использовать y=y0+12(v0y+vy)ty=y0+12(v0y+vy)t . Поскольку y0y0 равно нулю, это уравнение сводится к
y=12(v0y+vy)t.y=12(v0y+vy)t.
Обратите внимание, что конечная вертикальная скорость, vyvy, в самой высокой точке равна нулю. Следовательно,
t=2y(v0y+vy)=2(233 м)(67,6 м/с)=6,90 с.t=2y(v0y+vy)=2(233 м)(67,6 м/с)=6,90 с.
Обсуждение для (б)
Это время подходит и для больших фейерверков. Когда вы сможете увидеть запуск фейерверка, вы заметите, что пройдет несколько секунд, прежде чем снаряд взорвется. Другой способ найти время — использовать y=y0+v0yt−12gt2y=y0+v0yt−12gt2 и решить квадратное уравнение для tt.
Решение для (c)
Поскольку сопротивлением воздуха можно пренебречь, ax=0ax=0, а горизонтальная скорость постоянна. Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxtx=x0+vxt, где x0x0 равно нулю
x=vxt,x=vxt,
, где vxvx — составляющая x скорости, которая определяется выражением vx=v0cosθ0. vx=v0cosθ0. Теперь
vx=v0cosθ0=(70,0 м/с)(cos75∘)=18,1 м/с. vx=v0cosθ0=(70,0 м/с)(cos75∘)=18,1 м/с.
Время tt для обоих движений одинаково, поэтому xx равно
x=(18,1 м/с)(6,90 с)=125 м. x=(18,1 м/с)(6,90 с)=125 м.
Обсуждение для (c)
Горизонтальное движение имеет постоянную скорость в отсутствие сопротивления воздуха. Найденное здесь горизонтальное смещение может быть полезно для предотвращения падения фрагментов фейерверка на зрителей. После того, как снаряд взорвется, большое влияние оказывает сопротивление воздуха, и многие осколки приземлятся прямо под ним, в то время как некоторые из осколков теперь могут иметь скорость в направлении -x из-за сил взрыва.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Расскажите о проблеме с образцом. Обсудите переменные или неизвестные в каждой части задачи. Спросите учащихся, какие кинематические уравнения лучше всего подходят для решения различных частей задачи.
Выражение, которое мы нашли для yy при решении части (a) предыдущей задачи, работает для любой задачи о движении снаряда, где сопротивлением воздуха можно пренебречь. Назовите максимальную высоту y=hy=h; тогда
ч=v0y22g.h=v0y22g.
Это уравнение определяет максимальную высоту снаряда. Максимальная высота зависит только от вертикальной составляющей начальной скорости.
Рабочий пример
Расчет движения снаряда: снаряд Hot Rock
Предположим, что большой камень выбрасывается из вулкана, как показано на рис. 5.31, со скоростью 25,0 м/с25,0 м/с и под углом 35°35° над горизонталью. Скала ударяется о борт вулкана на высоте 20,0 м ниже его исходной точки. а) Вычислите время, за которое камень проходит этот путь.
Рисунок 5.31 На диаграмме показано движение снаряда большой скалы из вулкана.
Стратегия
Разбиение этого двумерного движения на два независимых одномерных движения позволит нам определить время. Время нахождения снаряда в воздухе зависит только от его вертикального движения.
Решение
Пока камень находится в воздухе, он поднимается, а затем падает в конечное положение на 20,0 м ниже начальной высоты. Мы можем найти время для этого, используя
y=y0+v0yt−12gt2.y=y0+v0yt−12gt2.
Если принять начальное положение y0y0 равным нулю, то конечное положение будет y=−20,0 м.y=−20,0 м. Теперь начальная вертикальная скорость представляет собой вертикальную составляющую начальной скорости, найденную из
v0y=v0sinθ0=(25,0 м/с)(sin35∘)=14,3 м/с. ∘)=14,3 м/с.
5,9
Замена известных значений дает .
Перестановка членов дает квадратное уравнение в tt
(4,90 м/с2)t2-(14,3 м/с)t-(20,0 м)=0,(4,90 м/с2)t2-(14,3 м/с)t-(20,0 м)=0.
Это выражение представляет собой квадратное уравнение вида at2+bt+c=0at2+bt+c=0, где константы равны a = 4,90, b = –14,3 и c = –20,0. Его решения даются квадратичной формулой
t=−b±b2−4ac2a.t=−b±b2−4ac2a.
Это уравнение дает два решения: t = 3,96 и t = –1,03. Вы можете проверить эти решения в качестве упражнения. Время t = 3,96 с или –1,03 с. Отрицательное значение времени подразумевает событие до начала движения, поэтому мы его отбрасываем. Следовательно,
t=3,96 с.t=3,96 с.
Обсуждение
Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 14,3 м/с14,3 м/с и приземлившийся на 20,0 м ниже начальной высоты, проведет в воздухе 3,96 с.
Практические задачи
11.
Если объект брошен горизонтально, движется со средней x-компонентой своей скорости, равной 5\,\text{м/с}, и не ударяется о землю, какой будет x-компонента смещения после 20\,\текст{ы}?
{-100}\,\текст{м}
{-4}\,\текст{м}
4\,\текст{м}
100\,\текст{м}
12.
Если мяч бросить вертикально вверх с начальной скоростью 20\,\text{м/с}, какой максимальной высоты он достигнет?
{-20,4}\,\текст{м}
{-1.02}\,\текст{м}
1.02\,\текст{м}
20,4\,\текст{м}
Тот факт, что вертикальное и горизонтальное движения независимы друг от друга, позволяет нам предсказать дальность полета снаряда. дальность — горизонтальное расстояние R , пройденное снарядом на ровной поверхности, как показано на рис. 5.32. На протяжении всей истории люди интересовались поиском диапазона снарядов для практических целей, например, для наведения пушек.
Рисунок 5.32 Траектории снарядов на ровной местности. (а) Чем больше начальная скорость v0v0, тем больше диапазон для данного начального угла. (б) Влияние начального угла θ0θ0 на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что любая комбинация траекторий, которая в сумме дает 90 градусов будет иметь тот же диапазон при отсутствии сопротивления воздуха, хотя максимальная высота этих путей различна.
Как начальная скорость снаряда влияет на его дальность? Очевидно, чем больше начальная скорость v0v0, тем больше диапазон, как показано на рисунке выше. Начальный угол θ0θ0 также сильно влияет на дальность. При пренебрежимо малом сопротивлении воздуха дальность RR снаряда на ровной местности составляет
R=v02sin2θ0g,R=v02sin2θ0g,
, где v0v0 — начальная скорость, а θ0θ0 — начальный угол относительно горизонтали. Важно отметить, что диапазон не применяется к задачам, в которых начальное и конечное положение y различаются, или к случаям, когда объект запускается строго горизонтально.
Виртуальная физика
Движение снаряда
В этой симуляции вы узнаете о движении снаряда, стреляя по объектам из пушки. Вы можете выбирать между такими объектами, как корпус танка, мяч для гольфа или даже Бьюик. Поэкспериментируйте с изменением угла, начальной скорости и массы и добавлением сопротивления воздуха. Сделайте игру из этой симуляции, пытаясь поразить цель. 9\цирк
Проверьте свое понимание
13.
Что такое движение снаряда?
Движение снаряда — это движение объекта, отброшенного в воздух и движущегося под действием силы тяжести.
Движение снаряда — это движение объекта, отбрасываемого в воздух и движущегося независимо от гравитации.
Снарядное движение — это движение объекта, проецируемого вертикально вверх в воздух и движущегося под действием силы тяжести.
Движение снаряда — это движение объекта, проецируемого горизонтально в воздух и движущегося независимо от силы тяжести.
14.
Какую силу испытывает снаряд после первоначальной силы, подбросившей его в воздух при отсутствии сопротивления воздуха?
- Ядерные силы
- Сила гравитации
- Электромагнитная сила
- Контактное усилие
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, достигают ли учащиеся целей обучения в этом разделе.
Leave A Comment