Радиус окружности описанной около прямоугольного треугольника равен 13: Радиус окружности, описанной около прямоугольного треугольника

Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:

Найдем длину отрезка СО, равного радиусу описанной окружности, из треугольника СОК:

В ответе требуется указать 

Ответ: 5

4. Задание B7 (№ 27950)

Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1.

Центр О описанной окружности лежит в точке пересечения медиан (высот и биссектрис) треугольника ABC.

Высота (она же медиана) ВК=3, следовательно, 

Ответ: 2.

5. Задание B7 (№ 27951)

Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.

Считаем клеточки: AC=3, BC=4. По теореме Пифагора

Ответ: 1.

И. \circ }\), то около этого четырехугольника можно описать окружность.

Около параллелограмма можно описать окружность тогда и только тогда, когда этот параллелограмм прямоугольник.

Задача 1. Сторона правильного треугольника равна \(\sqrt 3 \). Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 1.

Задача 2. Радиус окружности, описанной около правильного треугольника, равен \(\sqrt 3 \). Найдите сторону этого треугольника. Ответ ОТВЕТ: 3.

Задача 3. Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 2.

Задача 4. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника. Ответ ОТВЕТ: 4,5.

Задача 5. Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника. Ответ ОТВЕТ: 6.

Задача 6. Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника. Ответ ОТВЕТ: 8.

Задача 7. В треугольнике ABC угол С равен 90°, \(AC = 4,\;\;BC = 3.\)  Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 2,5.

Задача 8. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника. Ответ ОТВЕТ: 2.

Задача 9. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 30°.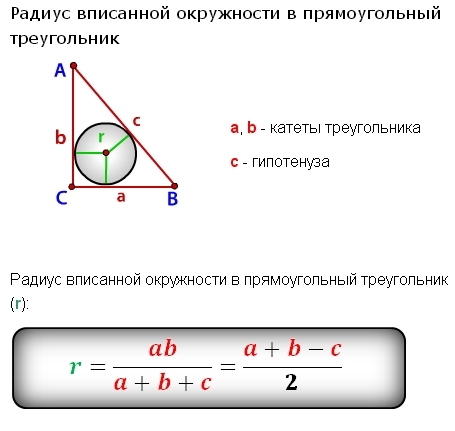 Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 1.

Задача 10. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах. Ответ ОТВЕТ: 30.

Задача 11. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30°. Найдите сторону AB этого треугольника. Ответ ОТВЕТ: 3.

Задача 12. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 150°. Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 1.

Задача 13. По данным на рисунке найдите площадь треугольника АВС, если точка О – центр описанной окружности, АС =  ВС, OD = 8 и АВ = 12. \circ },\)  \(\angle \,A:\angle \,B = 1:2\)  и  \(AC = 8\sqrt 3 .\) Ответ ОТВЕТ: 8.

Задача 16. Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах. Ответ ОТВЕТ: 122.

Задача 17. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95°, 49°, 71°, 145°. Найдите угол B этого четырехугольника. Ответ дайте в градусах. Ответ ОТВЕТ: 108.

Задача 18. Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4 : 2 : 3 : 6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах. Ответ ОТВЕТ: 60.

Задача 19. Четырехугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в градусах. Ответ ОТВЕТ: 70.

Задача 20. Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах. Ответ ОТВЕТ: 110.

Задача 21. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах. Ответ ОТВЕТ: 40.
Задача 22. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции. Ответ ОТВЕТ: 6.
Задача 23. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции. Ответ ОТВЕТ: 6.
Задача 24. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах. Ответ ОТВЕТ: 122.
Задача 25. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности. Ответ ОТВЕТ: 24.
Задача 26. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6? Ответ ОТВЕТ: 6.
Задача 27. Найдите радиус окружности описанной около равнобедренного треугольника, если боковые стороны равны 5, а основание 6. Ответ ОТВЕТ: \(\frac{{25}}{8}.\)
Задача 28. Найдите радиус окружности описанной около равнобедренного треугольника, если боковые стороны равны 5, а основание 8. Ответ ОТВЕТ: \(\frac{{25}}{6}.\)
Задача 29. Найдите площадь равнобедренного треугольника, боковая сторона которого равна \(8\sqrt 5 ,\) а радиус описанной окружности равен 10. Ответ ОТВЕТ: 128.
Задача 30. По данным на рисунке найдите ВС, если АВ = 5,  BD = 4  и  ОС = 5. Ответ ОТВЕТ: 8.
Задача 31. По данным на рисунке найдите радиус описанной окружности OR, если QM = 5, QR = 10  и  PQ = 12. Ответ ОТВЕТ: 12.
Задача 32. По данным на рисунке найдите радиус описанной окружности ОТ около трапеции KLMT, если LM = 12, KT = 16 и высота трапеции равна 2. \circ }\) и АС является биссектрисой угла BAD. Ответ ОТВЕТ: \(48\sqrt 3 .\)
Задача 34. По данным на рисунке найдите радиус описанной окружности ОМ около трапеции FKME,  если  КМ = 2,  FE = 14  и  FK = 10. Ответ ОТВЕТ: \(5\sqrt 2 .\)
Задача 35. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции. Ответ ОТВЕТ: 7 или 1.
Задача 36. Радиус окружности описанной около остроугольного треугольника АВС равен 9. Найдите радиус окружности описанной вокруг треугольника МВК, если АК и СМ – высоты треугольника, а АС = 12  и  МК = 4. Ответ ОТВЕТ: 3.
Задача 37. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1,2 раза больше стороны BC. Ответ ОТВЕТ: 15.
Задача 38. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 14, а сторона AC в 2 раза больше стороны BC. Ответ ОТВЕТ: 7.

Реклама

Мы Вконтакте

Поддержать нас

Математическая задача: Описание — вопрос № 735, геометрия, теорема Фалеса

Найдите радиус описанной окружности до прямоугольного треугольника с катетами 6 см и 3 см.

Правильный ответ:

Пошаговое объяснение:

a=6 см b=3 см c=a2+b2

​=62+32

902 ​=03 5 см≐6,7082 см c = 2⋅ r  r=c/2=6,7082/2=3,35 см

Попробуйте рассчитать с помощью нашего калькулятора треугольников.

Нашли ошибку или неточность? Не стесняйтесь

. Спасибо!

Советы по использованию связанных онлайн-калькуляторов

См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.

You need to know the following knowledge to solve this word math problem:

• geometry
• Thales’ theorem
• planimetrics
• Pythagorean theorem
• right triangle
• circle
• треугольник

Уровень задачи:

• практика для 13-летних
• практика для 14-летних
• старшая школа

  1

• Описанный 29561
  Постройте равнобедренный треугольник, если дана описанная окружность с радиусом r = 2,6 см.
• Додекагон
  Найдите площадь правильного двенадцатиугольника (n=12), если радиус описанной окружности равен 5 см.
• Описанный 7290
  Вычислите площадь правильного шестиугольника, если радиус описанного круга равен 6,8 см.
• RT стороны
  Найдите стороны прямоугольного треугольника, если катеты a + b = 17см и радиус написанного круга ρ = 2см.
• RT и окружности
  Решите прямоугольный треугольник, если радиус вписанной окружности равен r=9, а радиус описанной окружности равен R=23.
• Описанная 2671
  Радиус окружности, описанной прямоугольником, равен 5 см, а длина одной стороны прямоугольника составляет 6 см. Вычислите длину другой стороны и площадь прямоугольника.
• Кольцевая площадь
  Квадрат со стороной a = 1 вписан и описан окружностями. Найдите площадь кольца.
• Перпендикуляры 64574
  Вычислите радиус окружности, описанной прямоугольным треугольником, перпендикуляры которого равны 10 см и 24 см.
• n-угольник II
  Какова длина стороны правильной 5-угольной описанной окружности радиусом 11 см?
• Правильный n-угольник
  Какой правильный многоугольник имеет радиус описанной окружности r = 10 см и радиус вписанной окружности p = 90,962 см?
• Описанный 22713
  Вычислите длину окружности и площадь правильного десятиугольного многоугольника, если радиус описанного круга r = 20 см.
• Описанный 63824
  В правильном десятиугольнике диаметр описанного круга составляет 10 см. Определить радиус окружности, вписанной в этот треугольник.
• Диагонали пятиугольника
  Вычислите длину диагонали правильного пятиугольника: а) вписанного в окружность радиусом 12 дм; б) описанная окружность радиусом 12 дм.
• Описание описанной окружности к квадрату
  Найдите длину окружности, описанной вокруг квадрата со стороной 10 см. Сравните его с периметром этого квадрата.
• Описанная 35781
  Правильная шестиугольная призма высотой 2 см. Радиус окружности, описанной основанием, равен 8 см. Определить его объем и поверхность.
• Окружность 56291
  Вычислите длину окружности, описанной прямоугольным треугольником с квадратами длиной 10 см и 15 см.
• Квадрат и круги
  Квадрат со стороной 83 см описан и вписан в круги. Определить радиусы обеих окружностей.

Объяснение вписанных окружностей

Самая большая окружность, которая вписывается в треугольник, только касаясь три стороны треугольника называются вписанной окружностью или обвести. Эта статья о треугольниках, в которых длины все стороны и радиусы вписанных окружностей целы числа. В продолжение проблемы Incircles (февраль 2000 г.) о прямоугольных треугольниках мы теперь находим аналогичные результаты для равнобедренные треугольники.

Прежде чем читать дальше, найдите радиус вписанной окружность треугольника со сторонами длин 3, 4 и 5 единиц и затем найдите радиус вписанной окружности треугольника с стороны длин 5, 12 и 13 единиц? Эти числа пифагорейские тройки, треугольники прямоугольные, вписанная окружность первая имеет радиус 1 единицу, а вторая имеет радиус 2 единицы.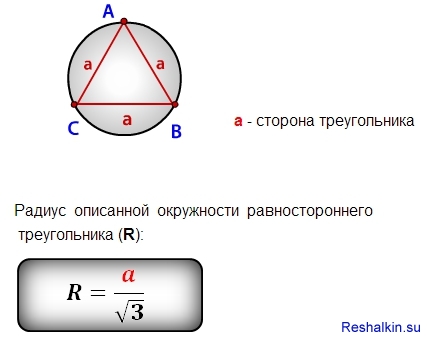 Так можно ли найти прямоугольный треугольник с радиусом вписанной окружности 3 единицы (или любое другое целое число), стороны которого являются примитивной пифагоровой тройной? Ответ на этот вопрос вы найдете здесь. 92+2k+1\\ \end{eqnarray}

Конечно, можно построить треугольники со сторонами a, b и c, которые дают целочисленное значение радиусу вписанной окружности, но которые не являются пифагоровой тройкой. Одним из таких является равнобедренный треугольник со сторонами 10, 10 и 12.

Образуется путем сложения двух треугольников спиной к спине, стороны которых задаются пифагорейской тройкой 6, 8, 10. Как и в решении задачи в исходной задаче радиус r вписанной окружности находится по формуле разделить треугольник на три части и найти его площадь

$$\Delta = ({1\более 2}ar +{1\более 2}br +{1\более 2}cr)$$. Следовательно

\begin{eqnarray} r &=& {2\Delta \over a+b+c}&&\\ &= &{2\times (12 \times 8)/2 \over 10+10+12}\\ &=& {96/32 = 3} \end{eqnarray}

Другой такой треугольник — это треугольник 39, 39, 30, который формируется из двух треугольников 39, 15, 36 (треугольник 5, 12, 13, увеличенный на коэффициент 3).