Связь центростремительного ускорения с линейной скоростью – Центростремительное ускорение, формулы и примеры

Центростремительное ускорение. Равнопеременное движение по окружности.

Вычислим величину ускорения при равномерном движении точки по окружности и найдем его направление. Пусть за некоторый промежуток времени t тело переместилось из точки А в точку А1 с постоянной по модулю скоростью. Изобразим вектора скорости в этих точках и найдем вектор изменения скорости . Рассмотрим треугольники АА1О и А1СВ. Эти треугольники равнобедренные и углы при их вершинах равны, т.к. АО┴СВ и А1О┴А1С (углы со взаимно перпендикулярными сторонами). Следовательно, эти треугольники подобны. Из подобия треугольников следует пропорция:  или, переходя к физическим обозначениям . Разделим правую и левую части равенства на промежуток времени, за которое совершено перемещение, и учтем, что  и . Тогда: .

Примеры: — Земля при вращении вокруг оси ацс=0,03 м/с2, — Земля при вращении вокруг Солнца ацс=0,006 м/с2, — Солнечная система при вращении вокруг центра Галактики ацс=3.10-10 м/с2.

Теперь определим направление ускорения. Т.к. мы должны для определения ускорения брать предел при Δt→0,  то из рисунка видно, что угол φ будет уменьшаться (→0), а b→900. Это значит, что прямая А1В (вектор ) будет стремиться наложиться на АО. Но вектор ускорения сонаправлен с вектором изменения скорости. Следовательно, вектор ускорения при равномерном движении по окружности направлен к центру окружности (центру вращения). Поэтому ускорение наз. центростремительным ускорением.

Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости. Используя связь между угловой и линейной скоростями, получим: .

www.eduspb.com

Поступательное и вращательное движения абсолютно твердого тела. Вектор бесконечно малого поворота. Вектор угловой скорости. Связь линейной и угловой скоростей. Ускорение при вращательном движении. Центростремительное и тангенциальное ускорение. Угловое ускорение и его связь с тангенциальным ускорением.

Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы.

При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной той же прямой, называемой осью вращения.Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.

Бесконечно малый поворот (dφ) — это поворот, который можно рассматривать как вектор.

Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

Легко найти связь между линейной скоростью точки v, ее угловой скоростью ω и радиусом r окружности, по которой она движется.

т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности.

При вращательном движении действуют: тангенциальное и центростремительное ускорения.

В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.

Центробежное ускорение можно вычислить по формуле:

Тангенциальное ускорение,касательное ускорение, составляющая ускорения, направленная по касательной к траектории тела.

где — путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.

Угловое ускорение — физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

Существует связь между тангенциальным и угловым ускорениями:

где R — радиус кривизны траектории точки в данный момент времени

Тангенциальное ускорение направлено по касательной в траектории движения тела, а нормальное — перпендикулярно ему.

malishev.info

Центростремительное ускорение — вывод формулы и практическое применение :: SYL.ru

Центростремительное ускорение сопровождает нас повсюду. Именно оно заставляет нашу Землю вращаться вокруг Солнца. Возникающая при этом сила тяжести позволяет нам существовать на этой планете. Как можно понять, что представляет собой центростремительное ускорение? Определение этой физической величины представлено ниже.

Наблюдения

Самый простой пример ускорения тела, движущегося по окружности, можно наблюдать, вращая камень на веревке. Вы тянете веревку, а веревка тянет камень к центру. В каждый момент времени веревка сообщает камню некоторое количество движения, и каждый раз – в новом направлении. Можно представить движение веревки в виде серии слабых рывков. Рывок – и веревка изменяет свое направление, еще рывок – еще раз изменение, и так по кругу. Если вы внезапно отпустите веревку, рывки прекратятся, а вместе с ними и прекратится изменение направления скорости. Камень будет двигаться в направлении касательной к кругу. Возникает вопрос: «С каким ускорением будет двигаться тело в это мгновение?»

Формула центростремительного ускорения

Прежде всего стоит заметить, что движение тела по окружности является сложным. Камень участвует в двух видах движения одновременно: под действием силы он движется к центру вращения, и одновременно по касательной к окружности, от этого центра удаляется. Согласно Второму закону Ньютона, сила, удерживающая камень на веревке, направлена к центру вращения вдоль этой веревки. Туда же будет направлен вектор ускорения.

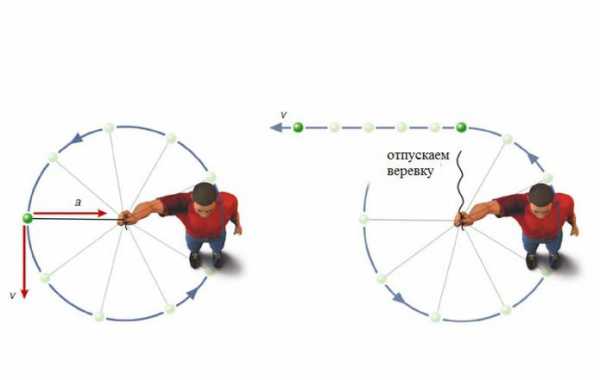
Пусть за некоторое время t наш камень, равномерно двигаясь со скоростью V, попадает из точки A в точку B. Предположим, что в момент времени, когда тело пересекало точку B, на него перестала действовать центростремительная сила. Тогда за промежуток времени оно попало бы в точку K. Она лежит на касательной. Если бы в тот же момент времени на тело действовали бы только центростремительные силы, то за время t, двигаясь с одинаковым ускорением, оно оказалось бы в точке O, которая расположена на прямой, представляющей собой диаметр окружности. Оба отрезка являются векторами и подчиняются правилу векторного сложения. В результате суммирования этих двух движений за отрезок времени t получаем результирующую движения по дуге AB.

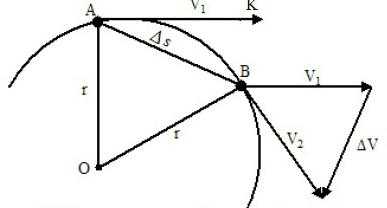
Если промежуток времени t взять пренебрежимо малым, то дуга AB будет мало отличаться от хорды AB. Таким образом, можно заменить движение по дуге движением по хорде. В этом случае перемещение камня по хорде будет подчиняться законам прямолинейного движения, то есть пройденное расстояние AB будет равно произведению скорости камня на время его движения. AB = V х t.

Обозначим искомое центростремительное ускорение буквой a. Тогда пройденный только под действием центростремительного ускорения путь можно рассчитать по формуле равноускоренного движения:

AO = at² / 2.

Расстояние AB равно произведению скорости и времени, то есть AB = V х t,

AO – вычислено ранее по формуле равноускоренного движения для перемещения по прямой: AO = at² / 2.

Подставляя эти данные в формулу и преобразуя их, получаем простую и изящную формулу центростремительного ускорения:

a = v² / R

Словами это можно выразить так: центростремительное ускорение тела, двигающегося по окружности, равно частному от деления линейной скорости в квадрате на радиус окружности, по которой вращается тело. Центростремительная сила в таком случае будет выглядеть так, как на картинке ниже.

Угловая скорость

Угловая скорость равна частному от деления линейной скорости на радиус окружности. Верно и обратное утверждение: V = ωR, где ω – угловая скорость

Если подставить это значение в формулу, можно получить выражение центробежного ускорения для угловой скорости. Оно будет выглядеть так:

a = ω²R.

Ускорение без изменения скорости

И все же, отчего тело с ускорением, направленным к центру, не движется быстрее и не перемещается ближе к центру вращения? Ответ кроется в самой формулировке ускорения. Факты говорят о том, что движение по окружности реально, но для его поддержания требуется ускорение, направленное к центру. Под действием силы, вызванной данным ускорением, происходит изменение количества движения, в результате чего траектория движения постоянно искривляется, все время меняя направление вектора скорости, но не изменяя ее абсолютной величины. Двигаясь по кругу, наш многострадальный камень устремляется внутрь, в противном случае он продолжал бы двигаться по касательной. Каждое мгновение времени, уходя по касательной, камень притягивается к центру, но не попадает в него. Еще одним примером центростремительного ускорения может стать водный лыжник, описывающий небольшие круги на воде. Фигура спортсмена наклонена; он как бы падает, продолжая движение и наклонившись вперед.

Таким образом, можно сделать вывод о том, что ускорение не увеличивает скорость тела, так как векторы скорости и ускорения перпендикулярны друг к другу. Добавляясь к вектору скорости, ускорение лишь меняет направление движения и удерживает тело на орбите.

Превышение запаса прочности

В предыдущем опыте мы имели дело с идеальной веревкой, которая не рвалась. Но, допустим, наша веревка самая обычная, и даже можно вычислить усилие, после которого она просто порвется. Для того чтобы рассчитать эту силу, достаточно сопоставить запас прочности веревки с нагрузкой, которую она испытывает в процессе вращения камня. Вращая камень с большей скоростью, вы сообщаете ему большее количество движения, а значит, и большее ускорение.

При диаметре джутовой веревки около 20 мм ее прочность на разрыв равна около 26 кН. Примечательно, что длина веревки нигде не фигурирует. Вращая груз размером в 1 кг на веревке радиусом в 1 м, можно вычислить, что линейная скорость, необходимая для ее разрыва равна 26 х 10³ = 1кг х V² / 1 м. Таким образом, скорость, которую опасно превышать, будет равна √26 х 10³ = 161 м/с.

Сила тяжести

При рассмотрении опыта мы пренебрегали действием силы тяжести, так как при таких больших скоростях ее влияние пренебрежимо мало. Но можно заметить, что при раскручивании длинной веревки тело описывает более сложную траекторию и постепенно приближается к земле.

Небесные тела

Если перенести законы движения по окружности в космос и применить их к движению небесных тел, можно заново открыть несколько давно знакомых формул. Например, сила, с которой тело притягивается к Земле, известна по формуле:

F= m*g.

В нашем случае множитель g и является тем самым центростремительным ускорением, которое было выведено из предыдущей формулы. Только в этом случае роль камня будет выполнять небесное тело, притягивающееся к Земле, а роль веревки – сила земного притяжения. Множитель g будет выражен через радиус нашей планеты и скорость ее вращения.

Итоги

Сущность центростремительного ускорения состоит в тяжелой и неблагодарной работе удержания движущегося тела на орбите. Наблюдается парадоксальный случай, когда при постоянном ускорении тело не изменяет величины своей скорости. Для неподготовленного ума такое заявление довольно парадоксально. Тем не менее и при расчете движения электрона вокруг ядра, и при вычислении скорости вращения звезды вокруг черной дыры, центростремительной ускорение играет не самую последнюю роль.

www.syl.ru

Формулы для равномерного движения по окружности. Центростремительное ускорение

Движение по окружности — движение тела (чаще всего с постоянной по модулю скоростью) вдоль траектории, имеющей форму окружности или части окружности.

Для движения по окружности вводятся свои кинематические характеристики, логическим образом похожие на характеристики поступательного (прямолинейного) движения (рис. 1). Попробуем ввести аналогию между этими двумя движениями:

• Если тело движется поступательно, то растёт параметр пути ()
• Если тело движется поступательно, то растёт параметр угла поворота ()

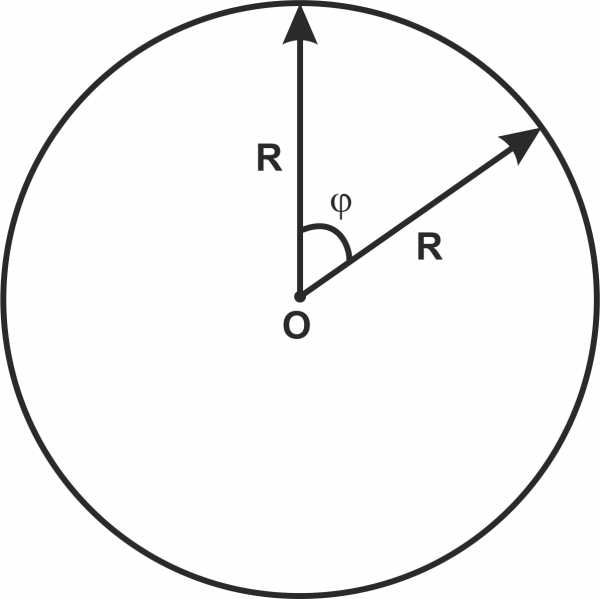
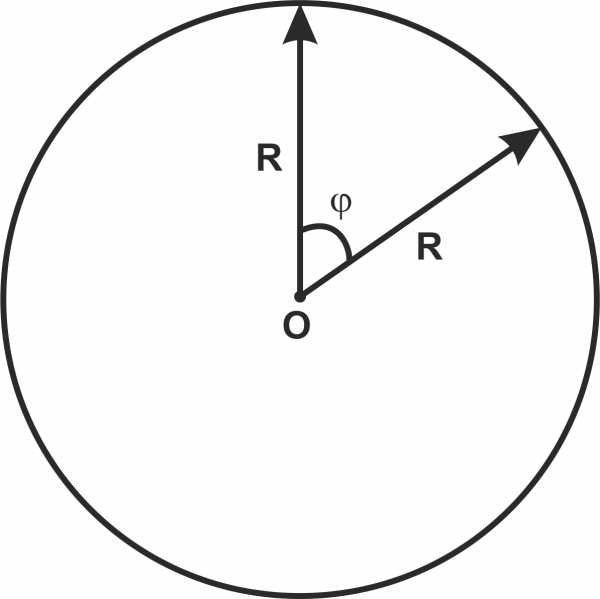
Рис. 1. Угловая скорость. Угол поворота

Если вводить скоростные характеристики движения:

• скорость движения (линейная скорость) —  — быстрота изменения положения тела со временем
• средняя угловая скорость поворота — — быстрота изменения угла поворота со временем

Визуально, формы поиска скорости похожи, этим можно пользоваться.

Для большинства задач школьной физики, тело вращается с постоянной угловой скоростью, поэтому

.

Кроме того, для вращательного движения вводится ряд уникальных характеристик:

Кроме того, существует связь между линейной и угловой скоростью вращения:

(1)

Исходя из (1), можно записать:

(2)

(3)

Вывод: задачи на движение по окружности касаются нахождения параметров периода, частоты и центростремительного ускорения. Переход от вращательного движения к поступательному осуществляется соотношением (1).

Поделиться ссылкой:

www.abitur.by

Конспект на тему «Центростремительное ускорение»

Казахско-Американский Университет Школа при КАУ Класс 9B Семестр осенний 2017-2018 учебный год Урок 5. Центростремительное ускорение Преподаватель: Шокпарбаева Э.Е

Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «

нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.

Наиболее простым примером центростремительного ускорения является вектор ускорения при равномерном движении по окружности (направленный к центру окружности).

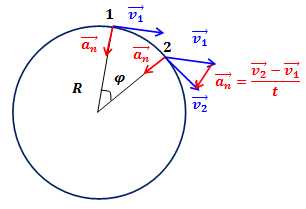
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Глоссарий

Вопросы:

1.Велосипедист едет по дороге со скоростью 10 м/с. Сколько оборотов за секунду делают колеса велосипеда, если они не скользят? Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?

Ответ: a_c ≈ 285 м/с².

2.Материальная точка подвешена на нити длиной м и равномерно движется в горизонтальной плоскости. При этом ее центростремительное ускорение 10 м/с . Определить период движения точки, если нить образует с вертикалью угол ϕ=60

Ответ: T=1.8 c.

3.Рабочее колесо турбины Красноярской ГЭС им. 50-летия СССР имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины?

Ответ: a_c ≈ 360 м/с².

4.Период вращения первого пилотируемого корабля-спутника «Восток» вокруг Земли был равен 90 мин. С каким ускорением двигался корабль, если его средняя высота над Землей 320 км? Радиус Земли принять равным 6400 км.

Ответ: a_c ≈ 9,1 м/с².

5.Угловая скорость вращения лопастей колеса ветродвигателя 6 рад/с. Найдите центростремительное ускорение концов лопастей, если линейная скорость концов лопастей 20 м/с.

Ответ: a_c ≈ 120 м/с².

СРС: упражнение в конце параграфа

Литература: Физика 9 класс

infourok.ru

3.6. Движение по окружности, центростремительное и тангенциальное ускорения. Угловое ускорение

В природе движение тела чаще происходит по кривым линиям. Почти любое криволинейное движение можно представить как по­следовательность движений по дугам окружностей. В общем случае, при движении по окружности скорость тела изменяется как по величине, так и по направлению.

Равномерное движение по окружности

Движение по окружности называется равномерным, если ве­личина скорости остается неизменной.

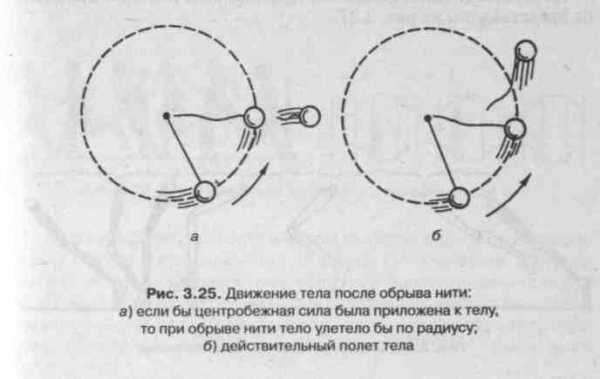
По третьему закону Ньютона всякое действие вызывает равное и противоположно направленное противодействие. Центростреми­тельной силе, с которой связь действует на тело, противодействует равная по модулю и противоположно направленная сила, с которой тело действует на связь. Эту силу F ₆ назвали центробежной, так как она направлена по радиусу от центра окружности. Центробеж­ная сила равна по модулю центростремительной:

Примеры

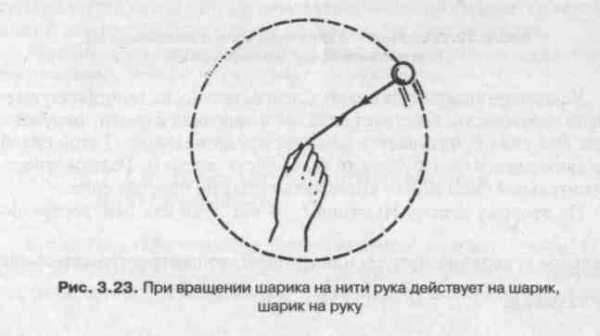
Рассмотрим случай, когда спортсмен вращает вокруг своей го­ловы предмет, привязанный к концу нити. Спортсмен ощущает при этом силу, приложенную к руке и тянущую ее наружу. Для удер­жания предмета на окружности спортсмен (посредством нити) тянет его внутрь. Следовательно, по третьему закону Ньютона, предмет (опять-таки посредством нити) действует на руку с равной и противоположно направленной силой, и это та сила, которую ощущает рука спортсмена (рис. 3.23). Сила, действующая на пред­мет — это направленная внутрь сила натяжения нити.

Другой пример: на спортивный снаряд «молот» действует трос, удерживаемый спортсменом (рис. 3.24).

Напомним, что центробежная сила действует не на вращающее­ся тело, а на нить. Если бы центробежная сила действовала на те­ло, то при обрыве нити оно улетело бы по радиусу в сторону от центра, как показано на рис 3.25, а. Однако на самом деле при об­рыве нити тело начинает двигаться по касательной (рис 3.25, б) в направлении скорости, которую оно имело в момент обрыва нити.

Центробежные силы находят широкое применение.

Центрифуга — устройство, предназначенное для тренировок и испытаний летчиков, спортсменов, космонавтов. Большой радиус (до 15 м) и большая мощность двигателей (несколько МВт) позво­ляют создавать центростремительное ускорение до 400 м/с². Цент­робежная сила при этом прижимает тела с силой, превосходящей нормальную силу тяжести на Земле больше чем в 40 раз. Человек может выдерживать временную перегрузку в 20—30 раз, если он ле­жит перпендикулярно направлению центробежной силы, и в 6 раз, если лежит вдоль направления этой силы.

3.8. Элементы описания движения человека

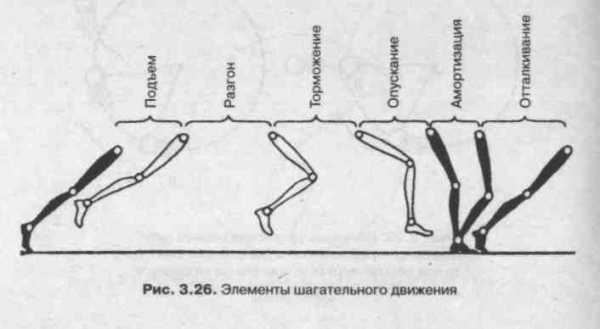
Движения человека носят сложный характер и с трудом под­даются описанию. Однако в ряде случаев можно выделить суще­ственные моменты, отличающие одни виды движений от других. Рассмотрим, например, чем отличается бег от ходьбы.

Элементы шагательных движений при ходьбе представлены на рис. 3.26. В шагательных движениях каждая нога поочередно быва­ет опорной и переносной. В опорный период входят амортизация (торможение движения тела по направлению к опоре) и отталки­вание, в переносной — разгон и торможение.

Последовательные движения тела человека и его ног при ходь­бе представлены на рис. 3.27.

Линии А и В дают качественное изображение движения стоп ног в процессе ходьбы. Верхняя линия А относится к одной ноге, нижняя линия В — к другой. Прямые участки соответствуют мо­ментам опоры стопы о землю, дугообразные участки — моментам движения стоп. В течение промежутка времени (а) обе ноги опи­раются на землю; затем (Ь) — нога А в воздухе, нога В продолжает опираться; а после (с) — вновь обе ноги опираются о землю. Чем быстрее ходьба, тем короче становятся промежутки (а и с).

На рис. 3.28 представлены последовательные движения тела человека при беге и графическое изображение движений стоп. Как видно на рисунке, при беге существуют промежутки времени {b, d, /), когда обе ноги находятся в воздухе, а промежутков од­новременного касания ног земли нет. Этим и отличается бег от ходьбы.

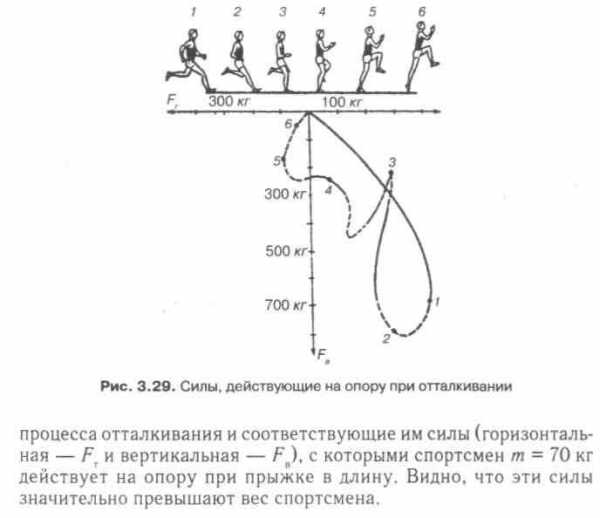
Другим распространенным видом движения является отталки­вание от опоры при различных прыжках. Отталкивание соверша­ется за счет выпрямления толчковой ноги, маховых движений рук и туловища. Задача отталкивания — обеспечить максимальную ве­личину вектора начальной скорости общего центра масс спортсме­на и его оптимальное направление. На рис. 3.29 показаны фазы

\ Глава 4

ДИНАМИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Динамикой называется раздел механики, в котором изучается движение тела с учетом его взаимодействия с другими телами.

В разделе «Кинематика» были введены понятия скорости и ус­корения материальной точки. Для реальных тел эти понятия нуж­даются в уточнении, так как для различных точек реального тела эти характеристики движения могут быть различны. Например, закрученный футбольный мяч не только движется вперед, но и вра­щается. Точки вращающегося тела движутся с разными скоростями. По этой причине сначала рассматривается динамика материальной точки, а затем полученные результаты распространяются на реаль­ные тела.

studfiles.net

4.5 Кинематика равномерного вращения по окружности

При движении по окружности с постоянной по величине линейной скоростью υ тело имеет направленное к центру окружности постоянное центростремительное ускорение

a_ц = υ²/R, (18)

где R – радиус окружности.

Вывод формулы для центростремительного ускорения

По определению .

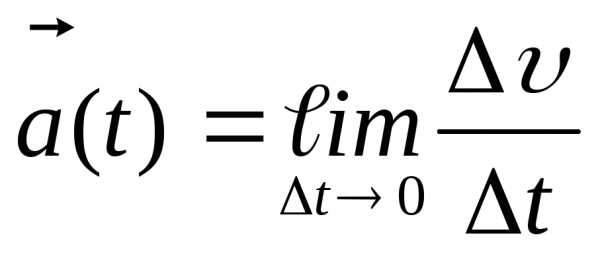(19)

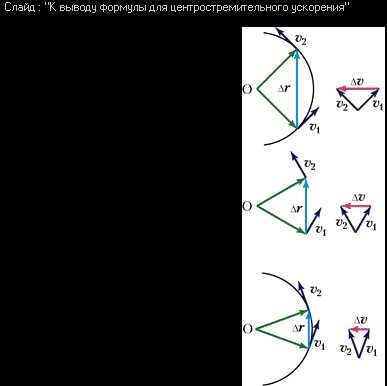
Рисунок 6 Вывод формулы центростремительного ускорения

На рисунке треугольники, образованные векторами перемещений и скоростей, подобны. Учитывая, что 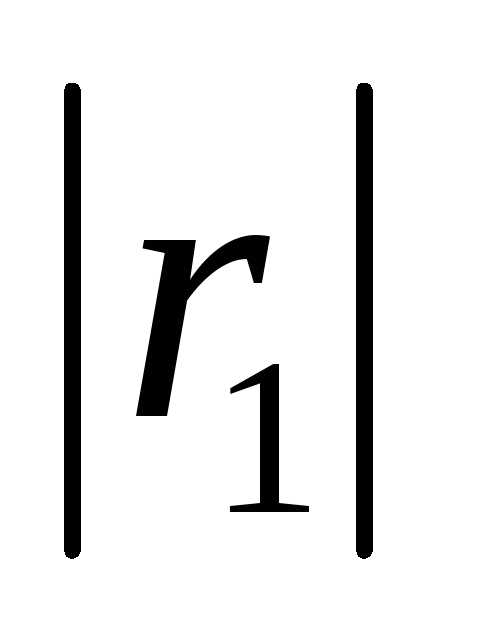==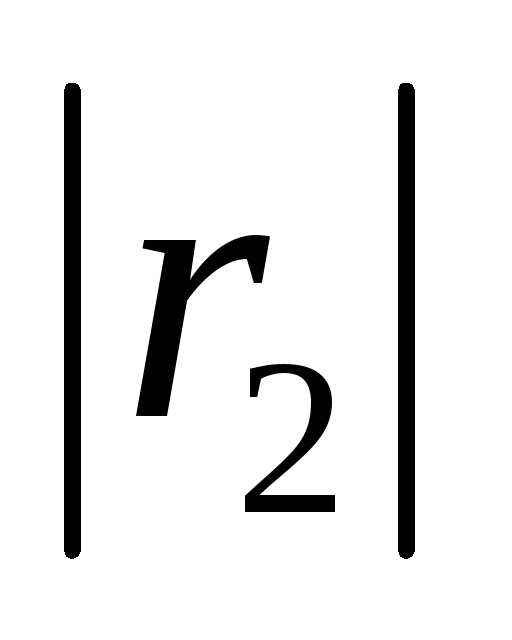 R и==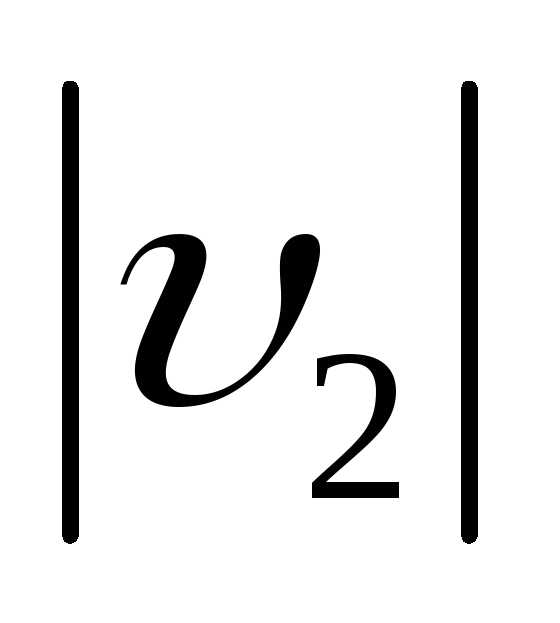 υ, из подобия треугольников находим:

(20)

откуда

(21)

Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом φ, измеряемым в радианах (рад), причем

x = R cos(φ + φ₀), y = R sin(φ + φ₀), (22)

где φ₀ определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).

В случае равномерного вращения угол φ, измеряемый в радианах, линейно растет со временем:

φ = ωt, (23)

где ω называется циклической (круговой) частотой. Размерность циклической частоты: [ω] = c^–1 = Гц.

Циклическая частота равна величине угла поворота (измеренного в рад) за единицу времени, так что иначе ее называют угловой скоростью.

Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде:

x= R cos(ωt + φ₀), (24)

y = R sin(ωt + φ₀).

Время, за которое совершается один оборот, называется периодом T.

Частота ν = 1/T. (25)

Размерность частоты: [ν] = с^–1 = Гц.

Связь циклической частоты с периодом и частотой: 2π = ωT, откуда

ω = 2π/T = 2πν. (26)

Связь линейной скорости и угловой скорости находится из равенства:

2πR = υT, откуда

υ = 2πR/T = ωR. (27)

Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом:

a_ц = υ²/R = ω²R = 4π²ν²R = 4π²R/T². (28)

4.6 Связь поступательного и вращательного движений

Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость υ и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение φ, угловая скорость ω и угловое ускорение ε (в случае, если тело вращается с переменной скоростью).

Из геометрических соображений вытекают следующие связи между этими характеристиками:

перемещение s → угловое перемещение φ = s/R;

скорость υ → угловая скорость ω = υ /R;

ускорение a → угловое ускорение ε = a/R.

Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например:

s = υt → φ = ωt, (29)

υ = υ₀ + at → ω = ω₀ + εt. (29а)

Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор , проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела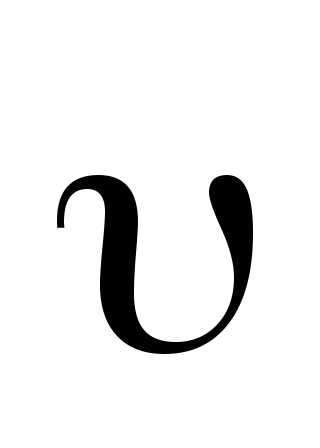, направленному по касательной к окружности в этой точке. Определим вектор, который по модулю равен угловой скорости ω и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора. Тогда связь трех взаимно перпендикулярных векторов,иможно записать с помощью векторного произведения векторов:

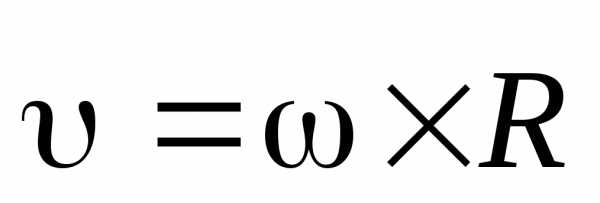. (30)

studfiles.net