Объем равен площадь на высоту: 404 — HTTP not found —

Онлайн калькулятор: Объем геометрических фигур

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

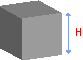Размеры куба

Формула:

Объем куба

Длина ребра куба (H)

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем прямоугольной призмы

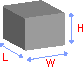Размеры прямоугольной призмы

Формула:

Объем прямоугольной призмы

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем пирамиды

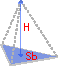Размеры пирамиды

Формула:

Объем пирамиды

Площадь основания

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем усеченной пирамиды

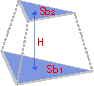Размеры усеченной пирамиды

Формула:

Объем усеченной пирамиды

Точность вычисления

Знаков после запятой: 5

Объем равен площадь на высоту

Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.

Объем фигуры — это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Объемы геометрических фигур.

Фигура	Формула	Чертеж

Параллелепипед.

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

Цилиндр.

Объем цилиндра равен произведению площади основания на высоту.

Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.

Пирамида.

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).

Правильная пирамида — это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

Правильная треугольная пирамида — это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Правильная четырехугольная пирамида — это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Тетраэдр — это пирамида, у которой все грани — равносторонние треугольники.

Усеченная пирамида.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S

1(abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

Куб.

Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 .

Конус — это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Усеченный конус получится, если в конусе провести сечение, параллельное основанию.

V = 1/3 πh (R 2 + Rr + r 2 )

Шар.

Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.

Призма.

Объем призмы равен произведению площади основания призмы, на высоту.

Сектор шара.

Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.

Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.

Сегмент шара — это часть шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом

1. Расчет объема куба

a — сторона куба

Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

3. Формула для вычисления объема шара, сферы

R — радиус шара

По формуле, если дан радиус, можно найти объема шара, (V):

4. Как вычислить объем цилиндра ?

h — высота цилиндра

r — радиус основания

По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):

5. Как найти объем конуса ?

R — радиус основания

H — высота конуса

Формула объема конуса, если известны радиус и высота (V):

7. Формула объема усеченного конуса

r — радиус верхнего основания

R — радиус нижнего основания

h — высота конуса

Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

8. Объем правильного тетраэдра

Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.

а — ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

9. Объем правильной четырехугольной пирамиды

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (

V):

10. Объем правильной треугольной пирамиды

Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):

11. Найти объем правильной пирамиды

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

Строительный объём

Расчет объемов работ в строительстве играет важную роль. В проектной документации указывают разные величины, например, отапливаемый объем, общую площадь, жилую площадь и так далее. Сегодня расскажем, как найти строительный объем здания , что это такое и зачем нужен показатель.

Общий строительный объем здания — что это такое

Правила подсчета показателя прописаны в СНиП 31-06-2009 года, а точнее — в их актуализированной редакции, СП 118.13330.2012 . В документе указано, что строительный объем здания определяется как сумма строительного объема выше отметки 0.00 — надземная часть — и ниже этой отметки — подземная часть. То есть величина — объем подземной и надземной части вместе. При этом учитываются все помещения — как жилые, так и нежилые, а фундамент не входит в формулы.

Строительный объем зданий указывают в кубических метрах. При подсчете полученные значения округляют до 1 м³. Например, если в результате получится цифра 4200,13 м², то в проектной документации будет отражено значение 4200 м³.

Зачем нужен строительный объем жилого дома и других зданий

🔸 Чтобы предварительно определить стоимость строительства или проверить работу подрядчиков — например, узнать, нет ли в смете серьезных ошибок.

🔸 Определить стоимость восстановительного ремонта жилого объекта.

🔸 Рассчитать затраты на обустройство систем кондиционирования, вентиляции и других.

Также строительный объем можно использовать в других сферах. Например, в качестве приблизительного значения его могут применять при обустройстве системы отопления для расчета необходимой мощности.

Какие показатели используют при расчете

Высота здания. Расстояние от проектной отметки земли до наивысшей точки отметки конструктивного элемента здания — например, конька или фронтона для скатных крыш.

Длина здания. Расстояние от одного торца здания до другого с учетом внешней отделки стен. В ряде случаев нужна внутренняя длина стен — ее измеряют от одного угла внешней стены до другого, без учета толщины внешних стен и отделки.

Общая площадь. Сумма площадей всех этажей, а также галерей, антресолей, веранд и других помещений, конструкций. Также в значение включают площадь открытых неотапливаемых планировочных элементов — например, наружных тамбуров или открытых лоджий.

Площадь застройки. Площадь горизонтального сечения по внешнему обводу здания по цоколю с учетом разных выступающих элементов, например, ступеней. Проезды под домом, площадь под ним, если здание расположено на столбах, выступающие элементы на уровне менее 4,5 м тоже включаются в площадь застройки. Если часть здания консольно выступает за пределы стены на высоте более 4,5 м, ее не учитывают.

Как считается строительный объем здания: основные правила

❗ Если здание состоит из надземной и подземной части, то сначала считают объем каждой части отдельно, а потом их суммируют.

❗ В расчетах можно использовать как и площадь застройки, так и общую площадь, но формулы для двух способов подсчета отличаются.

❗ Предусмотрены разные формулы расчета для зданий с чердачным перекрытием и без него.

❗ Надземной частью считается часть от пола первого этажа до верха крыши или чердачного перекрытия. Все, что ниже — подземная часть.

❗ Если в доме нет подвала или других помещений подземной части, высоту здания измеряют от уровня пола первого этажа.

❗ В строительный объем не входят объемы балконов, проездов и портиков, но включены объемы мансард, тамбуров, веранд и световых фонарей.

❗ Длина здания измеряется с учетом толщины облицовки и штукатурки.

❗ Если точных данных нет, можно посчитать объем по приблизительным с учетом поправочных коэффициентов.

Как посчитать строительный объем здания — примеры, инструкции, советы

Самый простой способ

Самый простой способ узнать ориентировочный строительный объем — это умножить площадь застройки на высоту здания. Точное значение площади застройки можно посмотреть в технических документах, проектной декларации. Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.

Например, есть рулетка для измерения длины, ширины и высоты здания. В результате измерений получились следующие данные:

высота — 3,4 м;
длина — 13 м;
ширина — 8 м.

Сначала перемножаем длину и ширину, получаем площадь — 104 м². Полученное значение умножаем на высоту: 3,4 м. Получаем 353,6 м³, округляем значение до 1 м³ и получаем строительный объем 353 м³.

Полученное значение далеко от реального результата, потому что не учитывает подземную часть, толщину перекрытий, толщину стен, индивидуальные особенности проектировки. Метод подсчета не соответствует требованиям к определению строительного объема, поэтому его нельзя использовать в проектной документации.

Более точный расчет строительного объема

Посчитать строительный объем дома точнее без специальных знаний и навыков помогут поправочные коэффициенты. В этом случае формула будет выглядеть так:

X = S¹ × (h + 0,2) × 1,2,

где 0,2 и 1,2 — поправочные коэффициенты, S¹ — общая площадь, а h — высота здания.

Как считать общую площадь здания , если она не указана в технической документации? Нужно найти площадь отдельно для каждого помещения, а потом сложить значения. Например, в доме есть 5 комнат площадью 10, 15, 10, 25 и 5 м². Суммарная площадь составит 65 м².

После того, как нашли площадь, нужно измерить или посмотреть высоту — допустим, она составляет 4,5 м. Добавляем к полученному значению 0,2 — примерную толщину перекрытий, получаем 4,7 м.

Теперь нужно перемножить полученные значения и умножить их на 1,2 — коэффициент перехода внутренней площади здания к внешней.

65 м² × 4,7 м × 1,2 = 306,7 или 307 м³.

Этот способ расчета более достоверный по сравнению с первым, но тоже не дает точных результатов. Он не учитывает индивидуальные конструктивные особенности здания: толщину перекрытий и стен. Зато позволяет быстро посчитать строительный объем для зданий необычной формы — например, многоугольной.

Дома с подземной частью

Если в доме есть подвал, технический этаж или другие помещения под землей, нужно отдельно посчитать строительный объем подземной части здания и наземной, а потом сложить полученные значения.

Для определения объема подземной части нужно знать площадь застройки или площадь горизонтального сечения подвала. Например, для подвала правильной прямоугольной формы площадь горизонтального сечения можно легко найти: нужно умножить длину на ширину. Например, длина составляет 23 м, ширина — 10 м. Площадь застройки или сечения дальне нужно умножить на высоту — ее измеряют от уровня пола подвала до пола первого этажа. Например, она составляет 3 м. Перемножаем площадь 230 м² на высоту 3 м и получаем объем 690 м³.

Чтобы определить объем надземной части, тоже нужно выяснить площадь горизонтального сечения и высоту. Сечение измеряем по внешней части здания. Например, длина составляет 23,6 м, ширина — 10,3 м. Высоту измеряем от пола первого этажа до начала теплоизоляционного слоя чердачного помещения, а если крыша плоская — до середины чердака. Допустим, она составила 13 м. Точно также находим площадь — она составила 243,08 м² — и умножаем ее на высоту. Получаем 3160,04 м³, или округленные 3160 м³.

Полученные значения складываем: прибавляем 690 м³ к 3160 м³ и получаем общий строительный объем: 3850 м³.

Здания без подвала

Если в доме нет подземной части, то строительный объем считается только по надземной части. Посчитать его можно по предыдущей формуле: находим сначала площадь горизонтального сечения, а затем умножаем ее на высоту.

Чтобы определить площадь поперечного сечения, тоже нужно проводить измерение по внешней части здания, с учетом штукатурки и облицовки. Если форма здания сложная, можно условно поделить его на отдельные геометрические фигуры. Например, если два параллельно расположенных здания соединены переходом в форме буквы «Н», можно рассчитать площадь отдельно каждого прямоугольника, а затем суммировать их и умножить на высоту.

Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м². Площадь перехода — 15 м². Складываем три площади: 450 + 450 + 15, получается 915 м². Если высота здания составляет 3 м, то строительный объем будет 2745 м³.

Здания с чердачными перекрытиями

Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:

В этом случае под S¹ понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.

Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.

Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м². Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м³.

Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.

Дома без чердачного перекрытия

Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:

S² — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.

L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.

Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м², а строительный объем — 552 м³.

Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.

Если известна общая площадь

Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.

Если известна общая площадь, можно использовать формулу:

В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.

H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.

К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.

То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м², а высота в свету — 15 м. В этом случае показатель составит 24000 м³ с учетом поправочного коэффициента.

Если известна площадь застройки

Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:

S¹ в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. H¹ — высота дома, в которой можно не учитывать выступающие части крыши.

S² и H² — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.

Дома с мансардами

Мансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.

Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.

Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м².

Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м².

Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.

Если здание имеет сложную форму

Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.

Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета. Если не хотите тратить время на это, обратитесь к профессионалам — они посчитают все быстрее и точнее.

Калькулятор для расчета площади

Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:

Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.

Полезные калькуляторы Конвертер единиц площади | Конвертер единиц длины

Расчет площади прямоугольника

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Расчет площади треугольника

Способ нахождения площади треугольника: По трем сторонам По одной стороне и высоте, опущенной на эту сторону По двум сторонам и углу между ними

Вычислить

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Расчет площади круга

Рассчитать площадь круга, если известен:

Вычислить

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Расчет площади параллелограмма

Способ нахождения площади параллелограмма:
По основанию и высоте параллелограмма По двум сторонам и углу между ними По двум диагоналям и углу между ними

Вычислить

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Расчет площади правильного многоугольника

Многоугольник с числом сторон n и длиной стороны а Многоугольник с числом сторон n, вписанный в окружность радиуса R Многоугольник с числом сторон n, описанный вокруг окружности радиуса r

Вычислить

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Расчет площади эллипса

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Расчет площади сектора круга

Рассчитать площадь сектора круга, если известен:

мм см м км фут ярд дюйм миля

θ=

мм см м км фут ярд дюйм миля

град. рад.

Вычислить

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Расчет площади трапеции

Способ нахождения площади трапеции: По двум основаниям a,b и высоте h По двум основаниям a,b и боковым сторонам c,d

Результат:

S= 1111 кв.мм кв.см кв.м кв.км кв.фут кв.ярд кв.дюйм кв.миля

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.

Метрические единицы измерения площади:
Квадратный метр, производная единица системы СИ 1 м² =	1 са (сантиар)
Квадратный километр — 1 км² =	1 000 000 м²
Гектар — 1 га =	10 000 м²
Ар (сотка) — 1 а =	100 м² (сотка как правило применяется для измерения земельных участков и равна 100 м² или 10м х 10м)
Квадратный дециметр, 100 дм² =	1 м²;
Квадратный сантиметр, 10 000 см² =	1 м²;
Квадратный миллиметр, 1 000 000 мм² =	1 м².

Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.

Как найти объем помещения. Как рассчитать, посчитать объем помещения

Как рассчитать, посчитать объем помещения.

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.

2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.

3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.

5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.

Формула объема помещения

Формула

Пример расчета объема помещения по формуле

Калькулятор площади стены или пола

Вставьте размеры помещения и получите результат.

Строительный объем здания: что это такое, как считается общий строительный объем

Здания с чердачными перекрытиями

Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:

X = S¹ × h.

Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.

Дома без чердачного перекрытия

Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:

X = S² × L

Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.

Если известна общая площадь

Если известна общая площадь, можно использовать формулу:

X = S × H × К

H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.

К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.

Если известна площадь застройки

X = S¹ × H¹ + S² × H²

Дома с мансардами

Если здание имеет сложную форму

Формулы объема, площади поверхности, объем конуса, объем цилиндра, объем шара

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Ты нашел то, что искал? Поделись с друзьями!

Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.

Например, такой важный факт:

Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.

(ведь , ).

Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.

1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.

Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.

формула для правильной и обычной фигуры

В данной публикации мы рассмотрим, как можно найти объем тетраэдра и разберем примеры решения задач для закрепления материала.

Формула вычисления объема тетраэдра

1. Общая формула (через площадь основания и высоту)

Объем (V) тетраэдра считается также, как и объем любой пирамиды. Он равняется одной третьей произведения площади любой грани и высоты, опущенной на нее:

S – площадь грани ABC, в данном случае выступающего в роли основания
h – высота, опущенная на грань ABC

2. Объем правильного тетраэдра

В правильном тетраэдре все грани являются равносторонними треугольниками. Объем данной фигуры равен одной двенадцатой произведения длины его ребра в кубе на квадратный корень из числа 2.

Т.к. это правильный тетраэдр, все его ребра равны (AB = BC = AC = AD = BD = CD).

Примеры задач

Задание 1
Площадь одной из граней тетраэдра равна 24 см², а высоту, опущенная на нее – 9 см. Найдите объем фигуры.

Решение:
Применим общую формулу и получаем:

Задание 2
Дан правильный тетраэдр, ребро которого равняется 8 см. Найдите его объем.

Решение:
Воспользуемся формулой для расчета объема правильной фигуры:

Как создать столбцы одинаковой высоты

Узнайте, как создавать столбцы одинаковой высоты с помощью CSS.

Как создать столбцы одинаковой высоты

Если у вас есть столбцы, которые должны отображаться рядом, вам часто нужно, чтобы они были одинаковой высоты (совпадающие с высотой самого высокого).

Попробуйте сами »

Шаг 1) Добавьте HTML:

Пример

Столбец 1
Hello World

Столбец 2

Привет, мир!

Hello World!

Столбец 3

Другой текст..

Другой текст ..

Шаг 2) Добавьте CSS:

Пример

.col-container {
дисплей: таблица; /* Сделать элемент контейнера ведет себя как таблица * /
width: 100%; / * Установите полную ширину, чтобы развернуть всю страницу * /
}

.col {
дисплей: таблица-ячейка; / * Заставляем элементы внутри контейнера вести себя как таблицы ячеек * /
}

Попробуй сам »

Отзывчивая равная высота

Столбцы, которые мы создали в предыдущем примере, являются адаптивными (если вы измените размер окна браузера в примере с пробной версией, вы увидите, что они автоматически подстраиваются под необходимую ширину и высоту).Однако для небольших экранов (например, смартфонов) вы можете разместить их вертикально, а не горизонтально:

На средних и больших экранах:

Привет, мир.

На маленьких экранах:

Привет, мир.

Для этого добавьте медиа-запрос и укажите значение пикселя точки останова, когда это должно произойти:

Пример

/ * Если размер окна браузера меньше 600 пикселей, делаем столбцы сверху друг друга * /
@media only screen и (max-width: 600px) {
.col {
дисплей: блок;
ширина: 100%;
}
}

Попробуй сам »

Равная высота и ширина с использованием Flexbox

Вы также можете использовать Flexbox для создания блоков одинаковой высоты:

Пример

.col-container {
дисплей: гибкий;
ширина: 100%;
}
.col {
гибкость: 1;
отступ: 16 пикселей;
}

Попробуй сам »

Примечание. Flexbox не поддерживается в Internet Explorer 10 и более ранних версиях.

Совет: Узнайте больше о гибких блоках в нашем руководстве по CSS Flexbox.

Калькулятор длины, ширины и высоты до объема

Нажмите, чтобы перезагрузить страницу с уникальным веб-адресом для добавления в закладки или обмена текущими настройками

✕ очистить настройки

К сожалению, здесь не удалось отобразить графику, потому что ваш браузер не поддерживает холст HTML5.

Сопутствующие инструменты

Руководство пользователя

Этот онлайн-инструмент рассчитывает объем прямоугольного ящика, исходя из его длины, ширины и высоты. Нет необходимости вводить все значения в одних и тех же единицах измерения, просто выберите желаемые единицы для каждого измерения и расчетного объема.

После ввода размеров длины, ширины и высоты рассчитанный объем будет показан в поле ответа. Также будет нарисовано изображение формы и размеров объема, которое будет обновляться каждый раз при изменении введенных значений.

Формула

Формула, используемая калькулятором для расчета объема прямоугольной коробки:

В = Д · Ш · В

Обозначения

V = Объем
L = длина
W = ширина
H = высота

Объемные размеры — длина, ширина и высота

Введите длину, ширину и высоту прямоугольного поля.

Следующие коэффициенты преобразования единиц СИ в метрах (м) используются для преобразования единиц измерения, указанных для длины, ширины и высоты:

нанометр (нм) — 0,000000001 м
микрометр (мкм) — 0,000001 м
миллиметр (мм) — 0,001 м
сантиметр (см) — 0,01 м
дюйма (дюйм) — 0,0254 м
фут (фут) — 0,3048 м
ярд — 0,9144 м
метр (м) — 1 м
километр (км) — 1000 м
миль (миль) — 1609.344 кв.м
морская миля (морская миля) — 1852 м

Расчет объема

Это объем прямоугольной коробки, который соответствует размерам, указанным для длины, ширины и высоты. Объем рассчитывается путем умножения каждого измерения и последующего преобразования его в выбранные единицы измерения объема.

Следующие коэффициенты пересчета в кубических метрах (м³) используются для перевода вычисленного объема в различные единицы измерения объема:

кубический нанометр (куб нм) — 1 x 10 ^-27 м³
кубический микрометр (куб мкм) — 1 x 10 ^-18 м³
кубический миллиметр (куб мм) — 1 x 10 ^-9 м³
кубический сантиметр (куб см) — 1 x 10 ^-6 м³
миллилитр (мл) — 1 x 10 ^-6 м³
кубических дюймов (у.е.) — 1.6387064 x 10 ^-5 м³
жидких унций (жидких унций, британских единиц) — 2,84130625 x 10 ^-5 м³
жидких унций (жидких унций, США) — 2,95735295625 x 10 ^-5 м³
пинта (пт, жидкость США) — 4,73176473 x 10 ^-4 м³
пинта (пинта, дюймовая) — 5,68 26125 x 10 ^-4 м³
литр (л) — 1 x 10 ^-3 м³
галлона (галлон, жидкость США) — 3,785411784 x 10 ^-3 м³
галлон (галлон) — 4.54609 x 10 ^-3 м³
кубических футов — 0,028316846592 м³
баррель (барр., Нефть) — 0,158987294928 м³
кубический ярд (cu yd) — 0,764554857984 м³
куб.м — 1 м³
кубический километр (куб км) — 1 x 10 ⁺⁹ м³
кубических миль (cu mi) — 4168181825,440579584 м³
кубическая морская миля (cu nmi) — 6352182208 м³

Приложения

Используйте этот калькулятор длины x ширины x высоты для определения объема в следующих приложениях:

Объем отправляемой посылки для включения в отгрузочные документы
Объем гравия, необходимый для заполнения дорожки, автостоянки или проезжей части.
Прямоугольный резервуар для хранения.
Вместимость грузового отсека легкового, грузового автомобиля или фургона.
Объем загрузки автомобиля для перемещения хранилища.
Максимальный объем резервуара для воды.
Сколько топлива необходимо для заправки бака.
Размер связки, необходимый для предотвращения утечек и разливов из контейнеров IBC.
Количество мешков, необходимых для каждого материала для строительного проекта.
Количество почвы, необходимое для заполнения ящика сеялки.
Количество воды, необходимое для наполнения аквариума / аквариума.
Заливная емкость для пруда.
Вместимость складского помещения из габаритов.
IBC.
Объем плавательного бассейна.
Возможное место для багажа внутри чемодана.
Цементная смесь, необходимая для заполнения фундаментов / опор.
Объем кузова пикапа.
Объем корпуса аудиодинамика.
Кормушка для кормления животных.
Садовый сарай, солярий или парник, объем цементной подушки.

Справка

Бак 25 x 10 x 12 дюймов в галлонах США

Сколько галлонов США вмещает резервуар шириной 10 дюймов, высотой 12 дюймов и длиной 25 дюймов?

Если исходить из внутренних размеров или отсутствия толщины стенок, объем резервуара составляет 12,987013 галлонов США.

Калькулятор площади поверхности тела

Калькулятор ниже вычисляет общую площадь поверхности человеческого тела, называемую площадью поверхности тела (BSA). Прямое измерение BSA затруднено, и поэтому было опубликовано множество формул для оценки BSA. Калькулятор ниже предоставляет результаты для некоторых из самых популярных формул.

Калькулятор RelatedArea | Калькулятор площади поверхности

Таблица средних BSA

	футов ²	м ²
Новорожденный	2.69	0,25
Двухлетний ребенок	5,38	0,5
Десятилетний ребенок	12,27	1,14
Взрослая женщина	17,22	1,6
Взрослый мужчина	20,45	1,9

BSA часто используется в клинических целях в зависимости от массы тела, потому что это более точный индикатор метаболической массы (потребности организма в энергии), где метаболическая масса может быть оценена как масса без жира, поскольку жировые отложения не метаболически активны.¹ BSA используется в различных клинических условиях, таких как определение сердечного индекса (чтобы связать работу сердца человека с размером его тела) или дозировки химиотерапии (категория лечения рака). Хотя дозировка для химиотерапии часто определяется с использованием BSA пациента, существуют аргументы против использования BSA для определения доз лекарств, имеющих узкий терапевтический индекс — сравнение количества вещества, необходимого для оказания терапевтического эффекта, с количеством, которое вызывает токсичность.

Ниже приведены некоторые из наиболее популярных формул для оценки BSA и ссылки на ссылки по каждой из них для получения более подробной информации об их выводе. Наиболее широко используемой из них является формула Дюбуа, которая, в отличие от индекса массы тела, показала свою эффективность для оценки жировых отложений как у пациентов с ожирением, так и у пациентов без ожирения. Если BSA представлен в м ² , W — это вес в кг , а H — это высота в см , формулы имеют следующий вид:

Формула Дюбуа:

BSA = 0.007184 × Ш ^0,425 × В ^0,725

Du Bois D, Du Bois EF (июнь 1916 г.). «Формула для оценки приблизительной площади поверхности, если известны рост и вес». Архив внутренней медицины 17 (6): 863-71. PMID 2520314. Проверено 9 сентября 2012 г.

Формула Мостеллера:

BSA = = 0,016667 × Ш ^0,5 × В ^0,5

Mosteller RD. «Упрощенный расчет площади поверхности тела». N Engl J Med 1987; 317: 1098. PMID 3657876.

Формула Хейкока:

BSA = 0,024265 × Ш ^0,5378 × В ^0,3964

Haycock GB, Schwartz GJ, Wisotsky DH «Геометрический метод измерения площади поверхности тела: формула роста и веса, проверенная на младенцах, детях и взрослых» J Pediatr 1978, 93: 62-66.

Формула Гехана и Джорджа:

BSA = 0,0235 × W ^0,51456 × H ^0,42246

Gehan EA, George SL, Cancer Chemother Rep 1970, 54: 225-235

Формула Бойда:

BSA = 0.03330 × Ш ^{(0,6157 — 0,0188 × log10 (Ш)} × В ^0,3

Бойд, Эдит (1935). Рост площади поверхности человеческого тела. Университет Миннесоты. Институт защиты детей, серия монографий, № x. Лондон: Oxford University Press

Формула Фудзимото:

BSA = 0,008883 × Ш ^0,444 × В ^0,663

Фудзимото С., Ватанабэ Т., Сакамото А., Юкава К., Моримото К. Исследования площади физической поверхности японцев.18. Расчетные формулы в три этапа для всех возрастов. Nippon Eiseigaku Zasshi 1968; 5: 443-50.

Формула Такахира:

BSA = 0,007241 × Ш ^0,425 × В ^0,725

Фудзимото С., Ватанабэ Т., Сакамото А., Юкава К., Моримото К. Исследования площади физической поверхности японцев. 18. Расчетные формулы в три этапа для всех возрастов. Nippon Eiseigaku Zasshi 1968; 5: 443-50.

Формула Шлиха:

Женщины BSA = 0.000975482 × Ш ^0,46 × В ^1,08

Мужчины BSA = 0,000579479 × W ^0,38 × H ^1,24

Schlich E, Schumm M, Schlich M: «3-D-Body-Scan als anthropometrisches Verfahren zur Bestimmung der spezifischen Korperoberflache». Эрнахрунгс Умшау 2010; 57: 178-183

1. Гринберг, JA., Boozer, CN. 1999. «Метаболическая масса, скорость метаболизма, ограничение калорийности и старение у самцов крыс Fischer 344». Elsevier 113 (2000): 37-48

ios — высота UITableView равна высоте contentSize

Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Общественные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним возможности технической карьеры
Талант Нанять технических талантов
реклама Обратитесь к разработчикам по всему миру

Загрузка…

Авторизоваться зарегистрироваться

Объем равен площадь на высоту: 404 — HTTP not found —

Онлайн калькулятор: Объем геометрических фигур

Объем куба

Объем куба

Объем прямоугольной призмы

Объем прямоугольной призмы

Объем пирамиды

Объем пирамиды

Объем усеченной пирамиды

Объем усеченной пирамиды

Объем равен площадь на высоту

1. Расчет объема куба

2. Найти по формуле, объем прямоугольного параллелепипеда

3. Формула для вычисления объема шара, сферы

4. Как вычислить объем цилиндра ?

5. Как найти объем конуса ?

7. Формула объема усеченного конуса

8. Объем правильного тетраэдра

9. Объем правильной четырехугольной пирамиды

10. Объем правильной треугольной пирамиды

11. Найти объем правильной пирамиды

Строительный объём

Общий строительный объем здания — что это такое

Зачем нужен строительный объем жилого дома и других зданий

Какие показатели используют при расчете

Как считается строительный объем здания: основные правила

Как посчитать строительный объем здания — примеры, инструкции, советы

Самый простой способ

Более точный расчет строительного объема

Дома с подземной частью

Здания без подвала

Здания с чердачными перекрытиями

Дома без чердачного перекрытия

Если известна общая площадь

Если известна площадь застройки

Дома с мансардами

Если здание имеет сложную форму

Калькулятор для расчета площади

Как найти объем помещения. Как рассчитать, посчитать объем помещения

Формула объема помещения

Калькулятор площади стены или пола

Строительный объем здания: что это такое, как считается общий строительный объем

Здания с чердачными перекрытиями

Дома без чердачного перекрытия

Если известна общая площадь

Если известна площадь застройки

Дома с мансардами

Если здание имеет сложную форму

Формулы объема, площади поверхности, объем конуса, объем цилиндра, объем шара

формула для правильной и обычной фигуры

Формула вычисления объема тетраэдра

1. Общая формула (через площадь основания и высоту)

2. Объем правильного тетраэдра

Примеры задач

Как создать столбцы одинаковой высоты

Как создать столбцы одинаковой высоты

Шаг 1) Добавьте HTML:

Пример

Столбец 2

Столбец 3

Шаг 2) Добавьте CSS:

Пример

Отзывчивая равная высота

Пример

Равная высота и ширина с использованием Flexbox

Пример

Калькулятор длины, ширины и высоты до объема

Сопутствующие инструменты

Руководство пользователя

Формула

Обозначения

Объемные размеры — длина, ширина и высота

Расчет объема

Приложения

Справка

Бак 25 x 10 x 12 дюймов в галлонах США

Калькулятор площади поверхности тела

Таблица средних BSA

ios — высота UITableView равна высоте contentSize

Share This Story, Choose Your Platform!