Информатика из двоичной в десятичную: Перевод чисел из одной системы счисления в любую другую онлайн

двоичная, восьмеричная, шестнадцатеричная — урок. Информатика, 8 класс.

Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую  информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Двоичной системой счисления называется позиционная система счисления с основанием \(2\).

Для записи чисел в ней использовали только две цифры:  \(0\) и \(1\).

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 —  число в двоичной системе счисления.

 

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием \(2\), например:

 

1012=1 ·22+0 ·21+1 ·20.

 

В десятичной системе счисления это число будет выглядеть так:

 

1012=4+0+1=5.

 

Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на \(2\) до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число \(13\) в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

 

 

Получили 1310=11012.

Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

 

\(224\)	\(112\)	\(56\)	\(28\)	\(14\)	\(7\)	\(3\)	\(1\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)	\(1\)	\(1\)	\(1\)

 

22410=111000002.

Восьмеричной системой счисления называется позиционная система счисления с основанием \(8\).

 

Для записи чисел в восьмеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\).

Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в восьмеричной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём восьмеричное число  154368 в десятичную систему счисления.

154368=1 ·84+5 ·83+4 ·82+3 ·81+6 ·80=694210

Пример:

Переведём десятичное число \(94\) в восьмеричную систему счисления.

 

 

9410=1368

Шестнадцатеричной системой счисления называется позиционная система счисления с основанием \(16\).

 

Для записи чисел в шестнадцатеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Для перевода целого десятичного числа в шестнадцатеричную  систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на \(16\) до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём шестнадцатеричное число \(2\)\(A7\) в десятичное.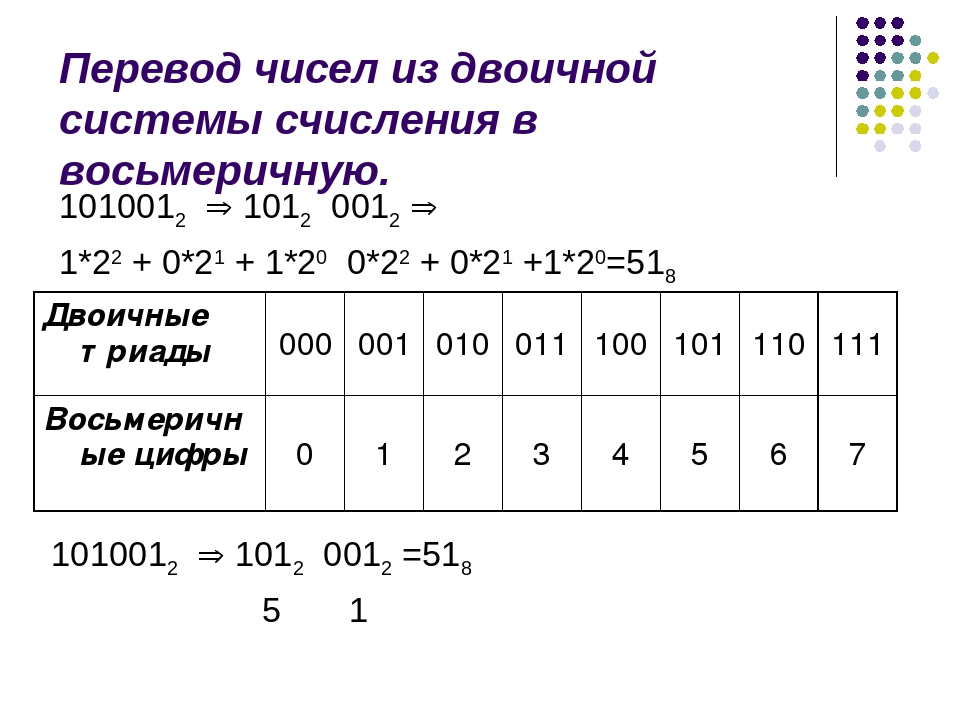

В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием \(16\):

2A716=2 ·162+10 ·161+7 ·160=512+160+7=679.

Пример:

Переведём десятичное число \(158\) в шестнадцатеричную систему счисления.

 

 

15810=9E16.

Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.

Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

Задача №1.

Перевод из одной системы в другую, сравнение чисел в различных системах.

Автор материалов — Лада Борисовна Есакова.

Системы счисления и их разновидности.

Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.

Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.

1. Непозиционные системы счисления.

В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.

Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке.

Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.

Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.

Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:

Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число

Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.

2. Позиционные системы счисления.

В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.

Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.

Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).

Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.

Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».

2.1. Однородные системы счисления.

В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.

2.2. Смешанные системы счисления.

В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.

Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т. е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т. е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Десятичные дроби и смешанные числа в разных системах счисления.

Автор — Лада Борисовна Есакова.

Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.

1. Перевод смешанного числа в десятичную систему счисления из любой другой.

Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.

Пример 1.

Переведите число 105,4 из восьмеричной системы в десятичную.

Решение:

Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :

Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:

Ответ:

2. Перевод десятичных дробей из десятичной системы счисления в любую другую.

Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.

Пример 2

Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.

Решение:

Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:

Ответ:

Пример 3.

Переведите десятичное число 0,8125 в восьмеричную систему.

Решение:

Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:

Ответ:

3. Перевод смешанных чисел из десятичной системы счисления в любую другую

Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.

Пример 4.

Сколько единиц в двоичной записи десятичного числа 14,125?

Решение:

Переведем целую часть числа в двоичную систему:

Переведем дробную часть числа в двоичную систему:

Соединим целую и дробную части:

14,12510 = 1110,0012

Количество единиц равно 4.

Ответ: 4

Ты нашел то, что искал? Поделись с друзьями!

Перевод двоичных чисел в десятичную систему счисления.

Работа с приложением Калькулятор

Казенное общеобразовательное учреждение Воронежской области

«Павловская школа-интернат №2

для обучающихся с ограниченными возможностями здоровья»

 

Открытый урок по информатике на тему:
 

«Перевод двоичных чисел в десятичную систему счисления»
Работа с приложением Калькулятор»

 

Провела учитель информатики

Юрова А.А.

Павловск 2016 г.

Тип урока: урок  изучения нового материала
Форма работы: фронтальная, групповая,  индивидуальная.
Методы: объяснительно-интерактивный.
Цели урока:
 Дидактическая – создать условия для усвоения нового материала, используя   интерактивный  метод обучения и работу в малых группах.
Образовательная  – познакомить со способами перевода двоичных чисел в десятичную систему счисления.
Развивающая – развивать умение школьников излагать свои мысли, аргументировать их.
Воспитательная – воспитывать общую культуру, эстетическое восприятие окружающего; создать условия для реальной самооценки учащихся, умение их давать объективную самооценку, социализация.

Коррекционная — коррекция внимания, мышления, памяти.
Задачи урока:
Воспитательная: развивать познавательный интерес, создать условия для формирования коммуникативной культуры.
Учебная: ввести новые понятия, расширить представления о возможностях приложения Калькулятор, закрепить основной программный материал в процессе выполнения заданий, осуществить первичный контроль.
Развивающая: развивать логическое мышление, расширять кругозор через различные задания для развития логического мышления, речи.

Оборудование:

компьютер;

проектор;

раздаточный материал (карточки).

Основные понятия:

двоичная система счисления;

двоичное кодирование.

Структура урока

Организационный момент (1 мин)

Актуализация опорных знаний учащихся, проверка, воспроизведение и коррекция знаний учащихся. (10 мин)

Сообщение темы, задач урока и мотивация учебной деятельности. (2 мин)

Изучение нового материала, его закрепление.
4.1 Восприятие и первичное осознание нового материала, осмысление связей и отношений в объектах изучения. (10 мин)

4. Гимнастика для глаз (2 мин)
   5. Компьютерный практикум(10 мин.)

6. Обобщение и систематизация знаний. (5 мин)

7. Домашнее задание, подведение итогов (рефлексия). (4 мин)

Ход урока

Организационный момент (1 мин)

Здравствуйте, ребята! Садитесь. Дежурный, назовите отсутствующих. Спасибо!

 Актуализация опорных знаний учащихся, проверка, воспроизведение и коррекция знаний учащихся. (10 мин)

Скажите пожалуйста, какую тему мы изучали на прошлом уроке? (Кодирование информации.

Перевод чисел из десятичной системы счисления в двоичную)

Что такое кодирование? (Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.)

Что такое декодирование? (Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.)

Что такое система счисления? (Система счисления – совокупность приемов и правил записи чисел с помощью определенного набора символов.)

Какие группы систем счисления вы знаете? (позиционные, непозиционные)

Что такое позиционные системы счисления? (Позиционные — количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.)

Что такое непозиционные системы счисления? (Непозиционные — количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра. )

Какие виды систем счисления вы знаете? (десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.)

Какие числа используются в десятичной системе счисления? (0-9)

Какие числа используются в двоичной системе счисления? (0,1)

С помощью какого действия мы переводим числа из десятичной системы счисления в двоичную? (делением на 2)

Сейчас я проверю как вы усвоили материал прошлого урока. Я раздаю карточки на которых написаны числа, которые надо перевести из десятичной системы счисления в двоичную. У кого появятся вопросы, поднимите руку, я подойду.

Справились с заданием? Молодцы!

2.1.Работа по карточкам. Проверка домашнего задания.

12610—X2	32410—X2	52810—X2
10010—X2	26810—X2	62310—X2
22810—X2	44410—X2	59710—X2

Сообщение темы, задач урока и мотивация учебной деятельности. (2 мин)

Как вы мне уже ответили мы переводим числа из десятичной системы счисления в двоичную при помощи действия деления. Скажите пожалуйста, а можем ли мы числа переводить из двоичной системы счисления в десятичную?

Конечно, а как вы думаете, какое действие мы при этом будем использовать? Молодцы! Конечно мы можем переводить числа как из десятичной системы в двоичную, так и наоборот. Запишите тему сегодняшнего урока: «Перевод чисел из двоичной системы счисления в десятичную»

 Изучение нового материала

4.2.Изучение нового материала, его закрепление.

Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа

Примеры перевода чисел из двоичной системы счисления в десятичную

Для примера переведем число 11011012 из двоичной системы счисления (далее СС) в десятичную. Нижний индекс 2 указывает, что число1101101 записано в двоичной системе счисления. 

1.Записываем число, которое необходимо перевести из двоичной системы счисления и справа налево над каждой цифрой числа ставим степень, начиная с нулевой:

2.Теперь умножаем каждую цифру числа на 2 в степени, которая стоит над числом и складываем результаты – получаем значение числа в десятичной системе счисления:

1*26 + 1*25 + 0*24 + 1*23 + 1*22 + 0*11 + 1*20 = 64 + 32 + 0 + 8 + 4 + 0 + 1 = 10910

При этом необходимо помнить, что любое число в нулевой степени равно единице:

4.3.Восприятие и первичное осознание нового материала, осмысление связей и отношений в объектах изучения.  (10 мин)

0001100111	11110001010	11111111
1000011001	00011111000	00000000
0111111000	00001101110	11110000

4. 4. Гимнастика для глаз

Компьютерный практикум (10 мин)

А теперь, опираясь на новые знания, проведем еще один эксперимент. А для этого нам понадобится сесть за компьютеры. Давайте вспомним основные правила ТБ при работе на ПК.
Практическая работа.
Перевод чисел из двоичной системы счисления в десятичную
Цель: закрепить знания по теме

Запустите приложение (Пуск – Программы – Стандартные – Калькулятор). Выполните команду Вид – Инженерный. Обрате внимание на группу переключателей, определяющих систему счисления:

Убедитесь, что Калькулятор настроен на работу в десятичной системе счисления (переключатель стоит на значении Dec). Введите в поле ввода произвольное двузначное число. Активизируйте переключатель Bin и проследите за изменениями в окне ввода. Вернитесь в десятичную систему счисления. Очистите поле вода.  

Настройте калькулятор на работу в двоичной системе счисления (поставить переключатель на значение Bin). Обратите внимания на то, какие кнопки Калькулятора и цифровые клавиши  клавиатуры вам доступны. Какие цифровые клавиши вам доступны? (0,1)

Переведите, при помощи калькулятора, числа из двоичной системы счисления в десятичную. Результат запишите на карточке.

001101011010	110011111001	00000111000000
01010101110	10110110001	1111111100111

Закройте приложение Калькулятор. 

Выставление отметок

Обобщение и систематизация знаний, полученных на уроке. (5 мин)

Итак, подведем итог нашего урока.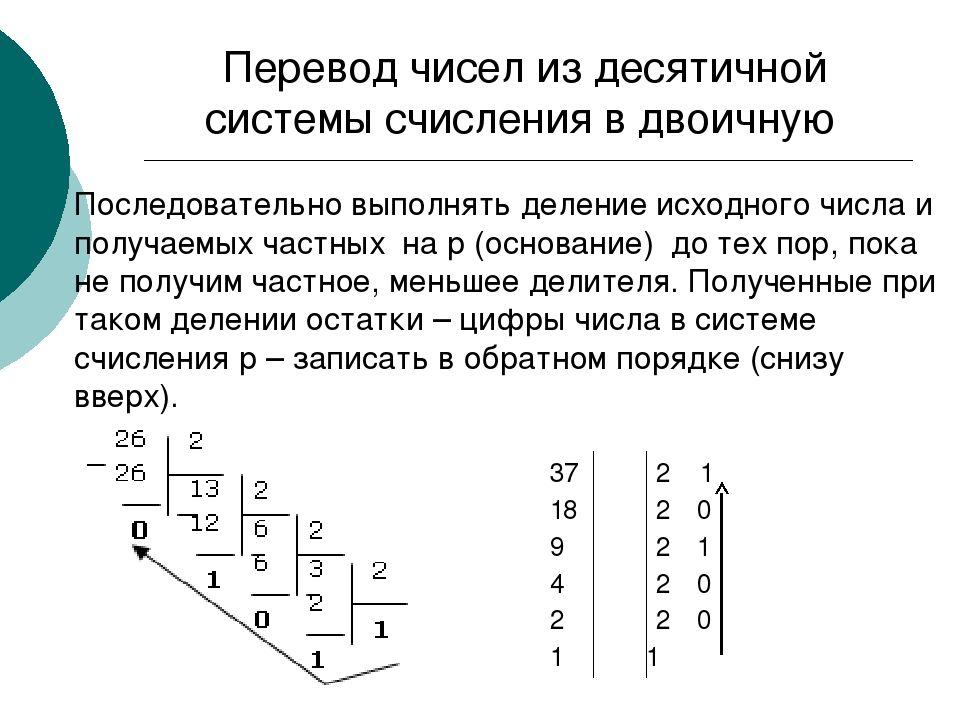

Ребята, я подготовила для вас несколько слов благодарности, но они закодировались, помогите мне пожалуйста восстановить фразу.

14		10000					1101				10000						5		11000				11101
3	29					10011				6			4			10000					5	1111		33
18		1	2		10000				20			1		1101						10
23		10000					18	10000							26			10000

Домашнее задание, подведение итогов (рефлексия). (4 мин)

Выставление отметок. Запишите домашнее задание, готовьтесь дома внимательно, вас ждет еще много интересных задач.

Перевод чисел | Практическая информатика

Наиболее часто встречающиеся системы счисления — это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Рассмотрим различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.

Пусть требуется перевести число 567 из десятичной в двоичную систему. Сначала определим максимальную степень двойки, такую, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, т. к. 2⁹=512, а 2¹⁰=1024, что больше начального числа. Таким образом, мы получим число разрядов результата. Оно равно 9+1=10. Поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 567-2⁹=55. Остаток сравним с числом 2⁸=256. Так как 55 меньше 256, то девятый разряд будет нулем, т. е. результат примет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 2⁷=128>55, то и он будет нулевым.

Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 2⁵=32<55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55-32=23 справедливо неравенство 2⁴=16<23, что означает равенство единице пятого разряда. Действуя аналогично, получаем в результате число 1000110111. Мы разложили данное число по степеням двойки:

567=1*2⁹+0*2⁸+0*2⁷+0*2⁶+1*2⁵+1*2⁴+0*2³+1*2² +1*2¹+1*2⁰

При другом способом перевода чисел используется операция деления в столбик. Рассмотрим то же самое число 567. Разделив его на 2, получим частное 283 и остаток 1. Проведем ту же самую операцию с числом 283. Получим частное 141, остаток 1. Опять делим полученное частное на 2, и так до тех пор, пока частное не станет меньше делителя. Теперь для того, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, то есть 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.

Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1000110111.

Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Для закрепления навыков рассмотрим перевод числа 567 в систему счисления с основанием 16.

Сначала осуществим разложение данного числа по степеням основания. Искомое число будет состоять из трех цифр, т. к. 16²=256 < 567 < 16³=4096. Определим цифру старшего разряда. 2*16²=512<567<3*16²=768, следовательно искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567-512). 3*16=48<55<4*16=64, значит во втором разряде находится цифра 3. Последняя цифра равна 7 (55-48). Искомое шестнадцатеричное число равно 237.

Второй способ состоит в осуществлении последовательного деления в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.

Конечно, не надо забывать и о том, что для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.

Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a₀*pⁿ + a₁*p^n-1 + … + a_n-1*p¹ + a_n*p⁰, где a₀ … a_n — это цифры данного числа в системе счисления с основанием p.

Пример

Переведем число 4A3F в десятичную систему. По определению, 4A3F= 4*16³+A*16²+3*16+F. Заменив A на 10, а F на 15, получим 4*16³+10*16²+3*16+15= 19007.

Пожалуй, проще всего осуществляется перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2ⁿ, нужно

• данное двоичное число разбить справа налево на группы по n-цифр в каждой;
• если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов;
• рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2ⁿ.

Двоично-шестнадцатеричная таблица

2-ная	0000	0001	0010	0011	0100	0101	0110	0111
16-ная	0	1	2	3	4	5	6	7
2-ная	1000	1001	1010	1011	1100	1101	1110	1111
16-ная	8	9	A	B	C	D	E	F

Двоично-восьмеричная таблица

2-ная	000	001	010	011	100	101	110	111
8-ная	0	1	2	3	4	5	6	7

Задания

1. Переведите в десятичную систему счисления:
   • а) 10001110₂;
   • б) 12345₈;
   • в) AA02D34B₁₆.
2. Сравните два числа:
   • а) 1026₈ и 216₁₆;
   • в) 11111₂ и 11111₃.

Простая информатика — Система счисления

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1.
 II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел). 

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.

Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 264 — трехразрядное число, 00010101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка — третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни. 

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
 0 – это ноль
 1 – это один (и это предел разряда)
 10 – это два
 11 – это три (и это снова предел)
 100 – это четыре
 101 – пять
 110 – шесть
 111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные. 

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 13710
Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
 38 / 2 = 19 (0 остаток)
 19 / 2 = 9 (1 остаток)
 9 / 2 = 4 (1 остаток)
 4 / 2 = 2 (0 остаток)
 2 / 2 = 1 (0 остаток)
 1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0
 001 – 1
 010 – 2
 011 – 3
 100 – 4
 101 – 5
 110 – 6
 111 – 7

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 1011101₂ = 1358.

Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.

100₈ = 1 0 0 = 001 000 000 = 001000000 = 10000002 

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

6728 = 6 * 8² + 7 * 8¹ + 2 * 8⁰ = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
 1008 = 1 * 8² + 0 * 8¹ + 0 * 8⁰ = 6410

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15). 

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

Например:
 10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):

4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.

FF = 15 * 161 + 15 * 160 = 240 + 15 = 255 

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

Информатика — Двоичная система счисления

В этом разделе всюду речь идет о двоичной записи чисел.

Главное: Двоичная запись числа N означает представление этого числа в виде суммы степеней двойки. Места, на которых стоит 1, показывают, какие степени двойки нужно брать.  Номер места отсчитывается справа налево и начиная с 0.

Примеры.
1)      25 = 16+8+1 = 2⁴ + 2³ + 2⁰ . Поэтому 25 = 11001₂ .
2)      66 = 64 + 2 = 2⁶ + 2¹ . Поэтому 66 = 1000010₂ .

Как переводить числа из десятичной системы в двоичную можно посмотреть, например, здесь.  Хорошая книга лежит здесь. Непонятно — пишите.
Другие свойства следуют из этого свойства. Вот несколько примеров.

 1. Четные числа оканчиваются на 0, нечетные – на 1.

  2. Число 2^k в двоичной системе счисления записывается единицей и k нулями.     Например, 32 = 2⁵ в двоичной системе счисления записывается так: 100000

 3. Число N делится на 2^k  <===>  число N оканчивается на k нулей

 

 4.  Число 2^k – 1 в двоичной системе счисления записывается k единицами. Например, 31 = 2⁵ – 1 в двоичной системе счисления записывается так: 11111  

 

5.   Двоичная запись числа N содержит ровно k цифр

                 тогда и только тогда, когда 

      Число N принадлежит интервалу 2^k-1 ≤ N ≤  2^k  — 1 

Действительно, пусть, например, k=5.   Наименьшее число, которое записывается 5-ю цифрами – это число 10000₂ = 2⁴ = 16₁₀. А наибольшее число, которое записывается 5-ю цифрами – это число 11111₂ = 2⁴+ 2³+ 2²+ 2¹+ 2⁰  = 16₁₀+8₁₀+4₁₀+2₁₀+1₁₀= 31₁₀ = 32 – 1 = 2⁵ – 1.

Еще один пример. Для числа 67 имеем:    64 = 2⁶ ≤ 67 ≤  2⁷  — 1 = 127. Двоичная запись числа 67 содержит 7 цифр: 64₁₀ = 1000011₂ = 2⁶ + 2¹ + 2⁰

 

 

 

 

 

Что думаете?

 

 

2.1 Представление информации в двоичной системе счисления

        В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

        Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

        В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

        Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

100010012 = 13710
Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

двоичных и десятичных чисел — AndyBargh.com

Компьютеры и электроника повсеместно используются в современной культуре (вы бы не читали этот пост, если бы они не были), и как новичок в разработке приложений для iOS вам в конечном итоге понадобятся некоторые знания базовых концепций информатики, которые лежат в основе не только Разработка приложений для iOS, но разработка программного обеспечения и компьютеров в целом.

Сегодня это первый из ряда постов, которые призваны дать вам эти знания, и в этом посте мы рассмотрим одну из самых основных концепций информатики — двоичных чисел .

Введение

Как вы, я уверен, вы знаете, компьютеры работают на электричестве.

Будь то сеть, аккумулятор или солнечная энергия, все эти устройства основаны на идее использования электричества для индивидуальной настройки миллиардов крошечных электронных компонентов в одно из двух состояний:

• На (который мы интерпретируем как 1 )
• Off (который мы интерпретируем как 0 )

По сути, каждый из этих отдельных компонентов используется для хранения одного « бит, » информации.

Теперь возможность хранить два значения, 0 и 1, — это хорошо, но далеко не уедет. А что насчет того, чтобы хранить большие значения?

Десятичное представление

Вы помните, когда впервые научились считать и писать числа в школе? Вы можете этого не делать, но для того, чтобы объяснить, как эти крошечные ячейки памяти используются для хранения больших чисел, нам нужно совершить быстрое путешествие по переулку памяти (извинения за глупые шутки!). Давайте посмотрим на пример.

Можете ли вы вспомнить различные числовые столбцы, которым вас учили в школе? Возможно, они ушли в смутное и далекое прошлое, но вас, вероятно, учили, что числа, такие как число 1234, можно записать, выразив их в терминах того, сколько раз нам нужны были столбцы с единицами, десятками, сотнями и тысячами и т. Д.

Итак, если бы мы выписали 1234 в более длинной форме, мы могли бы написать:

1234 = ( 1 x 1000) + ( 2 x 100) + ( 3 x 10) + ( 4 x 1)

Видите, как разные числовые столбцы являются частями выражения?

Теперь вы можете не знать, что мы можем разделить то же выражение еще дальше:

1234 = ( 1 * 10 ³ ) + ( 2 * 10 ² ) + ( 3 * 10 ¹ ) + ( 4 * 10 ⁰ )

Примечание: цифры в верхнем индексе называются показателем степени .Если вы никогда не сталкивались с показателями до этого, посетите https://en.wikipedia.org/wiki/Exponentiation для получения более подробной информации.

Вы видите, что жирные символы по-прежнему являются нашим исходным числом, но можете ли вы также видеть, как я разбил числовые столбцы, чтобы они были выражены как степени 10? Это все то же самое выражение, только в более длинной форме.

Когда мы пишем числа, такие как 1234 выше, мы записываем их в так называемой десятичной системе счисления (также называемой для краткости десятичной ).

Десятичное число , термин, происходящий от латинского decem , означающего 10, использует 10 символов (символы от 0 до 9) для обозначения чисел, и это нотация чисел, к которой привыкло большинство из нас.

Как вы, вероятно, можете видеть из приведенного выше примера, число 10 чрезвычайно важно в десятичной системе счисления и называется основанием системы счисления или основанием числа (http://en.wikipedia.org/wiki/Number_base). Все числа в десятичной системе счисления выражаются с помощью этой системы счисления .

Теперь вам может быть интересно, куда я иду с этим, и вот оно….

Что, если бы вместо 10 символов для выражения чисел мы использовали только два, символы 0 и 1, которые мы обсуждали в самом начале этого поста? Можем ли мы по-прежнему выразить все числа, которые мы хотели, используя только эти два символа?

Ну, как я уверен, вы уже догадались, ответ — да. Скажите «Привет» двоичной системе счисления .

Двоичное представление

Двоичная запись (часто сокращается до двоичная ), происходит от слова bi , означающего два.

В двоичном коде вместо 10 знаков или символов для выражения чисел используются только два символа: 0 и 1 .

Как и в десятичной системе счисления , все числа в двоичной системе счисления выражаются с помощью системы счисления или с основанием . В случае двоичного кода это основание равно 2.

Когда мы записываем двоичных чисел , мы иногда записываем их с основанием как нижний индекс.Это делается для того, чтобы отличить их от чисел в других основаниях (чаще всего, чтобы отличить их от чисел, записанных в десятичном формате ). Вот пример двоичного числа , которое показывает следующее: 101 ₂ .

Теперь предположим, что мы хотим представить десятичное число 27 в двоичном формате . Как бы мы это сделали?

Итак, мы знаем, что в десятичном формате у нас есть разные числовые столбцы (1, 10, 100, 1000 и т. Д.), И каждый из этих столбцов представляет собой значение возведения системы счисления в разную степень.Давайте посмотрим, как будут выглядеть эти столбцы для двоичного кода :

.

Мощность	2 7	2 6	2 5	2 4	2 3	2 2	2 1	2 0
Десятичное число Эквивалент	128	64	32	16	8	4	2	1

Теперь, аналогично decimal , мы можем выразить числа в двоичном формате , складывая вместе различные комбинации числовых столбцов.Однако двоичный отличается от десятичного тем, что вместо возможности использования определенного столбца до 9 раз вы можете использовать каждый столбец только один раз.

Учитывая это, слушайте тизер для вас. Как мы могли объединить столбцы с разными числами выше, чтобы в сумме получилось 27?

Ну, мы могли бы написать:

27 ₁₀ = ( 1 * 16) + ( 1 * 8) + ( 0 * 4) + ( 1 * 2) + ( 1 * 1)

Или альтернативно:

27 ₁₀ = ( 1 * 2 ⁴ ) + ( 1 * 2 ³ ) + ( 0 * 2 ² ) + ( 1 * 2 ¹ ) + ( 1 * 2 ⁰ )

Как и в случае с десятичным числом , если мы удалим часть числового столбца в каждом приведенном выше умножении, мы получим:

27 ₁₀ = 11011 ₂

И вот оно, 27 (которое также можно записать как 27 ₁₀ ), выраженное в двоичном формате !

А как насчет еще одного быстрого примера? Посмотрите, сможете ли вы справиться со следующей задачей самостоятельно.

Можете ли вы решить, как десятичное число 63 ₁₀ представить в двоичном формате?

Преобразование из десятичного в двоичное

Существует также второй, и, по мнению некоторых, более быстрый способ преобразования десятичного в двоичный , называемый методом деления . Давайте снова возьмем наш пример 27 ₁₀ .

Первый шаг в методе деления состоит в том, чтобы взять наше число и выполнить целочисленное деление , используя число 2, следя за остатком.

Примечание: вы можете знать или не знать, но целочисленное деление — это если вы посмотрите на максимальное количество раз, когда одно число впишется в другое вместе с любым остатком.

В нашем случае, если бы мы выполняли целочисленное деление, у нас было бы:

27/2 = 13 r 1.

В методе деления нас интересуют остатки, и мы в конечном итоге будем использовать каждый остаток как цифру в нашем двоичном числе . В этом случае цифра будет 1 .

Затем мы берем наше новое число 13 и снова делим его на 2, отслеживая новый результат и остаток. Это дает нам:

13/2 = 6 r 1.

Мы продолжаем повторять этот процесс, беря новое число, делим его на два и записываем остаток до тех пор, пока у нас не будет напоминания 0 или 1. Как только мы достигаем этой точки, мы также записываем эту последнюю цифру.

Если теперь мы прочитаем все остатки, которые мы отметили, в обратном порядке, мы получим двоичное число i.е. 11011 ₂ . Я написал полную таблицу работы ниже:

Расчет	Результат	остаток
27/2	13	1
13/2	6	1
6/2	3	0
3/2	1	1
1/2	0	1

Давайте попробуем другой пример.

На этот раз я пропущу описание, но посмотрим, сможете ли вы самостоятельно проработать приведенную ниже таблицу.

В этом примере мы попытаемся преобразовать десятичное число , число , число 126 (126, _{, 10,} ) в двоичное число , .

Расчет	Результат	остаток
126/2	63	0
63/2	31	1
31/2	15	1
15/2	7	1
7/2	3	1
3/2	1	1
1/2	0	1

Если считать остатки в обратном порядке, получим 1111110 ₂ .

Итак, теперь мы знаем, как преобразовать из десятичного в двоичного , но как насчет другого направления?

В следующем разделе мы рассмотрим аналог метода деления , который позволяет быстро преобразовать двоичный в десятичный .

Преобразование из двоичного в десятичное

Для преобразования из двоичного в десятичного есть также простой метод, но на этот раз вместо деления на 2 мы собираемся умножить на 2, отсюда и название: метод умножения .

Чтобы убедиться, что мы все поняли, мы воспользуемся нашим результатом из примера в предыдущем разделе и посмотрим, сможем ли мы вернуться к нашему начальному числу.

Давайте начнем с нашего двоичного числа 1111110 ₂ . Также начните с промежуточной суммы 0.

Первым шагом в методе умножения является умножение нашей промежуточной суммы на 2, а затем прибавление первой цифры из двоичного числа, чтобы получить новую промежуточную сумму.

Затем мы повторяем этот процесс для всех оставшихся цифр двоичного числа, умножая промежуточную сумму на два и затем добавляя следующую цифру.

После того, как мы добавили цифру из последнего столбца, мы закончили и должны получить наш десятичный эквивалент . Посмотрим, как получится:

Умножение	Двоичная цифра для добавления	Итого
0 * 2 = 0	1	1
1 * 2 = 2	1	3
3 * 2 = 6	1	7
7 * 2 = 14	1	15
15 * 2 = 30	1	31
31 * 2 = 62	1	63
63 * 2 = 126	0	126

И вот оно.Вернуться к нашему исходному результату 126 ₁₀

Давайте попробуем еще один пример. А как насчет двоичного числа 101101 ₂ ? Опять же, прежде чем смотреть на мои работы, посмотрите, сможете ли вы разобраться с этим самостоятельно.

Умножение	Двоичная цифра для добавления	Итого
0 * 2 = 0	1	1
1 * 2 = 2	0	2
2 * 2 = 4	1	5
5 * 2 = 10	1	11
11 * 2 = 22	0	22
22 * ​​2 = 44	1	45

В данном случае наш результат 45 ₁₀

Как видите, процесс перехода от двоичного эквивалента к его десятичному эквиваленту относительно прост, если вы изучите эту технику, и немного мысленной арифметики все будет готово!

Сводка

Мы оставим все здесь на сегодня, но, завершив сегодняшнюю публикацию, что мы узнали?

Мы рассмотрели двоичную систему счисления и десятичную системы счисления.Мы видели, как числа, записанные в определенной нотации, все выражаются в терминах этих нотаций с основанием системы счисления или с основанием счисления , и мы видели, как для десятичного числа с основанием равно 10 и для двоичного основание системы счисления равно 2.

Мы также узнали о двух методах преобразования: метод умножения для преобразования двоичных чисел в их десятичные эквиваленты и метод деления , который используется для преобразования десятичных чисел в двоичных чисел .В ходе публикации мы рассмотрели несколько примеров.

На этом я оставлю вас с двумя вещами.

Во-первых, если вы застряли в чем-то, что я объяснил в посте, свяжитесь с нами, и я сделаю все возможное, чтобы помочь вам с этим справиться.

Во-вторых, я оставлю вам одну из лучших (или худших) бинарных шуток, которые я знаю. После того, что вы узнали сегодня, это должно хотя бы вызвать у вас улыбку (или, может быть, это передергивает?)…

В мире есть 10 типов людей: те, кто понимает двоичный код, и те, кто нет.

Источник изображения: http://flic.kr/p/4zw5Zx

Преобразование из двоичной системы в десятичную — Двоичная — KS3 Computer Science Revision

Что такое денар

Люди используют десятичную (или десятичную) систему счисления в повседневной жизни. В этой системе есть 10 цифр, которые мы можем использовать: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Значение каждого разряда рассчитывается путем умножения на 10 (т. Е. На степень 10). Первые несколько значений разряда выглядят так:

Тысячи	Сотни	Десятки	Единицы
(1000s)	(100s)	(10997

Расчет значения 1024

19 119 1

Тысяч (1000 с)	Сотен (100 с)	Десятки (10 с)	Единицы (1 с)
4
1 × 1000 +	0 × 100 +	2 × 10 +	4 × 1

Преобразование из двоичного числа в денарное

Чтобы преобразовать двоичное число в десятичный, начните с записи из двоичных разрядов.В десятичной форме разряды равны 1, 10, 100, 1000 и т. Д. — каждое разовое значение в 10 раз больше предыдущего. В двоичном формате каждое разрядное значение в 2 раза больше предыдущего (т. Е. Увеличивается в степени 2). Первые несколько двоичных разрядов выглядят так:

Расчет значения 1010 1000:

128	64	32	16	8	4	2	1
1	0	1	0	1	0	0	0
1 × 128 +	0 10 641995 +	0 10 641995 +	0 × 16 +	1 × 8 +	0 × 4 +	0 × 2 +	0 × 1
128 +	0	32 +	0 +	8 +	0 +	0 +	0

Таким образом, 1010 1000 в двоичном формате равно 168 в денарном.

Как компьютер преобразует двоичное число в его десятичный эквивалент с дополнением до 2

Технически вы не можете преобразовать двоичное число в десятичное, потому что в компьютерах нет хранилища для представления десятичных чисел.

На практике это может показаться абсурдным, поскольку мы всегда имеем дело с числами в десятичном представлении. Но эти десятичные представления никогда не сохраняются в десятичном виде. Единственное, что делает компьютер, — это преобразовывает число в десятичное представление при его отображении.И это преобразование связано с построением программ и дизайном библиотек.

Приведу небольшой пример на языке Си. В C у вас есть целочисленные переменные со знаком и без знака. Когда вы пишете программу, эти переменные используются для хранения чисел в памяти. Кто знает об их приметах? Компилятор. В языках ассемблера есть операции со знаком и без знака. Компилятор отслеживает знак всех переменных и генерирует соответствующий код для подписанного и беззнакового регистра. Таким образом, ваша программа отлично работает со знакомыми или беззнаковыми целыми числами при компиляции.

Предположим, вы использовали предложение printf для печати целочисленной переменной и использовали преобразователь формата % d для печати значения в десятичном представлении. Это преобразование будет обрабатываться функцией printf , определенной в стандартной библиотеке ввода-вывода C. Функция считывает переменную из памяти, преобразует двоичное представление в десятичное, используя простой базовый алгоритм преобразования. Но целью алгоритма является последовательность символов, а не целое число.Таким образом, этот алгоритм выполняет две функции: он преобразует двоичное представление в десятичное; и он преобразует биты в значения char (или, точнее, коды ASCII). printf должен знать знак числа, чтобы успешно выполнить преобразование, и эта информация снова предоставляется конструкциями компилятора, размещенными во время компиляции. Используя эти конструкции, printf может проверить, подписано ли целое число или нет, и использовать соответствующий метод преобразования.

Другие языки программирования идут аналогичным путем.По сути, числа всегда хранятся в двоичном формате. Знаковое или беззнаковое представление известно компилятору / интерпретатору и, следовательно, общеизвестно. Десятичное преобразование выполняется только по косметическим причинам, и целью преобразования является последовательность символов или строка.

Компьютерные науки: двоичный

/ ru / информатика / аппаратно-программное обеспечение / содержание /

двоичный

На протяжении всей истории почти каждая цивилизация использовала десятичную систему счисления с 10 цифрами : от нуля до девяти.Все числа, которые мы можем придумать, используют некоторую комбинацию этих 10 цифр.

Компьютеры, однако, работают иначе. Вместо этого они используют систему счисления, в которой всего две цифры : единица и ноль. Эта система называется двоичной , и ваш компьютер использует ее постоянно.

Посмотрите видео ниже, чтобы узнать больше о том, как компьютеры используют двоичный код.

Компьютеры нуждаются в информации для того, чтобы делать то, что они делают. Эта цифровая информация, или данных , состоит из чего-то, что называется бит .Бит — это сокращение от двоичной цифры , что означает, что каждый бит на самом деле представляет собой просто одно число: либо , либо , либо , ноль .

Эти биты можно комбинировать для создания более крупных единиц, таких как байты, мегабайты и т. Д., Которые мы используем для измерения наших файлов. Чем больше файл, тем больше в нем бит. Так что что-то вроде видео с высоким разрешением на самом деле состоит из миллионов и миллионов единиц и нулей.

Но как именно эти единицы и нули объединяются и позволяют компьютеру работать? Давайте подумаем о двоичном коде как о выключателе .Представьте, что один представляет выключатель света на , а ноль представляет на . В двоичном режиме индикатор горит или выключен, других возможных состояний нет.

Эти биты объединены в различные комбинации единиц и нулей, и они образуют своего рода код . Затем ваш компьютер быстро обрабатывает этот код и переводит его в данные, сообщая ему, что делать.

Вам может быть интересно, почему компьютеры используют двоичную систему вместо десятичной, которую мы используем для подсчета вещей в нашей повседневной жизни.Как упоминалось выше, двоичный файл имеет два состояния: выключено и включено. Если бы компьютеры использовали десятичную систему, вместо этого было бы 10 состояний , и им пришлось бы работать с намного больше , чтобы обработать их все. Компьютерам легче обрабатывать двоичные файлы, к тому же они занимают меньше места.

Подобно тому, как атомы составляют все вокруг нас в реальном мире, все в цифровом мире можно разбить на двоичные. И хотя мы их не видим, это всего лишь куча единиц и нулей.

/ ru / информатика / языки программирования / содержание /

Типы компьютерных систем счисления: двоичная и десятичная

Отредактировано TheGuyLoveNY, Jen Moreau, SarMal, Sharingknowledge

Двоичные числа

Двоичные числа имеют базовое число, состоящее из единиц и нулей. Компьютеры сильно ограничены двоичными цифрами или битами. Память также представлена ​​в битах, например КБ, МБ, ГБ, ТБ, ПБ.Интересно, что у компьютеров всего два состояния: ON и OFF. Эти состояния представлены цифрами 1 (ВКЛ) и 0 (ВЫКЛ). Когда число передается из одной ячейки памяти в другую, например, a = 4, десятичное число 1 присваивается переменной a. Это десятичное число преобразуется в биты: (0100) 2. ЦП сигнализирует о передаче памяти. В этом случае переходит в память, где находится переменная a . 0100 бит присвоено переменной a.

Ну, это было легко, но настоящий вопрос в том, как компьютер узнает, что такое 1 и 0? Тот факт, что компьютер является электронным устройством, когда происходит питание или электричество, представлен.Когда нет электричества, означает 0 (ВЫКЛ). При присвоении (0100) «a» он должен быть (ВЫКЛ ВКЛ ВЫКЛ ВЫКЛ).

‘

Десятичные числа

Мы используем десятичные числа везде в нашей повседневной жизни. Цифры от 0 до 9 — это десятичные числа, также известные как денары. Люди работают с десятичными числами, а компьютеры — нет. Как объяснялось выше, компьютеры работают только с двоичными числами. Десятичные числа преобразуются в двоичные числа, чтобы хранить их на компьютерах. Всякий раз, когда они отображаются на экране, они преобразуются из двоичных в десятичные числа.

Шестнадцатеричные числа

Шестнадцатеричные числа — это числа с основанием 16 или шестнадцатеричные.Чаще всего они используются компьютерными программистами. Он состоит из цифр от 0 до 9, и оттуда он представлен как A для 10, B для 11 и так далее до F для 15.

Вот таблица из шестнадцатеричного в двоичное число:

Бинарное сложение

Бинарное сложение довольно просто. Два двоичных числа добавляются побитно.

• 1 + 1 = 0, 1 заимствуется в следующий бит.
• 0 + 1 = 1
• 1 + 0 = 1
• 0 + 0 = 0

Пример 1: Складываем (110110) 2 и (1110001) 2

Результат: (1101111) 2

Дополнение 2 Дополнение

до 2 используется для представления отрицательных двоичных чисел в памяти компьютера.Положительные числа напрямую представлены как есть, а отрицательные числа представлены с помощью дополнения до 2. Дополнение 2 использует дополнение 1.

2 Комплектация работ: Примените дополнение 1. Добавьте к битам 1 бит. Теперь дополнение 1 — это не что иное, как инвертирование битов, то есть с 1 до 0 и наоборот.

Например: Представьте (1101111) 2 в дополнении 2.

• Шаг 1: Инвертировать все биты (дополнение до единицы).

(1101111) 2 >>>>> (0010000) 2

• Шаг 2: Добавьте к битам 1 бит.

Дополнение 2 к (1101111) 2 — это (0010001) 2

Двоичное вычитание

Двоичное вычитание немного отличается в битах. Шаги в двоичном вычитании:

Шаг 1: Преобразуйте биты секунды в дополнение до 2. Шаг 2: сложите два бита. Шаг 3: Игнорируйте лишний бит из результата (если есть).

Пример 1:

Вычтите (10101) 2 и (01110) 2

• Шаг 1: Возьмите 2-е дополнение до 2-го значения.

Инвертировать все биты и добавить к нему 1 бит.

01110 >>>>>>>>> 10001

(10001) 2 + (00001) 2 = (10010) 2

• Шаг 2: Добавьте оба бита.

Результат: (00111) 2

Пример 2: Выполните двоичное вычитание для 010101 и 101010

• Шаг 1: Применение дополнения до 2 ко вторым битам.

Инвертировать все биты: (101010) >>>>>>> (010101)

Теперь добавьте к результату 1 бит: (010101) + (000001) = (010110)

• Шаг 2: Добавьте оба бита.

(010101) 2 + (010110) 2

Не было лишнего бита, который нужно было отбрасывать, поэтому результат: (101011) 2

Эта статья является частью серии, посвященной

Компьютерная организация и язык ассемблера (COAL) . Читайте полную серию здесь

Ссылка на эту статью

Если вам нужно ссылаться на эту статью в своей работе, вы можете скопировать и вставить следующее в зависимости от необходимого формата:

APA (Американская психологическая ассоциация)
Типы компьютерных систем счисления: двоичные и десятичные.(2017). В ScienceAid . Получено 22 февраля 2021 г. с https://scienceaid.net/Number_Systems

.

MLA (Ассоциация современного языка) «Типы компьютерных систем счисления: двоичные и десятичные». ScienceAid , scienceaid.net/Number_Systems По состоянию на 22 февраля 2021 г.

Чикаго / Турабиан ScienceAid.net. «Типы компьютерных систем счисления: двоичные и десятичные». По состоянию на 22 февраля 2021 г. https://scienceaid.net/Number_Systems.

Комментарии

Категории: Компьютерная организация и язык ассемблера

Последние редакции: SarMal, Jen Moreau, TheGuyLoveNY

двоичный — Computer Science Wiki

Из Википедии о компьютерных науках

Перейти к навигации Перейти к поиску

Это основная концепция информатики

В математике и цифровой электронике двоичное число — это число, выраженное в двоичной системе счисления или системе счисления с основанием 2, которое представляет числовые значения с использованием двух разных символов: обычно 0 (ноль) и 1 (единица).Система с основанием 2 представляет собой позиционную систему счисления с основанием 2. Из-за ее простой реализации в цифровых электронных схемах с использованием логических вентилей двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств. Каждая цифра называется битом. ^[1]

Это одно из лучших видео о двоичных файлах, которые я видел. Содержимое используется с благодарностью и разрешением: ^[2]

Основные определения [править]

• бит : бит представляет логическое состояние с одним из двух возможных значений
• байт : группа из 8 смежных двоичных цифр (8 бит), на которой компьютер работает как единое целое
• двоичная : двоичная система счисления является системой счисления с основанием 2.
• денарная / десятичная : десятичная система счисления (также называемая основанием 10 или иногда денарная) имеет основу десять. ^[3]
• шестнадцатеричный : В математике и вычислительной технике шестнадцатеричное (также основание 16 или шестнадцатеричное) — это позиционная система счисления с основанием 16 ^[4] . Щелкните здесь, чтобы увидеть отличное видео о шестнадцатеричном формате

Таблица двоичного перевода [править]

Я считаю полезным нарисовать эту таблицу, когда мне нужно преобразовать двоичный код в базу 10.Это также помогает при просмотре видео выше.

Полезная шпаргалка [править]

Как сложить два двоичных числа [править]

Добавить двоичный файл очень просто. Выровняйте числа, как если бы вы складывали числа с основанием 10.

Запомните это:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10, поэтому напишите 0 и перенесите 1 в следующий столбец.

Что вы должны знать [править]

Вы должны уметь правильно ответить на следующие вопросы:

• Определите термин: бит
• Определите термин: байт
• Определите термин: двоичный
• Определите термин: десятичный / десятичный (они относятся к одному и тому же)
• Определите термин: шестнадцатеричный

Почему это так важно? [Править]

Если мы можем представить числа как 1 и 0 , почему бы не представить числа как вкл. И выкл. ? Если мы можем представить буквы как числа (A = 65, B = 66), не могли бы мы также сказать A = 01000001 и B = 01000010? Мы можем следовать этой линии мышления и делать север / юг, вверх / вниз и вниз / вверх.Простые конструкции, которые мы можем использовать для представления более сложных чисел и даже букв.

Двоичное представление — это суть работы компьютеров.

Ресурсы [править]

Щелкните здесь, чтобы просмотреть слайды, хорошо освещающие эту тему

Ссылки [править]

преобразований

преобразований

Принципы CS

Это упражнение знакомит с концепцией, на которой построено абстракций. двоичные последовательности могут использоваться для представления всех цифровых данных .Также вводится концепция алгоритма . Это фокусируется на следующих целях обучения:

• 5б. Объяснение того, как системы счисления, включая двоичные и десятичные, используются для рассуждений о цифровых данных.
• 16а. Использование естественного языка, псевдокода, визуального или текстового языка программирования для выражения алгоритма.

Вступление

Этот урок предполагает, что вы выполнили домашнее задание по двоичному и шестнадцатеричные системы счисления.Эта домашняя работа описывала, как работают двоичные, десятичные и шестнадцатеричные системы счисления и показали, как конвертировать из одной системы счисления в другую.

В этом уроке мы хотим обобщить то, что мы узнали, увидев эти системы счисления как конкретные примеры более общей концепции, позиционная система счисления .

Мы разработаем алгоритмов , которые позволят вам выполнять преобразования из одной системы счисления в другую.

Тип обобщения, который мы делаем в этом уроке, — это еще один пример принципа абстракции в информатике — здесь мы сосредотачиваемся на общей схеме, которая верна для всех позиционные системы счисления.

Алгоритмы и псевдокод

Алгоритм — это пошаговая процедура для выполнения некоторых вычислений. Например, шаги, которые вы выполняете в приложении Hello Purr , когда кнопка clicked — это пример простого двухэтапного алгоритма:

Чтобы помочь нам рассказать об алгоритмах, мы будем использовать псевдокод, язык или обозначение, которые имеют многие структуры язык программирования, но его легко читать. Псевдокоды на полпути между естественными языками, такими как английский, и формальным программированием языков.

Системы позиционных чисел

Давайте рассмотрим некоторые ключевые моменты, которые вы усвоили в книге Хан Видео Академии.

• Наша десятичная система счисления (а также двоичная и шестнадцатеричная системы) являются частными примерами более общей концепции позиционный система счисления.
• В позиционной системе счисления один и тот же символ может представлять различные значения в зависимости от позиции (или позиции ) в цифра. Например, в 91 9 представляет 90 (10-е место). но в 19 он представляет собой 9 (первое место).Сравните это с тем, как символы работают в непозиционной системе, например римские цифры, где X всегда представляет 10.
• Основание числовой системы представляет собой количество символы:

  Имя	База	Символы
  Десятичный	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
  Двоичный	2	, 1
  Шестнадцатеричный	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
  Восьмеричный	8	0, 1, 2, 3, 4, 5, 6, 7

• В позиционных системах счисления используется возведение в степень от до определить значение символа в зависимости от его места.Мы можем использовать это Идея перевести из любой системы в десятичную:

  Система	База	Значение	Формула преобразования	Десятичное значение
  Десятичное число	10	104	(1 × 10 2 ) + (0 × 62) 10 1 4 × 10 0 )	100 + 0 + 4 = 104
  Двоичный	2	111	(1 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 )	4 + 2 + 1 = 7
  Восьмеричный	8	104	(1 × 8 2 ) + (0 × 8 1 ) + (4 × 8 0 )	64 + 0 + 4 = 68
  Шестнадцатеричный	16	FEC	(F × 16 2 ) + (E × 16 1 ) + (C × 8 0 )	15 × 256 + 14 × 16 + 12 × 1 = 3840 + 224 + 12 = 4076

Алгоритмы преобразования

Обобщим эти формулы преобразования, разработав общий алгоритм, который преобразует любую систему счисления в десятичную.

Алгоритм преобразования любого основания в десятичное основание 10

1. Пусть n будет количеством цифр в номере. Например, 104 состоит из 3 цифр, поэтому n = 3 .
2. Пусть b будет основанием числа. Например, 104 является десятичным, поэтому b = 10 .
3. Пусть с будет промежуточным итогом, изначально 0.
4. Для каждой цифры номера, работая слева направо:
   Вычтем 1 из n .
   Умножьте цифру на b ⁿ и прибавьте к s .
5. Когда вы закончите со всеми цифрами в номере, его десятичное значение будет с

Попробуем на двоичном числе 1011.

Пусть n = 4.
Пусть b = 2.
Пусть s = 0.
   Первая цифра, 1: n = 3, 1 × b  n  равно 1 × 2  3  = 8. Итак, s = 8.
   Вторая цифра, 0: n = 2, 0 × b  n  - это 0 × 2  2  = 0. Итак, s = 8.
   Третья цифра, 1: n = 1, 1 × b  n  равно 1 × 2  1  = 2. Итак, s = 10
   Последняя цифра, 1: n = 0, 1 × b  n  - 1 × 2  0  = 1.Итак, 1011  2  = 11  10 
 

06 062 × 2 900 = 1

Цифра	n	Значение = Цифра * b n	Итого
1	3	1 × 2 3 = 8	8
0 × 2 2 = 0	8
1	1	1 × 2 1 = 2	10
1	0
11

Попробуем на шестнадцатеричном числе 7E.

Пусть n = 2.
Пусть b = 16.
Пусть s = 0.
   Первая цифра, 7: n = 1, 7 × b  n  равно 7 × 16  1  = 7 × 16 = 112. Итак, s = 112.
   Последняя цифра, E: n = 0, 14 × b  n  составляет 14 × 16  0  = 14. Таким образом, s = 112 + 14 = 126. Итак, 7E  16  = 126  10 
 

E

Цифра	n	Значение = Цифра * b n	Итого
7	1	7 × 16 1 = 112	114
14 × 16 0 = 14	126

Попробуем на восьмеричном числе 124.

Пусть n = 3.
Пусть b = 8.
Пусть s = 0.
   Первая цифра, 1: n = 2, 1 × b  n  равно 1 × 8  2  = 1 × 64 = 64. Итак, s = 64.
   Вторая цифра, 2: n = 1, 2 × b  n  равно 2 × 8  1  = 2 × 8 = 16. Итак, s = 64 + 16 = 80.
   Последняя цифра, 4: n = 0, 4 × b  n  равно 4 × 8  0  = 4. Итак, s = 80 + 4 = 84. Итак, 124  8  = 84  10 
 

Цифра	n	Значение = Цифра * b n	Промежуточная сумма
1	2	1 × 8 2 = 64	64
2 × 8 1 = 16	80
4	0	4 × 8 0 = 4	84

Алгоритм преобразования десятичного числа в другое основание

1. Пусть n будет десятичным числом.
2. Пусть м будет числом, изначально пустым, в которое мы конвертируем. Мы будем составлять его справа налево.
3. Пусть b будет основанием числа, в которое мы конвертируем.
4. Повторяйте, пока n не станет 0
   Разделите n на b , пусть результат будет d , а остаток будет r .
   Запишите остаток r как крайнюю левую цифру числа b .
   Пусть d будет новым значением n .

Воспользуемся алгоритмом для преобразования 45 в двоичную форму.

Пусть n = 45.
Пусть b = 2.
Повторение
   45, деленное на b, составляет 45/2 = 22, остаток 1. Итак,  d = 22  и  r = 1 . Итак,  m = 1 , а новое  n  равно 22.
   22, разделенное на b, равно 22/2 = 11, остаток 0. Итак,  d = 11  и  r = 1 . Итак,  m = 01 , а новое  n  равно 11.
   11, разделенное на b, равно 11/2 = 5, остаток 1.Итак,  d = 5  и  r = 1 . Итак,  m = 101 , а новое  n  равно 5.
    5, деленное на b, составляет 5/2 = 2 остатка 1. Итак,  d = 2  и  r = 1 . Итак,  m = 1101 , а новое  n  равно 2.
    2, деленное на b, равно 2/2 = 1 остаток 0. Итак,  d = 1  и  r = 0 . Итак,  m = 01101 , а новое  n  равно 1.
    1, деленное на b, равно 1/2 = 0, остаток 1. Итак,  d = 0  и  r = 1 . Итак,  m = 101101 , а новое  n  равно 0.Итак, 45  10  = 101101  2 
 

Давайте воспользуемся им для преобразования 99 в двоичную форму.

Пусть n = 99.
Пусть b = 2.
Повторение
   99 разделить на b равно 99/2 = 49 остаток 1. Итак,  d = 49  и  r = 1 . Итак,  m = 1 , а новое  n  - 49.
   49, деленное на b, равно 49/2 = 24 остатка 1. Таким образом,  d = 24  и  r = 1 . Итак,  m = 11 , а новое  n  равно 24.
   24 делить на b равно 24/2 = 12, остаток 0.Итак,  d = 12  и  r = 0 . Итак,  m = 011 , а новое  n  равно 12.
   12, деленное на b, составляет 12/2 = 6 остаток 0. Итак,  d = 6  и  r = 0 . Итак,  m = 0011 , а новое  n  равно 6.
    6, деленное на b, составляет 6/2 = 3 остатка 0. Итак,  d = 3  и  r = 0 . Итак,  m = 00011 , а новый  n  равен 3.
    3, деленное на b, составляет 3/2 = 1 остаток 1. Итак,  d = 1  и  r = 1 . Итак,  m = 100011  и новое  n  равно 1.1, деленное на b, равно 1/2 = 0, остаток 1. Итак,  d = 0  и  r = 1 . Итак,  m = 1100011 , а новое  n  равно 0. Итак, 99  10  = 1100011  2 

 

Используем его для преобразования 45 в шестнадцатеричное.

Пусть n = 45.
Пусть b = 16.
Повторение
   45, деленное на b, дает 45/16 = 2 остатка 13. Итак,  d = 2  и  r = 13 . Итак,  m = D , а новое  n  равно 2.
    2, деленное на b, равно 2/16 = 0, остаток 2.Итак,  d = 0  и  r = 2 . Итак,  m = 2D , а новое  n  равно 0. Итак, 45  10  = 2D  16 .
 

Давайте воспользуемся им для преобразования 99 в шестнадцатеричное.

Пусть n = 99.
Пусть b = 16.
Повторение
   99, деленное на b, дает 99/16 = 6 остаток 3. Таким образом,  d = 6  и  r = 3 . Итак,  m = 3 , а новое  n  равно 6.
    6, деленное на b, составляет 6/16 = 0 остаток 6. Итак,  d = 0  и  r = 6 .Итак,  m = 63 , а новое значение  n  равно 0. Итак, 99  10  равно 63  16 .
 

Упражнения в классе

1. Преобразуйте следующие числа в десятичную систему.
   1. Двоичное число 111.
   2. Двоичное число 1011.
   3. Двоичное число 1011 1011.
   4. Шестнадцатеричное число 61.
   5. Шестнадцатеричное число DA.
   6. Шестнадцатеричное число FEE.
2. Преобразуйте следующие десятичные числа, как указано.
   1. Преобразование десятичного числа 12 в двоичное.
   2. Преобразовать десятичное число 44 в двоичное.
   3. Преобразование десятичного числа 254 в шестнадцатеричное.
   4. Преобразование десятичного числа 16 в шестнадцатеричное.
3. Задача: преобразовать десятичное 125 в восьмеричное (с основанием 8) .