Банк ЕГЭ | Открытый банк заданий
Банк ЕГЭ Банк решенных | ЕГЭ по математике В1 ● В2 ● В3 ● В4 ● В5 ● В6 ● В7 |
Полезные советы | Лента задачек | |
| С4Дан параллелограмм $ABCD$, сторона которого $AB=13$. Из углов $А$ и $В$ проведены биссектрисы, которые пересекаются в точке $O$. Расстояние от точки $O$ до отрезка АВ равно $\frac{60}{13}$. В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
Сумма углов треугольника — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике.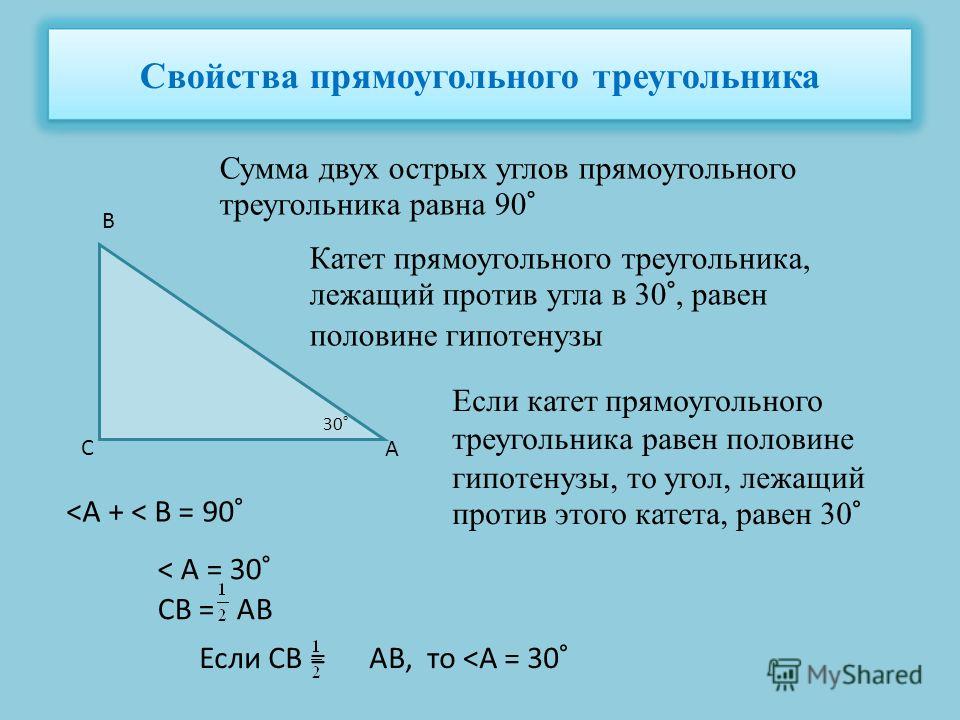 Базовый уровень Сложные задачи
Базовый уровень Сложные задачи
1. Сумма углов треугольника
Теорема. Сумма углов треугольника равна 180о.Доказательство. Для треугольника АВС через вершину С
проведем прямую, параллельную АВ. Тогда 1 = 4, 2
= 5, как внутренние накрест лежащие углы.
Следовательно, 1 + 2 + 3 = 4 + 5 + 3 = 180.
Следствие. Сумма острых
треугольника равна 90о.
углов
прямоугольного
2. Внешний угол треугольника
Теорема. Внешний угол треугольника равен сумме двухвнутренних, не смежных с ним.
4 1 3
3. Упражнение 1
В треугольнике ABC угол A равен 30o, угол Bравен 90o. Найдите угол C.
Ответ: 60о.
4. Упражнение 2
Один острый угол прямоугольного треугольника на32о больше другого. Найдите больший острый
угол.
Ответ: 61о.
5. Упражнение 3
Один острый угол прямоугольного треугольника вдва раза больше другого. Найдите меньший острый
угол.
Ответ: 30о.
6. Упражнение 4
Два острых угла прямоугольного треугольникаотносятся как 2:3.
 Найдите больший острый угол.
Найдите больший острый угол.Ответ: 54о.
7. Упражнение 5
В треугольнике ABC угол A равен 40o, AC = BC.Найдите угол C.
Ответ: 100о.
8. Упражнение 6
В треугольнике ABC угол C равен 120o, AC = BC.Найдите угол A.
Ответ: 30о.
9. Упражнение 7
Один из углов равнобедренного треугольникаравен 100о. Найдите один из других его углов.
Ответ: 40о.
10. Упражнение 8
В треугольнике ABC угол A равен 40o, внешнийугол при вершине B равен 100o. Найдите угол C.
Ответ: 60о.
11. Упражнение 9
В треугольнике ABC угол A равен 40o. Внешнийугол при вершине B равен 70o. Найдите угол C.
Ответ: 30о.
12. Упражнение 10
В треугольнике ABC AC = BC, угол C равен 50o.Найдите внешний угол CBD.
Ответ: 115о.
13. Упражнение 11
В треугольнике ABC AC = BC. Внешний уголпри вершине B равен 120o. Найдите угол C.
Ответ: 60о.
14. Упражнение 12
В треугольнике ABC AB = BC. Внешний уголпри вершине B равен 140o.
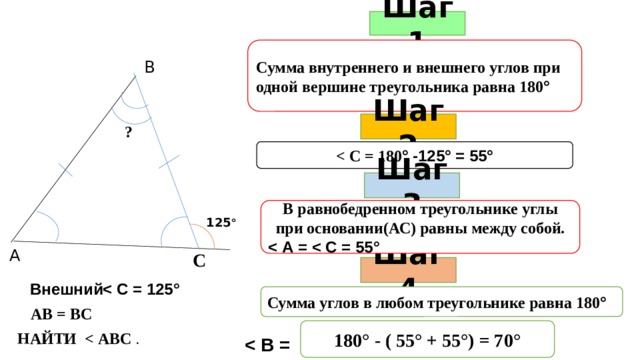 Найдите угол C.
Найдите угол C.Ответ: 70о.
15. Упражнение 13
Один из внешних углов треугольника равен 80о.Углы, не смежные с данным внешним углом,
относятся как 2:3. Найдите наибольший из них.
Ответ: 48о.
16. Упражнение 14
Сумма двух углов треугольника и внешнего угла ктретьему равна 30o. Найдите этот третий угол.
Ответ: 165o.
17. Упражнение 15
Углы треугольника относятся как 1:2:3. Найдитеменьший из них.
Ответ: 30о.
18. Упражнение 16
Один острый угол прямоугольного треугольника в5 раз больше другого. Найдите больший острый
угол.
Ответ: 75о.
19. Упражнение 17
Один острый угол прямоугольного треугольникана 20о больше другого. Найдите меньший острый
угол.
Ответ: 35о.
20. Упражнение 18
В треугольнике АВС угол C равен 90o, CH –высота, угол A равен 35o. Найдите угол BCH.
Ответ: 35о.
21. Упражнение 19
В треугольнике АВС угол А = 65o, угол В = 73o,CH – высота.
 Найдите разность углов ACH и
Найдите разность углов ACH иBCH.
Ответ: 8о.
22. Упражнение 20
В треугольнике АВС угол А равен 30o, CH –высота, угол BCH равен 20o. Найдите угол C.
Ответ: 40о.
23. Упражнение 21
В треугольнике АВС AD – биссектриса, угол Cравен 50o, угол CAD равен 30o. Найдите угол B.
Ответ: 70о.
24. Упражнение 22
В треугольнике АВС AD – биссектриса, угол Cравен 30o, угол BAD равен 20o. Найдите угол ADB.
Ответ: 50о.
25. Упражнение 23
В треугольнике АВС AC = BC, AD – высота, уголBAD равен 25o. Найдите угол C.
Ответ: 50о.
26. Упражнение 24
В треугольнике АВС CD – медиана, угол C равен90o, угол B равен 60o. Найдите угол ACD.
Ответ: 30о.
27. Упражнение 25
В треугольнике ABC угол A равен 70o, BD и CE –высоты, пересекающиеся в точке O. Найдите угол
DOE.
Ответ: 110o.
28. Упражнение 26
Два угла треугольника равны 60о и 70о. Какой уголобразуют между собой высоты, выходящие из
вершин этих углов?
Ответ: 50o.
29. Упражнение 27
В треугольнике ABC угол C равен 60o, AD иBE – биссектрисы, пересекающиеся в точке
O. Найдите угол AOB.
Ответ: 120o.
30. Упражнение 28
Острый угол прямоугольного треугольника равен30о. Найдите угол, образованный биссектрисами
этого и прямого углов треугольника.
Ответ: 60o.
31. Упражнение 29
Найдите углы между биссектрисами острыхуглов прямоугольного треугольника.
Ответ: 45o.
32. Упражнение 30
В треугольнике АВС CH – высота, AD –биссектриса, угол BAD равен 25o. Найдите угол
AOC.
Ответ: 115о.
33. Упражнение 31
В треугольнике АВС угол А равен 48o, угол Cравен 56o. На продолжении стороны АB
отложен отрезок BD = ВС. Найдите угол D
треугольника BCD.
Ответ: 38о.
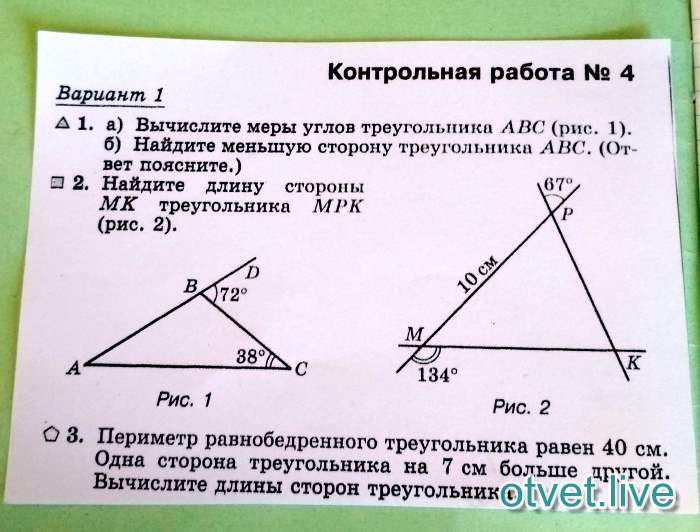
34. Упражнение 32
В треугольнике АВС угол А равен 48o, угол Вравен 56o. На продолжении стороны АС
отложены отрезки СЕ = ВС и AD = AB.
Найдите углы треугольника DEB.
Ответ: 24о, 38о, 118o.
35. Упражнение 33
Острые углы прямоугольного треугольника равны30о и 60о. Найдите угол между высотой и
биссектрисой, проведенными из вершины прямого
угла.
Ответ: 15о.
36. Упражнение 34
В прямоугольном треугольнике угол междувысотой и биссектрисой, проведенными из
вершины прямого угла, равен 20о. Найдите
меньший острый угол данного треугольника.
Ответ: 25о.
37. Упражнение 35
Острые углы прямоугольного треугольника равны25о и 65о. Найдите угол между высотой и
медианой, проведенными из вершины прямого
угла.
Ответ: 40о.
38. Упражнение 36
В прямоугольном треугольнике угол междувысотой и медианой, проведенными из вершины
прямого угла, равен 30о. Найдите больший из
острых углов этого треугольника.
Ответ: 60о.
39. Упражнение 37
Острые углы прямоугольного треугольника равны25о и 65о. Найдите угол между биссектрисой и
медианой, проведенными из вершины прямого
угла.

Ответ: 20о.
40. Упражнение 38
Угол между биссектрисой и медианойпрямоугольного треугольника, проведенными из
вершины прямого угла, равен 15о. Найдите
меньший острый угол этого треугольника.
Ответ: 30о.
41. Упражнение 39
В треугольнике ABC угол B равен 45o, угол C равен80o, AD – биссектриса, AE = AC. Найдите угол
BDE.
Ответ: 35o.
42. Упражнение 40
В треугольнике ABC угол A равен 30o, угол B равен85o, CD – биссектриса внешнего угла, СE = BC.
Найдите угол BDE.
Ответ: 55o.
43. Упражнение 41
На рисунке угол 1 равен 45о, угол 2 равен90о, угол 3 равен 30о. Найдите угол 4.
Ответ: 120о.
44. Упражнение 42
На рисунке 1 = 45о, 2 = 100о, 3 = 60о, 4= 30о . Найдите углы 5, 6.
Ответ: 110о, 140о.
45. Упражнение 43
На рисунке 1 = 45о, 2 = 110о, 3 = 70о, 4= 45о, 5 = 20о. Найдите угол 6.
English Русский Правила
Теорема по углам наружного угла — Формула и примеры
, написанные
Малкольм МакКинси
Проверка по фактам
Пол Маззола
Внешний угол.
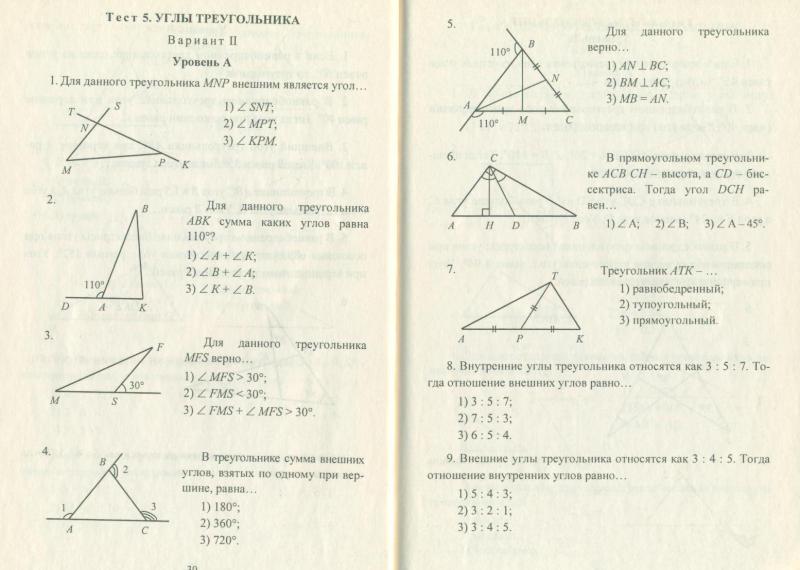 любой внешний угол треугольника равен сумме двух противоположных внутренних углов и что сумма всех трех внутренних углов треугольника равна 180° , сумме двух прямых углов (теорема о сумме треугольников).
любой внешний угол треугольника равен сумме двух противоположных внутренних углов и что сумма всех трех внутренних углов треугольника равна 180° , сумме двух прямых углов (теорема о сумме треугольников).Формула теоремы о внешнем угле
Теорема о внешнем угле основана на предложении 16 Евклида и предложении 32 его «Элементов». Вместе они дают нам теорему о внешнем угле, которую мы можем использовать для решения отсутствующих углов треугольников.
Теорема о внешнем углеВнешние углы треугольника
Чтобы понять теорему о внешнем угле, вы должны знать, что такое внешний угол любого многоугольника. Треугольник имеет три внутренних угла, но он также имеет шесть внешних углов, которые являются углами между стороной треугольника и продолжением смежной стороны.
Взяв по одному внешнему углу в каждой вершине, сумма трех внешних углов любого многоугольника всегда равна 360° . Это работает в любом направлении.
Доказательство теоремы о внешнем угле
Построим треугольник с внешним углом и докажем теорему о внешнем угле.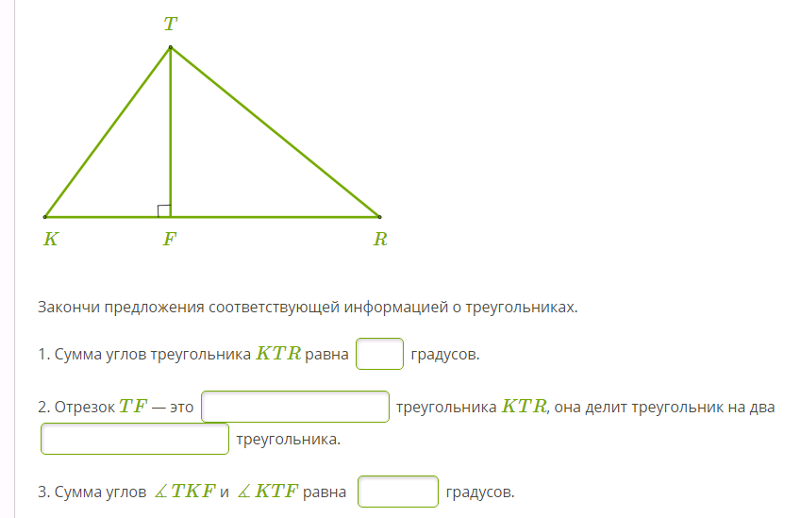
Вот △ABC , названный в честь трех углов: угол A , угол B и угол C . Мы расширили одну сторону, до н.э. , далеко за пределы треугольника:
Построение внешнего углаДобавляем Точку D на отрезок BC и получаем отрезок BD . Это дает нам внешний вид ∠ACD .
Далее построим отрезок, параллельный отрезку AB :
Доказательство теоремы о внешнем угле. Это означает ∠BAC и ∠ACE конгруэнтны, потому что они представляют собой чередующиеся внутренние углы двух параллельных прямых, пересеченных секущей.
Два угла, ∠ECD и ∠ABC , также равны, потому что они являются соответствующими углами.
Следовательно, ∠ACD равно сумме мер ∠BAC + ∠ABC , двух внутренних углов треугольника, противоположных внешнему ∠ACD .
Последний шаг, добавление внутреннего ∠ACB к ∠ACD чтобы получить отрезок прямой BD , показывает, что сумма трех внутренних углов треугольника составляет 180° .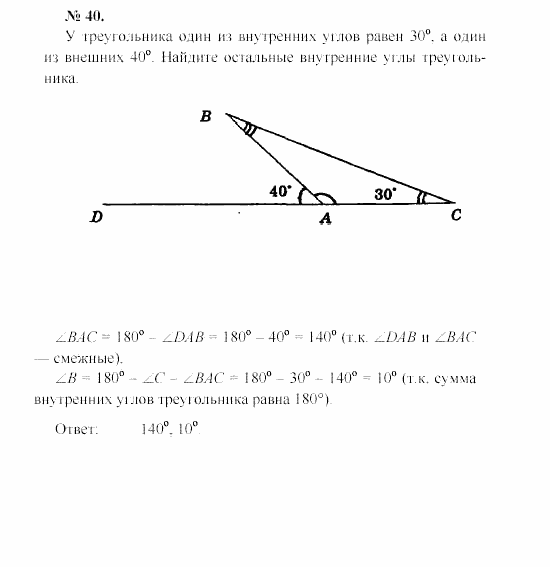
Пример теоремы о внешнем угле
Теорема о внешнем угле полезна для нахождения неизвестного угла любого треугольника. Если вам дана мера одного внешнего угла треугольника, J , и одного противоположного угла, F , вычитание даст вам недостающий угол, G . Символ, ∠ обозначает измеренный угол.
Вычтите известный внутренний угол из внешнего угла:
Предположим, что внешний угол равен 110° и вам сказали, что один из его противоположных внутренних углов равен 47° . Подставьте известные значения, чтобы найти неизвестное:
Теперь вы знаете два из трех внутренних углов и можете, при необходимости, легко найти третий внутренний угол, вычитая их из 180° :
Теорема о внешнем треугольникВы также можете использовать теорему, чтобы найти угол, прилегающий к внешнему углу, просто вычитая внешний угол из 180° .
Теорема о внешнем угле Часто задаваемые вопросы
Вы поняли это? Проверьте понимание, ответив на эти вопросы.
Сколько внешних углов у треугольника? Сколько внутренних углов?
Чему равна сумма внутренних углов треугольника?
Чему равна сумма одного набора внешних углов треугольника?
Внешний угол треугольника равен 145° , а один из его противоположных внутренних углов равен 51° . Чему равен другой противолежащий внутренний угол?
Внешний угол треугольника равен 139° . Чему равен прилежащий внутренний угол треугольника?
Пожалуйста, сделайте все возможное, прежде чем сверять свои ответы с нашими.
Треугольник имеет шесть внешние углы и три внутренних угла .
Сумма внутренних углов треугольника равна 180° (теорема о суммах треугольников).
Сумма одного набора внешних углов треугольника равна 360° .
Внешний угол треугольника равен 145° , а один из его противоположных внутренних углов равен 151° .
 Размер другого противоположного внутреннего угла равен 91°
Размер другого противоположного внутреннего угла равен 91° Внешний угол треугольника равен 139° . Прилежащий внутренний угол треугольника должен быть равен 41° . Это дополнительные углы.
Дополнительные уголки
Горячая математикаДополнительные углы два углы чьи меры складываются в 180 ° .
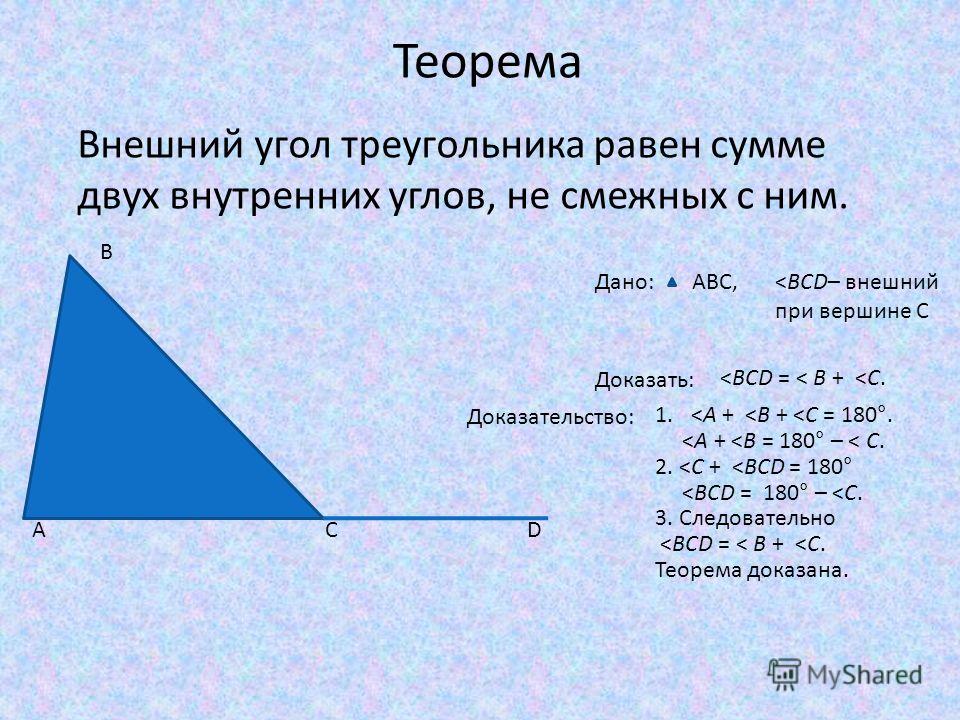
Два угла линейная пара , нравиться ∠ 1 и ∠ 2 на рисунке ниже всегда являются дополнительными.
Но два угла не обязательно должны быть смежными, чтобы быть дополнительными. На следующем рисунке ∠ 3 и ∠ 4 являются дополнительными, потому что их меры добавляют к 180 ° .
Пример 1:
Два угла являются дополнительными. Если градусная мера одного угла в два раза больше другого, найдите градусную меру каждого угла.
Если градусная мера одного угла в два раза больше другого, найдите градусную меру каждого угла.
Пусть мера одного из дополнительных углов равна а .
Мера другого угла 2 раз а .
Значит, мера другого угла 2 а .
Если сумма мер двух углов равна 180 ° , то углы дополнительные.
Так, а + 2 а «=» 180 °
Упрощать.
3 а «=» 180 °
Изолировать а , разделите обе части уравнения на 3 .
3 а 3 «=» 180 ° 3 а «=» 60 °
Мера второго угла равна
2 а «=» 2 × 60 ° «=» 120 °
Таким образом, меры двух дополнительных углов равны
60
°
и
120
°
.
Пример 2:
Находить м ∠ п и м ∠ Вопрос если ∠ п и ∠ Вопрос являются дополнительными, м ∠ п «=» 2 Икс + 15 , и м ∠ Вопрос «=» 5 Икс − 38 .
Сумма мер двух дополнительных углов равна 180 ° .
Так, м ∠ п + м ∠ Вопрос «=» 180 °
Заменять
2
Икс
+
15
для
м
∠
п
и
5
Икс
−
38
для
м
∠
Вопрос
.
2 Икс + 15 + 5 Икс − 38 «=» 180 °
Соедините подобные термины. Мы получаем:
7 Икс − 23 «=» 180 °
Добавлять 23 в обе стороны. Мы получаем:
7 Икс «=» 203 °
Разделите обе стороны на 7 .
7 Икс 7 «=» 203 ° 7
Упрощать.
Икс «=» 29 °
Найти м ∠ п , заменять 29 для Икс в 2 Икс + 15 .
2 ( 29 ) + 15 «=» 58 + 15
Упрощать.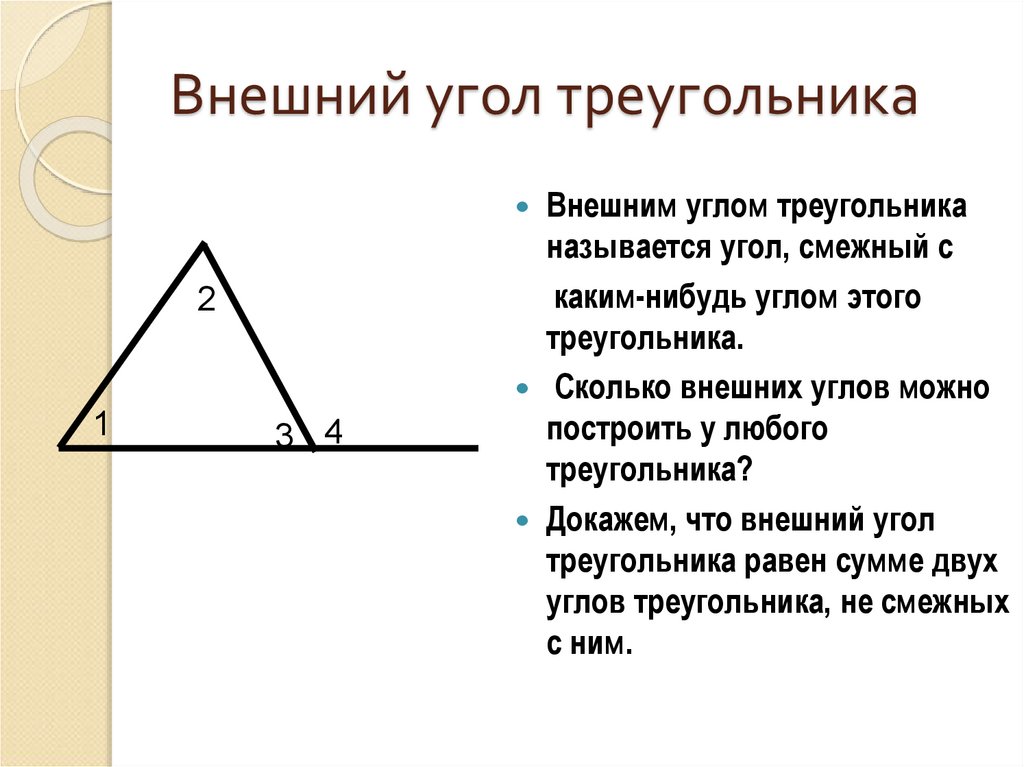

 wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.
wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.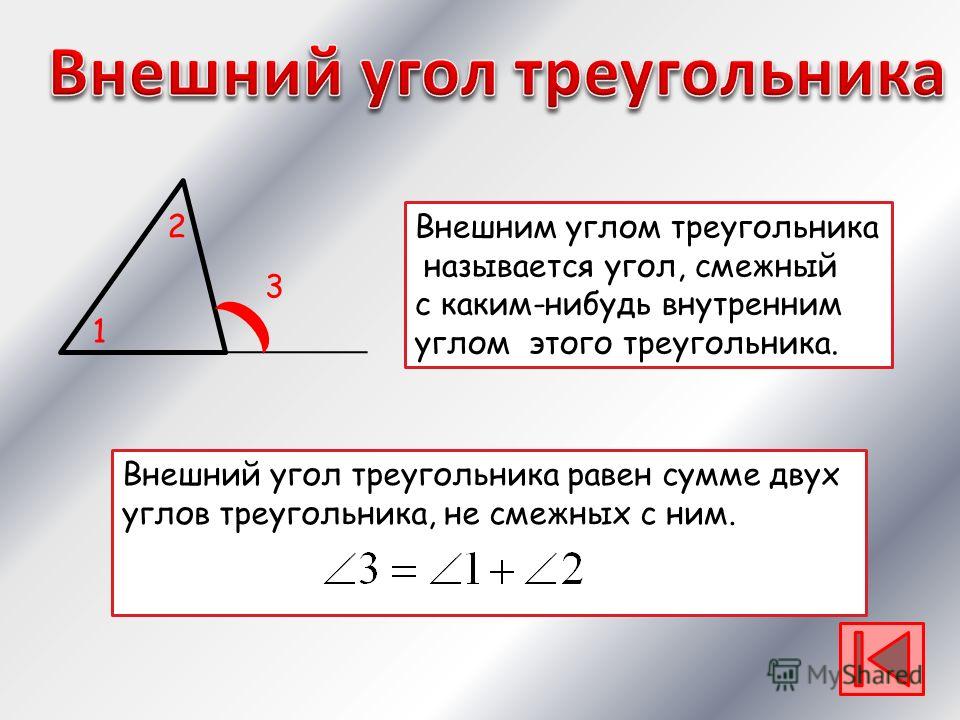 Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.
Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.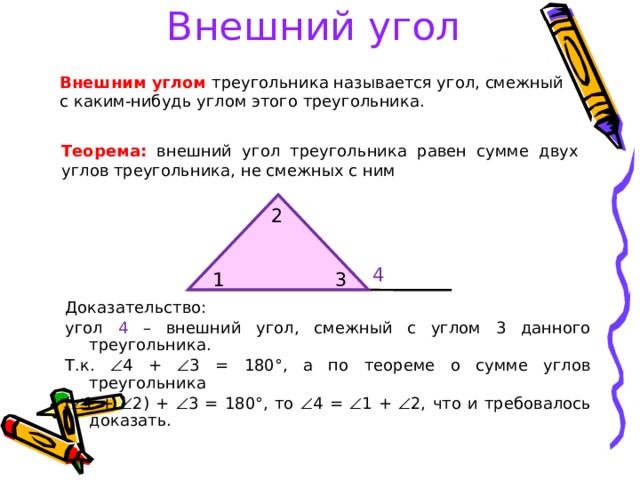
 Размер другого противоположного внутреннего угла равен 91°
Размер другого противоположного внутреннего угла равен 91°
Leave A Comment