Что такое Равнозамедленное движение?
Статьи › Чем отличается › Чем отличается равномерное и неравномерное движение?
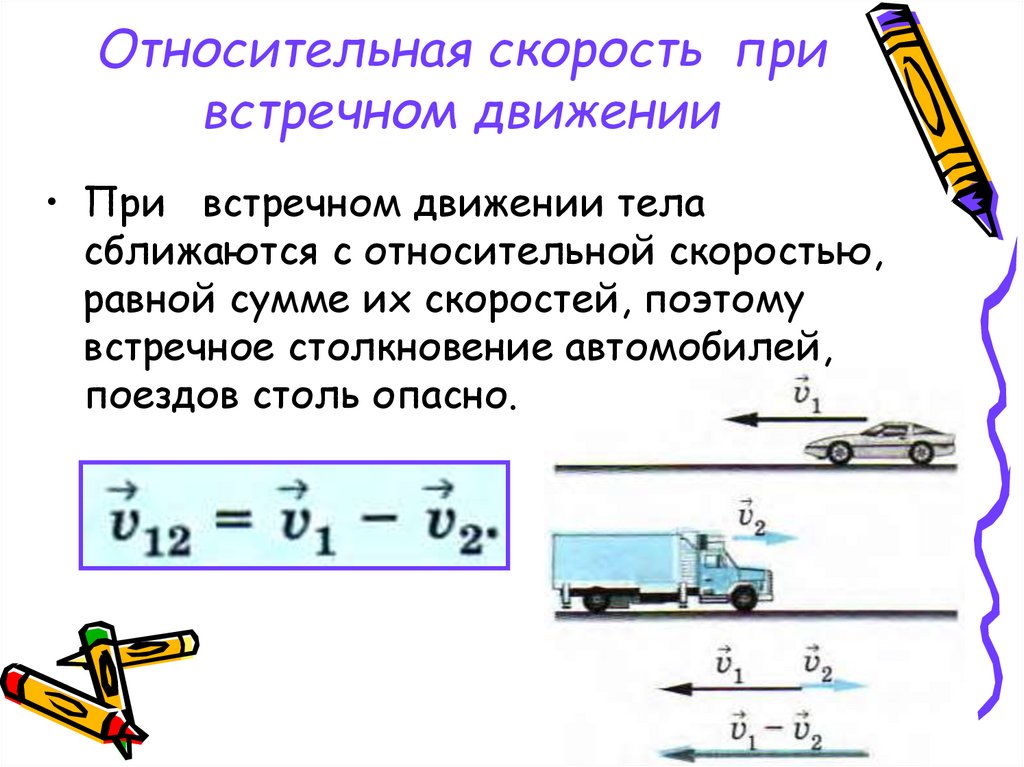
Равнозамедленное движение — движение, при котором модуль (величина) скорости равномерно меняется, а вектор ускорения остаётся постоянным и по модулю, и по направлению.
- Как найти Равнозамедленное движение?
- Что такое Равноускоренное и Равнозамедленное?
- Что такое Равнозамедленное прямолинейное движение?
- Чем Равноускоренное отличается от Равнозамедленного?
- В чем разница между равномерным и неравномерным движением?
- Что значит Равнопеременное движение?
- Какие виды Равнопеременного движения бывают?
- Какие виды движения вы знаете?
- Какое движение называется равномерным движением?
- Чем отличается замедленное движение от ускоренного?
- Какое движение называется равномерным Равноускоренным?
- Что называется равномерным Равноускоренным и Равнозамедленным движением?
- Какое движение называется равномерным приведите примеры?
- Что такое равномерное движение 7 класс?
- Какая формула равномерного движения?
- Что называется Равнопеременным прямолинейным движением?
- Что такое равномерное прямолинейное движение простыми словами?
- Что такое равномерное прямолинейное движение?
- Чему равно прямолинейное движение?
Как найти Равнозамедленное движение?
В физике, чтобы определить тип движения (равноускоренное или равнозамедленное), достаточно найти ускорение тела. Если ускорение тела получилось меньше нуля, значит оно направлено против движения тела, следовательно, движение является равнозамедленным, то есть тело снижает скорость.
Если ускорение тела получилось меньше нуля, значит оно направлено против движения тела, следовательно, движение является равнозамедленным, то есть тело снижает скорость.
Что такое Равноускоренное и Равнозамедленное?
Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину. При этом, если скорость увеличивается — движение называют равноускоренным, а если скорость уменьшается — равнозамедленным.
Что такое Равнозамедленное прямолинейное движение?
Это движение с постоянным по модулю и направлению ускорением. Равнопеременное прямолинейное движение бывает: равноускоренное (a → > 0) и равнозамедленное (a → < 0).
Чем Равноускоренное отличается от Равнозамедленного?
Равномерное — это когда два тела идут с одинаковой скоростью. Равноускоренное — это, когда в задаче еще добавляется ускорение. Равномерное — движение с одной скоростью. Равномерно ускоренное — увеличивающееся равномерно.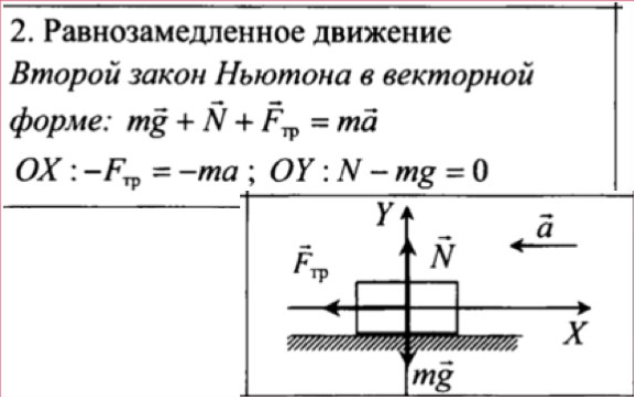
В чем разница между равномерным и неравномерным движением?
Если тело движется с постоянной скоростью и за любые равные промежутки времени проходит равные расстояния, то такое движение называется равномерным. А если скорость меняется, и проходимые расстояния оказываются неодинаковыми, то такое движение называется неравномерным.
Что значит Равнопеременное движение?
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением. изменение скорости, а Δt — промежуток времени.
Какие виды Равнопеременного движения бывают?
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает.Движения, совпадающие с направлением координатной оси:
- равноускоренноес начальной скоростью
- равноускоренное без начальной скорости
- равнозамедленное
- равнозамедленное
Какие виды движения вы знаете?
Различают следующие виды движений тел:
- поступательное;
- вращательное вокруг оси;
- плоское или плоскопараллельное;
- вращательное вокруг точки или сферическое;
- произвольное.
 2}\). Равноускоренное движение — это движение с постоянным ускорением: \(a=const\). Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: a → = v → − v 0 → t.
2}\). Равноускоренное движение — это движение с постоянным ускорением: \(a=const\). Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: a → = v → − v 0 → t.Что называется равномерным Равноускоренным и Равнозамедленным движением?
Равноускоренное движение тела
В этом случае имеется убыстрение, что отвечает за непрерывное повышение скорости. Ускорение перемещения остается постоянным, а темп регулярно и одинаково увеличивается. Кроме равноускоренного имеется также равнозамедленное перемещение, где модуль темп одинаково уменьшается.
Какое движение называется равномерным приведите примеры?
Равномерное движение — это движение при котором тело за оавнфе отрезки времени проходит равное расстояние. Примером равномерного движения может являться вращение планет вокруг своей оси.
Что такое равномерное движение 7 класс?
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным.

Какая формула равномерного движения?
Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения. v → = s → t. Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s → = v → ⋅ t.
Что называется Равнопеременным прямолинейным движением?
Прямолинейное движение с постоянным ускорением называется равнопеременным.
Что такое равномерное прямолинейное движение простыми словами?
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Что такое равномерное прямолинейное движение?
Равномерное прямолинейное движение Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени, совершает равные перемещения.
Чему равно прямолинейное движение?
Прямолинейное движение — механическое движение, происходящее вдоль прямой линии.
 То есть, при прямолинейном движении материальной точки траектория представляет собой прямую линию. равна нулю.
То есть, при прямолинейном движении материальной точки траектория представляет собой прямую линию. равна нулю.Равнопеременное прямолинейное движение
Равномерное прямолинейное движение
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением.
 В случае равноускоренного движения модуль скорости тела с течением времени
возрастает, направление ускорения совпадает с направлением скорости движения.
В случае равноускоренного движения модуль скорости тела с течением времени
возрастает, направление ускорения совпадает с направлением скорости движения.Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / t
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
= ‘
Проекция вектора скорости на ось ОХ:
vx = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
= ' = "
Учитывая, что 0 – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
Отсюда формула скорости равнопеременного движения в любой момент времени:
= 0 + t
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axt
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению.
 Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
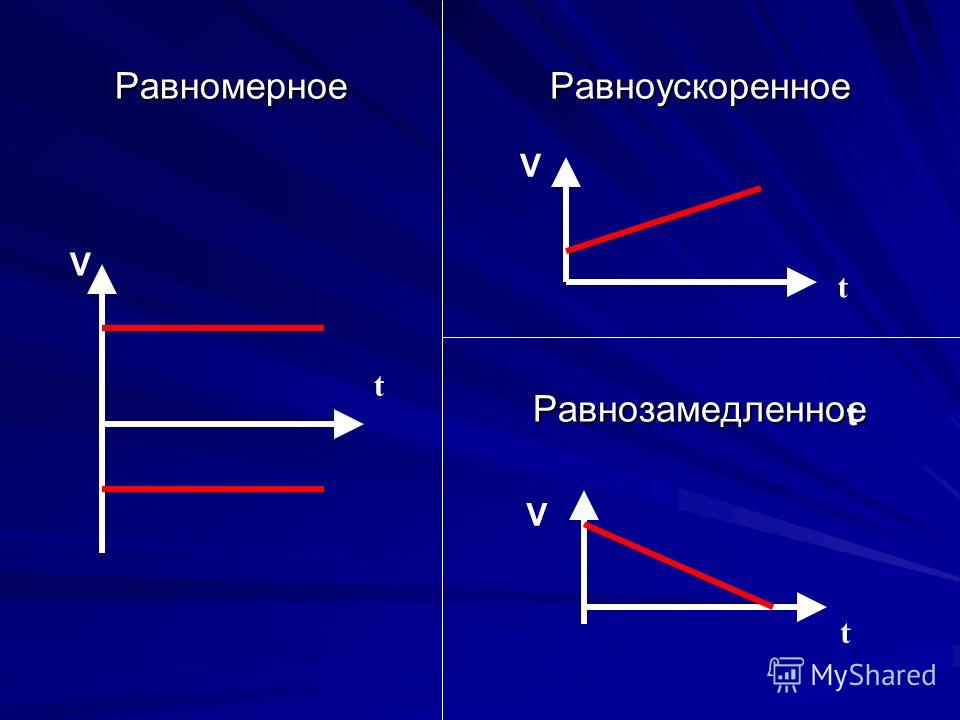
Аналогично записываются уравнения проекций вектора скорости на другие оси координат.Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат.
 При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).4.4 Равномерное круговое движение | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Находить центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
- Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение.
 Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости изменяется, или [латекс] d\overset{\to }{v}\text{/}dt\ne 0. [/latex] Это показано на (Рисунок). По мере того, как частица движется против часовой стрелки во времени [латекс] \текст{Δ}t [/латекс] по круговой траектории, ее вектор положения перемещается от [латекс] \overset{\to }{r}(t) [/латекс] к [латекс] \overset{\to}}{r}(t+\text{Δ}t). [/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex] \overset{\to }{v}(t) [/latex] до [latex] \overset{\to }{ v}(t+\text{Δ}t), [/latex] меняет только свое направление.
 Поскольку вектор скорости [латекс] \overset{\to }{v}(t) [/latex] перпендикулярен вектору положения [латекс] \overset{\to }{r}(t), [/latex] треугольники, образованные векторами положения и [латекс] \text{Δ}\overset{\to }{r}, [/latex] и векторами скорости и [латекс] \text{Δ}\overset{\to }{v } [/latex] похожи. Кроме того, поскольку [латекс] |\overset{\to }{r}(t)|=|\overset{\to }{r}(t+\text{Δ}t)| [/латекс] и [латекс] |\overset{\to }{v}(t)|=|\overset{\to }{v}(t+\text{Δ}t)|, [/latex] два треугольники равнобедренные. Из этих фактов мы можем сделать утверждение
Поскольку вектор скорости [латекс] \overset{\to }{v}(t) [/latex] перпендикулярен вектору положения [латекс] \overset{\to }{r}(t), [/latex] треугольники, образованные векторами положения и [латекс] \text{Δ}\overset{\to }{r}, [/latex] и векторами скорости и [латекс] \text{Δ}\overset{\to }{v } [/latex] похожи. Кроме того, поскольку [латекс] |\overset{\to }{r}(t)|=|\overset{\to }{r}(t+\text{Δ}t)| [/латекс] и [латекс] |\overset{\to }{v}(t)|=|\overset{\to }{v}(t+\text{Δ}t)|, [/latex] два треугольники равнобедренные. Из этих фактов мы можем сделать утверждение[латекс] \frac{\text{Δ}v}{v}=\frac{\text{Δ}r}{r} [/latex] или [латекс] \text{Δ}v=\frac{ v}{r}\text{Δ}r. [/latex]
Рисунок 4.18 (a) Частица движется по окружности с постоянной скоростью, с векторами положения и скорости в моменты времени [latex] t [/latex] и [latex] t+\text{Δ} т. [/latex] (b) Векторы скорости, образующие треугольник. Два треугольника на рисунке подобны. Вектор [латекс] \text{Δ}\overset{\to }{v} [/latex] указывает на центр окружности в пределе [латекс] \text{Δ}t\to 0.
 [/latex] 9{2}}{р}. [/latex]
[/latex] 9{2}}{р}. [/latex]Направление ускорения также можно определить, заметив, что по мере приближения [латекс] \текст{Δ}t [/латекс] и, следовательно, [латекс] \текст{Δ}\тета [/латекс] к нулю , вектор [латекс] \текст{Δ}\overset{\to }{v} [/latex] приближается к направлению, перпендикулярному [латексу] \overset{\to }{v}. [/latex] В пределе [latex] \text{Δ}t\to 0, [/latex][latex] \text{Δ}\overset{\to }{v} [/latex] перпендикулярно [latex ] \overset{\to}. [/latex] Поскольку [latex] \overset{\to }{v} [/latex] касается окружности, ускорение [latex] d\overset{\to }{v}\text{/}dt [/ латекс] указывает на центр круга. Подводя итог, частица, движущаяся по окружности с постоянной скоростью, имеет ускорение величиной 9{2}}{р}. [/latex]
Вектор ускорения направлен к центру окружности ((Рисунок)). Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему нижний индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».

Рисунок 4.19 Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Вектор скорости также показан и касается окружности.
Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения.
Пример
Создание ускорения 1
gСтруя летит со скоростью 134,1 м/с по прямой линии и делает поворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение 1 g по направлению к центру круговой траектории? 9{2}}=1835\,\text{м}=1,835\,\text{км}\text{.} [/latex]
Значение
реактивному самолету придется либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.
Проверьте свои знания
Радиус маховика составляет 20,0 см.
 {2}? [/латекс]
{2}? [/латекс]Показать решение
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в следующей таблице.
Типичные центростремительные ускорения Объект Центростремительное ускорение (м/с 2 или коэффициенты g ) Земля вокруг Солнца [латекс] 5,9{22} [/латекс] Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана ее вектором положения [латекс] \overset{\to }{r}(t).
 [/latex] (Рисунок) показывает частицу, совершающую круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс] \overset{\to }{r}(t) [/латекс], образующий угол [латекс] \тета [/латекс] с 9Ось 0039 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A=|\overset{\to }{r}(t)| [/латекс], а также радиус окружности, так что с точки зрения ее компонентов,
[/latex] (Рисунок) показывает частицу, совершающую круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс] \overset{\to }{r}(t) [/латекс], образующий угол [латекс] \тета [/латекс] с 9Ось 0039 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A=|\overset{\to }{r}(t)| [/латекс], а также радиус окружности, так что с точки зрения ее компонентов,[латекс] \overset{\to }{r}(t)=A\,\text{cos}\,\ омега т\шляпа{я}+А\,\текст{грех}\,\омега т\шляпа{j}. [/latex]
Здесь [latex] \omega [/latex] — константа, называемая угловой частотой частицы. Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду. Угол [латекс] \тета [/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс] \омега t [/латекс].

Если T — период движения или время, необходимое для совершения одного оборота ([латекс] 2\пи [/латекс] рад), то
[латекс] \омега =\фрак{2\пи }{ Т}. [/latex]
Рис. 4.20 Вектор положения частицы, совершающей круговое движение, с компонентами вдоль осей x и y. Частица движется против часовой стрелки. Угол [латекс] \тета [/латекс] — это угловая частота [латекс] \омега [/латекс] в радианах в секунду, умноженная на t.
Скорость и ускорение можно получить из функции положения дифференцированием:
[латекс] \ overset {\ to {v} (t) = \ frac {d \ overset {\ to {r} (t)} {dt} = \ text {−} A \ omega \, \ text{sin}\,\omega t\hat{i}+A\omega \,\text{cos}\,\omega t\hat{j}. [/latex]
Из (рис.) видно, что вектор скорости касается окружности в месте нахождения частицы с величиной [латекс] A\omega . [/latex] Точно так же вектор ускорения находится путем дифференцирования скорости:
[латекс] \overset{\to }{a}(t)=\frac{d\overset{\to}}{v}(t) }{dt} = \ text {−} A {\ omega} ^ {2} \, \ text {cos} \, \ omega t \ hat {i} -A {\ omega} ^ {2} \, \ text {грех}\,\омега т\шляпа{j}.
 [/латекс] 9{-7}\text{s}=200\,\text{ns}\text{.} [/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
[/латекс] 9{-7}\text{s}=200\,\text{ns}\text{.} [/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.Значение
Мы выбрали начальное положение частицы на оси x-. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно быть с постоянной скоростью. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе.
 В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:[латекс] {a}_{\text{T}}=\frac{d|\overset{\to}{v}| {дт}. [/latex]
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение , которое представляет собой векторную сумму центростремительного и тангенциального ускорений:
[латекс] \ overset {\ to }{a} = {\ overset {\ to }{a}} _ {\ text {C}} + {\ overset {\ to }{a}} _ {\ text {Т}}. [/latex]
Векторы ускорения показаны на (Рисунок). Обратите внимание, что два вектора ускорения [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\overset{\to }{a}}_{\ text{T}} [/latex] перпендикулярны друг другу, с [latex] {\overset{\to }{a}}_{\text{C}} [/latex] в радиальном направлении и [latex] {\overset{\to}{a}}_{\text{T}} [/latex] в тангенциальном направлении.
 Полное ускорение [латекс] \overset{\to }{a} [/latex] указывает на угол между [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/латекс]
Полное ускорение [латекс] \overset{\to }{a} [/latex] указывает на угол между [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/латекс]Рисунок 4.22 Центростремительное ускорение направлено к центру окружности. Тангенциальное ускорение касается окружности в месте нахождения частицы. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений, которые перпендикулярны.
Пример
Полное ускорение при движении по окружности
Частица движется по окружности радиусом r = 2,0 м. За интервал времени от t = 1,5 с до 9{2}},\enspace{c}_{1}=4.0\,\text{m}\text{/}\text{s,}\enspace{c}_{2}=6.0\,\text{ m}·\text{s}\text{.} [/latex]
Чему равно полное ускорение частицы в точке t = 2,0 с?
Стратегия
Нам известны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение.
 Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекса] |v(t)| [/latex] используя (Рисунок) и оценивая его на 9{-1}\frac{3.1}{1.5}=64\text{°} [/latex] от касательной к окружности. См. (Рисунок).
Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекса] |v(t)| [/latex] используя (Рисунок) и оценивая его на 9{-1}\frac{3.1}{1.5}=64\text{°} [/latex] от касательной к окружности. См. (Рисунок).Рисунок 4.23 Векторы тангенциального и центростремительного ускорения. Чистое ускорение [латекс] \overset{\to }{a} [/латекс] представляет собой векторную сумму двух ускорений.
Значение
Направления центростремительных и тангенциальных ускорений удобнее описывать в полярной системе координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге. 9{2}\text{/}р. [/латекс]
- Неравномерное круговое движение возникает, когда существует тангенциальное ускорение объекта, совершающего круговое движение, так что скорость объекта изменяется.
 Это ускорение называется тангенциальным ускорением [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/latex] Величина тангенциального ускорения – это скорость изменения во времени величины скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
Это ускорение называется тангенциальным ускорением [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/latex] Величина тангенциального ускорения – это скорость изменения во времени величины скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений. - Объект, совершающий равномерное круговое движение, может быть описан уравнениями движения. Вектор положения объекта: [латекс] \overset{\to }{r}(t)=A\,\text{cos}\,\omega t\hat{i}+A\,\text{sin} \,\omega t\hat{j}, [/latex], где A — величина [латекс] |\overset{\to }{r}(t)|, [/latex], которая также является радиусом окружность, а [латекс]\омега[/латекс] — угловая частота.
Концептуальные вопросы
Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?
Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?
Показать решение
Проблемы
Маховик вращается со скоростью 30 об/с. На какой угол в радианах поворачивается точка маховика за 40 с?
На какой угол в радианах поворачивается точка маховика за 40 с?
Частица движется по окружности радиусом 10 м с постоянной скоростью 20 м/с. Какова величина ускорения?
Показать решение
Кэм Ньютон из команды «Каролина Пантерз» делает идеальную футбольную спираль со скоростью 8,0 об/с. Радиус профессионального футбольного мяча составляет 8,5 см посередине короткой стороны. Чему равно центростремительное ускорение шнурков футбольного мяча?
Ярмарочный аттракцион вращает своих пассажиров внутри контейнера в форме летающей тарелки. Если горизонтальный круговой путь, по которому следуют всадники, имеет радиус 8,00 м, при каком числе оборотов в минуту всадники испытывают центростремительное ускорение, равное силе тяжести?
Показать решение
Бегун, участвующий в забеге на 200 м, должен обежать конец дорожки, имеющей дугу окружности с радиусом кривизны 30,0 м. Бегун начинает гонку с постоянной скоростью. Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы?
Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы?
Каково ускорение Венеры по отношению к Солнцу, если предположить, что она движется по круговой орбите?
Показать решение
Экспериментальная реактивная ракета летит вокруг Земли по экватору прямо над ее поверхностью. С какой скоростью должна двигаться струя, если модуль ее ускорения равен g ?
Вентилятор вращается с постоянной скоростью 360,0 об/мин. Чему равно ускорение точки одной из его лопастей на расстоянии 10,0 см от оси вращения?
Показать решение 9{2}. [/latex] Как далеко точка от оси вращения секундной стрелки?
Глоссарий
- угловая частота
- [латекс] \omega , [/латекс] скорость изменения угла, с которым объект движется по круговой траектории
- центростремительное ускорение
- составляющая ускорения объекта, движущегося по окружности, направленная радиально внутрь к центру окружности
- тангенциальное ускорение
- величина которого есть скорость изменения скорости во времени.
 Его направление касается окружности.
Его направление касается окружности.
- общее ускорение
- векторная сумма центростремительного и тангенциального ускорений
Скорость и скорость
Любой движущийся объект можно описать с помощью кинематических понятий, обсуждавшихся в Разделе 1 Урока физики. Движение движущегося объекта можно объяснить либо с помощью законов Ньютона (раздел 2 кабинета физики), либо векторных принципов (раздел 3 кабинета физики), либо с помощью теоремы о работе-энергии (раздел 5 кабинета физики). Те же концепции и принципы, которые используются для описания и объяснения движения объекта, могут быть использованы для описания и объяснения параболического движения снаряда. В этом разделе мы увидим, что те же самые понятия и принципы могут также использоваться для описания и объяснения движения объектов, которые либо движутся по кругу, либо могут быть аппроксимированы как движущиеся по кругу. Кинематические концепции и принципы движения будут применяться к движению объектов по кругу, а затем расширены для анализа движения таких объектов, как американские горки, футбольный игрок, делающий круговой оборот и планета, вращающаяся вокруг Солнца. Мы увидим, что красота и сила физики заключаются в том факте, что несколько простых понятий и принципов могут быть использованы для объяснения механики всей Вселенной. Урок 1 этого исследования начнется с развития кинематических и динамических идей, которые можно использовать для описания и объяснения движения объектов по кругу.
Мы увидим, что красота и сила физики заключаются в том факте, что несколько простых понятий и принципов могут быть использованы для объяснения механики всей Вселенной. Урок 1 этого исследования начнется с развития кинематических и динамических идей, которые можно использовать для описания и объяснения движения объектов по кругу.
Предположим, вы едете на машине с повернутым рулем таким образом, что ваша машина движется по идеальному кругу с постоянным радиусом. И предположим, что пока вы едете, ваш спидометр постоянно показывает 10 миль в час. В такой ситуации движение вашего автомобиля можно описать как равномерное круговое движение. Равномерное круговое движение — это движение объекта по окружности с постоянной или равномерной скоростью.
Расчет средней скорости
Равномерное круговое движение — круговое движение с постоянной скоростью — это одна из многих форм кругового движения. Объект, движущийся в равномерном круговом движении, будет преодолевать одно и то же линейное расстояние за каждую секунду времени. При движении по кругу объект проходит расстояние по периметру круга. Итак, если бы ваша машина двигалась по кругу с постоянной скоростью 5 м/с, то за каждую секунду времени машина проезжала бы 5 метров по периметру окружности. Расстояние одного полного цикла по периметру круга известно как окружность . При равномерной скорости 5 м/с автомобиль мог совершить полный цикл по кругу, длина окружности которого составляла 5 м. При этой равномерной скорости 5 м/с каждый цикл по кругу длиной 5 м потребует 1 секунду. При скорости 5 м/с круг окружностью 20 метров можно было сделать за 4 секунды; и при этой постоянной скорости каждый цикл по 20-метровой окружности будет длиться одинаковое время в 4 секунды. Эта взаимосвязь между длиной окружности, временем совершения одного цикла по кругу и скоростью объекта является просто расширением уравнения средней скорости, изложенного в Разделе 1 Учебного класса физики.
При движении по кругу объект проходит расстояние по периметру круга. Итак, если бы ваша машина двигалась по кругу с постоянной скоростью 5 м/с, то за каждую секунду времени машина проезжала бы 5 метров по периметру окружности. Расстояние одного полного цикла по периметру круга известно как окружность . При равномерной скорости 5 м/с автомобиль мог совершить полный цикл по кругу, длина окружности которого составляла 5 м. При этой равномерной скорости 5 м/с каждый цикл по кругу длиной 5 м потребует 1 секунду. При скорости 5 м/с круг окружностью 20 метров можно было сделать за 4 секунды; и при этой постоянной скорости каждый цикл по 20-метровой окружности будет длиться одинаковое время в 4 секунды. Эта взаимосвязь между длиной окружности, временем совершения одного цикла по кругу и скоростью объекта является просто расширением уравнения средней скорости, изложенного в Разделе 1 Учебного класса физики.
Длина окружности любого круга может быть вычислена из радиуса в соответствии с уравнением движение в равномерном круговом движении с радиусом окружности и временем совершения одного оборота по окружности ( период ).
где R представляет радиус окружности и T представляет период. Это уравнение, как и все уравнения, можно использовать как алгебраический рецепт решения задач. Его также можно использовать, чтобы направлять наши мысли о том, что переменные в уравнении связаны друг с другом. Например, уравнение предполагает, что для объектов, движущихся по кругам разного радиуса за один и тот же период, объект, пересекающий круг большего радиуса, должен двигаться с наибольшей скоростью. На самом деле средняя скорость и радиус окружности прямо пропорциональны. Двукратное увеличение радиуса соответствует двукратному увеличению скорости; трехкратному увеличению радиуса соответствует трехкратное увеличение скорости; и так далее. Для иллюстрации рассмотрим цепочку из четырех светодиодов, расположенных в разных местах вдоль нити. Прядь удерживается за один конец и быстро вращается по кругу. Каждый светодиодный свет пересекает круг разного радиуса. Но поскольку они подключены к одному и тому же проводу, период их вращения одинаков. Следовательно, светодиоды, которые находятся дальше от центра круга, перемещаются быстрее, чтобы охватить окружность большего круга за то же время. Если свет в комнате выключен, светодиоды создают дугу, которая может восприниматься как более длинная для тех светодиодов, которые перемещаются быстрее — светодиодов с наибольшим радиусом. Это показано на диаграмме справа.
Но поскольку они подключены к одному и тому же проводу, период их вращения одинаков. Следовательно, светодиоды, которые находятся дальше от центра круга, перемещаются быстрее, чтобы охватить окружность большего круга за то же время. Если свет в комнате выключен, светодиоды создают дугу, которая может восприниматься как более длинная для тех светодиодов, которые перемещаются быстрее — светодиодов с наибольшим радиусом. Это показано на диаграмме справа.
Объекты, движущиеся в равномерном круговом движении, будут иметь постоянную скорость. Но значит ли это, что они будут иметь постоянную скорость? Вспомните из раздела 1 курса физики, что скорость и скорость относятся к двум совершенно разным величинам. Скорость — это скалярная величина, а скорость — векторная величина. Скорость, будучи вектором, имеет как величину, так и направление. Величина вектора скорости — это мгновенная скорость объекта. Направление вектора скорости направлено в том же направлении, в котором движется объект. Поскольку объект движется по кругу, его направление постоянно меняется. В какой-то момент объект движется на север так, что вектор скорости направлен на север. Через четверть цикла объект будет двигаться на восток, так что вектор скорости будет направлен на восток. Как объект огибает круг, направление вектора скорости отличается от того, что было мгновением раньше. Таким образом, хотя величина вектора скорости может быть постоянной, направление вектора скорости меняется. Лучшим словом, которое можно использовать для описания направления вектора скорости, является слово тангенциальный . Направление вектора скорости в любой момент находится в направлении касательной, проведенной к окружности в месте расположения объекта. (Касательная линия — это линия, которая касается окружности в одной точке, но не пересекает ее.) На диаграмме справа показано направление вектора скорости в четырех разных точках для объекта, движущегося по часовой стрелке по окружности.
Направление вектора скорости направлено в том же направлении, в котором движется объект. Поскольку объект движется по кругу, его направление постоянно меняется. В какой-то момент объект движется на север так, что вектор скорости направлен на север. Через четверть цикла объект будет двигаться на восток, так что вектор скорости будет направлен на восток. Как объект огибает круг, направление вектора скорости отличается от того, что было мгновением раньше. Таким образом, хотя величина вектора скорости может быть постоянной, направление вектора скорости меняется. Лучшим словом, которое можно использовать для описания направления вектора скорости, является слово тангенциальный . Направление вектора скорости в любой момент находится в направлении касательной, проведенной к окружности в месте расположения объекта. (Касательная линия — это линия, которая касается окружности в одной точке, но не пересекает ее.) На диаграмме справа показано направление вектора скорости в четырех разных точках для объекта, движущегося по часовой стрелке по окружности. Хотя фактическое направление объекта (и, следовательно, вектора скорости) меняется, его направление всегда касается окружности.
Хотя фактическое направление объекта (и, следовательно, вектора скорости) меняется, его направление всегда касается окружности.
Итак, объект, движущийся в равномерном круговом движении, движется по периметру круга с постоянной скоростью. Пока скорость объекта постоянна, его скорость меняется. Скорость, будучи вектором, имеет постоянную величину, но изменяющееся направление. Направление всегда направлено по касательной к окружности, и когда объект поворачивает окружность, касательная всегда указывает в новом направлении.
Мы хотели бы предложить…
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения Uniform Circular Motion. Вы можете найти его в разделе Physics Interactives на нашем сайте.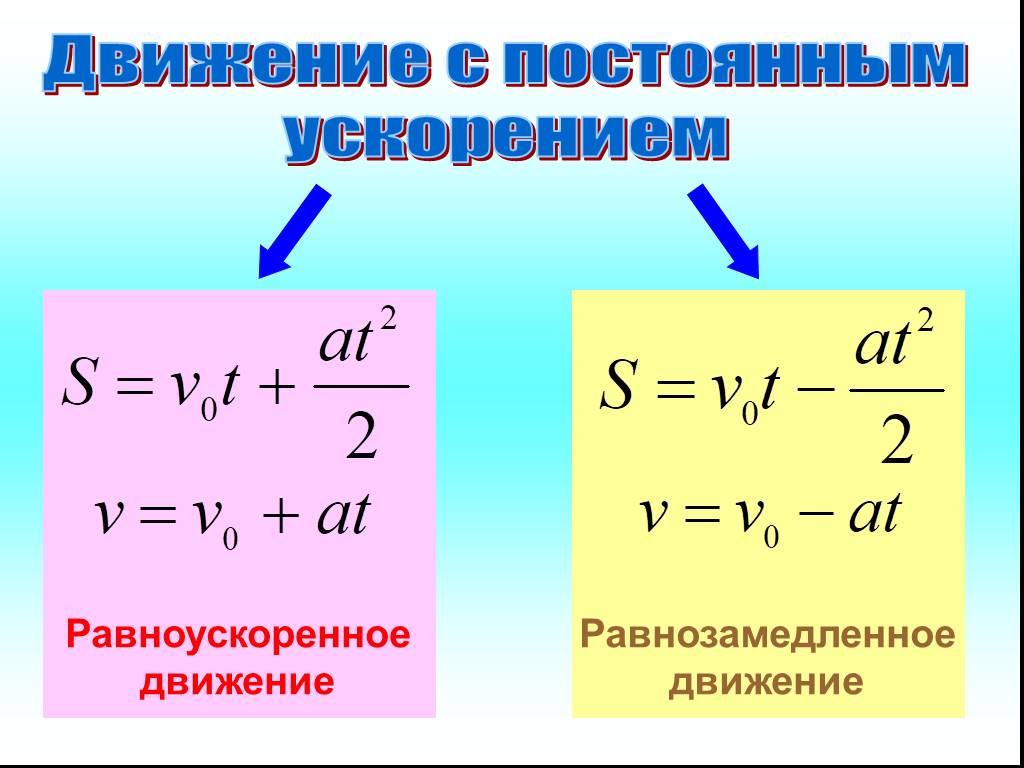

 2}\). Равноускоренное движение — это движение с постоянным ускорением: \(a=const\). Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: a → = v → − v 0 → t.
2}\). Равноускоренное движение — это движение с постоянным ускорением: \(a=const\). Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: a → = v → − v 0 → t.
 То есть, при прямолинейном движении материальной точки траектория представляет собой прямую линию. равна нулю.
То есть, при прямолинейном движении материальной точки траектория представляет собой прямую линию. равна нулю.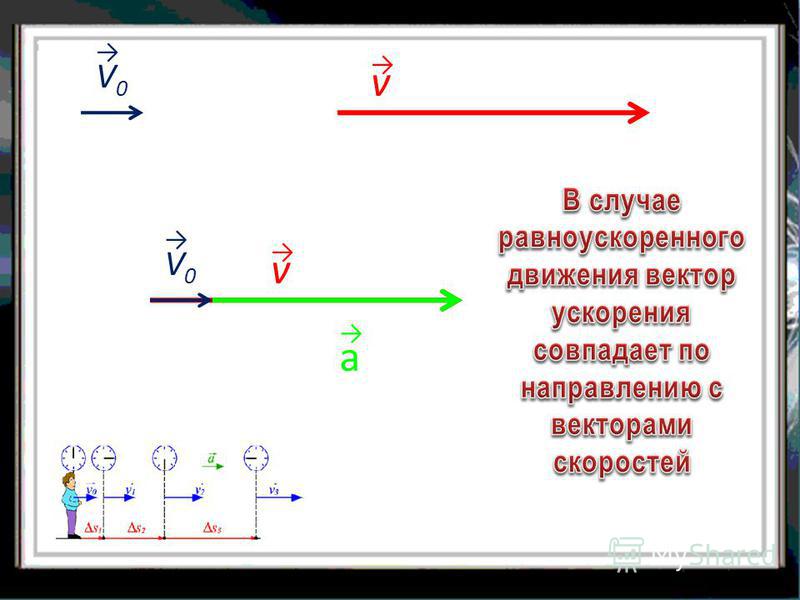 В случае равноускоренного движения модуль скорости тела с течением времени
возрастает, направление ускорения совпадает с направлением скорости движения.
В случае равноускоренного движения модуль скорости тела с течением времени
возрастает, направление ускорения совпадает с направлением скорости движения.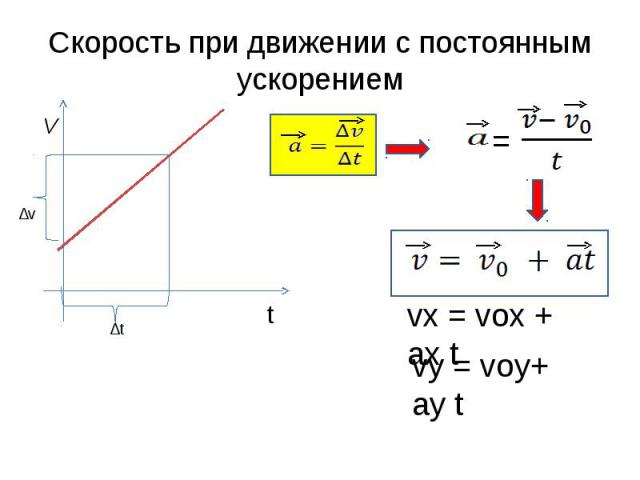
 Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
 При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).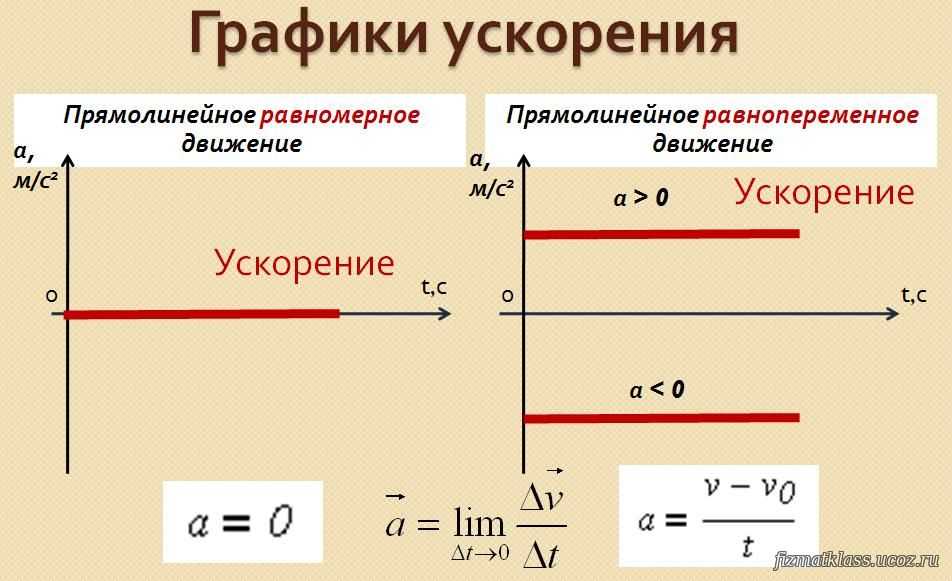 Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.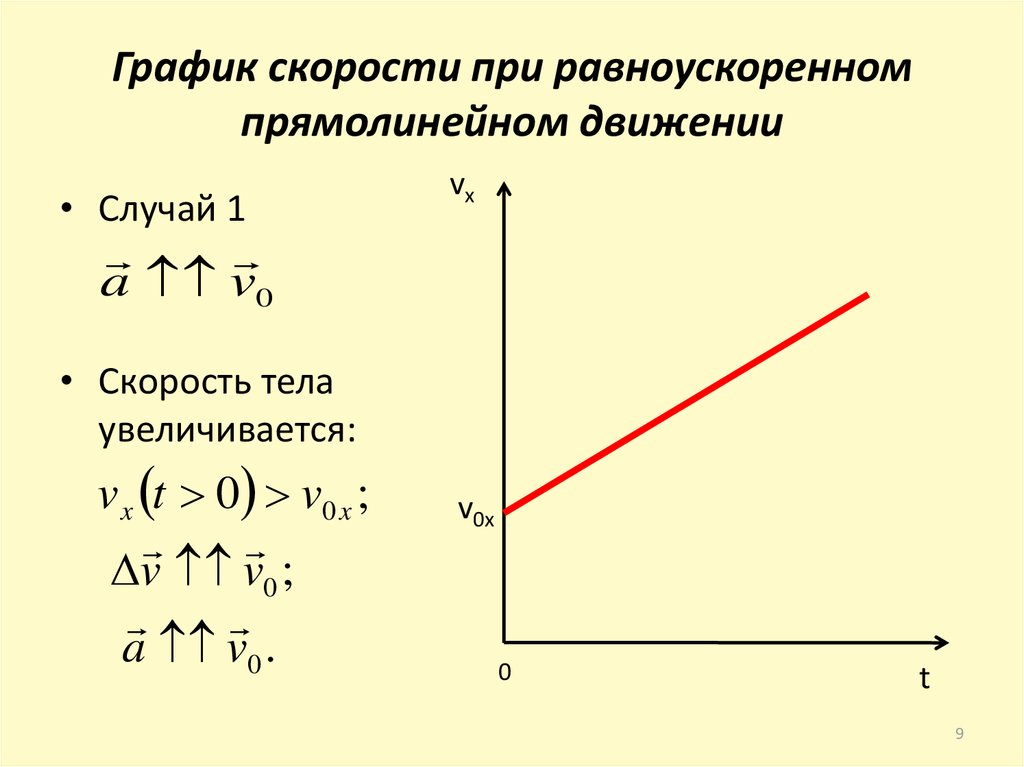 Поскольку вектор скорости [латекс] \overset{\to }{v}(t) [/latex] перпендикулярен вектору положения [латекс] \overset{\to }{r}(t), [/latex] треугольники, образованные векторами положения и [латекс] \text{Δ}\overset{\to }{r}, [/latex] и векторами скорости и [латекс] \text{Δ}\overset{\to }{v } [/latex] похожи. Кроме того, поскольку [латекс] |\overset{\to }{r}(t)|=|\overset{\to }{r}(t+\text{Δ}t)| [/латекс] и [латекс] |\overset{\to }{v}(t)|=|\overset{\to }{v}(t+\text{Δ}t)|, [/latex] два треугольники равнобедренные. Из этих фактов мы можем сделать утверждение
Поскольку вектор скорости [латекс] \overset{\to }{v}(t) [/latex] перпендикулярен вектору положения [латекс] \overset{\to }{r}(t), [/latex] треугольники, образованные векторами положения и [латекс] \text{Δ}\overset{\to }{r}, [/latex] и векторами скорости и [латекс] \text{Δ}\overset{\to }{v } [/latex] похожи. Кроме того, поскольку [латекс] |\overset{\to }{r}(t)|=|\overset{\to }{r}(t+\text{Δ}t)| [/латекс] и [латекс] |\overset{\to }{v}(t)|=|\overset{\to }{v}(t+\text{Δ}t)|, [/latex] два треугольники равнобедренные. Из этих фактов мы можем сделать утверждение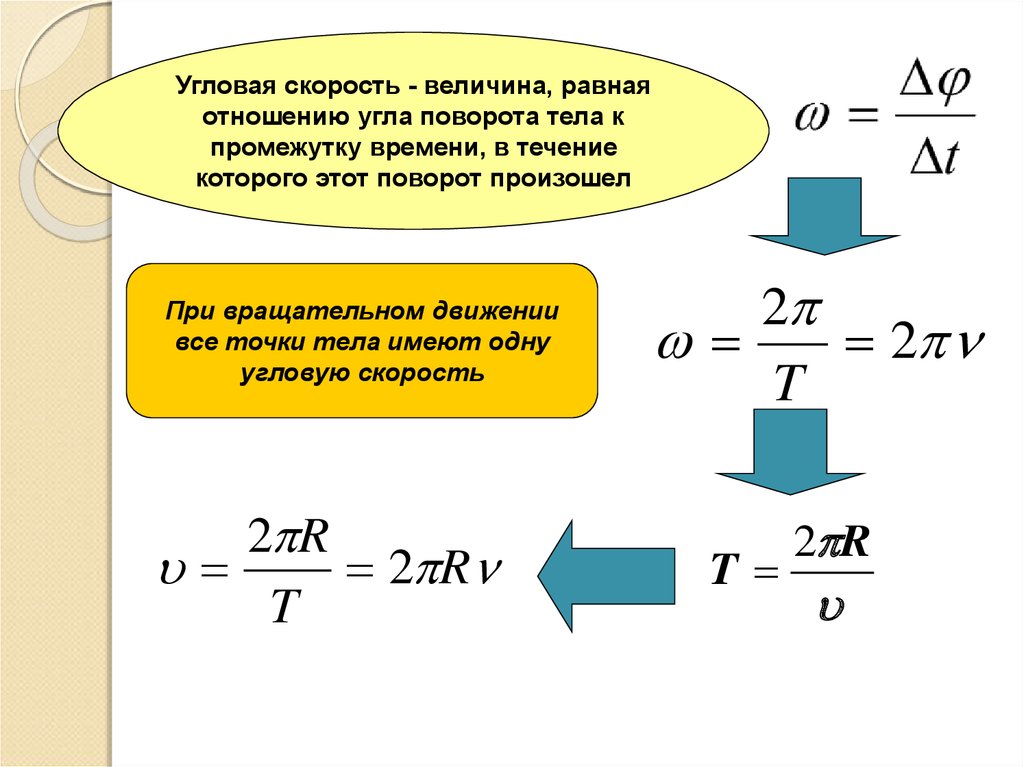 [/latex] 9{2}}{р}. [/latex]
[/latex] 9{2}}{р}. [/latex]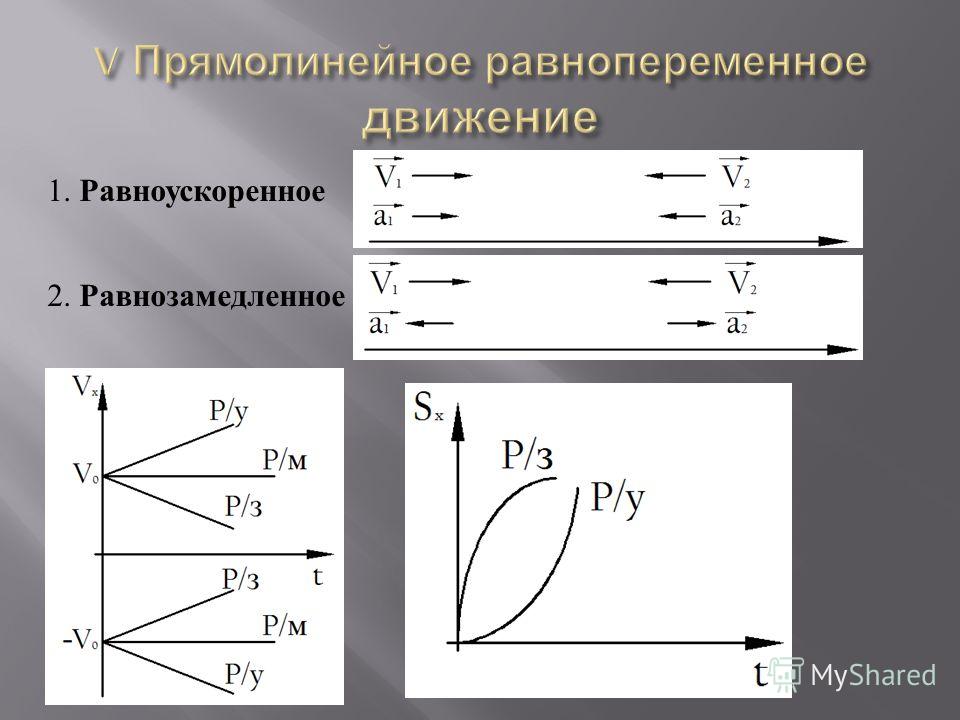
 {2}? [/латекс]
{2}? [/латекс]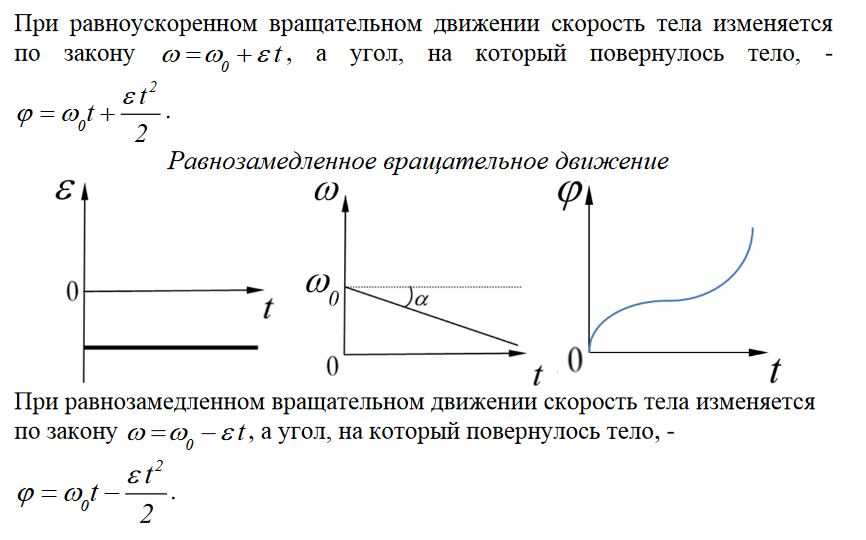 [/latex] (Рисунок) показывает частицу, совершающую круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс] \overset{\to }{r}(t) [/латекс], образующий угол [латекс] \тета [/латекс] с 9Ось 0039 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A=|\overset{\to }{r}(t)| [/латекс], а также радиус окружности, так что с точки зрения ее компонентов,
[/latex] (Рисунок) показывает частицу, совершающую круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс] \overset{\to }{r}(t) [/латекс], образующий угол [латекс] \тета [/латекс] с 9Ось 0039 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A=|\overset{\to }{r}(t)| [/латекс], а также радиус окружности, так что с точки зрения ее компонентов,
 [/латекс] 9{-7}\text{s}=200\,\text{ns}\text{.} [/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
[/латекс] 9{-7}\text{s}=200\,\text{ns}\text{.} [/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени: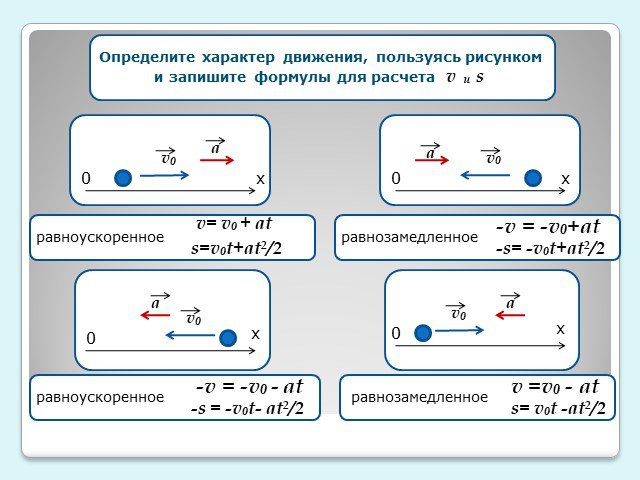 Полное ускорение [латекс] \overset{\to }{a} [/latex] указывает на угол между [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/латекс]
Полное ускорение [латекс] \overset{\to }{a} [/latex] указывает на угол между [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/латекс] Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекса] |v(t)| [/latex] используя (Рисунок) и оценивая его на 9{-1}\frac{3.1}{1.5}=64\text{°} [/latex] от касательной к окружности. См. (Рисунок).
Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекса] |v(t)| [/latex] используя (Рисунок) и оценивая его на 9{-1}\frac{3.1}{1.5}=64\text{°} [/latex] от касательной к окружности. См. (Рисунок). Это ускорение называется тангенциальным ускорением [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/latex] Величина тангенциального ускорения – это скорость изменения во времени величины скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
Это ускорение называется тангенциальным ускорением [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/latex] Величина тангенциального ускорения – это скорость изменения во времени величины скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.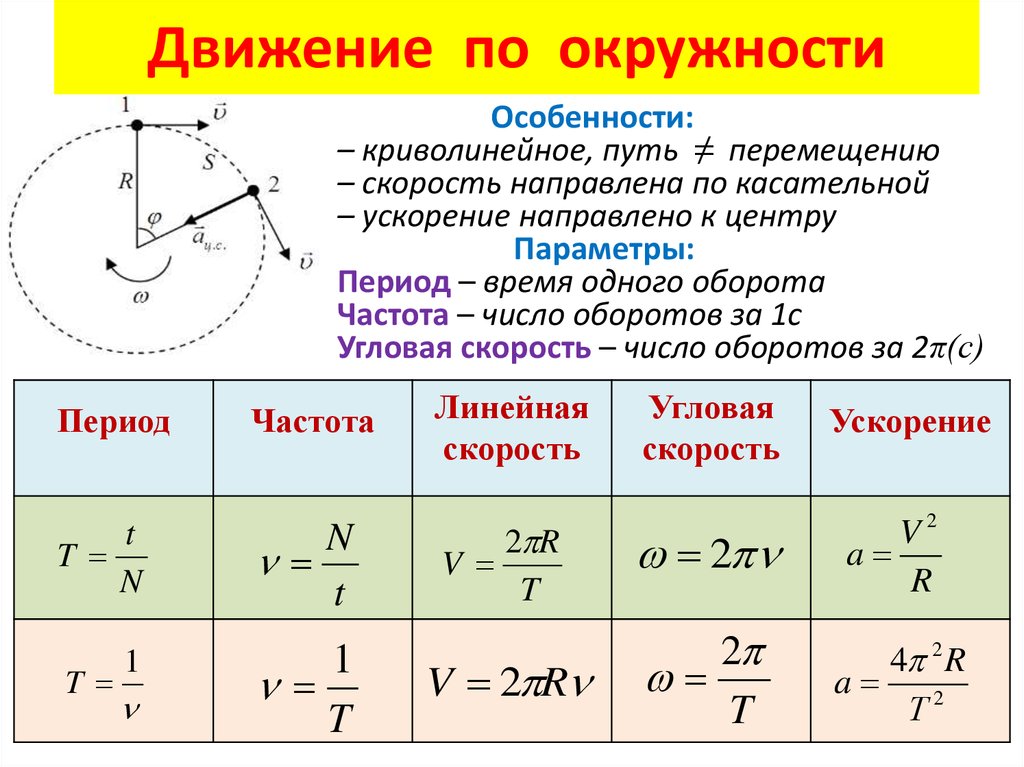 Его направление касается окружности.
Его направление касается окружности.
Leave A Comment