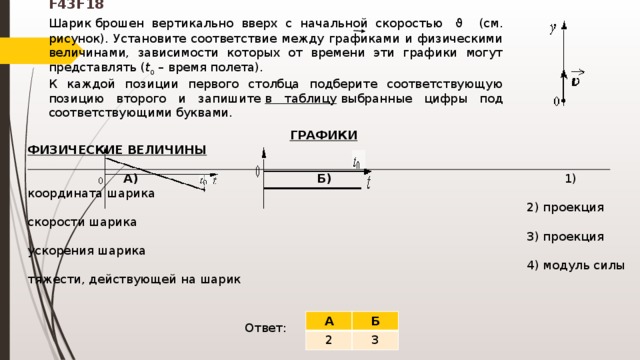
Движение тела брошенного горизонтально, теория и онлайн калькуляторы
Движение тела брошенного горизонтально, теория и онлайн калькуляторыПостановка задачи. Начальные условия
Рассмотрим движение тела, которое бросили с начальной скоростью ${\overline{v}}_0\ $параллельно Земле (горизонтально) рис.1. с некоторой высоты $h_0.$
Систему отсчета свяжем с Землей. Ось X направим параллельно Земле, ось Y перпендикулярно оси X, вверх. Тело движется под воздействием силы тяжести, если не учитывать силу трения, то другие силы на тело не действуют. Движение тела происходит в плоскости, в которой лежат векторы: начальной скорости тела ${\overline{v}}_0$ и ускорения $\overline{g}.\ $
Начальные условия при рассматриваемом нами движении точки:
\[при\ t=0\ c\left\{ \begin{array}{c} x_0=0, \\ y_0=h_0, \\ v_{0x}=v_0, \\ v_{0y}=0 \end{array} \right.\left(1\right).\]
Вектор ускорения при движении под действием силы тяжести считают постоянным:
\[\overline{a}=\overline{g}\left(2\right),\]
так как \textit{ }$\overline{g}$ направлен вертикально вниз, то:
\[\left\{ \begin{array}{c}
a_x=0, \\
a_y=g \end{array}
\right. 2}.$
2}.$
Кинематические уравнения движения тела брошенного горизонтально
Кинематическое уравнение для скорости равнопеременного движения в поле тяжести имеет вид:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(4\right),\]
где ${\overline{v}}_0$ — начальная скорость тела. Движение материальной точки в рассматриваемом случае можно представить сумму двух независимых движений по прямым линиям, в которых участвует тело, брошенное горизонтально. Это равномерное движение с неизменной скоростью ${\overline{v}}_0$ в горизонтальном направлении и равноускоренное движение с ускорением $\overline{g}$ без начальной скорости в направлении вектора ускорения свободного падения.
В проекциях на оси координат получаем:
\[\left\{ \begin{array}{c} v_x=v_0 \\ v_y=-gt \end{array} \left(5\right).\right.\]
Модуль скорости движения точки при этом равен:
\[v=\sqrt{v^2_x+v^2_y}=\sqrt{v^2_0+g^2t^2}\left(6\right). 2}{2}\to t_{pol}=\sqrt{\frac{2h_0}{g}}\left(10\right).\]
2}{2}\to t_{pol}=\sqrt{\frac{2h_0}{g}}\left(10\right).\]
Дальность полета (s) — это расстояние, которое тело преодолело по горизонтали (по оси X). Его найдем, подставив время полета в первое уравнение системы (8):
\[s=v_0\sqrt{\frac{2h_0}{g}}\ \left(11\right).\]
Примеры задач с решением
Пример 1
Задание. Маленький шарик бросили горизонтально со скоростью $v_0$. Какова высота, с которой бросили шарик, если он упал на землю, пролетев расстояние s по горизонтали в n раз большее, чем высота бросания?
Решение. Для решения задачи воспользуемся формулой, которую получили в теоретической части статьи, связывающую дальность полета тела и высоту, с которой это тело бросили горизонтально:
\[s=v_0\sqrt{\frac{2h}{g}}\ \left(1.1\right).\]
Воспользуемся условием, которое задано:
\[\frac{s}{h}{\rm =n}\to s=nh\ \left(1. 2}$
2}$
Читать дальше: движение тела под углом к горизонту.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Лабораторная работа № 4 «Изучение движения тела, брошенного горизонтально»
Цель работы: измерить начальную скорость, сообщенную телу в горизонтальном направлении при его движении под действием силы тяжести.
Если шарик брошен горизонтально, то он движется по параболе. За начало координат примем начальное положение шарика. Направим ось X горизонтально, а ось Y — вертикально вниз. Тогда в любой момент времени t
а
У =
Дальность полета l — это
значение координаты х, которое она будет иметь, если вместо t подставить время падения тела с высоты h. Поэтому можно записать:
Отсюда легко найти
время падения t и начальную скорость V0:
Если несколько раз пускать шарик в неизменных условиях опыта (рис. 177), то значения дальности полета будут иметь некоторый разброс из-за влияния различных причин, которые невозможно учесть.
177), то значения дальности полета будут иметь некоторый разброс из-за влияния различных причин, которые невозможно учесть.
В таких случаях за значение измеряемой величины принимается среднее арифметическое результатов, полученных в нескольких опытах.
Средства измерения: линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтой и лапкой; 2) лоток для пуска шарика; 3) фанерная доска; 4) шарик; 5) бумага; 6) кнопки; 7) копировальная бумага.
Порядок выполнения работы
1. С помощью штатива укрепите фанерную доску вертикально. При этом той же лапкой зажмите выступ лотка. Загнутый конец лотка должен быть горизонтальным (см. рис. 177).
2. Прикрепите к фанере кнопками лист бумаги шириной не менее 20 см и у основания установки на полоску белой бумаги положите копировальную бумагу.
3. Повторите опыт пять раз, пуская шарик из одного и того же места лотка, уберите копировальную бумагу.
4. Измерьте высоту h и дальность полета l. Результаты измерения занесите в таблицу:
|
Номер опыта |
h, м |
l, м |
lср, м |
v0ср, м/с |
5. Рассчитайте среднее значение начальной скорости по формуле
Рассчитайте среднее значение начальной скорости по формуле
6. Пользуясь формулами х =
найдите координату
х тела (координата у уже подсчитана) через каждые 0,05 с и постройте траекторию движения на листе бумаги, прикрепленном к фанерной доске:
|
t, с |
0 |
0,05 |
0,10 |
0,15 |
0,2 |
|
x, м |
0 | ||||
|
y, М |
0 |
0,012 |
0,049 |
0,110 |
0,190 |
7. Пустите шарик по желобу и убедитесь в том, что его траектория близка к построенной параболе.
Первой целью работы является измерение начальной скорости, сообщенной телу в горизонтальном направлении при его движении под действием силы тяжести. Измерение производится при помощи установки описанной и изображенной в учебнике. Если не принимать в расчет сопротивление воздуха, то тело, брошенное горизонтально, движется по параболической траектории. Если выбрать за начало координат точку начала полета шарика, то координаты его с течением времени изменяются следующим образом: х=V
Измерение производится при помощи установки описанной и изображенной в учебнике. Если не принимать в расчет сопротивление воздуха, то тело, брошенное горизонтально, движется по параболической траектории. Если выбрать за начало координат точку начала полета шарика, то координаты его с течением времени изменяются следующим образом: х=V
Расстояние, которое шарик пролетает до момента падения (l), это значение координаты х в момент, когда y = —h, где h — высота падения, отсюда можно получить в момент падения
Выполнение работы:
1. Определение начальной скорости:
|
№ опыта |
h, м |
l, м |
lср, м |
V0 м/с |
V0cp м/с |
|
1 |
|
0,16 |
0,15 |
0,79 |
0,74 |
|
2 |
0,2 |
0,14 |
0,69 | ||
|
3 |
0,2 |
0,15 |
0,74 | ||
|
4 |
0,2 |
0,135 |
0,67 | ||
|
5 |
0,2 |
0,165 |
0,82 | ||
|
|
0,2 |
0,145 |
0,71 |
Вычисления:
2. Построение траектории движения тела:
Построение траектории движения тела:
|
t, с |
0,5 |
1 |
1,5 |
2 |
|
x, м |
0,037 |
0,074 |
0,111 |
0,148 |
|
у, м |
-0,012 |
-0,049 |
-0,11 |
-0,19 |
Вычисления
1.
2.
3.
4.
Построение траектории:
Траектория, построенная вами, несколько отличается от реальной, которую вы можете наблюдать во время опытов, так как не учитывает сопротивления воздуха.
Источник:
Решебник
по
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №4
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ
Все задачи
← Лабораторная работа № 3 «Измерение коэффициента трения скольжения»
Лабораторная работа № 5 «Изучение движения тела по окружности под действием сил упругости и тяжести» →
Мяч брошен горизонтально с некоторой высоты с некоторой начальной скоростью в момент времени t = 0. Мяч многократно отскакивает от земли с коэффициентом восстановления меньше 1, как показано на рисунке. Пренебрегая сопротивлением воздуха и принимая направление вверх за положительное, какая фигура качественно изображает вертикальную составляющую скорости шаров (Vy) как функцию времени (t)?
KVPY ВОПРОСНИК ЗА ПРЕДЫДУЩИЙ ГОД 2013-ЧАСТЬ-II (ФИЗИКА)
11 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!
Обновлено: 27-06-2022
Текстовое решение
A
B
C
D
Ответ
Правильный ответ-B
Раствор
AS = uy-gt
.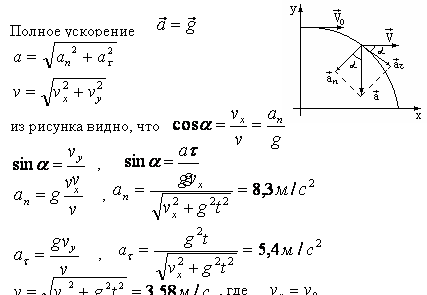
Ответьте
Пошаговое решение, разработанное экспертами, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
Похожие видео
Мяч брошен вертикально вверх. Какой из следующих графиков представляет график скорости мяча во время его полета (сопротивлением воздуха пренебрегается).
11487601
Мяч брошен вертикально вверх с вершины башни высотой h со скоростью v . Мяч ударяется о землю через некоторое время.
14527199
Мяч брошен вертикально вверх. Оно наблюдалось на высоте h дважды через интервал времени Deltat. Начальная скорость мяча
14626550
5Мяч брошен горизонтально с высоты 20 м. Он ударяется о землю со скоростью, в три раза превышающей начальную скорость. Начальная скорость мяча равна
14798225
Шар P брошен вертикально, а другой шар Q брошен горизонтально с той же скоростью и в то же время с той же высоты. Если пренебречь сопротивлением воздуха, то
15716480
Мяч, брошенный с земли вертикально вверх, находится на одной и той же высоте в моменты времени t_(1) и t_(2) . Скорость выброса мяча [без учета сопротивления воздуха]
Скорость выброса мяча [без учета сопротивления воздуха]
304589247
Мяч брошен вертикально вверх. Какой из следующих графиков представляет собой график скорости мяча во время его полета (сопротивлением воздуха пренебрегается)
565540493
Мяч брошен вертикально вверх. мяч во время полета (сопротивлением воздуха пренебрегаем)
612651285
Текст Решение
Мяч брошен вертикально вверх. Какой из следующих графиков представляет график зависимости скорости мяча от времени во время его полета (сопротивлением воздуха пренебрегается)
642673853
Мяч брошен вертикально вверх. Какой из следующих графиков представляет график скорости мяча во время его полета (сопротивлением воздуха пренебрегается)
642673864
Мяч, брошенный вертикально вверх с начальной скоростью u. Какой из следующих графиков правильно отображает скорость мяча как функцию времени?
(Направление вверх считать положительным)
642800679
Текст Решение
Мяч брошен вверх со скоростью A, u. При этом шар B, h сбрасывается с высоты вниз. t — скорость A относительно B в момент времени
При этом шар B, h сбрасывается с высоты вниз. t — скорость A относительно B в момент времени
642954248
Мяч брошен вертикально вверх. Это в два раза больше высоты, которую Deltat получает с течением времени. Начальная скорость мяча равна
642954253
Шар P брошен вертикально, а другой шар Q брошен горизонтально с той же скоростью и в то же время с той же высоты. Если пренебречь сопротивлением воздуха, то
643193151
Мяч брошен вертикально вверх с начальной скоростью u. Какой из следующих графиков правильно отображает скорость мяча как функцию времени? (Возьмите направление вверх как положительное)
644381497
Мяч брошен вертикально вверх с вершины башни высотой h со скоростью v . Мяч ударяется о землю через некоторое время.
644527590
Калькулятор горизонтального движения снаряда
Этот калькулятор горизонтального движения снаряда представляет собой инструмент для решения частного случая движения снаряда, когда объект запускается горизонтально с поднятой плоскости . Введите любые два значения, а остальные будут рассчитаны в мгновение ока! Кроме того, траектория будет отображаться под результатами.
Введите любые два значения, а остальные будут рассчитаны в мгновение ока! Кроме того, траектория будет отображаться под результатами.
Продолжайте прокручивать, чтобы узнать уравнения горизонтального движения снаряда и простой пример расчета — у вас не должно возникнуть проблем с упражнениями после прочтения нашего объяснения!
Уравнения горизонтального движения снаряда
Как мы уже говорили, уравнения горизонтального движения снаряда являются частным случаем общих формул. Нам не нужно указывать угол запуска, так как он параллелен земле (поэтому угол равен 0°). В результате имеем только одну составляющую начальной скорости – Vx=VV_x = VVx=V, тогда как Vy=0V_y = 0Vy=0. 92y=–21gt2, где ggg — ускорение свободного падения, а hhh — высота над уровнем моря.
Скорость
- Горизонтальная скорость равна VVV.
- Вертикальная скорость может быть выражена как –gt–g t–gt.
Ускорение
- Горизонтальное ускорение равно 0.

- Вертикальное ускорение равно -g-g-g (поскольку на снаряд действует только сила тяжести).
Уравнения горизонтального движения снаряда 92 = h31gt2=h. Из этого уравнения можно найти, что время полета равно:
t=2hgt = \sqrt{\frac{2h}{g}}t=g2h
r=Vt=v2hgr = Vt = v\sqrt{\frac{2h}{g}}r=Vt=vg2h
Опять же, эта формула будет сложнее, если угол не был установлен на 0 °. Если вам интересно это увидеть, проверьте калькулятор дальности полета снаряда.
Мы не будем вычислять здесь максимальную высоту (вместо этого см. калькулятор максимальной высоты), так как у нас нет начальной составляющей вертикальной скорости, а это значит, что максимальная высота та, с которой мы начинаем.
Во всех расчетах мы пренебрегали сопротивлением воздуха, действующим на снаряд. Таким образом, сохраняется сумма кинетической и потенциальной энергий. Подробнее о последнем вы можете прочитать в нашем калькуляторе потенциальной энергии.
Пример расчета горизонтального движения снаряда
Предположим, мы хотим рассчитать время полета и расстояние, пройденное мячом, брошенным с Эйфелевой башни только с горизонтальной скоростью, например, 7 м/с.
Введите скорость . В нашем случае это 7 м/с. При необходимости измените единицы измерения.
Введите начальную высоту, с которой начинается движение . Эйфелева башня имеет высоту 324 метра (1063 фута), но верхняя платформа находится на высоте 276 м (906 футов) над землей. Итак, вводим 276 м в нужное поле.
Наш калькулятор горизонтального движения снаряда показывает время полета, расстояние и траекторию! Мы выяснили, что мяч достигает земли за 7,5 секунды, а горизонтальное перемещение составляет ~52,52 м.
 Потрясающий!
Потрясающий!
Помните, что наши инструменты очень гибкие: просто введите любые два значения, и калькулятор горизонтального движения снаряда сделает свою работу. Вы можете, например, проверить, какая скорость необходима, чтобы бросить мяч на расстояние 100 м от основания башни.
Часто задаваемые вопросы
Как рассчитать горизонтальное расстояние при движении снаряда?
Чтобы рассчитать горизонтальное расстояние при движении снаряда, выполните указанные шаги:
Умножить вертикальную высоту
hна2и разделить на ускорение свободного паденияg.Возьмите квадратный корень из результата шага 1 и умножьте на начальную скорость проекции
u, чтобы получить горизонтальное расстояние.Вы также можете умножить на начальную скорость
uна время, необходимое снаряду, чтобы достичь землиt, чтобы получить расстояние по горизонтали.
Как рассчитать время полета снаряда при горизонтальном движении?
Для расчета времени полета снаряда при горизонтальном движении выполните следующие действия:
Узнать высоту по вертикали 902:34 ч откуда брошен снаряд.
Умножить
чна2и разделить результат наg, ускорение свободного падения.Возьмите квадратный корень из результата шага 2 , и вы получите время полета при горизонтальном движении снаряда.
Есть ли горизонтальное ускорение при движении снаряда?
Нет , горизонтального ускорения при движении снаряда нет. Скорость снаряда постоянна в горизонтальном направлении . Следовательно, ускорение также равно нулю в горизонтальном направлении.
Каково вертикальное ускорение снаряда при горизонтальном полете?
9,8 м/с² .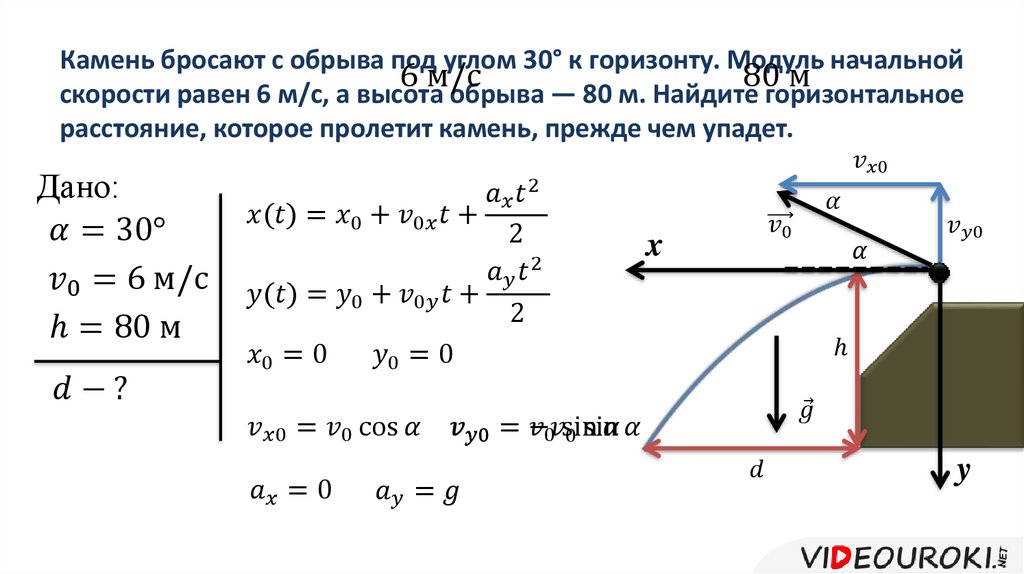


 Потрясающий!
Потрясающий!
Leave A Comment