Решение уравнений на ЕГЭ по Математике. Готовимся правильно!

В этом разделе – все основные способы и приемы решения уравнений на ЕГЭ по математике.

А встретиться вам могут всевозможные уравнения – квадратные, а также уравнения высших степеней. Дробно-рациональные уравнения. Уравнения, содержащие знак корня (иррациональные) или знак модуля. Показательные и логарифмические. И для каждого из этих типов – свои методы и секреты решения.

Десятиклассникам будут особенно полезны темы: «Алгебраические уравнения», «Уравнения с модулем», «Иррациональные уравнения», «Системы алгебраических уравнений».

Квадратные уравнения

Алгебраические уравнения

Системы алгебраических уравнений

Показательные уравнения

Логарифмические уравнения

Уравнения с модулем

Иррациональные уравнения

Простейшие тригонометрические уравнения, 1

Простейшие тригонометрические уравнения, 2

Тригонометрические уравнения. Методы решения

 

Запомним главное – что нужно знать при решении уравнений

— Корень уравнения – это такое число, при подстановке которого в уравнение получается верное равенство.

— Решить уравнение – значит найти все его корни или доказать, что их нет.

— Равносильными называются уравнения, множества решений которых совпадают.

— Если в уравнении есть дроби, корни четной степени, логарифмы – значит, не забываем про область допустимых значений (ОДЗ) уравнения. 

— Если в уравнении можно сделать замену переменной – сделайте замену переменной.

— Решение уравнения лучше всего оформлять в виде цепочки равносильных переходов.

— Решив уравнение, сделайте проверку. Действительно ли найденные вами ответы являются корнями уравнения?

— Если слева и справа в уравнении находятся функции разных типов – например, квадратичная и показательная, или логарифм и синус, — значит, оно решается или графически, или с использованием свойств этих функций, или методом оценки

Больше уравнений:

Задание 5 Профильного ЕГЭ по математике

Задание 13 Профильного ЕГЭ по математике

Калькулятор онлайн — Решение показательных уравнений. Описание

Знак умножения нужно вводить только между числами, во всех остальных случаях его можно не вводить.

При решении этой задачи используется большой и дорогой модуль одного «забугорного» сервиса. Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли. Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях. Единственное неудобство — на английском языке, но это не большая цена за качество.

Если вам что-то осталось не понятно обязательно напишите об этом в Обранной связи и мы дополним эту таблицу.

Функция Описание Пример ввода Результат ввода
pi Число \(\pi\) pi $$ \pi $$
e Число \(e\) e $$ e $$
e^x Степень числа \(e\) e^(2x) $$ e^{2x} $$
exp(x) Степень числа \(e\) exp(1/3) $$ \sqrt[3]{e} $$
|x|
abs(x)		 Модуль (абсолютное значение) числа \(x\) |x-1|
abs(cos(x))		 \( |x-1| \)
\( |\cos(x)| \)
sin(x) Синус sin(x-1) $$ sin(x-1) $$
cos(x) Косинус 1/(cos(x))^2 $$ \frac{1}{cos^2(x)} $$
tg(x) Тангенс x*tg(x) $$ x \cdot tg(x) $$
ctg(x) Котангенс 3ctg(1/x) $$ 3 ctg \left( \frac{1}{x} \right) $$
arcsin(x) Арксинус arcsin(x) $$ arcsin(x) $$
arccos(x) Арккосинус arccos(x) $$ arccos(x) $$
arctg(x) Арктангенс arctg(x) $$ arctg(x) $$
arcctg(x) Арккотангенс arcctg(x) $$ arcctg(x) $$
sqrt(x) Квадратный корень sqrt(1/x) $$ \sqrt{\frac{1}{x}} $$
root(n,x) Корень степени n
root(2,x) эквивалентно sqrt(x) 		root(4,exp(x)) $$ \sqrt[4]{ e^{x} } $$
x^(1/n) Корень степени n
x^(1/2) эквивалентно sqrt(x) 		(cos(x))^(1/3) $$ \sqrt[\Large 3 \normalsize]{cos(x)} $$
ln(x)
log(x)
log(e,x)		 Натуральный логарифм
(основание — число e)		 1/ln(3-x) $$ \frac{1}{ln(3-x)} $$
log(10,x) Десятичный логарифм числа x log(10,x^2+x) $$ log_{10}(x^2+x) $$
log(a,x) Логарифм x по основанию a log(3,cos(x)) $$ log_3(cos(x)) $$
sh(x) Гиперболический синус sh(x-1) $$ sh(x-1) $$
ch(x) Гиперболический косинус ch(x) $$ ch(x) $$
th(x) Гиперболический тангенс th(x) $$ th(x) $$
cth(x) Гиперболический котангенс cth(x) $$ cth(x) $$
ВыводПеревод, пояснение
Solve for x over the real numbersРешить относительно х в действительных числах (бывают ещё комплексные)
Multiply both sides by …Умножаем обе части на …
Equate exponents of … on both sidesПриравниваем степени … в обоих частях (с обоих сторон)
Simplify and substitute …Упрощаем и делаем подстановку …
Bring … together using the commom denominator …Приводим … к общему знаменателю …
The left hand side factors into a product with two termsЛевая часть разбивается на множители как два многочлена
Split into two equationsРазделяем на два уравнения
Take the square root of both sidesИзвлекаем квадратный корень из обоих частей
Subtract … from both sidesВычитаем … из обеих частей уравнения
Add … to both sidesПрибавляем … к обоим частям уравнения
Multiply both sides by …Умножаем обе части уравнения на …
Divide both sides by …Делим обе части уравнения на …
Substitute back for …Обратная подстановка для …
… has no solution since for all …… не имеет решения для всех …
Simplify the expressionУпрощаем выражение
AnswerОтвет
\(log(x)\)Натуральный логарифм, основание — число e. У нас пишут \(ln(x)\)
\(arccos(x)\) или \(cos^{-1}(x)\)Арккосинус. У нас пишут \( arccos(x) \)
\(arcsin(x)\) или \(sin^{-1}(x)\)Арксинус. У нас пишут \( arcsin(x) \)
\(tan(x)\)Тангенс. У нас пишут \(tg(x) = \frac{sin(x)}{cos(x)}\)
\(arctan(x)\) или \(tan^{-1}(x)\)Арктангенс. У нас пишут \(arctg(x)\)
\(cot(x)\)Котангенс. У нас пишут \(ctg(x) = \frac{cos(x)}{sin(x)}\)
\(arccot(x)\) или \(cot^{-1}(x)\)Арккотангенс. У нас пишут \(arcctg(x)\)
\(sec(x)\)Секанс. У нас пишут также \(sec(x) = \frac{1}{cos(x)}\)
\(csc(x)\)Косеканс. У нас пишут \(cosec(x) = \frac{1}{sin(x)}\)
\(cosh(x)\)Гиперболический косинус. У нас пишут \(ch(x) = \frac{e^x+e^{-x}}{2} \)
\(sinh(x)\)Гиперболический синус. У нас пишут \(sh(x) = \frac{e^x-e^{-x}}{2} \)
\(tanh(x)\)Гиперболический тангенс. У нас пишут \(th(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \)
\(coth(x)\)Гиперболический котангенс. У нас пишут \(cth(x) = \frac{1}{th(x)} \)

Решение задачи Коши онлайн · Как пользоваться Контрольная Работа РУ

UPD: Теперь вы можете вводить условия задачи Коши прямо в форму:

Решение задачи Коши онлайн - вводим условия в форму

Рассмотрим пример решения задачи Коши с помощью онлайн калькулятора «Контрольная-работа.Ру».

Внимание! Следуя этому примеру и подробно и внимательно читая вы сможете решить и свою задачу, просто следуя тем же шагам!

Возьмём задачу из контрольной «Решить задачу Коши для дифференциального уравнения второго порядка«:

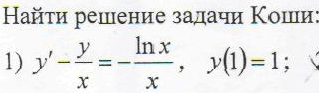
Задача Коши - пример решения онлайн

Для того, чтобы решить данную задачу откройте сервис решения дифференциальных уравнений онлайн

и введите в форму левую часть уравнения y’ — y/x

а в правую часть уравнения: -lnx/x

как на картинке:

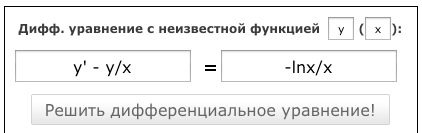
Задачи Коши в форме

Нажимаем кнопку «Решить дифференциальное уравнение!«

Видим ответ для этого дифф. ур-ния:


y(x) == C1*x + log(x) + 1

Но как вы знаете, это ещё не решение задачи Коши, это всего лишь решение дифференциального уравнения.

Теперь по начальным условиям y(1) = 1 надо найти C1.

Для этого воспользуемся сервисом по решению обычных уравнений онлайн

Вобъём в форму обычных уравнений в правую часть уравнения c*x + log(x) + 1, а в левую y

А также укажем, что уравнение с неизвестной c=C1

На рис. всё это видно:

Первоначальное условие в задаче Коши

Нажимаем кнопку «Решить уравнение!«

Получаем ответ для C1


y - log(x) - 1
──────────────
      x

Но и это ещё не всё.

Надо указать, что y = 1 и x = 1 (т.к. y(1)=1). Подставляем по той же ссылке как на рис. ниже:

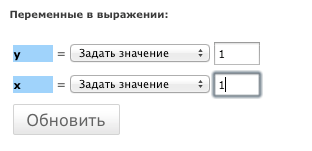
Начальное условие в задаче Коши

Нажимаем кнопку «Обновить«

И получаем окончательный ответ для C1:

C1 = c = 0

Подставляем это C1 в решение дифф. уравнения и мы получим решение нашей задачи Коши:


y(x) = C1*x + log(x) + 1 = 0*x + log(x) + 1 = log(x) + 1

 

Решение иррациональных уравнений онлайн · Как пользоваться Контрольная Работа РУ

Иррациональные уравнения бывают от простых до сложных — и всех их можно решить онлайн и с подробным решением с помощью калькулятора онлайн.

Итак:

Простые иррациональные уравнения

Будем считать, что простые уравнения будут содержат только одну часть иррациональности. Тогда рассмотрим пример:

2*x + sqrt(-x + 3)  = 3

Введём это уравнение в форму калькулятора

Решение иррациональных уравнений онлайн

Тогда, вы получите подробное решение:

Дано уравнение


  _______          
\/ 3 - x  + 2*x = 3

  _______          
\/ 3 - x  = 3 - 2*x

Возведём обе части ур-ния в(о) 2-ую степень

Перенесём правую часть уравнения левую часть уравнения со знаком минус

Это уравнение вида

Квадратное уравнение можно решить

с помощью дискриминанта.

Корни квадратного уравнения:


       ___    
     \/ D  - b
x1 = ---------
        2*a   

            ___
     -b - \/ D 
x2 = ----------
        2*a

где D = b^2 — 4*a*c — это дискриминант.

Т.к.

, то


(11)^2 - 4 * (-4) * (-6) = 25

Т.к. D > 0, то уравнение имеет два корня.


x1 = (-b + sqrt(D)) / (2*a)

x2 = (-b - sqrt(D)) / (2*a)

или

 

Т.к.


  _______          
\/ 3 - x  = 3 - 2*x

и

то

или

Тогда, окончательный ответ:

Средние иррациональные уравнения

Средними же будем считать уравнения, которые содержат две иррациональные части в уравнении.

Например,

sqrt(4*x + 1)  + sqrt(3*x — 2)  = 2

надо ввести в форму в калькуляторе

Иррациональное уравнение онлайн

Результат будет таким:

Дано уравнение


  _________     __________    
\/ 1 + 4*x  + \/ -2 + 3*x  = 2

Возведём обе части ур-ния в(о) 2-ую степень


                            2    
/  _________     __________\     
\\/ 1 + 4*x  + \/ -2 + 3*x /  = 4

или


 2                 _____________________    2              
1 *(3*x - 2) + 2*\/ (3*x - 2)*(4*x + 1)  + 1 *(4*x + 1) = 4

или


          __________________          
         /                2           
-1 + 2*\/  -2 - 5*x + 12*x   + 7*x = 4

преобразуем:


     __________________          
    /                2           
2*\/  -2 - 5*x + 12*x   = 5 - 7*x

Возведём обе части ур-ния в(о) 2-ую степень


                2            2
-8 - 20*x + 48*x  = (5 - 7*x) 

                2                   2
-8 - 20*x + 48*x  = 25 - 70*x + 49*x

Перенесём правую часть уравнения левую часть уравнения со знаком минус

Это уравнение вида

Квадратное уравнение можно решить

с помощью дискриминанта.

Корни квадратного уравнения:


       ___    
     \/ D  - b
x1 = ---------
        2*a   

            ___
     -b - \/ D 
x2 = ----------
        2*a

где D = b^2 — 4*a*c — это дискриминант.

Т.к.

, то


(50)^2 - 4 * (-1) * (-33) = 2368

Т.к. D > 0, то уравнение имеет два корня.


x1 = (-b + sqrt(D)) / (2*a)

x2 = (-b - sqrt(D)) / (2*a)

или

 

Т.к.


   __________________          
  /                2    5   7*x
\/  -2 - 5*x + 12*x   = - - ---
                        2    2

и


   __________________     
  /                2      
\/  -2 - 5*x + 12*x   >= 0

то

или

проверяем:


       __________     ___________    
-2 + \/ 1 + 4*x1  + \/ -2 + 3*x1  = 0

=


   _______________________      ________________________        
  /       /         ____\      /        /         ____\         
\/  1 + 4*\25 - 4*\/ 37 /  + \/  -2 + 3*\25 - 4*\/ 37 /  - 2 = 0

=

— тождество

Тогда, окончательный ответ:

Сложные иррациональные уравнения

Самыми сложными же будут уравнения с тремя частями иррациональностями, значит будет такой пример:

sqrt(x + 5)  — sqrt(x — 1)  = sqrt(2*x + 4)

В форме калькулятора это будет выглядеть так:

Подробное решение иррациональных уравнений

Тогда получите подробное объяснение

Дано уравнение


  _______     ________     _________
\/ 5 + x  - \/ -1 + x  = \/ 4 + 2*x

Возведём обе части ур-ния в(о) 2-ую степень


                        2          
/  _______     ________\           
\\/ 5 + x  - \/ -1 + x /  = 4 + 2*x

или


 2               _________________       2                  
1 *(x + 5) - 2*\/ (x + 5)*(x - 1)  + (-1) *(x - 1) = 4 + 2*x

или


         _______________                
        /       2                       
4 - 2*\/  -5 + x  + 4*x  + 2*x = 4 + 2*x

преобразуем:


      _______________    
     /       2           
-2*\/  -5 + x  + 4*x  = 0

преобразуем

Это уравнение вида

Квадратное уравнение можно решить

с помощью дискриминанта.

Корни квадратного уравнения:


       ___    
     \/ D  - b
x1 = ---------
        2*a   

            ___
     -b - \/ D 
x2 = ----------
        2*a

где D = b^2 — 4*a*c — это дискриминант.

Т.к.

, то


(4)^2 - 4 * (1) * (-5) = 36

Т.к. D > 0, то уравнение имеет два корня.


x1 = (-b + sqrt(D)) / (2*a)

x2 = (-b - sqrt(D)) / (2*a)

или

проверяем:


  ________     _________     __________    
\/ 5 + x1  - \/ -1 + x1  - \/ 4 + 2*x1  = 0

=


  _______     ________     _______    
\/ 5 + 1  - \/ -1 + 1  - \/ 4 + 2  = 0

=

— тождество


  ________     _________     __________    
\/ 5 + x2  - \/ -1 + x2  - \/ 4 + 2*x2  = 0

=


  _______     ________     ____________    
\/ 5 - 5  - \/ -1 - 5  - \/ 4 + 2*(-5)  = 0

=

— Нет

Тогда, окончательный ответ:

Решение кубических уравнений онлайн · Как пользоваться Контрольная Работа РУ

Рассмотрим два примера кубических уравнений, которые калькулятор уравнений умеет без проблем решать с подробным решением:

Пример простого кубического уравнения

Первый пример будет простым:

49*x^3 — x = 0

Решение кубических уравнений онлайн

После того, как вы нажмёте «Решить уравнение!», то вы получите ответ с подробным объяснением:

Дано уравнение:

преобразуем

Вынесем общий множитель x за скобки

получим:

тогда:

и также

получаем ур-ние

Это уравнение вида

Квадратное уравнение можно решить

с помощью дискриминанта.

Корни квадратного уравнения:


       ___    
     \/ D  - b
x2 = ---------
        2*a   

            ___
     -b - \/ D 
x3 = ----------
        2*a

где D = b^2 — 4*a*c — это дискриминант.

Т.к.

, то


(0)^2 - 4 * (49) * (-1) = 196

Т.к. D > 0, то уравнение имеет два корня.


x2 = (-b + sqrt(D)) / (2*a)

x3 = (-b - sqrt(D)) / (2*a)

или

Получаем окончательный ответ для -x + 49*x^3 = 0:


x3 = -1/7

 

Второй простой пример кубического уравнения будет таким:

8 = (1/2 + 3*x)^3

Кубическое уравнение онлайн

Получим подробное решение:

Дано уравнение:

преобразуем:

Вынесем общий множитель за скобки


              /               2\    
-9*(-1 + 2*x)*\7 + 12*x + 12*x /    
-------------------------------- = 0
               8

Т.к. правая часть ур-ния равна нулю, то решение у ур-ния будет, если хотя бы один из множителей в левой части ур-ния равен нулю.

Получим ур-ния

решаем получившиеся ур-ния:

1.

Переносим свободные слагаемые (без x)

из левой части в правую, получим:

Разделим обе части ур-ния на -9/4

Получим ответ: x1 = 1/2

2.

Это уравнение вида

Квадратное уравнение можно решить

с помощью дискриминанта.

Корни квадратного уравнения:


       ___    
     \/ D  - b
x2 = ---------
        2*a   

            ___
     -b - \/ D 
x3 = ----------
        2*a

где D = b^2 — 4*a*c — это дискриминант.

Т.к.

, то


(12)^2 - 4 * (12) * (7) = -192

Т.к. D < 0, то уравнение

не имеет вещественных корней,

но комплексные корни имеются.


x2 = (-b + sqrt(D)) / (2*a)

x3 = (-b - sqrt(D)) / (2*a)

или


               ___
       1   I*\/ 3 
x2 = - - + -------
       2      3   

               ___
       1   I*\/ 3 
x3 = - - - -------
       2      3

Тогда, окончательный ответ:


               ___
       1   I*\/ 3 
x2 = - - + -------
       2      3   

               ___
       1   I*\/ 3 
x3 = - - - -------
       2      3

Пример сложного кубического уравнения

Третьим примером будет более сложный — возвратное кубическое уравнение онлайн.

5*x^3 -8*x^2 — 8*x + 5 = 0

Чтобы решить такое возвратное кубическое уравнение, то введите данное уравнение в калькулятор:

Возвратное кубическое уравнение

Дано уравнение:


             2      3    
5 - 8*x - 8*x  + 5*x  = 0

преобразуем


   3          2                  
5*x  + 5 - 8*x  + 8 - 8*x - 8 = 0

или


   3         3      2          2              
5*x  - 5*(-1)  - 8*x  - -8*(-1)  - 8*x - 8 = 0

  / 3       3\     / 2       2\                
5*\x  - (-1) / - 8*\x  - (-1) / - 8*(x + 1) = 0

          / 2           2\                                     
5*(x + 1)*\x  - x + (-1) / + -8*(x + 1)*(x - 1) - 8*(x + 1) = 0

Вынесем общий множитель 1 + x за скобки

получим:


        /  / 2           2\                \    
(x + 1)*\5*\x  - x + (-1) / - 8*(x - 1) - 8/ = 0

или


        /              2\    
(1 + x)*\5 - 13*x + 5*x / = 0

тогда:

и также

получаем ур-ние

Это уравнение вида

Квадратное уравнение можно решить

с помощью дискриминанта.

Корни квадратного уравнения:


       ___    
     \/ D  - b
x2 = ---------
        2*a   

            ___
     -b - \/ D 
x3 = ----------
        2*a

где D = b^2 — 4*a*c — это дискриминант.

Т.к.

, то


(-13)^2 - 4 * (5) * (5) = 69

Т.к. D > 0, то уравнение имеет два корня.


x2 = (-b + sqrt(D)) / (2*a)

x3 = (-b - sqrt(D)) / (2*a)

или


            ____
     13   \/ 69 
x2 = -- + ------
     10     10  

            ____
     13   \/ 69 
x3 = -- - ------
     10     10

Получаем окончательный ответ для 5 — 8*x — 8*x^2 + 5*x^3 = 0:


            ____
     13   \/ 69 
x2 = -- + ------
     10     10  

            ____
     13   \/ 69 
x3 = -- - ------
     10     10

РЕШЕНИЕ УРАВНЕНИЙ

РЕШЕНИЕ УРАВНЕНИЙ

В этом разделе показан процесс решения уравнений различных форм. Он также показывает вам, как проверить свой ответ тремя разными способами: алгебраически, графически и с использованием концепции эквивалентности. В следующей таблице приведены частичные списки типичных уравнений.

ЛИНЕЙНЫЕ УРАВНЕНИЯ — Решите относительно x в следующих уравнениях.

  1. x — 4 = 10 Решение
  2. 2 x — 4 = 10 Решение
  3. 5x — 6 = 3 x — 8 Решение
  4. Решение
  5. Решение
  6. 2 (3 x — 7) + 4 (3 x + 2) = 6 (5 x + 9) + 3 Решение
  7. Решение

УРАВНЕНИЯ , СОДЕРЖАЩИЕ РАДИКАЛЬНЫЕ (S) — Решите для x следующим образом уравнения.

  1. Решение
  2. Решение
  3. Решение
  4. Решение
  5. Решение
  6. Решение
  7. Решение

УРАВНЕНИЯ , СОДЕРЖАЩИЕ АБСОЛЮТНЫЕ ЗНАЧЕНИЯ — Решите для x в следующие уравнения.

  1. Решение
  2. Решение
  3. Решение
  4. Решение
  5. Решение

КВАДРАТИЧЕСКИЕ УРАВНЕНИЯ — Решите для x следующим образом уравнения.

  1. х Решение
  2. Решение
  3. Решение
  4. Решение
  5. Решение

УРАВНЕНИЯ , ВКЛЮЧАЮЩИЕ ДОБИ — Решите для x следующим образом уравнения.

  1. Решение
  2. Решение
  3. Решение
  4. Решение
  5. Решение

ЭКСПОНЕНЦИАЛЬНЫЕ УРАВНЕНИЯ — Решите для x следующие уравнения.

  1. Решение
  2. Решение
  3. Решение
  4. Решение
  5. Решение
  6. Решение
  7. Решение

ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ — Решите для x следующим образом уравнения.

  1. Решение
  2. Решение
  3. Решение
  4. Решение
  5. Решение
  6. Решение
  7. Решение

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ — Решите для x следующим образом уравнения.

  1. Решение
  2. Решение
  3. Решение
  4. Решение
  5. Решение
  6. Решение
  7. Решение
  8. Решение
  9. Решение
  10. Решение
  11. Решение
  12. Решение
[Алгебра] [Тригонометрия] [Геометрия] [Дифференциальные уравнения] [Исчисление] [Комплексные переменные] [Матричная алгебра] С.Домашняя страница O.S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

Автор: Нэнси Маркус
Авторское право 1999-2020 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час ,

Решение уравнений со сложными решениями

  2. Образование
  3. Математика
  4. Алгебра
  5. Решение уравнений со сложными решениями

Мэри Джейн Стерлинг

Вы часто сталкиваетесь с уравнениями, у которых нет реальных решений, или с уравнениями, которые могут дать гораздо больше реальных решений, чем они есть на самом деле. Например, уравнение x 2 + 1 = 0 не имеет реальных решений.Если вы запишете это как x 2 = –1 и попытаетесь извлечь квадратный корень из каждой стороны, вы столкнетесь с проблемами.

Только когда у вас есть мнимые числа, вы не сможете написать, что решение этого уравнения: x = +/– i . Уравнение имеет два комплексных решения.

Пример уравнения без достаточного количества реальных решений: x 4 — 81 = 0. Это уравнение множится в ( x 2

— 9) ( x 2 + 9) = 0.Два реальных решения этого уравнения — 3 и –3. Два комплексных решения: 3 i и –3 i .

Чтобы найти комплексные решения уравнения, вы используете факторизацию, свойство квадратного корня для решения квадратичных уравнений и формулу корней квадратного уравнения.

Примеры вопросов

  1. Найдите все корни, действительные и комплексные, уравнения x 3 — 2 x 2 + 25 x — 50 = 0.

    x = 2, 5 i , –5 i . Сначала разложите уравнение на множители, чтобы получить x 2 ( x — 2) + 25 ( x — 2) = ( x — 2) ( x 2 + 25) = 0 Используя нулевое свойство умножения, вы определяете, что

    x — 2 = 0 и x = 2. Вы также получаете x 2 + 25 = 0 и x 2 = –25. Извлеките квадратный корень из каждой стороны и получим

    Упростим радикал, используя эквивалент для i , и комплексные решения будут

    Действительный корень равен 2, а мнимый корень равен 5 i и –5 i .

  2. Найдите все корни, действительные и мнимые, уравнения 5 x 2 — 8 x + 5 = 0.

    x = 0,4 + 0,6 i , 0,4 — 0,6 i . Квадратичный коэффициент не учитывается, поэтому вы используете квадратную формулу:

    Сложны только два решения: 0,4 + 0,6 i и 0,4 — 0,6 i .

Практические вопросы

  1. Найдите все корни, действительные и мнимые, из x 2 + 9 = 0.

  2. Найдите все корни, действительные и мнимые, x 2 + 4 x + 7 = 0.

  3. Найдите все корни, действительные и мнимые, из 5 x 2 + 6 x + 3 = 0.

  4. Найдите все корни, действительные и мнимые, для x 4 + 12 x 2 — 64 = 0.

Ниже приведены ответы на вопросы практики:

  1. Ответ:

    x = 3 i , –3 i .

    Добавьте –9 к каждой стороне, чтобы получить x 2 = –9. Извлеките квадратный корень из каждой стороны. Затем упростите выражение, используя i для отрицательного значения под корнем:

  2. Ответ:

    Используйте формулу корней квадратного уравнения, чтобы найти x . Упростите выражение, используя i для отрицательного значения под корнем:

  3. Ответ:

    Используйте формулу корней квадратного уравнения, чтобы найти x .Упростите выражение, используя i для отрицательного значения под корнем:

  4. Ответ: x = 2, –2, 4 i , –4 i .

    Фактор левой части: ( x 2 + 16) ( x 2 — 4) = ( x 2 + 16) ( x — 2) ( x + 2 ) = 0. Получите два действительных корня, установив x — 2 и x + 2 равными 0. Когда x 2 + 16 = 0, вы обнаружите, что x 2 = –16 ,Извлечение квадратного корня из каждой стороны и использование i вместо –1 под корнем дает два мнимых корня.

,

Тем по алгебре: Решение уравнений

Урок 8: Решение уравнений

/ ru / algebra-themes / упрощающие-выражения / content /

Решение уравнений

В предыдущем разделе мы говорили о упрощающих выражениях . В этом разделе мы поговорим о решениях уравнений. Уравнения

— это два выражения, равных друг другу с использованием знака равенства (=). Когда мы упрощаем выражения, наша конечная цель состоит в том, чтобы не осталось никаких операций.

Когда мы решаем уравнения, наша конечная цель состоит в том, чтобы выяснить, чему равна переменная (или буква), поместив переменную отдельно по одну сторону от знака равенства и само число с другой. Мы собираемся достичь этой цели, выполнив два важных шага:

  1. Упростите каждое выражение по обе стороны от знака равенства.
  2. Используйте обратные операции для отмены.

Звучит сложно? Мы разберем его, чтобы было легче. Давайте посмотрим на пример:

5x — 4x — 6 = 18

Мы можем начать решать так же, как начинали бы упрощать выражение, проверяя порядок операций.Мы хотим максимально упростить каждую сторону знака равенства сначала . Глядя на наше уравнение, нет скобок или показателей степени и нечего умножать или делить, поэтому мы просто начнем складывать и вычитать. Первая часть проста: 5 x — 4 x — 1 x , или просто x .

Отмена с обратными операциями

Теперь у нас осталось это уравнение:

х — 6 = 18

Мы не можем вычесть 6 из x , потому что они не , как термины (наш урок чтения алгебраических выражений объясняет это более подробно).Но x

— 6 = 18 все еще недостаточно упрощен. В конце концов, мы ищем значение x , а не значение x — 6.

Чтобы решить это уравнение, нам нужно получить только x по одну сторону от знака равенства. Чтобы переместить -6 на другую сторону от знака равенства, мы можем использовать , обратное — или противоположное — -6. Это будет 6. Другими словами, мы можем прибавить шесть к обеим сторонам уравнения.

В левой части уравнения -6 плюс 6 равно 0, а x -0 равно x .Справа 18 плюс 6 равно 24, поэтому x = 24. Теперь наше уравнение упрощено. Мы упростили его, используя , инверсный , от которого мы хотели избавиться.

Это также называется , отменяющим , потому что оно позволяет вам отменить или избавиться от части уравнения. Это не значит, что вы можете просто зачеркнуть любую часть уравнения, которую не хотите решать (хотя это значительно упростит алгебру!). Вы должны соблюдать несколько правил.

Во-первых, вы заметили, что мы добавили 6 к обеим сторонам нашего уравнения? Это потому, что обе стороны уравнения всегда должны быть равными — в конце концов, это то, что означает знак равенства. Каждый раз, когда вы делаете что-то дополнительно к одной стороне уравнения, вы должны делать то же самое с другой. Поскольку мы добавили 6 к -6 на левой стороне , нам также пришлось добавить ее к 18 на правой стороне .

Во-вторых, помните, как мы прибавили шесть, где в исходном выражении говорилось, что вычесть ? Мы сделали это, потому что 6 — это противоположность -6.Чтобы отменить часть выражения, вам нужно использовать ее противоположность или инверсию. Противоположность вычитания — , сложение , и, как вы могли догадаться, противоположность сложения — , вычитание .

Посмотрите видео ниже, чтобы увидеть, как эта проблема решена.

А как насчет умножения и деления? Это тоже противоположности, и их тоже можно отменить. Например, как получить a только в этом уравнении слева от знака равенства?

5a = 30

Поскольку a — это , умноженное на на 5, вы можете разделить с обеих сторон задачи на 5. 5 a разделить на 5 равно a и 30 разделить на 5 равно 6, поэтому упрощенная версия этого уравнения будет выглядеть как

.

Решение квадратных уравнений

Решение квадратных уравнений

Квадратное уравнение — это уравнение, которое можно записать как

топор 2 + bx + c = 0

, когда a 0.

Существует три основных метода решения квадратных уравнений: факторинг, использование формулы квадратиков и завершение квадрата.

Факторинг

Чтобы решить квадратное уравнение на множители,

  1. Поместите все члены с одной стороны от знака равенства, оставив ноль с другой стороны.

  2. Коэффициент

    .

  3. Установите каждый коэффициент равным нулю.

  4. Решите каждое из этих уравнений.

  5. Проверьте, подставив свой ответ в исходное уравнение.

Пример 1

Решить x 2 — 6 x = 16.

Следуя инструкциям,

x 2 — 6 x = 16 становится x 2 — 6 x — 16 = 0

Коэффициент

.

( x -8) ( x + 2) = 0

Установка каждого коэффициента на ноль, equation

Затем для проверки, equation

Оба значения, 8 и –2, являются решениями исходного уравнения.

Пример 2

Решить y 2 = — 6 y — 5.

Устанавливая все члены равными нулю,

y 2 + 6 y + 5 = 0

Коэффициент

.

( y + 5) ( y + 1) = 0

Установка каждого коэффициента на 0, equation

Для проверки, y 2 = –6 y — 5

equation

Квадратичный с отсутствующим членом называется неполным квадратичным (до тех пор, пока не пропущен член ax 2 ).

Пример 3

Решить x 2 — 16 = 0.

Коэффициент

.

equation

Для проверки, x 2 — 16 = 0

equation

Пример 4

Решить x 2 + 6 x = 0.

Коэффициент

.

equation

Для проверки, x 2 + 6 x = 0

equation

Пример 5

Решить 2 x 2 + 2 x — 1 = x 2 + 6 x — 5.

Во-первых, упростите, поместив все термины в одну сторону и объединяя похожие термины.

equation

А теперь фактор.

equation

Для проверки, 2 x 2 + 2 x — 1 = x 2 + 6 x — 5

equation

Квадратичная формула

Многие квадратные уравнения не могут быть решены факторизацией. Обычно это верно, когда корни или ответы не являются рациональными числами.Второй метод решения квадратных уравнений включает использование следующей формулы: equation

a, b, и c берутся из квадратного уравнения, записанного в его общем виде

топор 2 + bx + c = 0

, где a — это число перед x 2 , b — это число перед x , а c — это число без переменной рядом с ним (a ,k.a., «постоянная»).

При использовании формулы корней квадратного уравнения вы должны знать о трех возможностях. Эти три возможности отличаются частью формулы, называемой дискриминантом. Дискриминант — это значение под знаком корня, b 2 — 4 ac . Квадратное уравнение с действительными числами в качестве коэффициентов может иметь следующее:

  1. Два разных действительных корня, если дискриминант b 2 -4 ac является положительным числом.

  2. Один действительный корень, если дискриминант b 2 -4 ac равен 0.

  3. Нет действительного корня, если дискриминант b 2 — 4 ac является отрицательным числом.

Пример 6

Решите для x : x 2 — 5 x = –6.

Установка всех членов равными 0,

x 2 -5 x + 6 = 0

Затем замените 1 (который, как предполагается, стоит перед x 2 ), –5 и 6 вместо a , b и c, соответственно в формуле квадратов и упростите.

equation

Поскольку дискриминант b 2 — 4 ac положительный, вы получаете два разных действительных корня.

Пример производит рациональные корни. В примере , квадратная формула используется для решения уравнения, корни которого нерациональны.

Пример 7

Найти y : y 2 = –2y + 2.

Установка всех членов равными 0,

y 2 + 2 y — 2 = 0

Затем замените 1, 2 и –2 на a , b и c, соответственно в формуле корней квадратного уравнения и упростите.

equation

Обратите внимание, что два корня иррациональны.

Пример 8

Решить относительно x : x 2 + 2 x + 1 = 0.

Подставляя в формулу корней квадратного уравнения,

equation

Поскольку дискриминант b 2 -4 ac равен 0, уравнение имеет один корень.

Квадратичная формула также может использоваться для решения квадратных уравнений, корни которых являются мнимыми числами, то есть они не имеют решения в действительной системе счисления.

Пример 9

Найдите x : x ( x + 2) + 2 = 0 или x 2 + 2 x + 2 = 0.

Подставляя в формулу корней квадратного уравнения,

equation

Поскольку дискриминант b 2 — 4 ac отрицателен, это уравнение не имеет решения в действительной системе счисления.

Но если бы вы выразили решение с помощью мнимых чисел, решений было бы equation.

Завершение квадрата

Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.

  1. Запишите уравнение в виде ax 2 + bx = — c .

  2. Убедитесь, что a = 1 (если a ≠ 1, умножьте уравнение на equation, прежде чем продолжить).

  3. Используя значение b из этого нового уравнения, прибавьте equation к обеим сторонам уравнения, чтобы получился полный квадрат в левой части уравнения.

  4. Найдите квадратный корень из обеих частей уравнения.

  5. Решите полученное уравнение.

Пример 10

Решить относительно x : x 2 — 6 x + 5 = 0.

Оформить в виде

equation

Поскольку a = 1, добавьте equation, или 9, к обеим сторонам, чтобы завершить квадрат.

equation

Извлеките квадратный корень из обеих частей.

х — 3 = ± 2

Решить.

equation

Пример 11

Решить относительно y : y 2 + 2 y — 4 = 0.

Оформить в виде

equation

Поскольку a = 1, добавьте equation или 1 к обеим сторонам, чтобы завершить квадрат.

equation

Извлеките квадратный корень из обеих частей.

equation

Решить.

equation

Пример 12

Решите относительно x : 2 x 2 + 3 x + 2 = 0.

Оформить в виде

equation

Поскольку — это ≠ 1, умножаем уравнение на equation.

equation

Добавьте equation или equation с обеих сторон.

equation

Извлеките квадратный корень из обеих частей.

equation

В действительной системе счисления нет решения. Возможно, вам будет интересно узнать, что завершение квадратного процесса для решения квадратных уравнений использовалось для уравнения ax 2 + bx + c = 0 для вывода формулы квадратичного уравнения.

,